轨道发射器利用强脉冲电流在强磁场中产生巨大洛伦兹力把模拟小车加速到每秒几百米的速度,使其具有巨大的瞬时动能以模拟撞击实验。但是,发射器发射过程中由于瞬时大电流的作用,导致轨道承受很大的冲击力和瞬时的焦耳热。通以液态水进行循环冷却,或利用液态水受热汽化的相变潜热进行冷却。轨道发射器模拟小车发射中轨道产生的焦耳热和摩擦热被喷水雾冷却带走。文献[1]比较系统介绍了国内外喷雾学研究的进展,空气雾化喷嘴即采用高速的空气射流将工质破碎成微细液滴[2],对于不同的喷雾冷却系统,喷雾角度、喷雾高度、系统压力、冷却表面结构等因素都会对喷雾冷却效果带来影响[3 – 6]。喷雾冷却是一种前景非常广阔的新型冷却技术,具有散热能力强、换热温差小等一系列优点[7]。由于喷雾冷却传热机理的复杂性,目前关于其传热特性的研究主要是采用实验方法[8]。尽管对喷雾冷却的各方面都进行了大量的研究[9],但轨道发射器应用喷雾冷却的散热机理及试验涉及不多。
本文主要研究目的是通过试验测量获得空气雾化在不同的喷水时间、喷气时间、喷气压力、喷水流量工况下的喷雾冷却特性。为了得到雾化冷却的实际性能参数,搭建轨道表面喷淋试验平台对轨道表面进行冷却试验,采集轨道表面温度变化数据,从宏观上分析喷雾冷却特性,并给出了有关试验结果,分析它们的特点。
1 试验装置方案设计 1.1 轨道内表面传热机理由于轨道的长度远大于外直径,而热量沿轨道轴向传递的速率很低,可以忽略轴向传热,热量不断沿径向传递。假设轨道的温度场具有轴向及角度对称性。这样,热传导问题被简化为一维稳定导热问题[10]。从热力学基本定理和能量守恒的角度分析,采用赋值法估算了轨道表面经强制喷淋冷却到规定温度时单位面积消耗的冷却介质,计算中采用了如下假设:
1)根据上述分析,对轨道表面峰值温度、冷却厚度、强制冷却温度等初始条件进行赋值;
2)高初速的初始温度冷却介质与需要冷却的轨道内表面充分浸润,急速升温、汽化热交换过程中无热量损失;
3)由于水蒸气的导热系数很低,短时间内轨道内表面仅与表层气膜发生热交换,因此忽略冷却介质汽化后的换热效应以及辐射传热;
4)由于冷却温度Ts大于冷却介质汽化温度时需要考虑冷却介质相变吸热Hw,根据方程
| ${Q_w} = {Q_r}{\text{,}}$ | (1) |
| ${Q_w} = {\rho _w}{V_w}\left[ {\left( {{T_s} - {T_w}} \right){c_w}} \right] + {H_w}{\text{,}}$ | (2) |
| ${Q_r} = {\rho _r}{S_r}\Delta t{c_r}\left( {{T_h} - {T_s}} \right){\text{。}}$ | (3) |
综合评价过程中难免存在主观性的成分,主观性是综合评价的固有属性,综合评价是以客观性为基础,保证评价结果的一致性,有效性,客观性。指标选取应遵循目的性,全面性,层次性,可行性,定性指标与定量指标相结合、不相容性6个基本原则。
1)目的性原则
所选用的指标目的很明确。选取的评价指标确实能或多或少地反映评价目标、评价对象的内容。整个冷却特性的评价指标体系必须紧紧围绕着综合评价目的即表面喷淋综合效能层层展开,使由指标体系得出的结论真实可靠的反映评价目标。
2)全面性原则
选择的一级指标要尽量涵盖评价的内容,有所遗漏就会使评价结果出现偏差。当然指标体系应该截取主要的、关键的、有代表性的技术指标。即评价指标体系必须反映被评价项目的各个方面且选取的指标要尽可能全面且具有代表性,但也绝不是面面俱到,抓主要矛盾。
3)层次性原则
即综合评价指标体系要具有层次性,递阶目标树图可以清晰把握整体或侧面的评价效果。
4)可行性原则
通俗来讲就是可操作性。虽然有些指标比较合适但无法得到,这样就要从指标体系中剔除。即冷却特性的评价指标体系既要系统全面,又要简单可行,能使评价者对综合评价指标体系方便准确地进行分析计算。
5)定性指标与定量指标相结合原则
即冷却特性的评价指标体系使定性指标、定量指标共存。对于某些量化难度较大的指标可以采用定性指标来描述。为利于对评价对象作出科学的评价结论,需要根据实际情况,结合定性指标与定量指标,从质和量的角度对项目评价进行综合分析。
6)不相容性原则
冷却特性的评价指标指标众多,应该尽量避免各指标间的重叠度,若指标重叠或交叉就会增大重叠部分的权重使决策失真,各指标要具有较高的独立性避免耦合性,做到评价指标简洁概括、具有一般性。
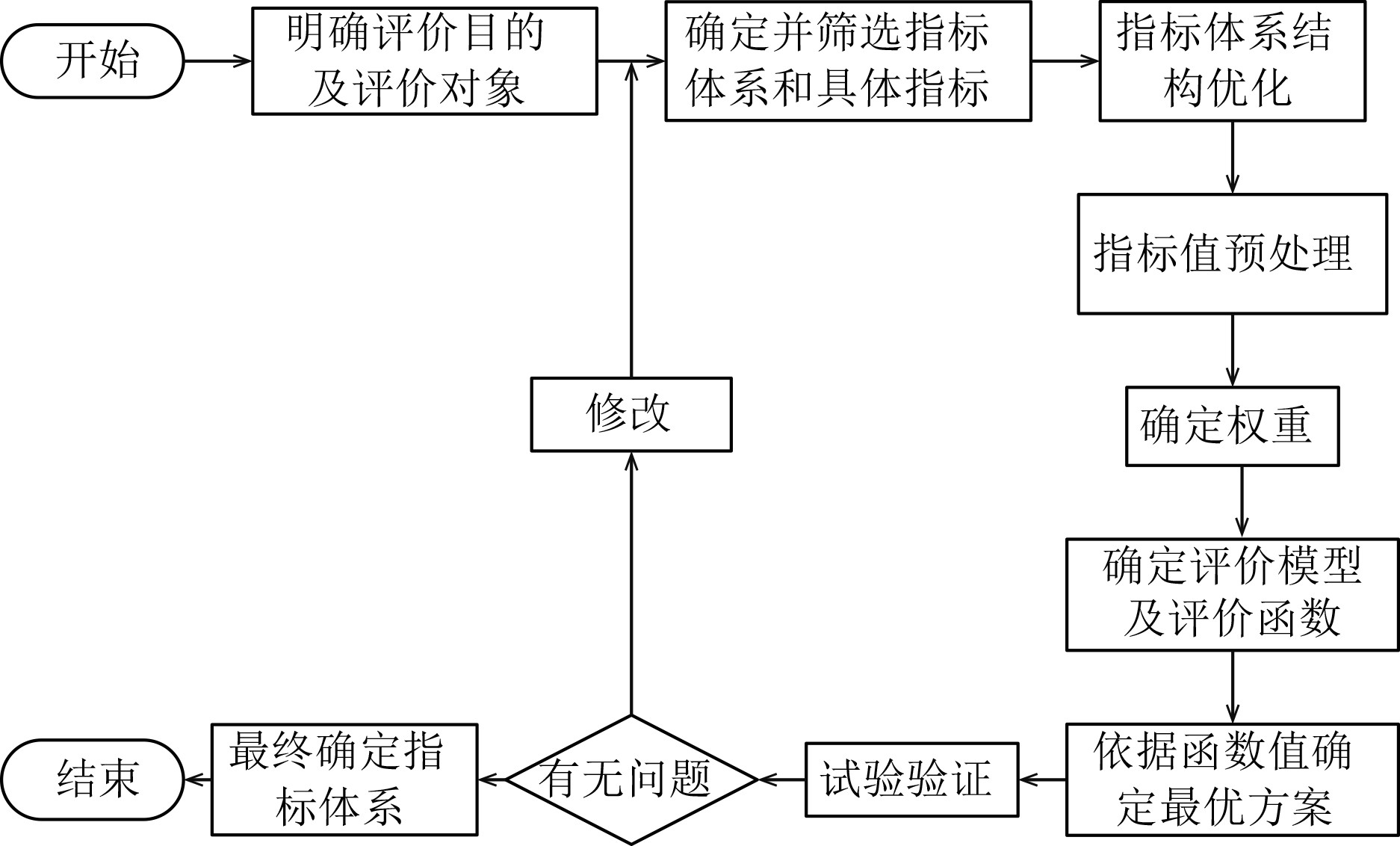
2.2 综合评价指标体系构造的流程构成综合评价问题的6个要素分别为评价指标、评价对象、评价目标、权重系数、综合评价模型及评价者。根据总目标评价者分解评价载体直到与方案直接相关的指标形成清晰的指标层次结构是体系构造的基础,采用一定的方法对各分解后的子指标确定权重并进行指标值处理,通过一定的评价模型将多个单项评价指标值及权重合成为判断方案优劣性的综合评价指标值,最后与客观试验结果比较修正评价体系。综合评价过程是一个主客观信息集成、各要素信息流动的闭环、动态的过程。该过程的流程结构如图1所示。
|
图 1 综合评价指标体系构造流程图 Fig. 1 Construction flow chart of comprehensive evaluation index |
从试验数据分析得知,表面喷淋的参数变量喷水时间、喷气压力、喷气时间、喷水流量分别对冷却效果和绝缘性能的影响趋势正负相关性不尽相同,因此在满足目标要求冷却效果和绝缘性能的前提下,需要引进评价方法对初步遴选的3种方案进行优选(见表1),从而得到4个参数变量耦合后的最佳方案。
|
|
表 1 三种方案 Tab.1 Three kinds of solutions |
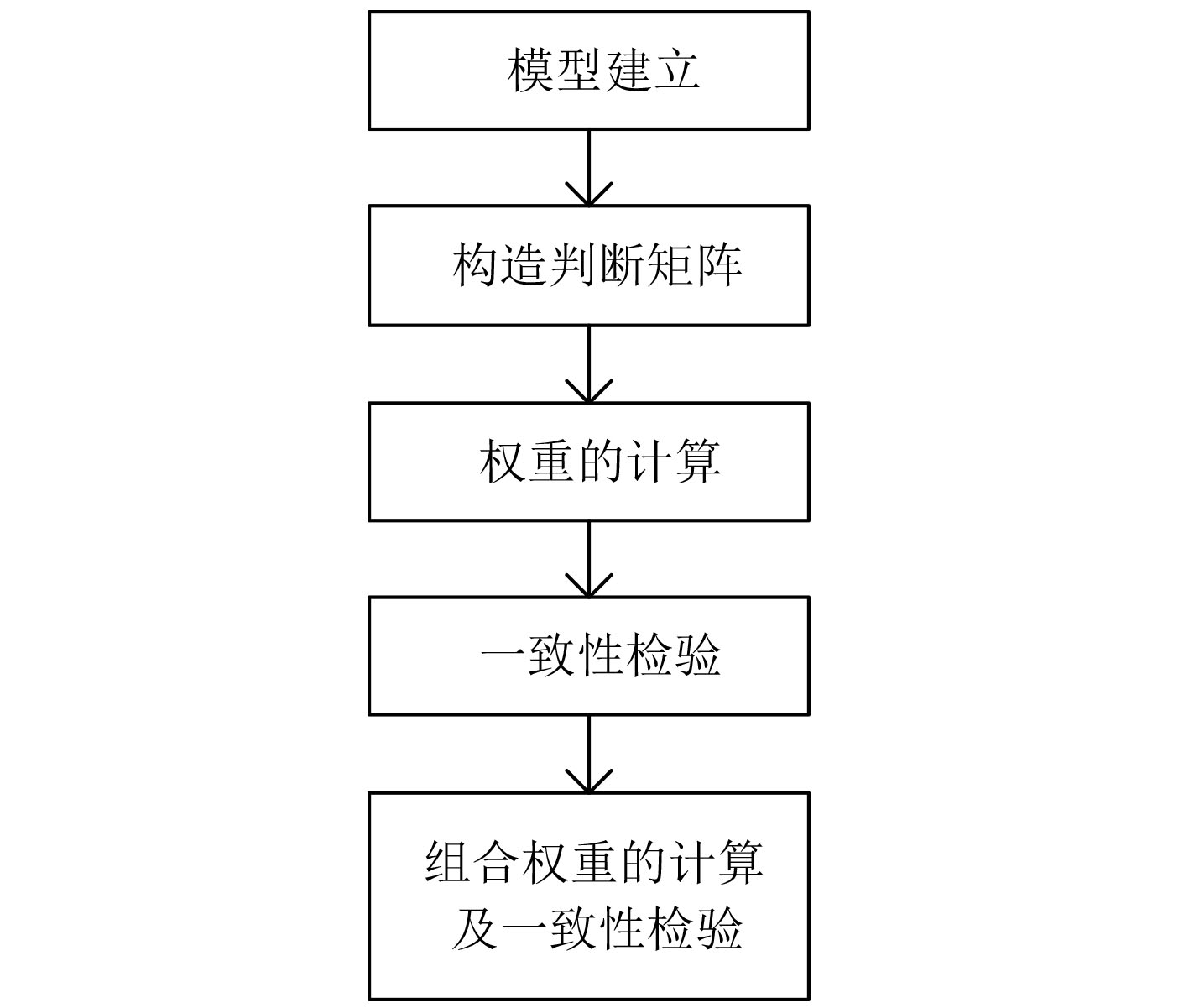
层次分析法(Analytic Hierarchy Process,AHP)是由运筹学家Saaty T.L.首先提出的一种多指标综合评价方法[11]。该方法是在对评价对象主要环节深入剖析的前提下,对评价目标逐层分解,构造判断矩阵将各指标的重要性量化得到权重,并进行一致性检验。基本步骤如图2所示.
|
图 2 AHP基本步骤 Fig. 2 Basic steps of AHP |
在深入分析评价对象及评价目标的基础上,将评价目标逐层分解,每一因素直接支配从属于此因素的若干子指标,最终形成由目标层、准则层、指标层组成的递阶层次结构。模型的建立是以拓扑图形式展示,将问题评价目标作为目标层即顶层,中间可有一个或几个层次,通常为准则层和指标层,最底层为具体方案层。
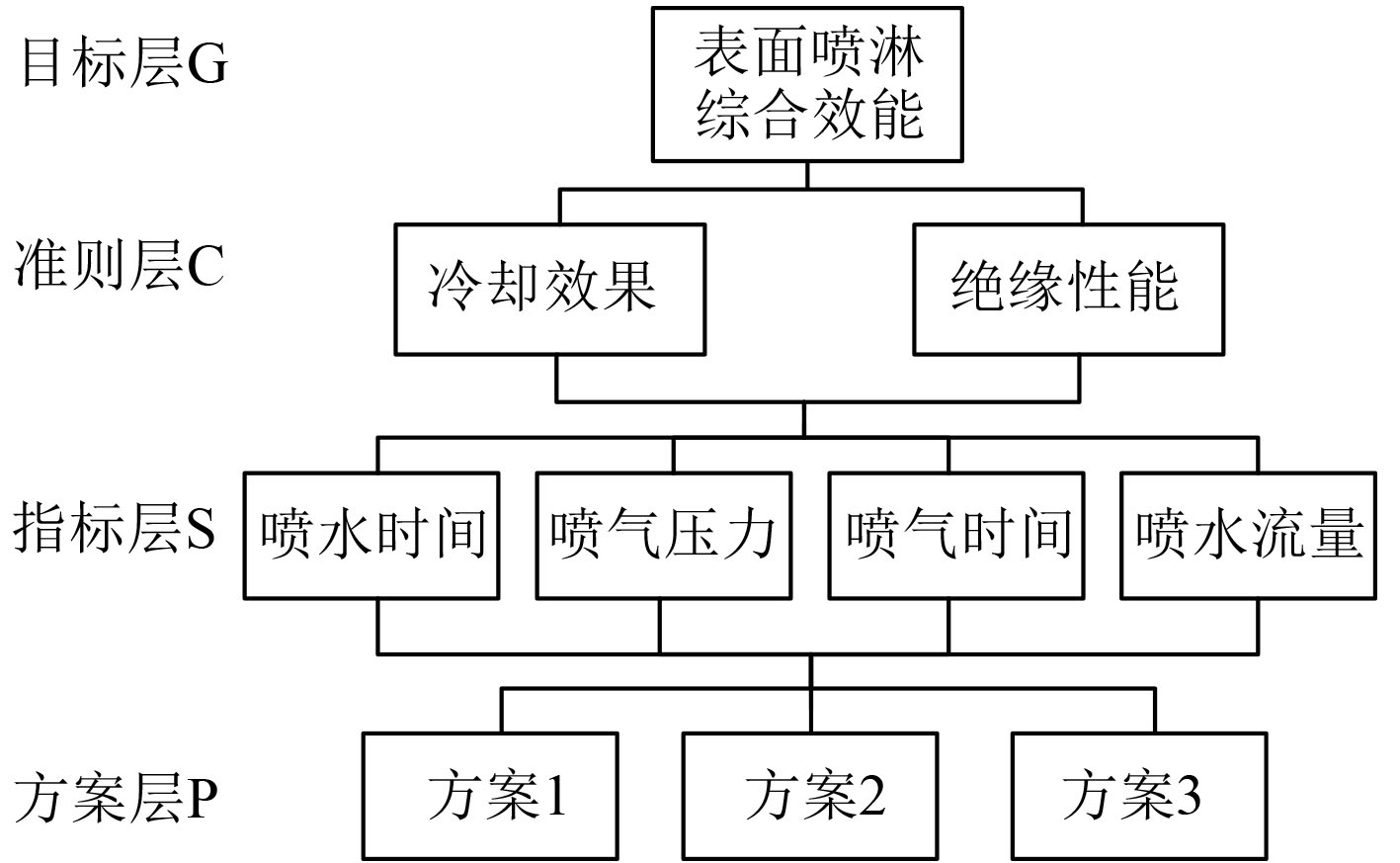
表面喷淋综合效能评价的递阶层次结构如图3所示,其中最高层为评价目标表面喷淋综合效能;第2层为衡量表面喷淋综合效能的2个准则,从左至右依次记为
|
图 3 表面喷淋综合效能评价体系的拓扑图 Fig. 3 The topography of the evaluation system of surface spray comprehensive efficiency |
判断矩阵的构造是指递阶层次结构图中同被一个因素直接支配的同一层次子指标之间重要性的比较,并根据9级标度两两判断量化,从而对上一层指标有直接支配关系的下一层次指标按其相对重要性赋予相应的权重。程序从层次模型的第2层开始直到最下层。一定主观因素的存在是AHP固有的属性。构造判断矩阵是权重排序的基础,因此是AHP法中最为关键的一步。
判断矩阵的构造是指拓扑图中被同一个因素直接支配的同一层次子指标之间重要性的比较,并根据9级标度两两判断量化,9级标度具体内容如表2所示。构造判断矩阵是权重排序的基础,是AHP中较为关键的一步[12 – 13]。
|
|
表 2 9级标度及其含义 Tab.2 Scale 9 and its meaning |
对表面喷淋综合效能的2个准则进行专家经验判断,根据其对表面喷淋综合效能的贡献大小做两两比较,形成准则层相对于评价目标的判断矩阵,如表3所示。
|
|
表 3 准则层相对于目标层的判断矩阵 Tab.3 Judgment matrix of criterion layer relative to target layer |
同理,形成指标层相对于准则层冷却效果的判断矩阵,如表4所示。
|
|
表 4 指标层相对于准则层冷却效果的判断矩阵 Tab.4 Judgment matrix of index layer relative to criterion layer cooling effect |
同理,形成指标层相对于准则层绝缘性能的判断矩阵,如表5所示。
|
|
表 5 指标层相对于准则层绝缘性能的判断矩阵 Tab.5 Judgment matrix of index layer relative to criterion layer insulation performance |
准则层相对于目标层的判断矩阵记为G,计算判断矩阵每行元素乘积的n次方根
指标层相对于准则层的判断矩阵记为C1,C2,同理,判断矩阵C1,C2对应的权重向量
一致性检验的内涵就是判断在两两比较中是否出现不合逻辑的情况,通常引入相对一致性指标CR:
| $CR = \frac{{CI}}{{RI}}{\text{,}}$ | (4) |
| $CI = \frac{{{\lambda _{\max }} - n}}{{n - 1}}{\text{。}}$ | (5) |
式中:
|
|
表 6 判断矩阵的RI值 Tab.6 The RI value of the judgment matrix |
CR越小,判断矩阵的一致性越好。对于判断矩阵C1,C2,求得CR1=0.00344<0.1、CR2=0.005278<0.1,则判断矩阵的一致性可以接受。
比较3种方案主要环节的优缺点并对每种模块的主要环节专家百分制打分,然后选择线性隶属函数对专家打分值进行无量纲化处理。无量纲化值如表7所示。
|
|
表 7 无量纲化处理值 Tab.7 Dimensionless processing value |
| ${y_{ij}} = \frac{{{a_{ij}}}}{{\sum\limits_{i = 1}^3 {{a_{ij}}} }}{\text{,}}\left( {\text{指标}{{i}} = 1,2,3,4,\text{模块}{{j}} = 1,2,3} \right){\text{。}}$ | (6) |
式中:
因此,若设上述无量纲化值表格数据为矩阵C,则总评价值E=CP。由Matlab计算可得:
| $\begin{array}{l} E = CP = \left[ {\begin{array}{*{20}{c}} {0.159}&{0.167}&{0.160}&{0.168}\\ {0.161}&{0.162}&{0.160}&{0.168}\\ {0.157}&{0.149}&{0.143}&{0.151} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {0.368}\\ {0.143}\\ {0.262}\\ {0.227} \end{array}} \right]=\\ \; \;\;\;\;\;\;\;\;\;\;\;\;\;\; {\left( {0.1624,0.1625,0.1508} \right)^{\rm T}}{\text{。}} \end{array}$ |
显然,3种方案的总排序为
AHP-模糊综合评价法具有客观性和合理性的特点[14]。对方案2进行评级可最大限度避免人为的误差。
评价对象的因素论域
|
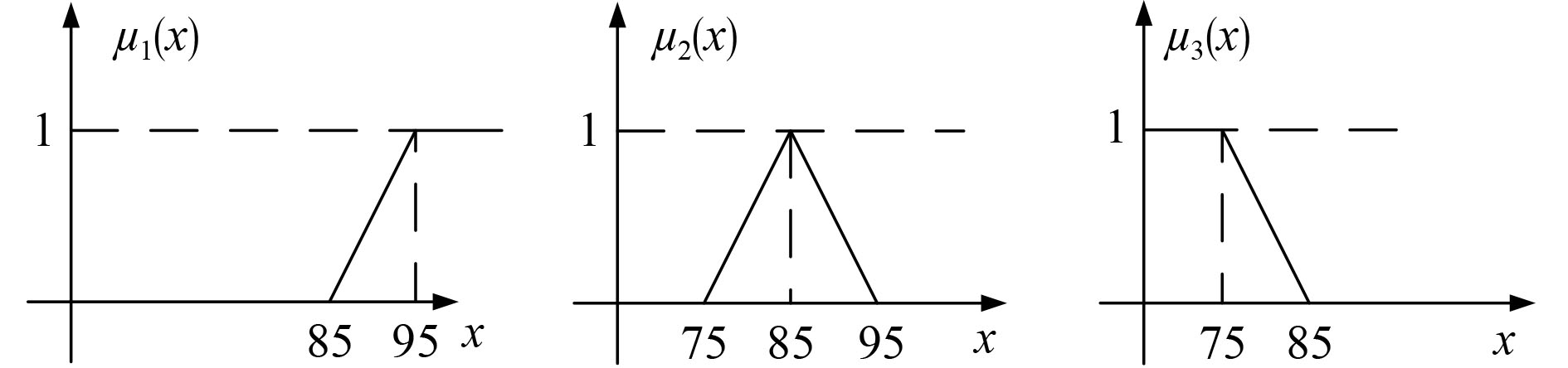
图 4 隶属函数图 Fig. 4 The diagram of the membership function |
| ${\mu _1}\left( x \right) = \left\{ {\begin{array}{*{20}{l}} {0,}&{x \leqslant 85}{\text{,}}\\ {\left( {x - 85} \right)/10,}&{x \in \left( {85,95} \right)}{\text{,}}\\ {1,}&{x \geqslant 95}{\text{,}} \end{array}} \right.$ |
| ${\mu _2}\left( x \right) = \left\{ {\begin{array}{*{20}{l}} {0,}&{x \leqslant 75\text{或}x \geqslant 95}{\text{,}}\\ {\left( {x - 75} \right)/10,}&{x \in \left( {75,85} \right]}{\text{,}}\\ {\left( {95 - x} \right)/10,}&{x \in \left( {85,95} \right)}{\text{,}} \end{array}} \right.$ |
| ${\mu _3}\left( x \right) = \left\{ {\begin{array}{*{20}{l}} {1,}&{x \leqslant 75}{\text{,}}\\ {\left( {85 - x} \right)/10,}&{x \in \left( {75,85} \right)}{\text{,}}\\ {0,}&{x \geqslant 85}{\text{。}} \end{array}} \right.$ |
把方案2中的各单项指标值即专家打分代入隶属函数公式可以得到模糊关系矩阵R,矩阵R中的元素rij第i种单项指标值被评为第j等级的可能性,即i对j的隶属度,最终求得的模糊关系矩阵
| $ \begin{array}{l} \begin{array}{*{20}{l}} {}&{}&{{v_1}}&{{v_2}}&{{v_3}}&{} \end{array}\\ R = \left[ {\begin{array}{*{20}{c}} {0.8}&{0.2}&0\\ {0.7}&{0.3}&0\\ {0.7}&{0.3}&0\\ 0&1&0 \end{array}} \right] \begin{array}{*{20}{c}} {{S_1}}\\ {{S_2}}\\ {{S_3}}\\ {{S_4}} \end{array} \end{array}\!\!\!\!\!{\text{。}} $ |
又由AHP得到的模糊权向量
| $ \begin{align} &B = {P^{\rm T}} \cdot R = \left( {0.368,0.143,0.262,0.227} \right)\left[ { \begin{array}{*{20}{c}} {0.8}&{0.2}&0 \\ {0.7}&{0.3}&0 \\ {0.7}&{0.3}&0 \\ 0&1&0 \end{array}} \right] =\\ & \left( {0.5779,0.4221,0} \right){\text{。}} \end{align}$ |
可见方案2评价等级为一级,与AHP评价结果比较来看具有令人满意的一致性。这也就从侧面证明了方案2在3种方案中是最优方案。
4 结 语为研究轨道发射器轨道表面冷却的壁面换热机理,探索高效冷却方法,搭建设计了轨道表面喷淋试验平台,引入层次分析法评价优选出了表面喷淋冷却综合效能最优方案,得到了4个参数变量耦合后的最佳配合方案,即喷水时间5 s、喷气压力5 MPa、喷气时间10 s、喷水流量6 L/s。为减少主观因素的作用,利用基于AHP-模糊数学理论对该方案进行了检验,进一步证明了该方案是最优方案的判断,为表面喷淋方案在轨道发射器冷却系统中的应用积累了经验并指明方向。
| [1] |
曹建明. 喷雾学[M]. 北京: 机械工业出版社, 2006: 23–28.
|
| [2] |
KIM J. Spray Cooling Heat Transfer: the State of the Art[J]. International Journal of Heat Fluid Flow, 2016, 13/14: 80-85. |
| [3] |
ESTES K A, MUDAWAR I. Correlation of Sauter mean diameter and critical heat flux for spray cooling of small surfaces[J]. International Journal of Heat and Mass Transfer, 2015, 16(38): 2985-2996. |
| [4] |
BOSTANCI H, RINI D P, KIZITO J P, et al. High Heat flux spray cooling with ammonia: Investigation of enhanced surfaces for CHF[J]. International Journal of Heat and Mass Transfer, 2015, 13/14: 3849-3856. |
| [5] |
CHEN R H, CHOW L C, NAVEDO J E. Effects of characteristics on critical heat flux in subcooled water spray cooling[J]. International Journal of Heat and Mass Transfer, 2012, 19(45): 4033-4043. |
| [6] |
LIN L, PONNAPPAN R. Heat transfer characteristics of spray cooling in a closed loop[J]. International Journal of Heat and Mass Transfer, 2013, 20(46): 3737-3746. |
| [7] |
王亚青. 喷雾冷却换热机理和影响换热性能的因素[J]. 强激光与粒子束, 2011, 23(9): 2277-2281. WANG Ya-qing. Heat transfer mechanism and influencing factors in spray cooling[J]. High power laser and particle beams, 2011, 23(9): 2277-2281. |
| [8] |
程文龙. 系统压力影响下的喷雾冷却特性及温度均匀性[J]. 化工学报, 2010, 61(12): 3086-3091. CHENG Wen-long. Effect of system pressure on spray cooling heat transfer and surface temperature uniformity[J]. CIESC Journal, 2010, 61(12): 3086-3091. |
| [9] |
马腾跃. 喷雾冷却高热流密度散热传热特性研究[J]. 科技导报, 2012, 30(21): 34-37. MA Teng-yue. Heat transfer characteristics of spray cooling with high heat flux dissipation[J]. Science and technology review, 2012, 30(21): 34-37. DOI:10.3981/j.issn.1000-7857.2012.21.004 |
| [10] |
陈礼. 流体力学与热工基础[M]. 北京: 清华大学出版社, 2012: 128-135.
|
| [11] |
郭亚军. 综合评价理论、方法及应用[M]. 北京: 科学出版社, 2007: 28-35.
|
| [12] |
吕跃进, 张维. 指数标度在AHP标度系统中的重要作用[J]. 系统工程学报, 2003(5): 14-17. LV Yue-jin, ZHANG Wei. Exponential scale plays an important role in AHP scale system[J]. Journal of systems engineering and electronics, 2003(5): 14-17. |
| [13] |
李礼. 建筑材料绿色性的6E综合评价体系研究[D]. 大连: 大连理工大学, 2012: 38-46. LI Li. Research on 6E comprehensive evaluation system of greening building materials[D]. Dalian: Dalian university of technology, 2012: 38-46. |
| [14] |
邱东. 多指标综合评价方法的系统分析[M]. 杭州: 杭州大学出版社, 1997: 55-61.
|
 2019, Vol. 41
2019, Vol. 41
