0 引　言

随着中口径火炮射速的不断提高，对排壳的速度要求也更加严苛。排壳速度的提高，药筒初始能量随之增加^[1]。在高速排壳过程中，保证药筒残余速度和零件结构强度是优化排壳机构的关键。

中口径火炮要求排壳初始速度达到40 m/s，采用一种前排壳的方式将药筒以一定的速度排出火炮装置。运用ADAMS和Abaqus软件分析排壳过程的运动学和动力学特性，刚柔耦合仿真结果作为排壳相关结构优化的参考数据^{[2 – 4]}。

1 多体系统动力学理论

多体系统动力学由多刚体系统动力学与多柔体系统动力学组成。多刚体系统动力学的研究对象是由多个刚体组成的系统，刚体之间以某种形式的约束连接，主要解决多个刚体组成的系统动力学问题。多柔体系统动力学的研究对象则是由刚体和柔体共同组成的系统，可以看作是多刚体系统动力学的自然延伸。根据多柔体系统组成特点，一般以多刚体系统动力学的研究为基础，对系统中柔性体进行不同的处理^{[5 – 6]}。

多体系统动力学微分-代数方程组可表示为：

$ {{ M}}\left( {{{q}},{{t}}} \right){{\ddot q}} + \emptyset _{{q}}^{{\rm T}}\left( {{{q}},{{t}}} \right){\rm{\lambda }} - {{ Q}}\left( {{{q}},{{\dot q}},{{t}}} \right){\text{，}} $

(1)

$ \emptyset \left( {{{q}},{{t}}} \right){\rm{\lambda }} = 0{\text{。}} $

(2)

式中：q， ${\dot{{ q}}}$ ， ${\ddot {{q}}} \in {{{R}}^{\rm{n}}}$ 分别是系统的广义坐标及其对时间的一、二阶导数；λ∈R^m是拉格朗日乘子；M∈R^n×n为系统广义质量阵； ${\emptyset _{\rm{t}}} \in {{{R}}^{{\rm{m}} \times {\rm{n}}}}$ 为约束雅可比矩阵；Q∈Rⁿ为外力列阵； ${\emptyset } \in {{{R}}^{{\rm{m}} }}$ 为位置约束方程列阵。首先利用运动学关系消除非独立变量，使微分方程只含有独立变量，然后直接积分求解；求出独立变量的位移、速度和加速度后再通过运动学关系求出非独立变量的位移、速度和加速度；积分过程采用Runge-Kutta法求解。

2 仿真模型的建立

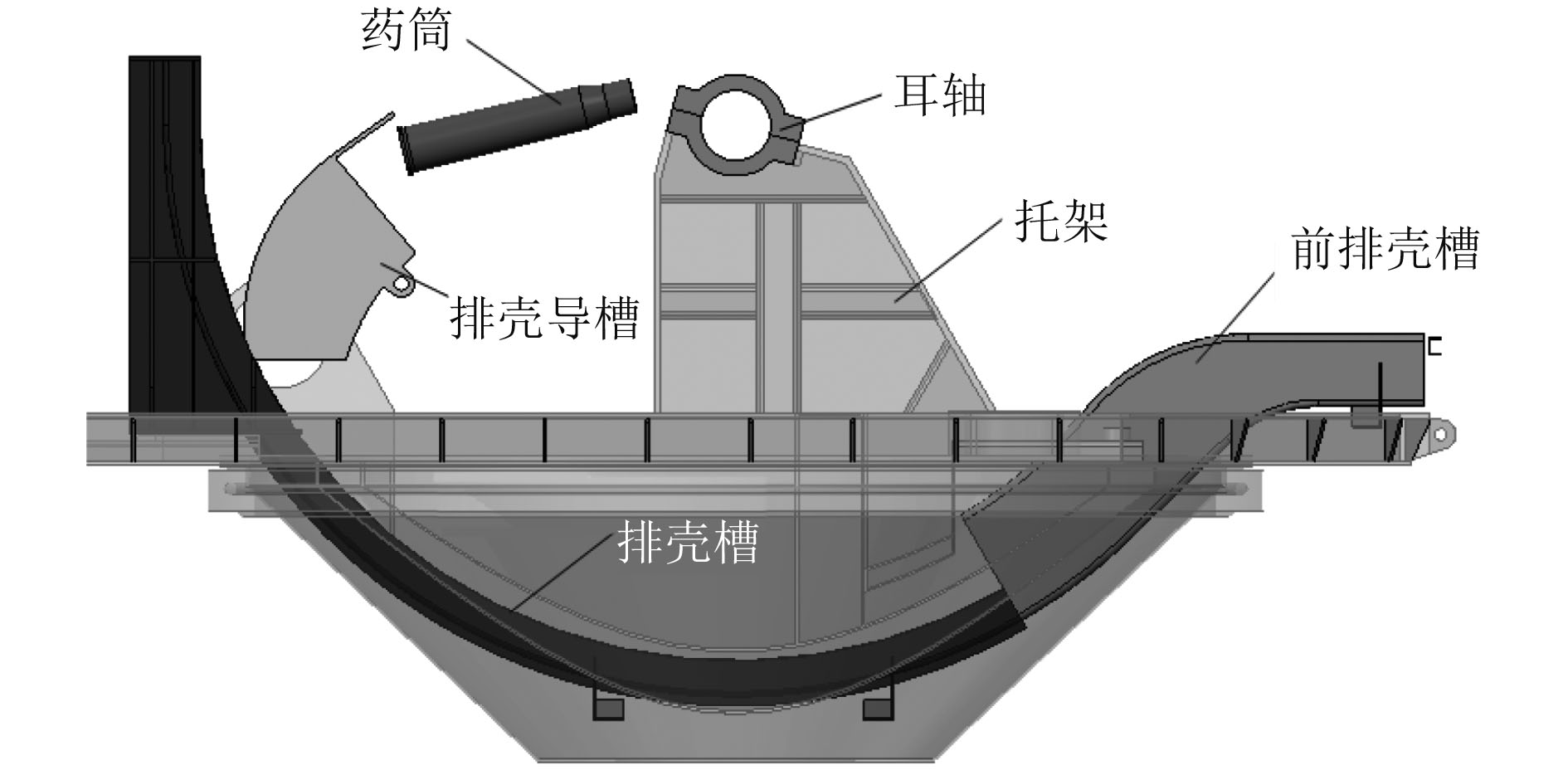
利用三维软件建立排壳机构装配模型，在ADAMS和Abaqus软件中，添加零件约束，施加载荷，得到排壳机构多刚体动力学模型，如图1所示。

图1中，排壳槽和前排壳槽固定在托架上，排壳导槽和药筒可以随发射系统绕耳轴转动，火炮高低运动范围为0°～85°，图1为高低0°角的位置。由于排壳导槽和药筒绕耳轴旋转的速度远小于40 m/s，对排壳机构动力学影响较小，可以忽略，因此，仿真分析时将排壳导槽和药筒高低角度固定在0°～85°之间的某个位置即可。设置模型属性、约束、接触、驱动速度等参数，如表1所示。

3 仿真结果分析 3.1 运动学仿真结果分析

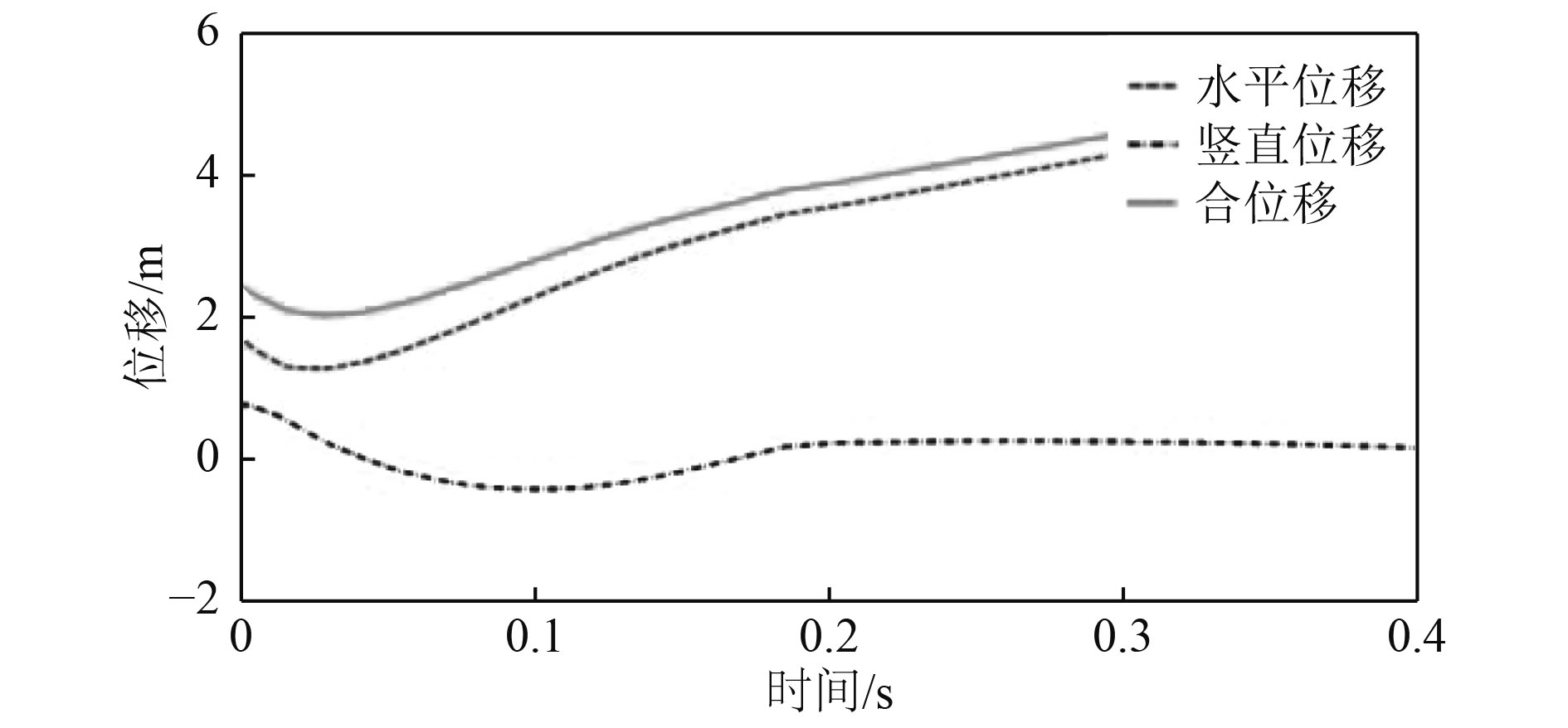
药筒在排壳导槽、排壳槽和前排壳槽的约束下运动位移先减小后增大，在0.25 s之后药筒排出系统做自由落体运动，药筒位移呈线性增加。药筒位移-时间曲线如图2所示。

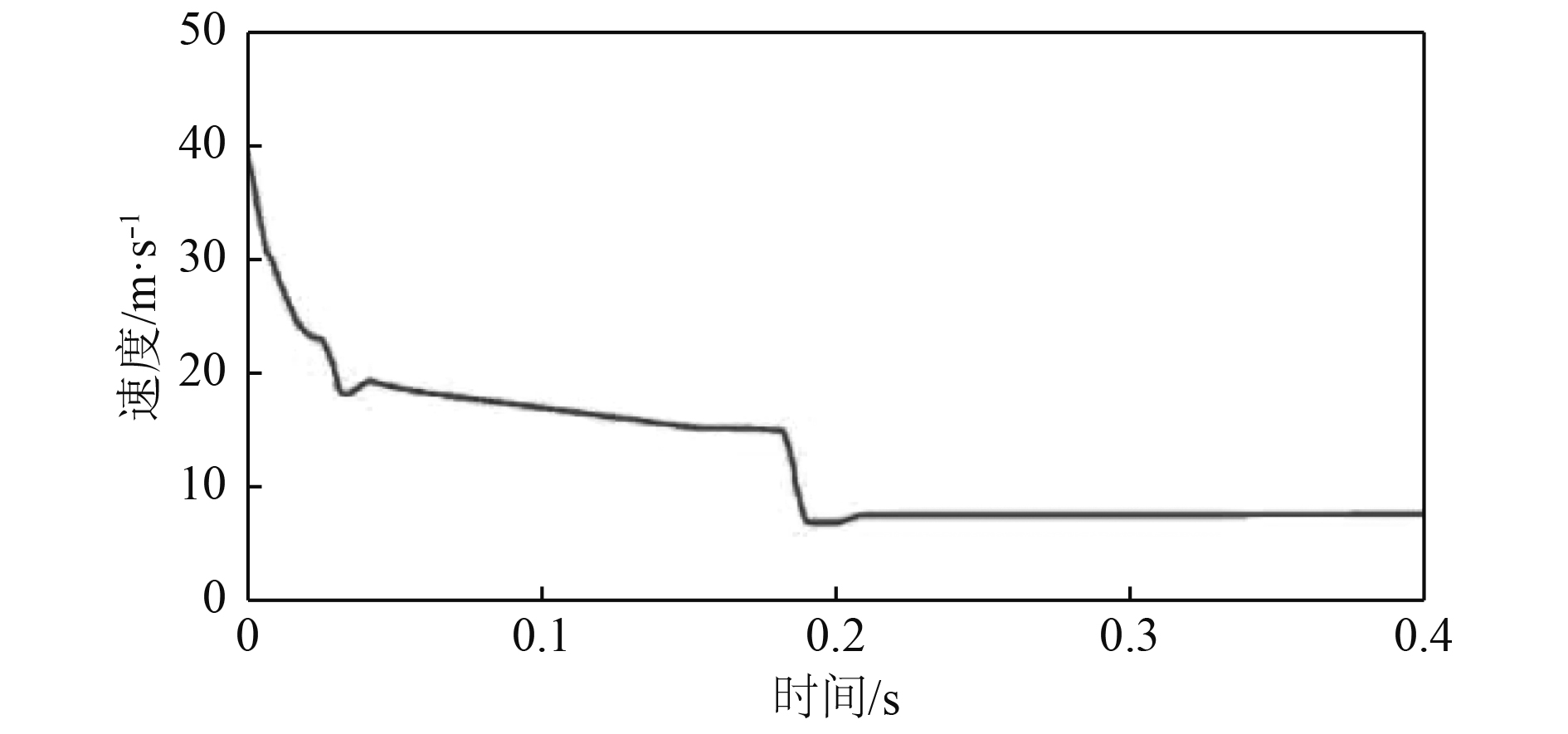
由药筒速度-时间曲线（见图3）可以看出，药筒在0.003 1 ～0.003 3 s之间存在第1次较大的速度突变，此处为药筒与排壳导槽第1次碰撞，是潜在的危险点之一。在0.029 4 ～0.029 6 s之间存在第2次较大的速度突变，此处为药筒过渡到排壳槽零件上的碰撞过程。在0.185 6 ～0.186 3 s之间存在第3次较大的速度突变，此处为药筒进入前排壳槽内在弯角处产生的撞击。3次速度突变的过程为能量损失较大的过程，是结构强度校核的重点位置。通过图3还可以得出，药筒排出火炮装置的末端速度为7.68 m/s。通过以上仿真结果可以得出，药筒可以一定的末端速度排出火炮装置，达到功能要求，排壳过程中药筒存在3次速度急剧变化的区域，此区域为结构强度的危险点。

3.2 动力学仿真结果分析

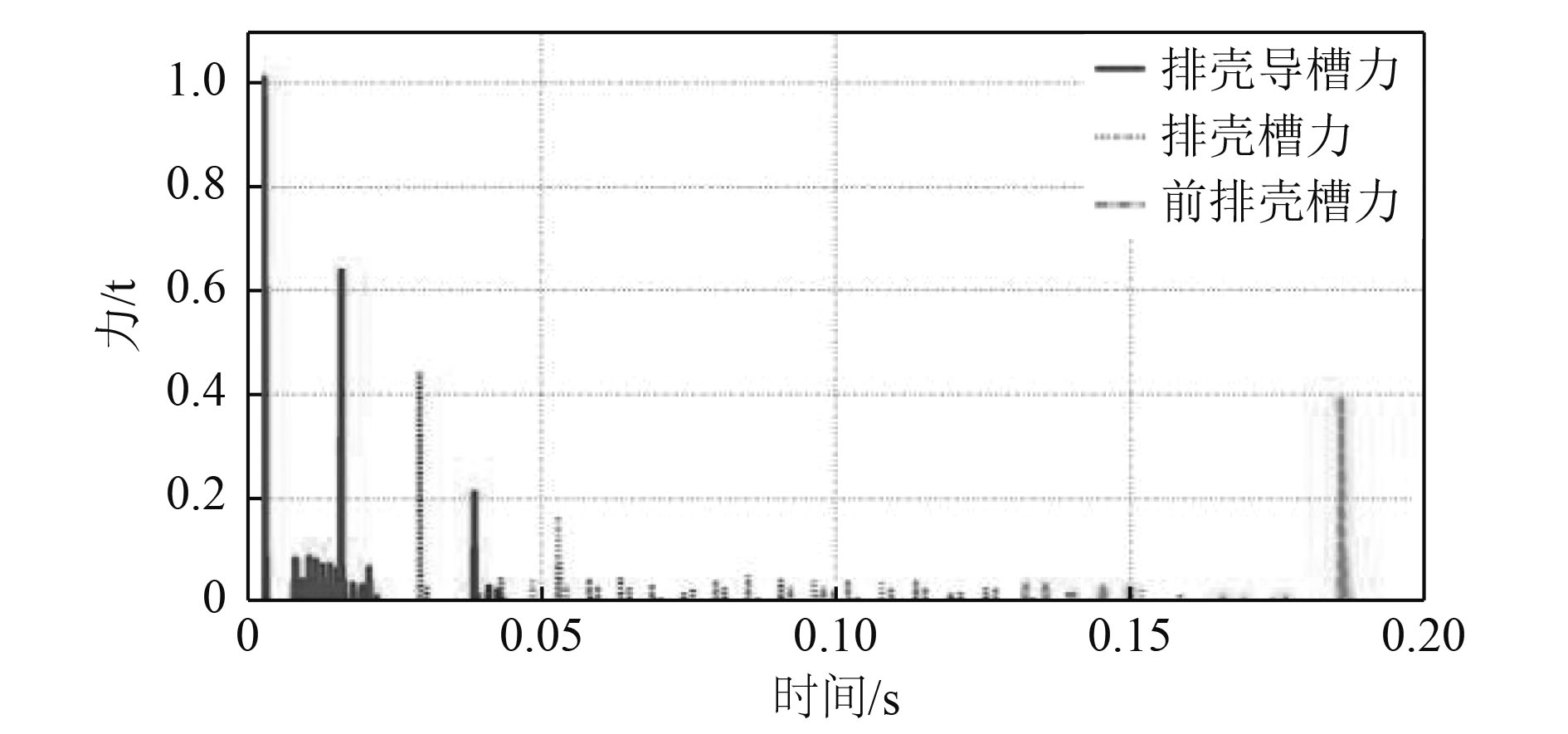
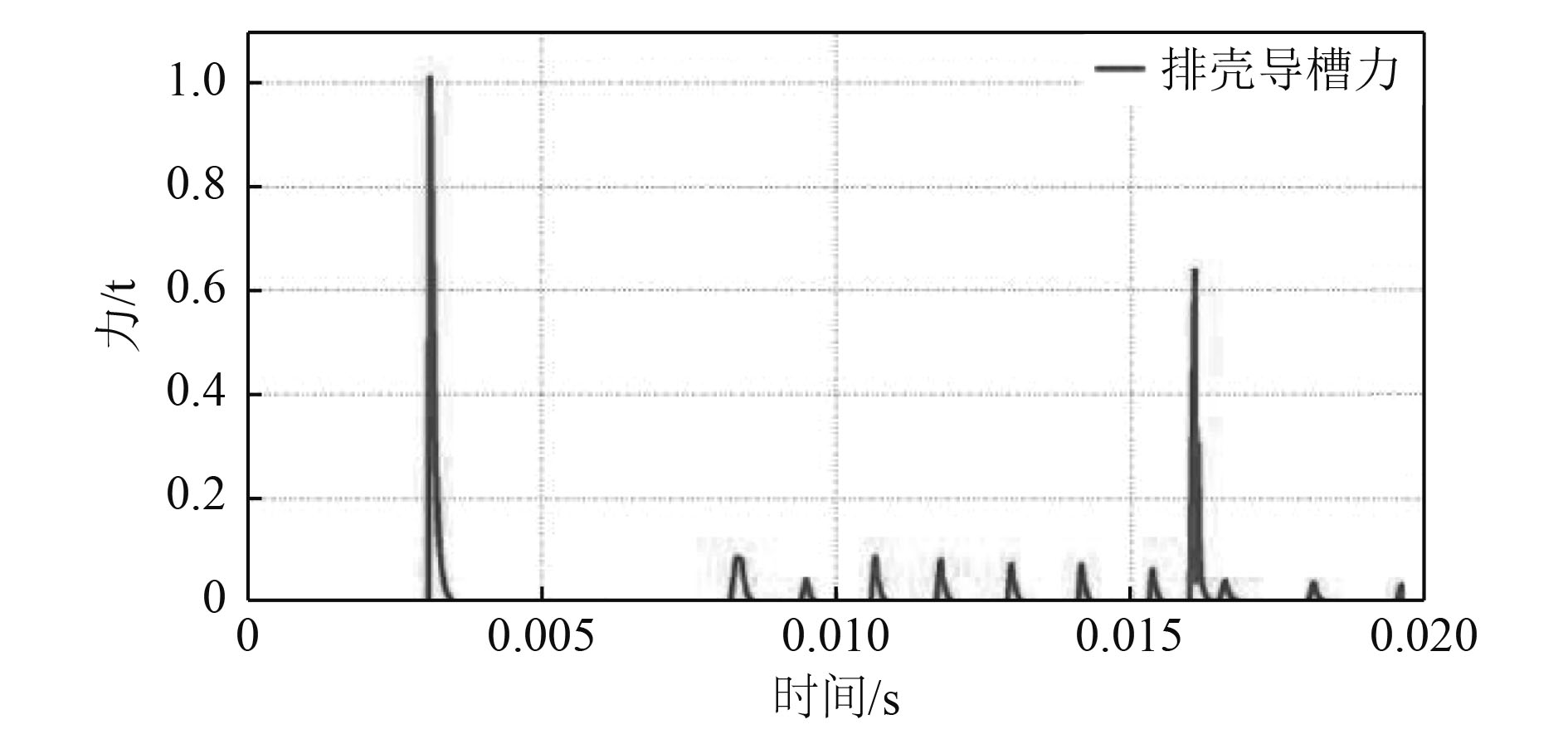
本文在ADAMS中采用impact函数定义接触力，如图4为刚性排壳机构力-时间曲线，存在7个峰值，其中第1次撞击时接触力最大，为排壳机构结构强度的危险点。图5为刚性排壳导槽力-时间曲线，即为药筒与排壳导槽第1次撞击峰值时力的历程曲线。

图4和图5作用力存在如下特点：力的峰值较大，但作用时间短，是一个瞬态过程。由于在ADAMS仿真计算中采用的是刚体模型，力的峰值存在偏大的可能，所得结果可以作为有限元分析的定性参考。

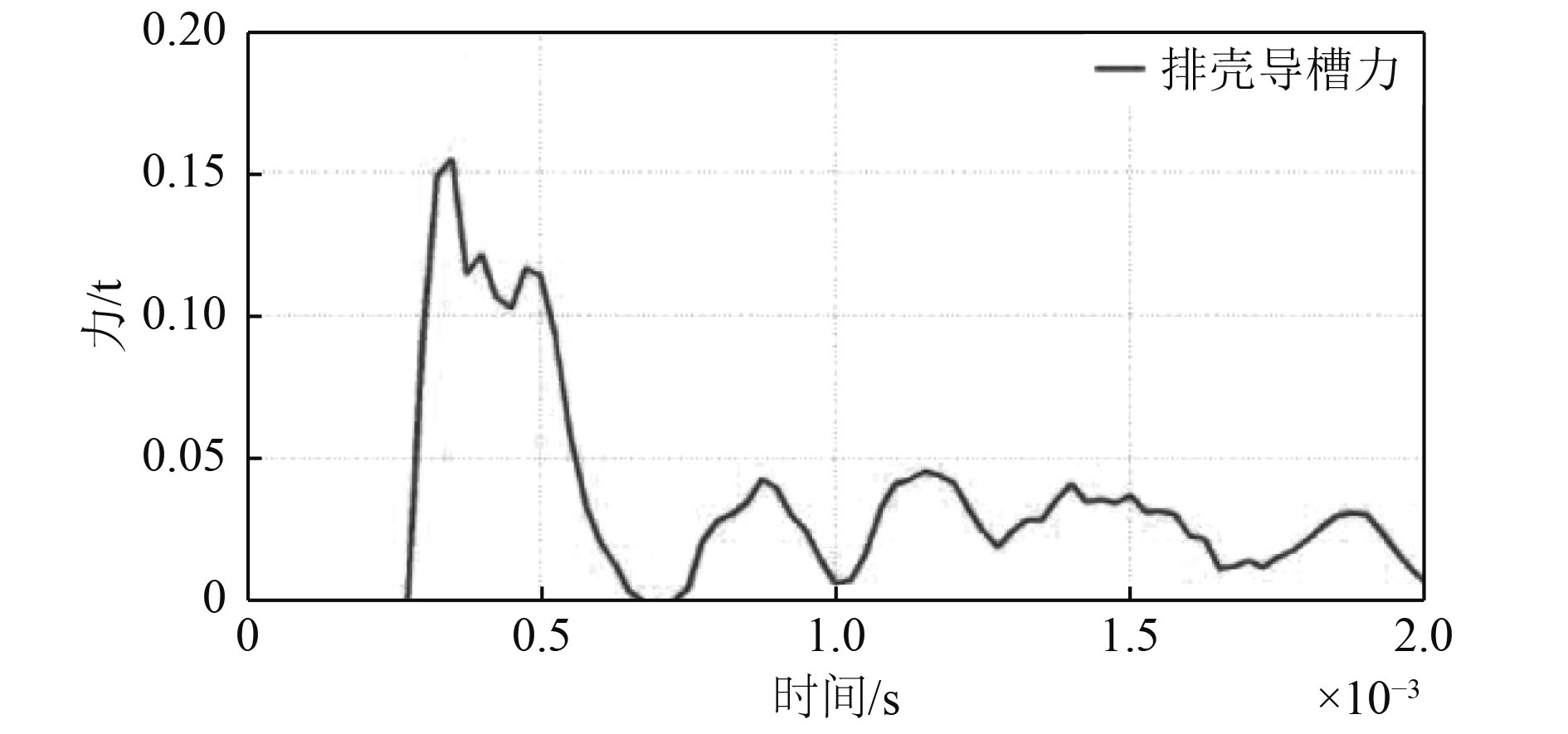
通过上述分析，确定第1次撞击排壳导槽与药筒撞击为危险点，采用柔性体模拟撞击过程。在Abaqus软件中创建有限元模型，添加边界条件，进行有限元仿真计算，计算碰撞时的作用力和零件内部的应力。图6为柔性排壳导槽力-时间曲线，柔性排壳导槽历程曲线同刚性排壳导槽历程曲线整体趋势相近，但峰值大小不同，柔性体峰值更小。

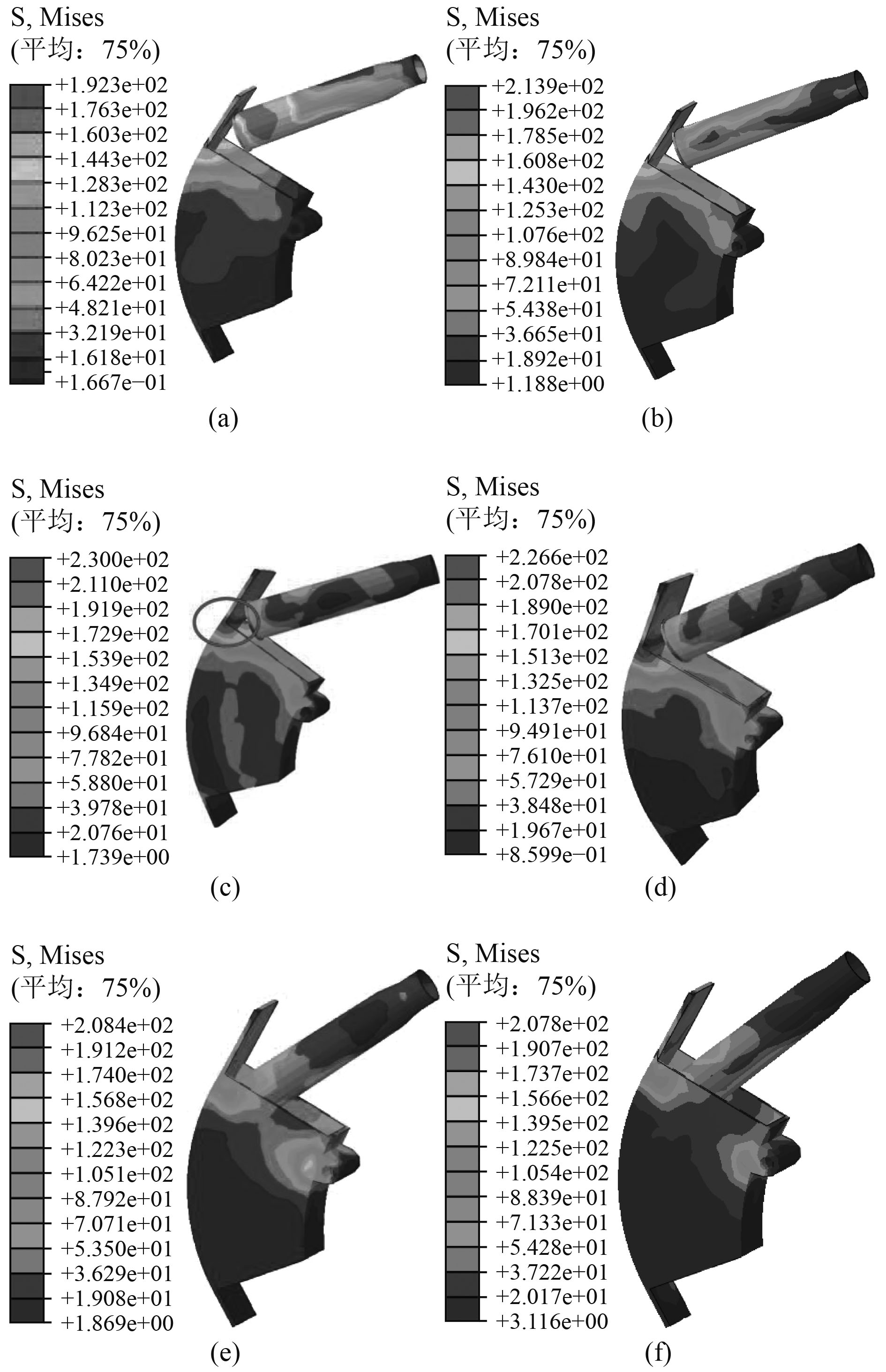
图7为排壳导槽历程应力云图，在整理撞击历程中，最大应力值只出现在某个瞬态，出现的位置在排壳导板拐角处，如图7（c）指示区域，最大瞬态应力值为230 MPa。其中，排壳导槽材料极限为345 MPa，通过式（3）计算可得安全系数为1.5。

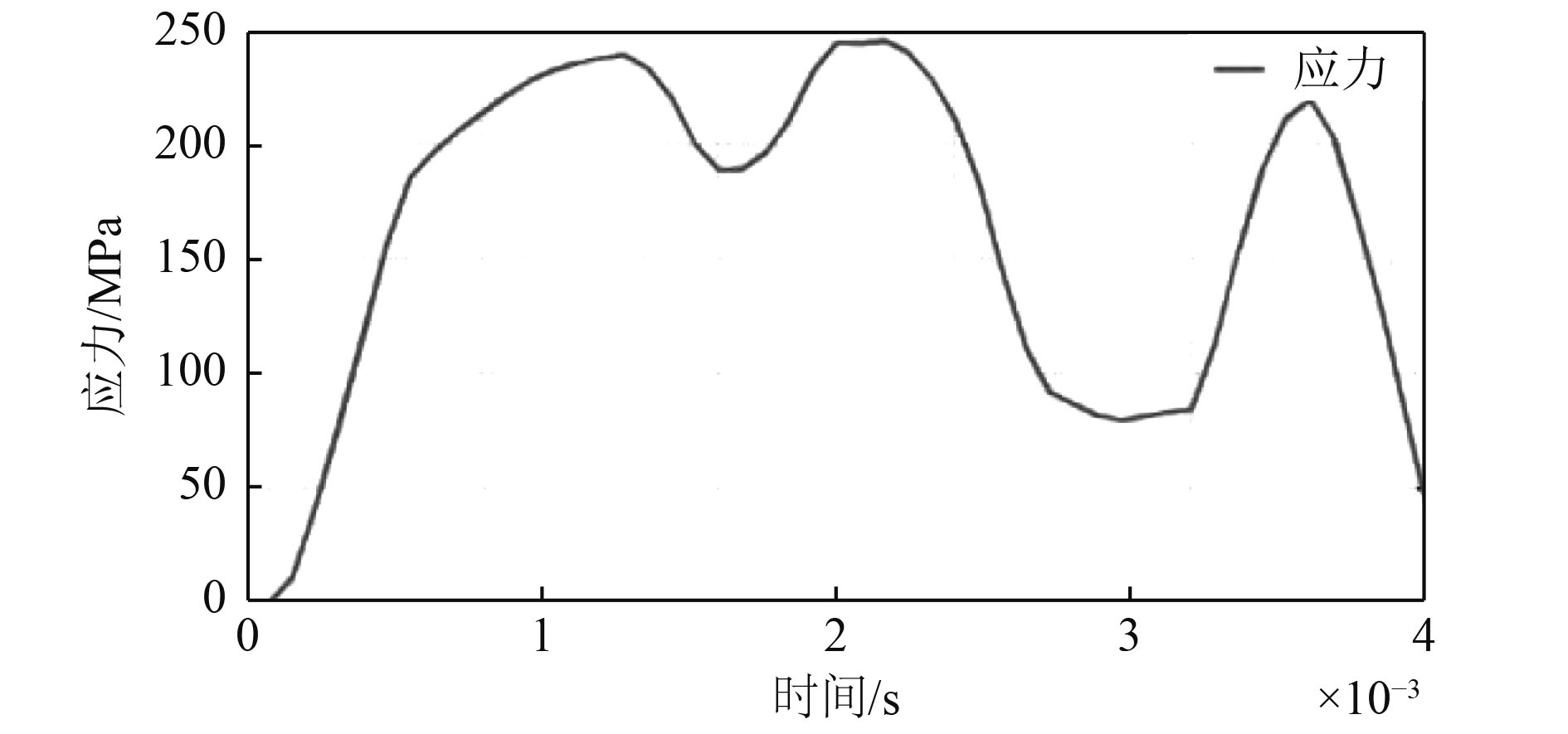
图8为危险点应力-时间曲线，从曲线中可以得出在撞击的过程中，应力处于波动状态，波动峰值为230 MPa，波动周期约为2 ms。

4 结　语

通过对高速排壳机构的运动学仿真分析，得出一种前排壳机构可以完成初速为40 m/s药筒的排壳功能，药筒末端速度为7.68 m/s。通过对高速排壳机构的动力学仿真分析，将刚体和柔性体结合分析，得出高速排壳机构排壳过程中应力变化曲线，最大瞬态应力为230 MPa，进一步计算得出该排壳机构在排壳过程中的安全系数为1.5。