0 引　言

在某发射动力系统连接结构中，螺栓连接以其连接刚性好，安装方便等诸多优点得到广泛的应用，但是螺栓连接件会影响结构局部刚度和整机的动力学性能，所以建立准确的动力学连接模型是准确计算结构动态特性与响应的前提。

螺栓连接的有限元建模方法主要分为两类：非参数化建模方法和参数化建模方法。非参数化建模将连接刚度和连接阻尼等效为对结构动力学特性作用相同的附加外力的形式^{[1 – 4]}，缺点是无法揭示连接处的微观特性。与非参数化建模不同的是参数化建模是根据连接处的物理特性和连接界面的微观滑移、碰撞等特性建立连接模型，因为能够深刻揭示连接的特性而得到越来越多的研究。参数化建模分为零厚度单元（Zero thickness element）、一般单元（Generic element）和薄层单元（Thin layer element）3种类型。零厚度单元用集中质量、弹簧和摩擦滑块来表示连接界面处的力—位移关系。Iwan^[5]模型因为能够表示连接处的粘滑运动而被广泛应用；Ahmadian和Jalali^[6]采用一般单元模拟连接处的特性，并通过实验频响函数对连接参数进行了识别；薄层单元理论最早应用于岩石接触的力学分析^[7]，Mayer和Gaul^[8]研究表明薄层单元能够有效模拟机械连接面的接触特性。

在连接的不确定性方面，国内外学者进行了大量的研究。Gangaharan^[9]提出一种基于统计学的参数识别方法，运用系统静力学响应来进行参数识别；Qiao LS^[10]采用迟滞模型研究了非自治系统的刚度不确定性；Guo Qin tao和Zhang Ling mi^[11] 将连接结构的接触刚度及接触阻尼作为随机分布参数处理，然后基于响应面法的模型修正方法和分布代数方法进行参数识别；姜东和费庆国^[13]基于薄层单元理论，提出了一种螺栓连接接触面不确定性参数识别方法；C.Zang^[13]基于鲁棒性设计研究了两自由度结构的动力学不确定性问题。本文以某发射动力系统连接结构为研究对象，针对薄层单元连接模型，通过Taguchi方法研究了薄层单元的厚度、弹性模量和密度不确定性。

1 薄层单元基本理论

薄层单元建模方法把2个连接件接触面的部分等效为连续的厚度非常薄的单元，如图1所示。

对于尺寸为 ${l_1} \times {l_2} \times d$ 的薄层单元，根据虚位移原理得到虚功方程：

$ \begin{split} \delta {W_I} =& \int\nolimits_0^{{l_1}} {\int\nolimits_0^{{l_2}} {\int\nolimits_0^d {{{\left\{ \delta \right\}}^{\rm T}}\left\{ {\delta \varepsilon } \right\}{\rm d}x{\rm d}y{\rm d}z} } }= \\ \;\;\;\;\;\;\; & \delta \left\{ u \right\}_{nodal}^{\rm T}\left[ K \right]{\left\{ u \right\}_{nodal}} \text{。} \end{split} $

(1)

式中： ${l_1}$ ， ${l_2}$ 分别为薄层单元在局部坐标系 $x$ 和 $y$ 方向的长度； $d$ 为薄层单元在局部坐标系 $z$ 方向的厚度； $K$ 为通过等参变换得到的在自然坐标系 $\xi $ ； $\eta $ ， $\zeta $ 下的单元刚度矩阵：

$\left[ K \right] = \int\nolimits_{ - 1}^1 {\int\nolimits_{ - 1}^1 {\int\nolimits_{ - 1}^1 {{{\left[ B \right]}^{\rm T}}\left[ C \right]\left[ B \right]\det \left( {\left[ J \right]} \right){\rm d}\xi {\rm d}\eta {\rm d}\zeta } } }\text{。} $

(2)

式中： $\left[ { J} \right]$ 为雅克比矩阵，由局部坐标转换到自然坐标的等参变换得到，二者方向一致时 $\left[ J \right]$ 的表达式为：

$\begin{split} \left[ { J} \right] =& \left[ {\begin{array}{*{20}{c}} {\partial x/\partial \xi }&{\partial y/\partial \xi }&{\partial z/\partial \xi } \\ {\partial x/\partial \eta }&{\partial y/\partial \eta }&{\partial z/\partial \eta } \\ {\partial x/\partial \zeta }&{\partial y/\partial \zeta }&{\partial z/\partial \zeta } \end{array}} \right] =\\ & \left[ {\begin{array}{*{20}{c}} {{l_1}/2}&0&0 \\ 0&{{l_2}/2}&0 \\ 0&0&{{l_3}/2} \end{array}} \right] \text{。} \end{split} $

(3)

对式（2）运用2节点高斯积分可得到刚度矩阵的数值表达式：

$\begin{split} \left[ K \right] =& \sum\limits_{i = 1}^2 {\sum\limits_{i = 1}^2 {\sum\limits_{i = 1}^2 {\left[ {B{{\left( {{\xi _i},{\eta _j},{\zeta _k}} \right)}^{\rm T}}\left[ C \right]B\left( {{\xi _i},{\eta _j},{\zeta _k}} \right)} \right]} } }\times \\ & \det \left( {\left[ {J\left( {{\xi _i},{\eta _j},{\zeta _k}} \right)} \right]} \right){w_{\xi ,i}}{w_{\eta ,j}}{w_{\zeta ,k}}\text{。} \end{split} $

(4)

式中： ${w_{\xi ,i}}$ ， ${w_{\eta ,j}}$ ， ${w_{\zeta ,k}}$ 为高斯积分权函数。

对于薄层单元，假设厚度 $d$ 远远小于长度 ${l_1}$ 和宽度 ${l_2}$ ，文献[15 – 16]表明当厚度 $d$ 趋近于零时单元应变 $\left( {{\varepsilon _x},{\varepsilon _y},{\varepsilon _{xy}}} \right)$ 和单元应力 $\left( {{\delta _x},{\delta _y},{\delta _{xy}}} \right)$ 可以忽略。此时可以把接触面法向 ${\left\{ e \right\}_n}$ 和接触面切向 ${\left\{ e \right\}_{Tx}}$ ， ${\left\{ e \right\}_{Ty}}$ 分别定义为局部坐标 $x$ ， $y$ 和 $z$ 的方向；同理，应力 ${\delta _z}$ ， ${\delta _{xz}}$ 和 ${\delta _{yz}}$ 分别对应 ${t_n}$ ， ${t_{Tx}}$ 和 ${t_{Ty}}$ ；应变 ${\varepsilon _z}$ ， $2{\varepsilon _{xz}}$ 和 $2{\varepsilon _{yz}}$ 分别对应 ${\varepsilon _n}$ ， ${\gamma _{Tx}}$ 和 ${\gamma _{Ty}}$ ，则本构方程可以转化为：

$\left\{ {\begin{array}{*{20}{c}} {{t_n}} \\ {{t_{Tx}}} \\ {{t_{Ty}}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} {{E_n}}&0&0 \\ 0&{{G_T}}&0 \\ 0&0&{{G_T}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\varepsilon _n}} \\ {{\gamma _{Tx}}} \\ {{\gamma _{Ty}}} \end{array}} \right\}\text{。}$

(5)

式中： ${E_n}$ 和 ${G_T}$ 分别为弹性模量，剪切模量。此时 ${E_n}$ 和 ${G_T}$ 为2个独立的参数，如果要求两者的耦合关系，可在本构关系式（5）中加入耦合项实现。

薄层单元建模的关键在于薄层厚度的确定，当薄层厚度 $d$ 趋近于零时，雅克比矩阵的行列式 $\det \left( {\left[ J \right]} \right)$ 趋近于零， $\left[ J \right]$ 无法求逆导导致无法计算致力和位移关系矩阵 $\left[ B \right]$ 。文献[14]认为薄层厚度 $d$ 可以根据薄层长度 ${l_1}$ 和 ${l_2}$ 来决定，并定义了比例系数为：

$R = \frac{{\max ({l_1},{l_2})}}{d}\text{。}$

(6)

研究表明 $R$ 取值为10～100时能获得较准确结果，但是如何精确选择薄层单元厚度 $d$ 以获得准确的仿真结果，国内外尚无定论。本文运用鲁棒设计方法，对薄层厚度 $d$ ，弹性模量 $E$ 和密度 $\rho $ 的不确定关系进行研究，确定不确定性因素对连接件动力学响应的影响。

2 Taguchi设计方法

鲁棒设计是在不减弱或消除不确定性因素影响的情况下，寻找合理的设计值，使响应对参数变化不敏感的设计方法。结构动力学鲁棒设计问题属于不确定结构动力学分析的反问题。Taguchi设计是一种重要的鲁棒设计方法，最早由日本学者田口谷一提出^[15]。这种设计方法把统计学的实验设计方法应用到了工业设计中，通过较少的实验设计来减少设计人员的工作量，同时设计出较高质量的产品。Taguchi方法将工程优化过程和产品设计过程分为3步：系统设计、参数设计和容差设计，具体设计过程见文献[16]。

Taguchi利用信噪比考虑结构性能的鲁棒性以及产品的综合经济性。根据产品的质量特性，信噪比分为3类：望目特性的信噪比，望小特性的信噪比和望大特性的信噪比。

望目特性的信噪比：

$\eta = 10\log \left( {\frac{{\overline y }}{{s_y^2}}} \right)\text{；}$

(7)

望小特性的信噪比：

$\eta = - 10\log \left( {\frac{1}{n}\sum\limits_{i = 1}^n {\frac{1}{{y_i^2}}} } \right)\text{；}$

(8)

望大特性的信噪比：

$\eta = - 10\log \left( {\frac{1}{n}\sum\limits_{i = 1}^n {y_i^2} } \right)\text{。}$

(9)

通过信噪比分析，可以初步得到一组参数组合，经过进一步优化分析，最终确定最优化参数组合。

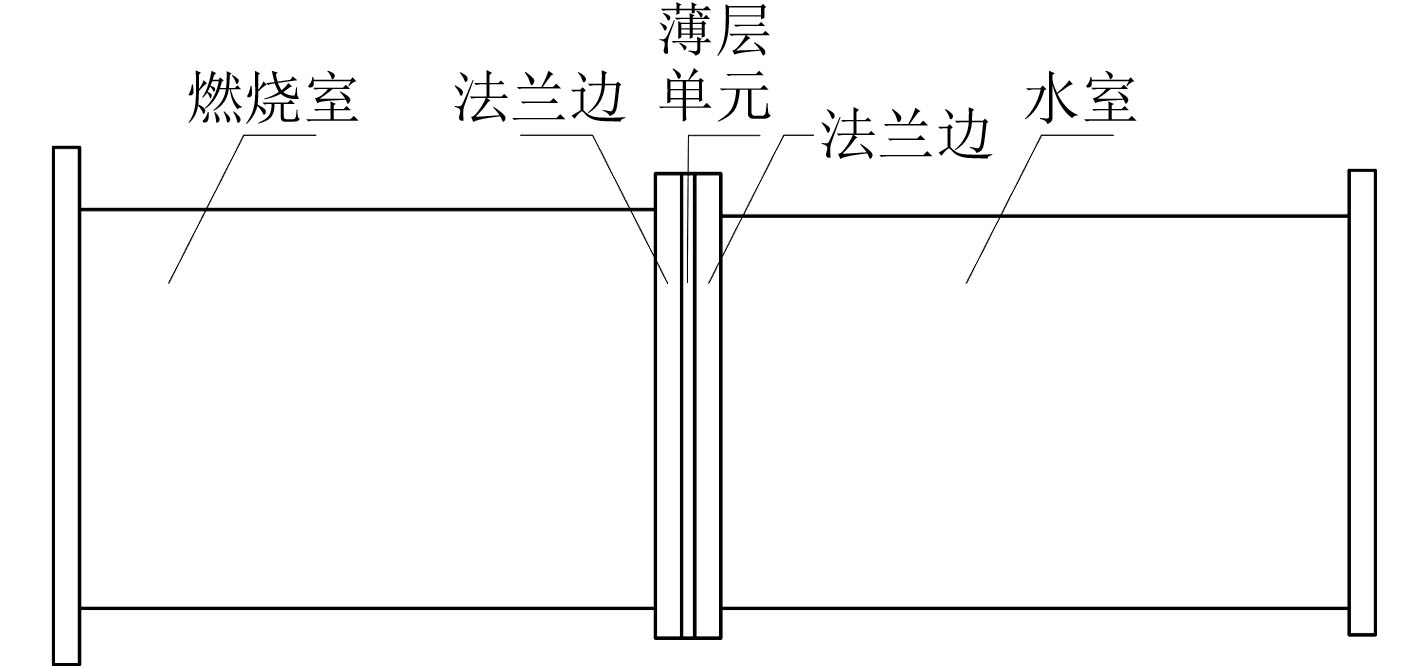
3 薄层单元的鲁棒设计 3.1 设计模型

某发射动力系统连接结构模型如图2所示，连接件由前后2个结构组成，2个结构的法兰边通过薄层单元进行连接。考虑到螺栓连接对连接结构局部刚度影响比较大，而局部刚度的变化对连接结构整体影响非常大。在连接结构的建模中，薄层的厚度对建模的准确性至关重要，对连接结构的整体响应影响巨大。而目前国内外对于如何准确确定薄层厚度尚无定论。本文对连接结构的整体动力学响应为研究目标，以薄层厚度 $d$ ，弹性模量 $E$ 和密度 $\rho $ 为设计变量，对发射动力系统连接结构进行鲁棒设计。

3.2 信噪比分析

通过正交设试验和方差分析的方法，对薄层单元的厚度 $d$ ，弹性模量 $E$ 和密度 $\rho $ 进行灵敏度分析。将3个设计参数参数分为3个水平，则将该问题转化为3个参数、3个水平的实验设计问题。其输入参数的水平设置如表1所示。选用L9正交表进行试验设计，并用望小特性的信噪比对连接结构振动响应的第3阶和第5阶频率进行分析，计算结果如表2所示。

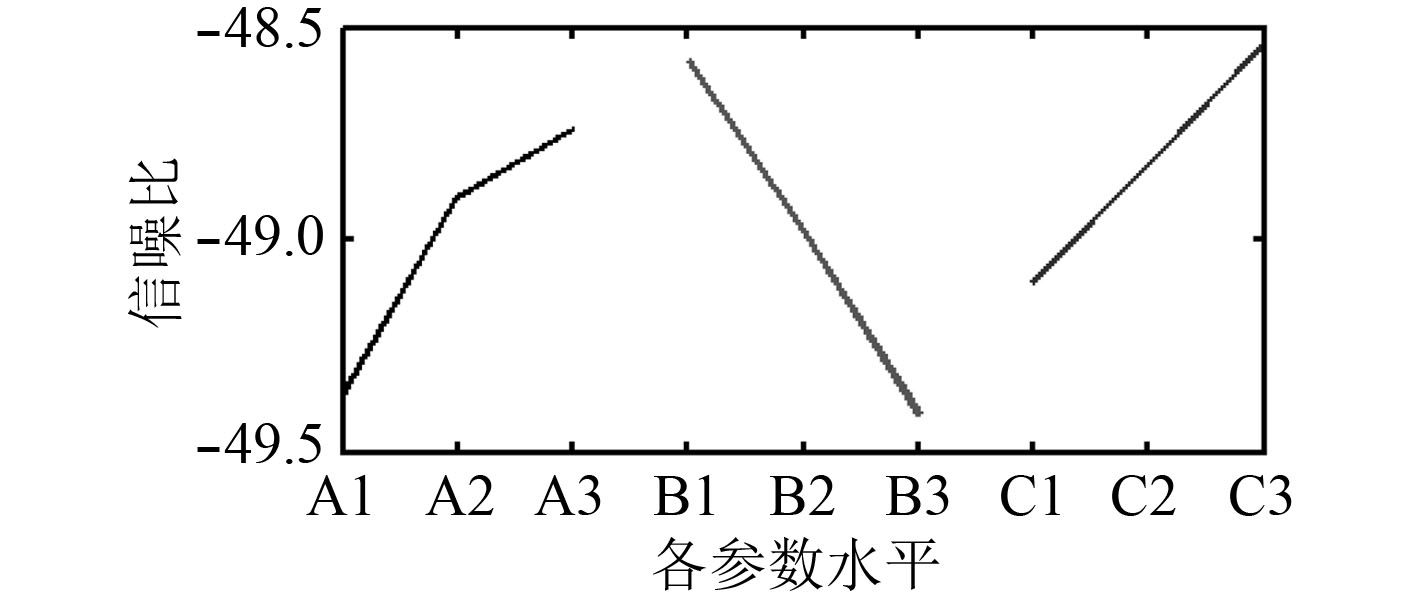
正交试验的信噪比分析结果如图3和图4所示，表示各参数值在各水平位置时对输出结果的影响大小，其中 $xi$ 表示输入参数 $x$ 在 $i$ 水平的信噪比均值，如图3中 $A1$ 表示厚度 $d$ 在1水平的信噪比均值。可知，3个输入参数对连接结构第3阶频率和第5阶频率影响均比较大，并且可以初步得到一组较优的组合 $A1B3C1$ 。

3.3 优化分析

对正交试验结果进行回归分析，通过回归分析运用最小二乘法可以得到表示固有频率关于厚度、弹性模量和密度的经验公式：

$F_3 = 320 - 2.55^*d + 8.06^*E - 0.0043^*\rho \text{，}$

(10)

$F_5 = 399 - 5.20^*d + 3.24^*E - 0.0036^*\rho\text{。} $

(11)

以 $F_3$ 和 $F_5$ 的设计值作为优化的目标，通过权重系数法把多目标优化问题转化为单目标优化问题，目标函数如下：

$D = {\left( {{d_1} \times {d_2} \times \ldots {d_n}} \right)^{\frac{1}{n}}} = {\left( {\prod\limits_{i = 1}^n {{d_i}} } \right)^{\frac{1}{n}}}\text{。}$

(12)

式中： $d$ 为测试的响应值， $n$ 为实验的次数。

4 结　语

1）薄层单元的厚度、弹性模量和密度等因素对连接结构的动力学响应影响较大。在弹性模量和密度保持不变时，随着厚度的增加，连接结构的模态频率逐渐减小；在厚度保持不变时，随着弹性模量的增加，连接结构的模态频率逐渐增大；在薄层厚度和弹性模量保持不变时，连接结构的模态频率逐渐减小；

2）通过回归分析，运用最小二乘法建立了连接结构动力学响应关于薄层厚度、弹性模量和密度的经验公式；

3）对薄层参数进行了优化分析，经过优化，建立了精确的连接模型。