船舶的发展史就是其动力系统的发展进化史,动力系统的好坏直接关系到整个舰船的安全稳定航行。正是因为船舶的动力系统对于船舶至关重要,对于动力系统的改造优化也就成为船舶设计中值得重点关注和研究的问题。对于动力系统的优化设计,既要坚持科学的原则,又要根据船舶具体的类型和航行特点有所针对性,从而实现对船舶动力系统配置的合理优化[1 – 3]。
动力系统优化的主要方向就是对于能源控制技术的改良优化。不同的能源动力系统采用的控制技术也完全不同,对于船舶的航行速度,航行稳定性和航行安全性的要求也与日俱增,需要通过更加先进的方法对于船舶的动力系统进行全面的优化升级改造。在这样的背景下,人工神经网络作为目前人工智能领域最为常见的智能算法脱颖而出[4]。
1 船舶动力系统的概念阐述主要动力系统和辅助配套系统是构成船舶前进驱动的两大部分,这两部分相互协调工作,都需要进行科学的优化设计[5]。
1.1 主要装置主动力系统主要包括发动机,其中又涵盖了原始动力系统和辅助动力系统,原始动力系统又包括燃气轮机,汽油机,传动系统主要包括主推器,还有推进器,螺旋桨,泵式推进器,这部分结构主要功能是实现船舶的动力能转换。除此以外,配套装置还有离合器,减速器,管系设备以及轴系设备等。这些设备是为了保障传动装置能够更稳定的运行,同时能够保障船舶发挥良好的转向、制动和减震的作用[6 – 8]。
1.2 辅助装置除了原动系统,配套系统也是发动机必不可少的组成部分,发电机,锅炉和自动化操控装置构成了发动机配套系统,这些装置的主要目的是为了实现船舶的良好可操控性[9 – 10]。
|
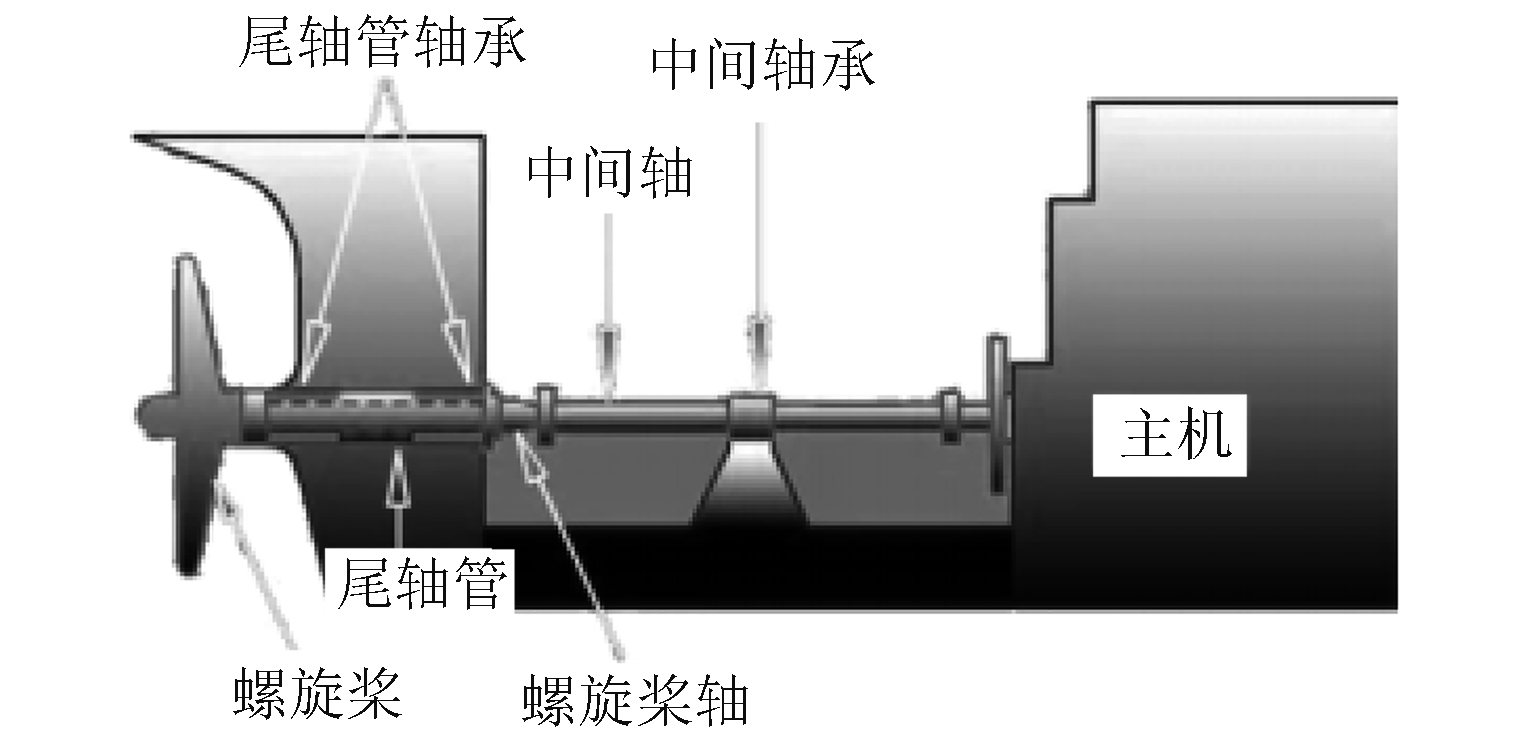
图 1 船舶动力系统结构图 Fig. 1 Ship power system structure |
众多精密复杂的机电设备组成的电气化系统构成了整个动力系统,这就会出现一个严重的设备间干扰问题。特别是大型电器设备运行会形成磁场,对于周围电器设备运行,特别是精密的设备运行产生影响。这就需要对于整个主动力系统电气系统进行设备结构的优化改造。为此需要配套不同的子系统,并且诸多子系统都要按照同样的原则进行设计,才能避免系统间内扰动,具体的国际标准系统设计方案如下:
1)首先对于动力系统目标进行优化,明确船舶动力系统所需要完成的目标需求,进行针对优化设计,主要从动力和经济两方面考虑,同时还需要兼顾安全和稳定性能。
2)进一步明确船舶所需要承载负荷需求,同时考虑船舶主要日常用途,航行线路特点以及特定性需求等。
3)根据船舶归属国家相关船舶设计规定,对于船舶的性能进行进一步的对比设计,制定一系列约束条件,从而保障船舶设计的合理性。
4)根据之前确定好的最佳方案参数,在将技术可行性,建造成本,建造时间和性能指标等附加条件纳入考虑范围,最终确定船舶的动力系统优化设计方案[15]。
2 神经网络技术在系统优化配置中的应用 2.1 神经网络优化原理以人工智能技术为代表的第三次信息技术革命正在改变过去传统领域。特别是具有代表性的人工神经网络技术,其具有优良的非线性模型拟合能力。在各个方面的实际应用中已经取得了良好的效果。
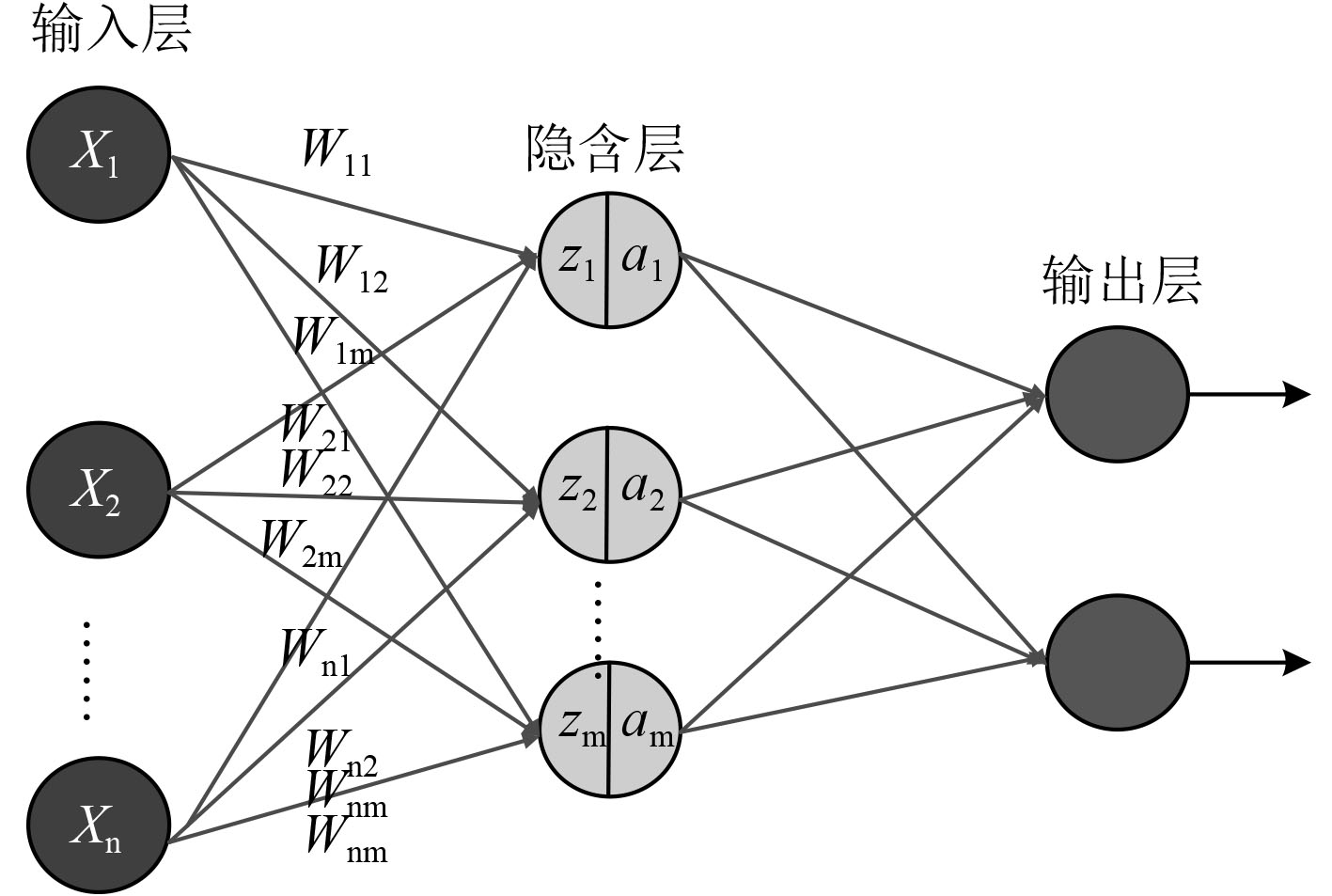
人工神经网络没有一个具体固定的结构标准,往往根据不同的物理问题通过数据训练得到成熟的模型。但是一般的神经网络主要分为3个层次,按照数据输入顺序分别是输入层,隐含层和输出层构成的,每个层之中含有若干个神经元,一般结构如图2所示。
|
图 2 一般神经网络结构 Fig. 2 Gerenal structure of neunal network |
图中W为输入层和中间层的连接权值,通过对于每个神经元的输入进行赋权,调整不同输入信息在整个模型的影响程度,得到单个神经元输入z和将z通过激活函数进行非线性转化为a,使用激活函数的原因是因为线性模型(无法处理线性不可分的情况)的表达能力不够,所以通常需要利用Sigmoid函数来加入非线性因素得到神经元的输出值。
根据本文研究的船舶具体情况,采用前馈神经网络ELM算法进行优化设计,该算法结构简单,只有一层隐含层,同时ELM算法可以支持向量机操作,模型内部神经元参数不需要不断调整,可以根据随机函数设定具体目标而自动生成,保证该模型能够具有较高的计算效率,比较适合船舶动力系统这样复杂结构的优化设计[11 – 13]。ELM算法具有以下2个特点:
1)所有的隐含层节点参数相互独立,与训练数据集无关;
2)ELM模型的优点是无需任何先验信息。假设ELM单隐层前馈神经网络具有L个隐节点输出,其表达式为
式中:ai和bi分别为隐含节点的学习训练参数;θi∈Rm为第i个隐节点连接到输出节点时的权重向量值;F(x, ai, bi)为第i个隐节点在输入为x时的输出函数。
本文对于动力系统优化算法的激活函数为[14]:
| $ F\left( {x,{a_i},{b_i}} \right):R \to R{\text{。}} $ |
在对优化算法进行数据驱动训练时,第一种数据样本(xj,tj)如果一共存在L个隐含层单元,并且ELM算法网络结构误差较小。那么模型中的θi,ai与bi满足下式:
| $ \sum\limits_i^L {{\theta _i}} F\left( {x,{a_i},{b_i}} \right) = {t_j}{\text{。}} $ |
经过简化处理,可以得到
式中:F为单隐层前馈神经网络中的输出向量矩阵。
F矩阵的第i列分别与x1,x2,…,xl的第i个隐含节点的输出向量相对应;F矩阵的第j行分别与输入xj的隐含性输出向量相对应。
3 仿真设计针对本文研究的船舶动力系统优化问题进行仿真建模,通过建模得到动力系统的三维仿真图[15],如图3所示。

|
图 3 船舶动力系统仿真界面 Fig. 3 Simulation face of ship power system |
在系统优化仿真前先设定仿真对象的数学模型,输入满足如下关系:
| $ yout(k) = \frac{{a(k)yout(k - 1)}}{{1 + you{t^2}(k - 1)}} + u(k - 1){\text{。}} $ |
图4为神经网络训练后的输出曲线,图5为优化后的结果对比曲线,可以看出,通过ELM神经网络优化以后,船舶动力系统输出性能有了较为明显的改善。

|
图 5 控制作用下的输出振幅曲线对比图 Fig. 5 Output curve comperation under control |
本文首先简要介绍船舶的动力系统组成,提出ELM神经网络算法对于船舶动力系统优化设计,并且通过三维仿真进行实验验证。结果表明,船舶动力系统输出性能有了较为明显的改善,对于提升船舶性能,提高船舶航行安全稳定性具有一定价值。
| [1] |
洪声振. 大连海事大学航海类专业教学计划资料汇编(1909-2009) 第二部分 新中国成立后的60年(1949-2009年)[J]. 航海教育研究, 2014, 4. DOI:10.3969/j.issn.1006-8724.2014.03.038 |
| [2] |
张磊. LNG船舶推进装置发展介绍[J]. 珠江水运, 2014, 18. DOI:10.3969/j.issn.1672-8912.2014.01.029 |
| [3] |
彭岩, 朱玉崧. LNG船舶推进装置对比分析[J]. 世界海运, 2008, 2. DOI:10.3969/j.issn.1006-7728.2008.01.019 |
| [4] |
陈永道. 船舶动力系统现状及发展趋势[J]. 机械制造与自动化, 2013, 2. DOI:10.3969/j.issn.1671-5276.2013.01.055 |
| [5] |
郭爱红, 彭中立. 船舶动力系统运用工程的基础理论探析[J]. 科技风, 2012, 18. DOI:10.3969/j.issn.1671-7341.2012.01.052 |
| [6] |
严新平, 袁成清. 船舶动力系统运用工程的基础理论体系[J]. 中国造船, 2011, 2. DOI:10.3969/j.issn.1000-4882.2011.01.027 |
| [7] |
王扬. 船舶动力系统现状及发展趋势[J]. 中国设备工程, 2017, 24. DOI:10.3969/j.issn.1671-0711.2017.01.080 |
| [8] |
徐立华. 探究6S管理在船舶动力系统中的应用[J]. 内燃机与配件, 2018, 4. DOI:10.3969/j.issn.1674-957X.2018.01.079 |
| [9] |
王扬. 船舶动力系统控制器的研究与设计[J]. 国防制造技术, 2017, 4. DOI:10.3969/j.issn.1674-5574.2017.01.018 |
| [10] |
振宇, 陈艳明, 曹鹏飞, 等. 船舶动力系统" 一元”培训模式的探讨与实践[J]. 科技风, 2018, 29. |
| [11] |
宋大雷, 孟祥冬, 齐俊桐, 等. 3自由度旋翼飞行机械臂系统动力学建模与预测控制方法[J]. 机器人, 2015, 2. |
| [12] |
肖国宝, 严宣辉. 一种基于改进Theta~*的机器人路径规划算法[J]. 智能系统学报, 2013(1). |
| [13] |
陈洋, 赵新刚, 韩建达. 移动机器人3维路径规划方法综述[J]. 机器人, 2010(4). |
| [14] |
柯良. 日本船舶推进装置新技术介绍[J]. 造船技术, 1990, 7. |
| [15] |
曾庆东. 国际排放法对船舶动力系统技术提升的要求与对策[J]. 武汉理工大学学报(交通科学与工程版), 2015(2). |
 2019, Vol. 41
2019, Vol. 41
