目前,中高压、大功率船舶电力推进系统变频器主要采用控制技术相对成熟的全桥逆变器或者传统的多电平换流器,对单个开关器件的耐压能力要求较高,输出波形谐波含量大,影响控制系统的整体性能[1]。MMC相比于传统的多电平换流器,模块化配置易于扩展、谐波性能优异;子模块冗余设计能够提高换流器的故障处理能力,是目前中高压交流调速系统的研究热点[2~3]。
文献[4]建立MMC上下桥臂子模块电容电压可变控制原理数学模型,提出一种根据电机运行速度灵活调节MMC电容电压的新型控制策略,增加系统控制灵活性,降低系统损耗。文献[5]通过向MMC输出电压中注入高频共模电压,同时控制桥臂环流,有效解决MMC驱动船舶推进电机过程中出现的子模块电容电压低频脉动问题,但其推进电机负载转矩直接给定,没有构建出完整的船舶电力推进系统。本文基于不对称全桥型MMC,设计相应的永磁同步电机调速系统。在Matlab/Simulink环境下,对基于不对称全桥型MMC的船舶电力推进系统进行仿真研究,验证系统的静动态性能。
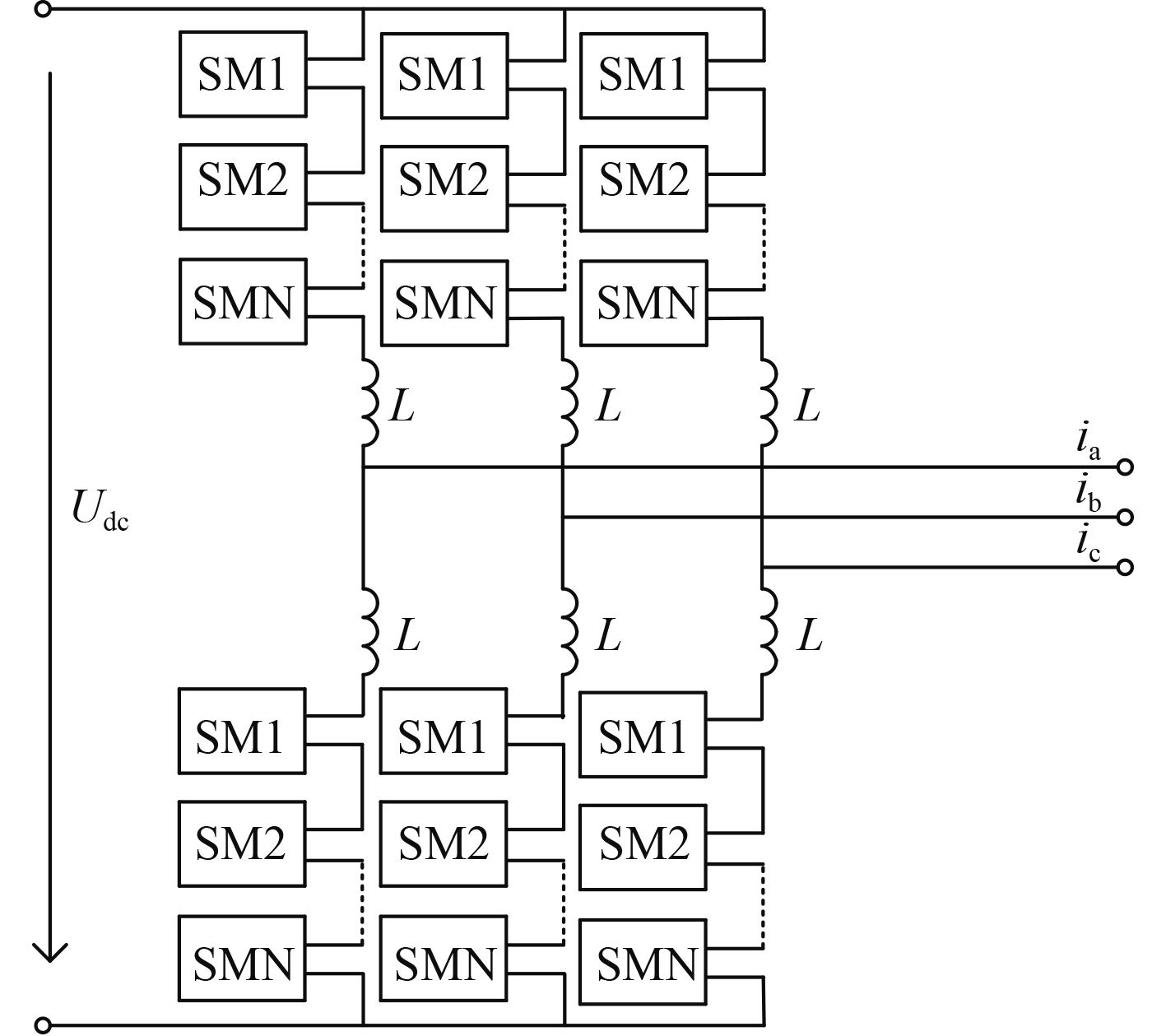
1 不对称全桥型MMC拓扑结构设计MMC基本拓扑结构如图1所示。三相六桥臂拓扑,每个桥臂由N个子模块和1个桥臂电抗器级联而成。不对称全桥型子模块电路结构如图2所示。与全桥型子模块相比,其左下桥臂直接由二极管D3代替。正常工作情况下,T1一直处于导通状态,T2和T4开关状态相反。闭锁模式下,不对称全桥型MMC具备直流故障自清除能力。表1所示为不对称全桥型子模块工作模式。
|
图 1 MMC拓扑结构 Fig. 1 Topology of MMC |

|
图 2 不对称全桥型子模块电路结构 Fig. 2 Topology of asymmetric full-bridge sub module |
|
|
表 1 不对称全桥型子模块工作模式 Tab.1 Operating mode of asymmetric full-bridge SM |
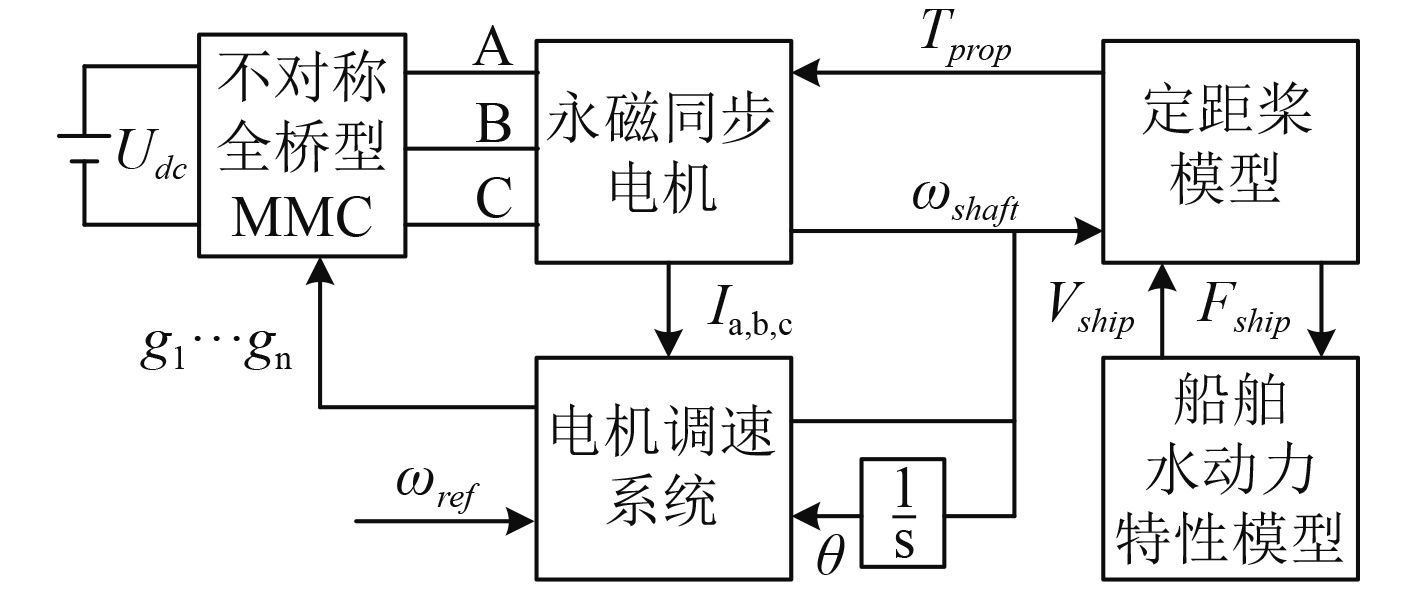
本文选用功率密度高、运行噪声小的永磁同步电机作为推进电机,螺旋桨采用瓦格宁根B系列定距桨,电机调速系统采用电流滞环比较PWM控制,推进系统控制框图如图3所示。MMC直流侧接直流电压源Udc,交流侧为永磁同步电机三相定子绕组供电,电机转轴带动螺旋桨以转速ωshaft旋转,同时螺旋桨为电机提供负载转矩Tprop。电机调速系统通过转速控制信号ωref和推进电机转速反馈信号ωshaft的误差值经PI调节生成三相电流参考值,与采集的三相定子电流比较,生成MMC控制信号。
|
图 3 基于不对称全桥型MMC的船舶永磁电机推进系统框图 Fig. 3 Scheme of marine permanent magnet motor propulsion system |
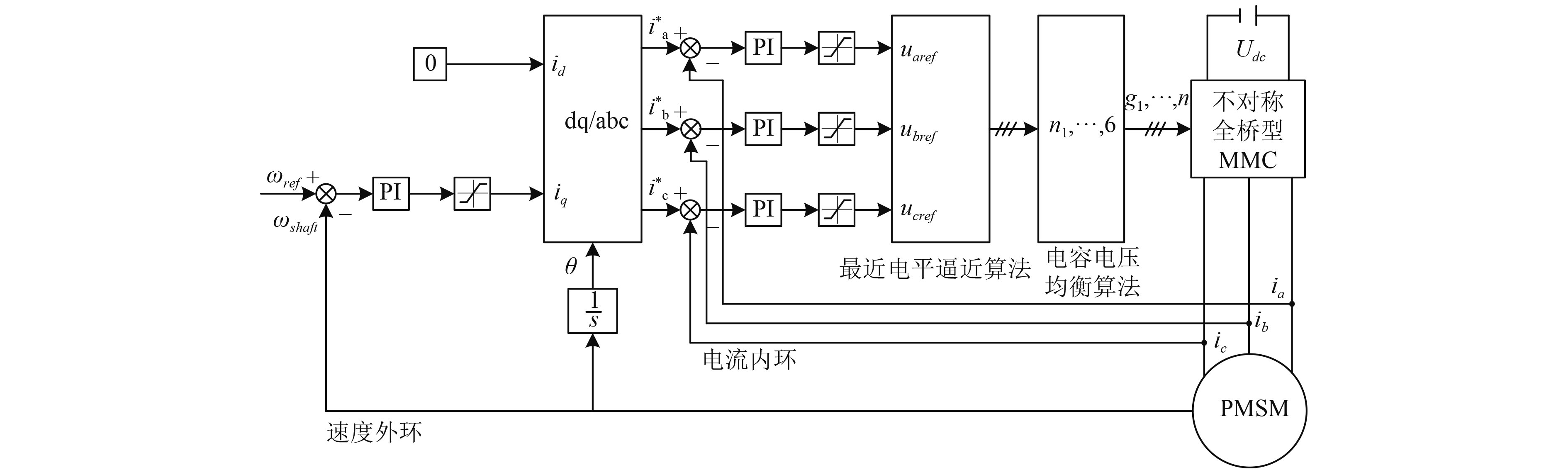
永磁同步电机转子无励磁绕组,矢量控制环节无励磁控制,控制系统相对简单。结合MMC驱动原理,本文设计的永磁同步电机不对称全桥型MMC调速系统控制器如图4所示,由速度外环控制和电流内环控制组成。速度外环通过转速调节器对速度误差进行调节,得到无功电流分量的参考值,有功电流分量参考值id设定为0,经派克反变换得到三相电流参考值,变换角θ为同步电机转角。由于本文采用不对称全桥型MMC作为电机驱动器,需要向调制策略环节输入三相电压参考值进行最近电平逼近调制。因此,本文将原电流滞环比较环节的滞环比较器更改为PI控制器,以此对电流误差进行调节输出MMC交流侧三相电压参考值uiref(i=a,b,c)。通过最近电平逼近算法,输出三相六桥臂的子模块导通个数ni(i=1,2,
|
图 4 永磁同步电机MMC调速系统 Fig. 4 Permanent magnet synchronous motor speed regulating system based on MMC |
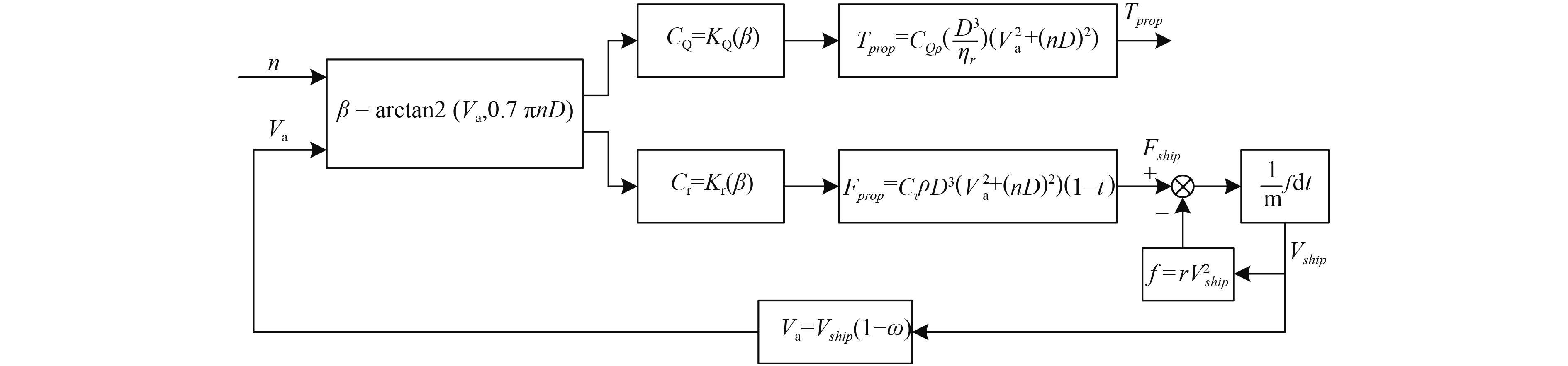
参考文献[6–8]对推进电机螺旋桨负载特性研究,本文推进系统中的船桨数学模型如图5所示。数学模型的输入为螺旋桨转速n(单位:rpm),输出为Tprop。β表示螺旋桨进程角,范围为0~2π,通过四象限反正切函数求得,其中Va为螺旋桨进速、D为螺旋桨直径。CT,CQ分别为推力和转矩系数,通过式(1)所示的切比雪夫多项式得出,系数AT,BT,AQ和BQ参考文献[6]中B3-65型号螺旋桨参数。ρ为海水密度,t为推力减额系数,m为船舶质量,f为船舶航行阻力,r为船舶阻力系数,Vship为船速。由于本文主要验证不对称全桥型MMC调速性能,以电机达到指定转速为系统完成标志,因此,船速较小,伴流系数ω简化取0。
|
图 5 船桨数学模型 Fig. 5 Mathematical model of ship-propeller |
| $ \begin{align} & {C_T} = \frac{1}{{100}}\sum\limits_{k = 0}^{30} {\{ {A_T}(k)\cos (k\beta ) + {B_T}(k)\sin (k\beta )\} }{\text{,}} \\ & {C_Q} = \frac{{ - 1}}{{1\;000}}\sum\limits_{k = 0}^{30} {\{ {A_Q}(k)\cos (k\beta ) + {B_Q}(k)\sin (k\beta )\} } {\text{。}} \end{align} $ | (1) |
本文以某万吨级单桨电力推进船舶为研究对象, 在Matlab/Simulink中对推进系统进行仿真,分析船舶在不同工况下电力推进系统的调速性能以及螺旋桨负载特性,具体参数见表2。
|
|
表 2 仿真参数 Tab.2 Simulation parameters |
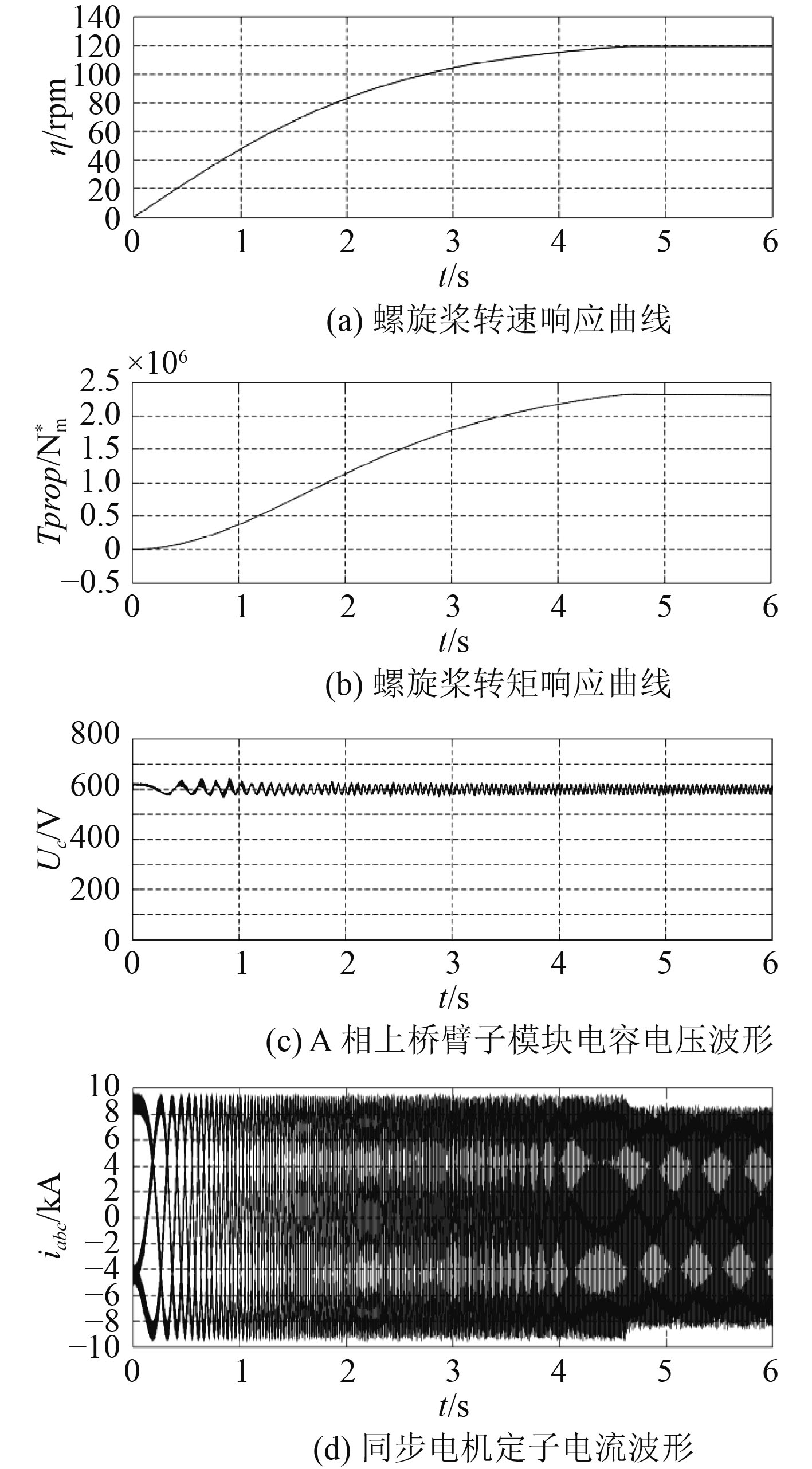
船舶正车启动时,螺旋桨工作在第1象限(X轴转速、Y轴船速,下同),转速和船速同时为正。启动过程可分为直接正车启动和分级正车启动使船舶达到稳定航速,本文重点验证不对称全桥型MMC在电力推进系统中的运行可靠性,为节约仿真时间,以螺旋桨达到额定转速为启动完成标志。图6和图7分别给出船舶直接正车启动和分级正车启动过程的螺旋桨负载动态响应曲线图、不对称全桥型MMC子模块电容电压波形以及推进电机定子电流波形。
|
图 6 直接启动仿真结果 Fig. 6 Simulation results of direct start |
|
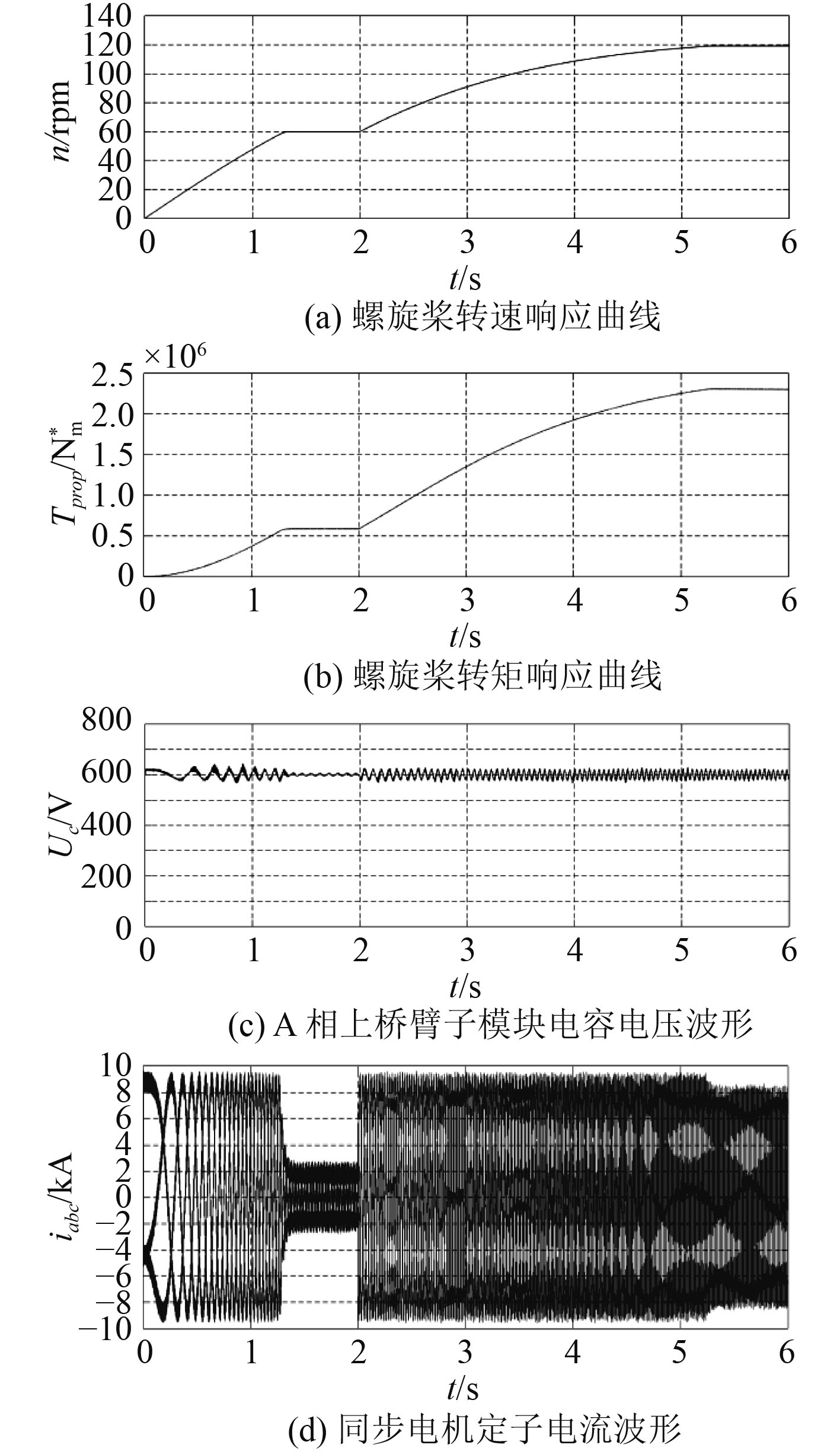
图 7 分级启动仿真结果 Fig. 7 Simulation results of grading start |
图6船舶直接正车启动时,螺旋桨5 s内可以达到额定转速,转速响应曲线无超调,静差率保持在1%以下。电机启动时,定子电流较大,电流频率随着启动过程逐渐增大,稳定运行时,定子电流达到额定值。推进电机启动初期子模块电容电压波动较大,当达到额定转速时,子模块电容电压波动率维持在±5%左右。图7船舶分级启动过程,螺旋桨在1.5 s内达到一半的额定转速,2 s后螺旋桨开始加速,5.5 s前达到额定转速。同样分级启动过程中转速响应无超调,静差率保持在1%以下。定子电流波形同直接启动过程类似,当电机保持1/2转速稳态运行时,定子电流幅值较小。当推进电机保持低速运行时,MMC工作稳定,子模块电容电压波动率保持在±2%以内,电压均衡效果较好。
3.2 船舶停车船舶正航停车过程中螺旋桨工作在第1象限,同样以螺旋桨转速降到0为标志分为直接停车和分级停车模式。图8和图9分别给出了额定转速下实行直接停车和分级停车过程中螺旋桨负载动态响应曲线图、不对称全桥型MMC子模块电容电压波形以及推进电机定子电流波形。

|
图 8 直接停车仿真结果 Fig. 8 Simulation results of direct stop |

|
图 9 分级停车仿真结果 Fig. 9 Simulation results of grading stop |
图8直接停车过程,螺旋桨在2 s内由额定转速降为0,定子电流频率逐渐变小。子模块电容电压随着转速下降,波动逐渐变大,当转速接近0时,电容电压均衡效果较差。转速降为0后,不对称全桥型MMC停止工作。图9分级停车过程,螺旋桨在1 s内降低至1/2额定转速,8 s后转速开始下降为0。同直接停车类似,第一级停车过程中,子模块电容电压随着转速下降,波动逐渐变大,但当螺旋桨保持在一半额定转速时,子模块电容电压波动率较小,保持在±2%以内,电容电压均衡效果较好。进入停车第二阶段时,子模块电容电压开始波动较大,直至不对称全桥型MMC停止工作。比较2种停车过程,直接停车较分级停车缺少转速保持环节,当转速接近0时,子模块电容电压不均衡现象较严重,容易引起MMC相间环流,增加MMC运行损耗。
3.3 船舶倒航船舶倒航是船舶航行的重要环节之一,螺旋桨依次工作在第1、2、3象限,推进电机需要克服螺旋桨阻力矩进行反转。图10和图11分别给出紧急倒车、分级倒车过程螺旋桨负载动态响应曲线、子模块电容电压波形以及定子电流波形。

|
图 10 紧急倒车仿真结果 Fig. 10 Simulation results of emergency reverse |

|
图 11 分级倒车仿真结果 Fig. 11 Simulation results of grading reverse |
图10船舶紧急倒车过程中,螺旋桨在3.5 s内完成由额定转速下降至0并反转至1/2额定转速的过程,螺旋桨转矩跟随转速下降,转矩过零点时较平稳。倒车过程中,定子电流频率出现由大变小,再由小变大的过程,频率最小点对应转速过零点。同样,子模块电容电压充放电频率跟随定子电流频率,6 s开始子模块电容电压波动变大,电压均衡效果变差,对应转速过零点时刻,子模块电容电压出现较大的不均衡程度。其后螺旋桨反转加速过程,子模块电容电压均衡效果逐渐改善,稳态运行时子模块电容电压波动率维持在±2%以内。图11分级倒车过程,螺旋桨在1 s内下降至1/2额定转速,8 s后减速至0并反转加速至1/2额定转速。螺旋桨转矩响应曲线同直接倒车类似,跟随转速平稳下降。分级倒车第1阶段转速下降过程,子模块电容电压波动类似于紧急倒车,转速稳定后,子模块电容平稳充放电,电容电压保持均衡。8 s后随着转速继续下降,子模块电容电压波动率逐渐变大。相比于紧急倒车,分级倒车过程中转速过零点时,子模块电容电压均衡效果较好,未出现较大的波动现象。随着螺旋桨反转加速,子模块电容逐渐稳定充放电。
4 结 语本文将不对称全桥型MMC应用于船舶电力推进系统,在Matlab/Simulink环境下,对不同工况下的船舶电力推进系统进行仿真研究,分析不对称全桥型MMC电机调速性能以及螺旋桨转矩特性。仿真结果表明,采用不对称全桥型MMC驱动的推进电机具有良好的控制精度以及动态响应能力,不对称全桥型MMC在电机低频运行时具有较小的电容电压纹波。采用分级运行模式对推进系统进行启动、停车、倒车过程,有利于减缓MMC电容电压波动,减小MMC相间环流,降低MMC运行损耗。
为了简化控制系统复杂程度,本文的MMC控制器未加入环流抑制环节,下一步研究可以将环流抑制环节加入。此外,可以将电力推进系统接入中压直流电网,结合能量管理系统,分析推进电机变工况运行对于船舶中压直流电网稳定性影响。
| [1] |
张洋, 杨平西, 刘林生, 等. 船舶电力推进同步发电机-推进变流器系统谐波特性仿真[J]. 舰船科学技术, 2010, 32(8): 196-199. ZHANG Yang, YANG Ping-xi, LIU Lin-sheng, et al. Harmonic characteristic simulation of the synchronous generator-propulsion converter system in electric propulsion[J]. Ship Science and Technology, 2010, 32(8): 196-199. DOI:10.3404/j.issn.1672-7649.2010.08.041 |
| [2] |
WANG Z, LIAO K, ZHANG K, et al. An improved ripple suppression method based on flying-capacitor modular multilevel converter for high performance MV drivers[C]//2017 IEEE Applied Power Electronics Conference and Exposition (APEC). Tampa, FL. 2017: 2571–2575.
|
| [3] |
LI B, ZHOU S, XU D, et al. A hybrid modular multilevel converter for medium-voltage variable-speed motor drives[J]. IEEE Transactions on Power Electronics, 2017, 32(6): 4619-4630. DOI:10.1109/TPEL.2016.2598286 |
| [4] |
台丙勇, 高聪哲, 刘向东, 等. 基于MMC的永磁同步电机驱动系统新型电容电压控制策略[J]. 北京理工大学学报, 2017, 37(08): 836-841. TAI Bing-yong, GAO Cong-zhe, LIU Xiang-dong, et al. A novel capacitor voltage control strategy of MMC applied for permanent magnet synchronous motor drive[J]. Transactions of Beijing Institute of Technology, 2017, 37(08): 836-841. |
| [5] |
SPICHARTZ M, STAUDT V, STEIMEL A. Modular multilevel converter for propulsion system of electric ships[C]//2013 IEEE Electric Ship Technologies Symposium (ESTS), Arlington, VA, 2013: 237–242.
|
| [6] |
RODDY R F, HESS D E, FALLER W. Neural network predictions of the 4-quadrant wageningen propeller series[R]. 2006: B-8.
|
| [7] |
PIVANO L, JOHANSEN T A, SMOGELI Ø N. A four-quadrant thrust estimation scheme for marine propellers: theory and experiments[J]. IEEE Transactions on Control Systems Technology, 2009, 17(1): 215-226. DOI:10.1109/TCST.2008.922602 |
| [8] |
许爱德, 孙建波. 基于回归算法的船舶电力推进系统中螺旋桨负载特性仿真[J]. 大连海事大学学报, 2014, 40(3): 64-68. XU Ai-de, SU Jian-bo. Marine propeller load characteristics simulation based on regression algorithm[J]. Journal of Dalian Maritime University, 2014, 40(3): 64-68. DOI:10.3969/j.issn.1006-7736.2014.03.014 |
 2019, Vol. 41
2019, Vol. 41
