渤海海域现役的3艘16万吨级单点系泊FPSO“渤海世纪”号、“海洋石油112”号、“海洋石油113”号,作业海域水深仅20 m左右,大型FPSO在我国浅水海域的广泛应用使浅水浮体水动力学引起了学术界和工程界的广泛关注。通过实际观测以及物模试验发现,FPSO在浅水中的运动响应较为剧烈[1],垂直面内的运动幅度较大,发生触底或者与软刚臂发生碰撞的概率较大,这些都将导致严重后果,浅水环境下FPSO的运动响应特性及其与软刚臂系泊结构的相互耦合需要深入研究。
本文采用AQWA软件,基于三维势流理论,计算了FPSO在不同水深下的附加质量、阻尼系数、运动幅度以及波浪力等水动力参数;利用多体动力学方法,将FPSO和软刚臂视为2个刚体,进行整个系统的运动响应和载荷分析。这种分析方法,一方面可以准确模拟软刚臂的具体结构形式,另一方面能充分考虑FPSO与软刚臂之间的耦合效果,从而更准确的预报船体及系泊结构的运动响应[2]。基于多体动力学方法求解的船体运动响应与试验值较为接近,此前已有学者进行过验证。
1 计算理论 1.1 线性波理论势流理论基于理想流体假设,流域的边界条件满足Laplace方程[3],将运动学和动力学边界条件线性化处理之后可以得到:
| $ \displaystyle\frac{{{\partial ^2}\emptyset }}{{\partial {t^2}}} + g\displaystyle\frac{{\partial \emptyset }}{{\partial z}} = 0{\text{,}} $ | (1) |
当速度势以圆频率ω作简谐振荡时,在z=0处得到:
| $ - {\omega ^2}\emptyset + g\displaystyle\frac{{\partial \emptyset }}{{\partial z}} = 0{\text{。}} $ | (2) |
对于有限水深一阶波浪速度势函数为:
| $ {\emptyset ^{\left( 1 \right)}} = Re\left[ {\displaystyle\frac{{ - igA}}{\omega }\displaystyle\frac{{\cos hk\left( {z + d} \right)}}{{\cos hkd}}{e^{i(kx\cos\theta + ky \sin\theta - \omega t}}} \right]{\text{,}} $ | (3) |
自由液面处的波形为:
| $ {\eta ^{\left( 1 \right)}} = A{\rm cos}\left( {kx{\rm cos}\theta + ky{\rm sin}\theta - \omega t} \right){\text{。}} $ | (4) |
水动力参数、波激力和力矩均可以通过三维势流理论求解得到。一般将流体速度势分解为入射势、绕射势和辐射势。
基于单色波与浮体相互作用的第一阶边界值问题,整体势函数求解问题表述为:
| $ \begin{split} & {\emptyset ^{\left( 1 \right)}} = \left( {\emptyset _I^{\left( 1 \right)} + \emptyset _D^{\left( 1 \right)} + \emptyset _R^{\left( 1 \right)}} \right) = \\ & Re\left\{ {\left[ {\varphi _I^{\left( 1 \right)}\left( {x,y,z} \right) + \varphi _D^{\left( 1 \right)}\left( {x,y,z} \right) + \varphi _R^{\left( 1 \right)}\left( {x,y,z} \right)} \right]{e^{ - i\omega t}}} \right\}{\text{。}} \end{split}$ | (5) |
分别求解3个速度势,即可得到流域内整体的速度势。通过对物面波压的直接积分可以得到力和力矩向量的6个分量:
| $ \begin{split} & F_{j}^{\left( 1 \right)}\left( t \right)=-\rho g\mathop{\iint{z{{n}_{j}}ds}}^{}-\rho Re\left\{ \underset{j=1}{\overset{n}{\mathop \sum }}\,i\omega {{\zeta }_{j}}{{e}^{-i\omega t}}\mathop{\iint }^{}{{\varphi }_{j}}{{n}_{j}}{\rm d}s \right\}-\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \\ & \rho Re\left\{ i\omega A{{e}^{-i\omega t}}\mathop{\iint{\left( {{\varphi }_{I}}+{{\varphi }_{D}} \right)}}^{}{{n}_{j}}{\rm d}s \right\}{\text{,}}j=1-6 {\text{。}} \end{split} $ | (6) |
综合考虑风、浪、流以及单点系泊系统回复力的联合作用,FPSO的时域运动方程[4]为:
| $ \begin{array}{l} \displaystyle\mathop \sum \limits_{i = 1}^6 \left[ {{ M} + { A}\left( \infty \right)} \right]\ddot x\left( t \right) + \int_0^t {{ r}\left( {t - \tau } \right)} \dot x\left( \tau \right){\rm d}\tau + { D}\dot x\left( t \right) +\\ { K}x\left( t \right) ={F^{\left( {1,2} \right)}}\left( t \right) + {F_W}\left( t \right) + {F_C}\left( t \right) + {F_{SPM}}\left( t \right){\text{。}} \end{array} $ | (7) |
式中:r(t)为辐射阻尼的脉冲响应函数矩阵;D为FPSO慢漂阻尼矩阵;K为FPSO静水回复力刚度矩阵;
在不规则波浪下,作用于结构物上的瞬时波浪力可以写为:
| $ {F^{\left( {1,2} \right)}}\left( t \right) = {F^{\left( 1 \right)}}\left( t \right) + {F^{\left( 2 \right)}}\left( t \right){\text{,}} $ | (8) |
| $ {F^{\left( 1 \right)}}\left( t \right) = \mathop \int \nolimits_0^t h\left( {t - \tau } \right)\eta \left( \tau \right){\rm d}\tau {\text{。}} $ | (9) |
| $ \begin{split} &{F^{\left( 2 \right)}}\left( t \right) = \displaystyle\mathop \sum \limits_{j = 1}^{NSPL} \displaystyle\mathop \sum \limits_{k = 1}^{NSPL} {A_j}{A_k}\biggr\{ P_{jk}^ - \cos \left[ { - \left( {{\omega _j} - {\omega _k}} \right)t -}\right. \\ &\left.{\left( {{\varepsilon _j} - {\varepsilon _k}} \right)} \right] +Q_{jk}^ - {\rm{sin}}\left[ { - \left( {{\omega _j} - {\omega _k}} \right)t - \left( {{\varepsilon _j} - {\varepsilon _k}} \right)} \right]\biggr\} {\text{,}} \end{split} $ | (10) |
式中:η(τ)为海浪随机波面升高的时域历程;h(t)为脉冲响应函数,由1阶波浪力传递函数通过傅里叶变换得到,即
| $ \begin{array}{l} {f_w}\left( {\rm{\omega }} \right) = \mathop \int \nolimits_{ - \infty }^{ + \infty } h\left( t \right){e^{ - i\omega t}}{\rm{d}}t{\text{,}}\\ \;\;\;h\left( t \right) = \displaystyle \frac{1}{{2{\text{π}} }}\mathop \int \nolimits_{ - \infty }^{ + \infty } {f_w}\left( \omega \right){e^{ - i\omega t}}{\rm d}t{\text{。}} \end{array} $ | (11) |
若已知整个频率范围内的fw(ω),即可按上式求得h(t),然后按波浪时历η(τ),根据(11)式求得1阶波浪力。
2 设计输入及耦合模型建立 2.1 设计输入以“渤海明珠”号FPSO为例,在某装载情况下,计算模型主要参数如表1所示。百年一遇极端环境条件参数见表2。
|
|
表 1 FPSO主要参数 Tab.1 The main dimensions of FPSO |
|
|
表 2 环境条件 Tab.2 The marine environment conditions |
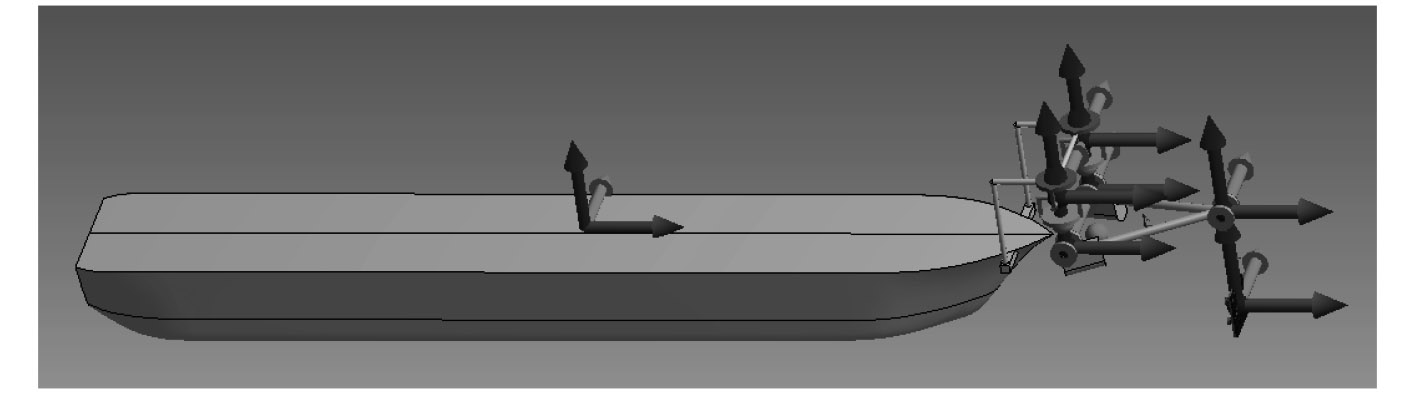
采用三维建模软件建立船体三维模型,导入Ansys-Workbench,建立系泊支架、系泊腿、系泊刚臂及导管架(用立柱表示)的全耦合模型,坐标原点取在船尾中纵剖线与水面交点,从船尾指向船首为X轴,船体左舷为Y轴,垂直向上为Z轴,满足右手定则。FPSO与系泊腿之间采用2个万向节连接,释放横摇和纵摇2个自由度,系泊刚臂与系泊腿、系泊刚臂与导管架之间采用球铰接,具有3个自由度,导管架与大地固结,关节之间进行力和运动的传递。建立全耦合模型之后划分网格,设置相关参数,耦合模型计算网格如图2所示。
|
图 1 耦合模型建立 Fig. 1 The model of FPSO |

|
图 2 耦合模型计算网格 Fig. 2 The finite element model of FPSO |
保持吃水不变,改变水深,分别计算15 m,16.3 m,18 m,20 m和30 m这5种水深下FPSO的水动力参数,得到不同水深下FPSO六个自由度的附加质量、辐射阻尼系数、以及RAO。
3.1.1 附加质量随水深的变化特性
|
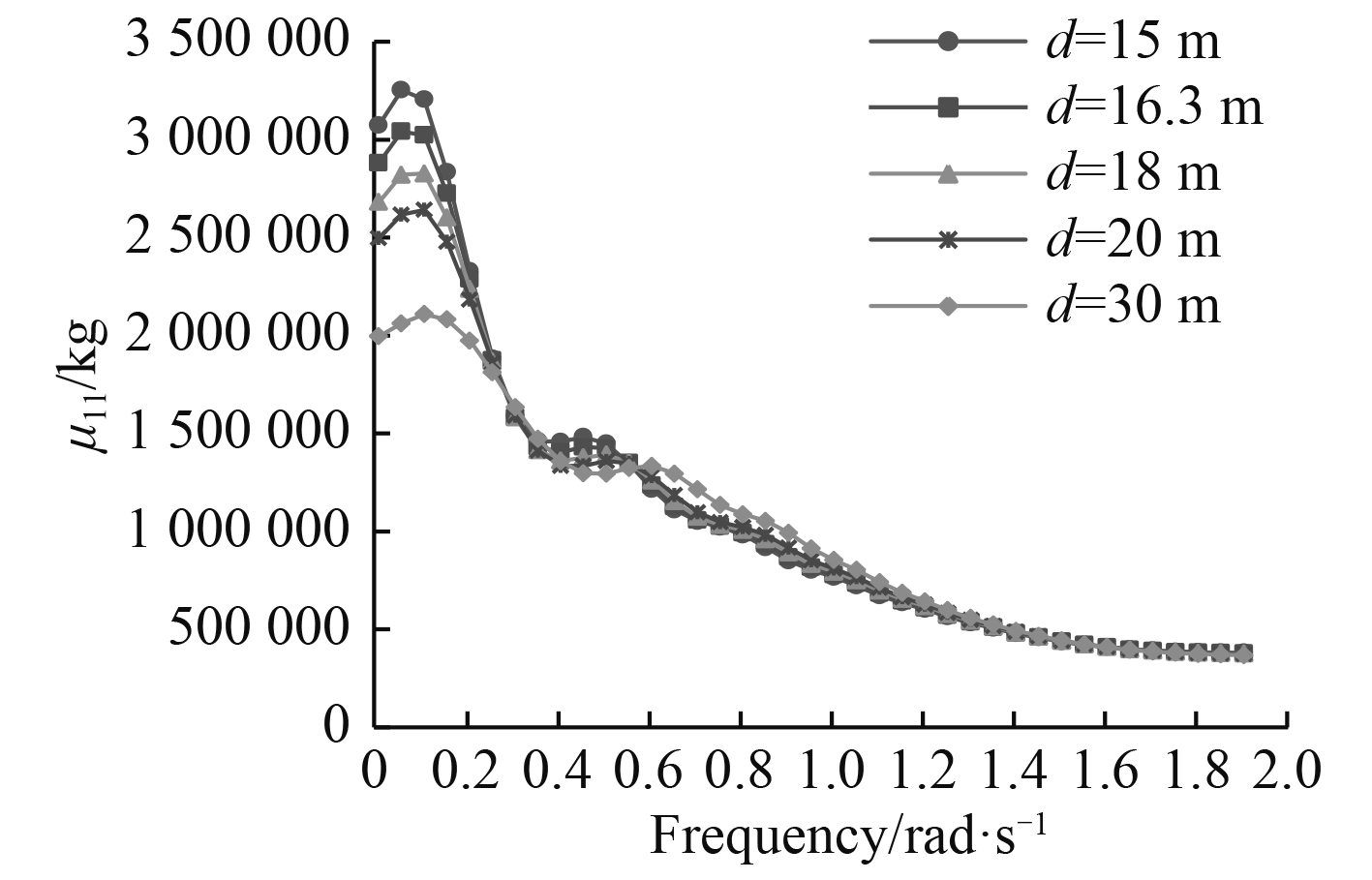
图 3 附加质量μ11随水深的变化曲线 Fig. 3 Added mass μ11 in different water depth |
|
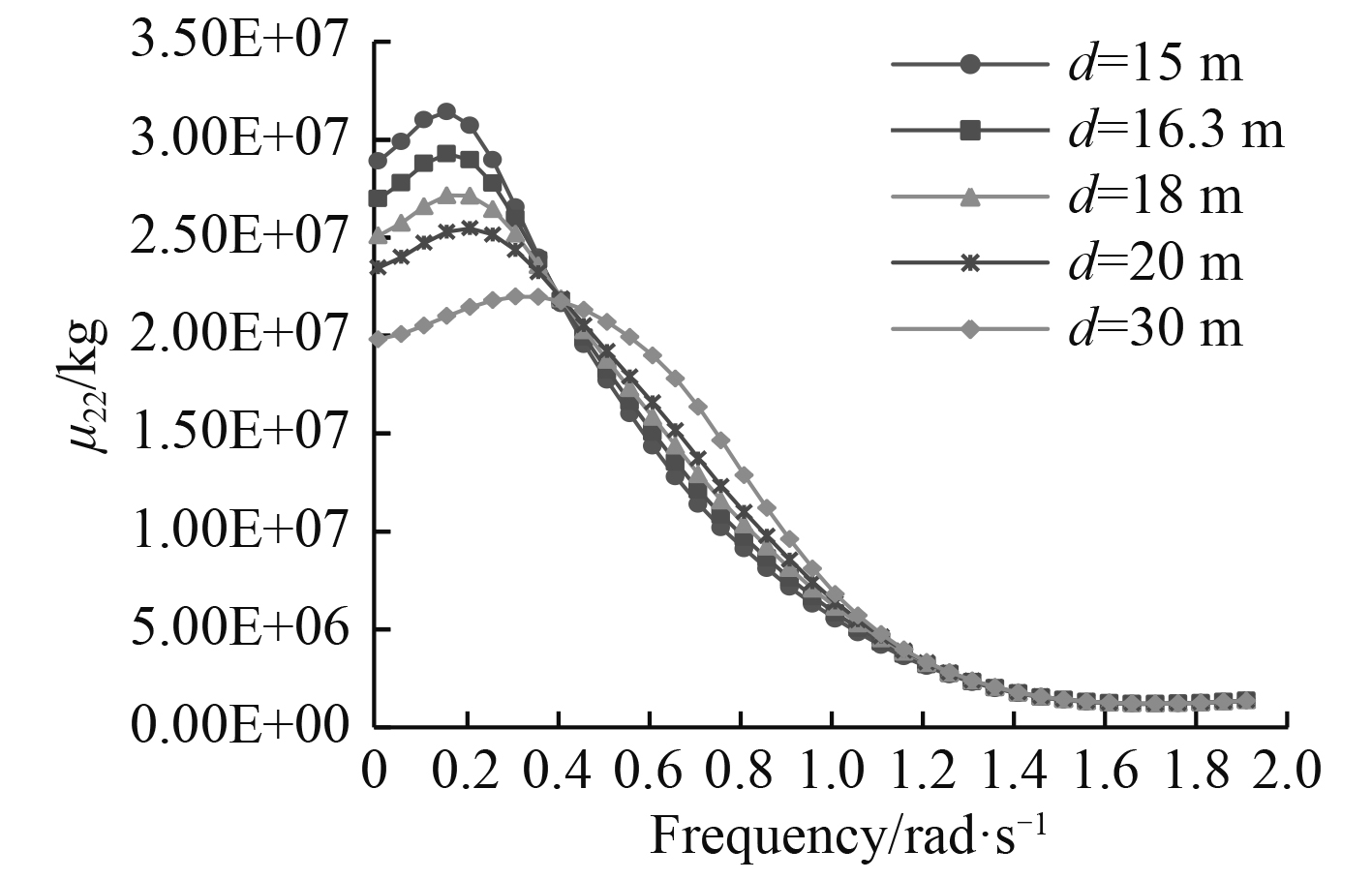
图 4 附加质量μ22随水深的变化曲线 Fig. 4 Added mass μ22 in different water depth |
|
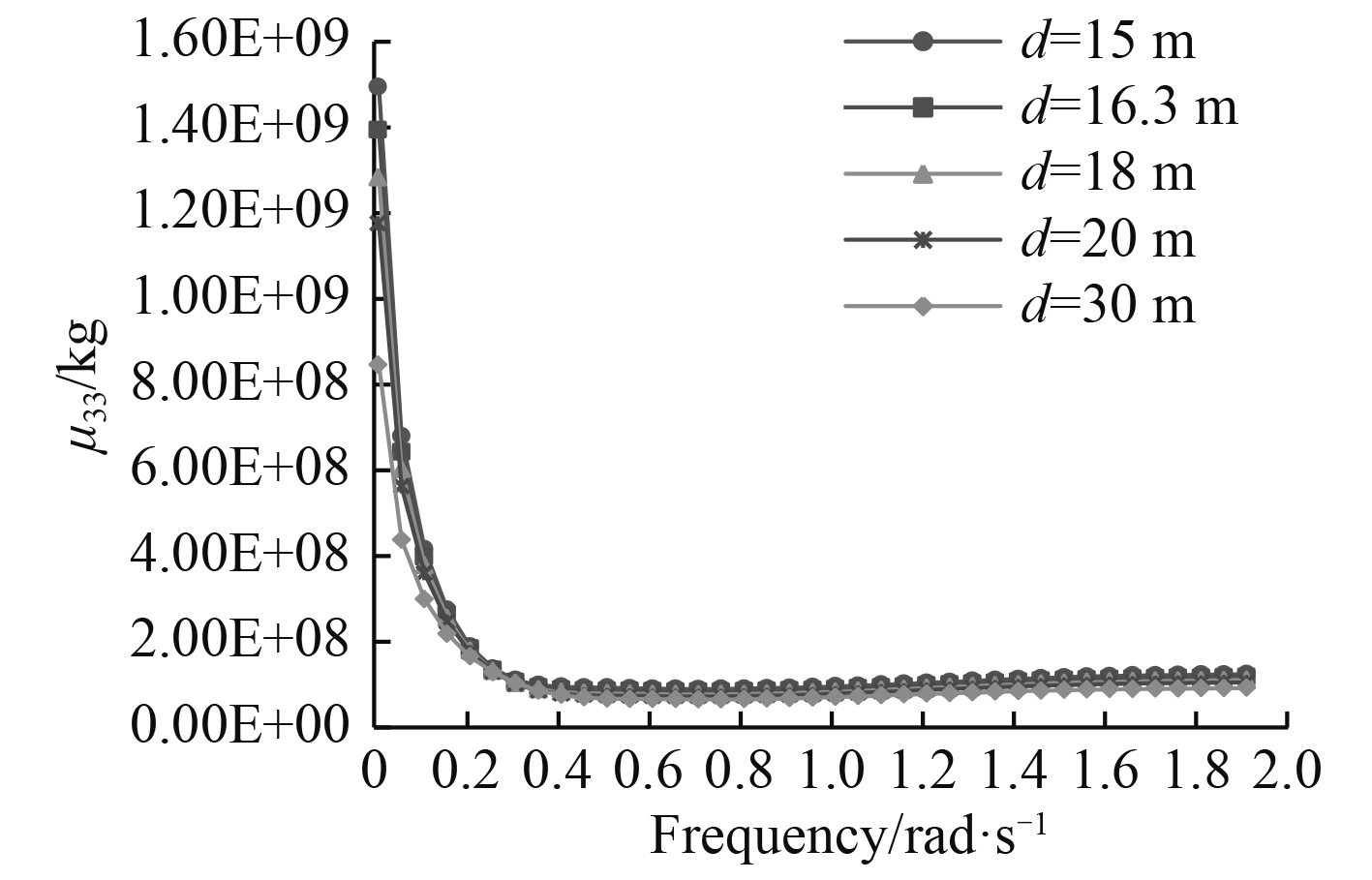
图 5 附加质量μ33随水深的变化曲线 Fig. 5 Added mass μ33 in different water depth |
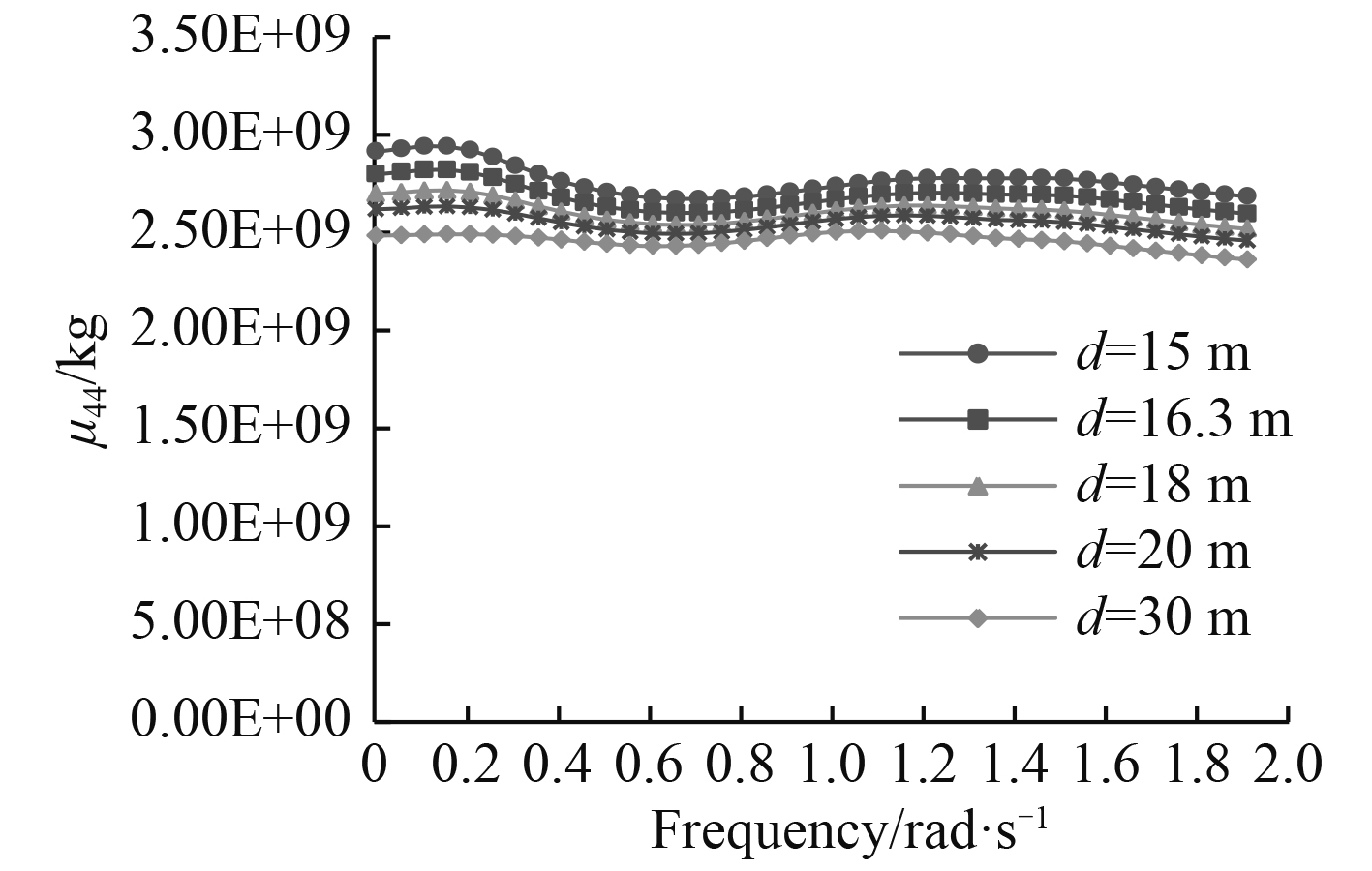
|
图 6 附加质量μ44随水深的变化曲线 Fig. 6 Added mass μ44 in different water depth |
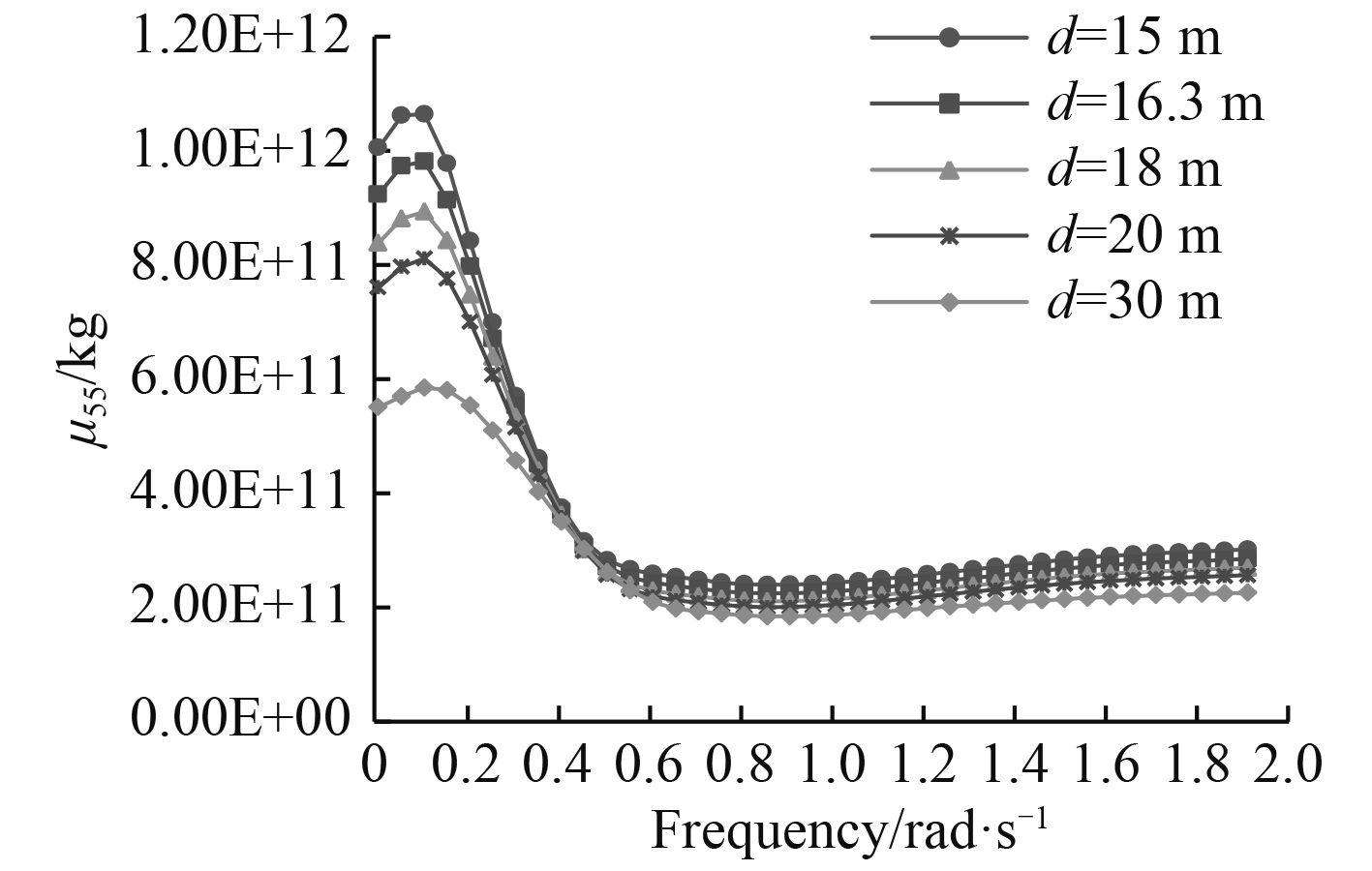
|
图 7 附加质量μ55随水深的变化曲线 Fig. 7 Added mass μ55 in different water depth |
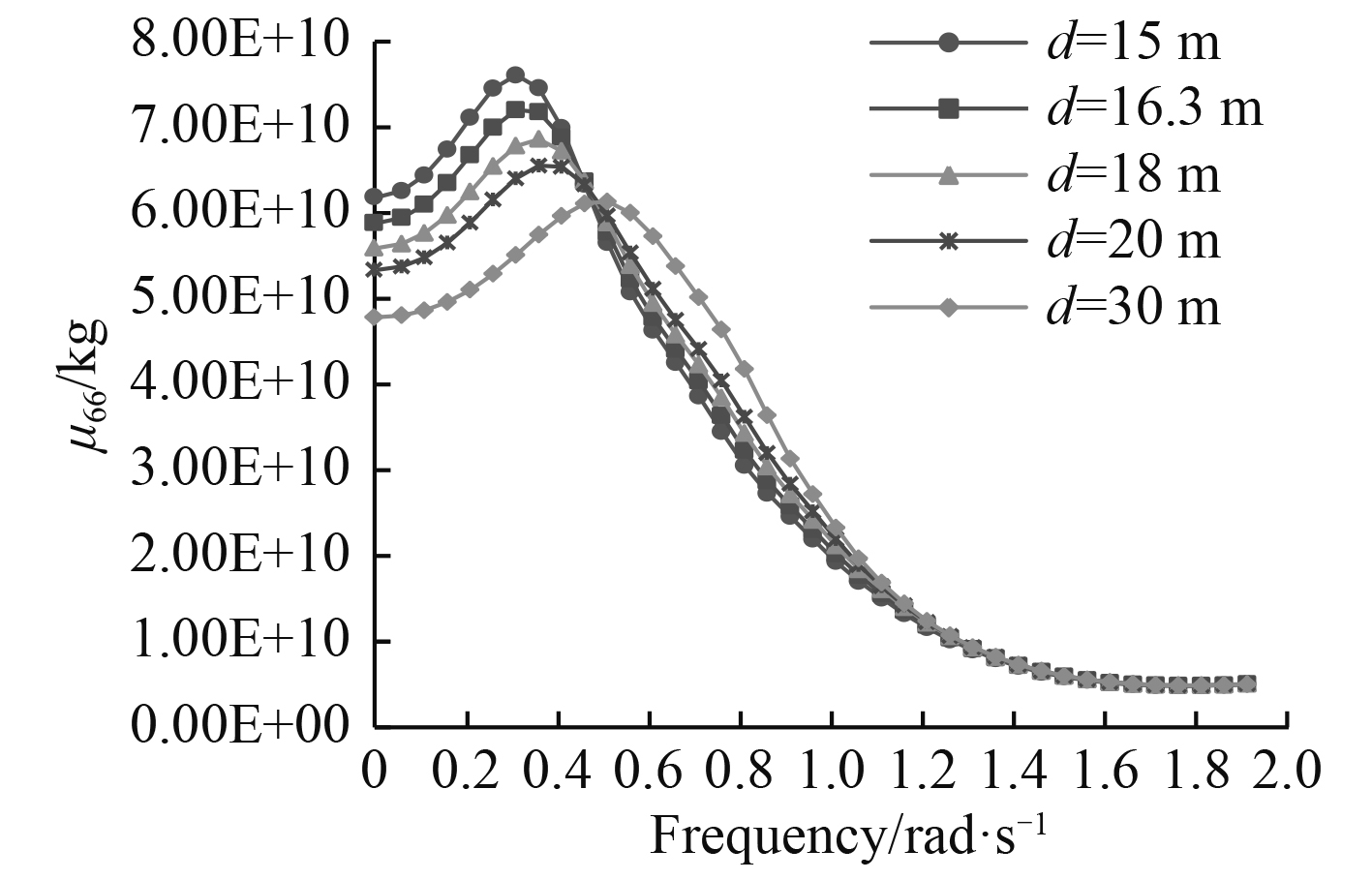
|
图 8 附加质量μ66随水深的变化曲线 Fig. 8 Added mass μ66 in different water depth |
可以看出,随着频率的增加,FPSO六个自由度的附加质量整体呈变小趋势,并趋于稳定,低频附加质量明显大于高频。随着水深的减小,在整个频率范围内,横摇和纵摇附加质量明显增大;当频率小于0.4 rad/s时,随着水深的减小,附加质量显著增大;当频率大于1.2 rad/s时,水深对附加质量基本无影响。结果表明,低频附加质量对水深更为敏感。FPSO沿3个坐标轴转动的附加质量均比绕3个轴平动的附加质量大2-3个数量级[5]。
3.1.2 辐射阻尼系数随水深的变化特性图9~图14展示了FPSO六个自由度下辐射阻尼系数随水深的变化。
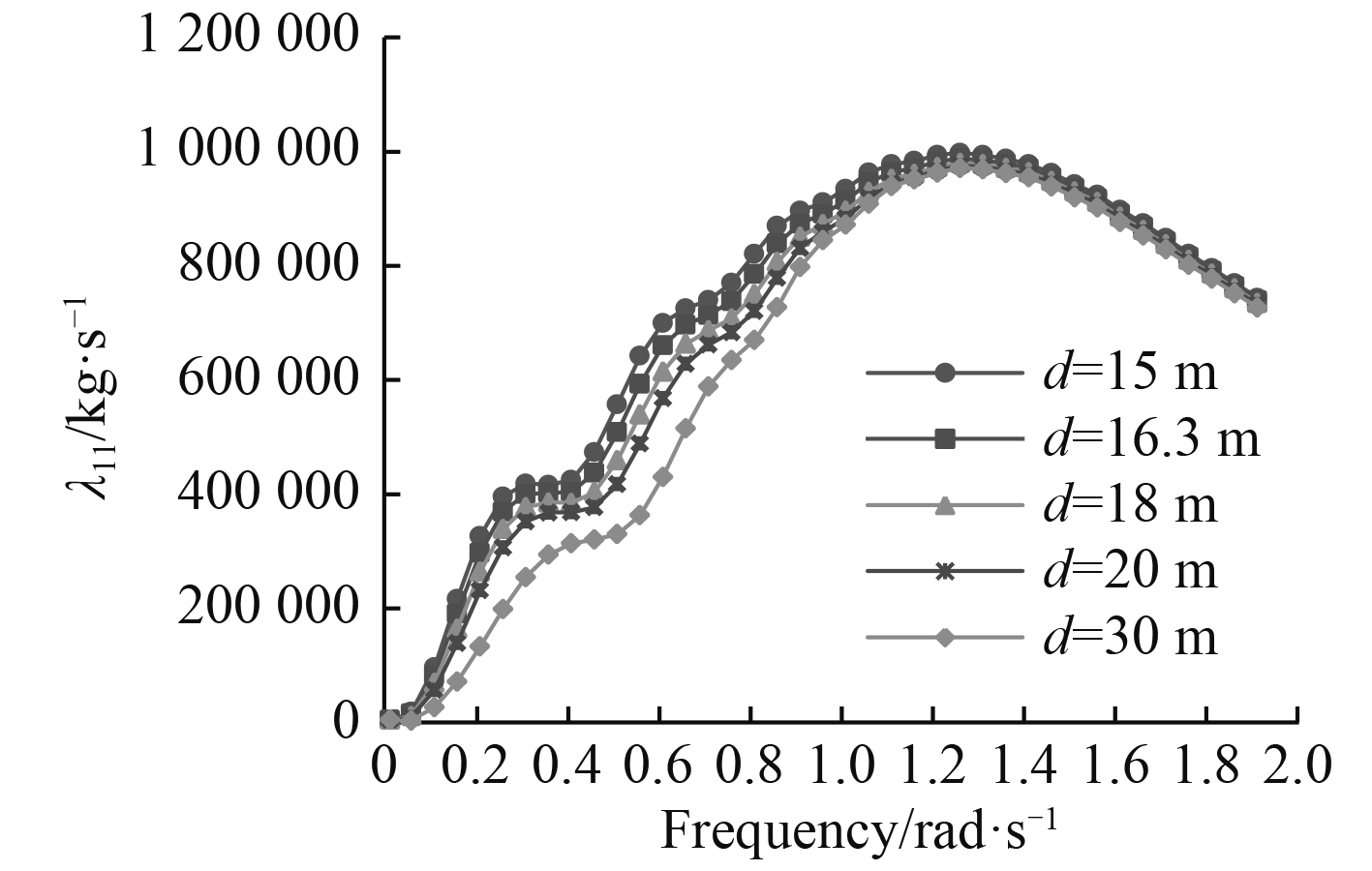
|
图 9 辐射阻尼λ11随水深的变化曲线 Fig. 9 Radiation damping λ11 in different water depth |

|
图 10 辐射阻尼λ22随水深的变化曲线 Fig. 10 Radiation damping λ22 in different water depth |
|
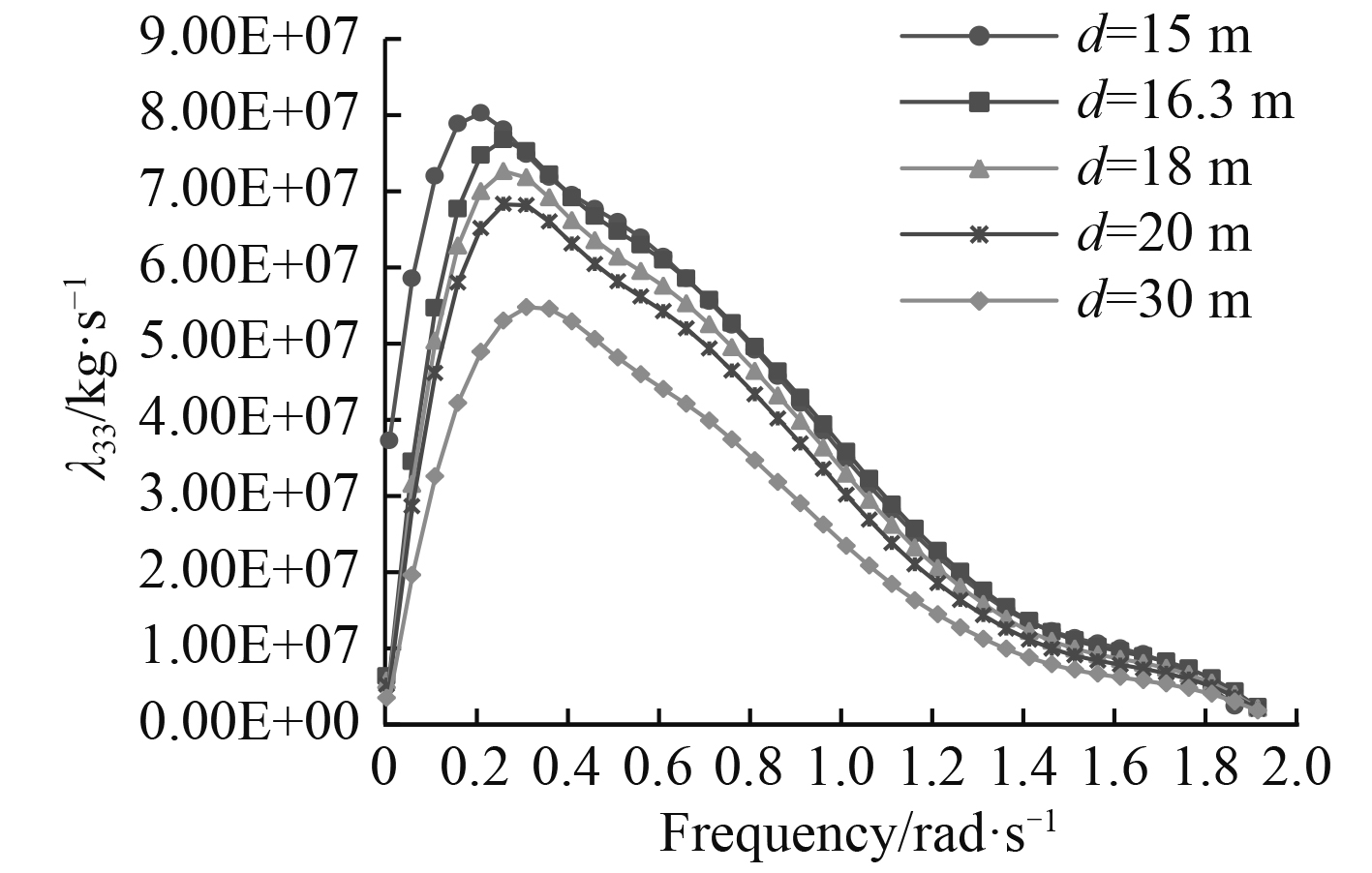
图 11 辐射阻尼λ33随水深的变化曲线 Fig. 11 Radiation damping λ33 in different water depth |
|
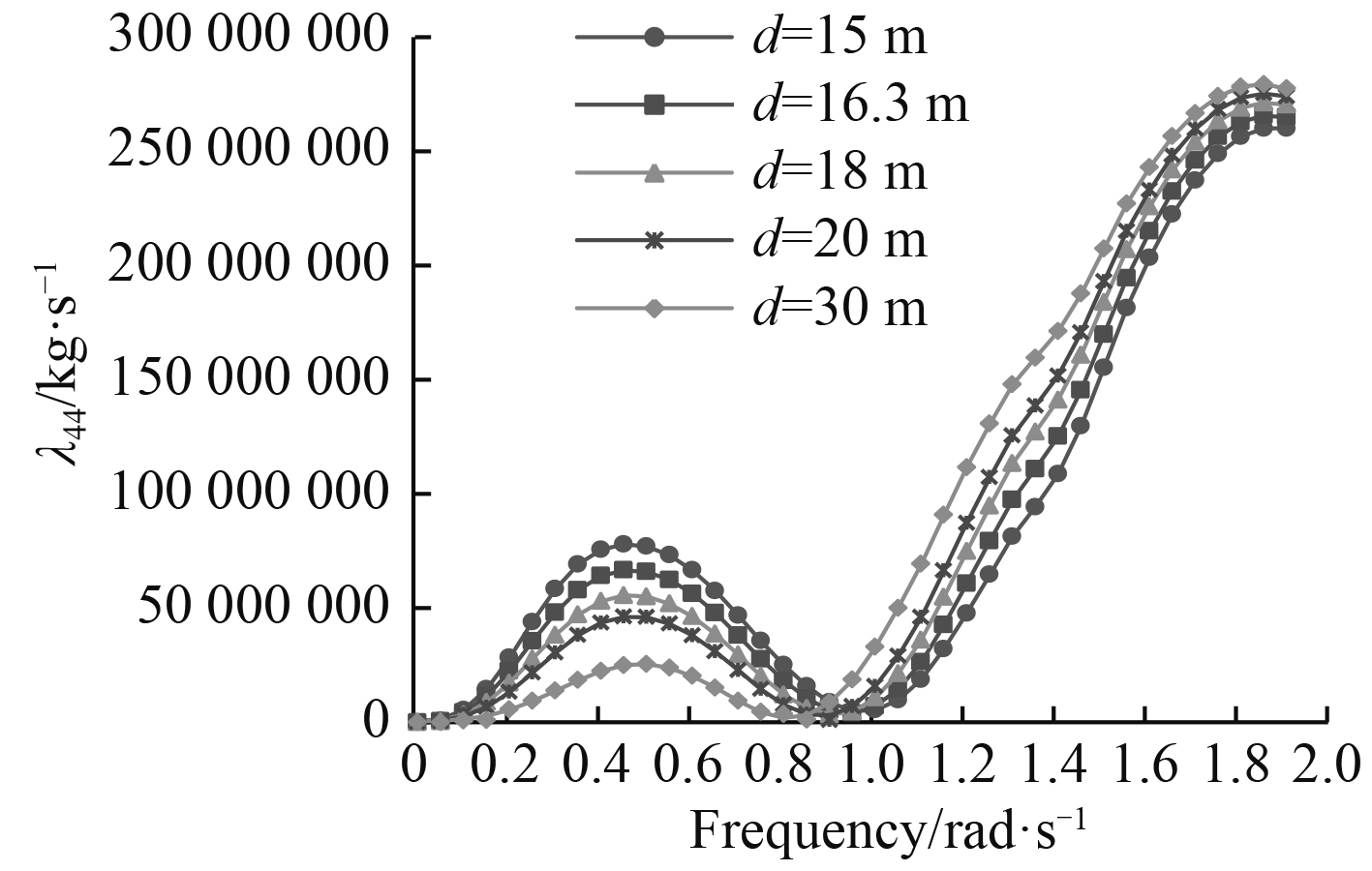
图 12 辐射阻尼λ44随水深的变化曲线 Fig. 12 Radiation damping λ44 in different water depth |
|
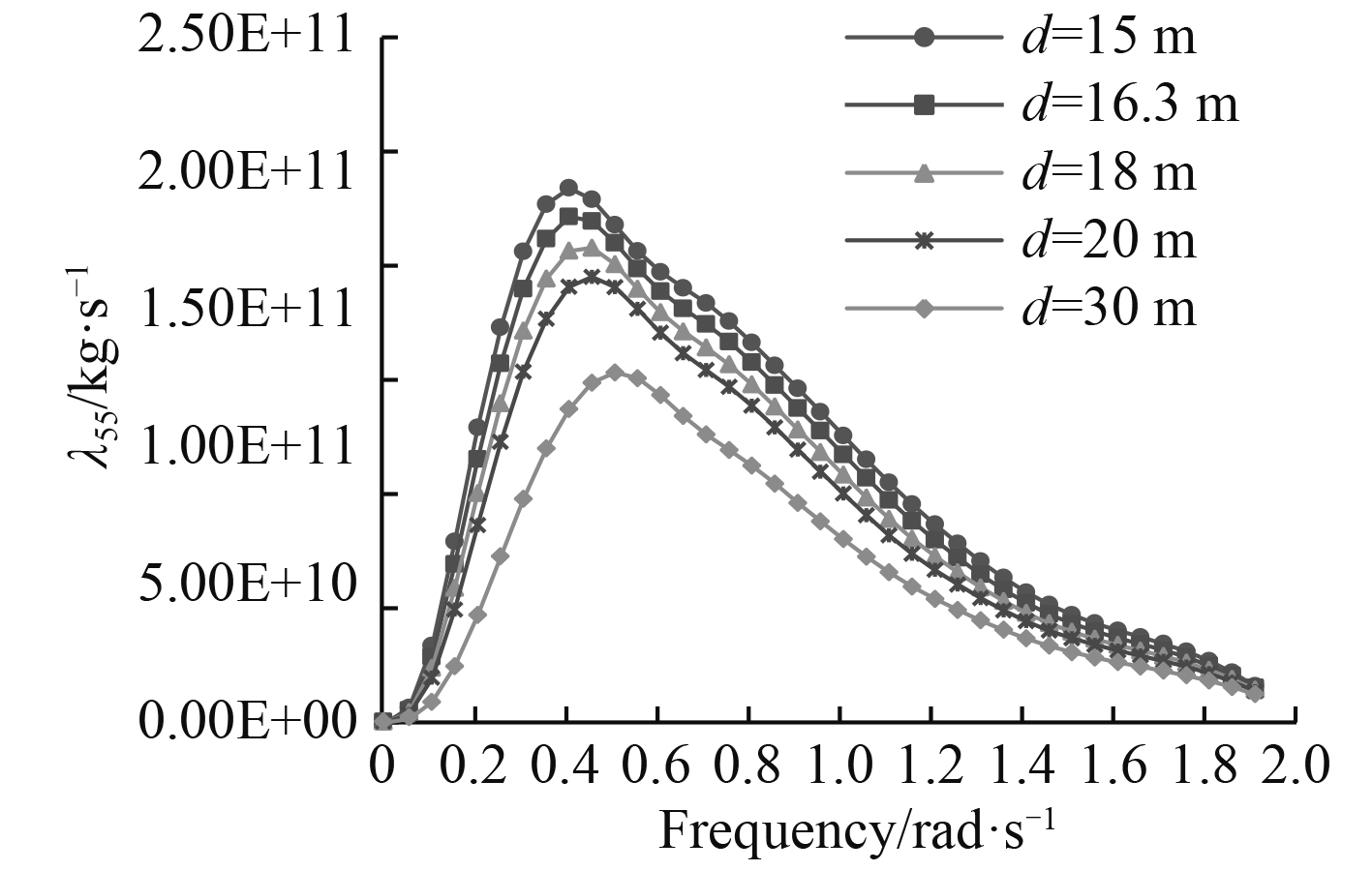
图 13 辐射阻尼λ55随水深的变化曲线 Fig. 13 Radiation damping λ55 in different water depth |

|
图 14 辐射阻尼λ66随水深的变化曲线 Fig. 14 Radiation damping λ66 in different water depth |
可以看出,FPSO六个自由度上的阻尼系数整体上随着频率的增大,先增大后减小。随着水深的减小,6个自由度上的阻尼呈增大趋势,且在低频时变化比较明显。当频率接近于0或者趋于无穷大时,辐射阻尼都趋于0,这说明在极低频率和极高频率时都不会产生大的辐射波[5]。与附加质量的结果类似,绕3个轴转动的阻尼系数比沿3个轴平动的阻尼系数大2~3个数量级。
3.1.3 运动响应幅值算子随水深的变化特性图15~图20展示了FPSO六个自由度下RAOs随水深的变化曲线。

|
图 15 纵荡RAO随水深的变化曲线 Fig. 15 Surge RAO in different water depth |
|
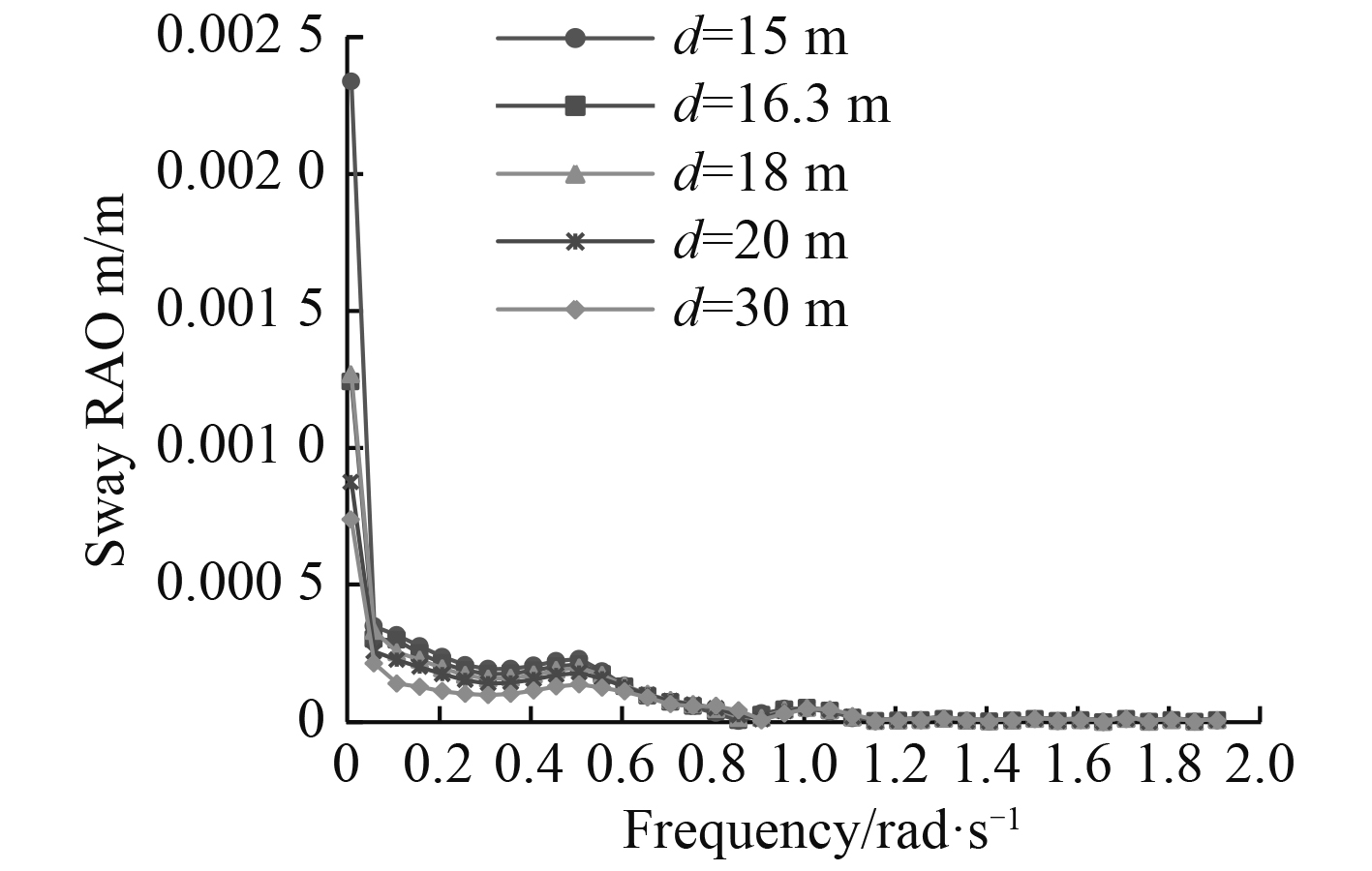
图 16 横荡RAO随水深的变化曲线 Fig. 16 Sway RAO in different water depth |
|
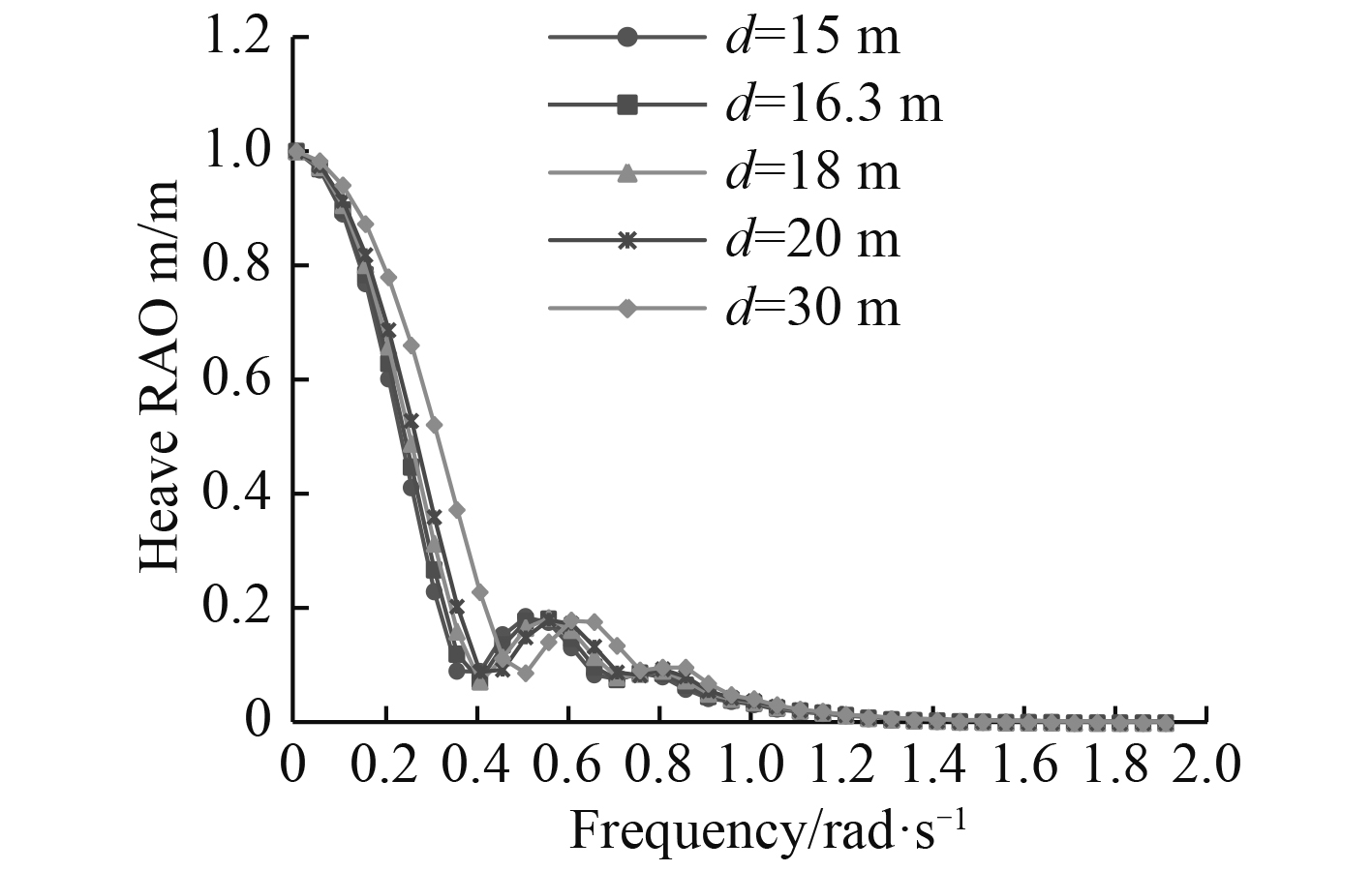
图 17 垂荡RAO随水深的变化曲线 Fig. 17 Heave RAO in different water depth |
|
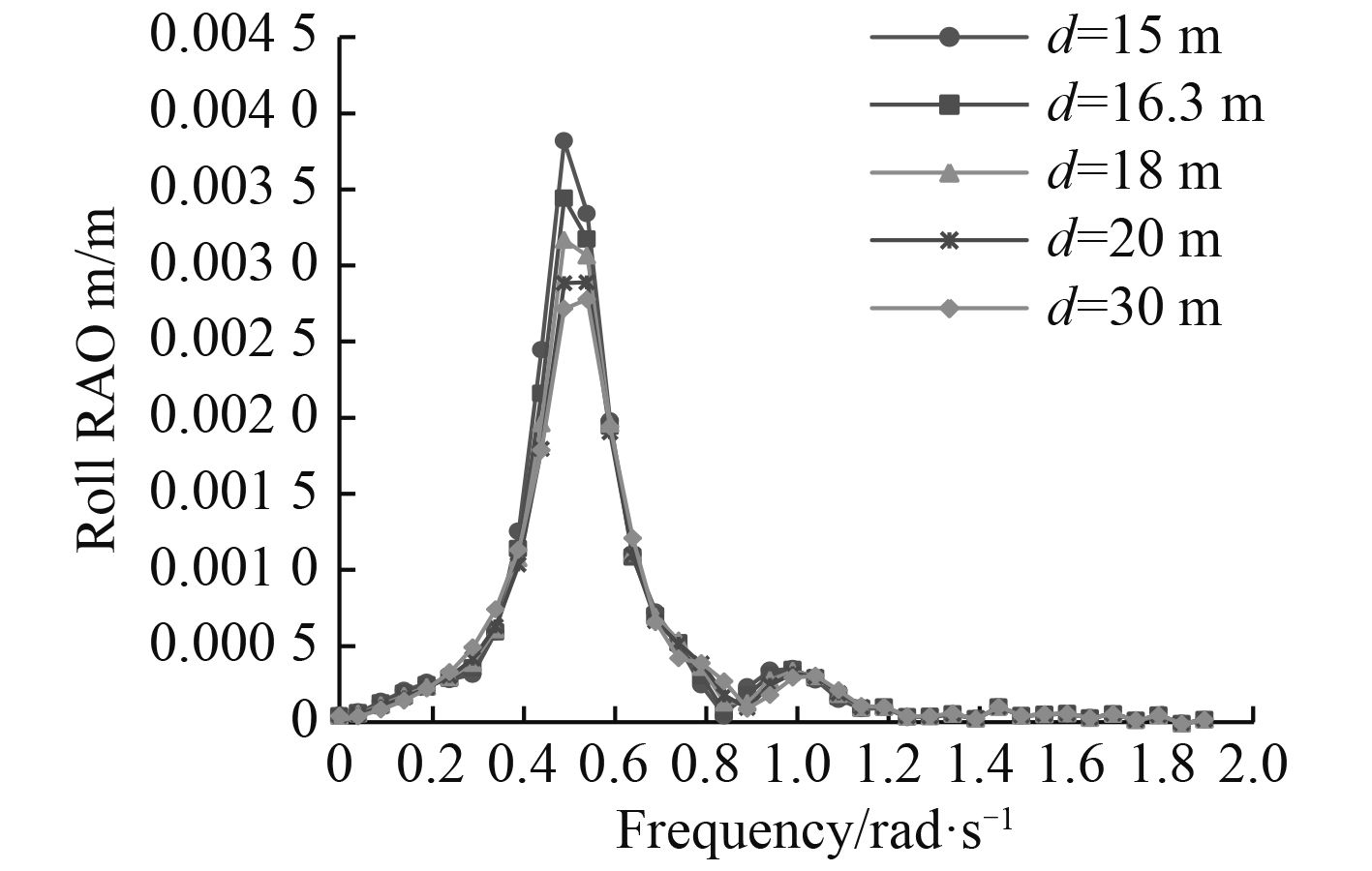
图 18 横摇RAO随水深的变化曲线 Fig. 18 Roll RAO in different water depth |
|
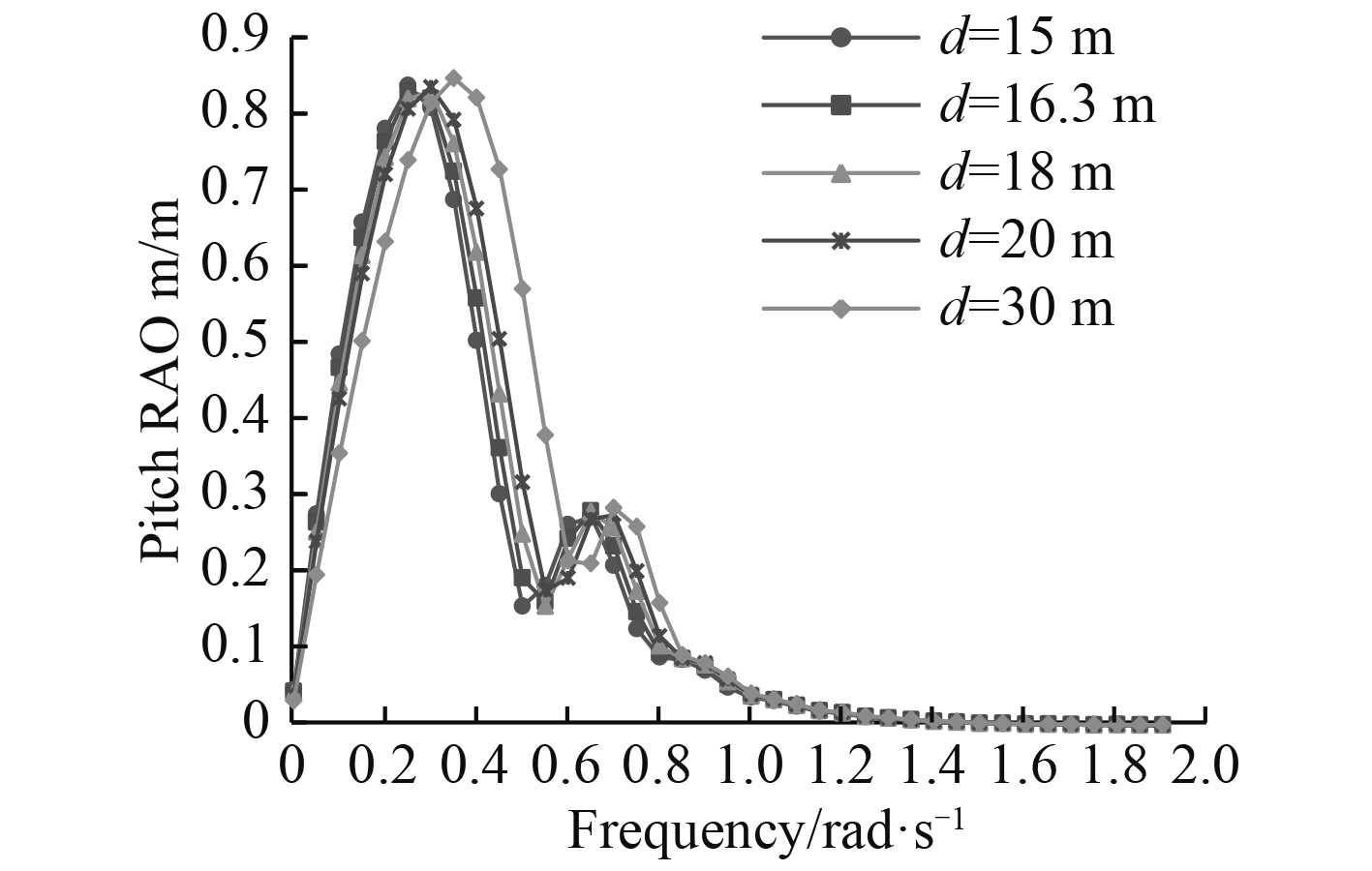
图 19 纵摇RAO随水深的变化曲线 Fig. 19 Pitch RAO in different water depth |
|
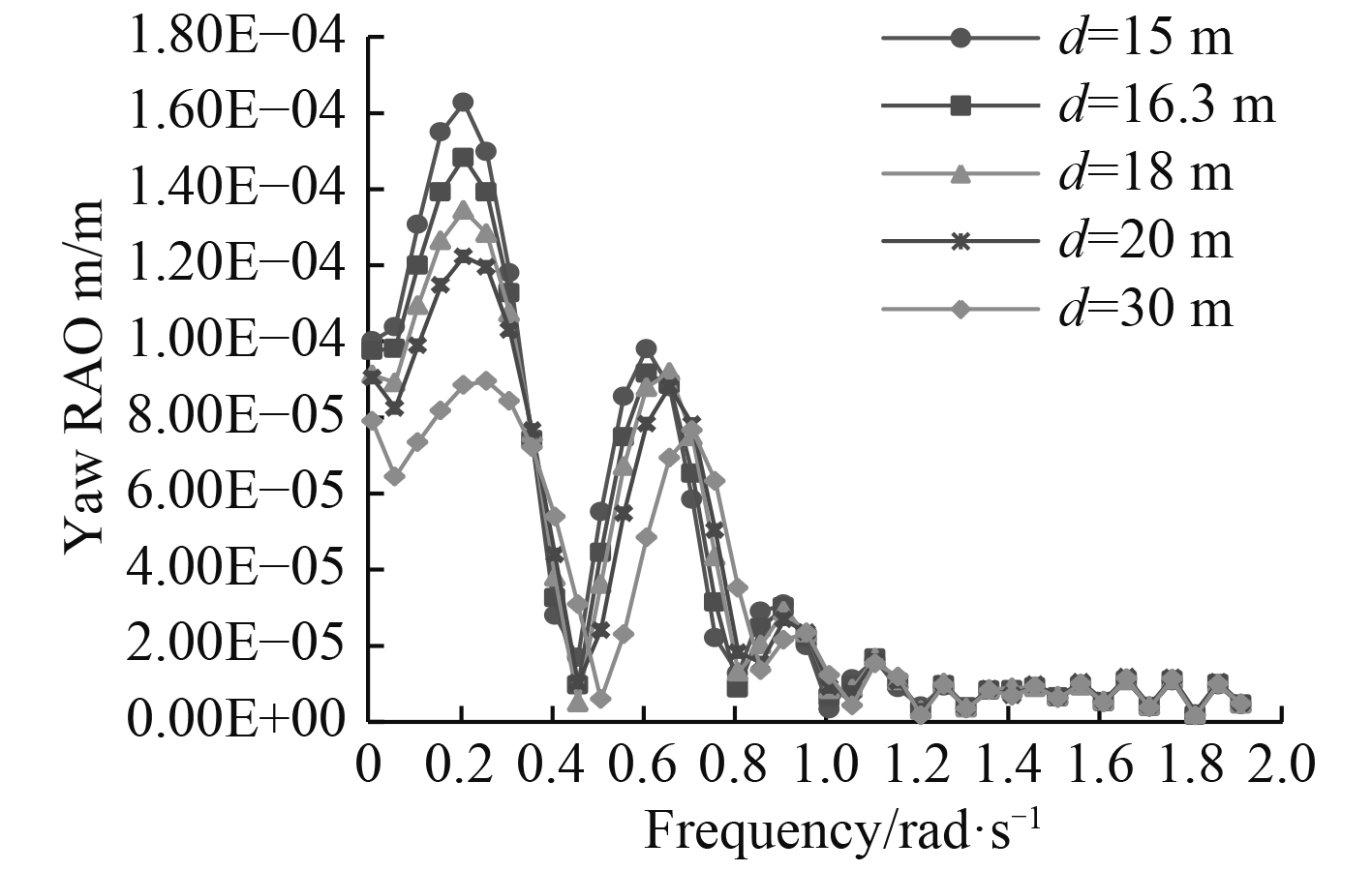
图 20 首摇RAO随水深的变化曲线 Fig. 20 Yaw RAO in different water depth |
从计算结果看,纵荡响应幅值在低频时远大于高频,说明纵荡运动幅度主要受低频波浪力影响。随着水深的减小,深沉运动响应减小,横摇和首摇响应幅值增大,纵摇响应幅值变化不大,峰值对应的频率减小。
3.2 时域分析结果在时域内对FPSO和软刚臂系泊系统进行15 m,16.3 m,18 m三种水深下的动态耦合计算,得出了这3种水深情况下FPSO和软刚臂系泊系统的运动响应。计算总时间3 h,时间步长0.2 s。
船体运动计算结果如表3所示。系泊力计算结果与试验结果对比如表4所示。
|
|
表 3 FPSO运动统计结果 Tab.3 Motion statistics of FPSO |
|
|
表 4 系泊力极值对比 Tab.4 Extrem value of mooring force |
从表3的结果来看,随着水深的减小,各运动平均值均增大,纵荡运动极值显著增大。说明水深主要影响纵荡运动。从表4的结果来看,随着水深的减小,系泊力显著增大。模型试验、计算及现场单点使用情况均表明,当油田水深过浅时,系泊力和纵荡运动将显著增大。低频波浪在浅水中引发的FPSO船运动量远大于深水情况[6],这是由于低频波浪成分会诱导2阶低频波浪力,从而使得总的低频波浪慢漂激励大幅度增大,最终导致单点系泊FPSO低频共振纵荡运动响应以及由此产生的系泊力相比于深水大幅增加[7]。
4 结 语本文运用AQWA软件,基于三维势流理论和多体动力学基础,分别进行了频域分析和时域耦合计算。得出如下结论:
1)在整个频率范围内,随着水深的减小,横摇和纵摇附加质量明显增大;频率小于0.4 rad/s时,随着水深的减小,附加质量显著增大;频率大于1.2 rad/s时,水深对附加质量基本无影响。附加质量在低频范围内对水深更为敏感;
2)FPSO六个自由度上的阻尼系数整体上随着频率的增大,先增大后减小。随着水深的减小,6个自由度上的阻尼均增大,且在低频时变化比较明显;
3)纵荡响应幅值在低频时远大于高频,纵荡运动幅度主要受低频波浪力影响;
4)随着水深的减小,纵荡运动极值和系泊力均显著增大,各运动平均值有所增大。
| [1] |
李欣, 杨建民, 范模. 渤海油田浅水软刚臂系泊FPSO触底分析[J]. 海洋工程, 2004, 2(22): 51-57. |
| [2] |
李淑一, 王树青. 基于多体分析的浅水FPSO和水下软刚臂系泊系统运动特性研究[J]. 中国海洋大学学报(自然科学版), 2011, 41(9): 095-102. |
| [3] |
李淑一, 浅水软钢臂系泊FPSO水动力性能和运动响应数值研究[D]. 青岛: 中国海洋大学, 2011.
|
| [4] |
刘成义, 唐友刚, 李焱, 等. 浅水单点系泊FPSO软刚臂参数敏感性分析[J]. 中国舰船研究, 2014, 9(5): 69-76. DOI:10.3969/j.issn.1673-3185.2014.05.012 |
| [5] |
刘晓健. FPSO单点系泊系统运动响应分析[D]. 镇江: 江苏科技大学, 2013.
|
| [6] |
肖龙飞, 杨建民, 范模, 等. 160 kDWT FPSO在极浅水中运动安全性研究[J]. 船舶力学, 2006, 10(1): 7-14. DOI:10.3969/j.issn.1007-7294.2006.01.002 |
| [7] |
肖龙飞, 杨建民, 胡志强. 极浅水单点系泊FPSO低频响应分析[J]. 船舶力学, 2010, 14(4): 372-377. DOI:10.3969/j.issn.1007-7294.2010.04.007 |
 2019, Vol. 41
2019, Vol. 41
