2. 船舶动力工程技术交通行业重点实验室,湖北 武汉 430063
2. School of Energy and Power Engineering, Wuhan 430063, China
随着我国海洋工程实力不断提升,越来越多的海上作业平台和深海工程装备被投入使用[1],由此进行海上人员转移也更为频繁,每年仅在海上石油和天然气领域,全世界就有超过1 000万次海上人员转移作业。复杂的海洋环境是转移作业中的关键挑战,传统的海上转移作业主要应用直升机、船舶、起重机和吊篮等,然而传统方式在安全和经济性等方面表现不佳。随着科技的进步,具有动力定位系统的海洋工程船搭载大型波浪补偿舷梯装置提供一种更加安全可靠、经济有效的人员转移解决方案,近年来广泛应用于海上船舶与平台之间人员转移作业[2]。
本文为明确补偿舷梯运动规律,提出补偿舷梯运动学建模方法,分析了舷梯运动部件的运动特性,为后续舷梯执行机构选型及控制系统的研究提供参考。
1 概述海上作业船舶由于受到风和海浪的影响,船舶不可避免地产生显著的升沉、摇摆、平移运动。虽然借助船舶的动力定位系统使得横荡、纵荡得到一定程度上的控制,但对于船舶升沉、摇摆方向上的运动仍很难控制[3]。
波浪补偿舷梯通过监测船舶和控制舷梯执行机构的运动对船舶的摇摆和升沉运动进行补偿,并且克服这些运动互相耦合的影响,保持舷梯在船舶与离岸设施之间平稳固定,使海上人员转移变得更加安全方便,降低海上生产作业的成本,提高了作业效率[4],典型的大型波浪补偿舷梯结构如图1所示。

|
图 1 国外某大型波浪补偿舷梯 Fig. 1 Example of motion compensated gangways |
大型舷梯的补偿模式分为随动式与主动式[5]。随动式具体工作方式为:舷梯臂尖端伸入到海上设施登入口,通过操作人员将舷梯尖端通过钢绳坚固连接登入口。舷梯尖端一旦连接,控制方式换为跟随模式,允许舷梯在船舶和设施之间漂浮,此时液压执行机构管路打开,为非控制浮动状态,系统无压力,舷梯臂自然随着船的摆动而摆动。主动式具体工作方式为:液压执行机构为主动控制状态,通过检测船体的摆动位置情况,进行实时位置跟踪控制,使舷梯尖端始终保持与海上设施登入口同一水平线,同时通过伸缩臂执行机构始终有往外伸的力使尖端与登入口始终保持接触。主动式控制模式下不需要人为的固定操作,因而大大增加了作业的安全性与经济性,并且在恶劣海况下可随时脱离,保证人员安全和舷梯不受到破坏。
大型舷梯的工作模式可划分为对接、工作、紧急脱离三类。当搭载补偿舷梯的海洋工程船通过动力定位系统靠近海上设施合适位置时,调节舷梯姿态,使工程船与海上设施在一定区域内准确对接,该区域根据船舶的尺寸、舷梯在船甲板上的安装位置以及海况等因素确定。工作时,补偿舷梯与海上设施保持连接,通过液压执行机构运动,补偿船舶的运动,保证工程船与海上设施始终连接,从而保证人员安全转移而避免发生危险;当海况超过舷梯运行安全值,保护系统启动,向操作员发出声或光报警信号,立即停止人员转移作业,通过补偿舷梯配有的紧急脱离系统,切断舷梯伸缩臂首段与海上设施的连接,舷梯伸缩臂向上抬起,锁定在安全位置,避免船舶过大移动而破坏补偿舷梯。
国外在相关船舶工程领域有丰富的经验,拥有先进的技术以及优良的补偿舷梯设备,基本上垄断全球海洋工程登离舷梯设备领域。我国自身工业基础条件比较薄弱,起步较晚,现只针对一些深海石油开采、海上吊装操作的波浪补偿设备进行研究,主要关注点在升沉方向上的补偿,对于补偿舷梯尚处于初级理论研究阶段[6 – 7],相关应用主要依赖进口设备。
2 波浪补偿舷梯运动学建模建立准确的运动学模型是进行运动学分析的基础,是进行机构动力特性评价及动力学优化设计的必要条件,同时也是实现舷梯装置高精度控制的前提。
2.1 补偿舷梯模型简介本文大型补偿舷梯设计基于DNVGL-ST-0358(2015)海上舷梯设计规范,满足6级海况工作要求,工作范围如下:
舷梯臂工作长度范围为7 ~ 10 m;
俯仰操作角度为–15° ~ +25°。
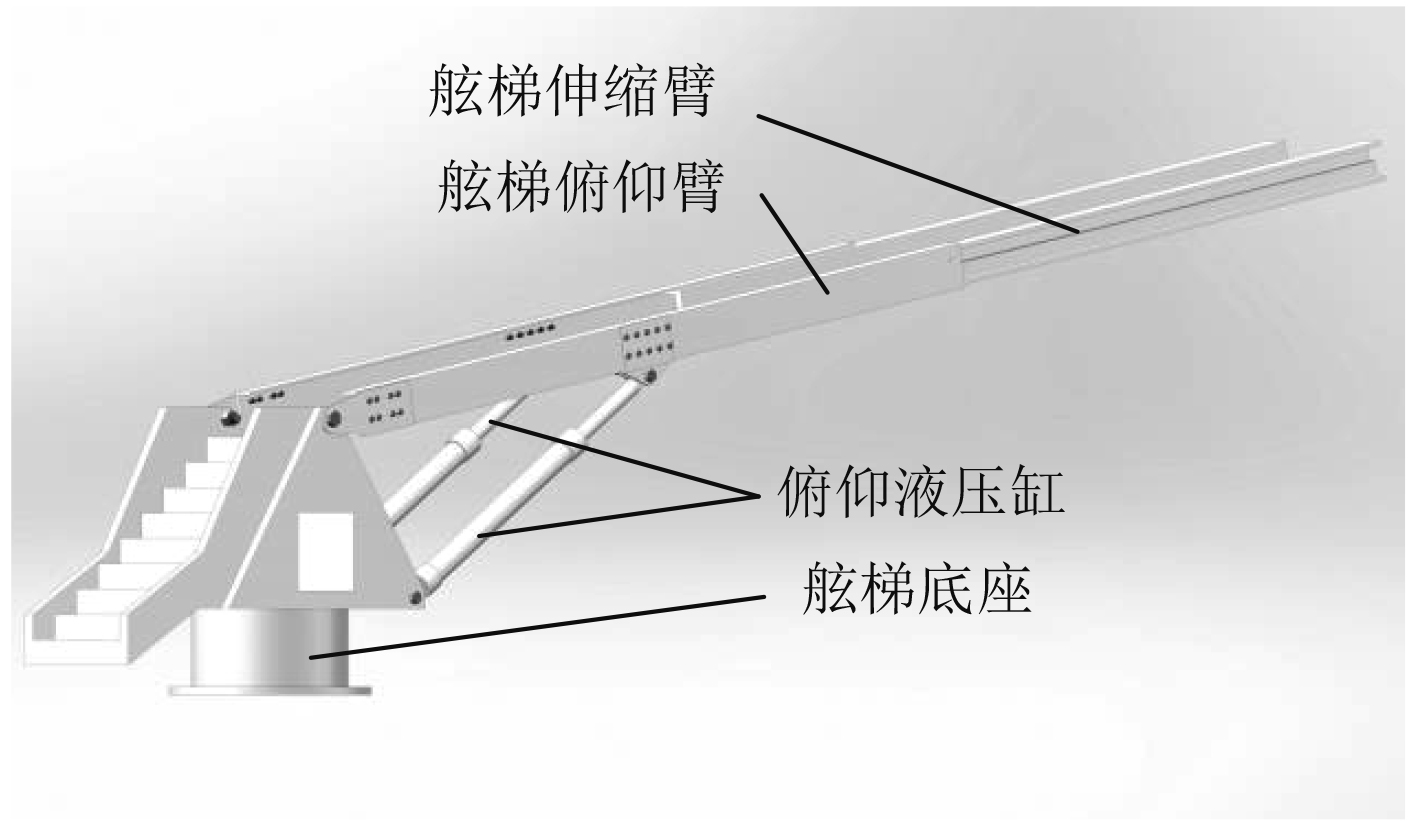
设计的大型补偿舷梯执行机构主要包括舷梯俯仰臂、舷梯伸缩臂、舷梯底座和液压执行器。其中液压执行器包括2个俯仰液压缸,分别通过舷梯底座与舷梯伸缩臂连接,是舷梯补偿船舶运动发挥作用的主要部分。俯仰臂与伸缩臂相连,伸缩臂设有液压马达驱动系统及弹簧阻尼系统,通过齿条驱动伸缩臂进行伸缩运动。弹簧阻尼系统主要起抗冲减振、应对高频率运动及降低大幅度横摇运动的作用。舷梯底座连接海上工作船甲板,在底座水平面内安装回转液压系统实现补偿舷梯整机的旋转运动。
为后续运动学分析方便,通过SolidWorks软件对大型补偿舷梯进行建模。因为运动学是探讨一个物体或一个系统的运动情况,所以运动学建模时不将质量和力量因素列入考虑,即只分析舷梯装置在空间中的位置与时间的关系,因此省略了护栏等一些不影响运动学分析的零件,简化后的模型如图2所示。为了防止模型出现运动干涉现象,装配完之后模型进行干涉检查,确认模型的正确性。
|
图 2 Solidworks舷梯模型设计图 Fig. 2 Solidworks model of designed gangway |
由于大型补偿舷梯的复杂性,一些研究基于几何分析法或CAD模型直接仿真,误差较大。本文根据补偿舷梯的机械结构,创新性地将补偿舷梯运动学分析类比机械臂,运用机械臂运动学研究中最常用的Denavit-Hartenberg参数齐次变换法(D-H参数法)进行合理建模。
D-H参数法指:用齐次坐标来描述舷梯各关节相对于参考坐标系的空间集合关系,用4×4的齐次变换矩阵来描述相邻两关节i和i–1的空间几何关系,从而推导出补偿舷梯尖端坐标系相对于参考坐标系的空间位姿关系。
| $ {}_{ {i}}^{{ {i - 1}}}\!{ T}\! \!=\! \left[\!\! {\begin{array}{*{20}{c}} {{\cos }{\theta _{ {i}}}}\!\!&\!\!{{{ - \sin}}{\theta _{ {i}}}}\!\!&\!\!{0}\!\!&\!\!{{\alpha _{{ {i - 1}}}}} \\ \!\!\!\! {{\cos }{\alpha _{{ {i - 1}}}}{\sin }{\theta _{{i}}}}\!\!&\!\!{{\cos }{\alpha _{{{i - 1}}}}{\cos }{\theta _{{i}}}}\!\!&\!\!{{{ - \sin}}{\alpha _{{{i - 1}}}}}\!\!&\!\!{{{ - }}{{\rm{d}}_{{i}}}{\sin }{\alpha _{{{i - 1}}}}} \\ \!\!\!\! {{\sin }{\alpha _{{{i - 1}}}}{\sin }{\theta _{{i}}}}\!\!&\!\!{{\sin }{\alpha _{{{i - 1}}}}{\cos }{\theta _{{i}}}}\!\!&\!\!{{\cos }{\alpha _{{{i - 1}}}}}\!\!&\!\!{{{\rm{d}}_{{i}}}{\cos }{\alpha _{{i}}}} \\ \!\!\!\! {0}\!\!&\!\!{0}\!\!&\!\!{0}\!\!&\!\!{{1}} \end{array}}\!\!\! \!\!\! \right]{\text{。}} $ | (1) |
一旦确定了坐标系,且得到相应的关节参数,就可以直接推导出运动学方程式并计算出各个关节的变换矩阵。然后,将各变换矩阵乘在一起便可得到坐标系{n}相对于基座标系的变换矩阵。
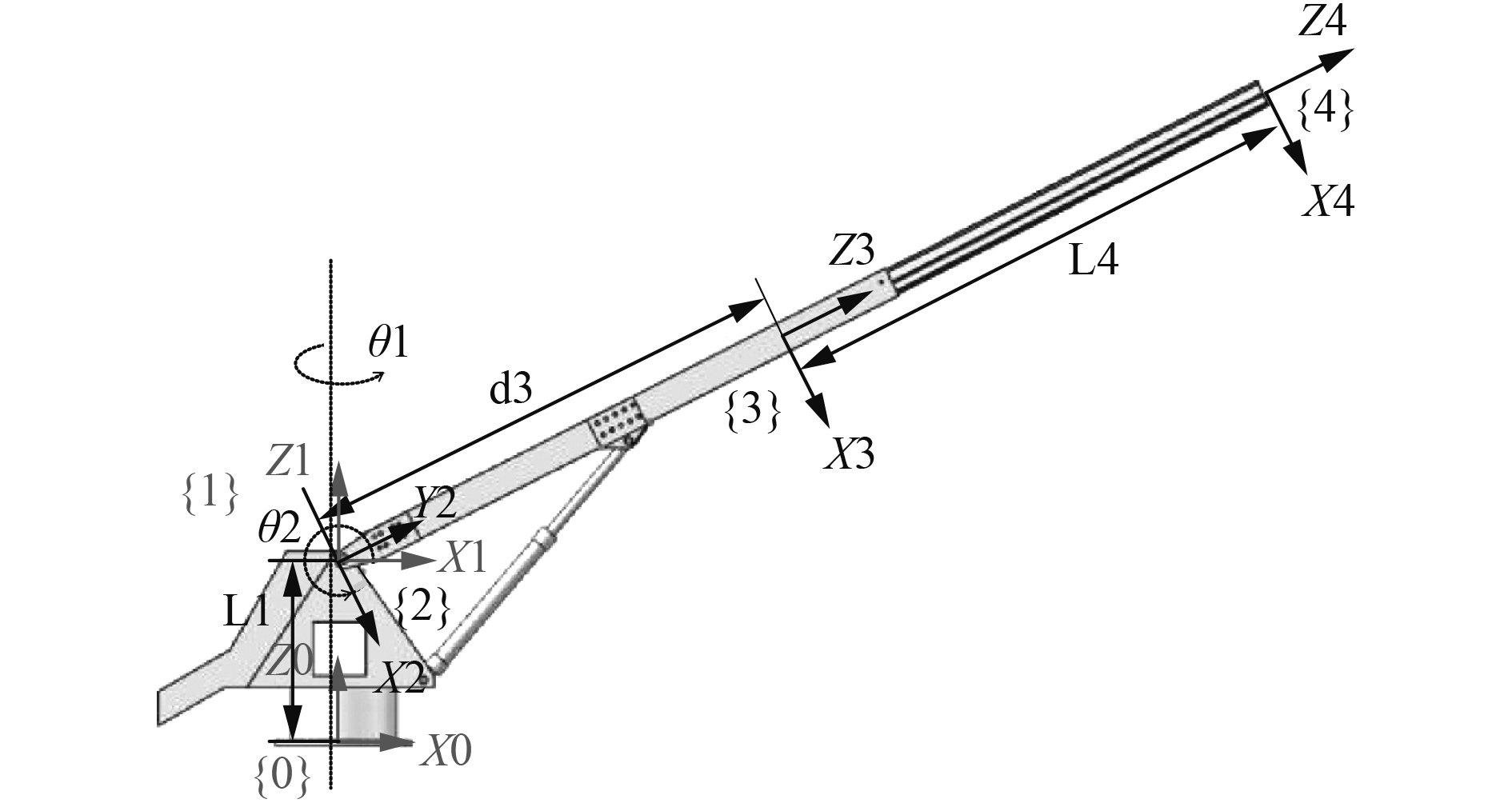
根据以上设计的舷梯,所研究的补偿舷梯由2个旋转关节和1个移动关节组成,分别为舷梯底座旋转关节1,俯仰臂旋转关节2和伸缩臂的移动关节3。将底座底部的中心作为基础坐标系{0}的原点,底座与舷梯俯仰臂连接点中心作为坐标系{1}和{2}的原点,舷梯俯仰臂与舷梯收缩臂尾端接触部分中心设立坐标系{3},舷梯收缩臂尖端中心设立坐标系{4}。其中L1为1 820 mm,L4为5 650 mm。按照D-H参数法的定义,建立补偿舷梯运动学模型图如图3所示。
|
图 3 舷梯系统简化D-H图 Fig. 3 The D-H sketch of simplified gangway system |
根据设计,每个关节的工作范围如表1所示。
|
|
表 1 各关节的变量范围 Tab.1 The operational range of joint variables |
D-H矩阵参数如表2所示。
|
|
表 2 舷梯D-H参数表 Tab.2 D-H parameters of gangway system |
一般而言,运动学可分为正向运动学与逆向运动学两部分,正逆向运动学分析是做大型波浪补偿舷梯控制前重要的一个环节。
3.1 正向运动学求解正向运动学是知道每个液压执行机构的位移后,进而求出舷梯尖端在空间中的位置。将表2中的相关参数代入舷梯变换矩阵,在Matlab中进行矩阵运算,得出坐标系{1}相对于基座基坐标系{0}变换矩阵如下:
| ${{ }}{}_{{1}}^{0}{ T} = \left[ {\begin{array}{*{20}{c}} {c1}&{ - s1}&0&0 \\ {s1}&{c1}&0&0 \\ 0&0&1&{L1} \\ 0&0&0&1 \end{array}} \right]\text{,}$ | (2) |
其中s1为sinθ1,c1为cosθ1。坐标系{2}相对于坐标系{1}变换矩阵为:
| $_{{2}}^{{1}}{ T} = \left[ {\begin{array}{*{20}{c}} {c2}&{ - s2}&0&0 \\ 0&0&{ - 1}&0 \\ {s2}&{c2}&0&0 \\ 0&0&0&1 \end{array}} \right]\text{,}$ | (3) |
其中s2为sinθ2,c2为cosθ2。同理,坐标系{3}相对于坐标系{2}变换矩阵与坐标系{4}相对于坐标系{3}变换矩阵分别为:
| $_{{3}}^{{2}}{ T} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&0&1&{D3} \\ 0&{ - 1}&0&0 \\ 0&0&0&1 \end{array}} \right]\text{,}$ | (4) |
| ${}_{{4}}^{{3}}{ T} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&1&{L4} \\ 0&0&0&1 \end{array}} \right]\text{。}$ | (5) |
由此得坐标系{4}相对于基座基坐标系{0}变换矩阵为:
| $\begin{aligned} {}_{{4}}^{0}{ T} &= {}_{{1}}^{0}{ T}{}_{{2}}^{{1}}{ T}{}_{{3}}^{{2}}{ T}{}_{{4}}^{{3}}{ T} = \\ & \left[ {\begin{array}{*{20}{c}} {c1c2}&{ - s1}&{ - c1s2}&{ - c1s2(D3 + L4)} \\ {s1c2}&{c1}&{ - s1s2}&{ - s1s2(D3 + L4)} \\ {s2}&0&{c2}&{L1 + (D3 + L4)c2} \\ 0&0&0&1 \end{array}} \right] {\text{。}} \end{aligned} $ | (6) |
式(6)即所要求的补偿舷梯正运动学方程,表达了舷梯尖端点的位置和姿态与舷梯基坐标系{0}之间的变换关系。其中:N=[c1c2 s1c2 s2]T为舷梯基座坐标系{0}相对于坐标系{4}在X轴上的方向矢量;O=[–s1 c1 0]T为舷梯基座坐标系{0}相对于坐标系{4}在Y轴上的方向矢量;A=[–c1
因此,舷梯基座坐标系{0}中表示的通道顶端位置由式(6)给出:
| $\begin{gathered} {P_X} = - c1s2(D3 + L4){\text{,}} \\ {P_Y} = - s1s2(D3 + L4){\text{,}} \\ {P_Z} = L1 + (D3 + L4)c2 {\text{。}} \end{gathered} $ | (7) |
取舷梯初始水平位置:θ1=180°,θ2=270°,D3=3650 mm,代入式(6)得到初始位姿矩阵为:
| ${}_{{4}}^{0}{ T} = \left[ {\begin{array}{*{20}{c}} {0}&{0}&{{1}}&{{{9300}}} \\ {0}&{{1}}&{0}&{0} \\ {{{ - 1}}}&{0}&{0}&{{{1820}}} \\ {0}&{0}&{0}&{{1}} \end{array}} \right]{\text{。}}$ |
这与补偿舷梯所处初始状态的位姿是一致的,所得运动学模型和补偿舷梯实际情况相符,验证了D-H参数法的正确性。
继续对PX,PY,PZ中的θ1,θ2,D3进行求导得舷梯顶端的速度雅可比矩阵为:
| ${{ J}_{{V_P}}} = \left[ {\begin{array}{*{20}{c}} {s1s2(D3 + L4)}\!\!&\!\!{ - c1c2(D3 + L4)}\!\!&\!\!{ - c1s2} \\ { - c1s2(D3 + L4)}\!\!&\!\!{ - s1c2(D3 + L4)}\!\!&\!\!{ - s1s2} \\ 0\!\!&\!\!{ - s2(D3 + L4)}\!\!&\!\!{c2} \end{array}} \right]{\text{。}} \!\!\!\!$\!\! | (8) |
式(6)是机械臂运动学正解,它是接下来进行运动学分析的数学基础,式(8)舷梯顶端的速度雅可比矩阵可为求解补偿舷梯的各关节驱动力矩以及各坐标系相互之间的速度、加速动和力的转换关系找到一个很好的方法。
3.2 逆向运动学求解逆向运动学主要解决舷梯尖端欲达到特定位置时,其每个液压执行机构需要的运动,如补偿舷梯目标为舷梯末端点位移至海上设施登入口的点,逆向运动学可以解出在这个过程中,舷梯的每个液压执行机构所需的位移。
整理式(6),将含有θ1的部分移到方程左边得:
| ${}_2^1{{ T}^{ - 1}}{}_1^0{{ T}^{ - 1}}{}_4^0{ T} = {}_3^2{ T}{}_4^3{ T}{\text{,}}$ | (9) |
即式(9)左边为:
| $\left[\!\!\!\! {\begin{array}{*{20}{c}} {{\rm{c}}1c2}&{c2s1}&{s2}&{ - L1s2}\!\! \\ { - c1c2}&{ - s1s2}&{c2}&{ - L1c2}\!\! \\ {s1}&{ - c1}&0&0\!\! \\ 0&0&0&1\!\! \end{array}} \!\!\!\!\right]\!\left[\!\!\!\! {\begin{array}{*{20}{c}} {c1c2}&{ - s1}&{ - c1s2}&{{P_X}}\!\! \\ {s1c2}&{c1}&{ - s1s2}&{{P_Y}}\!\! \\ {s2}&0&{c2}&{{P_Z}}\!\! \\ 0&0&0&0\!\! \end{array}} \!\!\!\!\right]{\text{,}}$ | (10) |
式(9)右边为:
| ${}_4^2T = {}_3^2T{}_4^3T = \left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&0&1&{D3 + L4} \\ 0&{ - 1}&0&0 \\ 0&0&0&1 \end{array}} \right]{\text{。}}$ | (11) |
令式(10)和式(11)两边的元素(3,4)相等得:
| $s1{P_X} - c1{P_Y} = 0{\text{,}}$ | (12) |
通过进行三角恒等变换求解这种形式的方程,设
| ${\theta _1} = A\tan 2({P_Y}, {P_X}){\text{,}}$ | (13) |
同理,令式(10)和式(11)两边的元素(1,4),(2,4)相等,得:
| $ \begin{split} c1c2{P_X} + c2s1{P_Y} + s2{P_Z} = &0 - c1c2{P_X} - s1s2{P_Y} + \\ &c2{P_Z} = D3 + L4 {\text{,}} \end{split} $ | (14) |
根据舷梯的要求考虑操作范围,求得:
| $\begin{aligned} & {\theta _2} = A\tan 2({P_X}, \cos ({\theta _1})(L1 - {P_Z})) {\text{,}} \\ & D3 = \frac{{{P_X}}}{{ - \cos ({\theta _1})\sin ({\theta _2})}} - L4 {\text{。}} \end{aligned} $ | (15) |
通过求解上面的系统方程并根据要求考虑操作范围,对于给定的舷梯顶端位置,求得符合舷梯运动的运动学逆解如下:
| $\begin{aligned} & {\theta _1} = A\tan 2({P_Y}, {P_X}) {\text{,}} \\ & {\theta _2} = A\tan 2({P_X}, \cos ({\theta _1})(L1 - {P_Z})) {\text{,}} \\ & D3 = \frac{{{P_X}}}{{ - \cos ({\theta _1})\sin ({\theta _2})}} - L4 {\text{。}} \end{aligned} $ | (16) |
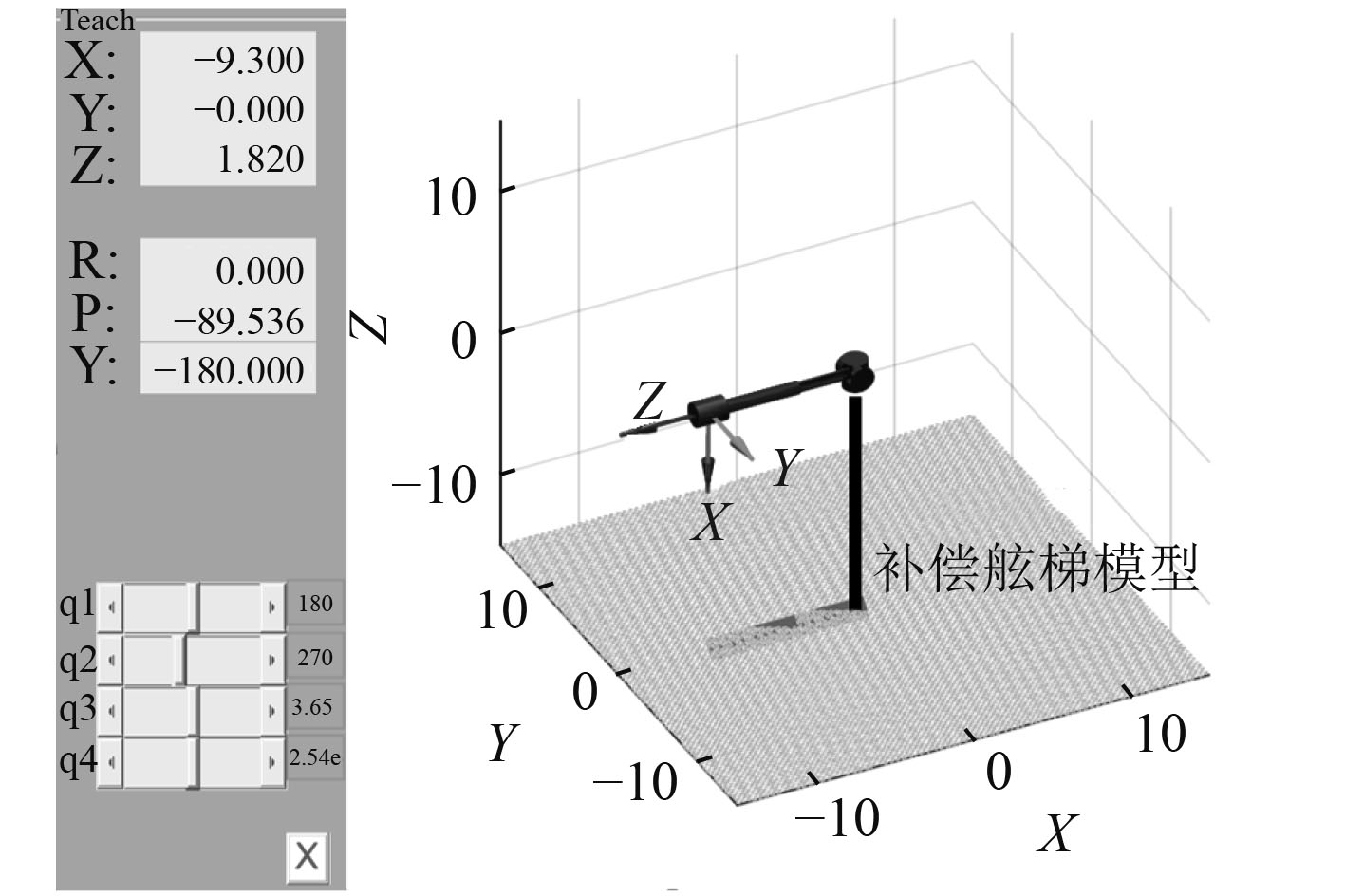
D-H参数法求运动学正逆解可以通过Matlab中的Robotics Toolbox组件进行计算验证。把补偿舷梯参数输入到Robotics Toolbox组件中得到其在运动空间中的活动范围,如图4所示。通过移动组件中q1,q2,q3,q4按钮,可以验证舷梯运动可行性和以上正逆解计算的正确性。
|
图 4 Robotics Toolbox中舷梯运动学模型 Fig. 4 Gangway model in Robotics Toolbox |
由于补偿舷梯系统通过俯仰和伸缩运动来抵消波浪引起的船舶运动,因此船舶运动方程是设计补偿舷梯的前提和重要因素。
船舶在波浪影响下典型的运动为竖直方向的上下升沉伴有横摇、纵摇和偏航,以上下升沉和横摇为主,运动规律类似正弦运动[8]。本文模拟1 000 t海洋工程船在航向角为90°,海况等级为6级,义波高为5.7 m的海洋环境下,假设船在舷梯基坐标系{0}的Y方向和Z方向的移动近似于正弦曲线,在Y方向上做频率为0.1 Hz,振幅为10°的横摇运动,Z方向做频率为0.1 Hz,振幅为1 200 mm的升沉运动。
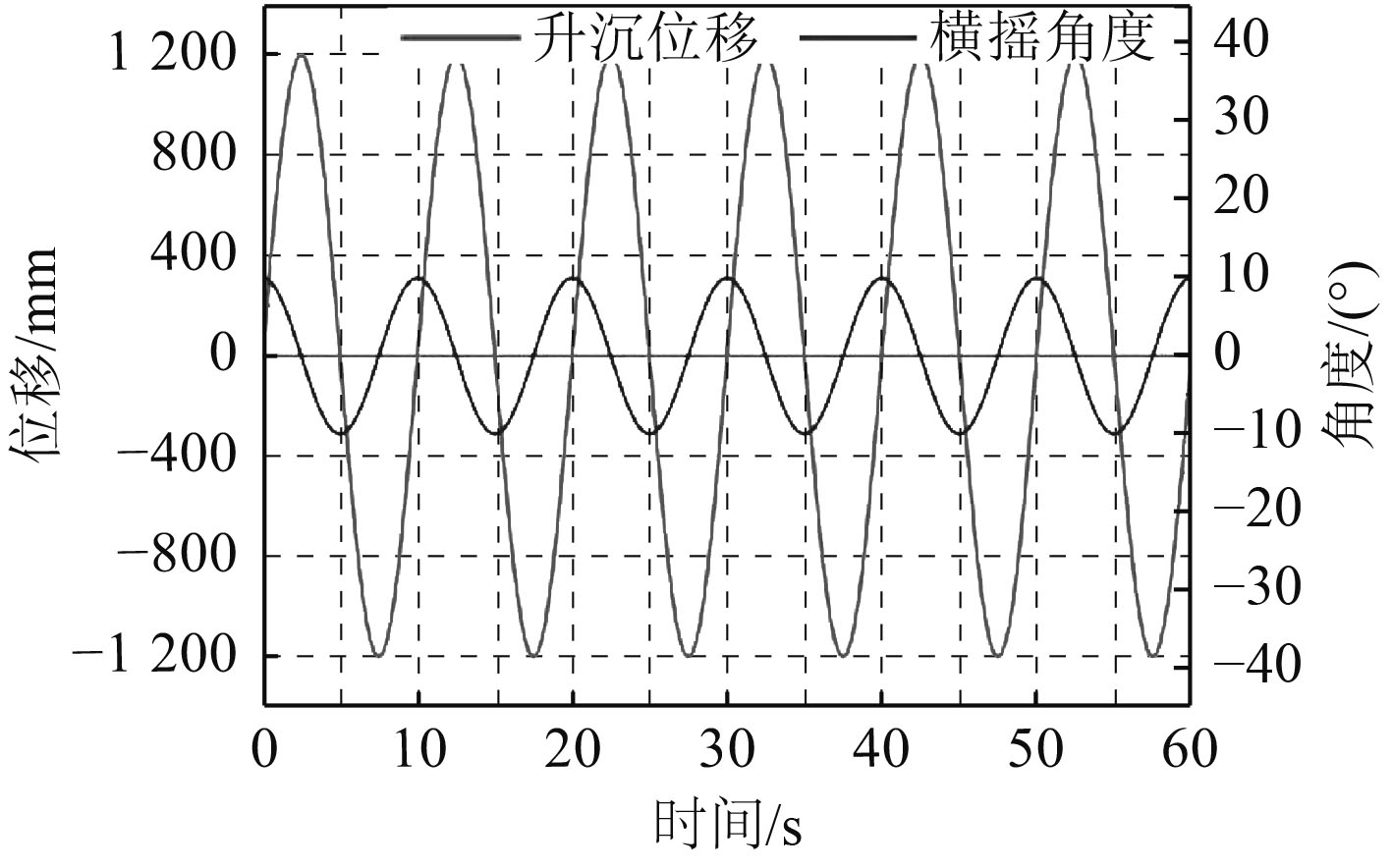
由于波浪的作用,船舶在横摇与升沉运动之间存在一定的相位差,可简化地认为当船舶处于波浪的波峰或波谷时,横摇角正好处于0的位置,当船舶处于平衡位置时,横摇角却正好是最大值,由此Z轴方向的升沉运动与绕Y轴的横摇运动两者频率相同,相位角相差90°,海洋工程船做此复合运动时的运动曲线如图5所示。
|
图 5 复合运动时的运动曲线 Fig. 5 The compound motion curve |
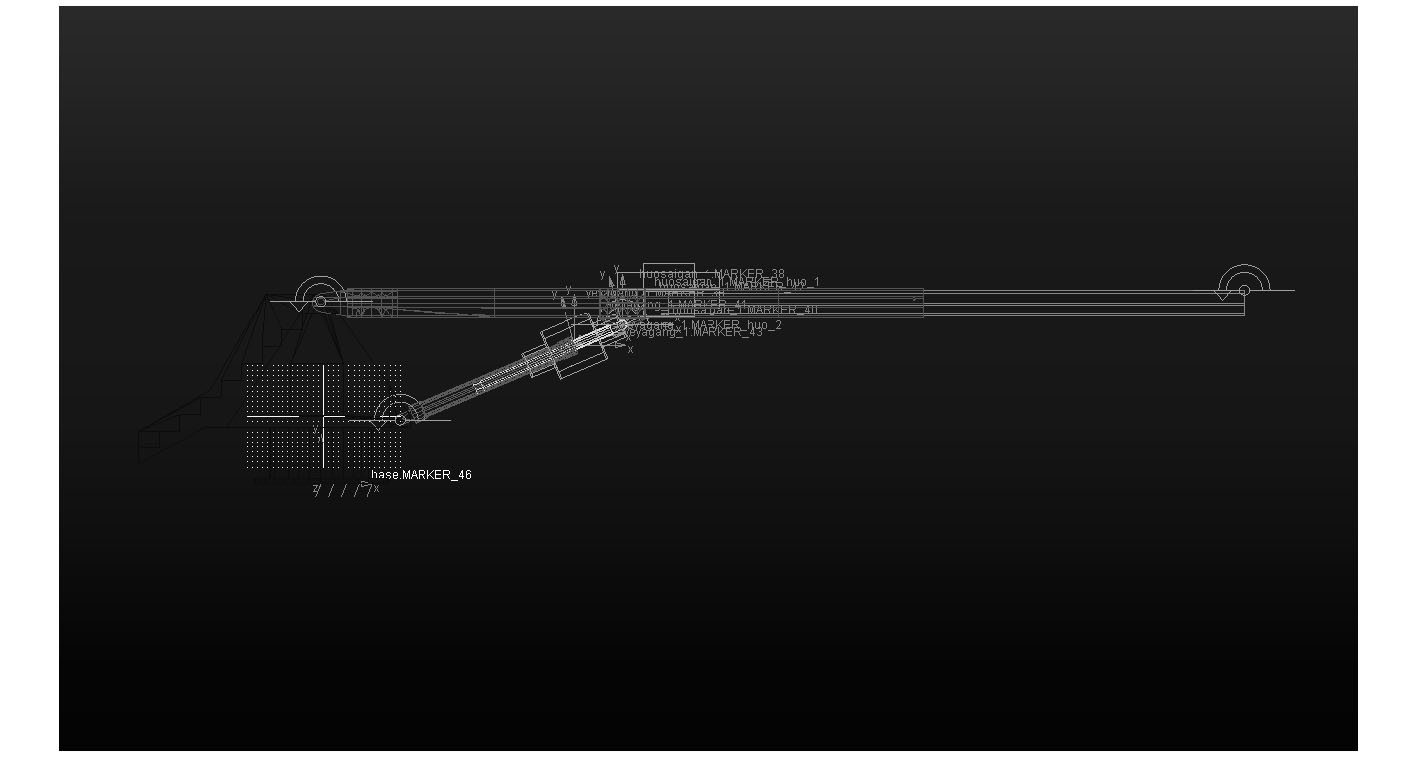
将SolidWorks中建立的补偿舷梯以Parasolid形式导入到ADAMS中,在ADAMS中建立补偿舷梯虚拟样机,如图6所示。在建立虚拟样机之前,首先对软件进行环境设置,包括坐标系、加速度、质量、力、角度、时间进行设置,统一使用MMKS(mm/kg/N/s)单位制[9]。
|
图 6 补偿舷梯ADAMS虚拟样机模型 Fig. 6 Virtual prototype of gangway system in ADAMS |
在Solidworks中建立的模型导入ADAMS后其物理属性会全部丢失,故在ADAMS软件中需要重新对模型进行实体化及添加驱动和运动副才能完成运动学仿真[10]。根据补偿舷梯运动的实际工况为虚拟样机模型添加运动副,驱动后舷梯可以按照设计的轨迹运动,其约束分配情况如表3所示。
|
|
表 3 补偿舷梯各构件之间的约束 Tab.3 Constraints between components of gangway system |
为了模拟补偿舷梯的实际工作环境,将船舶运动的数据导入到ADAMS运动仿真当中,设置舷梯顶端的初始位置如下:
|
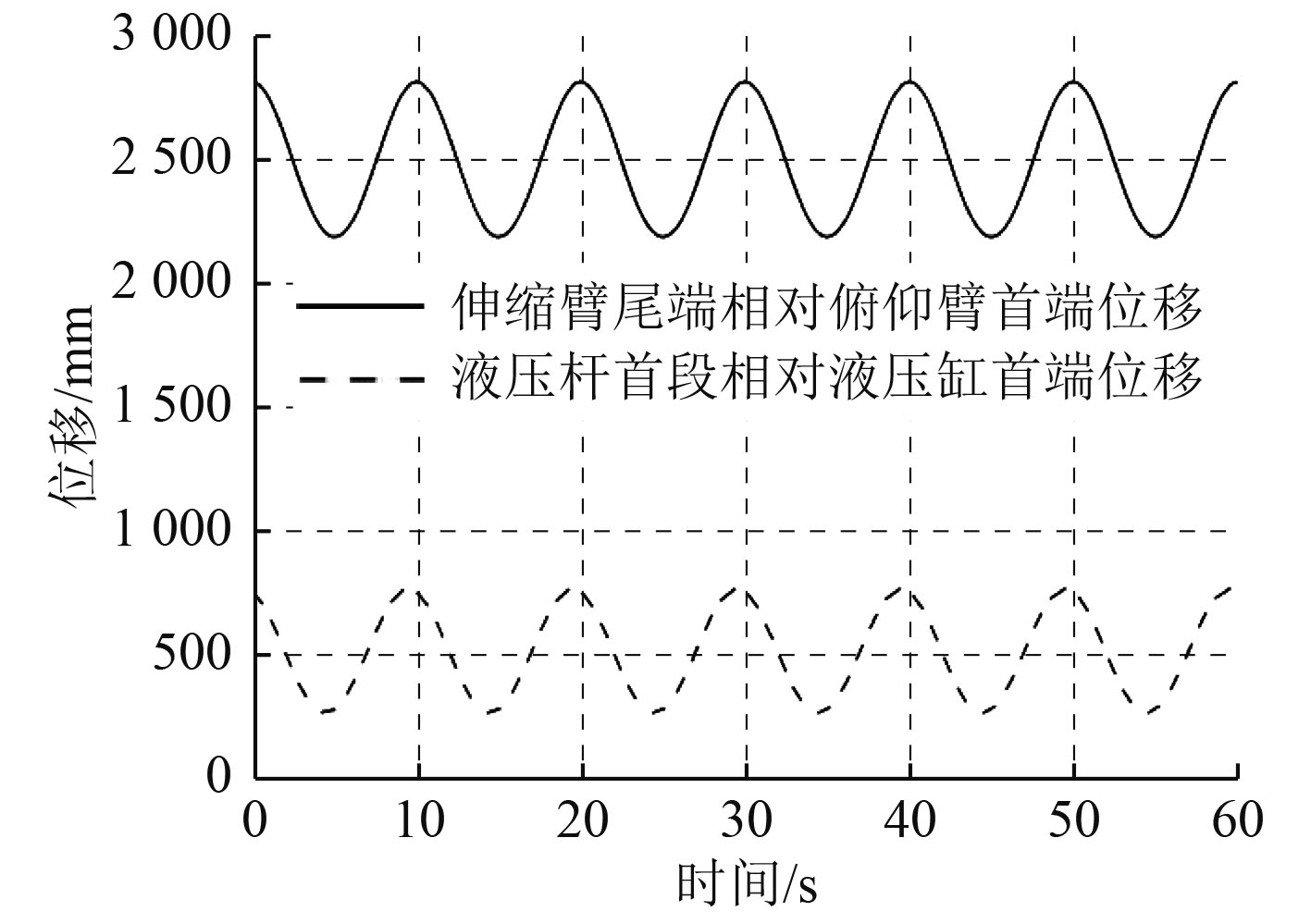
图 7 俯仰臂与伸缩臂位移曲线 Fig. 7 Displacement curve of gangway system |
|
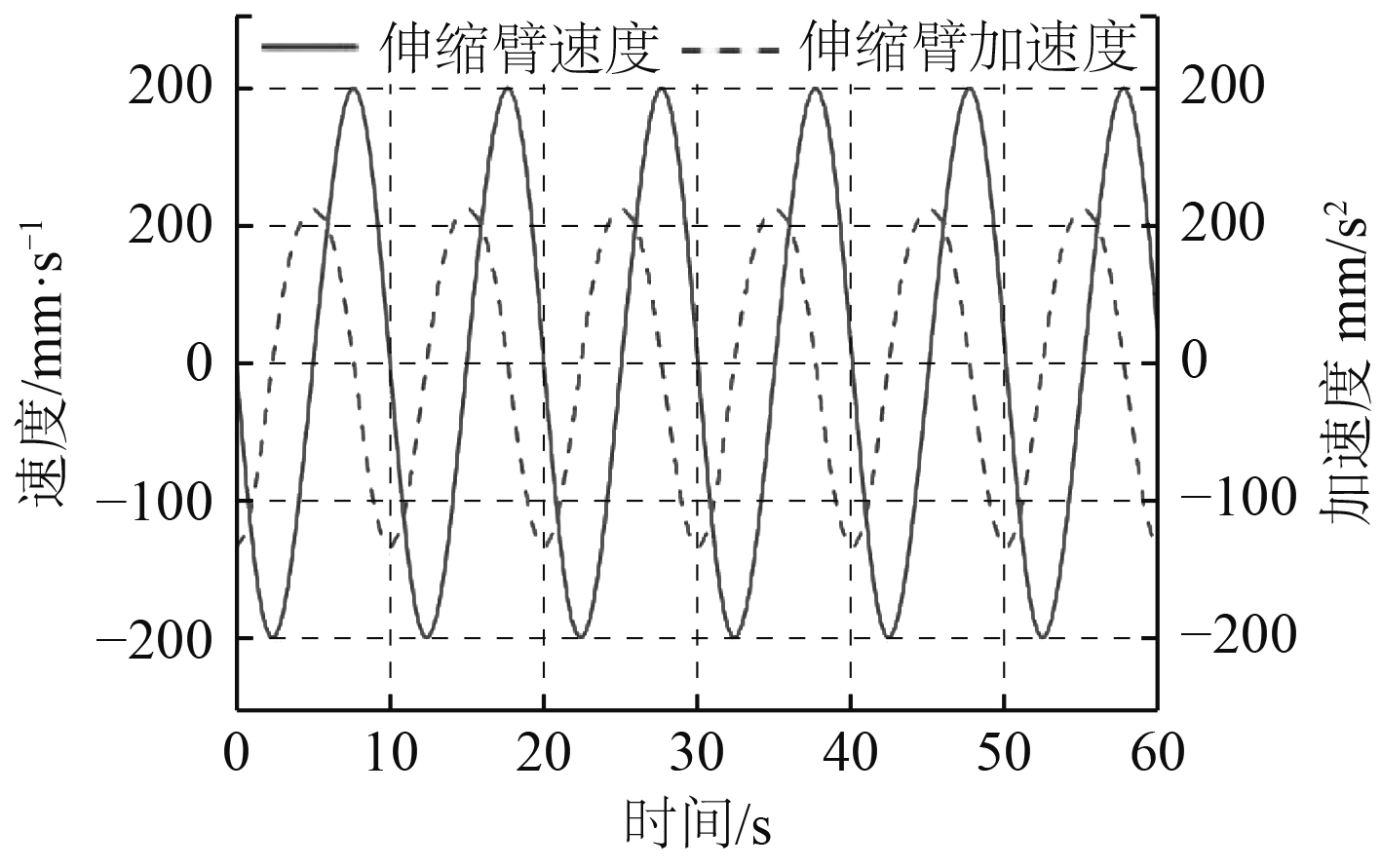
图 9 伸缩臂运动曲线 Fig. 9 Motion curve of telescopic arm |
|
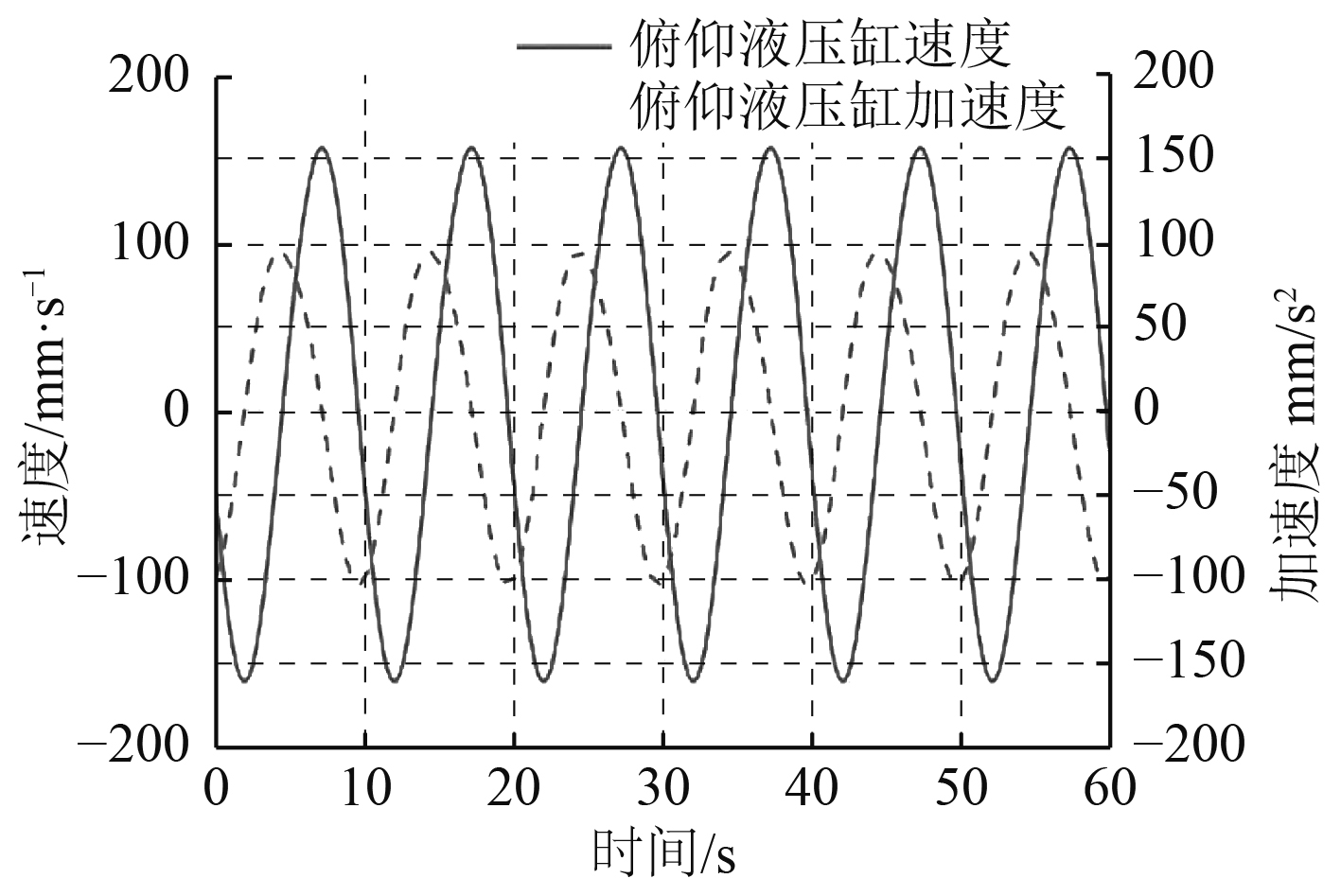
图 8 俯仰臂运动曲线 Fig. 8 Motion curve of pitch arm |
通过以上仿真可以得出各个关节在正常工作时的位置变化,得出俯仰臂液压缸与伸缩臂的位移峰值,俯仰臂液压缸最大位移为247.18 mm,伸缩臂最大位移为311.43 mm,为机械臂后续的结构设计和优化提供依据。从仿真结果可以看出,波浪补偿舷梯俯仰液压缸和伸缩臂的运动规律均呈周期性变化,其中在静止到启动阶段和换向时刻加速度较大。
5 结 语本文基于DNVGL-ST-0358设计规范设计一大型补偿舷梯,并在Solidworks中建立简化模型。研究了补偿舷梯运动学建模方法,根据D-H参数法推导出其空间运动的变换矩阵,对补偿舷梯正逆运动学进行求解并验证,证明了该算法的有效性和可行性。通过ADAMS运动学仿真出各执行器运动曲线,分析了舷梯运动部件的运动特性,为后续大型补偿舷梯执行机构选型及控制系统的研究提供参考。
| [1] |
刘赐贵. 坚决扛起建设海洋强国的历史使命[J]. 求是, 2016, 15: 20-22. DOI:10.3969/j.issn.1003-4641.2016.03.04 |
| [2] |
王哲骏, 谢金辉, 高剑, 等. 波浪补偿技术现状和发展趋势[J]. 舰船科学技术, 2014(11): 1-7. DOI:10.3404/j.issn.1672-7649.2014.11.02 |
| [3] |
边信黔. 船舶动力定位[M]. 北京: 科学出版社, 2011.
|
| [4] |
D. J. CERDA SALZMANN. Development of the access system for offshore wind turbines[D]. Technische Universiteit Delft, 2010.
|
| [5] |
Feilong YU. Modeling, Simulation and control of motion compensated gangway in offshore operations[D]. Norwegian University of Science and Technology, 2017.
|
| [6] |
白玉, 胡永攀. 海上并靠补给波浪补偿技术发展趋势[J]. 船舶与海洋工程, 2016, 32(5): 1-4. |
| [7] |
顾永凤, 邱广庭, 谢荣, 等. 6级海况下波浪补偿装置平台的机构优化设计[J]. 舰船科学技术, 2017, 39(21): 141-145. |
| [8] |
黄瑞佳, 邵宇鹰, 施光林. 具有波浪补偿功能的电液提升控制系统仿真研究[J]. 机电一体化, 2014, 20(4): 7-11. DOI:10.3969/j.issn.1007-080x.2014.04.002 |
| [9] |
陈峰华. ADAMS 2012虚拟样机技术从入门到精通[M]. 北京: 清华大学出版社, 2013: 21-32.
|
| [10] |
陈罡, 周奇才, 吴菁. 七自由度机械臂的ADAMS/MATLAB联合仿真研究[J]. 系统仿真学报, 2017, 29(1): 99-106. |
 2019, Vol. 41
2019, Vol. 41
