0 引　言

我国首艘海洋核动力平台（以下简称平台）是搭载有核动力装置的非自航船型浮式平台，采用软刚臂长期系泊于渤海海域，可为周围采油平台等用户提供电能和淡水。

为保证平台安全以及核安全，需要在设计阶段针对平台可能遭受到的极限环境载荷进行估算，从而使平台具有足够的结构强度。一般情况下，环境载荷中的波浪载荷是校核平台结构强度的关键载荷，因此选取科学合理的方法计算平台的波浪载荷至关重要^[1]。

结构物在波浪作用下，波浪载荷具有随机性和复杂动力性，难以精确计算。目前普遍采用动态力静力化或用准静力的方法等效设计出一定概率水平的规则波施加在平台上，用于波浪载荷计算和校核结构强度，即所谓的等效设计波法^[2]。

本文采用确定性法、随机性法和长期预报对平台波浪载荷进行计算，并得到不同方法对应的设计波参数，为平台的结构设计与强度校核提供参考。

1 设计波法原理

设计波法一般是根据波浪载荷等效原则确定一组规则波，使得结构物在该规则波下受到一定概率水平的最大波浪载荷，该方法的关键在于如何确定设计波参数（波高、频率、浪向角和相位角）。

1.1 载荷控制参数

强度校核一般只针对几种主要波浪载荷进行，因此选取这些主要波浪载荷作为设计波法的载荷控制参数。ABS，BV和DNV规范^{[3 – 5]}对载荷控制参数的规定如表1所示。

载荷控制参数不同，其校核的船体构件侧重也不同。本文选取ABS规范规定的5种波浪载荷用于设计波的计算。

1.2 浪向角和频率

设计波法的计算主要分为两部分：载荷控制参数RAO的计算和载荷极值预报^[6]。其中，采用三维势流理论计算船体在单位规则波中的载荷幅值响应算子RAO是载荷极值预报的基础，因此选取合理的浪向角和频率的范围和步长至关重要。

确定性法和随机性法认为各动载荷成分的RAO包含所有可能遇到的浪向角，考虑到船体的对称性，因此浪向角的选取范围为0°（随浪）到180°（迎浪），步长15°^[7]。但对于长期预报，在拖航状态时，认为各浪向出现的概率相同，在单点系泊状态作业时，应根据具体海域和作业情况确定各个浪向角的发生概率。

波浪频率的范围需根据作业海域具体的波浪条件进行选取，一般推荐的做法是从0.2 rad/s到1.8 rad/s，步长0.05 rad/s。

1.3 确定性法

确定性法以给定的极限规则波波陡为基础来确定设计波波高^[8]。由于只考虑了规则波，因此该方法计算简便，主要流程如下：

1）由选定的频率范围按照给定的波陡公式生成一系列极限规则波；

2）在某一浪向下，将极限规则波波幅与对应的载荷控制参数RAO相乘得到载荷预报值；

3）在选定的浪向范围内，取载荷预报最大值对应的频率和波高作为设计波的频率和波高；

4）取载荷控制参数RAO最大值对应的浪向和相位角作为设计波的浪向和相位角，为区分船体的受力状态，相位角分为中拱相位和中垂相位。

DNV规范规定，对于短期不规则波海况，平均波陡由下式确定：

$ {S_s} = {{2{\text{π}} {H_s}}/{\left( {gT_z^2} \right)}}{\text{。}} $

(1)

式中： ${S_s}$ 为平均波陡； ${H_s}$ 为有义波高； ${T_z}$ 为平均跨零周期。

对于中国渤海海域，由于缺乏针对性的规则波波陡统计，因此本文基于已知的渤海万年一遇短期海况参数 ${S_s} = 8.5\;{\rm{m}}$ 和 ${T_z} = 9.03\;{\rm{s}}$ ，采用式（1）得到渤海海域的平均波陡为 ${S_s} = 0.066\;75$ 。

对于在某一持续时间（一般取3 h）内保持稳定的短期海况，用 ${T_z}$ 将其割分为 $N$ 个波，则 $N$ 个波高的期望平均最大值的近似表达式为：

$ E\left( {{H_N}} \right) = 2\left[ {\sqrt {2\ln N} + \frac{\gamma }{{\sqrt {2\ln N} }}} \right]\sqrt {{m_0}} {\text{。}} $

(2)

式中： $\gamma $ 为欧拉常数， $\gamma = 0.577\;2$ 。

由式（2）计算得到渤海万年一遇规则波的最大波高为：

${H_{\max }} = E\left( {{H_{1196}}} \right) = 16.65\;{\rm{m}}{\text{。}} $

(3)

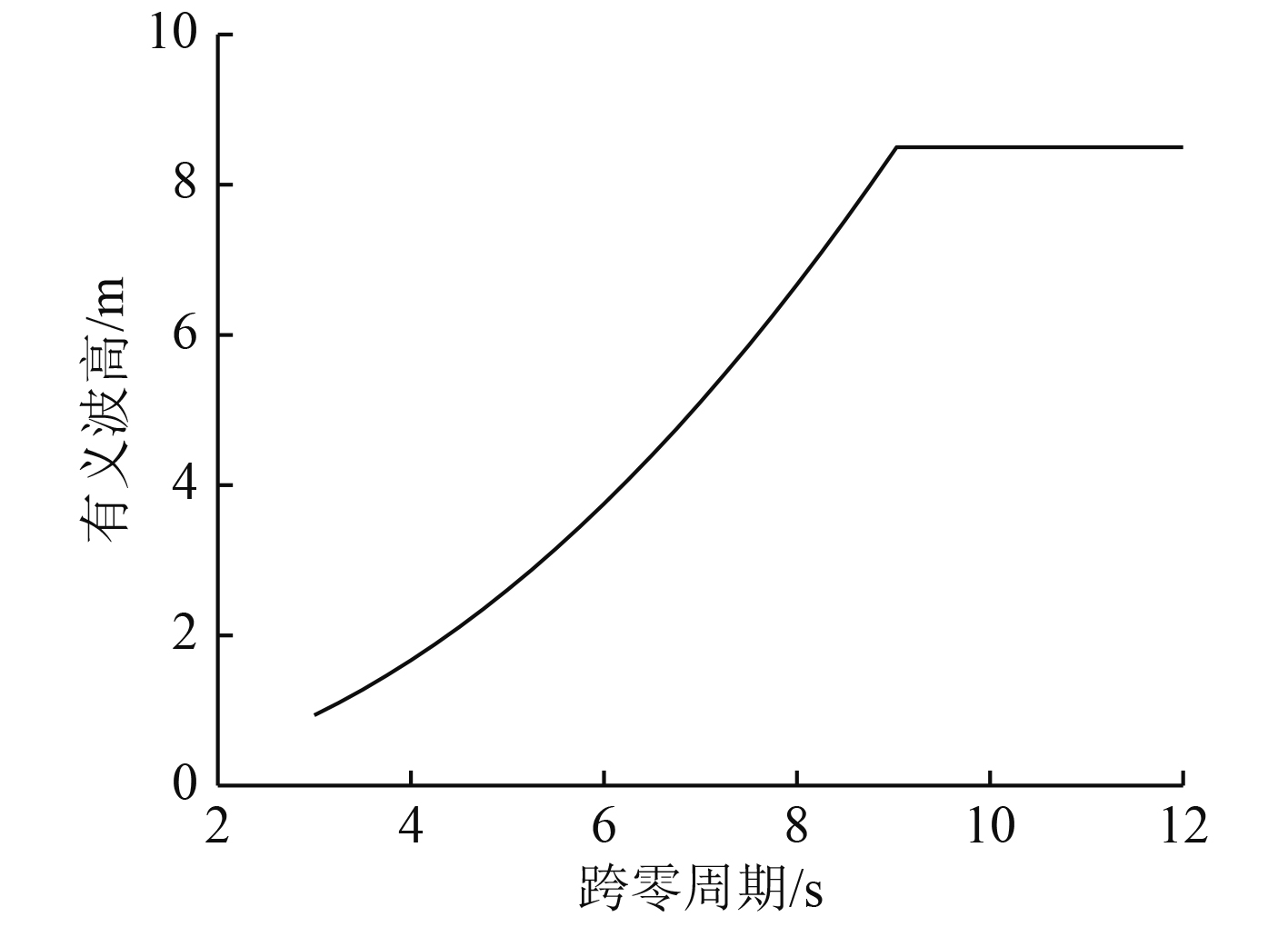
基于波陡不随频率变化的推荐方法，由选定的频率范围和已知的渤海平均波陡由式（1）生成极限规则波。但应注意，波高不得超过渤海万年一遇规则波的最大波高，因此合理的做法是将极限规则波波高进行截断，最终得到的极限规则波如图1所示。

1.4 随机性法

当波浪以谱的形式表示时，一般采用随机性法来确定设计波参数，该方法是以短期预报，即每个载荷控制参数的短期响应最大值为基础的^[9]。由于考虑了波浪的随机性和不规则性，因此该方法更加科学、合理。

在缺乏海况长期预报的情况下，由给定波陡生成一系列短期海况，采用合适的波浪谱，并结合载荷控制参数RAO曲线，最终得到该载荷参数的响应谱，计算公式如下式：

${S_R}\left( \omega \right) = {\left[ {RAO\left( \omega \right)} \right]^2}{S_W}\left( \omega \right){\text{。}} $

(4)

式中： ${S_R}\left( \omega \right)$ 为载荷参数响应谱； ${S_W}\left( \omega \right)$ 为波浪谱。

基于波浪载荷响应的幅值服从Rayleigh分布的前提条件，概率密度特征参数由响应谱的零阶矩决定，因此某一短期海况下波浪载荷响应的最大值为：

${R_{\max }} = \sqrt {2\ln N} \sqrt {{m_0}} {\text{。}}$

(5)

式中： ${m_0} = \displaystyle\int_0^\infty {{S_R}\left( \omega \right)} {\rm d}\omega $ 为响应谱零阶矩；循环次数 $N = {D/{{T_R}}}$ ， $D$ 为波浪持续时间（一般取3 h）， ${T_R}$ 为平均响应跨零周期， ${T_R} = 2{\text{π}}\sqrt {{{{m_0}}/{{m_2}}}} $ 。

由Rayleigh分布的特性可知，波浪载荷响应大于由式（5）计算得到的最大值的概率大约为63.2%，即危险率为63.2%。所以在设计中，有时为了计及海况资料的不可靠性或从使用要求进一步考虑船体结构的安全性，往往引入更小的危险率 $\alpha $ ，此时波浪载荷响应最大值为：

${R_{\max }} = \sqrt {2\ln {N/\alpha }} \sqrt {{m_0}} {\text{，}}$

(6)

设计波波幅由 $i$ 个短期海况预报的 ${\left( {{R_{\max }}} \right)_i}$ 中的最大值 ${R'_{\max }}$ 与该载荷响应 $RA{O_{\max }}$ 比值得到：

${A_D} = \left( {{{{{R'}_{\max }}}/{RA{O_{\max }}}}} \right) \cdot LF{\text{。}} $

(7)

式中 $LF$ 为载荷参数，在1.1～1.3之间取值，本文取1.2。设计波的频率、浪向和相位角由RAO最大值决定。

1.5 长期预报

短期预报认为浪向是等概率发生的，但对于单点系泊船体，风标效应使得船体基本都处于迎浪状态，因此在计算过程中需要计及浪向概率分布。长期预报认为不同海况组成的短期预报是互相独立的，波浪载荷的长期预报值是各短期预报值和浪向概率分布的加权组合，如下式：

$ \begin{split} & P\left( {X \!>\! x} \right) \!=\\ & \sum\limits_i {\sum\limits_j {\sum\limits_k {{p_i}\left( {{H_s},{T_z}} \right){p_j}\left( \beta \right)} } } {p_k}\left( V \right)\exp \left( {{{ - {x^2}}/{2{\sigma ^2}}}} \right) \end{split}{\text{。}} $

(8)

式中： $P\left( {X > x} \right)$ 为超越概率； ${p_i}\left( {{H_s},{T_z}} \right)$ 为短期海况 $\left( {{H_s},{T_z}} \right)$ 发生的概率； ${p_j}\left( \beta \right)$ 为浪向概率分布； ${p_k}\left( V \right)$ 为航速发生的概率，一般取为1，即认为航速为定值； ${\sigma ^2} = 2{m_0}\left( {{H_s},{T_z},{\beta _j},{V_k}} \right)$ ； ${m_0}$ 为波浪载荷的方差；通过对波浪载荷的谱分析得到，本文选用JONSWAP谱。

给定重现期和 ${T_z}$ 就可以确定重现期内波浪的个数 $N$ ，从而可以得到该重现期内超越概率为 ${1/N}$ 对应的载荷最大值。本文选取渤海海域万年一遇海况参数，其中 ${T_z} = 9.03\;{\rm{s}}$ ，由此可得 $P{\rm{ = 2}}{\rm{.86E - 11}}$ 。

设计波的波幅由载荷预报最大值和 $RA{O_{\max }}$ 的比值求得，频率、浪向角和相位角由 $RA{O_{\max }}$ 决定。长期预报需要给定作业海域以短期海况出现次数的长期统计为基础的波浪散布图，目前中国渤海海域的波浪统计主要为方钟圣编写的西北太平洋波浪统计集中的B1区块，本文只考虑该区块全年所有方向的波浪统计。

2 计算参数

平台的水动力模型如图3所示，选取4种典型的装载工况：工作状态（LC1）、工作结束（LC2）、拖航离港（LC3）和拖航到港（LC4），其中LC1和LC2为正浮状态，LC3和LC4会有小幅的首倾。

3 计算结果与分析 3.1 RAO计算结果

RAO的计算结果分为两部分：适用于确定性法和随机性法的0°～180°浪向等概率分布的RAO结果，如表2～表5所示，和适用于长期预报的具有浪向概率分布的RAO结果，其中LC1和LC2中180°，165°和150°的浪向概率分布分别为60%，30%和10%，如表4～表7所示。

3.2 计算结果

3种方法得到的设计波参数和载荷最大值如表8和表9所示，其中确定性法对应的设计波浪向角和相位角以及随机性法对应的设计波频率，浪向角和相位角同表2～表5，长期预报对应的设计波频率，浪向角和相位角同表4～表7。

3.3 结果分析

综合表8和表9中的设计波参数，分析如下：

1）在LC1和LC2时，由于考虑的浪向概率分布，长期预报的RAO幅值一般比确定性法和随机性法小，而对应的频率比较大。

2）3种方法得到的载荷最大值由大到小依次为确定性法、随机性法和长期预报，对应的设计波波高大小趋势与载荷最大值相同，这符合计算方法越合理，计算结果越小的趋势。由确定性法和长期预报得到的同一载荷控制参数对应的设计波波高相差1倍左右。

3）对于随机性法，引入的危险率越小，最终得到的设计波波高和载荷最大值也就越大。危险率为5%时的载荷最大值和设计波波高比危险率为63.2%的结果增大20%，进一步考虑了平台结构的安全性。

4 结　语

1）确定性法步骤简单，得到的设计波波高和载荷最大值也比较大，偏于保守，适合设计初期对波浪载荷的估算。

2）随机性法由于考虑了波浪的随机性和不规则性，比确定性法较为合理，在计算中可根据实际情况选取合适的危险率。

3）长期预报在3个方法中最科学合理，可作为最终波浪载荷计算和校核平台结构强度的计算输入。