概率假设密度(PHD)滤波是一种基于随机有限集理论的多目标贝叶斯滤波,对多目标跟踪过程中的目标随机出现、分裂、消失、漏检和虚警杂波等现象有着严格的数学描述,它代表着多目标跟踪技术的一个新方向[1]。通常,实现递推传递概率假设密度函数的多目标跟踪算法比较困难,Vo等利用粒子滤波技术给出了PHD滤波器的近似实现形式[2],简称为PF-PHD滤波算法,这就加快了PHD滤波的工程应用。
文献[3]中将势分布概率假设密度滤波(CPHD)应用于水下多目标跟踪,并针对传感器量测的不确定性,在CPHD滤波的框架下引入量测的幅值信息,增加数据关联的可靠性。文献[4]探究了基于多波束前视声呐数据的2种不同多目标跟踪方法,一种方法是给每个目标分配卡尔曼滤波器,通过设定量测门限和数据关联技术进行目标跟踪,另一种是应用PF-PHD滤波算法结合数据关联技术的目标状态估计。仿真表明PHD滤波器比传统卡尔曼滤波方法更优越。文献[5]利用声信号得到目标的距离测量信息,采用蒙特卡罗方法实现的PHD滤波器成功地跟踪3个水下自主航行器(AUV)。文献[6]通过单一的水下传感器获得目标位置量测信息,针对杂波存在时,通常的跟踪算法仅依赖当前的位置观测,故使用高斯混合概率假设密度(PHD)前向-后向平滑算法,它是利用多个量测数据对滤波值进行平滑,进而减小目标估计的位置误差。结果表明在高密度杂波的水下环境中该算法表现良好。
目前大部分文献侧重研究目标的主动跟踪,实际上,被动跟踪在某些方面更具应用价值。本文采用PF-PHD滤波算法对监测区域内目标进行跟踪,并利用双被动声呐[7]来获得目标的方位角信息。
1 双被动声呐系统观测模型假设二维监测区域内有多个目标,采用匀速运动(CV)模型模拟每个目标的位置变化情况。采样时间为
| ${x_k} = { F}{x_{k - 1}} + { G}{w_k}\text{,}$ | (1) |
其中,
假设观测平台上装备有仅得到目标角度观测信息的2部被动声呐基阵,等效于雷达跟踪中的2个测向传感器,那么这里传感器个数为2,接下来文中描述的单个传感器均指单被动声呐基阵,并且假设被跟踪目标与声呐设备在一个平面上,以便研究算法特性。令
| ${\beta _{k,s}} = {\rm arc}\tan \frac{{{\rm{x}} - {a_s}}}{{{\rm{y}} - {b_s}}}\text{,}$ | (2) |
则对于第
| ${z_{k,s}} = {h_s}({x_k}) + v_k^s = {\beta _{k,s}} + v_k^s\text{,}$ | (3) |
式中:
多目标跟踪中当每一时刻目标数、杂波或虚警个数不同时,状态空间和量测空间的维数也会随之变化,此时目标跟踪的模型应表示为各个目标状态和量测的集合。基于随机集理论的跟踪模型有着坚实的数学基础,能准确地描述多目标跟踪中目标产生、消失、衍生等现象。
假设在采样时刻
| $ {X_k} \!\!= [\mathop \cup \limits_{{x_{k - 1}} \in {X_{k - 1}}} \!\!\!\!\!\!\!{S_{k\left| {k - 1} \right.}}({x_{k - 1}})] \cup [\mathop \cup \limits_{{x_{k - 1}} \in {X_{k - 1}}} \!\!\!\!\!\!\!\!{B_{k\left| {k - 1} \right.}}({x_{k - 1}})] \cup {\varGamma _k}\text{。}\!\!\!\!\! $ | (4) |
其中:
| ${Z_k} = {K_k} \cup [\mathop \cup \limits_{{x_{k - 1}} \in {X_{k - 1}}} {\Theta _k}({x_{k - 1}})]\text{。}$ | (5) |
其中:
针对多目标跟踪中Bayes公式难求解的问题,Mahler提出了概率假设密度(PHD)滤波近似实现多目标Bayes滤波器,PHD滤波通过递推多目标后验密度的一阶统计矩来降低计算复杂度。
在
PHD滤波预测方程:
| $\begin{split} & {D_{k\left| {k - 1} \right.}}(x\left| {{Z_{k - 1}}} \right.) = \\ & \int {{\phi _{k\left| {k - 1} \right.}}} (x,{x_{k - 1}}){D_{k - 1\left| {k - 1} \right.}}({x_{k - 1}}\left| {{Z_{k - 1}}} \right.){\rm d}{x_{k - 1}} + {\gamma _k}(x)\end{split}\text{,}$ | (6) |
| ${\phi _{k\left| {k - 1} \right.}}(x,\xi ) = {b_{k\left| {k - 1} \right.}}(x\left| \xi \right.) + {e_{k\left| {k - 1} \right.}}(\xi ){f_{k\left| {k - 1} \right.}}(x\left| \xi \right.)\text{。}$ | (7) |
其中:
PHD滤波更新方程:
| $\begin{split} & {D_k}(x\left| {{Z_k}} \right.) = \Bigg[1 - {P_{D,k}} +\Bigg.\\ & \Bigg.\sum\limits_{z \in {Z_k}} {\frac{{{\psi _{k,z}}(x)}}{{{K_k}(z) + \langle {\psi _{k,z}},{D_{k\left| {k - 1} \right.}}\rangle }}}\Bigg] \cdot {D_{k\left| {k - 1} \right.}}(x\left| {{Z_{k - 1}}} \right.)\end{split}\text{。}$ | (8) |
其中:
对式(8)中的PHD函数
PF-PHD滤波是利用一系列离散的带权重的样本近似相应的PHD函数,通过聚类算法提取目标的状态估计,当粒子数目达到一定程度,PF-PHD滤波逼近Bayes最优估计,文献[2]详细介绍了粒子滤波实现PHD滤波的原理及具体步骤。
传统的PHD滤波器的应用前提是单传感器,对于多传感器的情况,也有相应的算法提出,比如一种利用所有传感器的量测更新PHD的迭代更新近似算法[8],以及Mahler提出的一种乘积形式的多传感器PHD滤波算法[9],这些算法的共同缺点是计算复杂度大。本文根据文献[10],采用集中式融合策略,在第k时刻,将各个传感器的观测统一送至数据融合中心,假定量测数据已完成配准及关联,这样就可以将多传感器问题转化为单传感器问题,进一步简化多目标跟踪算法。
3 仿真实验考虑二维监测区域范围为[–3000 m,3000 m] × [–3000 m,3000 m],进入监测区域的目标都作匀速直线运动且航速约40 kn,即20
1)实验1 单目标跟踪
假设监测区域内只有一个目标,沿横坐标
仿真中单个目标在
二维搜索得到的结果是当两传感器间距和目标初始链距以
进一步分析数据标准差,判断目标估计均方根误差对参数变化的敏感程度。固定每一个传感器间距
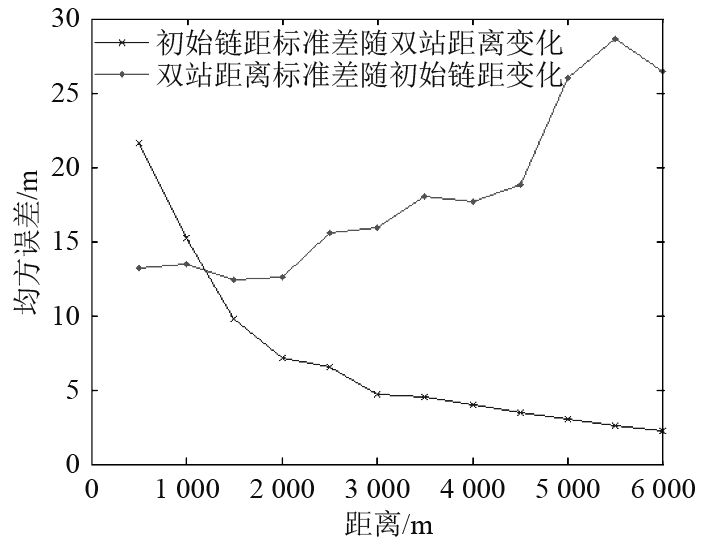
|
图 1 数据标准差变化 Fig. 1 Standard deviation of data |
图2表示目标估计均方根误差均值随传感器间距变化情况,其中均值指的是各初始链距对应均方根误差的均值。将实验2和实验3的传感器间距设置为
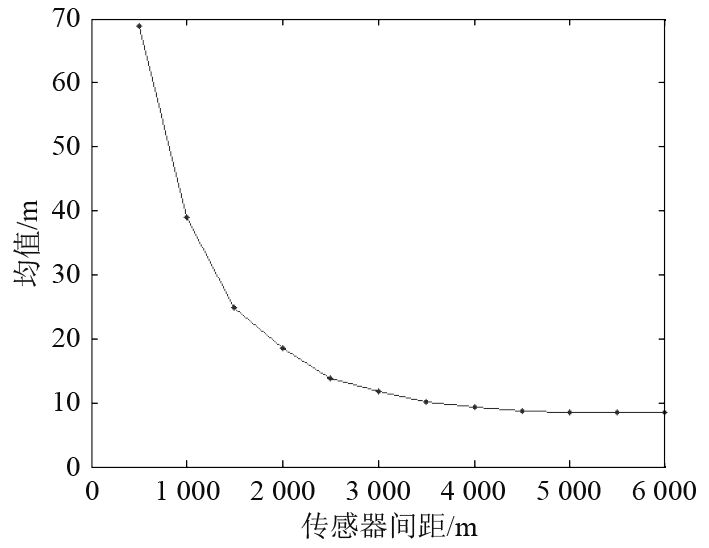
|
图 2 均方根误差均值变化 Fig. 2 Mean value of root mean square error |
2)实验2 多目标编队航行的场景
假设目标编队航行,各目标的间距为
假设监测区域内存在3个目标,位置单位为
图3描述了不同
|
图 3
不同
|
3)实验3 航迹交叉的场景
假设监测区域内存在3个目标,位置单位为
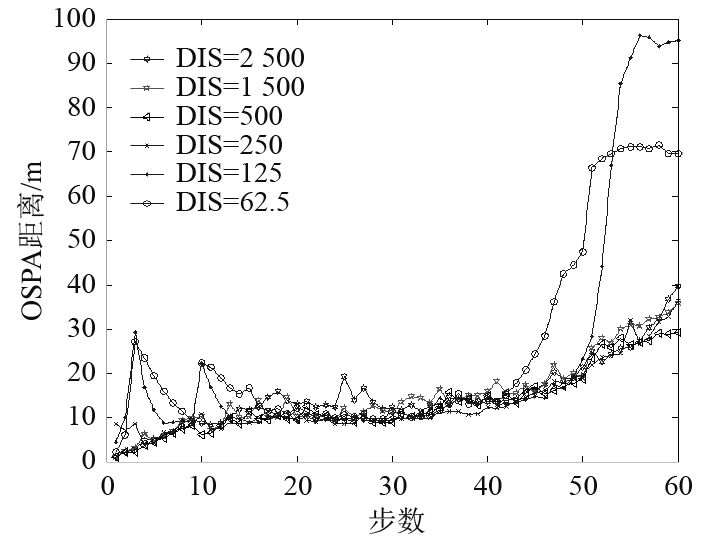
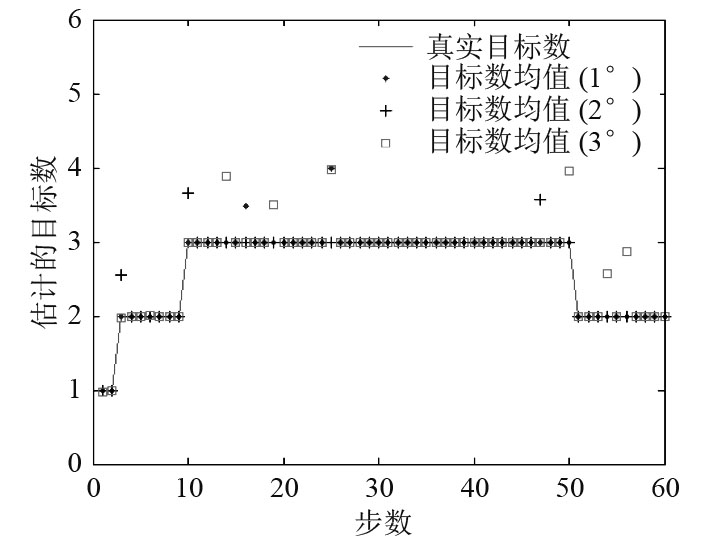
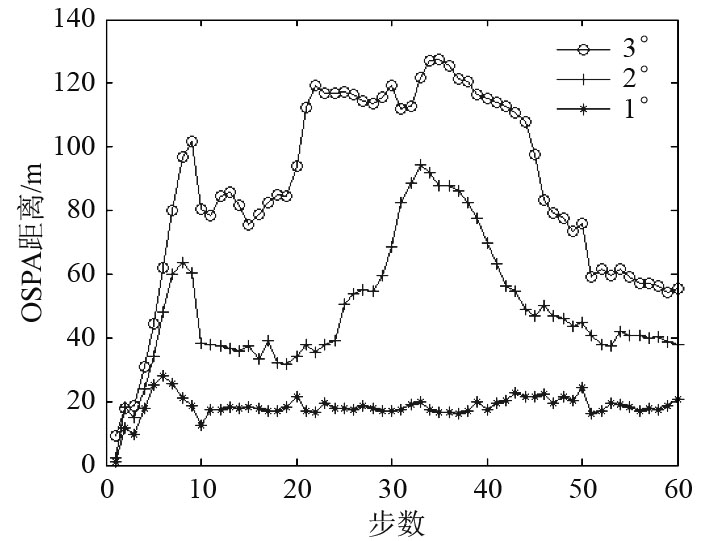
由图4~图6知,当目标航迹发生交叉时,量测角度误差保持在2°以下时,采用PF-PHD算法能够对监测区域内每时刻存在的目标进行跟踪,且目标跟踪精度很高。对于角度量测误差超过一定范围时,在航迹交叉点和交叉区域内目标跟踪偏离程度高,效果很差,因此算法对于声呐基阵的测向精度有一定要求。
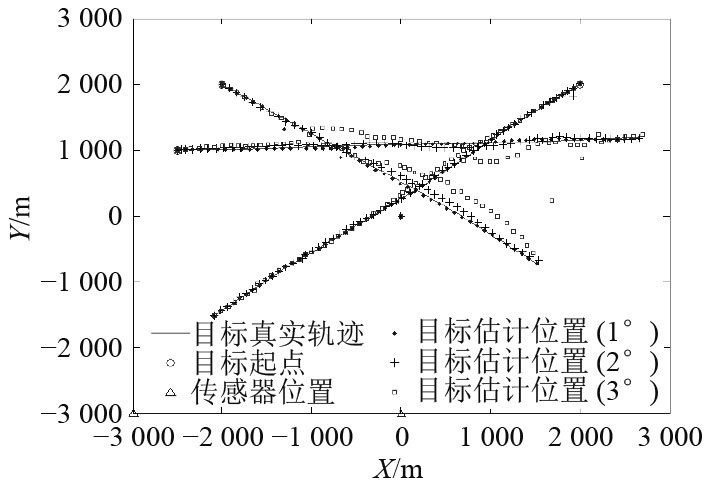
|
图 4 目标位置估计 Fig. 4 Target position estimate |
|
图 5 目标数估计 Fig. 5 Target number estimate |
|
图 6 OSPA距离 Fig. 6 OSPA distance |
本文研究了基于概率假设密度滤波的水下多目标跟踪技术,针对算法中两声呐距离和目标初始链距2个重要参数取值的问题,提出的二维搜索法能够有效指导实际目标跟踪中算法的参数选取,并且通过数据分析得出单目标跟踪的精度对于目标初始链距的变化比两声呐间距变化更敏感这一重要结论。同时,对于多目标编队航行和航迹交叉情况,仿真结果表明算法的高效性和稳定性。
| [1] |
MAHLER R. Random set theory for target tracking and identification. Data Fusion Hand Book. Boca Raton: CRC Press, 2001. 1–33.
|
| [2] |
VO B N, SINGH S, DOUCET A. Sequential Monte Carlo methods for multitarget filtering with random finite sets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1224-1245. DOI:10.1109/TAES.2005.1561884 |
| [3] |
章飞. 舰载多被动声纳多目标跟踪算法研究[D]. 南京: 东南大学, 2011.
|
| [4] |
CLARK D, RUIZ I T, PETILLOT Y, et al. Particle PHD filter multiple target tracking in sonar image[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(1): 409-416. DOI:10.1109/TAES.2007.357143 |
| [5] |
MELO J, MATOS A. A PHD filter for tracking multiple AUVs[C]//Oceans. IEEE, 2015: 1–8.
|
| [6] |
ZHANG S, ZHANG X, YU Y. A forward-backward PHD smoother for tracking multiple AUVs[C]//Oceans. IEEE, 2016: 1–6.
|
| [7] |
关欣, 何友, 衣晓. 双基阵纯方位水下被动目标跟踪性能仿真分析[J]. 系统仿真学报, 2003, 15(10): 1465-1466. |
| [8] |
MAHLER R P S. Multitarget Bayes filtering via first-order multitarget moments[J]. IEEE Transactions on Aerospace and Electronic Systems, 2004, 39(4): 1152-1178. |
| [9] |
MAHLER R. Approximate multisensor CPHD and PHD filters[C]//Information Fusion. IEEE, 2010: 1–8.
|
| [10] |
赵欣. 基于随机集理论的被动多传感器多目标跟踪技术[D]. 西安: 西安电子科技大学, 2009.
|
 2019, Vol. 41
2019, Vol. 41
