拖曳系统的振动传递不仅危害到拖曳缆的安全性,也对拖曳系统的运动稳定性能产生影响,由于拖曳系统在直航拖曳过程中是低阻尼和高刚度的系统,如Niedzwecki[1]的模拟结果所示,拖曳缆在规则波中运动形成的张力历程也服从规则的正余弦分布规律。但是在母船进行水平面操纵运动时,由于水流阻力沿着拖曳缆发生了变化,造成拖曳体沉深变化和冲击等现象,Ablow[2]模拟了较短拖曳缆回转运动中的拖曳体沉深历程,Huang[3]基于凝集参数法模拟了拖曳系统的全回转运动,具体的运动规律是拖曳系统完成回转运动的过程中,存在拖曳缆的大范围失速和跌落,造成了拖曳体的沉深陡增,尤其是回转半径较小的情况下,拖曳体的沉深显著增大,其中也包含了部分非线性响应行为。Zhu[4]模拟了母船完成指定的水面操纵运动轨迹情况下拖曳体的运动和张力历程,但是基于有限元的数值模型中采用了瑞利阻尼模型,这与水面操纵运动中的响应缆段部分失速造成的阻尼力差异较大。王志博[5]利用质量、刚度、阻尼的归纳方法建立动力学模型模拟了拖曳体在规则波中的运动响应。Wang[6]采用Ablow[2]的动力学模型模拟了母船水平面操纵参数对水下拖曳体的影响。由于Ablow方法将缆的运动受力高度耦合,不用给出基于经验的瑞利模型的参数,对拖曳系统进入回转运动后拖曳系统的响应计算更为准确。然而引起从冲击效应的结构出发建立模型,王志博[7]模拟了拖曳系统受强迫振动冲击作用。Huang[8],Chiou[9]和Driscoll[10]应用凝集参数法模拟了不同波浪运动状态下的冲击张力。Huang等[11]着重分析了拖曳缆受到的冲击对拖曳体运动稳定性的影响,但是上述研究基于长响应周期,缺乏瞬态冲击的效应描述。
本研究分析对瞬态冲击效应,通过应用改进的自适应数值模拟技术,模拟在短时内发生的回转冲击现象。由于缆的冲击张力现象和拖曳体的空间运动密不可分,本研究将拖曳体的空间运动与母船端的张力历程结合分析,对拖曳体沉深和侧向位移的变化与缆内张力的变化过程结合在一起进行分析。
1 动力学模型拖曳缆的放缆长度大缆的弯曲和扭转作用随着缆长的增大而逐渐变得微弱,本文将缆简化为柔性圆形横截面质量均匀分布的缆,在缆上任意截取微元ds,在缆元的切线方向、法线方向和副法线方向,按照右手法则建立当地坐标系O-tnb,在当地坐标系下缆受到水流阻力、水中重量(重力和浮力的差)、附加质量力、缆内张力的作用,依据牛顿第二定律Ablow对缆元受力建立了动力学模型,进而建立固定联结在大地的坐标系O-XYZ,应用欧拉转换关系可将当地坐标系转换到全局坐标系中。
任意缆元处Ablow推导的动力学方程控制方程可写成:
| ${M_{6 \times 6}}\frac{{\partial {Y_{6 \times 1}}}}{{\partial s}} = {N_{6 \times 6}}\frac{{\partial {Y_{6 \times 1}}}}{{\partial t}} + {Q_{6 \times 1}}\text{。}$ |
转换到全局坐标系O-XYZ中,系数矩阵M的非零元素包括:
| ${M_{1,1}} \!= \!{M_{2,2}} \!=\! {M_{3,3}} \!=\!{M_{4,4}} = 1,\;\;{M_{5,5}} \!=\! - T\cos \varphi ,\;\;{M_{6,6}} \!=\! T, $ |
非对角线的非零系数为:
| $ \begin{aligned} {M_{2,5}} =& {v_b}\cos \varphi ,{M_{2,6}} = - {v_n},{M_{3,5}} = - {v_b}\sin \varphi ,\;\;\\&{M_{3,6}} = {v_t},\;\;{M_{4,5}} = - {v_t}\cos \varphi + {v_n}\sin \varphi \text{。} \end{aligned}$ |
时间相关系数矩阵的非零变量为:
| $ {N_{1,1}} = - k{v_t},{N_{1,2}} = m,{N_{1,5}} = - {N_{6,5}} = {m_a}{v_b}\cos \varphi, $ |
| $\begin{aligned} &{N_{1,6}} = - {m_a}{v_n},{N_{2,1}} = e,{N_{3,6}} = e/k,\\&{N_{4,5}} = - e/k\cos \varphi ,{N_{5,1}} = - {m_a}k{v_b}, \end{aligned}$ |
| $ {N_{5,5}} = {m_a}{v_n}\sin \varphi - {m_a}{v_t}\cos \varphi ,{N_{6,1}} = - k{m_a}{v_n},{N_{6,6}} = m{v_t}\text{。} $ |
源项为缆元受到的水流阻力、水中重力和海流作用力分别写成:
| ${Q_1} = - w\sin \varphi + \frac{1}{2}\rho {\text{π}} d(1 + eT){C_t}{u_t}\left| {{u_t}} \right|\text{,}$ |
| ${Q_5} = {C_n}{(1 + eT)^{1/2}}{u_b}{(u_b^2 + u_n^2)^{1/2}} - \rho A{J_b}\text{,}$ |
| ${Q_6} = - w\cos \varphi + \frac{1}{2}{C_n}{u_n}{(u_b^2 + u_n^2)^{1/2}} - \rho A{J_n}\text{。}$ |
其中:w为单位缆长重量;ma为缆的附加质量系数;A为缆元迎流面积;
未知变量为缆内张力T、缆的运动速度
| $Y = {\left[ {\begin{array}{*{20}{c}} T&{{v_t}}&{{v_n}}&{{v_b}}&\theta &\varphi \end{array}} \right]^{\rm T}}\text{,}$ |
根据牛顿第二定律将拖曳体简化成为质点运动写成:
| ${M_b}\frac{{{d^2}S}}{{d{t^2}}} = F\text{。}$ |
质量系数矩阵写成:
| $ {M_{b1,1}} = m + {m_{ax}},\;\;{M_{b2,2}} = m + {m_{ay}},\;\;{M_{b3,3}} = m + {m_{az}}\text{,} $ |
| $ S = {\left[ {\begin{array}{*{20}{c}} X&Y&Z \end{array}} \right]^{\rm T}},F = {\left[ {\begin{array}{*{20}{c}} {{X_F}}&{{Y_F}}&{{Z_F}} \end{array}} \right]^{\rm T}}\text{,} $ |
| $ {X_F} = \frac{1}{2}\rho {U^2}L_x^2,{Y_F} = \frac{1}{2}\rho {U^2}L_y^2,{Z_F} = \frac{1}{2}\rho {U^2}L_z^2 + mg - \rho gV\text{。} $ |
其中:m为拖曳体质量;
本研究以Burgess推导的盒式格式为基础,在每一个时间步长内增加松弛因子,在时间步长内多次迭代计算满足求解精度要求,求解离散方程。
| $\begin{aligned} & \left[ {M_{j + 1}^{i + 1} + M_j^{i + 1}} \right]\frac{{Y_{j + 1}^{i + 1} - Y_j^{i + 1}}}{{\Delta {S_j}}} + \left[ {M_{j + 1}^i + M_j^i} \right]\frac{{Y_{j + 1}^i - Y_j^i}}{{\Delta {S_j}}}= \\ & \left[ {N_{j + 1}^{i + 1} + N_{j + 1}^i} \right]\frac{{Y_{j + 1}^{i + 1} - Y_{j + 1}^i}}{{\Delta {t_k}}} + \left[ {N_j^{i + 1} + N_j^i} \right]\frac{{Y_j^{i + 1} - Y_j^i}}{{\Delta {t_k}}} +\\ & Q_{j + 1}^{i + 1} + Q_j^{i + 1} + Q_{j + 1}^i + Q_j^i \text{。}\\ \end{aligned} $ |
在拖曳缆受到外界扰动作用下,观察结构矩阵M可知,拖曳系统内的张力随时间发生大幅度的振荡导致该结构矩阵M的性质发生了变化,从而造成数值求解的困难。为了克服每个时间步长内的张力求解值差别大,造成数值求解不稳定问题,采用自适应时间步长的方法求解上述盒式差分格式。首先取时间步长为某一个初始时间步长,如令k=1进行计算。
| $\Delta {t_k} = \frac{{{T_0}}}{k}\text{。}$ |
若在
| $\varepsilon = \frac{{{Y_{k + 1}} - {Y_k}}}{{{Y_k}}} < {\varepsilon _0}\text{。}$ |
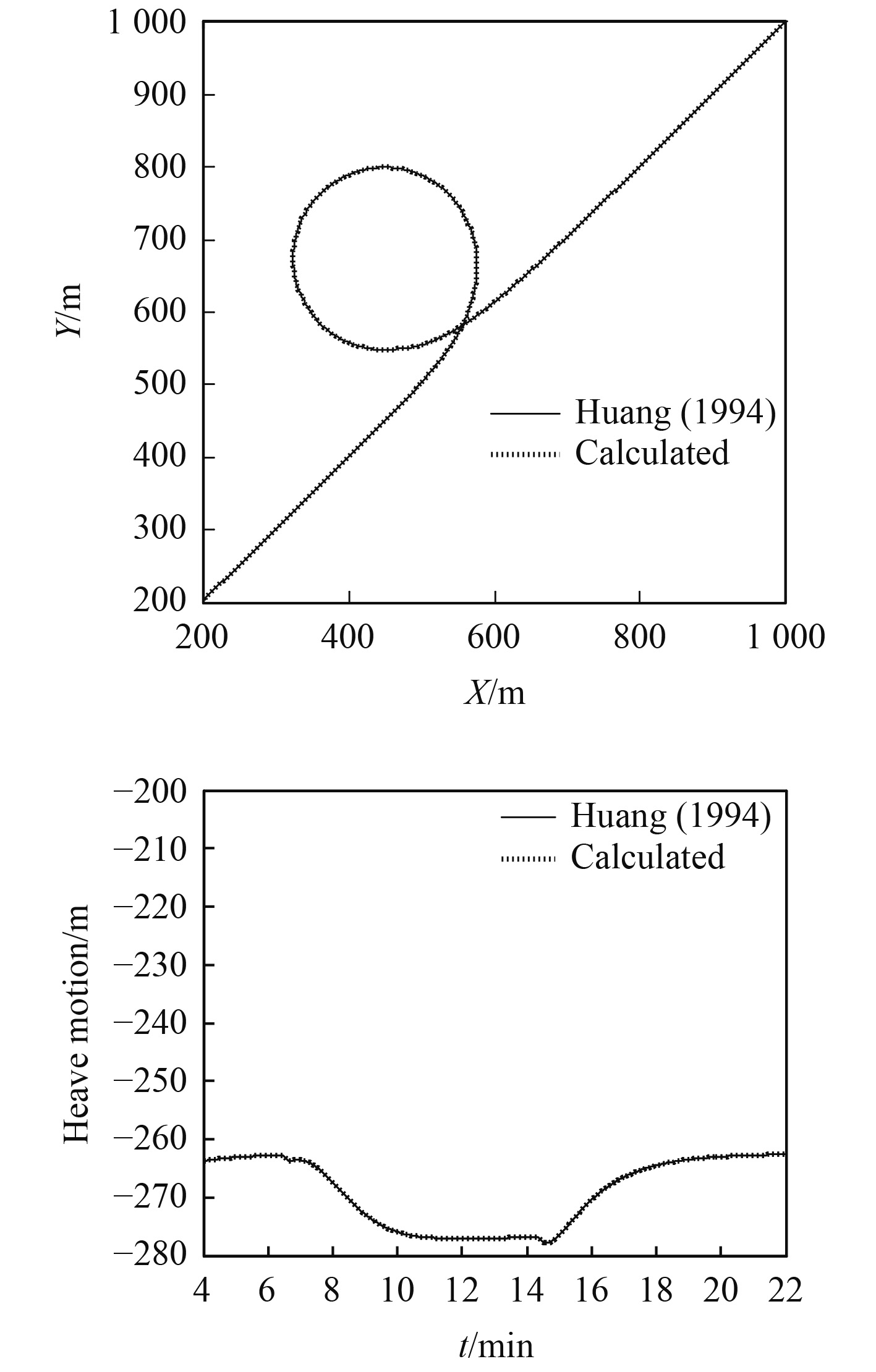
本文利用表1所示的Huang给出的算例进行验证,在该拖曳系统基础上扩展进行加速运动的振动响应计算。拖曳缆水下端在O-XY水平面的运动轨迹和水深Z向的升沉历程计算结果对比如图1所示。通过比较可知,拖曳体的升沉运动与水平面内的运动轨迹基本一致,验证了本模型对应程序的正确性。
|
|
表 1 拖曳系统结构参数与操纵参数(缆的总质量和拖曳体的质量比) Tab.1 Structural and maneuverable parameters oftowed cable system |
|
图 1 拖曳体水下端回转轨迹和升沉历程的数值计算结果与Huang(1994)的计算结果的对比 Fig. 1 Validation of numerical model with Huang (1994) bysimulating turning path of towed system |
在回转运动中历经了2个张力振荡的冲击阶段,一是拖曳系统进入回转运动的过程中,拖曳缆内的张力振荡,另一个是拖曳系统完全回转运动后,进入直航拖曳状态时,拖曳缆内的张力振荡。
拖曳体在回转过程中的运动基本规律如图1所示,拖曳系统进入回转运动的过程中,拖曳体的回转圈直径要小于母船的回转圈直径,也就是拖曳体在母船的内侧,那么缆运动的线速度下降,必然造成拖曳体沉深增大。同时拖曳体的沉深增大,直到回转运动结束后,拖曳体才缓慢回复到之前的沉深,由于缆的空间运动和缆内张力高度耦合,缆受到的水流阻力减小产生失速效应,那么拖曳缆内的张力必然是先增大后减小。
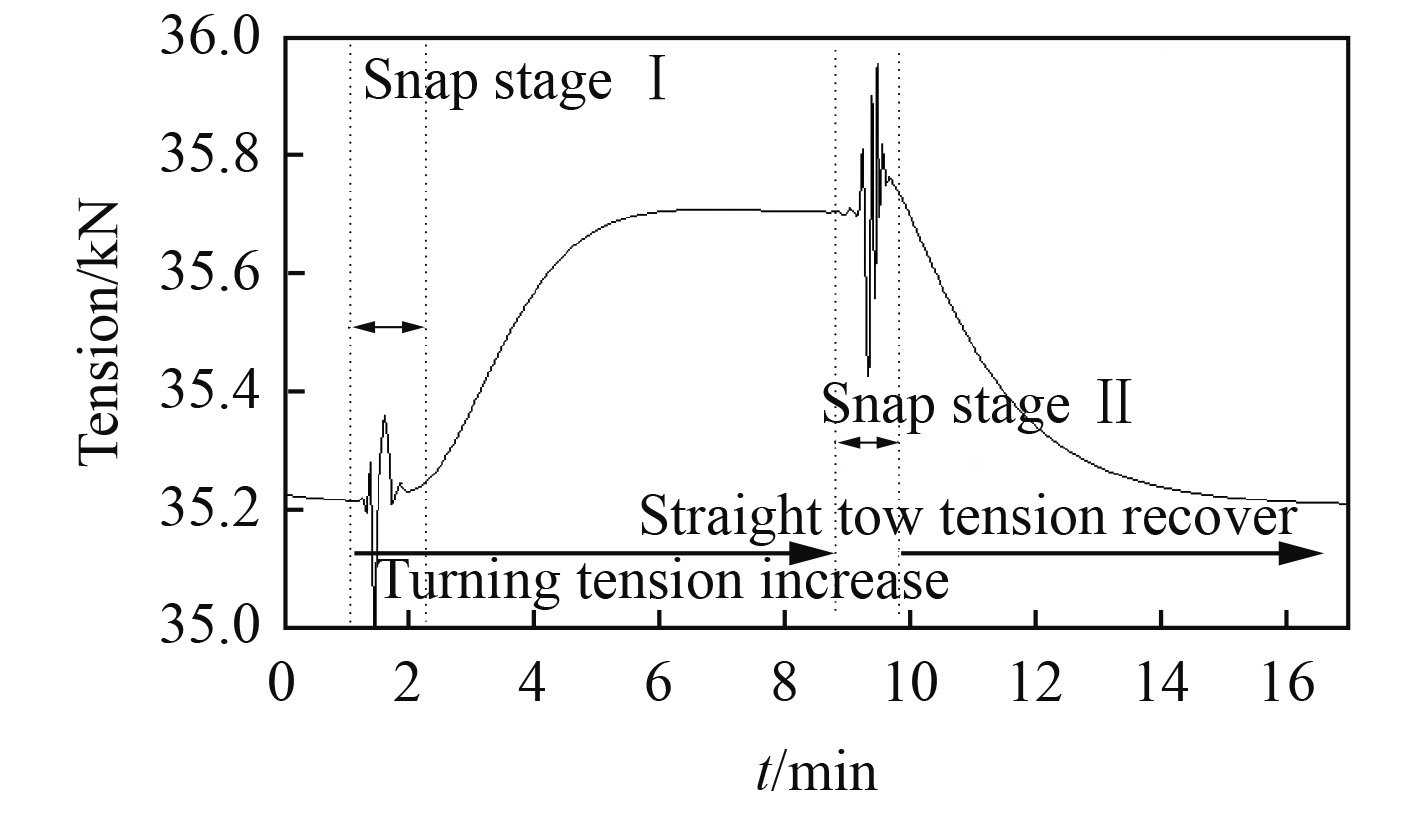
如图2所示,由于进入回转状态下,拖曳缆的运动速度下降,缆受到的水流作用力陡降,拖曳缆内的张力产生振荡,随着缆运动速度下降,缆内的张力逐步增大,这称为缆的失速效应。失速效应对应的冲击阶段成为第1冲击阶段;在完成回转运动后,拖曳系统又进入直航状态,缆在获得水流作用力的同时产生了冲击作用,此阶段的冲击效应成为第2冲击阶段。显然第2阶段的冲击效应要显著大于第1阶段。也就是失速冲击效低于加速冲击效应。
|
图 2 回转过程中拖曳缆水面端的张拉力时间历程 Fig. 2 Tension history in cable surface end during full turns |
以上验证算例是在较大的回转直径情况下拖曳体形成了完整的回转圈,本研究考查在较小回转圈下存在冲击现象。仍然以Huang给出的验证算例为基础,通过修改拖曳系统的操纵参数和拖曳体的质量,分析拖曳系统在回转运动过程中形成的冲击张力随着设计参数的变化规律。修改拖曳系统的操纵参数和结构参数包括回转圈的直径、回转速度、拖曳体的重量。
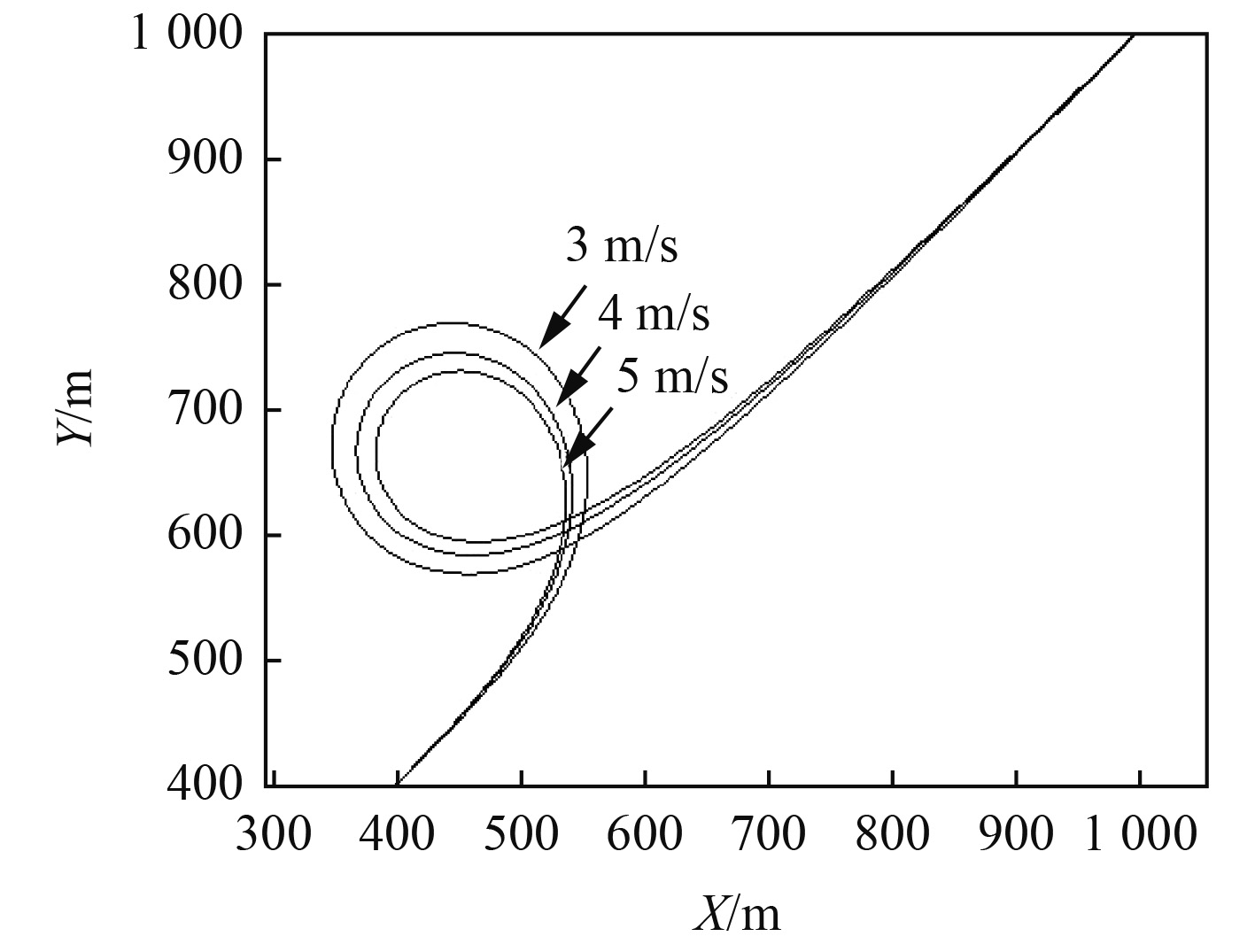
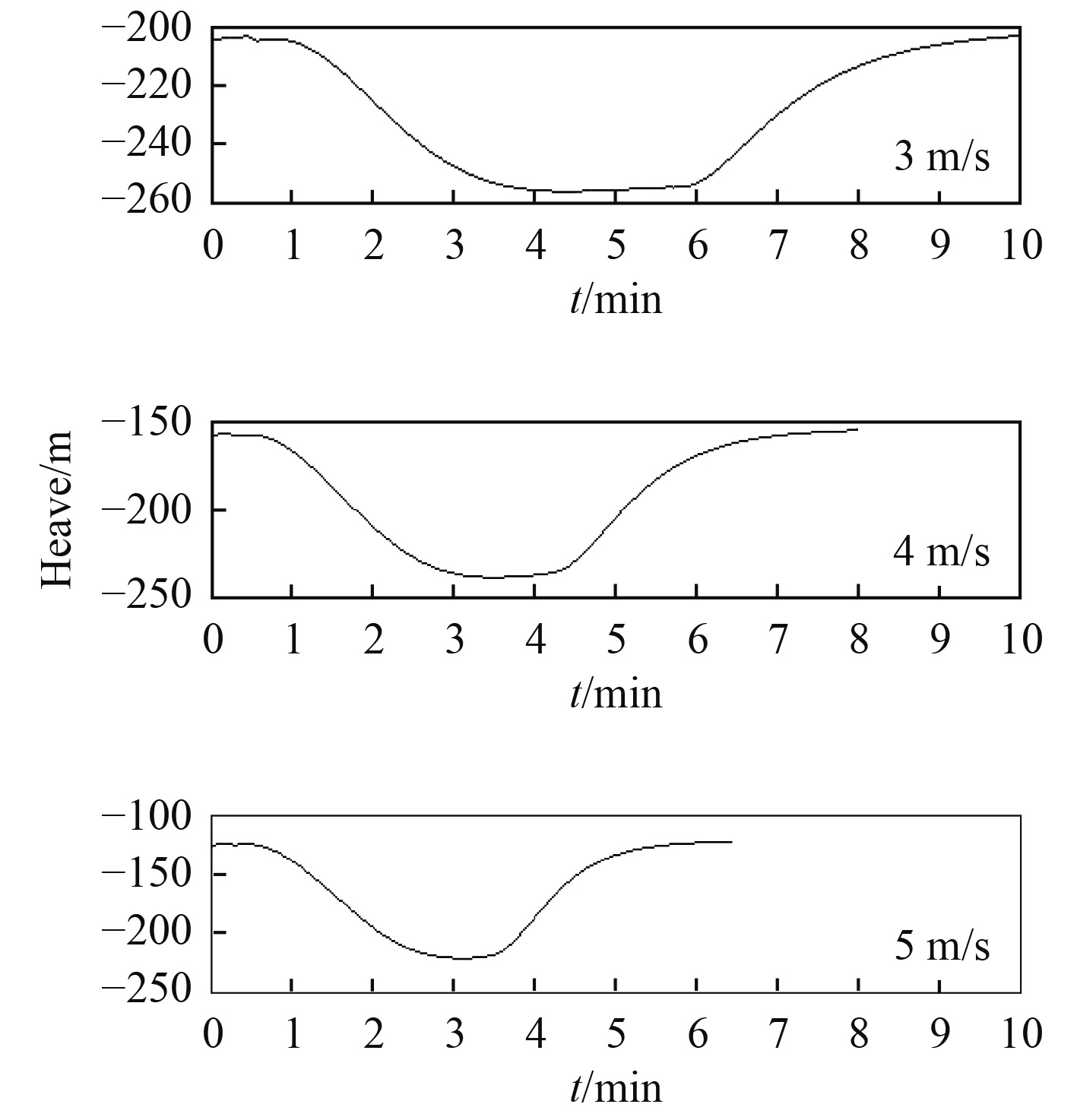
3.1 同一回转半径不同回转速度时的冲击规律图3为回转运动的水平运动轨迹,图4为拖曳体的升沉历程。随着拖曳速度的提升,拖曳体向回转圈内侧的侧向位移逐渐增加,拖曳体的侧向移动增大。随着拖曳速度的增大拖曳体的下潜段将在更短的时间内完成,这需要水流作用力在较短的时间内使拖曳体恢复到原先的潜深,拖曳速度越大,拖曳体的潜深变化越大而完成沉深恢复的时间却缩短了,如图5所示存在2个冲击阶段,拖曳缆内必然形成较大的冲击峰值。然而冲击持续的时间却没有显著增大,这是由于快速进入直航拖曳后拖曳体的运动将趋于稳定。
|
图 3 不同拖曳速度下的拖曳体水平回转轨迹 Fig. 3 Horizontal trajectory of towed body in differenttowed velocity |
|
图 4 不同拖曳速度对应的拖曳体升沉历程 Fig. 4 Heaving history of towed body in different towed velocity |
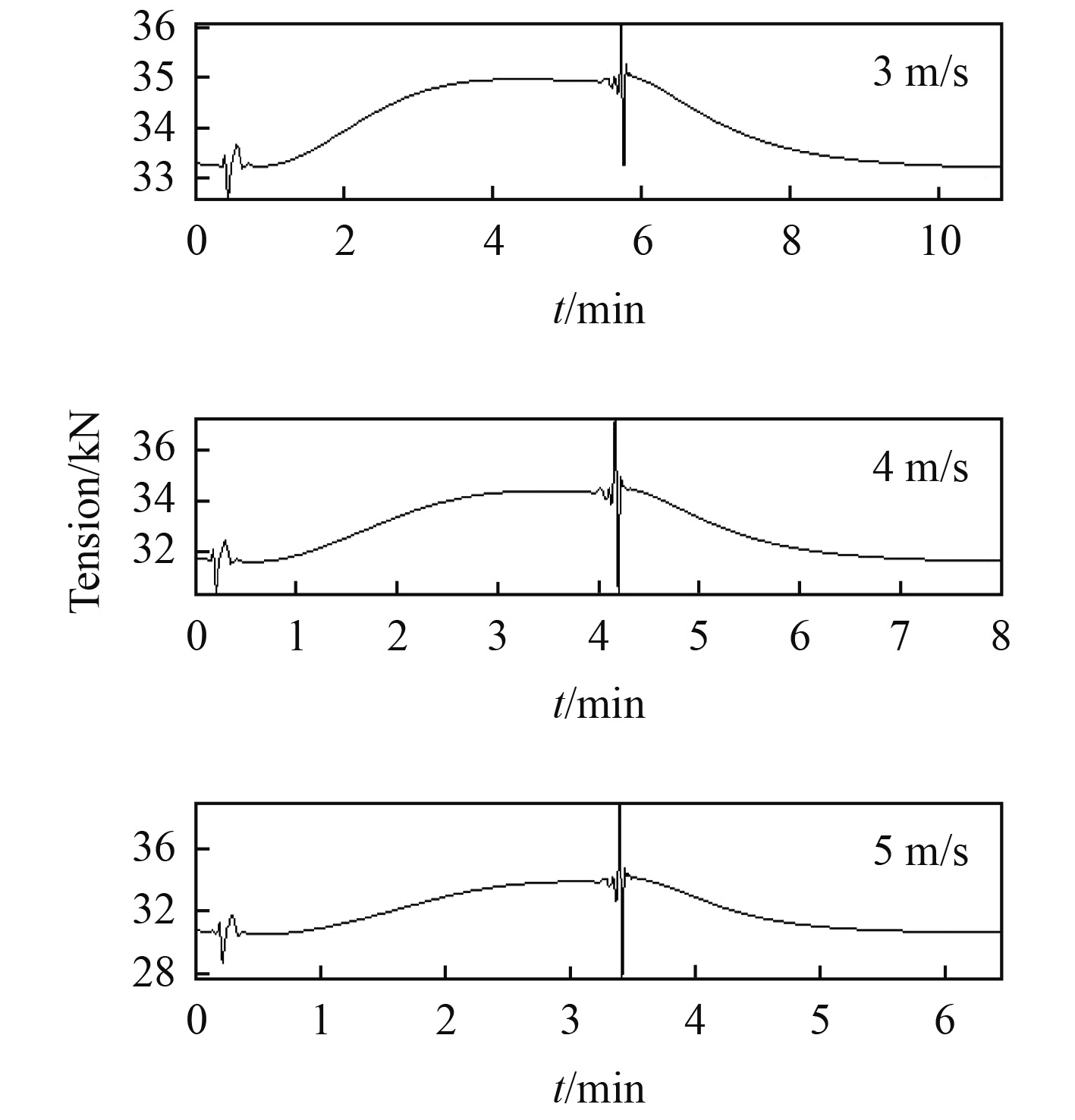
|
图 5 不同拖曳速度对应的张力历程 Fig. 5 Cable surface end tension history in different towed velocity |
维持拖曳速度为2 m/s,改变回转半径,考察2个阶段的冲击行为。当回转半径满足R/L<0.4时,图6为拖曳体并未呈现出完整的回转圈运动,图7为拖曳系统在小回转圈运动时,拖曳体历经了多次的升沉运动、这个升沉运动形成了多段冲击效应,在这一阶段拖曳系统受到的冲击行为呈现出一定的非线性行为,由于缆在空间的一部分未参与到回转圈运动,造成部分缆段的多次失速,形成了多次冲击。如图8所示,当回转半径较小时,拖曳缆内的张力在回转过程中历经多次的振荡,在完成整个小回转圈的运动过程中几乎不存在张力稳定的阶段。
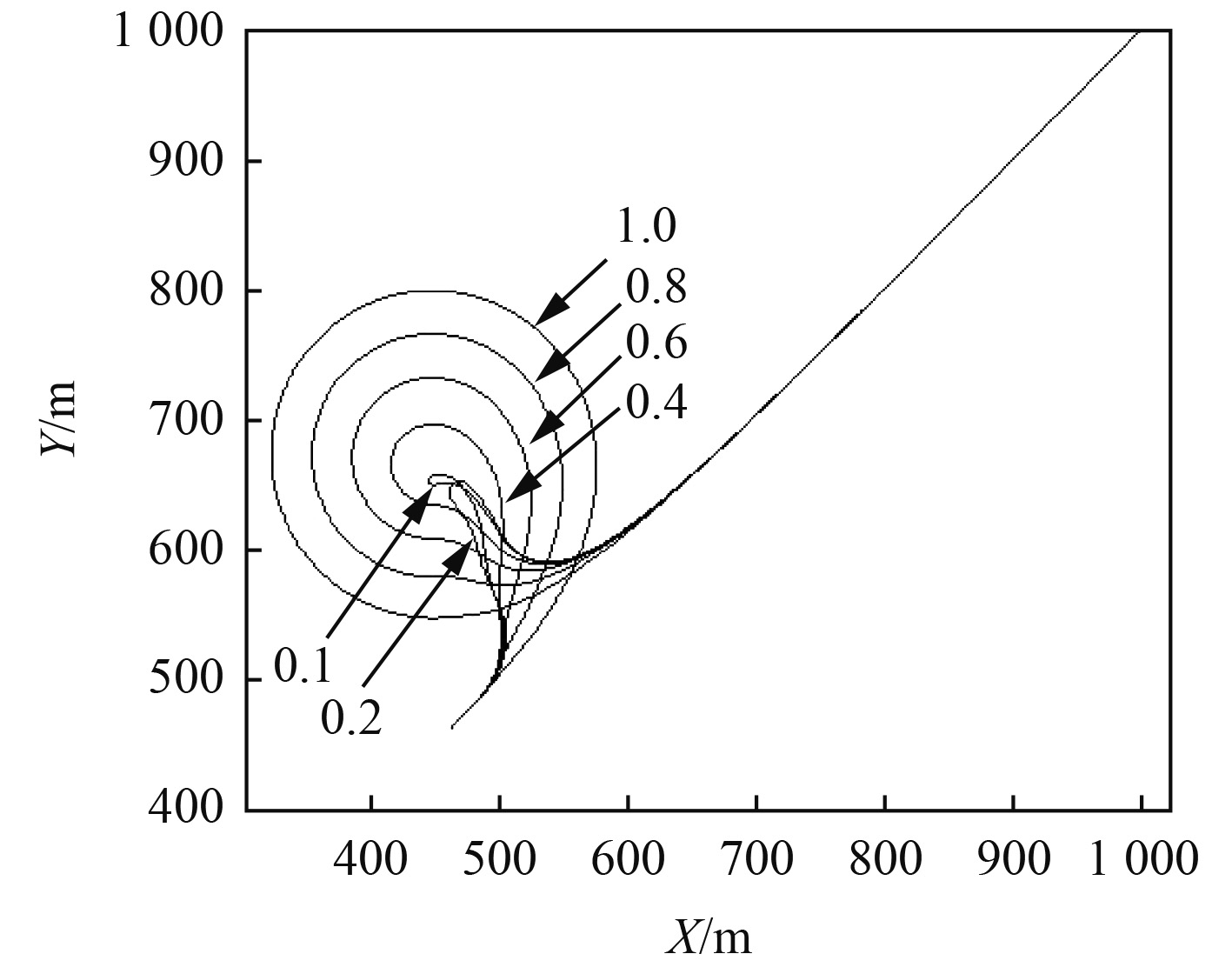
|
图 6 不同回转半径下的拖曳体的水平面运动轨迹 Fig. 6 Horizontal trajectory of towed body in differenttowed velocity |
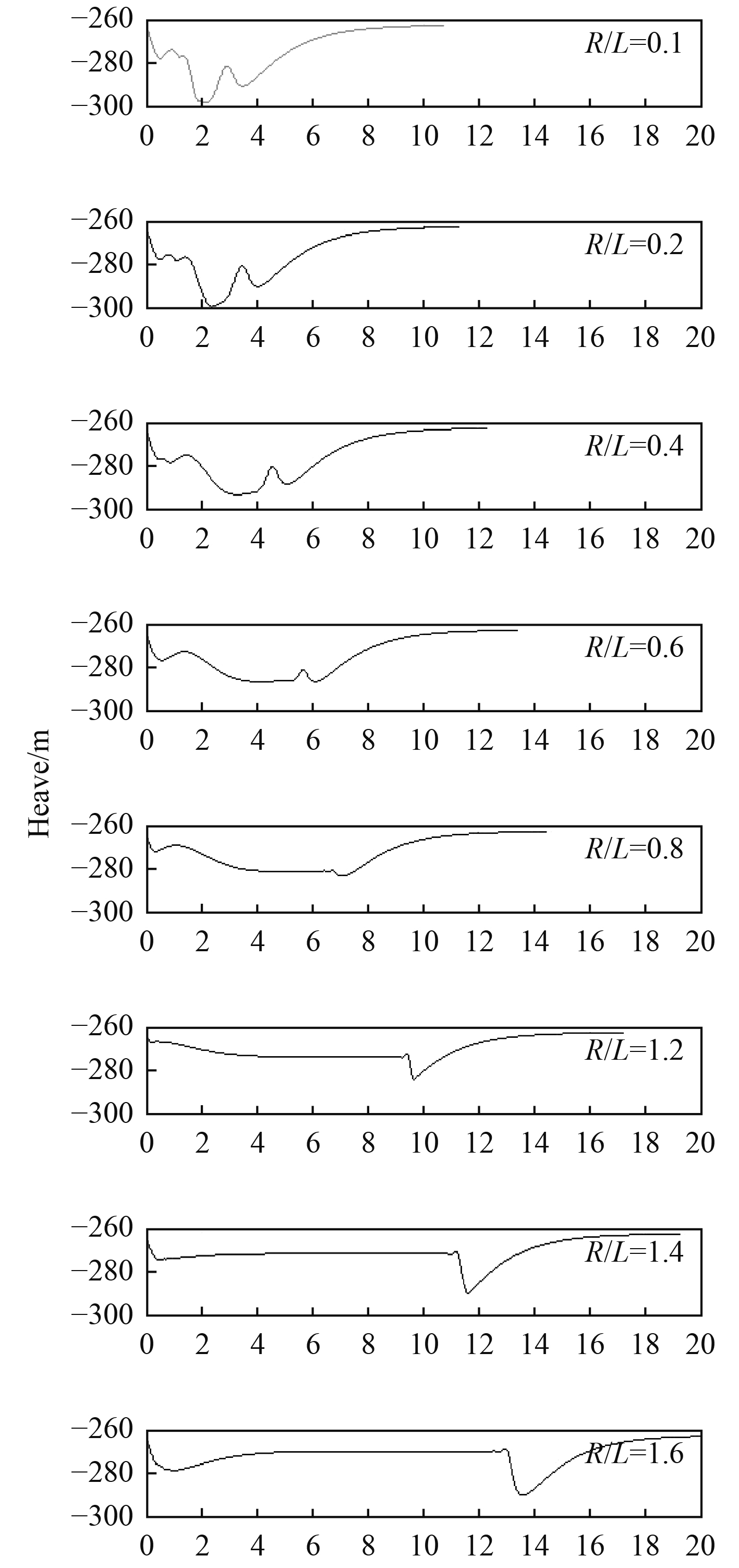
|
图 7 不同回转半径对应的拖曳体升沉历程 Fig. 7 Heaving history of towed body in different turning radius |
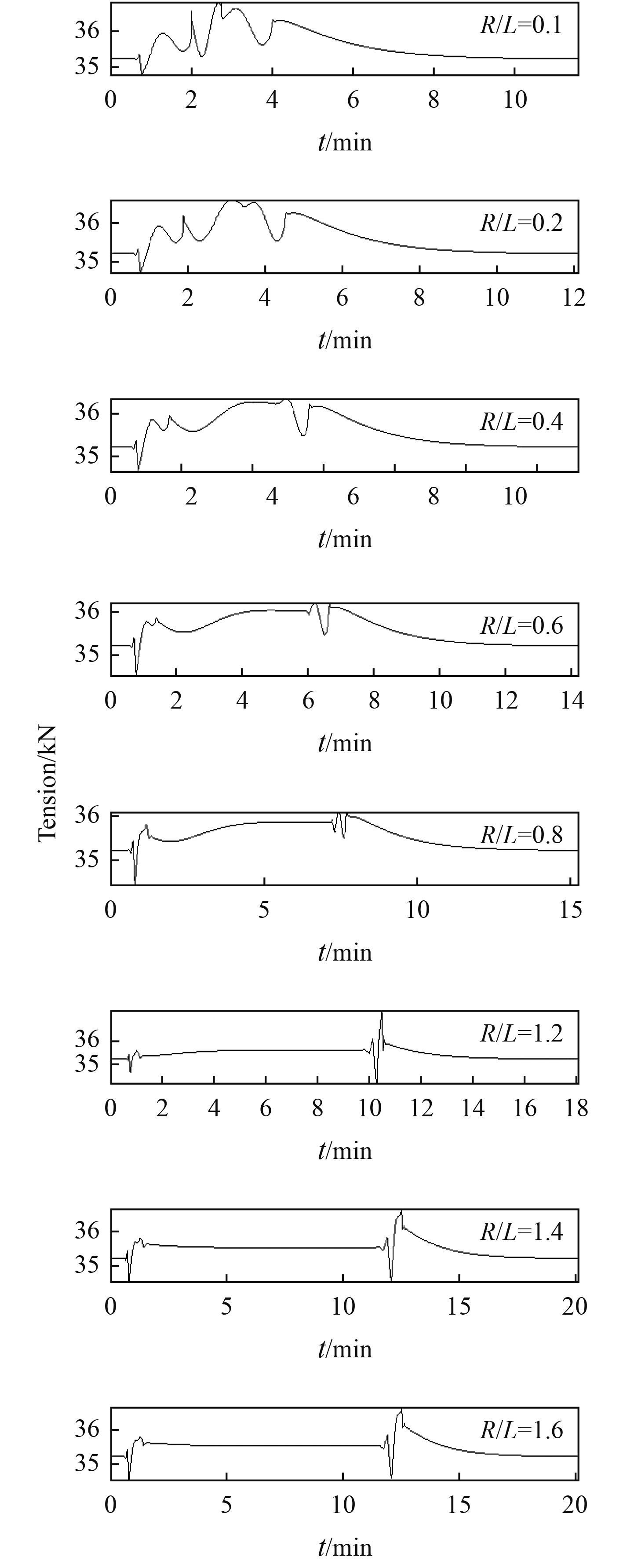
|
图 8 不同的回转半径对应的冲击张力的历程 Fig. 8 Cable surface end tension history in different turning radius |
然而在R/L>0.4后逐渐呈现出了2个阶段的冲击效应,拖曳体在回转过程中不仅形成了完整的回转圈,而且形成了稳定的沉降深度。
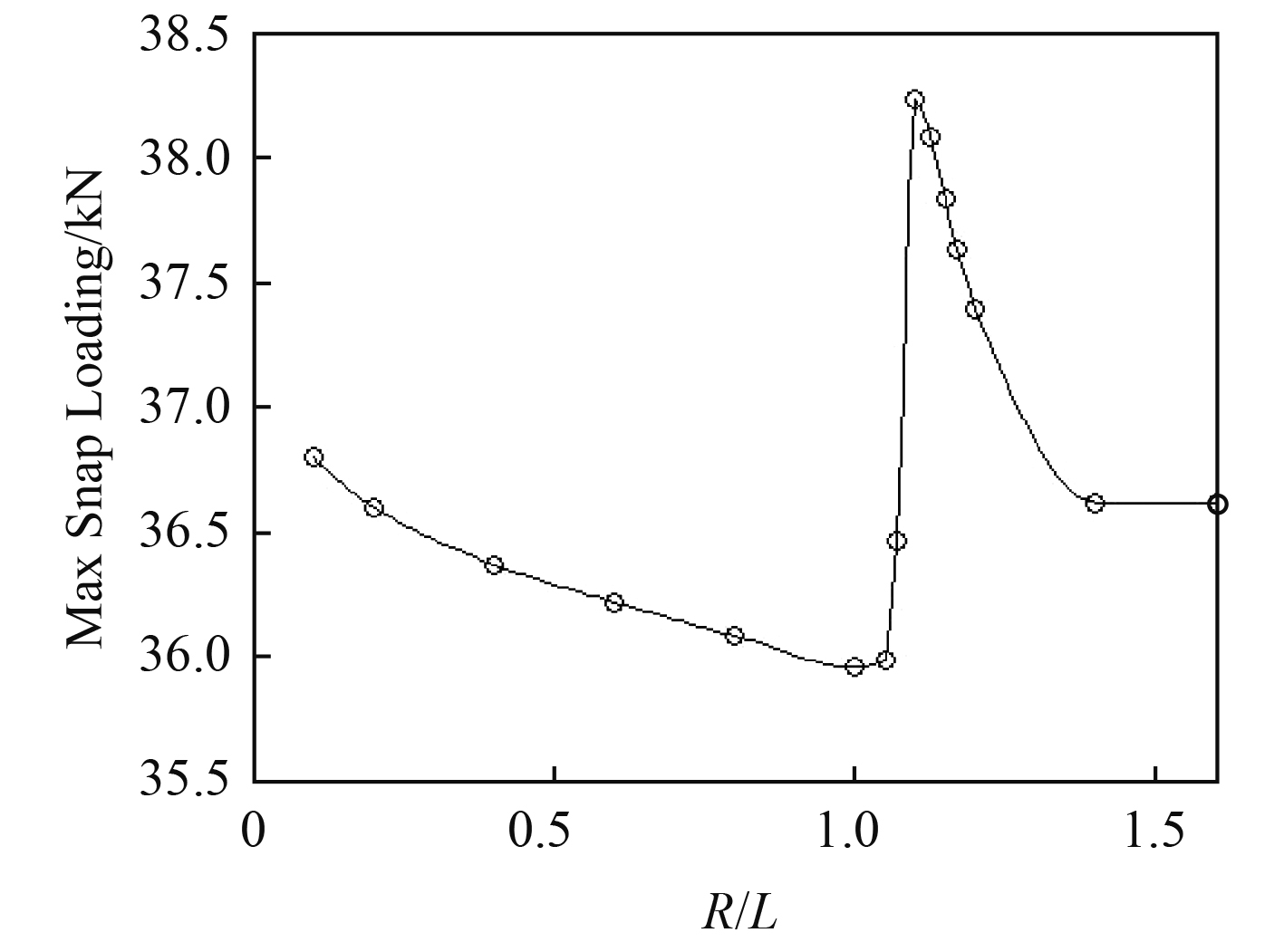
然而在R/L>0.8之后进入新的直航拖曳状态时,拖曳体出现了一定的短时跌落和回升,这种跌论必然造成冲击峰值。图9为拖曳系统在不同回转半径下冲击峰值的分布规律,这种冲击在R/L接近1时出现最大冲击量。
|
图 9 最大冲击张力随着回转圈运动的变化 Fig. 9 The maximum snap loading in cable surfaceend vs. turning radius |
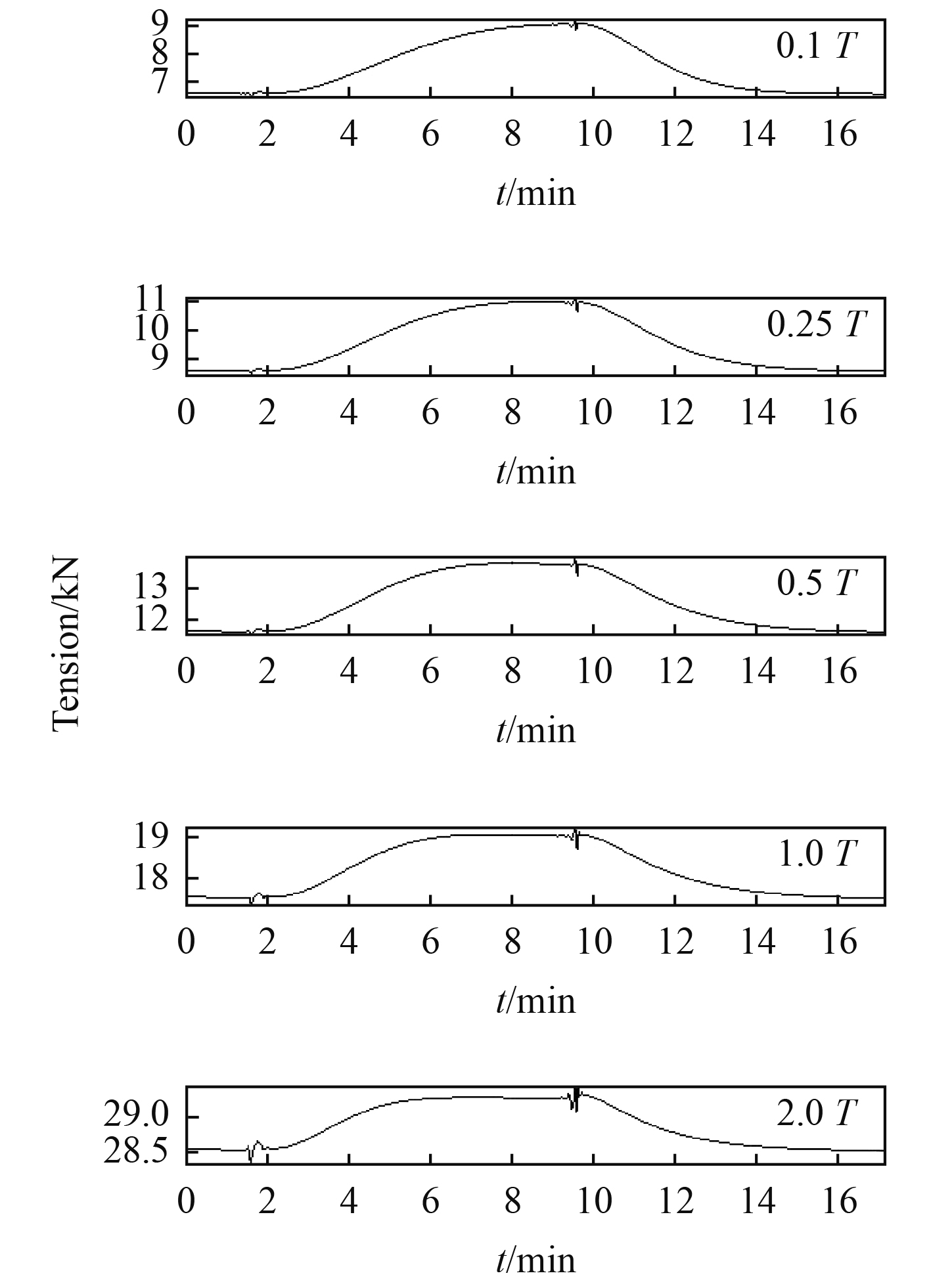
Wang[5]的研究显示回转圈半径和缆长组合形成操纵参数,另一个操纵参数是拖曳体的水中重量和缆重量的比值,这反映了拖曳缆的质量分布情况。改变拖曳体的重量从而调整质量集中程度,可以改变拖曳系统的惯性效应。如图10所示,分别取不同的拖曳体水中重量,考查对2个冲击阶段的影响规律,在较小的拖曳体重量的情况下第1阶段的冲击效应几乎观察不到,第2阶段的冲击效应也较为微弱,随着拖曳体重量的增大,2个阶段的冲击效应逐渐凸显,可见拖曳系统的质量集中效应引起了较高水平的势能向动能的转化,从而造成了拖曳系统的冲击效应越来越显著。
|
图 10 不同的拖曳体重对应的冲击张力历程(R/L=1.0) Fig. 10 The snap loading in cable surface end ofdifferent towed body mass |
本研究在建立相应数值方法的基础上,改变拖曳系统的的结构参数和操纵参数。拖曳系统完成一次全回转运动的过程中拖曳缆历经多次冲击作用,在较大回转圈时对应了2个冲击阶段,而在较小的回转圈时,存在多次的冲击效应体现了小回转圈情况下的非线性行为。在进入较大的回转圈运动时,拖曳系统历经的冲击效应尤其在R/L=1.0附近出现了冲击极值,这是由于进入直航拖曳过程中缆形的恢复延迟造成的。
拖曳系统的质量分布对冲击效应的影响规律较为明显,呈现低质量集中程度下的弱冲击行为,高质量集中度的冲击效应显著。
| [1] |
NIEDZWECKI J M, THAMPI S K. Snap loading of marine cable systems *[J]. Applied Ocean Research, 1991, 13(5): 210-219. DOI:10.1016/S0141-1187(05)80045-8 |
| [2] |
ABLOW C M, SCHECHTER S. Numerical simulation of undersea cable dynamics[J]. Ocean Engineering, 1983, 10(6): 443-457. DOI:10.1016/0029-8018(83)90046-X |
| [3] |
HUANG S. Dynamic analysis of three-dimensional marine cables[J]. Ocean Engineering, 1994, 21(6): 587-605. DOI:10.1016/0029-8018(94)90008-6 |
| [4] |
ZHU Z H. Dynamic modeling of cable system using a new nodal position finite element method[J]. International Journal for Numerical Methods in Biomedical Engineering, 2010, 26(6): 692-704. |
| [5] |
WANG Z, SUN G. Parameters influence on maneuvered towed cable system dynamics[J]. Applied Ocean Research, 2015, 49: 27-41. DOI:10.1016/j.apor.2014.10.009 |
| [6] |
王志博, 侯德永. 拖曳系统运动传递计算[J]. 船舶力学, 2015(4): 389-396. WANG Zhi-bo, HOU De-yong. Motion transmission calculation of towing system[J]. Ship Mechanics, 2015(4): 389-396. DOI:10.3969/j.issn.1007-7294.2015.04.006 |
| [7] |
王志博, 顾华, 侯德永, 等. 拖缆冲击张力和拖体运动的求解[C]// 全国水动力学研讨会并周培源诞辰110周年纪念大会. 2012. WANG Zhi-bo, GU Hua, HOU De-yong, et al. The solution of towing impact tension and dragging motion. [C]// national hydrodynamics workshop and Zhou Peiyuan's 110th Anniversary Birthday Commemorative Conference. 2012. |
| [8] |
王志博. 海洋水下拖曳体的设计要点[J]. 船舶与海洋工程, 2017, 33(4): 5-8. WANG Zhibo. Key factors of design of marine towed vehicle[J]. Ship and Marine Engineering, 2017, 33(4): 5-8. |
| [9] |
HUANG S, VASSALOS D. A numerical method for predicting snap loading of marine cables[J]. Applied Ocean Research, 1993, 15(4): 235. DOI:10.1016/0141-1187(93)90012-M |
| [10] |
CHIOU R. Nonlinear hydrodynamic response of curved singly-connected cables[J]. Computer Modelling in Ocean Engineering, 1989. |
| [11] |
HUANG S. Stability analysis of the heave motion of marine cable-body systems[J]. Ocean Engineering, 1999, 26(6): 531-546. DOI:10.1016/S0029-8018(98)00003-1 |
| [12] |
DRISCOLL F R, LUECK R G, NAHON M. Development and validation of a lumped-mass dynamics model of a deep-sea ROV system[J]. Applied Ocean Research, 2000, 22(3): 169-182. DOI:10.1016/S0141-1187(00)00002-X |
 2019, Vol. 41
2019, Vol. 41

