航路规划是指在特定约束条件下,寻找运动体从初始点到目标点并且满足某种性能指标最优的运动轨迹。针对汽车、无人机、水下机器人等的路径规划方法很多。其中根据规划范围[1]分为全局路径规划和局部路径规划;根据环境信息的准确性可分为确定性路径规划和不确定性路径规划。根据具体的算法不同[2],可分为基于几何模型的方法,如Voronoi图、可视图、栅格法;基于虚拟势场和导航函数的方法,如人工势场法;基于数学优化的方法;基于智能的方法[3 – 4],如蚁群算法、遗传算法、粒子群算法、神经网络算法,以及几种算法的改进、组合[5]。
导航装备的发展及信息渠道的多元化使得潜航器智能航路规划成为非常重要的课题。结合潜航器实际航行环境,建立多约束多指标的潜航器三维规划模型,改进蚁群算法信息素更新策略,避免路径搜索陷入局部最优。基于单目标动态威胁建立局部避障航路规划模型,所得航路能很好规避动态障碍。
1 潜航器航路规划问题描述潜航器航路规划是保证潜艇安全航行和执行任务的手段,过去指的是人为依据海图在出航前或出航时规划出一条航线。随着导航技术的发展及海上信息获取渠道的增加,潜航器航路规划与人工智能的结合表现出更多的优异性。蚁群算法[6 – 8]是一类不确定算法,含有随机因素,主要依靠蚂蚁遗留信息素来完成寻优的过程,因此容易陷入局部最优,但蚁群算法具有较强的鲁棒性、分布式计算机制、自组织性和进化性,现已应用到航路规划领域并取得很好的效果。
潜航器的航行安全性是其完成各项训练和作战任务的重要前提和基础保障,安全性受潜航器的内部因素和外部因素共同影响。潜航器航行安全是指首先要避免与沉船、暗礁、岛屿等障碍物发生碰撞;其次要采取必要的措施提高自己的隐蔽性从而避免被敌方探测设施捕获;最后还要尽量快速地到达目的地。由此可以看出,潜航器航行安全主要包括安全性、隐蔽性和快速性。
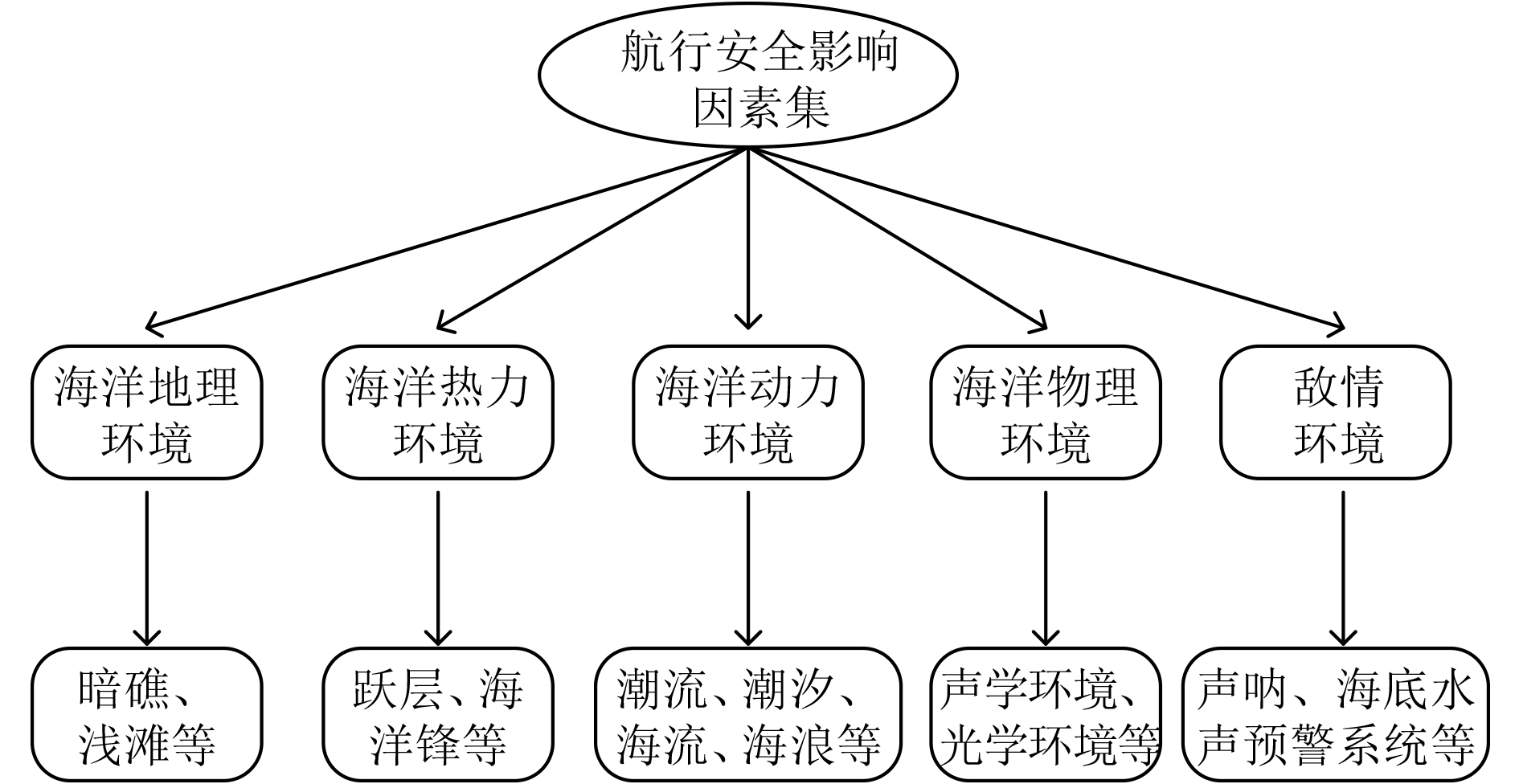
|
图 1 航行安全影响因素集 Fig. 1 Navigation safety impact factor set |
潜航器进行航路规划,要详细了解航行海区的海洋地理、地质、水文气象、声学环境等情况,以便于采取合理的战术机动,确保潜航器航行安全,需要注意一些对潜航器航行有安全影响的自然地理等因素。
2 蚁群改进策略的水下路径规划 3.1 信息素更新机制蚁群算法等仿生智能算法是通过进化的思想来实现全局搜索,同时由具体问题的代价函数决定最优解。但传统蚁群算法在搜索过程中信息素收敛速度过快,易陷入局部最优。因此为保证信息素在每次更新过程中得到合理的分配,引入混合启发式蚁群—微分进化模型,将微分进化算法中的变异、交叉操作用于信息素更新机制。假设蚂蚁种群规模为M,这样关于信息素的变异操作为:在每次所有蚂蚁完成一次循环后,使用从实验以来全局最优的蚂蚁走过路径的信息素分布对其他蚂蚁走过路径的信息轨迹进行更新,更新规则为:
| $ {\tau _{{r_1}}} = {\tau _{{r_2}}} + F \cdot ({\tau _{{r_{best}}}} - {\tau _{{r_3}}}){\text{。}} $ | (1) |
其中:
| ${\tau _{{l_j}}} = \left\{ {\begin{array}{*{20}{c}} {{\tau _{{r_1}j}}\;\;, \;\;randb \leqslant CR{\text{或}}j = randj}{\text{,}}\\ {{\tau _{ij}}\;\;,\;\;randb > CR{\text{或}}j \ne randj}{\text{。}} \end{array}} \right.$ | (2) |
式中:
当前全局最优解的信息素按下式进行更新:
| $ {\tau _{ij}}(t + 1) = (1 - \rho ) \cdot {\tau _{ij}}(t) + \Delta \tau _{ij}^{best}{\text{。}} $ | (3) |
其中:
考虑潜航器的特殊性,其航路规划过程中的启发因子总结为3个方面:
1)规避式启发因子。水下航行环境较为复杂,岛礁等碍航物存在处水深浅,属不可通行区域,由水深判断下一待选点的可航性:
| $ Qfz(1) = \left\{ {\begin{array}{*{20}{c}} 0{\text{,}}&{{\text{下一点航行深度}}>{\text{水深}}}{\text{,}}\\ 1{\text{,}}&{{\text{下一点航行深度}}<{\text{水深}}}{\text{。}} \end{array}} \right. $ | (4) |
2)保持式启发因子。潜航器在航渡过程中不可能频繁地上浮或者下潜,其具有保持同一深度面航行的特性:
| $ Qfz(2) = \frac{1}{{|{z^*} - z| + 1}}{\text{。}} $ | (5) |
其中:
3)距离启发因子。潜航器航渡过程中,都希望规划的航路尽可能短,以缩短完成任务的时间,因此计算可见度时加入待选点与终点的距离这一指标:
| $ \begin{split} & Qfz(3) = \frac{1}{{\sqrt {{{(N_x^* - {N_x})}^2} + {{(N_y^* - {N_y})}^2} + {{(N_z^* - {N_z})}^2}} }}+ \\ & \frac{1}{{\sqrt {{{(N_x^* - {E_x})}^2} + {{(N_y^* - {E_y})}^2} + {{(N_z^* - {E_z})}^2}} }}{\text{,}} \end{split} $ | (6) |
总的启发因子
| $ Qfz = Qfz(1)*Qfz(2)*Qfz(3){\text{,}} $ | (7) |
状态转移概率
| $ {p_i} = \frac{{Qf{z_i} \cdot {\tau _i}}}{{\displaystyle\sum\limits_{k \in allowe{d_k}} {(Qf{z_k} \cdot {\tau _k})} }}{\text{。}} $ | (8) |
其中,
在完成全局静态航路规划后,若航行器在行进过程中发现敌方机动目标,则需建立动态规避模型[9 – 11]。模型以敌我当前位置连线为路径规划的基准线进而确定下一时刻的可行域,以步长为半径、基准线为中心线画圆弧,圆弧弧度为120 °,此圆弧即为可行域,离散化可行域,在基准线两边间隔一定角度
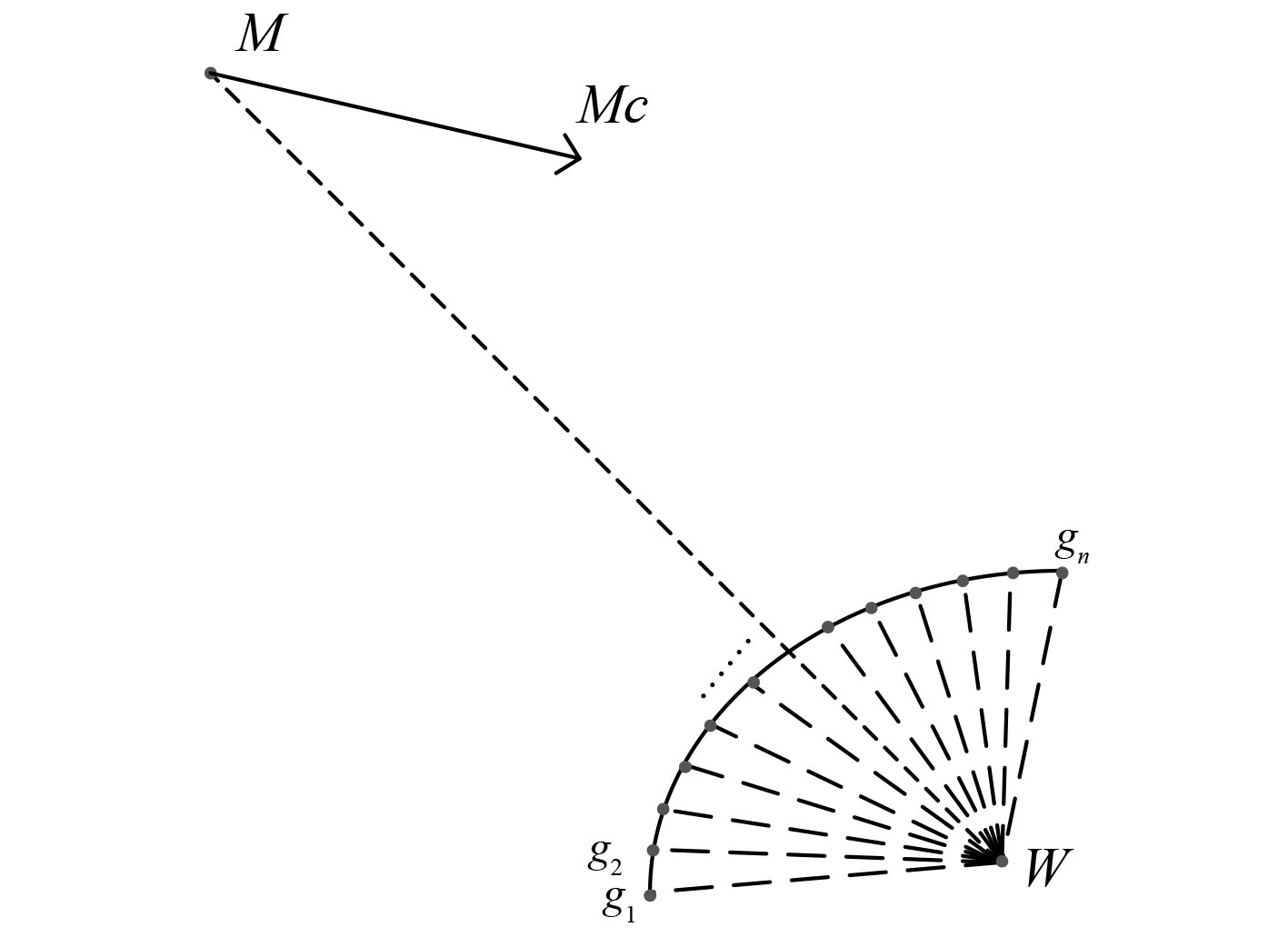
|
图 2 规避机动可行域 Fig. 2 Evading maneuverable domain |
设潜航器运动步长为l,当前位置为
1)计算敌方位角
| $ \gamma = a\tan ((Mx - Wx)/(My - Wy)){\text{,}} $ | (9) |
其中
| $ \left\{ {\begin{array}{*{20}{l}} {\gamma = \gamma + {\text{π}} {\text{,}}\;\;\;\;\;\;\;\;\;\;\;My < Wy}{\text{,}}\\ {\gamma = \gamma {\text{,}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;M{{y}} \geqslant W{{y}}} {\text{。}}\end{array}} \right. $ | (10) |
2)离散化可行域
基准线以左:
| $ \begin{split} g(i,1:2) =& [Wx + l*\sin (\gamma - i*\sigma /180*pi),\\ & Wy + l*\cos (\gamma - i*\sigma /180*pi)]{\text{,}} \\ &(i = 1,2, \cdots ,12) {\text{。}} \end{split} $ | (11) |
基准线以右:
| $ \begin{split} g(i,1:2) =& [Wx + l*\sin (\gamma - (i - 12)*\sigma /180*pi),\\ & Wy + l*\cos (\gamma - (i - 12)*\sigma /180*pi)]\\ & (i = 1,2, \cdots ,12){\text{。}} \end{split} $ | (12) |
设
| $ I(x,y) = C(x,y) \times B(x,y) \times L(x,y) {\text{。}} $ | (13) |
式中:
| $ C(x,y) = {e^{(dis1)}}{\rm{*(1/(}}m + diff - range{\rm{))}} {\text{。}} $ | (14) |
式中:
潜航器在规避机动过程中除考虑声呐的作用距离时,也必须考虑到声呐的作用范围,以此时监测敌方的运动状态。潜航器声呐并不是可对周围区域进行全方位听测,其对潜航器侧后方存在一定的盲区,为保证我方安全,必须时刻将敌置于我方声呐可听测范围内。因此设计
| $ B(x,y) = \left\{ {\begin{array}{*{20}{l}} {0{\text{,}}\;\;\;\;\;\;angle(x,y) > \theta }{\text{,}} \\ {1{\text{,}}\;\;\;\;\;\;angle(x,y) \leqslant \theta } {\text{。}} \end{array}} \right.$ | (15) |
式中:
| $ L(x,y) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{1}{{{e^{({d_{\min }} - dis)}}}}{\text{,}}\;\;\;\;\;(dis < {d_{\min }})}{\text{,}} \\ {1{\text{,}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(dis \geqslant {d_{\min }})} {\text{。}} \end{array}} \right. $ | (16) |
式中:
1)我方航行器转向机动,纯方位法解算目标运动要素,包括位置
2)运动要素解算完毕,开始进行规避机动。计算航行器当前可行域
3)计算所有可选航路点的代价值
4)判断是否继续规避机动。以开始机动时我方位置点及我方航向作直线,计算航路点到直线的距离,若此距离相比上一航路点到直线的距离减小,则停止规避机动,转到步骤5,否则,转到步骤2。
5)计算原航路上开始规避机动点与其下一点连线的斜率k0,依次计算后续点之间连线的斜率,直到找到斜率不同于k0的目标点作为规避机动后需转到的原航向上的目标点。
4 仿真分析 4.1 全局路径规划仿真分析参数设置:蚁群规模PopNumber = 30。信息素强度Q=8;挥发系数
首先利用插值拟合仿真海底三维地形,在仿真空间中的起始点和终点之间设置若干个吸引区域和排斥区域如图3所示,其中白色区域为有利隐蔽的吸引区域,黑色区域为敌方探测区域,考虑航程及安全因素,最终得到潜航器的全局航路规划结果如图4所示。可见,规划出的全局路径很好地规避了海底地形障碍和敌方探测区域,且有效地利用有利隐蔽区域,实现了规划的安全性、隐蔽性、快速性。
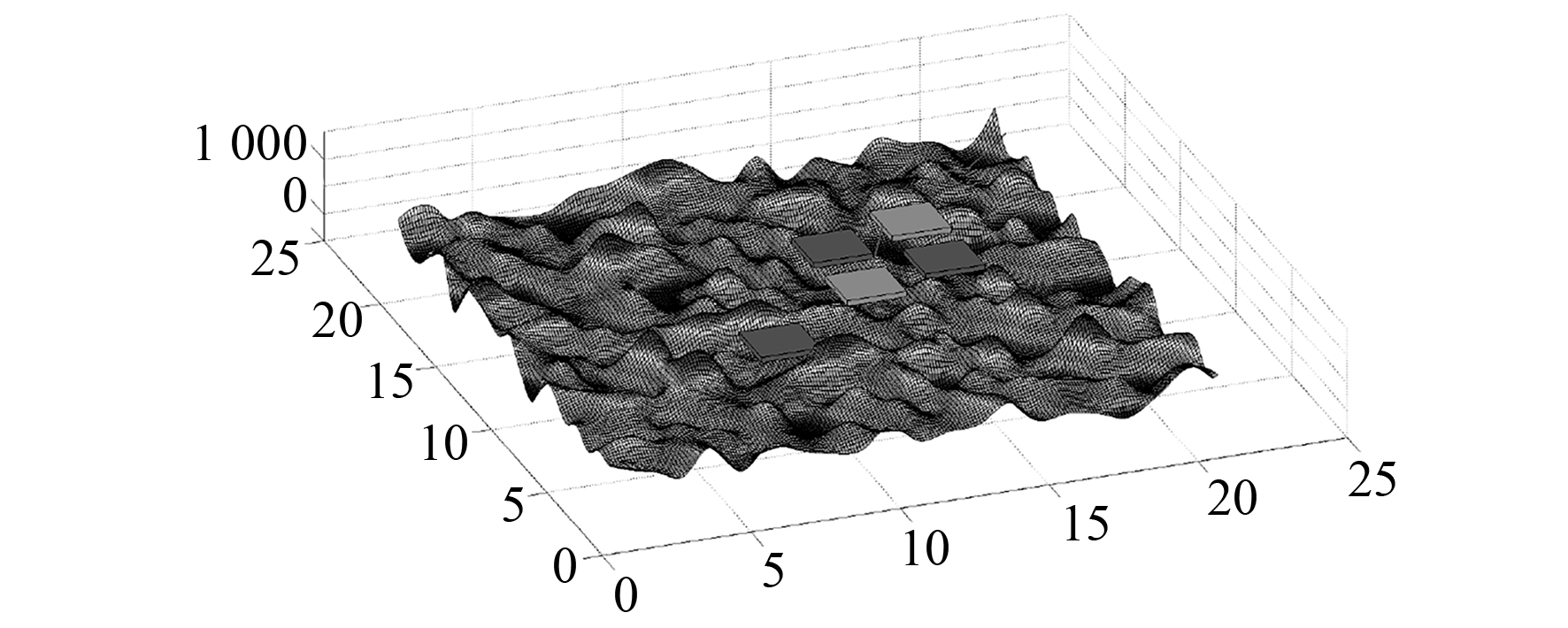
|
图 3 蚁群算法规划航路 Fig. 3 Ant colony algorithm planning route |
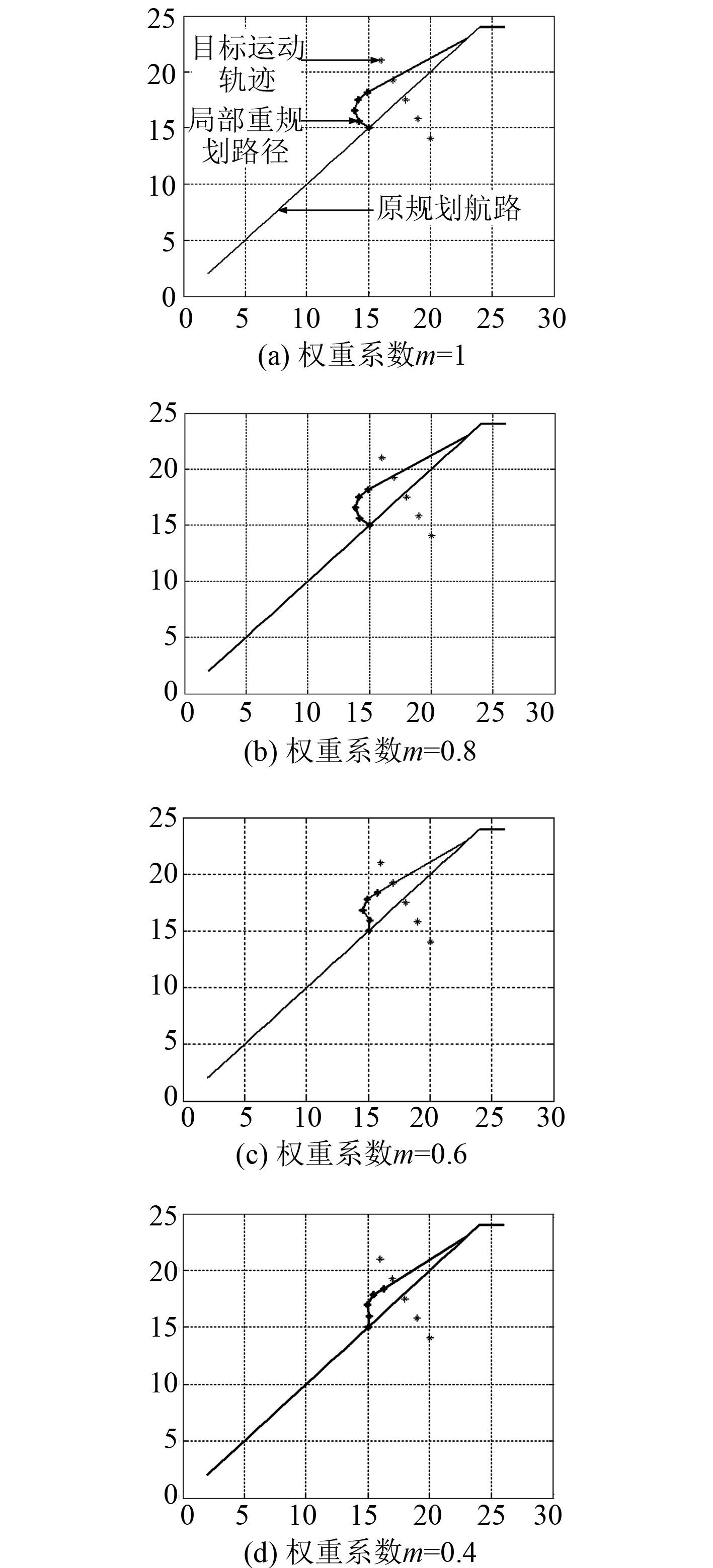
|
图 4 局部在线航路规划图 Fig. 4 Local online route planning |
假设单威胁为敌方舰艇(潜艇),或对潜航器航行有影响的第三方军用舰艇,对航路局部在线规划算法进行模拟与仿真。
仿真条件设定:取威胁因子航向160;步长2( nmile/10 min);步长0.5(nmile/10 min)。
由仿真试验结果可见,基于动态威胁的潜航器局部航路在线规划方法能够较好地实现动态威胁规避,且通过调整权重系数,潜航器可以与威胁目标的距离始终保持在需要的可靠范围内。
5 结 语本文通过改进蚁群算法的信息素更新机制和对启发因子进行重设,结合潜航器航行特点和环境影响因素集,考虑航行的安全性、隐蔽性,建立了基于静态环境的潜航器全局航路规划模型。并针对突发动态单威胁目标,考虑敌我距离变化量、我方当前位置与目标点的距离、我方声呐盲区、敌我距离最小量4个因数,建立基于单目标动态威胁的局部航路规划模型。进一步仿真验证了本文提出的潜航器全局航路规划算法和动态局部航路规划算法的有效性。
| [1] |
朱大奇, 颜明重. 移动机器人路径规划技术综述[J]. 控制与决策, 2010, 25(7): 961-967. |
| [2] |
王奎民. 水下潜器的航路规划技术综述[J]. 智能系统学报, 2014, 9(6): 653-658. |
| [3] |
Athina N. BRINTAKI, Ioannis K. NIKOLOS. Coordinated UAV Path PlanningUsing Differential Evolution[J]. Operational Research. An International Journal. Vol.5, No.3 (2005), pp.487-502.
|
| [4] |
Hai-bin DUAN, Ya-xiang YU, Xiang-yin ZHANG, et al. Three-dimension path planning for UCAV using hybrid meta-heuristicACO-DE algorithm[J]. Simulation Modelling Practice and Theory, 2010, 18: 1104-1115. DOI:10.1016/j.simpat.2009.10.006 |
| [5] |
Han-lin NIU, Yu LU, SAVVARIS A, et al. Efficient path planning algorithms for unmanned surface vehicle[J]. IFAC-Papers Online, 2016, 49-23: 121-126. |
| [6] |
DORIGO M, STÜTZLE T. Ant colony optimization: overview and recent advances[J]. Technical Report TR/IRIDIA/2009-013, IRIDIA, Université Libre de Bruxelles, Brussels, Belgium, May 2009.
|
| [7] |
孙涛, 谢晓方, 乔勇军. 基于二维自由空间蚁群算法的反舰导弹航路规划仿真[J]. 系统仿真学报, 2008, 20(13): 3586-3592. |
| [8] |
王沛栋, 冯祖洪, 黄新. 一种改进的机器人路径规划蚁群算法[J]. 机器人, 2008, 30(6): 555-560. |
| [9] |
俞炅, 旻吴, 超赵敏, 等. 重于水型AUV模糊路径规划与优化[J]. 舰船科学技术, 2017, 39(12): 76-80. DOI:10.3404/j.issn.1672-7649.2017.12.016 |
| [10] |
杨敬辉, 洪炳镕, 朴松昊. 基于遗传模糊算法的机器人局部避障规划[J]. 哈尔滨工业大学学报, 2004, 07: 946-948. DOI:10.3321/j.issn:0367-6234.2004.07.033 |
| [11] |
毛宇峰, 庞永杰, 李晔, 等. 速度矢量坐标系下水下机器人动态避障方法[J]. 哈尔滨工程大学学报, 2010(2): 159-164. DOI:10.3969/j.issn.1006-7043.2010.02.005 |
 2019, Vol. 41
2019, Vol. 41
