0 引　言

对于四边固支矩形板的弹性解答，很多学者已进行了较为深入的研究，主要针对承受均布载荷的矩形板^[1]，钟阳^[2]提出利用辛几何法推导得到均布载荷下四边固支矩形弹性薄板弯曲问题的解答；李元媛^[3]提出采用多项式函数结合Navier方法来得到近似的矩形薄板弯曲挠度，IMRAK^[4]结合三角函数和双曲函数，在忽略高阶小量的前提下求解了四边固支矩形板受均布载荷的最大位移。均布载荷下四周刚性固定矩形板解答可用于对船体中板格进行分析，如承受分布货物荷重的甲板板。但一些特殊情况下，比如海洋平台或军用船舶上直升机的起降，滚装船上轮印载荷的作用^[5]，以及极地船舶舷侧加强部分承受冰载荷的作用^[6]等，此时分布载荷只作用于板格局部位置，不能再将板格视为承受均布载荷四周刚性固定矩形板求解，将其简化为局部分布载荷下矩形板的问题近似考虑更为合理。对于承受局部分布载荷的刚性固定矩形板，张文福^[7]曾尝试给出了板中弯矩和挠度的计算用表，但仅适用于泊松比为0.2，矩形板的长宽比a/b为1，1.2，1.4，1.6，1.8和2，局部载荷的边长与对应矩形板边长比c/a为0.2，0.4，0.6，0.8和1的部分情况，应用具有局限性。

本文基于能量法，推导了局部载荷作用下四边固支矩形板弹性阶段的解答方程组，利用Matlab编程可方便得到挠度计算值。对于冰级船舶，由于与冰的遭遇工况多，如果采用非线性直接计算，在工况繁多的情况下计算工作量会很大。结合极限载荷准则，将本文提出的解答应用于极地船舶极限冰载荷的快速校核中^[8]，可提高初步设计阶段的效率。

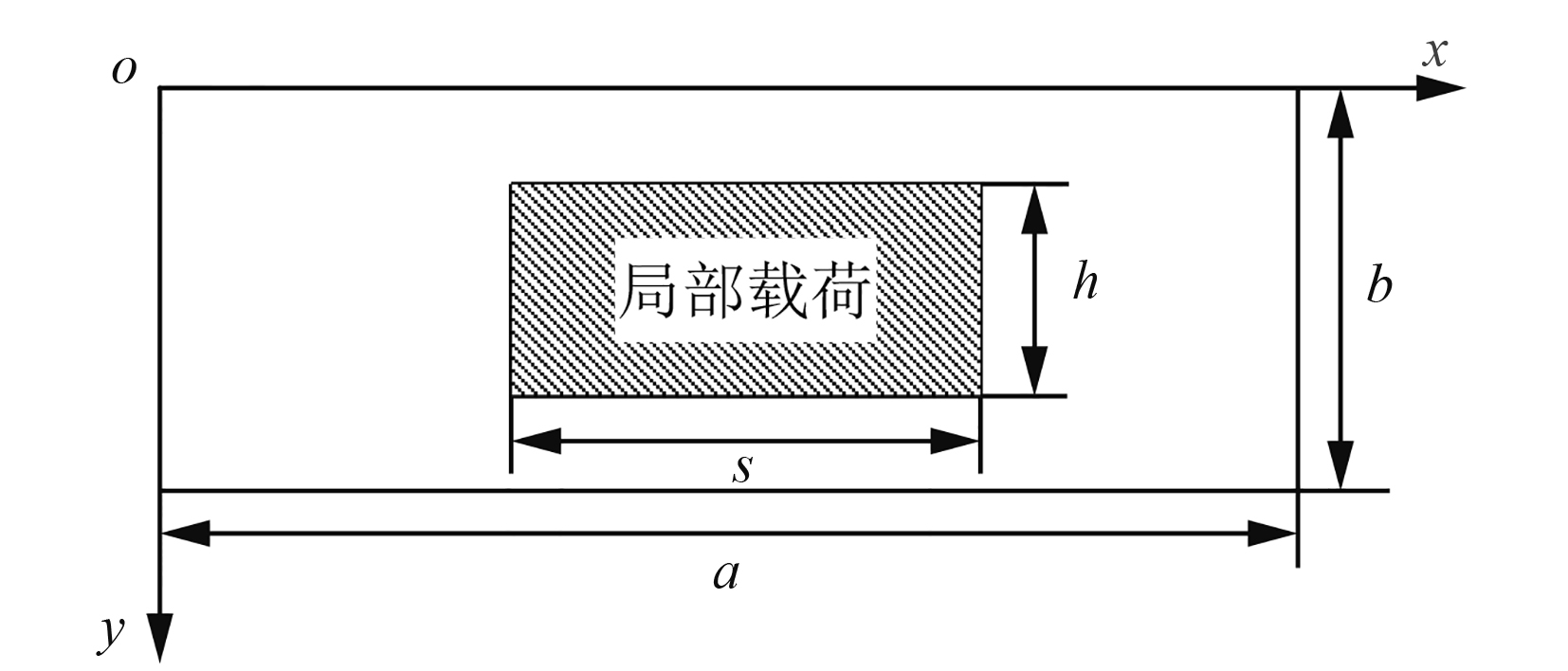
1 局部载荷作用下四边固支矩形板的理论解答

对于如图1所示局部载荷作用下板厚为 $t$ ，长宽分别为a和b的四边固支矩形板，所受局部分布载荷为 $q$ ，作用尺寸分别为 $s$ 和 $h$ 。

满足位移边界条件的挠度 $w$ 表达式为：

$w = \sum\limits_1^M {\sum\limits_1^N {{a_{mn}}\left(1 - \cos \frac{{2m{\text{π}} x}}{a}\right)\left(1 - \cos \frac{{2n{\text{π}} y}}{b}\right)} }\text{。} $

(1)

其中： $M$ ， $N$ 分别为 $x$ ， $y$ 方向展开的项数； ${a_{mn}}$ 为基函数的系数。

板的应变能为：

$V = \frac{D}{2}\iint {{{\left(\frac{{{\partial ^2}w}}{{\partial {x^2}}} + \frac{{{\partial ^2}w}}{{\partial {y^2}}}\right)}^2}{\rm d}x{\rm d}y}\text{。}$

(2)

式中： $D = \displaystyle\frac{{E{t^3}}}{{12(1 - {\mu ^2})}}$ 为弯曲刚度，其中E为弹性模量，μ为泊松比。

力函数为：

$U = \int_{\frac{{{\rm{a - s}}}}{2}}^{\frac{{a + s}}{2}} {\int_{\frac{{b - h}}{2}}^{\frac{{b + h}}{2}} {qw{\rm d}x{\rm d}y} }\text{，} $

(3)

将挠度表达式代入总位能公式中得到：

$ \begin{align} &\Pi =\frac{D}{2}\\ &\left(\!\int_0^a {\int_0^b {{{\left(\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{a_{mn}}{{\left(\frac{{2m{\text{π}} }}{a}\right)}^2}} }\!\!\! \cos \frac{{2m{\text{π}} x}}{a}\left(1 - \cos \frac{{2n{\text{π}} y}}{b}\right)\right)}^2}} } \!\!\!{\rm d}x{\rm d}y+\right. \\ & \int_0^a {\int_0^b {{{\left(\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{a_{mn}}{{\left(\frac{{2n{\text{π}} }}{b}\right)}^2}} } \cos \frac{{2n{\text{π}} y}}{b}\left(1 - \cos \frac{{2m{\text{π}} x}}{a}\right)\right)}^2}} } {\rm d}x{\rm d}y \\ & +2\int_0^a \int_0^b \left(\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{a_{mn}}{{\left(\frac{{2m{\text{π}} }}{a}\right)}^2}} } \cos \frac{{2m{\text{π}} x}}{a}\left(1 - \cos \frac{{2n{\text{π}} y}}{b}\right)\right)\\ & \left. \times \left(\sum\limits_{s = 1}^M {\sum\limits_{t = 1}^N {{a_{st}}{{\left(\frac{{2s{\text{π}} }}{a}\right)}^2}} } \cos \frac{{2s{\text{π}} x}}{a}\left(1 - \cos \frac{{2t{\text{π}} y}}{b}\right)\right) {\rm d}x{\rm d}y\right)\text{，} \end{align} $

(4)

根据最小势能原理 $\displaystyle\frac{{\partial \Pi }}{{\partial {a_{mn}}}} = 0$ 以及三角函数的正交性，任意一组（ $m$ ， $n$ ）都满足

$ \begin{align} &4D{{\text{π}} ^4}ab\left\{ \left[ {3{{\left( {\frac{m}{a}} \right)}^4} + 3{{\left( {\frac{n}{b}} \right)}^4} + 2{{\left( {\frac{m}{a}} \right)}^2}{{\left( {\frac{n}{b}} \right)}^2}} \right]{a_{mn}}\right.+ \\ & \left. \sum\limits_{r = 1,r \ne {\rm{n}}}^N {2{{\left( {\frac{m}{a}} \right)}^4}{a_{mr}} + \sum\limits_{s = 1,s \ne m}^M {2{{\left( {\frac{n}{b}} \right)}^4}{a_{sn}}} } \right\} -\\ & q\left(s - \frac{{a\cos (m{\text{π}} )\sin \left(\displaystyle\frac{{sm{\text{π}} }}{a}\right)}}{{m{\text{π}} }}\right)\left(h - \frac{{b\cos (n\pi )\sin \left(\displaystyle\frac{{hn{\text{π}} }}{b}\right)}}{{n{\text{π}} }}\right) = 0 \text{。} \end{align} $

(5)

由此得到关于系数 ${a_{mn}}$ 的线性方程组。

2 局部载荷作用下四边固支矩形板的近似解

随着项数 $M$ ， $N$ 的增加，挠度计算精度也不断增加直至收敛，同时随着项数的增加，求解式（5）的计算量也会陡增，故此借助Matlab程序进行求解。

将式（5）改写成如式（6）的形式求解，

${ K { A}} = { P}\text{ ，}$

(6)

其中： ${ K} = 4D{\pi ^4}ab\left({K_1} + \displaystyle\frac{2}{{{a^4}}}{K_2} + \displaystyle\frac{2}{{{b^4}}}{K_3}\right)$ ，为方程组系数矩阵， $ A$ 为基函数待定系数矩阵，

$ \begin{align} &P \!=\! \left[ {{p_{11}}}\,{p{}_{12}}\, \ldots {{p_{1N}}} \ldots {{p_{i1}}}\,{{p_{i2}}}\, \ldots {{p_{iN}}} \ldots {{p_{M(N - 1)}}}\,{{p_{MN}}} \right]_{(M \times N) \times 1}^{\rm{T}}\\ &{\text{且}}{p_{ij}} = q\left(s - \frac{{a\cos (i\pi )\sin \left(\displaystyle\frac{{is{\text{π}} }}{a}\right)}}{{i{\text{π}} }}\right)\left(h \!-\! \displaystyle\frac{{b\cos (j\pi )\sin \left(\displaystyle\frac{{jh{\text{π}} }}{b}\right)}}{{j{\text{π}} }}\right){\text{。}} \end{align} $

并有

$ {K_1} = \frac{3}{{{a^4}}}{K_{11}} + \frac{3}{{{b^4}}}{K_{12}} + \frac{2}{{{a^2}{b^2}}}{K_{13}}\text{，} $

${{ K}_{11}} = {\left[ {\begin{aligned} & {{{\left[ {\begin{array}{*{20}{c}} 1&{}&{} \\ {}& \ldots &{} \\ {}&{}&1 \end{array}} \right]}_{N \times N}}} \\ & \quad\quad \ldots & \\ & {{{\left[ {\begin{array}{*{20}{c}} {{i^4}}&{}&{} \\ {}& \ldots &{} \\ {}&{}&{{i^4}} \end{array}} \right]}_{N \times N}}}&{}&{} \\ & \quad\quad \ldots &{} \\ & {{{\left[ {\begin{array}{*{20}{c}} {{M^4}}&{}&{} \\ {}& \ldots &{} \\ {}&{}&{{M^4}} \end{array}} \right]}_{N \times N}}} \end{aligned}} \right]_{_{(M \times N) \times (M \times N)}}}$

${{ K}_{12}} = {\left[ {\begin{aligned} & {{{\left[ {\begin{array}{*{20}{c}} 1&{}&{} \\ {}& \ldots &{} \\ {}&{}&{{N^4}} \end{array}} \right]}_{N \times N}}} \\ &\quad\quad \ldots \\ &{{{\left[ {\begin{array}{*{20}{c}} 1&{}&{} \\ {}& \ldots &{} \\ {}&{}&{{N^4}} \end{array}} \right]}_{N \times N}}} \\ &\quad\quad \ldots &{} \\ &{{{\left[ {\begin{array}{*{20}{c}} 1&{}&{} \\ {}& \ldots &{} \\ {}&{}&{{N^4}} \end{array}} \right]}_{N \times N}}} \end{aligned}} \right]_{_{(M \times N) \times (M \times N)}}}$

${{ K}_{13}} = {\left[ {\begin{aligned} & {{{\left[ {\begin{array}{*{20}{c}} \!\!\!\!\! {{1^2} \times {1^2}}\!\!\!\!\!\!\!\!\!\!&{}&{}&{} \\ \!\!\! {}&{{1^2} \times {2^2}}\!\!\!\!\!\!\!\!\!\!&{}&{} \\ \!\!\! {}&{}& \ldots \!\!\!\!\!\!\!\!\!\!&{} \\ \!\!\! {}&{}&{}&{{1^2} \times {N^2}} \!\!\!\!\! \end{array}} \right]}_{N \times N}}}\!\!\!\!\!\!\!\!\!&{}&{}&{}&{} \\ & \quad\quad\quad\quad \ldots \\ & {{{\left[ {\begin{array}{*{20}{c}}\!\!\!\!\! {{i^2} \times {1^2}}\!\!\!\!\!\!\!\!\!\!&{}&{}&{} \\ \!\!\! {}&{{i^2} \times {2^2}}\!\!\!\!\!\!\!\!\!\!&{}&{} \\ \!\!\! {}&{}& \ldots\!\!\!\!\!\!\!\!\!\! &{} \\ \!\!\! {}&{}&{}&{{i^2} \times {N^2}} \!\!\!\!\! \end{array}} \right]}_{N \times N}}}\!\!\!\!\!\!\!\!\!&{}&{} \\ \!\!\! & \quad\quad\quad\quad \ldots \\ & {{{\left[ {\begin{array}{*{20}{c}}\!\!\!\!\! {{M^2} \times {1^2}}\!\!\!\!\!\!\!\!\!\!&{}&{}&{} \\ \!\!\! {}&{{M^2} \times {2^2}}\!\!\!\!\!\!\!\!\!&{}&{} \\ \!\!\! & \ldots\!\!\!\!\!\!\!\!\! &{} \\ \!\!\! {}&{}&{}&{{M^2} \times {N^2}}\!\!\!\!\! \end{array}} \right]}_{N \times N}}} \end{aligned}} \right]_{(M \times N) \times (M \times N)}}$

${{ K}_2} = {\left[ {\begin{aligned} & {\left[ {\begin{array}{*{20}{c}} {}&1&1 \\ 1&{}&1 \\ 1&1&{} \end{array}} \right]} \\ & \quad \ldots \\ & {\left[ {\begin{array}{*{20}{c}} {}&{{i^4}}&{{i^4}} \\ {{i^4}}&{}&{{i^4}} \\ {{i^4}}&{{i^4}}&{} \end{array}} \right]}&{}&{} \\ & \quad\quad \ldots &{} \\ & {\left[ {\begin{array}{*{20}{c}} {}&{{M^4}}&{{M^4}} \\ {{M^4}}&{}&{{M^4}} \\ {{M^4}}&{{M^4}}&{} \end{array}} \right]} \end{aligned}} \right]_{_{(M \times N) \times (M \times N)}}}$

$ \begin{aligned} &{K_3}{\rm{ = }} {\left[ {\begin{array}{*{20}{c}} 0&{\widetilde k}&{\widetilde k}& \ldots &{\widetilde k}\\ {\widetilde k}&0&{\widetilde k}& \ldots &{\widetilde k}\\ {\widetilde k}&{\widetilde k}&0&{\widetilde k}& \ldots \\ \ldots & \ldots &{\widetilde k}&0&{\widetilde k}\\ {\widetilde k}&{\widetilde k}& \ldots &{\widetilde k}&0 \end{array}} \right]_{M \times M}}\\ & \widetilde k = {\left[ {\begin{array}{*{20}{c}} 1&{}&{}&{}&{}\\ {}& \ldots &{}&{}&{}\\ {}&{}&{{i^4}}&{}&{}\\ {}&{}&{}& \ldots &{}\\ {}&{}&{}&{}&{{N^4}} \end{array}} \right]_{N \times N}} \end{aligned}$

求出系数 $A$ 后，代入式（1）即可求得矩形板的挠度 $w$ ，该方法可以求任意载荷面积下的矩形板挠度。

2.1 均布载荷作用下解答验证

为验证本文方法的正确性，与四边刚性固定矩形板受均布载荷作用的经典解答进行对比。弹性解答矩形板中点的挠度为 ${w_{\max }} = {k_1}\displaystyle\frac{{q{b^4}}}{{E{t^3}}}$ ， ${k_1}$ 取值见表1^[9]。

将本文的计算方法退化到均布载荷情况，即取 $ s = a,h = b$ ，选取 $b = 100\;{\rm mm}$ ， $t = 4\;{\rm mm}$ ， $E = 2.06 \times $ 10⁵ MPa进行验证，2种方法计算结果如表2所示。

可以发现2种方法得到的结果非常一致，本文解答在均布载荷的特殊情况下是正确的。

2.2 局部载荷作用下本文解答与数值解的一致性验证

取 $t = 4\;\rm mm$ ， $E = 206\,000\;{\rm MPa}$ ， $P = 2\;{\rm MPa}$ ，改变矩形板和局部载荷的尺寸，得到本文方法与有限元法解答，如表3所示。

可知，本文解答与数值解差别很小。

3 局部载荷作用下四边固支矩形板弹性解答的应用 3.1 基于2倍弹性斜率法的快速校核方法

近年来，随着极地环境不断变化，越来越多的目光转向极地船舶的发展。在求解极地船舶所受极限冰载荷作用时，可使用有限元软件进行非线性有限元计算，但冰船遭遇情况复杂，工况繁多，且对网格精度要求高，需要极大的工作量。陈伟杰等^[10]提出结合载荷-变形曲线和2倍弹性斜率准则得到极地船舶强度评估方法，由此快速得到极限冰载荷的初步设计值，现将本文的矩形板弹性解答应用于该校核方法中。

修正后的矩形板载荷-变形公式的塑性阶段解析解^[10]

$p = \frac{{16{M_P}}}{{{b^2}{K_h}}} \cdot {K_P} \cdot {K_m} \cdot {f_B} \cdot C\text{。}$

(16)

其中： ${M_P}$ 为塑性弯矩； ${K_p}$ 为局部载荷高度调整系数； ${K_m}$ 为矩形板的薄膜效应系数； ${f_B}$ 为矩形板的弯曲系数； $C$ 为修正系数； ${K_h}$ 为局部载荷长度调整系数； $b$ 为矩形板的宽度。

由本文矩形板弹性解答，结合塑性阶段的计算公式，得到如下基于2倍弹性斜率的快速校核方法。

1）利用弹性阶段公式得到曲线 $Oa$ ；

2）利用塑性阶段公式得到曲线 $bc$ ；

3）根据 $Oa$ 直线，计算相对于载荷轴的2倍斜率得到曲线 $Od$ ；

4）直线 $Od$ 和 $bc$ 交点的纵坐标值即为极限载荷值 $U$ 。

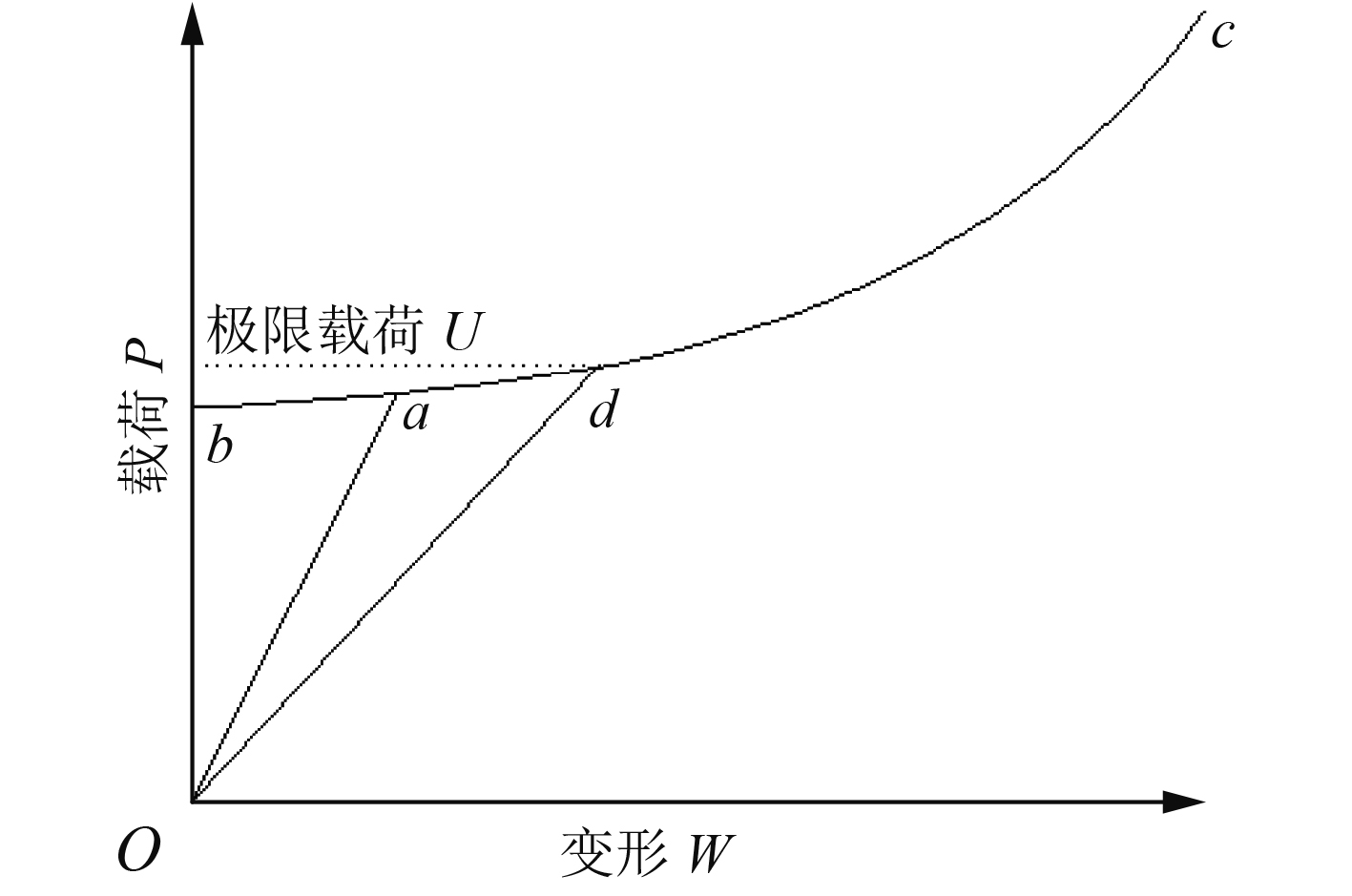
快速校核方法求解极限示意图如图2所示。

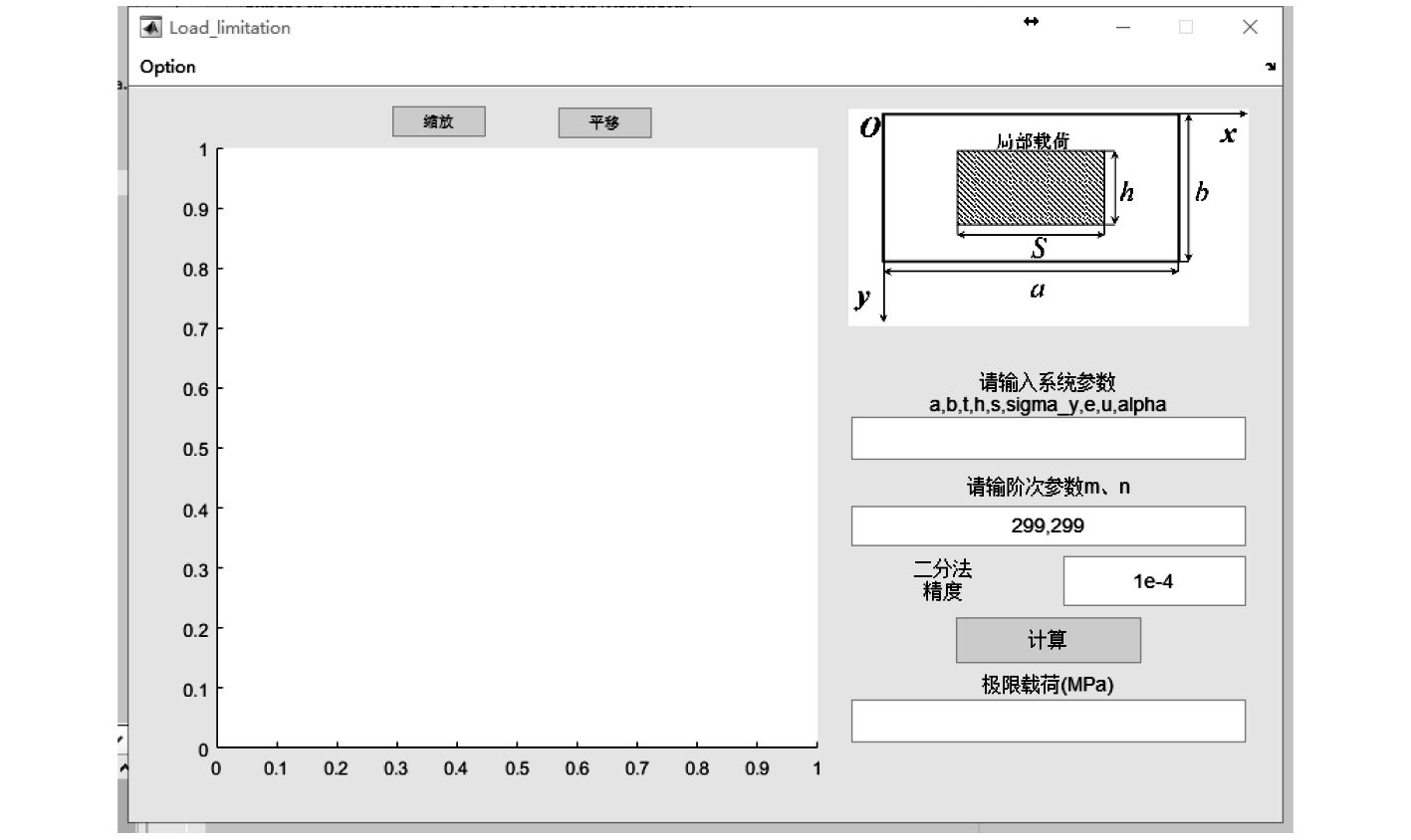
通过Matlab编程实现如图3所示的可视化界面，只需输入简单的参数即可快速得到极限载荷值。

3.2 算例

某极地船舷侧结构如图4所示。

选取以下6种工况进行2种方法的对比，结果如表4所示。

从上面的对比结果可以看到，快速校核方法获取的舷侧冰区加强板格可承受的极限载荷与非线性有限元方法结果相差很小，作为一种快速评估方法，适用于初步设计阶段。

5 结　语

本文应用能量法推导了局部载荷作用下四边固支矩形板的跨中挠度公式，并利用Matlab编程得到任意矩形板尺寸与局部载荷尺寸下的载荷-挠度曲线。通过快速校核方法的算例可以看出文中所给的方法快速且精确，可供工程设计人员在初步设计时参考。