2. 中国船舶重工集团公司第七一四研究所,北京 100012;
3. 哈尔滨工程大学,黑龙江 哈尔滨 150001
2. The 714 Research Institute of CSIC, Beijing 100012, China;
3. Harbin Engineering University, Harbin 150001, China
舱室噪声是影响船员生活的重要因素,国际海事组织(IMO)MSC.337(91)[1]对船舶舱室噪声等级提出了严格要求,在船舶设计阶段准确预报船舶舱室噪声水平已成为关键一步。舱室噪声组成中中高频噪声占主要部分,因此解决如何准确预报中高频舱室噪声问题刻不容缓。
大量学者在船舶舱室噪声特性规律方面做了相关研究[2 – 4]。苏楠[5]基于统计能量法分析了某船振动激励源和空气激励源对于机舱平台附近居住舱室噪声特性的影响,研究结果表明离考核舱室越近的振动激励源对舱室噪声的贡献量越大。温华兵,冯博等[6 – 8]应用统计能量分析方法对不同类型船舶或海洋平台进行了舱室噪声预报,并针对不满足舱室噪声限值的舱室采取降噪措施,使其能够在设计阶段满足舱室噪声限值要求,对实际工程应用具有指导作用。张文春[9]对中高频振声问题采用统计能量分析(SEA)求解,引入SEA系统传递路径的概念,并结合图论提出了舱室噪声传递的SEA赋权图法,揭示了能量在结构和声腔中的传播机理。赵楠[10]结合在船舶建造中遇到的低频主机排气噪声问题,从排气噪声控制角度对船舶柴油机排气系统设计提出了建议。
上述研究表明,大量学者采用统计能量方法进行了船舶舱室噪声预报分析,但鲜有学者探究主机排放噪声对舱室噪声的影响;而主机排放噪声水平往往高于舱室内部空调设备、风机盘管设备等,且可通过空气介质辐射至附近舱室及上层建筑,从而对船舶噪声产生影响。为此,本文以某船为例,分析主机排放噪声对船舶舱室噪声的影响,给出了主机排放噪声对船舶典型舱室噪声的影响规律,旨在为船舶舱室噪声控制提供参考。
1 统计能量方法统计能量法是将一个完整的系统离散成多个子系统,在外界激励作用下,子系统通过边界进行能量交换,建立整个系统能量平衡方程,求解得到各子系统响应。将船舶复杂结构系统离散后,可得各子系统与其相邻子系统的功率流方程:
| $ {P_{i{n_i}}} = {P_{dis{s_i}}} + {P_{ij}}{\text{。}} $ | (1) |
式中:
由一系列的子系统功率流方程式联立,则可得到方程组:
| $ \begin{split} & \omega \left[\!\!\!\! \begin{array}{*{20}{c}} {\left( {{\eta _1} + \displaystyle\sum\limits_{i = 1,i \ne j}^N {{\eta _{1i}}} } \right){n_1}}&{ - {\eta _{12}}{n_1}}& \cdots &\!{ - {\eta _{1N}}{n_1}}\\ { - {\eta _{21}}{n_2}}&{\left( {{\eta _2} + \displaystyle\sum\limits_{i = 1,i \ne j}^N {{\eta _{2i}}} } \right){n_2}}& \cdots &{ - {\eta _{2N}}{n_2}}\\ \vdots & \vdots & \ddots & \vdots \\ { - {\eta _{N1}}{n_N}}&{ - {\eta _{N2}}{n_N}}& \cdots &{\left( {{\eta _N} + \displaystyle\sum\limits_{i = 1,i \ne j}^N {{\eta _{Ni}}} } \right){n_N}} \end{array}\!\!\!\! \right] \times\\ &\left[ {\begin{aligned} {\frac{{{{\bar E}_1}}}{{{n_1}}}}\\ {\frac{{{{\bar E}_2}}}{{{n_2}}}}\\ \vdots \\ {\frac{{{{\bar E}_N}}}{{{n_N}}}} \end{aligned}} \right]= \left[ \begin{array}{*{20}{c}} {{{\bar P}_{i{n_1}}}}\\ {{{\bar P}_{i{n_2}}}}\\ \vdots \\ {{{\bar P}_{i{n_N}}}} \end{array} \right]\text{。} \end{split} $ | (2) |
式中:
对于结构子系统而言:
| $ {E_i}{\rm{ = }}{m_i}v_i^2{\text{。}} $ | (3) |
式中:
对于声腔子系统而言:
| $ {E_i}{\rm{ = }}\frac{{{p_i}^2}}{{\rho {c^2}}}{V_i}{\text{。}} $ | (4) |
式中:
求解上述方程即得到子系统的振动响应或声场响应。
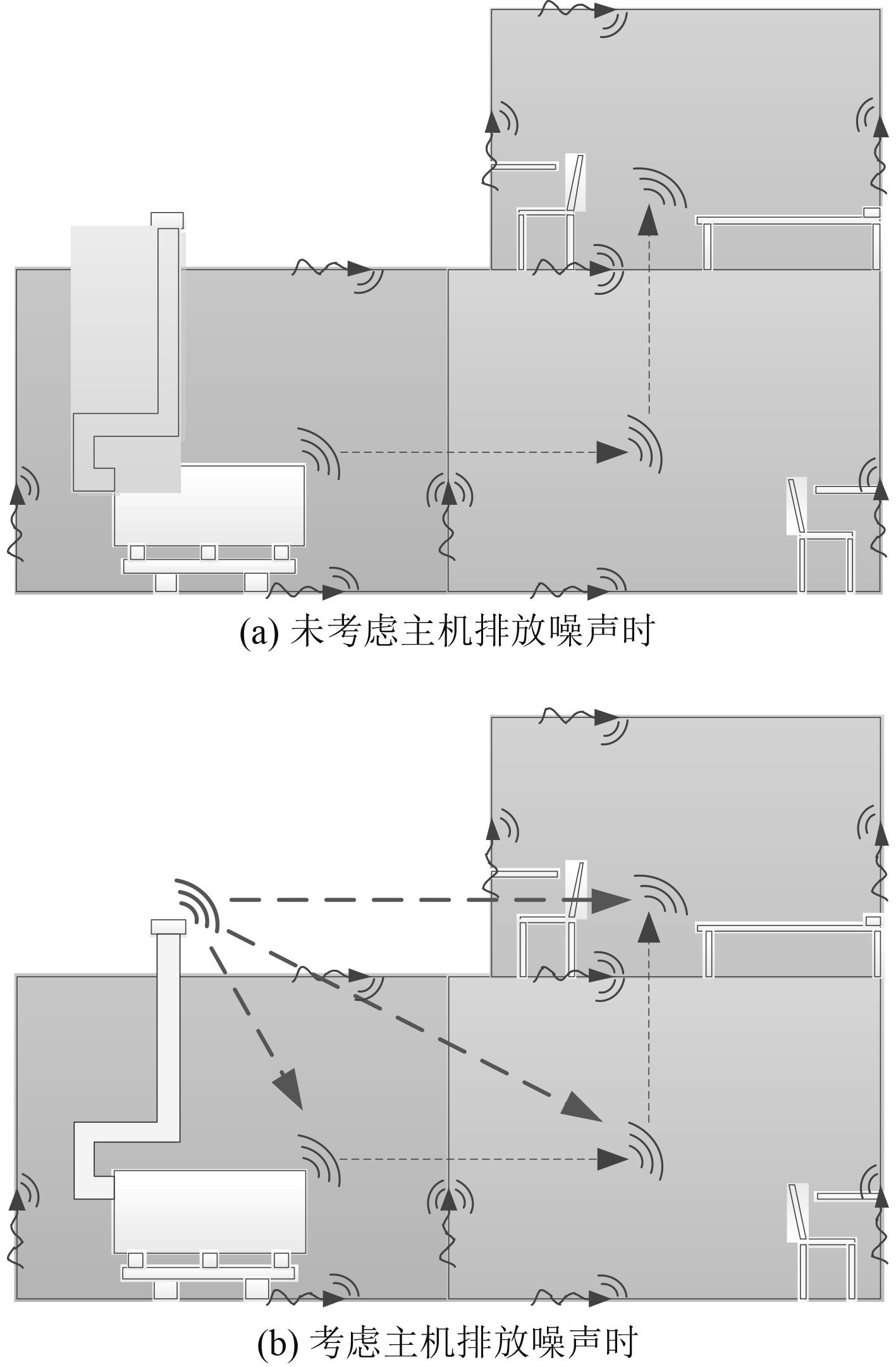
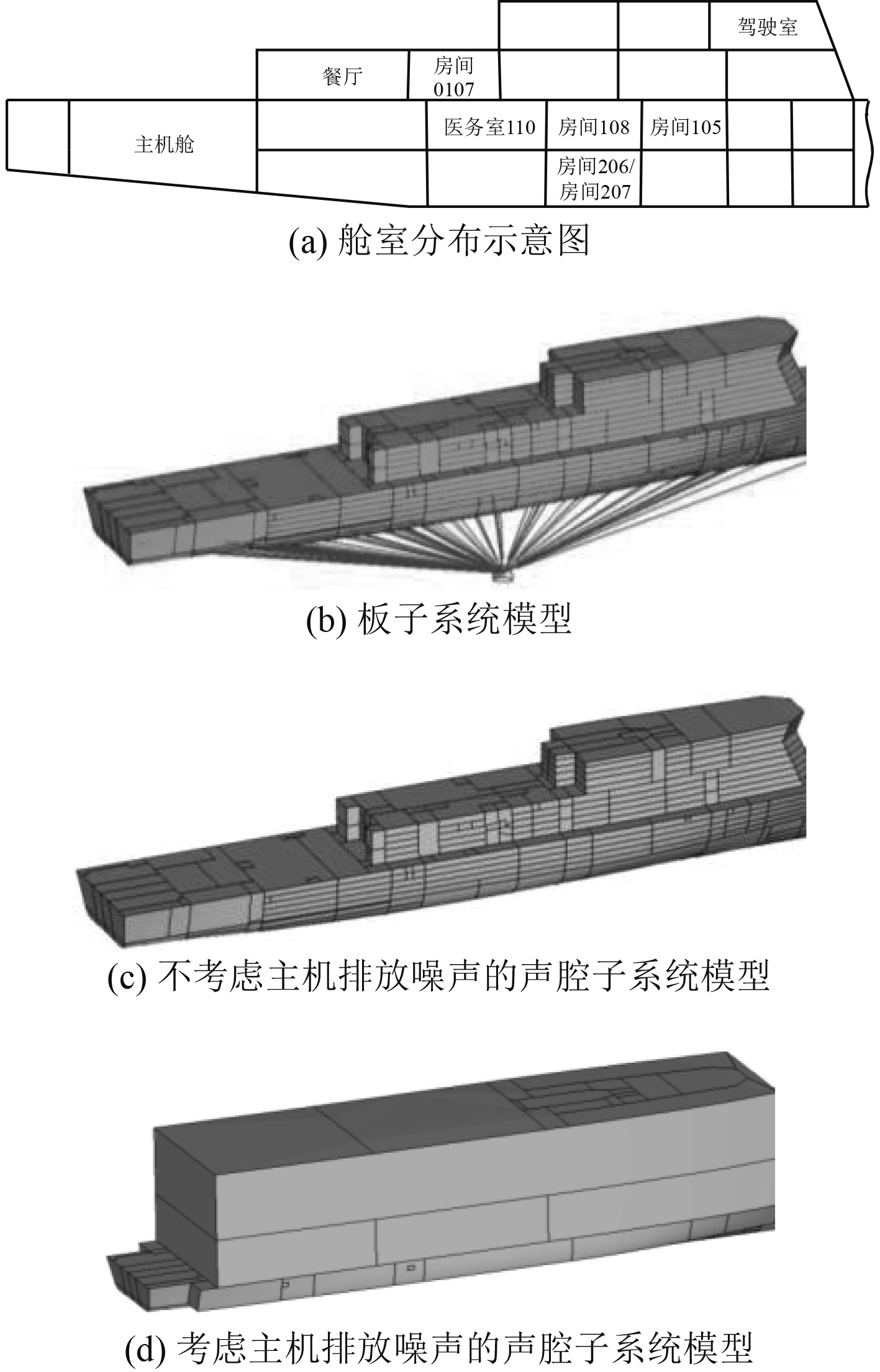
2 船舶舱室噪声分析模型 2.1 统计能量模型本文以某船为研究对象,该船总长88.2 m,型深5.8 m,型宽11.4 m。未考虑主机排放噪声及考虑主机排放噪声时船舱噪声能量传递示意图如图1所示。依据船舶结构图、总布置图、舾装图等资料,建立船舶舱室噪声预报模型,如图2所示。其中考虑主机排放噪声模型建立了外部辅助声腔,模型子系统共2 048个。
|
图 1 舱室噪声能量传递示意图 Fig. 1 Diagram of cabin noise energy transfer |
|
图 2 某船统计能量模型 Fig. 2 Statistical energy model of ship |
结构损耗因子包括内损耗因子及耦合损耗因子。结构内损耗因子采用经验公式

|
图 3 结构内损耗因子 Fig. 3 Structure's internal loss factor |
|
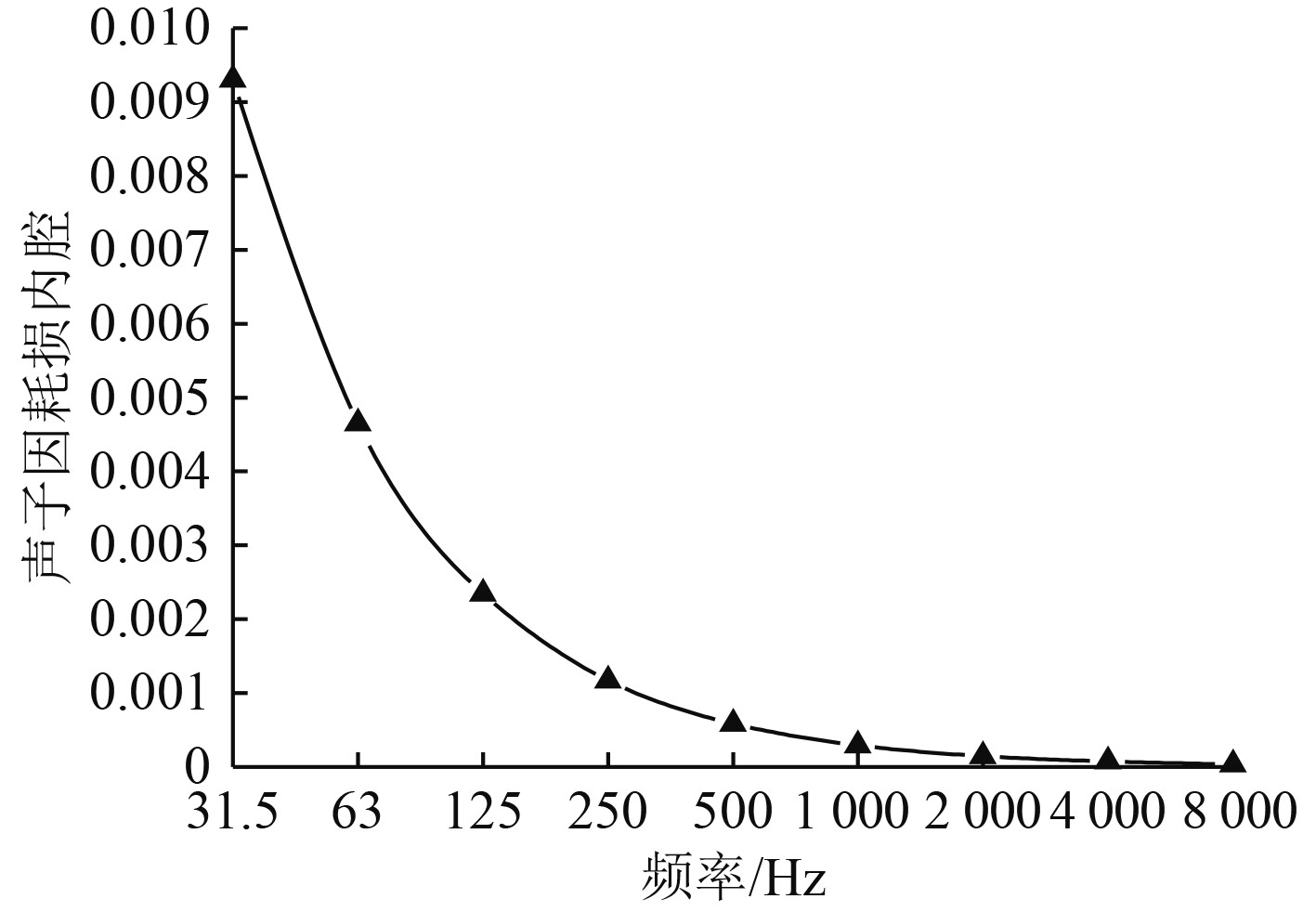
图 4 声腔内损耗因子 Fig. 4 Acoustic cavity's internal loss factor |
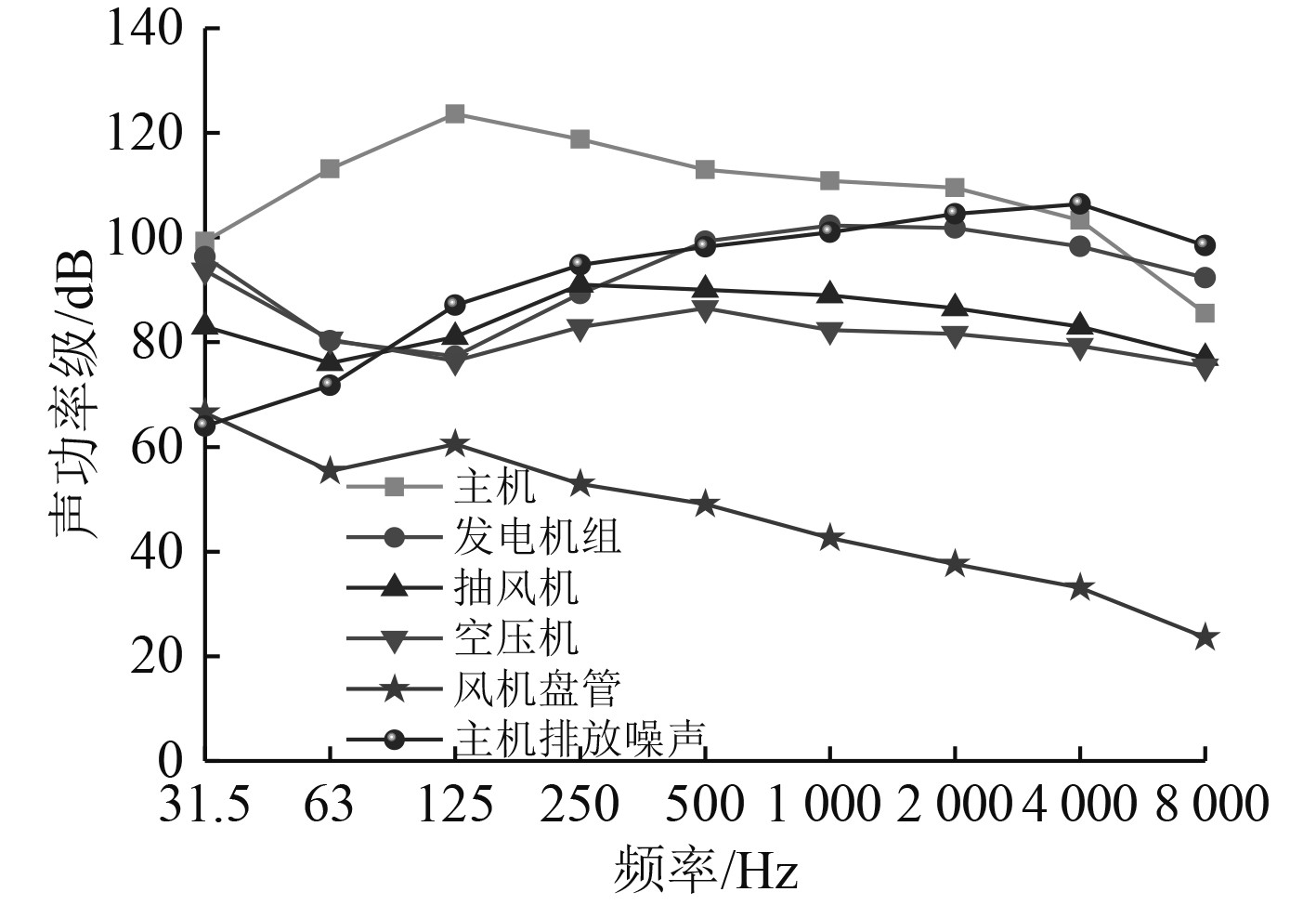
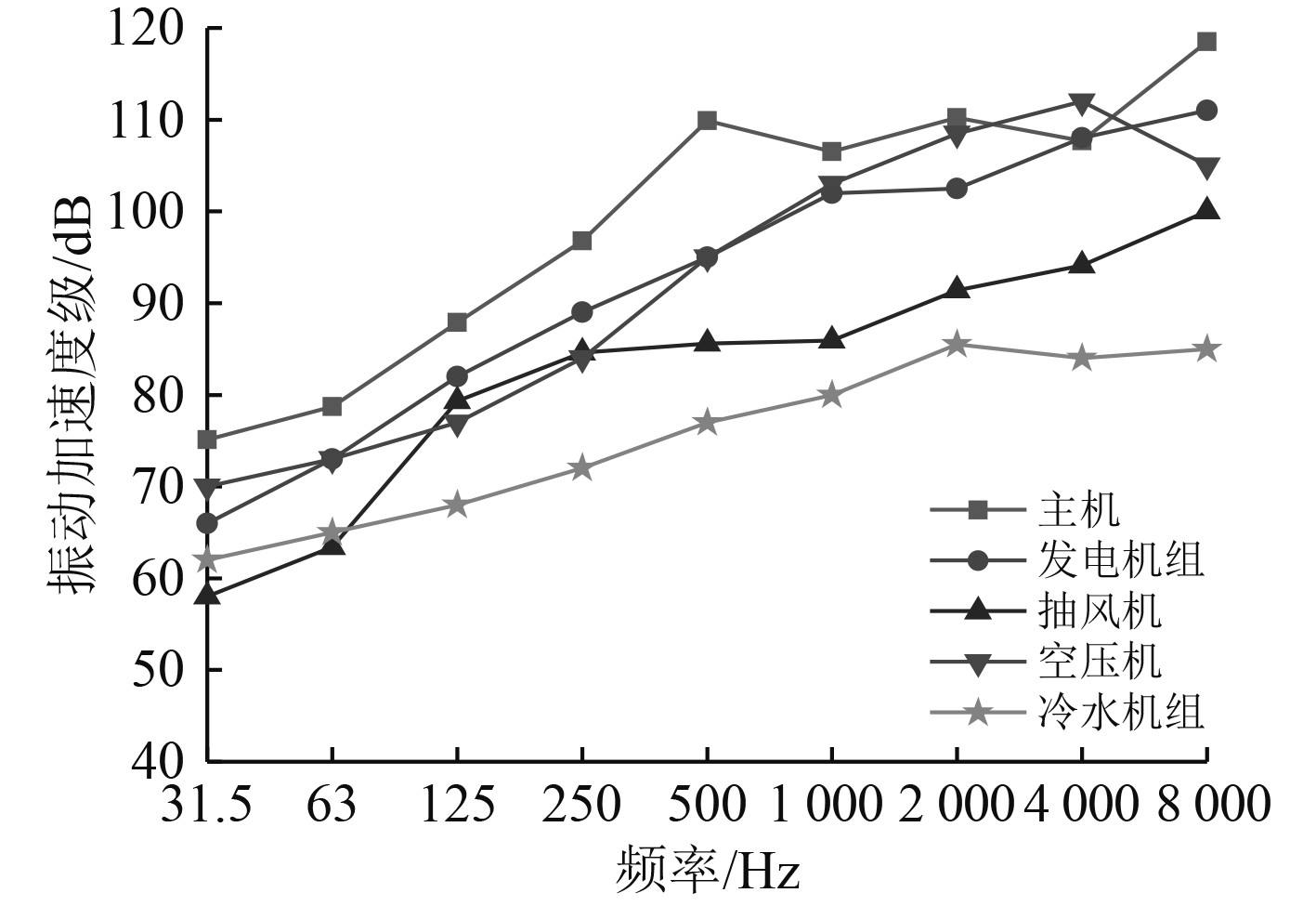
引起船舱噪声的激励载荷按激励类型可分为空气激励载荷及振动激励载荷。空气激励载荷以声功率的形式加载于设备处声腔子系统,其中主机排放噪声载荷加载于烟囱位置;振动激励载荷以振动加速度的形式加载于设备基座处。图5和图6分别给出了部分噪声源设备声功率级频谱曲线及振动加速度级频谱曲线。
|
图 5 设备声功率级曲线 Fig. 5 Equipment's sound power level curve |
|
图 6 设备振动加速度级曲线 Fig. 6 Equipment's vibration acceleration level curve |
本文为分析主机排放噪声对舱室噪声的影响,共设置5种计算工况,如表1所示。工况1、工况3计算模型中声腔建立如图2(c)所示,工况2和工况4及工况5计算模型中声腔建立如图2(d)所示。
|
|
表 1 计算工况表 Tab.1 Calculation condition |
计算工况1、工况2下全船舱室噪声水平,并与实船试验测试结果对比,部分舱室噪声总级计算结果如表2所示。结果表明,工况2计算结果更接近测试值,且结果差异小于3 dB,即考虑主机排放噪声及外部辅助声腔的计算结果更真实合理。部分房间舱室噪声响应曲线如图7所示。
|
|
表 2 典型舱室噪声预报及测试结果对比 Tab.2 Comparison of typical cabin noise prediction and test results |

|
图 7 舱室噪声变化曲线 Fig. 7 Curve of cabin noise |
由图7可以看出,主机排放噪声对舱室噪声有影响,特别是对高频段噪声影响较大,频点噪声差值最大达到6 dB以上。因此,开展船舶舱室噪声预报分析时应考虑主机排放噪声的影响。
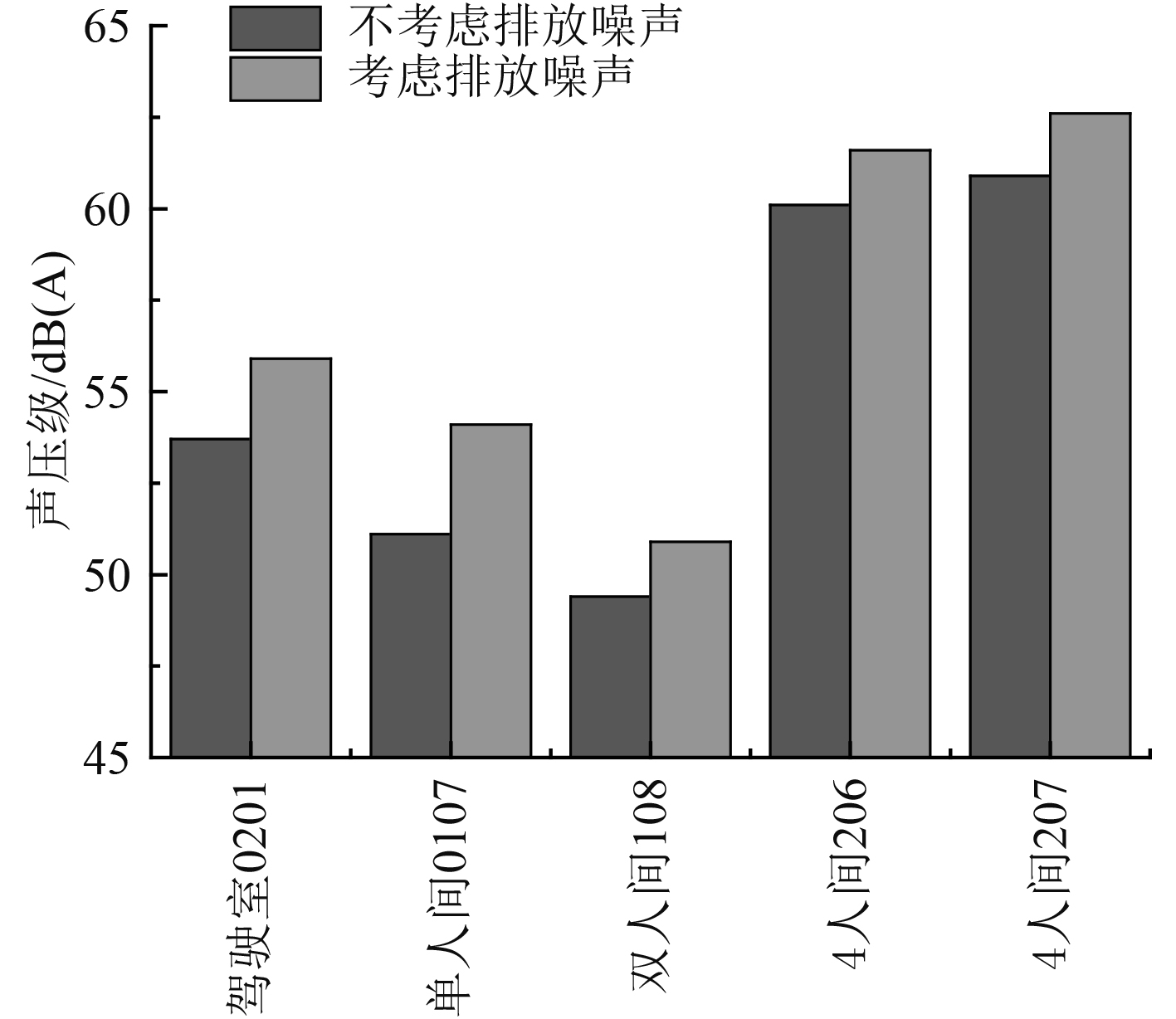
3.2 主机排放噪声对舱室空气噪声的影响船舶舱室噪声组成包括结构噪声及空气噪声,准确分析舱室噪声组成及主导分量是进行舱室声学防护设计的关键一步,而主机排放噪声是引起船舶舱室空气噪声的成分之一,为此分析主机排放噪声对船舶舱室空气噪声的影响。计算工况3与工况4下船舶舱室噪声水平,得到典型舱室空气噪声水平如图8所示。结果表明,考虑主机排放噪声相比不考虑排放噪声舱室噪声较高,部分舱室噪声总级相差3 dB以上。
|
图 8 舱室空气噪声水平对比图 Fig. 8 Comparison of cabin air noise level |
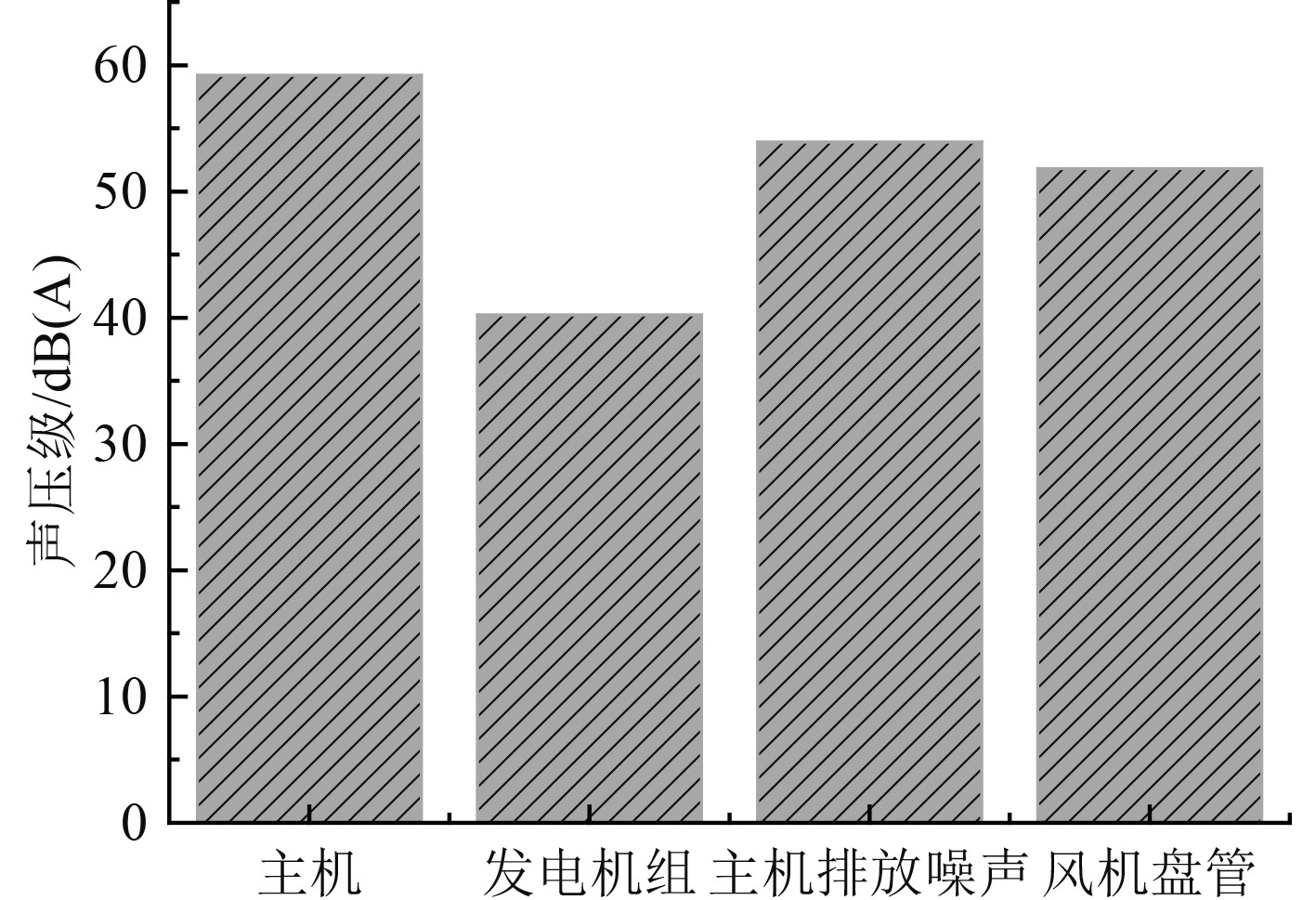
以4人间207为例,其附近主要空气噪声源设备有主机、发电机组、主机排放噪声及风机盘管,对其进行单机噪声分析,得到各设备对4人间207舱室噪声贡献量如图9所示。可以看出,主机排放噪声对4人间207舱室噪声贡献量较大,仅次于主机噪声。
|
图 9 单机贡献量对比图 Fig. 9 Comparison of Single machine contribution |
由图8和图9可知,主机排放噪声在距离较近舱室空气噪声中占比较高,进行舱室声学防护设计时,应考虑主机排放噪声对舱室噪声的影响。
3.3 主机排放噪声激励下舱室噪声水平部分船级社对船舶舱室噪声限值设定如图10所示。可以看出,噪声标准对居住室、医务室要求较高,其中DNV COMF-C1等级或ABS HAB++(WB)等级对人员居住室舱室噪声限值要求为50 dB。为此,探究仅主机排放噪声单独作用时全船舱室噪声分布规律以及需要考虑主机排放噪声的舱室大致范围。

|
图 10 舱室噪声限值 Fig. 10 Limit of cabin noise |
计算工况5下全船舱室噪声,得到仅主机排气噪声激励时全船噪声分布,其中250 Hz下全船舱室噪声分布如图11所示。可以看出,距离主机舱室越近,由主机排放噪声引起的舱室噪声越大。

|
图 11 250 Hz舱室噪声分布图 Fig. 11 Distribution of cabin noise in 250 Hz |
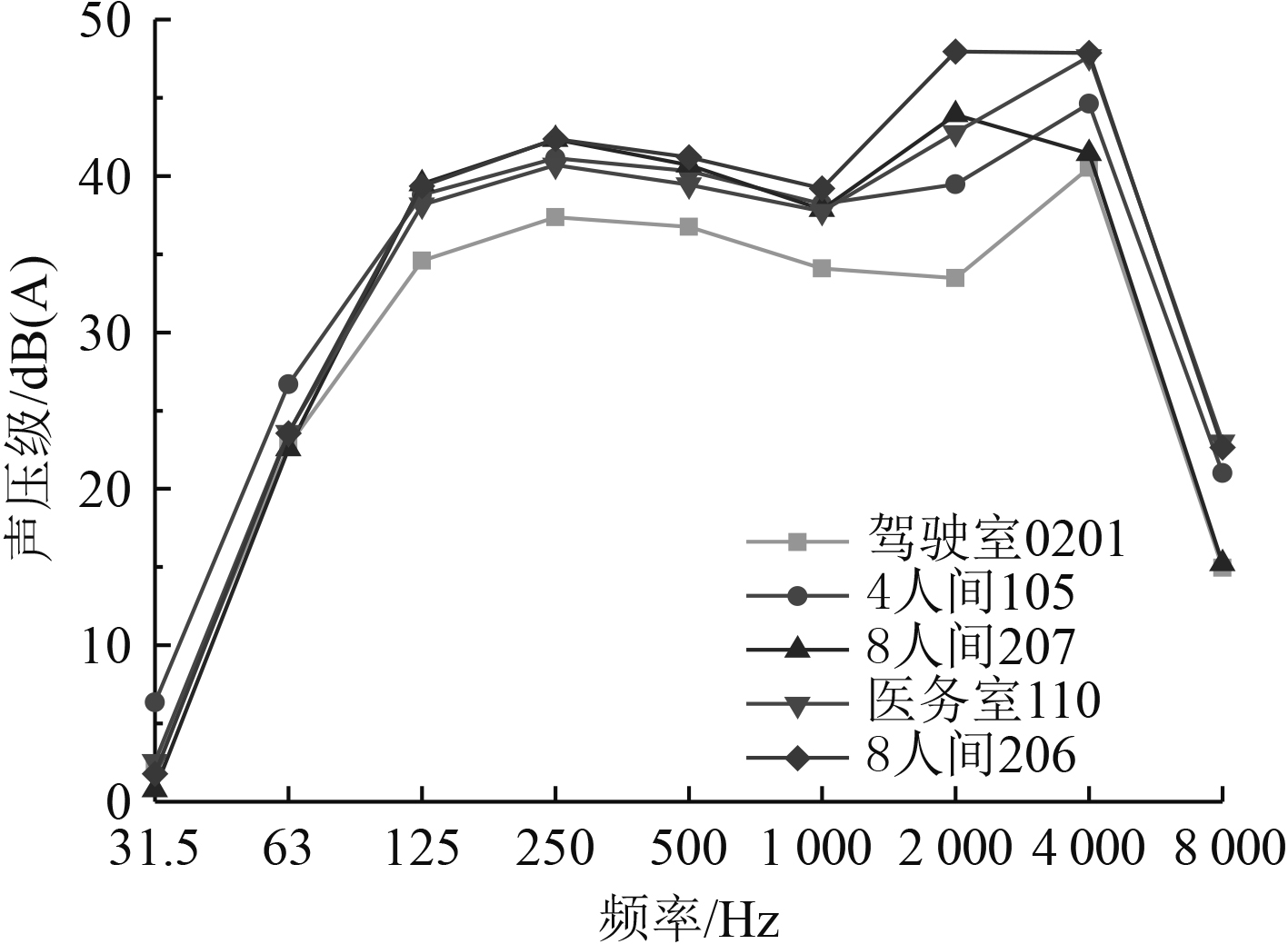
船上设置人员主要活动舱室共26间,其中舱室噪声总级大于50 dB的舱室共9个,达到全船舱室数量的1/3以上,部分舱室噪声响应如图12所示。以主机舱所在甲板为例,计算舱室噪声水平沿船长方向的分布情况,如图13所示(设船首方向为正向)。可以看出,在距离主机舱25 m内的舱室噪声均大于50 dB,超出部分噪声限值标准。因此,对该区域的居住舱室、医务室进行声学防护设计时主机排放噪声不可忽略。
|
图 12 舱室噪声响应曲线 Fig. 12 Curve of cabin noise response |

|
图 13 舱室噪声分布曲线 Fig. 13 Curve of cabin noise distribution |
本文以某船为例,建立舱室噪声预报模型,基于统计能量法分析了主机排放噪声对舱室噪声计算结果的影响,并探究主机排放噪声对舱室噪声的影响规律,得出如下结论:
1)考虑主机排放噪声的舱室噪声计算结果相较于未考虑其影响的计算结果,更接近实船测试值,且误差小于3 dB。
2)距离主机舱越近,由主机排放噪声引起的舱室噪声越大,且主机排放噪声造成的舱室空气噪声仅次于主机引起的舱室空气噪声,在进行声学防护设计时应加以考虑。
3)对于居住室、医务室等对噪声限值要求较严格的舱室而言,需考虑主机排放噪声的影响。就本文所研究船舶而言,距主机舱25 m内的居住室及医务室应考虑主机排放噪声的影响。
| [1] |
International Marine Organization (IMO). Code on noise levels on board ships (IMO MSC.337(91)). 2012.
|
| [2] |
温华兵, 倪杰, 刘甄真. 全回转工作船舱室中频噪声预测分析[J]. 中国造船, 2016, 57(1): 85-93. DOI:10.3969/j.issn.1000-4882.2016.01.010 |
| [3] |
李泽成, 廖久宁, 吴文伟, 等. 海洋工程船的舱室噪声评估[J]. 舰船科学技术, 2015, 37(S1): 69-72. |
| [4] |
于大鹏, 赵德有, 汪玉. 船舶声学建模和阻尼结构对舱室噪声影响研究[J]. 船舶力学, 2010, 14(5): 539-548. DOI:10.3969/j.issn.1007-7294.2010.05.013 |
| [5] |
苏楠, 庞福振, 黄木, 等. 机舱平台附近居住舱室自噪声特性分析[J]. 船海工程, 2014, 43(3): 21-25. DOI:10.3963/j.issn.1671-7953.2014.03.005 |
| [6] |
温华兵, 刘甄真, 陈宁. 全回转拖轮舱室振动噪声预报与控制[J]. 船舶力学, 2018, 22(10): 1292-1299. DOI:10.3969/j.issn.1007-7294.2018.10.014 |
| [7] |
冯博, 桂洪斌, 杨群. 船舶尾部舱室噪声预报及控制分析[J]. 舰船科学技术, 2017, 39(15): 22-27. |
| [8] |
尤小健, 刘依明, 董斌, 等. 基于统计能量法的海洋平台舱室噪声预报及控制[J]. 舰船科学技术, 2018, 40(9): 26-30. |
| [9] |
张文春, 段树林, 邢辉, 等. 基于SEA赋权图的舱室噪声传递路径分析[J]. 振动与冲击, 2017, 36(23): 164-169+180. |
| [10] |
赵楠. 船舶中速主机低频排气噪声控制研究[J]. 船舶工程, 2018, 40(3): 37-40. |
| [11] |
HYNNA P, KLINGE P, NIEMINEN M. Statistical energy analysis with finite element model for noise prediction in ships[C]// Stockholm, Sweden: International Cooperation on Marine Engineering Systems (ICMES), 1987.
|
| [12] |
PLUNT J. Methods for predicting noise levels in ships: experiences from empirical and sea calculation methods[M]. Noise Level Prediction Methods for Ships, Based on Empirical and data, 1980.
|
 2019, Vol. 41
2019, Vol. 41
