2. 江苏科技大学 能源与动力学院,江苏 镇江 212003
2. Jiangsu University of Science and Technology, College of Energy and Power, Zhenjiang 212003, China
穿浪高速双体船(以下简称WPC)是结合普通高速双体船和小水线面船的船型特点设计的,特殊的设计赋予它速度高、稳性好、耐波和回转性能好以及运载能力高等特点,加上制造工艺简单和使用成本低,因此在军事作战和民用运输中得到广泛的应用[1 – 2]。
20世纪80年代初,WPC由澳大利亚人赫克斯和克利福德首先提出并经试验取得成功,随后,澳大利亚AMD公司进行了WPC船型系列实验研究,日本NKK公司开展了薄壁连接桥的WPC船型研究[3]。国内对WPC船的研究开始于20世纪80年代末,哈尔滨工程大学和大连理工大学开展了对WPC船水动力性能的理论与系列实验研究[4]。在片体干扰因子确定方面,赵连恩等[5]提出用兰金(Rankine)体的波幅函数代替实际船型的波幅函数;在兴波阻力和波形数值计算方面,马健等[6 – 7]提出了基于面元法的势流计算方法;张晓阳等[8]利用Michell积分的复积分形式对兴波阻力和片体干扰进行数值计算,并进行船模实验数据对比,这些研究成果为本文的阻力计算和兴波干扰因子的确定提供有力支撑。
本文提出一种基于阻力性能分析的穿浪双体船优化设计分析方法,通过选用不同的片体间距比k/b,选择一个最合适的k/b值,使兴波干扰始终处于有利条件,兴波阻力随航速的增大而逐渐减小。在此基础上选择适当的片体长宽比L/b来减小船舶在航行中的阻力,得到更优化的双体船船型参数,为双体船及多体船设计提供一种可利用的参考方法。
1 主尺度的确定与建模以某穿浪双体船为参考船型(参数见表1),按18.288 m船长对其进行比例缩放,并对外形进行适当简化,完成双体船的船型初步设计。
|
|
表 1 船型参数 Tab.1 Ship parameters |
考虑到运行的需求,选取船长L为18.288 m。型深D对航速的影响不是很突出,通常与船的总纵强度和储备浮力有关,影响稳性;型深D不能太小,必须满足最小干舷的要求,若型深D取得过大,重心升高,影响高速航行时的回转性能,对快速航行不利,综合考虑,型深D取2.500 m。船宽主要影响船舶稳心位置、船舶受到浮力和舱容的大小,从快速性的角度说,保持其他船型参数不变,高速双体船可以适当的减小
选取的穿浪双体船基本主尺度如下:船长L=18.288 m,最大船宽B=8.522 m,型深D=2.500 m,设计水线长

|
图 1 设计船型 Fig. 1 Design ship |
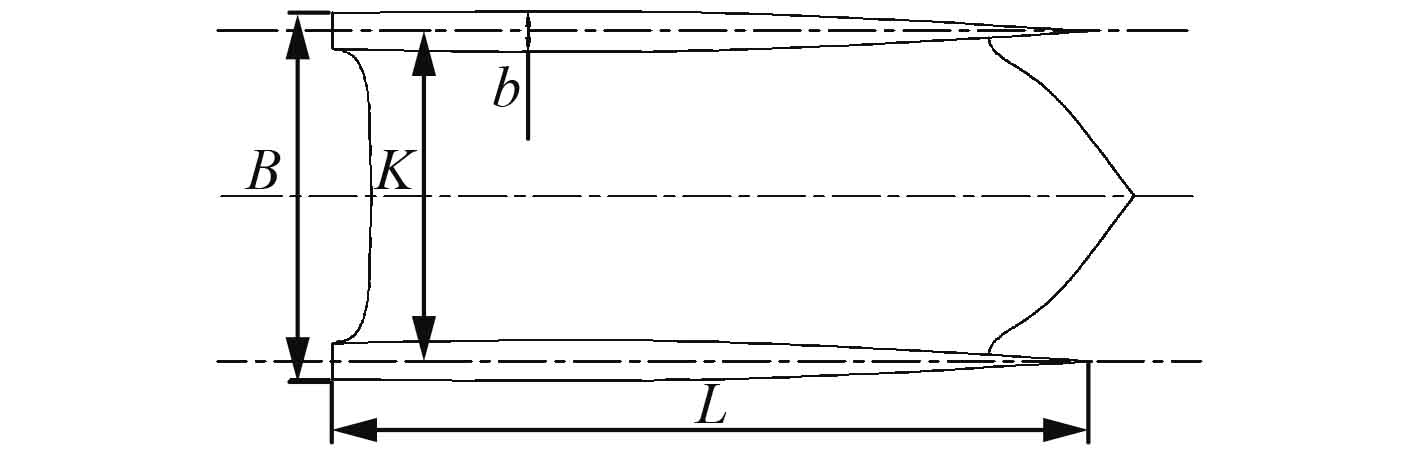
|
图 2 船型主尺度 Fig. 2 Main scale of ship |
双体船在静水中航行时受到的阻力,除了普通单体船舶所受阻力外,还存在着干扰阻力[9],分析时不计空气阻力和附体阻力,总阻力可以表达为:
| ${R_t} = {R_f} + {R_r} + \Delta R\;\Delta R = \Delta {R_{\rm{w}}} + \Delta {R_v}\text{。}$ | (1) |
式中:
采用三因次法,双体船的黏性阻力可表达为
| ${C_{tcat}} = (1 + \beta k){C_f} + \tau {C_w}\text{。}$ | (2) |
式中:
粘性阻力由粘压阻力和摩擦阻力两部分组成,这里采用ITTC–1957摩擦阻力公式计算粘性阻力,其计算公式为:
| ${R_v} = 1/2(1 + k){C_f}\rho {v^2}s\text{。}$ | (3) |
英国南安普顿大学科学系的A.E.Molland等对双体船形状修正因子进行研究得出以下公式和结果[10]:
| $ 1 + \beta k=3.03{({L / {{\Delta ^{1/3}}}})^{ - 0.40}}=1.328 \text{。} $ | (4) |
斯利金斯基和伦德根据流体静力学的“映像”假设,把2条相同并列等速平行运动的船舶用一条平行竖直运动的情况来代替,导出了双体“薄船”的兴波阻力积分公式。高速双体船的片体长宽比L/b比较大,属于瘦长型船舶,符合双体“薄船”阻力公式的应用[11]。
| ${R_{wcat}} = \displaystyle\frac{{8\rho {{\rm{g}}^2}}}{{{\text{π}} {V^2}}}\int_1^\infty {({I^2}} \!+\! {J^2})[1 \!+\! \cos (2{C_0}{k_0}\lambda \sqrt {{\lambda ^2} \!- \!1} )\displaystyle\frac{{{\lambda ^2}{\rm d}\lambda }}{{\sqrt {{\lambda ^2} - 1} }}\text{,}$ | (5) |
| $I = \int_{ - d}^0 {\int_{ - L/2}^{L/2} {{f_x}(x, z)} } \exp ({k_0}{\lambda ^2}z)\sin ({k_0}\lambda x){\rm d}x{\rm d}z\text{,}$ | (6) |
| $J = \int_{ - d}^0 {\int_{ - L/2}^{L/2} {{f_x}(x, z)} } \exp ({k_0}{\lambda ^2}z)\cos ({k_0}\lambda x){\rm d}x{\rm d}z\text{。}$ | (7) |
高速双体船的兴波阻力由2部分组成,即
| ${R_{w0}} = \frac{{8\rho {g^2}}}{{{\text{π}} {V^2}}}\int_1^\infty {({I^2} + {J^2})} \frac{{{\lambda ^2}{\rm d}\lambda }}{{\sqrt {{\lambda ^2} - 1} }}\text{,}$ | (8) |
| $\Delta {R_i} = \frac{{8\rho {g^2}}}{{{\text{π}} {V^2}}}\cos (2{C_0}{k_0}\lambda \sqrt {{\lambda ^2} - 1} )\frac{{{\lambda ^2}{\rm d}\lambda }}{{\sqrt {{\lambda ^2} - 1} }}\text{。}$ | (9) |
模型导入船舶分析软件进行阻力仿真分析,计算方法采用瘦体解析法,使用Molland对双体船形状修正并计及黏性干扰,摩擦阻力采用ITTC–1957计算公式,为了能够捕捉整个航速范围内的阻力及干扰,航速范围取0~33 kn。
双体船的阻力由片体自身的摩擦阻力
选取适当的L/b和k/b并与
双体船片体间距比k/b,主要受附加兴波干扰阻力的影响。航速较低时,k/b对双体船干扰阻力不明显且无规律,k/b的选择完全以总布置要求来决定,一般取k/b>2,当k/b>6时,片体间的干扰阻力接近0。中高速航行时的双体船k/b影响兴波干扰明显增加,此时引入兴波干扰因子

|
图 3 不同k/b下兴波阻力系数变化曲线图 Fig. 3 Curve of wave-making resistance coefficient under different k/b |
由图3可以看出,随着航速的增加,兴波阻力系数出现3次较大波动,分别在
随着片体间距比k/b的增大,双体船兴波阻力的峰值依次减小,总体呈下降趋势,因此可以通过增加k/b来减少兴波干扰。结果显示k/b越大,其对应的
为了更进一步分析在不同傅汝德数
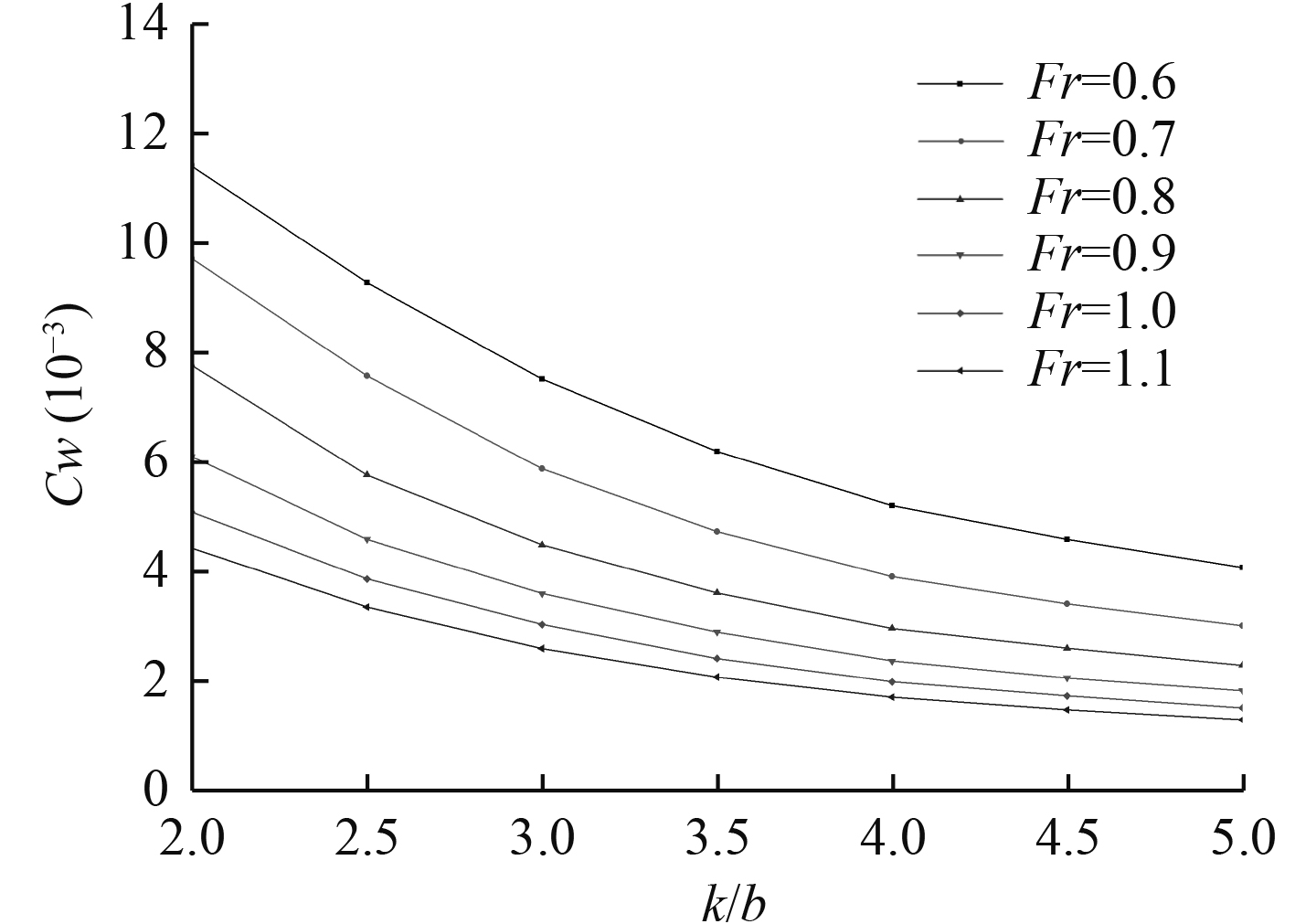
|
图 4
不同
|
可以看出:
1)傅汝德数越小,其兴波阻力受k/b的影响就越大,随着傅汝德数增大,兴波阻力变化愈趋于平缓;
2)当k/b>3.2时,兴波阻力曲线斜率趋于平缓,继续增大片体间距对兴波阻力的影响效果不明显。所以k/b适合的取值范围在3.2~4之间,若继续增大k/b值,兴波阻力系数
双体船具有不同的长宽比也就意味着其修长系数
从阻力和载重量上综合考虑,取L/b=9–15。根据片体间距对阻力的影响分析知道,k/b在3~4之间兴波阻力较小,这里选取k/b=3.5分别绘制片体长宽比L/b=9.0,10.0,11.0,12.0,13.0,14.0,15.0时的剩余阻力系数
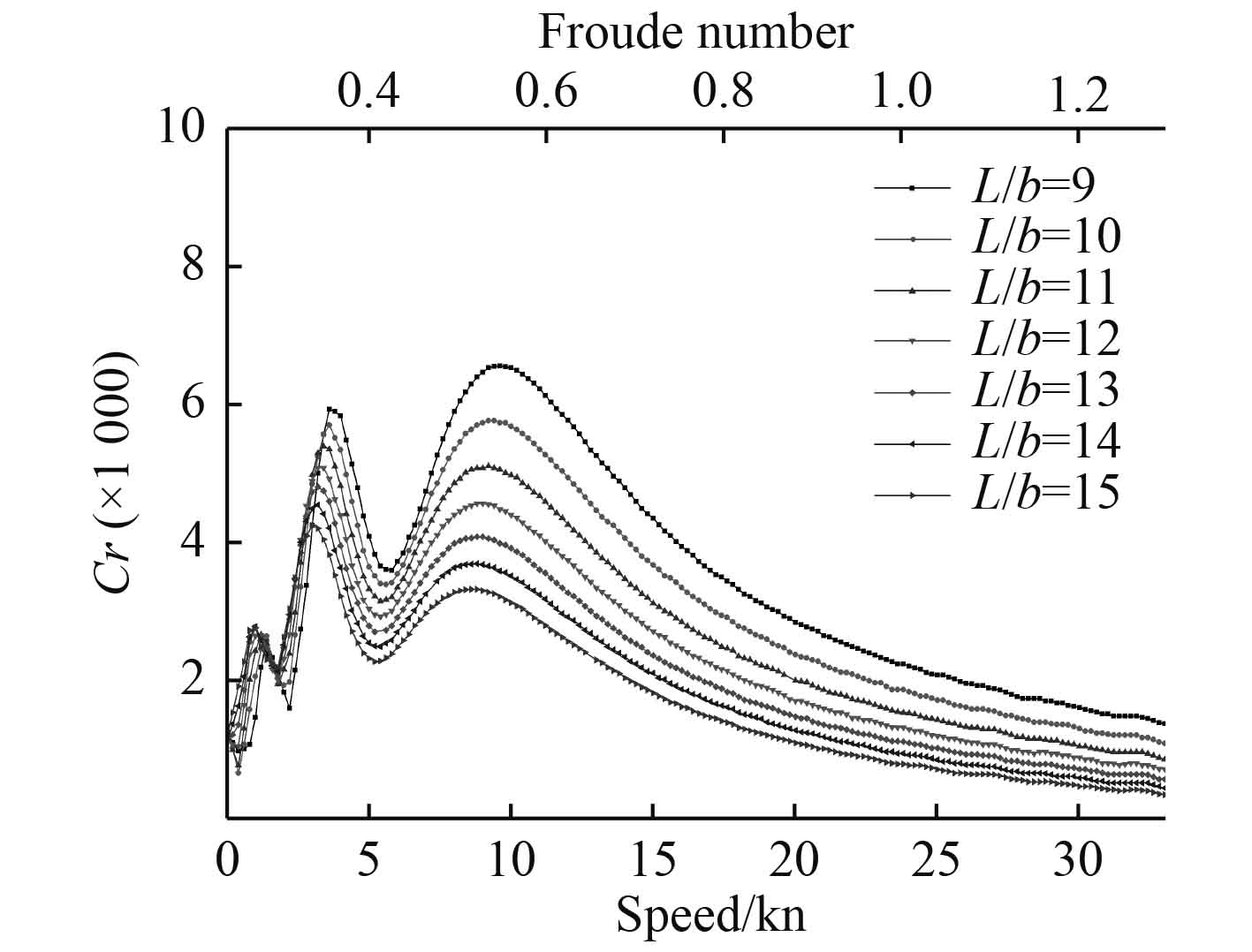
|
图 5 不同L/b下剩余阻力系数变化曲线图 Fig. 5 Curve of residual drag coefficient under different L/b |
可以看出,随着航速的增加,剩余阻力系数出现3次较大波动,分别在
在片体间距比相同时,片体长宽比的变化对剩余阻力系数影响随着航速的变化有所浮动,当
同样分析在一定傅汝德数
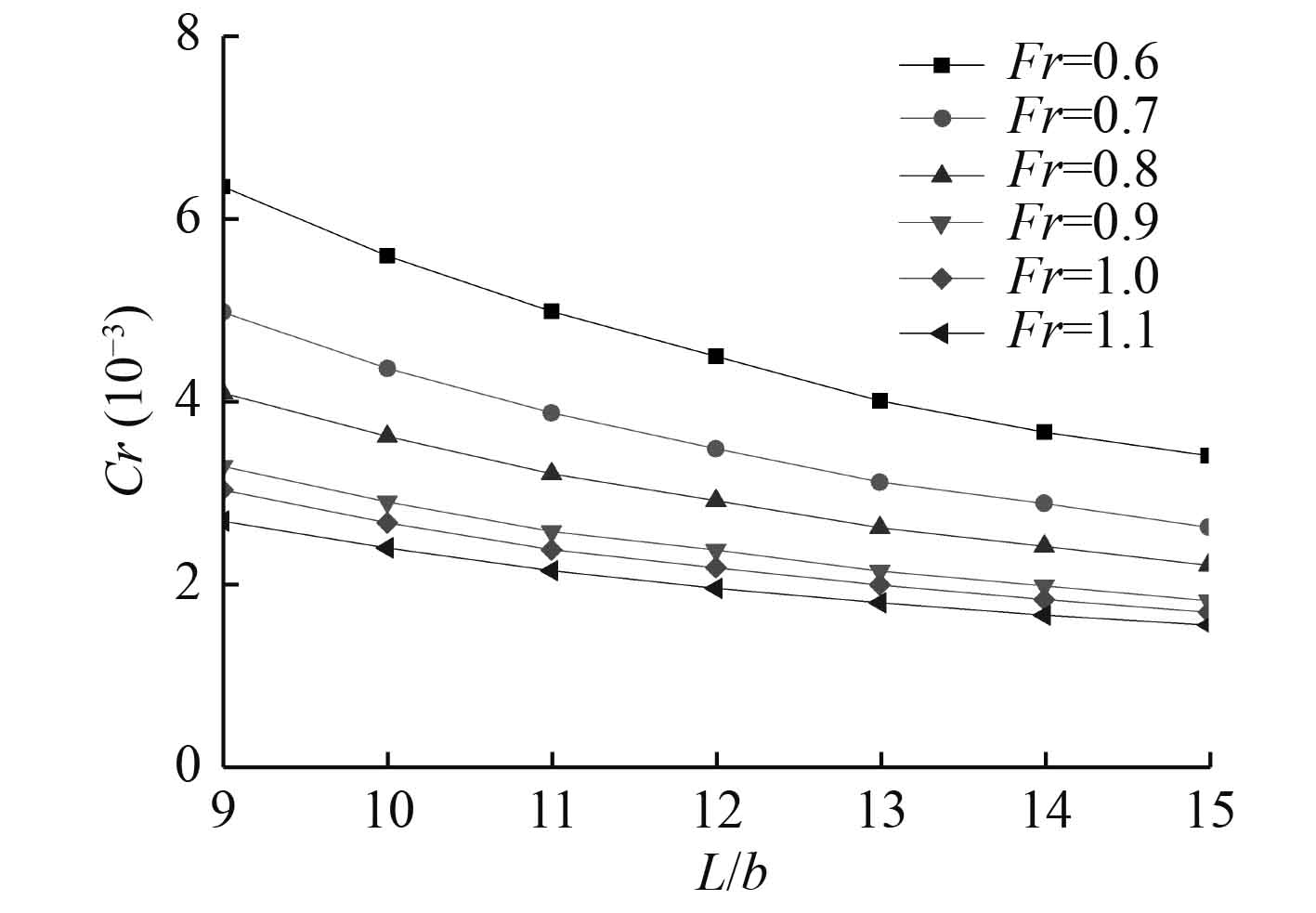
|
图 6
不同
|
由图6可以得知,航速越小,剩余阻力系数L/b的影响越大,随着航速增加,剩余阻力系数变化越来越小。此外可以看到,当L/b≥12时,剩余阻力系数随L/b的变化趋于平缓,所以L/b值选择在12~13之间比较合适。
4 结 语在
对于双体船兴波干扰影响最大的区间为
由于船型限制,没有考虑菱形系数对于船舶快速性的影响,且没有结合耐波性等其他性能对该船型进行全面分析,以后会增加控制变量的数目,以进行更全面的分析。此外,没有进行相关的船模试验数据对比分析,这也是下一步研究的方向。
| [1] |
杨帅, 谢伟, 许晟. 不同附体对穿浪双体船阻力和耐波性影响研究[J]. 舰船科学技术, 2015, 37(7): 20-23. DOI:10.3404/j.issn.1672-7649.2015.07.005 |
| [2] |
赵连恩, 谢永和. 高性能船舶原理与设计[M]. 北京: 国防工业出版社. 2009: 122–125.
|
| [3] |
苏红宇. 穿浪船的发展概况[J]. 船舶工业技术经济信息, 2004, 226(2): 6-9. |
| [4] |
赵连恩, 何义. 穿浪多体船运动性能研究[J]. 中国造船, 1997, 139(4): 20-28. |
| [5] |
赵连恩, 杜振煌, 应业炬. 基于兴波理论与阻力图谱资料的高速双体船阻力预报方法[J]. 船舶力学, 2006, 10(5): 17-23. DOI:10.3969/j.issn.1007-7294.2006.05.003 |
| [6] |
马健, 左文锵. 穿浪双体船兴波阻力数值计算[J]. 中国舰船研究, 2007, 2(1): 52-55. DOI:10.3969/j.issn.1673-3185.2007.01.012 |
| [7] |
马健, 高高. 基于NURBS高阶面元法的浅水船舶兴波阻力计算[J]. 武汉理工大学学报, 2006, 6(3): 444-447. DOI:10.3963/j.issn.2095-3844.2006.03.021 |
| [8] |
张晓阳, 李铁骊, 林焰. 穿浪双体船阻力性能预报与模型实验分析[J]. 大连理工大学学报, 2009, 49(3): 396-400. |
| [9] |
邓芳, 邓魏彬. 双体船阻力性能计算及船型设计优化[J]. 青岛科技大学学报(自然科学版), 2015, 36(1): 72-76. |
| [10] |
COUSER P, WELLICOME J F, MOLLAND A F. An Improved Method for the Theoretical Prediction of the Wave Resistance of Transom-stern Hulls using a Slender Body Approach[J]. International Shipbuilding Progress, 1998, 45(444): 1-18. |
| [11] |
陈京普, 朱德祥, 何术龙. 双体船兴波阻力数值预报方法研究[J]. 船舶力学, 2006, 10(2): 25-28. |
 2019, Vol. 41
2019, Vol. 41
