0 引　言

声学覆盖层广泛运用于潜艇等水下平台，敷设的声学覆盖层可吸收入射声波，降低潜艇目标强度，提高潜艇声隐身性^[1]。目前对于敷设声学覆盖层的复杂结构体的目标强度已经开展了大量研究，形成了针对中高频率目标强度的计算方法和实用的软件，采用声学覆盖层技术可以有效控制中高频段的目标强度^[2]。而对于低频段，传统声学覆盖层的吸声特性不佳，相关的研究也较少。研究表明，很多情况下传统吸声材料可以等效为具有等效密度和等效动态模量的均匀黏弹性材料或者多层均匀黏弹性材料^[3]。目前已经有很多研究采用实验方法测定材料等效参数，并用于相关计算和预报^[4]。考虑到黏弹性材料的特性，采用有限元方法可以准确的对黏弹性材料进行建模，因此本文采用有限元方法分析敷设声学覆盖层的标准潜艇低频目标强度。

1 声-壳-结构耦合有限元法

采用有限元方法计算敷设声学覆盖层的标准潜艇的目标强度，涉及到海水环境、潜艇主结构和声学覆盖层3种不同的材料，适用不同的物理模型，因此需要采用多物理场耦合的有限元方法。海水环境采用线弹性声学模型，潜艇主结构采用中厚板壳模型；声学覆盖层^[5]采用三维固体力学模型。由于有限元方法的具体表达式非常复杂，因此只列出控制方程。

1.1 线弹性声学模型

标准潜艇外部以及标准潜艇内壳和外壳之间为海水，基本方程为各项同性Helmholtz方程：

${\nabla ^2}{p_t}\left( {{r}} \right) + {k^2}{p_t}\left( {{r}} \right) = 0{\text{。}}$

(1)

其中： ${p_t}\left( {{r}} \right)$ 为总声压； ${{r}}$ 为空间中任意点的位矢； $k \!=\! {{2{\text{π}} f} / c}$ 为波数；f为频率；c为声速。对目标强度的计算，实际上是计算在特定入射声波 ${p_i}\left( {{r}} \right)$ 的条件下，标准潜艇的散射声波 ${p_s}\left( {{r}} \right)$ 。由于入射声波的声源通常在远场，因此采用平面波作为入射声波 ${p_i}\left( {{r}} \right)$ ，这样散射声波为 ${p_s}\left( {{r}} \right){ { = }}$ ${p_t}\left( {{r}} \right) - {p_i}\left( {{r}} \right)$ 。此外，标准潜艇的外部为无限大海水空间，采用完美匹配层（PML）技术模拟无限大空间。

1.2 中厚板壳模型

标准潜艇的主结构为钢板，根据相关研究，钢板的振动主要为反对称Lamb波，当频厚比满足 $ fd < 2{\rm{ kHz}} \cdot {\rm{m}}$ 时，物理模型可以采用Mindlin-Reissner中厚板壳模型^[5]，其中d为板厚度。中厚板壳模型的控制方程为

$\rho \displaystyle \frac{{{\partial ^2}{{u}}\left( {{r}} \right)}}{{\partial {t^2}}} = \nabla \cdot {\bf{\sigma }}\left( {{r}} \right) + {{{F}}_V}\left( {{r}} \right){\text{。}}$

(2)

其中： ${{u}}\left( {{r}} \right)$ 为任意一点的位移矢量， ${\bf{\sigma }}\left( {{r}} \right)$ 为应力张量； ${{{F}}_V}\left( {{r}} \right)$ 为体载荷；ρ为密度；t为时间，此外 ${{u}}\left( {{r}} \right)$ 和 ${\bf{\sigma }}\left( {{r}} \right)$ 满足线弹性材料的本构关系。中厚板壳模型中的位移矢量 ${{u}}\left( {{r}} \right)$ 满足方程

${{u}}\left( {{r}} \right) = {{{u}}_s}\left( {{r}} \right){{ + }}{\xi _z}{{a}}\left( {{r}} \right){\text{。}}$

(3)

其中： ${{{u}}_s}\left( {{r}} \right)$ 为板壳中面上任意一点的位移矢量； ${{a}}\left( {{r}} \right)$ 为 ${{r}}$ 点的位移旋转矢量； ${\xi _z}$ 为板壳局部坐标系中厚度方向的坐标。

结合式（2）和式（3），中厚板模型将三维空间上的计算转换为二维中面上的计算，实际建模中只需对中面进行建模，可以极大地减小计算量。此时体载荷转换为面载荷 ${{{F}}_A}\left( {{r}} \right)$ ，即 ${{{F}}_V}\left( {{r}} \right) = {{{{{F}}_A}\left( {{r}} \right)} / d}$ ，此外忽略板壳局部坐标系中厚度方向应力分量，即 ${\sigma _z} = 0$ 。

1.3 固体力学模型

声学覆盖层在几何上也属于板壳，但根据相关研究，声学覆盖层所采用的高分子橡胶材料在频率很低时也会产生高阶Lamb波分量，因此不适用于板壳模型，而需要采用三维固体力学模型。固体力学模型的控制方程为

$\rho \displaystyle \frac{{{\partial ^2}{{u}}\left( {{r}} \right)}}{{\partial {t^2}}} = \nabla \cdot {\bf{\sigma }}\left( {{r}} \right){\text{。}}$

(4)

位移矢量 ${{u}}\left( {{r}} \right)$ 和应力张量 ${\bf{\sigma }}\left( {{r}} \right)$ 满足黏弹性材料的本构关系，固体力学的载荷作为边界条件给出。

1.4 物理场耦合边界条件

耦合有限元模型中涉及多个物理场，物理场与物理场之间的边界条件对于求解目标强度至关重要。对于线弹性声学模型与固体力学模型，在其边界应满足法向位移连续条件。此外还需满足动力学平衡条件，对于线弹性声学模型有

${{n}} \cdot \displaystyle \frac{{\nabla {p_t}\left( {{r}} \right)}}{\rho } = \pm {{n}} \cdot \displaystyle \frac{{{\partial ^2}{{u}}\left( {{r}} \right)}}{{\partial {t^2}}}, {{ }}{{r}} \in \partial \varOmega {\text{。}}$

(5)

其中： ${{n}}$ 为边界法向单位矢量； $\partial \varOmega $ 为物理场边界。等号右侧的正负号取决于 ${{n}}$ 的方向，若 ${{n}}$ 指向线弹性声学模型方向，则取正号，反之取负号；对于固体力学模型有

${{{F}}_A}\left( {{r}} \right) = \pm {p_t}\left( {{r}} \right){{n}}, {{ }}{{r}} \in \partial \varOmega {\text{。}}$

(6)

其中： ${{{F}}_A}\left( {{r}} \right) = {{n}} \cdot {\bf{\sigma }}\left( {{r}} \right)$ ，等号右侧的正负号取决于 ${{n}}$ 的方向，若 ${{n}}$ 指向线弹性声学模型方向，则取负号，反之取正号。对于线弹性声学模型与中厚板壳模型，在其边界同样应满足法向位移连续条件和动力学平衡条件，即式（5）和式（6），只是其中 ${{{F}}_A}\left( {{r}} \right) = {{{F}}_V}\left( {{r}} \right)d$ 。对于固体力学模型与中厚板壳模型，在其边界同样应满足位移连续条件。

2 标准潜艇模型设定

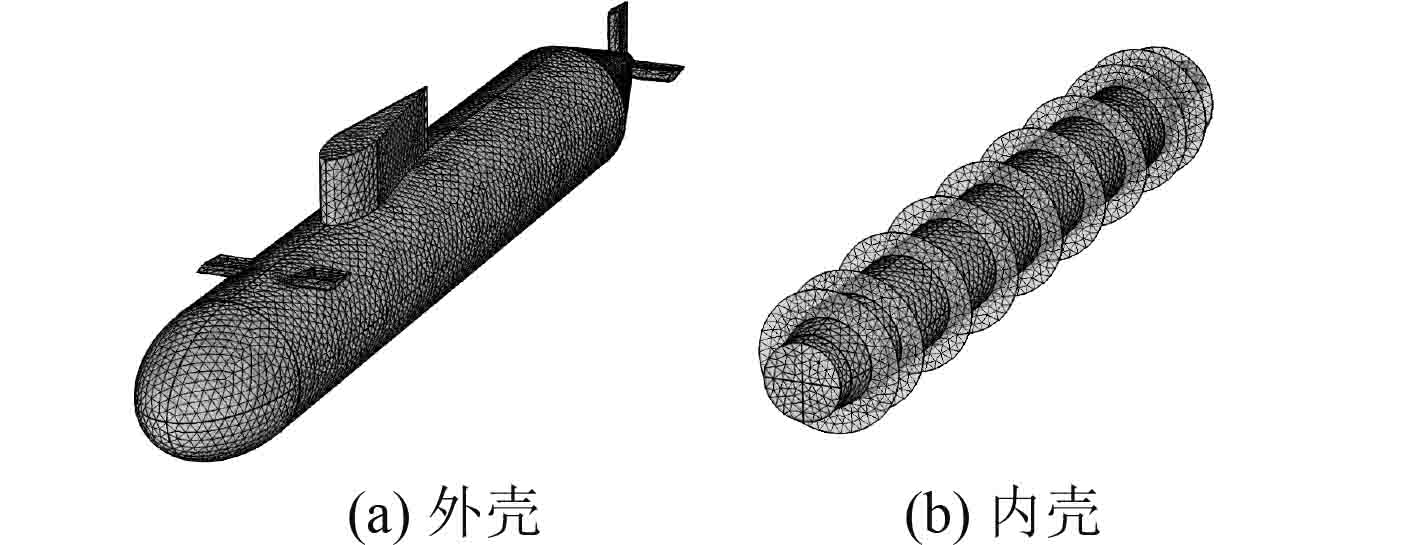
计算采用的标准潜艇模型为BeTSSi-simple模型，如图1（a）所示，这是一个外壳模型，模型全长为62 m，艇体部分的直径为7.5 m。计算采用的内壳模型如图1（b）所示，全长为51.9 m，主体部分直径为5 m，内壳和外壳之间还包括10个环肋^[6]。此外规定首部方向为0°，右舷方向为90°，尾部方向为180°，左舷方向为270°。根据有限元理论，一个波长范围内应至少划分6个网格以保证计算的准确性^[7]。取最大计算频率为500 Hz，这样整个耦合有限元模型的自由度约为200万。

分别计算单壳体和双壳体标准潜艇的目标强度，参照相关文献[8]对标准潜艇的主结构和声学覆盖层进行设定。单壳体标准潜艇仅包含外壳，外壳采用40 mm厚的耐压钢板，敷设50 mm厚的声学覆盖层。外壳外部为海水，内部为空气。双壳体标准潜艇包含外壳、内壳和环肋，其中外壳为10 mm厚的非耐压轻外壳钢板，内壳为40 mm厚的耐压钢板，环肋为30 mm厚的钢板，外壳和内壳均敷设50 mm厚的声学覆盖层。外壳外部以及内壳和外壳之间为海水，内壳内部为空气。

参照相关文献[9]对标准潜艇模型的材料参数进行设定：钢密度为 ${\rho _s} = 7\,850\;{\rm{ kg/}}{{\rm{m}}^3}$ ，杨氏模量为 ${E_s} = 2 \times $ $1{{{0}}^{{{11}}}}\;{\rm{ Pa}}$ ，泊松比为 ${\nu _s} = 0.33$ ；声学覆盖层密度为 ${\rho _a} = 1\,100\;{\rm{ kg/}}{{\rm{m}}^3}$ ，杨氏模量为 ${E_a} = 2 \times 1{{{0}}^7}\;{\rm{ Pa}}$ ，泊松比为 ${\nu _a} = 0.497$ ，损耗因子为 ${\delta _a} = 0.5$ 。此外设定海水参数为：密度 ${\rho _w} = 1\,024\;{\rm{ kg/}}{{\rm{m}}^3}$ ，声速 $c = 1\,500\;{\rm{ m/s}}$ 。此外空气域近似为真空。

3 耦合有限元模型验证

为了验证耦合有限元模型的准确性，分别计算2个敷设声学覆盖层的球壳目标强度。第1个球壳参照双壳体标准潜艇内壳的几何和结构特性，壳体内径设定为5 m，壳体厚度为40 mm，声学覆盖层厚度为50 mm；第2个球壳参照双壳体标准潜艇外壳的几何和结构特性，壳体内径设定为7.5 m，壳体厚度为10 mm，声学覆盖层厚度为50 mm。壳体内部为空气，壳体外部为水。

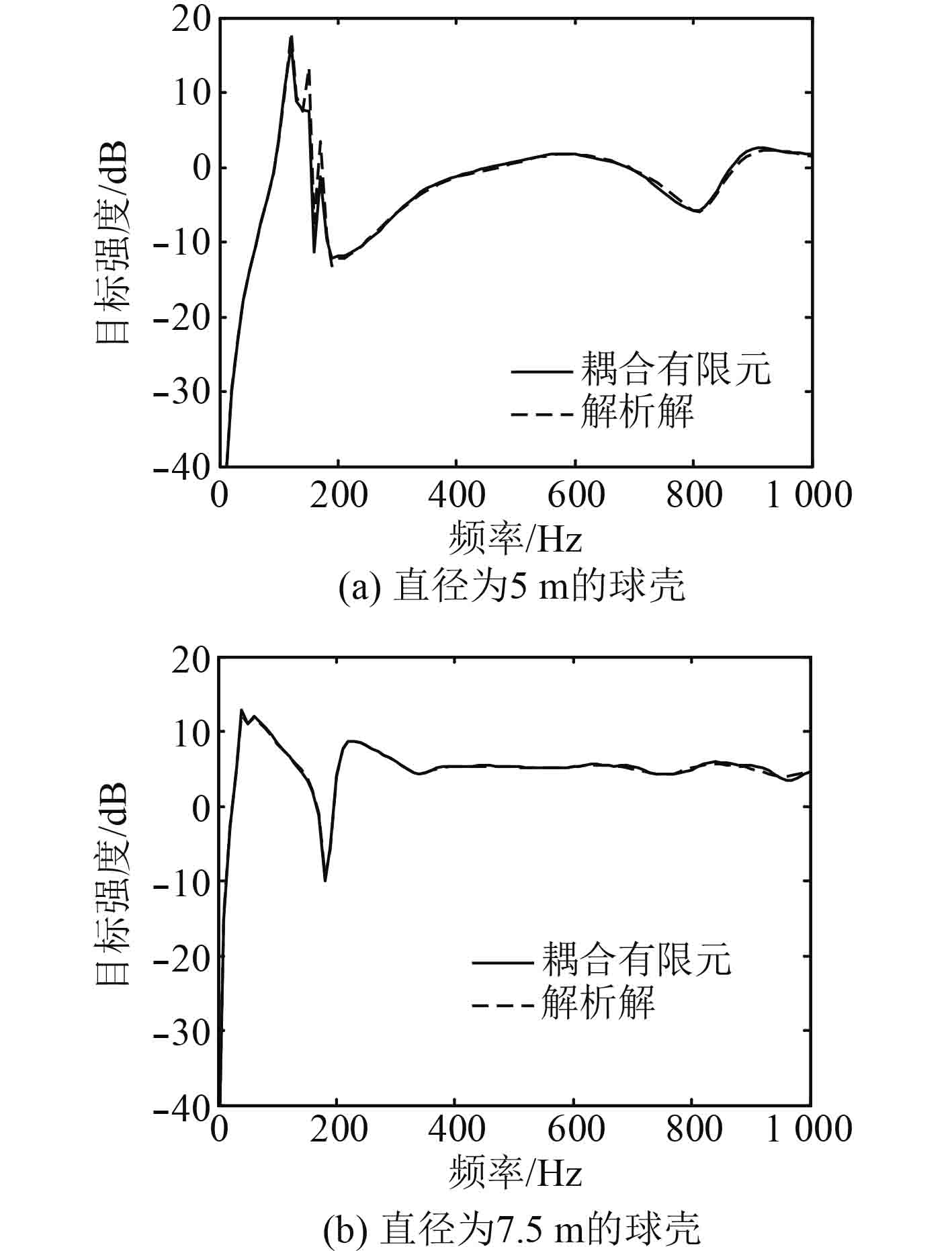
图2为2个球壳的目标强度，并与解析解进行比较，这里解析解为Mitri推导的双层球壳声散射的级数解^[10]。由图2可知，采用耦合有限元计算得到的目标强度与解析解非常接近。对于直径为5 m的球壳，目标强度的平均误差为0.4 dB；对于直径为7.5 m的球壳，目标强度的平均误差为0.15 dB。由此可见，耦合有限元模型具有较高的计算精度。

4 目标强度的计算结果与分析 4.1 单壳体

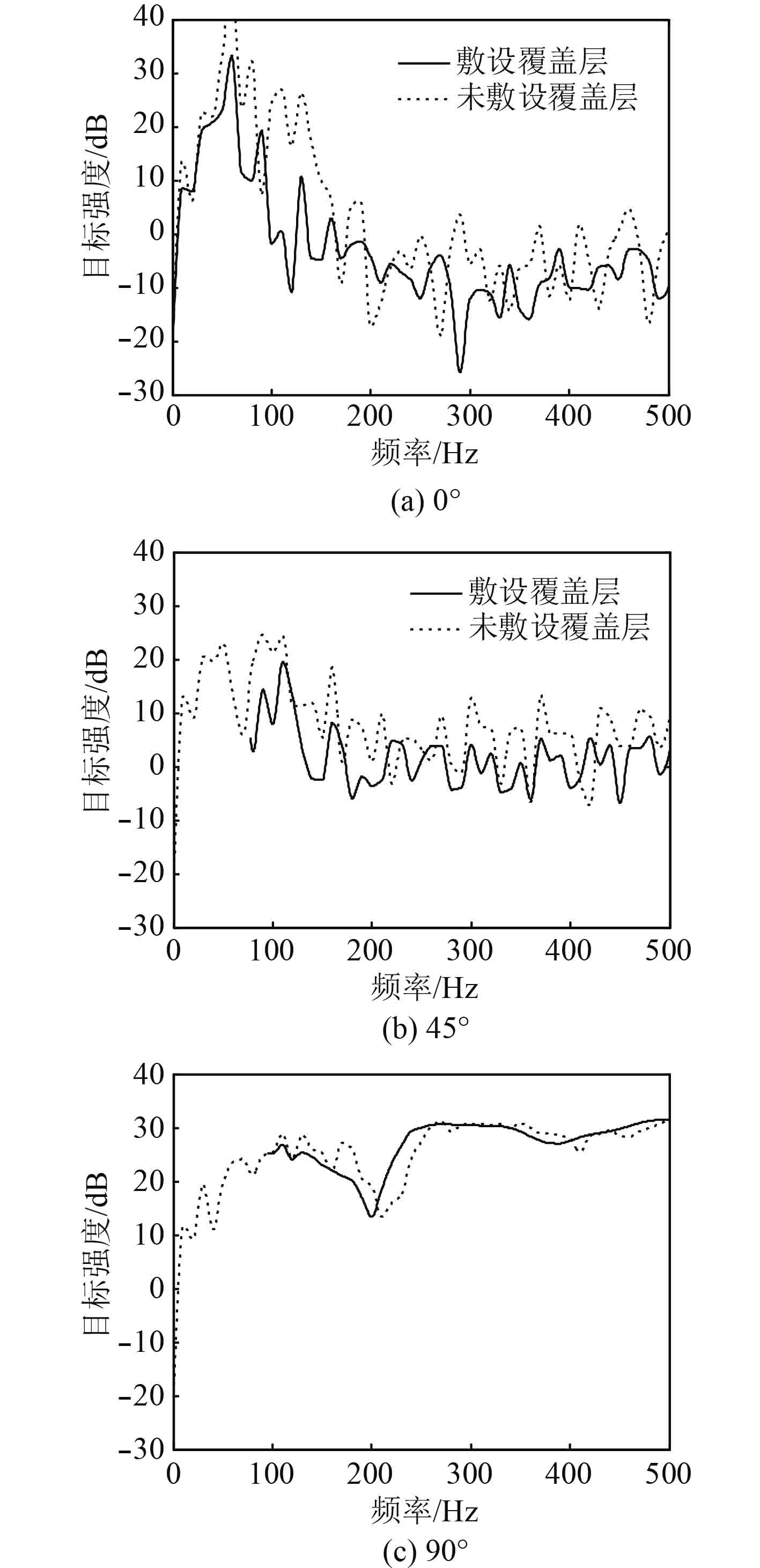
计算不同频率收发合置单壳体标准潜艇目标强度，由图3可知声学覆盖层可以明显改变目标强度曲线的起伏特性，这主要还是由于声学覆盖层改变了结构的振动特性。在某些频率点，敷设声学覆盖层的目标强度甚至比未敷设更大。进一步计算声学覆盖层对500 Hz以下低频目标强度的平均影响：0°，45°，90°，135°，180°入射时，敷设声学覆盖层相较于未敷设，目标强度分别降低5.7 dB，4.7 dB，0.1 dB，3.4 dB，2.9 dB。由此可见，在500 Hz以下低频段，敷设声学覆盖能降低目标强度，但是降幅较小。

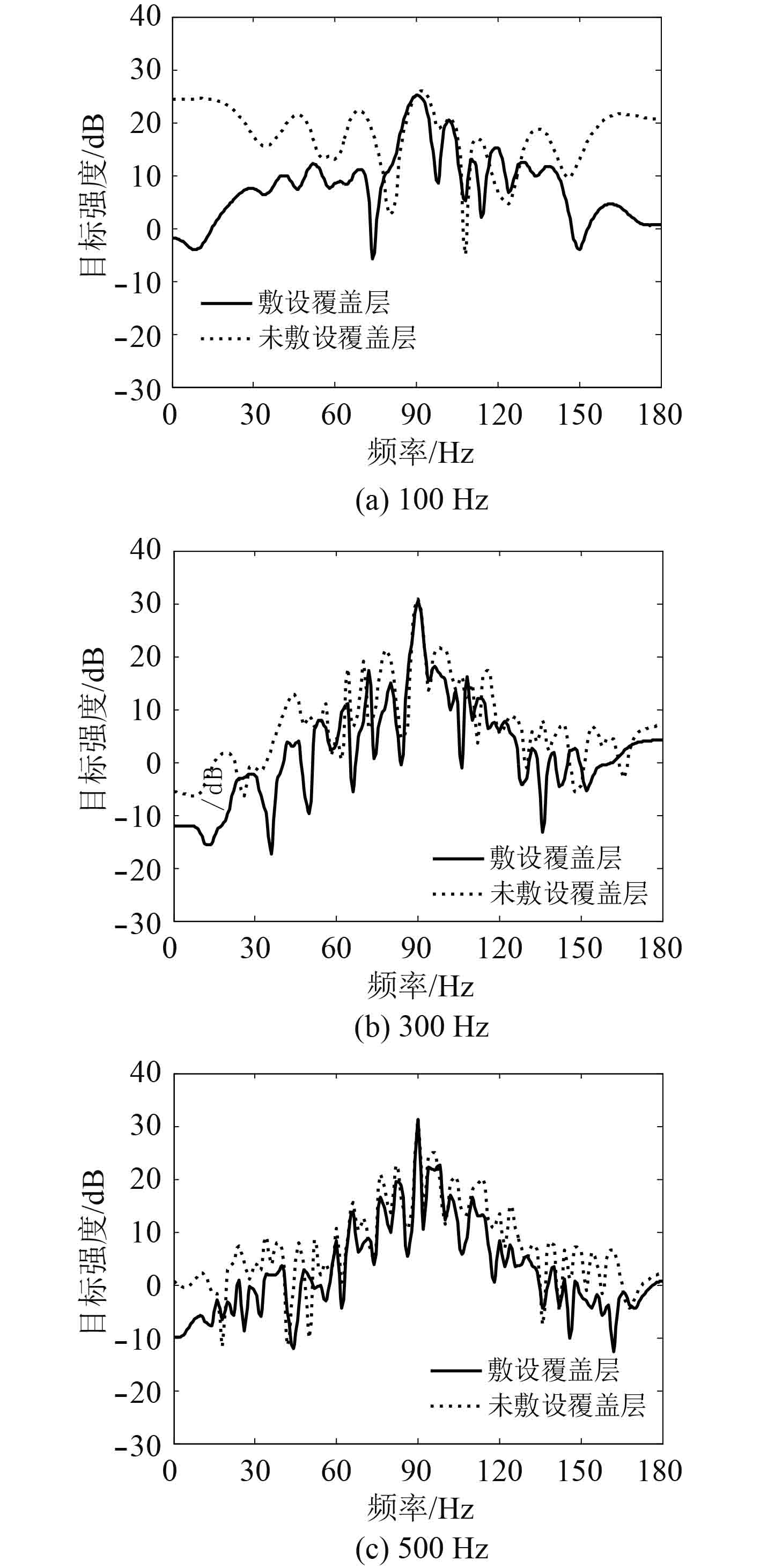
计算不同入射方向收发合置单壳体标准潜艇目标强度，由图4可见首部（0°）和尾部（180°）方向附近入射时目标强度相对较小，而正横（90°）方向入射时目标强度较大，这主要是由于首部和尾部的散射截面较小，而正横方向的散射截面较大。此外，频率越高，目标强度曲线变化越剧烈。同样，敷设声学覆盖层会改变目标强度曲线的起伏特性。进一步计算声学覆盖层对目标强度的平均影响：100 Hz，300 Hz，500 Hz时，敷设声学覆盖层相较于未敷设，目标强度分别降低10.1 dB，4.6 dB，4.3 dB，由此可见敷设声学覆盖可以降低目标强度。

4.2 双壳体

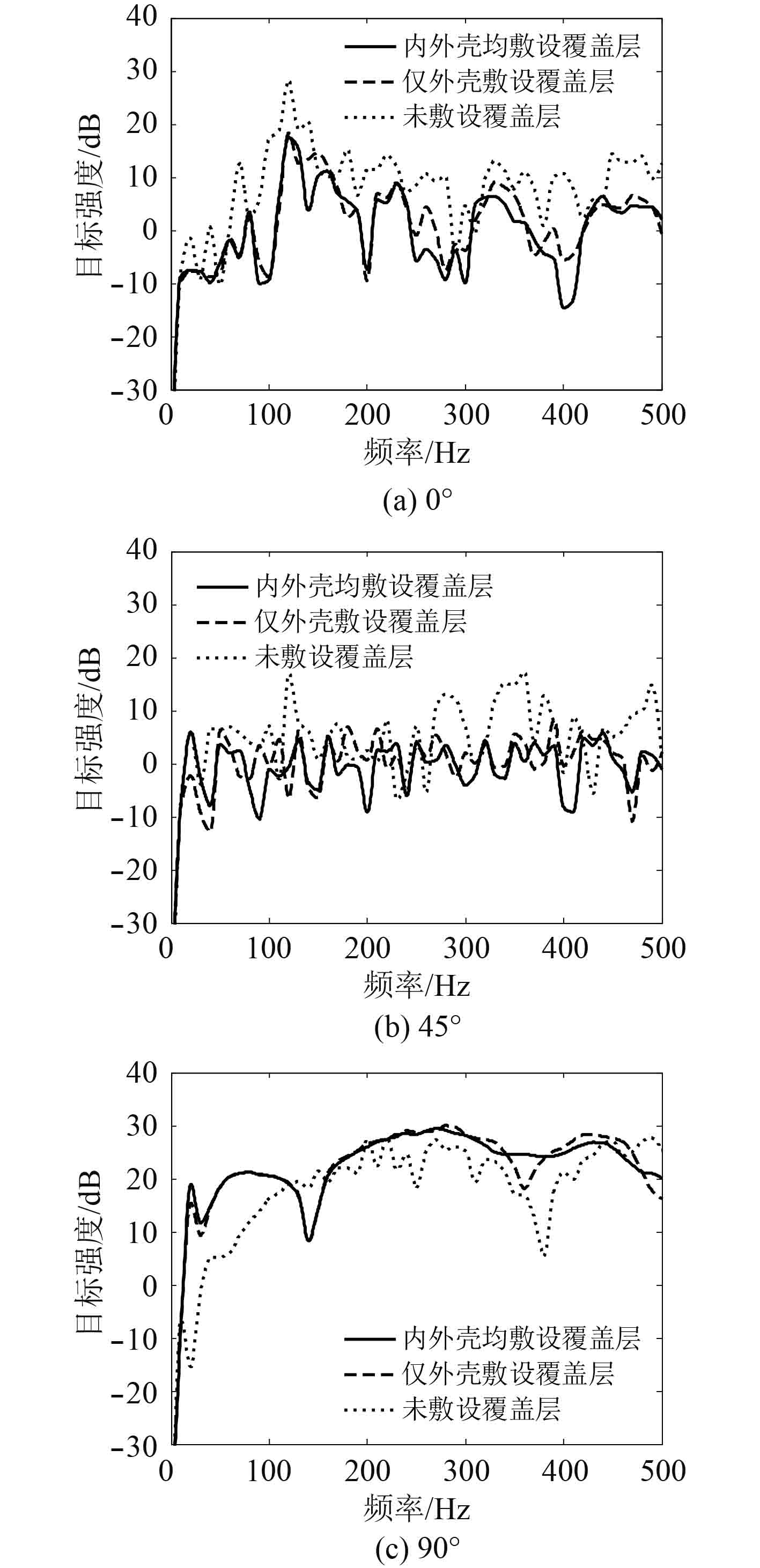
计算不同频率收发合置双壳体标准潜艇目标强度，由图5可见外壳敷设声学覆盖层可以明显改变目标强度曲线的起伏特性。进一步计算外壳声学覆盖层对500 Hz以下低频目标强度的平均影响：0°，45°，90°，135°，180°入射时，外壳敷设声学覆盖层相较于未敷设时，目标强度分别降低6.6 dB，4.7 dB，4.1 dB，9.3 dB，8.7 dB。在外壳敷设声学覆盖层的基础上，再增加内壳声学覆盖层，目标强度曲线几乎不变。进一步计算内壳声学覆盖层对500 Hz以下低频目标强度的平均影响：再增加内壳声学覆盖层，目标强度分别降低1.3 dB，1.0 dB，0.0 dB，2.5 dB，3.1 dB。

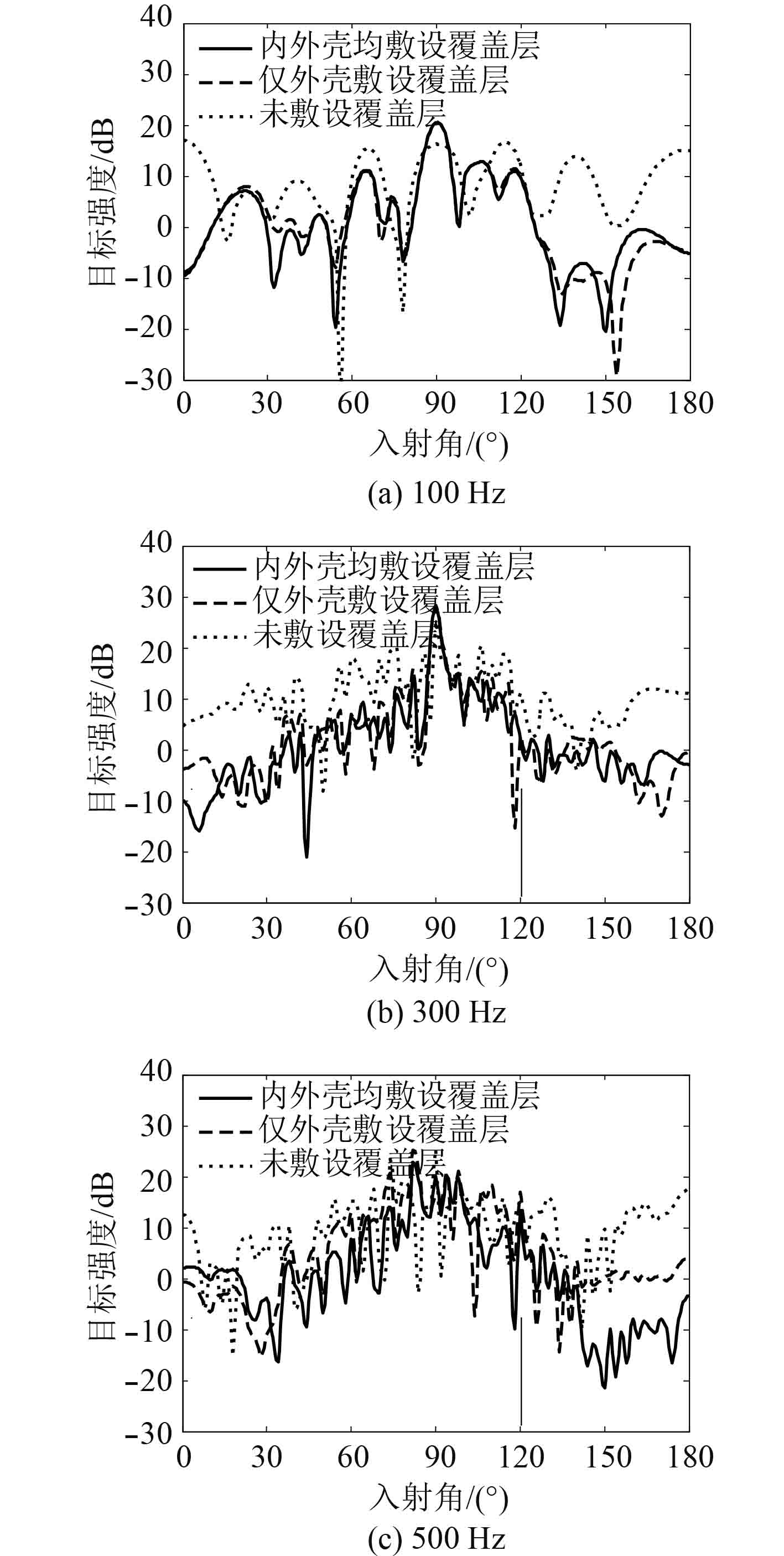
计算不同入射方向收发合置双壳体标准潜艇目标强度，如图6所示。与图5类似，外壳敷设声学覆盖层会改变目标强度曲线的起伏特性。进一步计算外壳声学覆盖层对目标强度的平均影响：100 Hz，300 Hz，500 Hz时，外壳敷设声学覆盖层相较于未敷设时，目标强度分别降低7.1 dB，8.2 dB，4.5 dB。而再增加内壳声学覆盖层，目标强度曲线几乎不变。进一步计算内壳声学覆盖层对目标强度的平均影响：再增加内壳声学覆盖层，目标强度分别降低0.3 dB，0.7 dB，3.8 dB。

5 结　语

本文采用耦合有限元模型分析了敷设声学覆盖层标准潜艇的目标强度。首先，建立耦合有限元模型，并验证其有效性。其次，计算敷设声学覆盖层的单壳体标准潜艇的低频目标强度，结果表明敷设声学覆盖层可以改变潜艇结构的振动参数，进而改变标准潜艇的声散射特性和目标强度曲线的起伏特性，在某些频率点或者入射角度，敷设声学覆盖层时目标强度甚至更大；进一步分析了声学覆盖层对低频目标强度的平均影响，结果表明敷设声学覆盖层可以略微降低平均目标强度。最后，分析了双壳体标准的低频目标强度，结果表明外壳敷设声学覆盖层可以改变潜艇结构振动参数和目标强度的起伏变化，并且可以略微降低平均目标强度。而再增加内壳声学覆盖层，则对潜艇模型的声散射特性几乎没有影响，因而对目标强度也几乎没有影响。

未来的工作中，应对目前各种层出不穷的新型吸声材料，研究各种声学覆盖层对目标强度的影响。此外，在所有壳体上敷设同样的声学覆盖层可能不是最有效的方式，因此探索更高效的声学覆盖层敷设方式是未来的另一个工作方向。