0 引　言

近年来，国内外众多学者对水下爆炸结构毁伤的力学机理进行了系统的研究^{[1 – 2]}，但对于在水下爆炸载荷作用下应力波在舰船结构中的传播特性研究甚少。目前，对于应力波在变截面结构中传递规律的研究主要以变截面杆为主，其中，王礼立等^[3]运用一维杆中应力波的初等理论对应力波在锥形放大器中传播特性进行了理论分析，指出了Leftheris计算公式的错误之处并与实验值进行对比，验证了理论值的正确性，但计算得到的峰值应力比实测值偏大。周光泉、刘孝敏等^{[4 – 5]}在此基础上运用二维理论研究该问题并取得了较好的结果。但是，数值模拟与理论推导相比有着特殊的优势，如果模型比较复杂并且载荷呈现强非线性时则难以利用理论推导出某处的应力状态。另外，近年来随着SHPB实验装置研究领域的拓宽，其传统的2个基本假定（一维应力假定和均匀性假定）均受到挑战^{[6 – 8]}，而数值模拟对于优化实验设计有着明显的优势，一方面数值模拟可以为实验提供预测，如果数值模拟精度足够的话完全可以代替实验；另一方面在数值模拟中可以对应力波在不同材料、不同截面压杆中的传播特性进行系统的数值分析^[9]。此外，在水下爆炸冲击载荷作用下研究变截面杆以及舷侧外板结构中应力波传播的问题仍比较少见。因此，本文尝试结合应力波理论，同时借助有限元的CEL方法来探讨在水下爆炸载荷作用下弹性波在变截面杆以及舷侧外板结构中的传播特性问题，并且利用冲击响应谱分析方法探讨舷侧外板结构中的响应规律，为舰船遭遇水下爆炸后结构中应力波的传播特性以及冲击响应规律研究提供参考。

1 变截面杆中的应力波理论

本节在材料为线弹性的基础上利用冲量定理、牛顿第三定律分析了弹性波在变截面杆中的反射和透射规律。

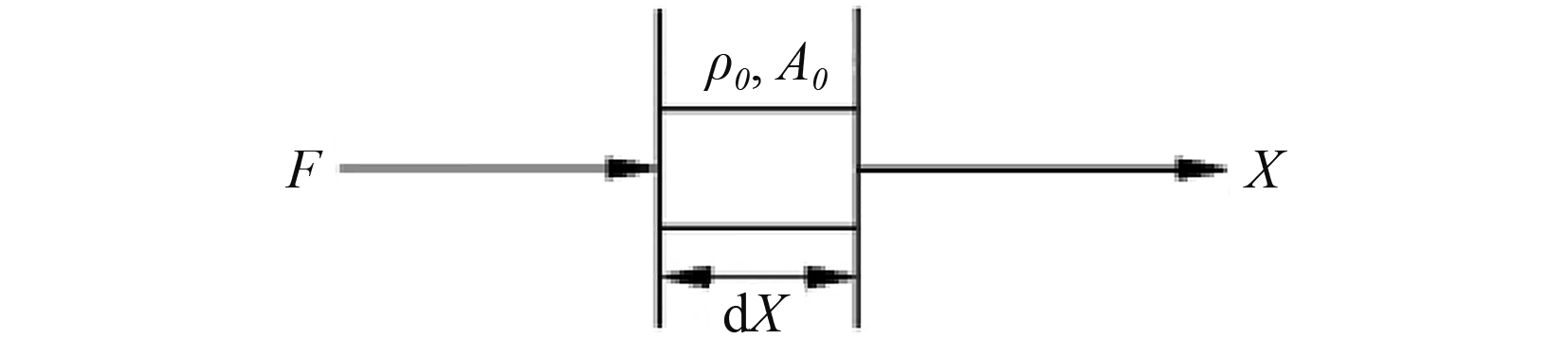
在如图1所示坐标系中研究一等截面均匀杆微元段在应力波下的纵向运动，其中A₀为截面面积， ${\rho _0}$ 为密度，F为力。

在推导控制方程之前，先作2个基本假设：

1）杆在变形时横截面保持为平面；

2）应力和应变之间遵循胡克定律。

规定应力和应变均以拉为正，质点速度以X轴正向为正。

根据冲量定理，有

$F{\rm d}t = {\rho _0}{A_0}{\rm d}Xv\text{，}$

(1)

进而

$\frac{F}{{{A_0}}} = \sigma = {\rho _0}\frac{{{\rm d}X}}{{{\rm d}t}}v = {\rho _0}Cv\text{。}$

(2)

设弹性波从一个截面A₁传播到另一个截面A₂，当入射波扰动 ${\sigma _I}$ 到达变截面时，会向2种截面传播反射波扰动 ${\sigma _R}$ 和透射波扰动 ${\sigma _T}$ 。根据连续条件和牛顿第三定律，在变截面处经反射、透射后的质点速度应相等，应力应相等^[10]，假设 ${v_I}$ 为入射波作用下杆中质点速度， ${v_R}$ 为反射波作用下杆中质点速度， ${v_T}$ 为透射波作用下杆中质点速度， ${A_1}$ ， ${A_2}$ 分别为杆两端截面面积， ${\rho _{\rm{0}}}$ ， ${C_{\rm{0}}}$ 分别为杆的密度和波速，则

${v_I} + {v_R} = v{}_T\text{，}$

(3)

${A_1}({\sigma _I} + {\sigma _R}) = {A_2}\sigma {}_T\text{。}$

(4)

将式（2）代入式（3）可得

$\frac{{{\sigma _I}}}{{{{\left( {{\rho _0}{C_0}} \right)}_1}}} - \frac{{{\sigma _R}}}{{{{\left( {{\rho _0}{C_0}} \right)}_1}}} = \frac{{{\sigma _T}}}{{{{\left( {{\rho _0}{C_0}} \right)}_2}}}\text{，}$

(5)

联立式（4）和式（5）得

$\left\{ \begin{gathered} {\sigma _R} = \frac{{{A_2} - {A_1}}}{{{A_1} + {A_2}}}{\sigma _I} \hfill \text{，}\\ {v_R} = - \frac{{{A_2} - {A_1}}}{{{A_1} + {A_2}}}{v_I} \hfill\text{。} \\ \end{gathered} \right.$

(6)

$\left\{ \begin{gathered} {\sigma _T} = \frac{{2{A_1}{A_2}}}{{{A_2}({A_1} + {A_2})}}{\sigma _I} \hfill\text{，} \\ {v_T} = \frac{{2{A_1}{A_2}}}{{{A_2}({A_1} + {A_2})}}{v_I} \hfill \text{。}\\ \end{gathered} \right.$

(7)

由此，若已知入射波作用下杆所受应力 ${\sigma _I}$ ，通过式（6）和式（7）就可以求出反射波作用下杆所受应力 ${\sigma _R}$ 和透射波作用下杆所受应力 ${\sigma _T}$ 。

2 水下爆炸流固耦合作用的CEL方法 2.1 CEL方法介绍

基于网格的数值方法有拉格朗日方法和欧拉方法，这2种方法各有优缺点，拉格朗日方法能够很好描述物质结构的运动，而欧拉方法能够较好处理流体大变形的问题。由于拉格朗日方法和欧拉方法具有互补的性质，于是发展形成了拉格朗日方法和欧拉方法相互耦合的CEL方法（耦合的欧拉-拉格朗日方法）。在CEL算法中，欧拉网格和拉格朗日网格相互独立。欧拉网格固定不动，材料在网格里流动，材料运动的同时它的各个物理量被映射到欧拉网格中，欧拉网格是独立于空间位置的“监测点”实时追踪流体的通量。而在拉格朗日网格中，网格节点固定在材料内部，网格随着材料的变形而变形，质量、动量和能量随着网格单元的运动而传递。在CEL计算时，结构利用拉格朗日方法求解，流体采用欧拉方法求解。在流体和结构相互耦合的界面上，拉格朗日单元受到欧拉材料给予的压力载荷，欧拉单元接受拉格朗日单元施加的几何约束，二者计算信息交换通过2组网格之间的映射实现。基于以上原理，CEL算法在解决物体的大位移，如碰撞、流体动力学及流体与固体之间的相互作用时，具有明显优势^[11]。

2.2 控制方程

在CEL方法中，拉格朗日数值方法的控制方程^[12]如下：

根据质量守恒有

$\frac{{D\rho }}{{Dt}} + \rho \nabla \cdot {v} = 0\text{，}$

(8)

根据动量守恒有

$\rho \frac{{D{v}}}{{Dt}} = \nabla \cdot {\sigma} + \rho {b}\text{，}$

(9)

根据能量守恒有

$\frac{{De}}{{Dt}} = {\sigma} :(\nabla \otimes {v})\text{。}$

(10)

式中： $\rho \text{，}{v}\text{，}{\sigma }\text{，}{b}\text{，}e$ 分别为拉格朗日流体介质的密度，速度，应力，质量力和内能。

在CEL方法中，欧拉数值方法的控制方程^[12]如下：

欧拉算法中，材料在固定的网格里流动，根据质量守恒定律，有连续性方程

$\tfrac{{\partial \rho }}{{\partial t}} + \nabla \cdot (\rho {v}) = 0\text{，}$

(11)

根据动量守恒有

$\frac{{\partial \rho {v}}}{{\partial t}} + \nabla \cdot (\rho {v} \otimes {v}) = \nabla \cdot {\sigma} + \rho {b}\text{，}$

(12)

根据能量守恒有

$\frac{{\partial e}}{{\partial t}} + \nabla \cdot (e{v}) = {\sigma} :(\nabla \otimes {v})\text{。}$

(13)

式中： $\rho {\text{，}}{v}{\text{，}}{\sigma }{\text{，}}{b}{\text{，}}e$ 分别为密度速度，应力，质量力和内能。

2.3 欧拉体积分数法

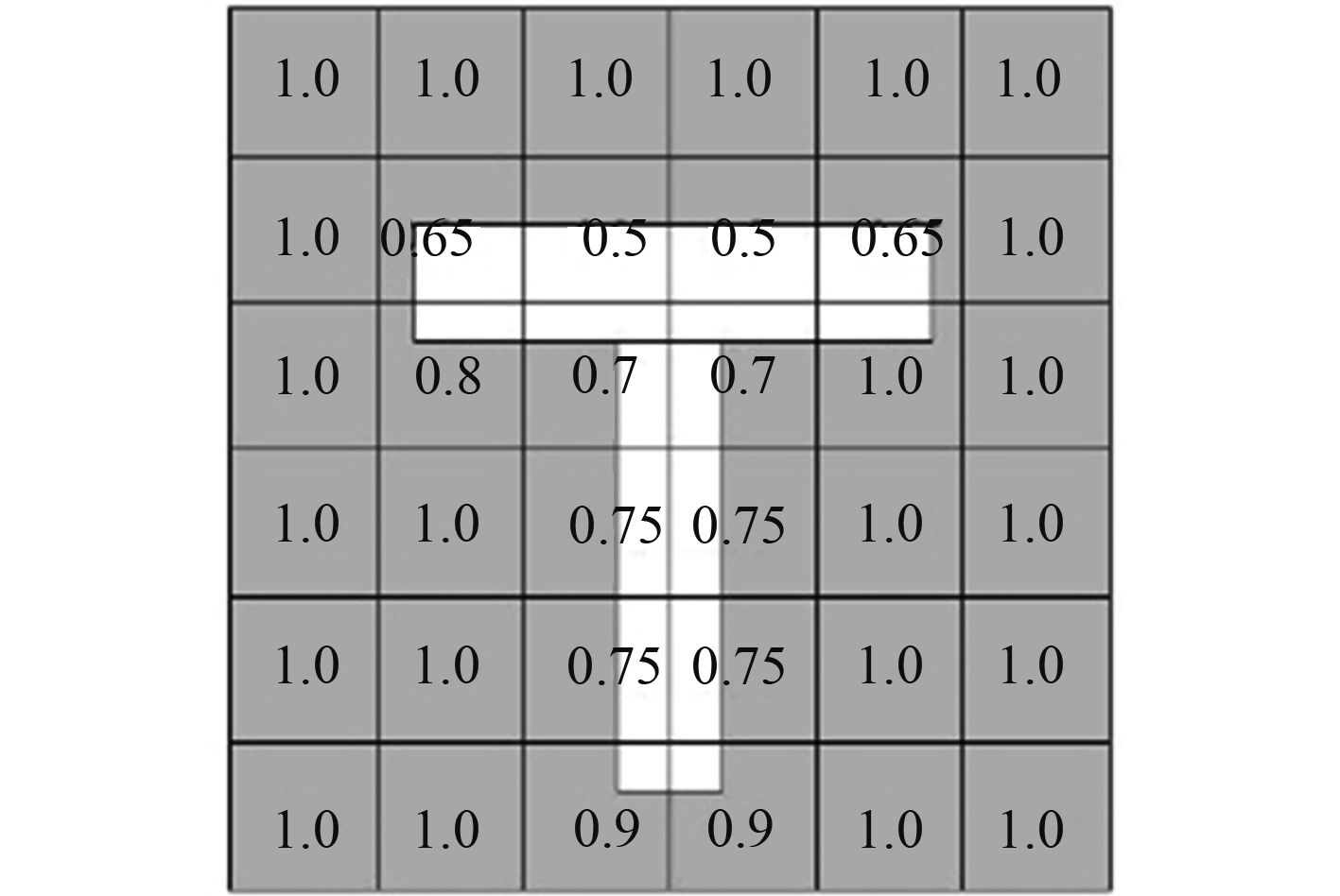
在CEL中，材料在每一个增量步都会计算每个单元材料的分布以此来描述流体的变形状态，而材料的初始分布情况在Abaqus中利用“体积分数工具”进行计算。该工具对欧拉体与参考体之间进行布尔运算来确定材料的分布。图2中利用“体积分数工具”将T型材作为参考体映射到欧拉体后计算得到的欧拉体积分数示意图，图中灰色部分代表在欧拉网格中填充“水”材料，数字代表“水”在欧拉单元中所占的体积分数，白色部分代表T型材结构其材料的敷设在拉格朗日体中进行。后处理中通过EVF选项卡来观察流体的运动情况。

2.4 罚函数接触方法

在CEL方法中，欧拉域与拉格朗日域之间的接触是通过罚函数接触方法实现的。拉格朗日单元边和面上建立节点，欧拉材料表面建立锚点，二者通过“硬”接触-压力过盈行为建立耦合关系^[13]。这种方法允许欧拉材料和拉格朗日体之间存在一些微小的渗透。节点与锚点之间的接触力F_p正比于二者的渗透距离d^[14]。

${F_p} = kd\text{，}$

(14)

式中：k为罚函数刚度系数，取决于拉格朗日和欧拉材料的属性。

2.5 CEL方法验证

本节采用自由场水下爆炸模型，以仿真值与经验公式值对比的方式对CEL方法进行验证，具体的几何模型如图3所示。

球形TNT的药量为0.055 g，装药密度 $\rho =$ 1 600 kg/m³，爆速 $D = 6\,\,\,930\,\,\,{\rm{m}}/{\rm{s}}$ 。爆轰产物的压力与爆轰产物相对比容和比内能之间的关系釆用JWL状态方程表示^[13]。方程中参数具体值见表1。

水的密度 $\rho = 1\;000\;{\rm{kg}}/{{\rm{m}}^3}$ ，粘性系数为0.001，采用U_S-U_P形式的EOS状态方程，其中，水的声速C₀=1 480 m/s。

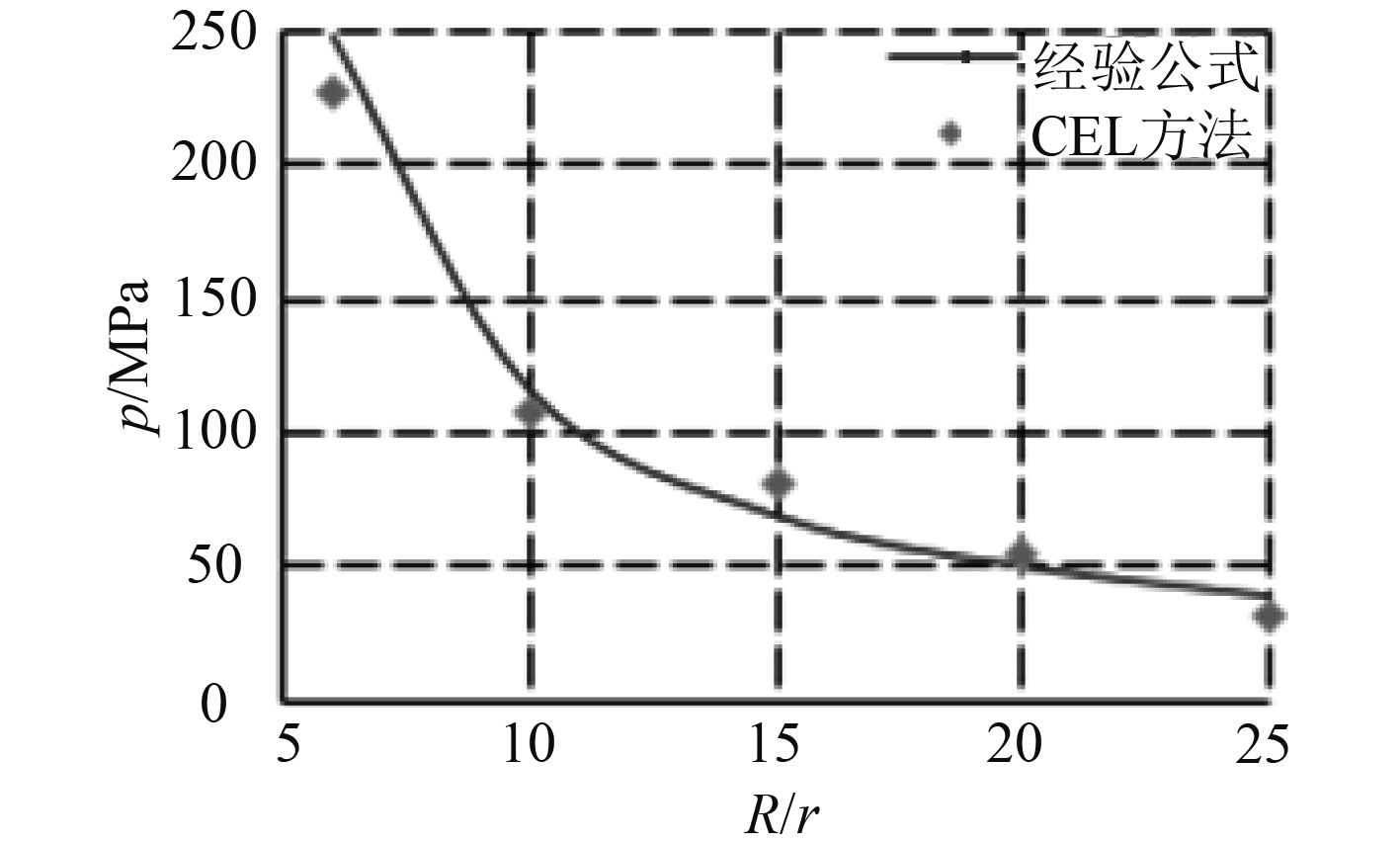
为减小边界对冲击波影响，计算欧拉域的所有边界都设定为流出无反射边界，在无边界效应影响的水域进行爆炸，其产生冲击波的波阵面压力峰值p_m可由Cole和Zamyshlyayev给出的经验公式^{[15 – 16]}表示。图4为在不同距离处CEL计算压力峰值与经验公式计算压力峰值的对比。

从图中可以发现，CEL方法计算出来的结果与Cole和Zamyshlyayev给出的经验公式计算结果相似，准确度较高。因此，采用CEL方法可以充分模拟水下爆炸冲击载荷。

3 水下爆炸载荷作用下变截面杆中应力波的传播特性

下面采用CEL方法模拟出水下爆炸冲击载荷，然后通过有限元方法模拟冲击波在变截面杆中的传播问题。此问题涉及液固相互作用并且水下爆炸载荷呈现非线性难以利用理论公式得到解析解，本节运用CEL方法来处理流固耦合问题以期达到研究变截面杆在受到水下爆炸载荷下弹性波传播特性的目的。

本节建立1根两段等长L的变截面杆，L为200 mm，杆左端直径D为4 mm，杆的截面比为2∶1，杆的材料为普通钢（不考虑塑性），杆的两端均为自由端，在距杆左端50 mm处建立和第2.5节一样的TNT炸药模型，最后建立一足够大的Euler域以保证TNT炸药具有足够的传播空间，Euler域四周均设置无反射边界条件，具体模型示意图如图5和图6所示。

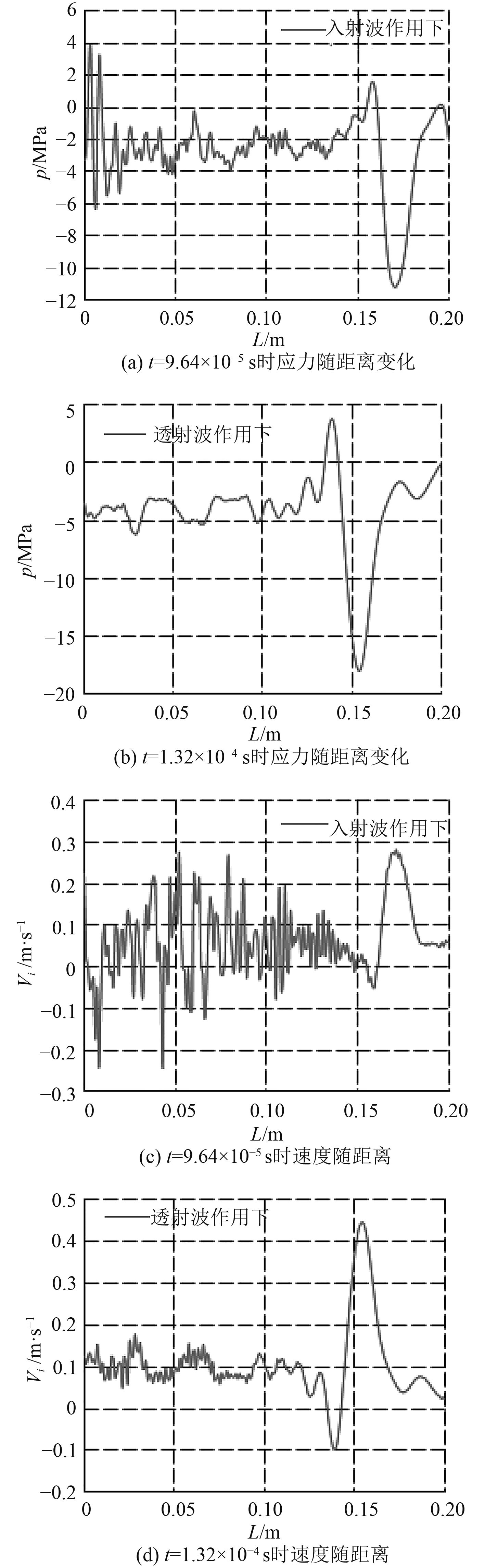
图7~图9给出了爆炸冲击波从开始进入到杆的左端、传递到变截面附近、传递到杆右端附近3个典型位置图。当时间t=9.64×10^–5 s时，提取出入射波作用下杆左端到右端的应力随距离传递曲线和速度随距离传递曲线，计算距离从0~0.2 m对应的应力峰值作为 ${\sigma _I}$ =–11.2 MPa，速度峰值作为 ${v_I}$ =0.28 m/s。当时间t=1.32×10^–4 s时，提取出透射波作用下杆左端到右端的应力随距离传递曲线和速度随距离传递曲线，计算距离从0.2~0.4 m对应的应力峰值作为 $\sigma {}_T$ =–17.95 MPa，速度峰值作为 ${v_T}$ =0.445 m/s。各曲线如图10所示，与理论解进行对比如表2所示。可以发现变截面杆在受到水下爆炸载荷作用下弹性波规律十分接近理论解，并且可以看出当应力波由大截面向小截面传播时，透射波扰动强度大于入射波扰动，这种结构起到“聚波”作用。由于在t=1.32×10^–4 s时，杆左端到杆变截面处存在反射波与部分入射波的叠加，所以难以提取反射波作用下杆的应力传递曲线和速度传递曲线，在此不予处理。

4 水下爆炸载荷作用下舷侧外板中应力波的传播特性 4.1 模型建立

本节借助CEL方法以期达到研究舷侧外板在受到水下爆炸载荷下弹性波传播特性的目的。此问题与上节变截面杆模型相比，不仅涉及液固相互作用而且模型更为复杂，无法利用理论公式得到解析解。

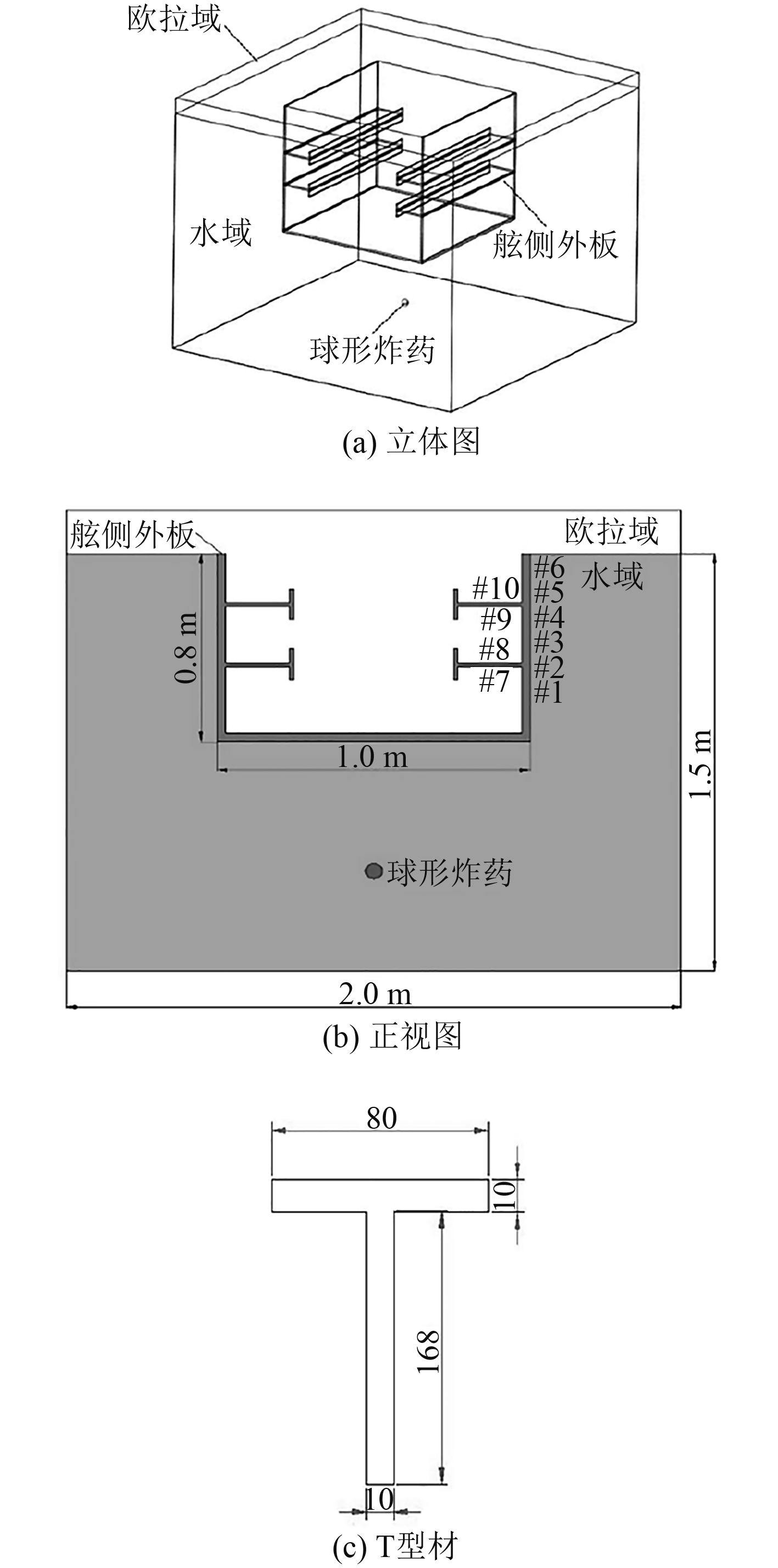
建立计算仿真模型如图11所示。欧拉计算域尺寸为 $2\;{\rm{m}} \times 2\;{\rm{m}} \times 1.6\;{\rm{m}}$ ，其中水域深度为1.5 m，水的材料与第2.5节相同。欧拉域四周均设置无反射边界条件。球形炸药药包半径为0.0195 m，爆心距离左端水域1 m，爆心距离结构下端面中心0.49 m，TNT材料与第2.5节保持一致。舷侧外板结构尺寸为1 m×1 m×0.8 m，板厚12 mm，结构沉浸在水域中，结构上端面与自由液面保持水平，结构材料与变截面杆保持一致，其中，#1-#10为布置的测点。#1，#2，#3，#4测点位于T型材根部附近，#5，#6测点位于外板结构上端面附近，#7，#8测点位于第1个T型材腹板中间处，#9，#10测点位于第2个T型材腹板中间处，详见图11（b）。T型材之间相距0.2 m，T型材几何示意图见图11（c）所示。

4.2 应力波从舷侧外板到T型材腹板传播的特性及冲击响应谱分析

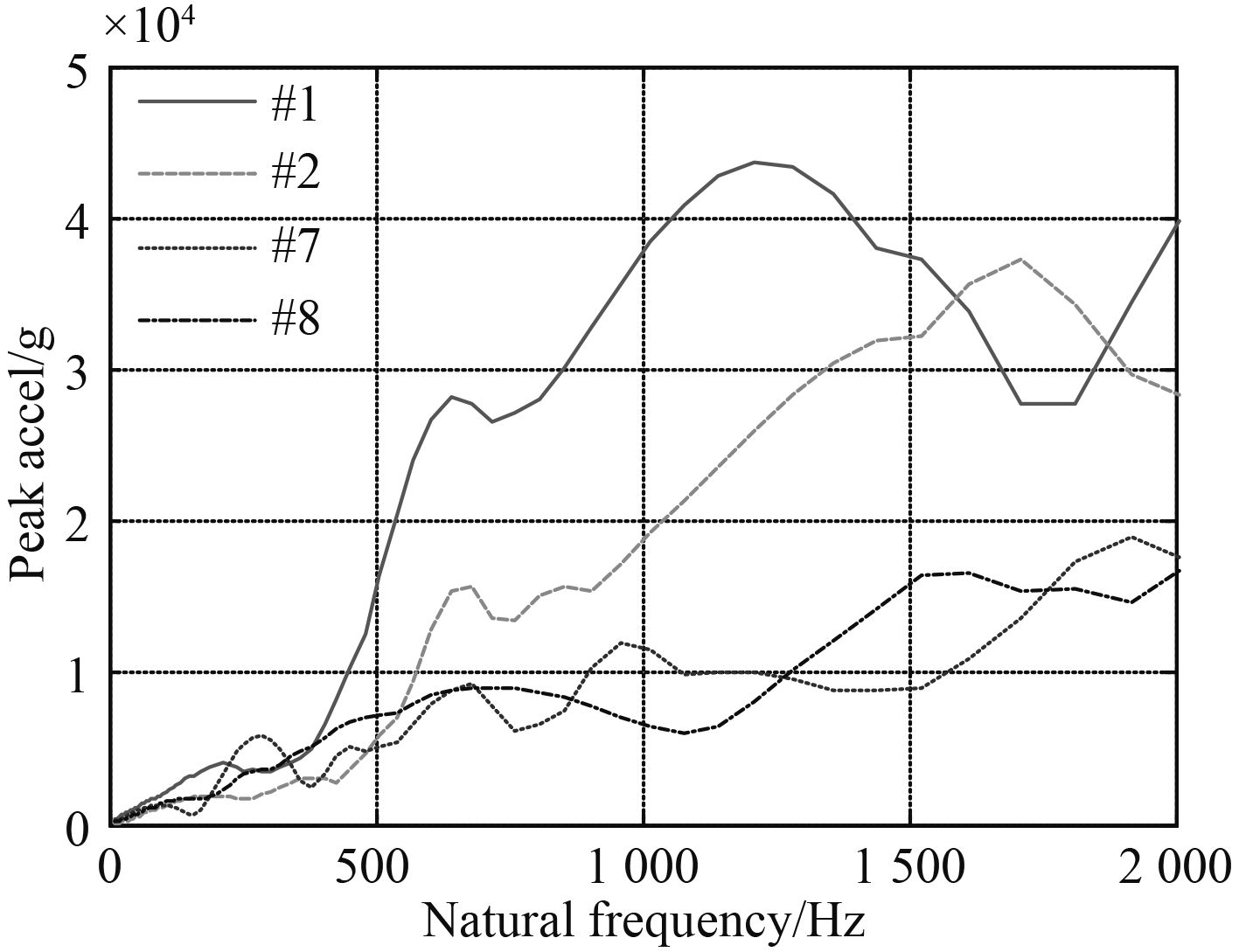
采用频谱分析方法和冲击响应谱分析方法，探究应力波从舷侧外板结构往T型材腹板中的传播特性。分别提取出#1，#2，#7，#8四个测点的加速度随时间变化的数据，并进行快速傅里叶变换得到对应的频谱曲线，如图12所示。从图中可以看出，在[500, 2 000] Hz较高频率范围内的应力波从舷侧外板经过第1个T型材后传递到T型材腹板处的强度大为减小，而[0, 500] Hz内的应力波强度则相差不大。这说明应力波在经过第1个从小到大截面时滤掉了大部分高频信号。

将以上测点的加速度时历数据进行转换得到冲击响应谱曲线，如图13所示。可以发现，对于[500, 2 000] Hz较高频率范围内的冲击响应经过第1个T型材后呈大幅衰减趋势。这说明舷侧外板在受到水下爆炸载荷作用下[500, 2 000] Hz内的T型材腹板的结构响应与外板结构响应相比大为减小。而[0, 500] Hz内的响应相对来说变化则较为平缓。总体来看，从舷侧外板到第1个T型材，低频段的结构响应谱值两者相差不大，而在高频段外板的谱值远高于T型材腹板中的谱值。

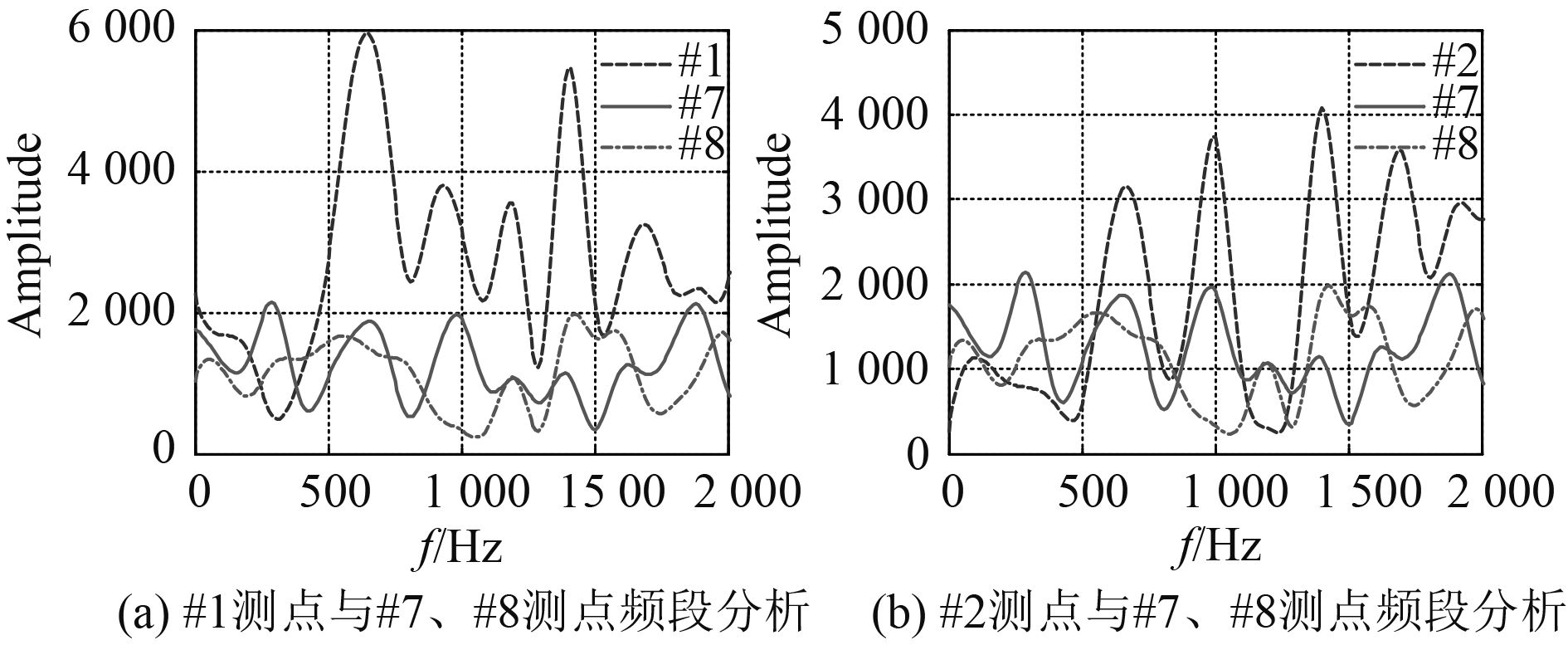
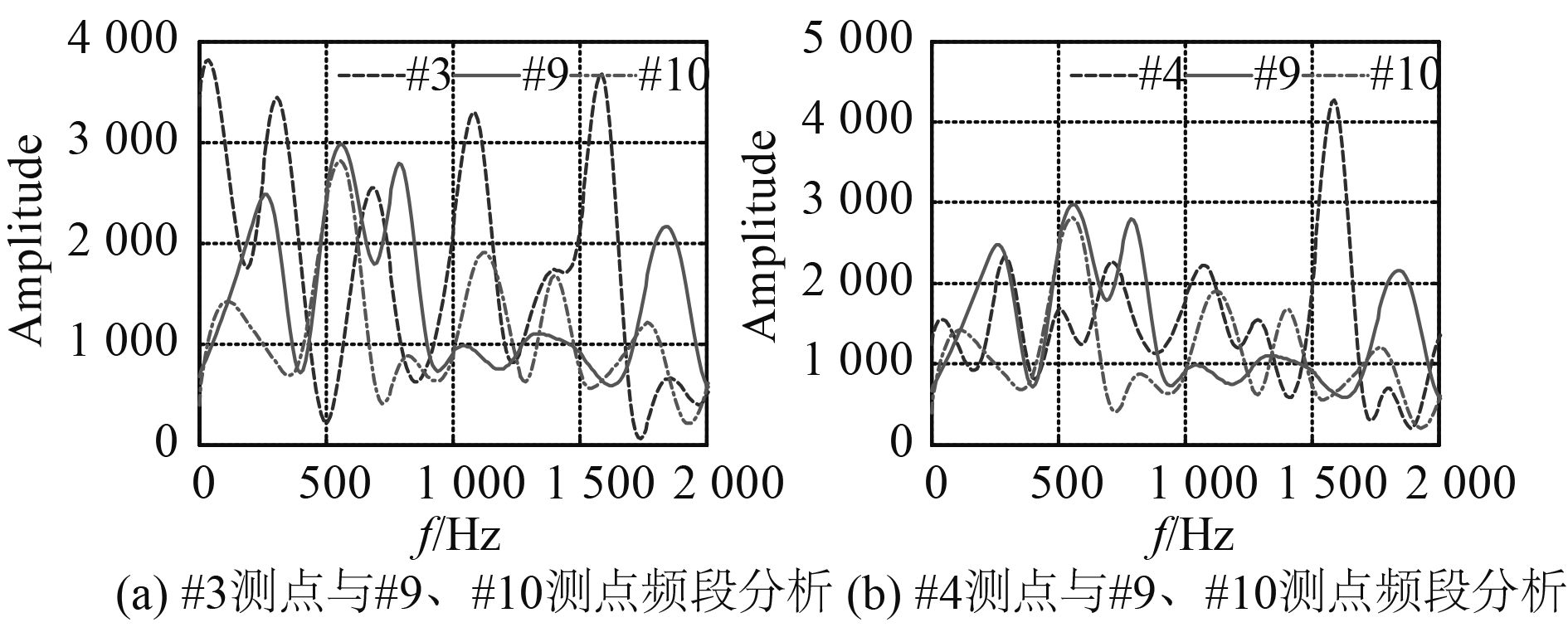
分别提取出#9，#10测点的加速度随时间变化的数据，并进行快速傅里叶变换，得到对应的频谱曲线，并与#3，#4进行对比，如图14所示。可以看出，在[0, 500] Hz的应力波从舷侧外板经过第2个T型材后传递到T型材腹板处的强度大为减小，而在其他频段中腹板的应力波强度与外板相比相差不大。这说明当应力波再次经过从小到大截面形式的变化时滤掉了大部分低频信号。

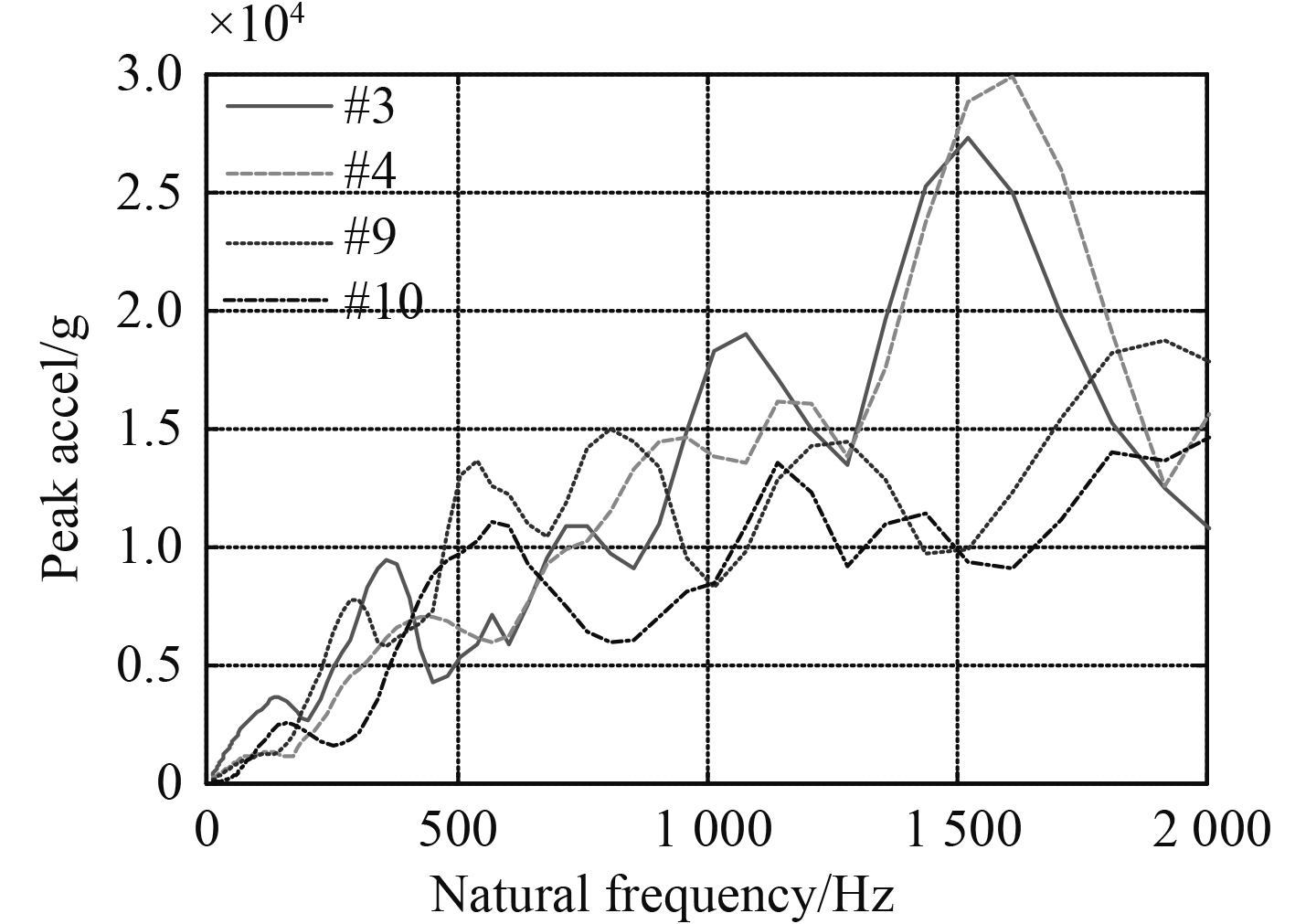
将以上测点的加速度时历数据进行转换得到冲击响应谱曲线，如图15所示。可以看出，冲击响应规律与经过第1个T型材后的规律不同，舷侧外板在受到水下爆炸载荷作用下，只有[1 300, 1 800] Hz内的结构响应才大于腹板的响应，在其他频段两者则呈波动交替趋势，幅值相差不大。

结合上述描述可以得出，当应力波再次经过从小到大截面形式的变化时，舷侧外板产生的中高频段冲击响应大于T型材腹板中的响应，而其他频段的响应相差不大。

4.3 应力波在舷侧外板中的传播特性及冲击响应谱分析

本节采用上节相同的分析方法，进一步探究应力波在舷侧外板结构中的传播特性。

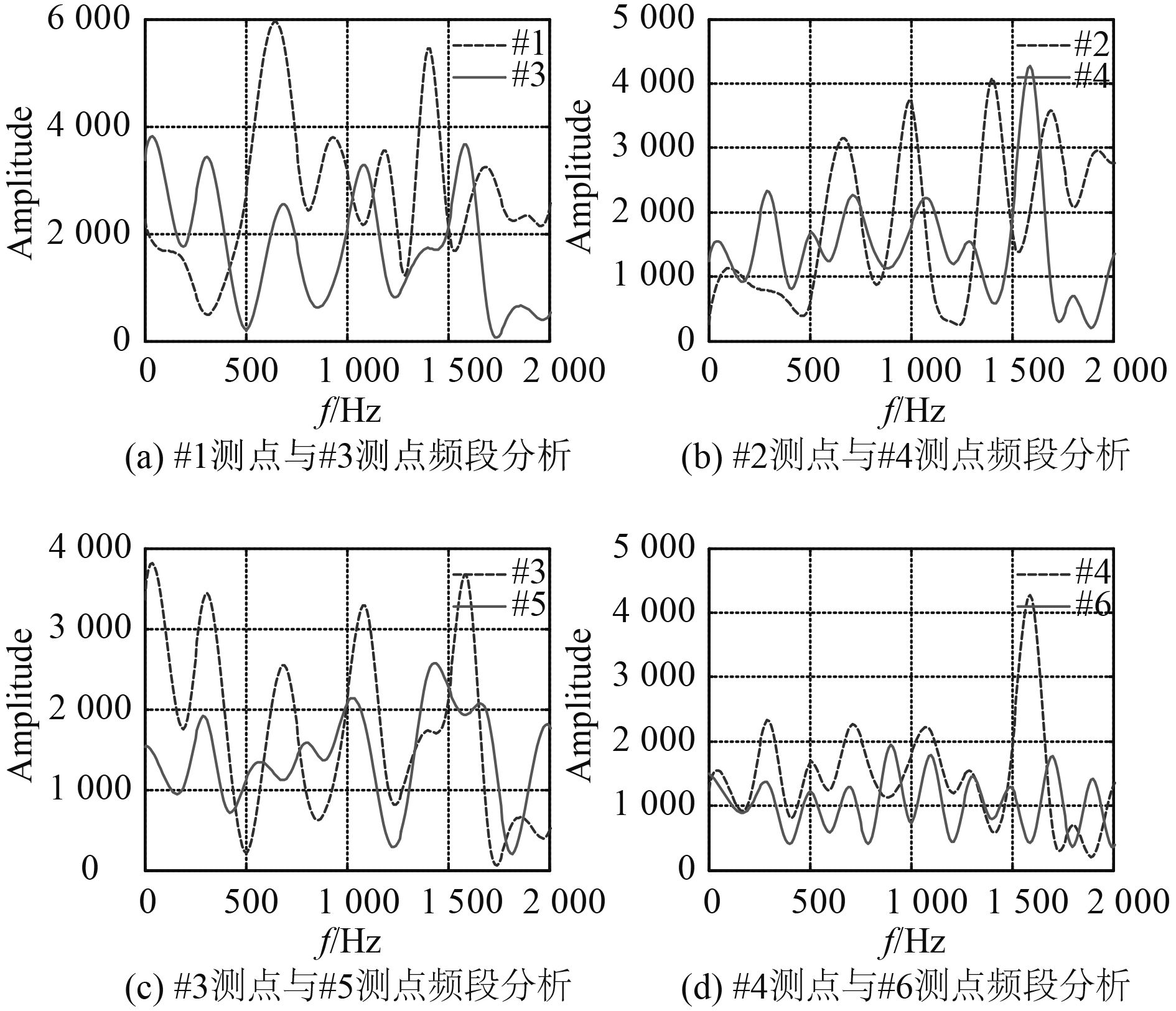
分别提取出#1～#6六个测点的加速度随时间变化的数据，并进行快速傅里叶变换，得到对应的频谱曲线，如图16所示。

通过图16（a）与图16（b）两组测点相互对比可以发现，在[500, 2 000] Hz内#3，#4测点的幅值比#1，#2测点小，这说明在该频率范围内的应力波经过第1个T型材后强度呈大幅衰减趋势，衰减幅度约60%，而#3，#4测点在[0, 500] Hz内的幅值比对应的#1，#2测点大，这说明在该频率范围内的应力波经过第1个T型材后强度略微增强。结合这两点，说明当应力波经过第1个T型材后滤掉了大部分高频信号，而增强了低频信号，前者是由于应力波在经过第1个从小截面到大截面形式的变化时会滤掉高频信号的特性所导致，后者是因为应力波从大截面进入小截面其强度会增强的原理所导致。

从图16（c）与图16（d）可以发现，#5，#6测点在[0, 500] Hz内的幅值比对应的#3，#4测点小，这说明在该频率范围内的应力波经过第2个T型材后强度呈衰减趋势，衰减幅度约50%，而#5，#6测点在[500, 2 000] Hz内的幅值相对于#3，#4测点来说衰减幅度并不大。基于此，这说明应力波再次经过相同截面形式的T型材后会滤掉大部分低频信号，这与4.2节的结论相吻合。

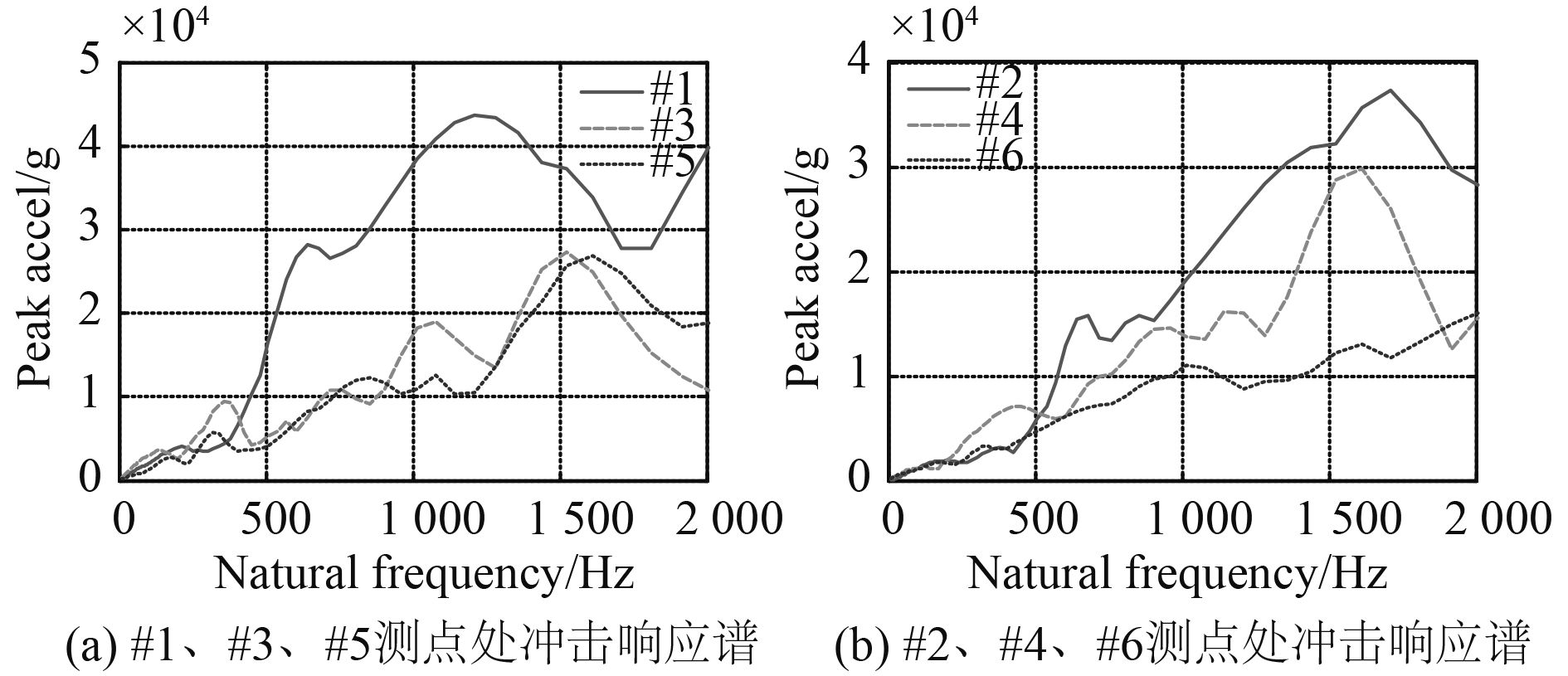
将以上测点的加速度时历数据进行转换得到其对应的冲击响应谱曲线，如图17所示。可以看出，#1，#3，#5测点处冲击响应谱曲线与#2，#4，#6测点处冲击响应谱曲线规律相似。为方便起见，下面以#2，#4，#6测点处冲击响应谱曲线规律进行阐述。在[0, 2 000] Hz内，#2，#4，#6测点的谱峰值依次减小，说明舷侧外板在受到水下爆炸载荷作用下，在[0, 2 000] Hz内的结构响应峰值在经过2个T型材后呈衰减趋势。具体说来，在[0, 500] Hz内#2测点的谱峰值小于#4，则说明舷侧外板在受到水下爆炸载荷作用下[0, 500] Hz内的结构响应在经过第1个T型材后呈放大趋势，而#6测点的谱峰值小于#4测点，这说明舷侧外板在受到水下爆炸载荷作用下[0, 500] Hz内的结构响应在经过第2个T型材后呈衰减趋势。对于[500, 2 000] Hz较高频率范围内的冲击响应经过2个T型材后整体呈衰减趋势。

综上所述，舷侧外板中低频段的冲击响应谱峰值沿着从下往上的方向先升高再下降而高频段的谱峰值则依次下降。

5 结　语

本文基于应力波理论，结合CEL方法，首先研究了在水下爆炸载荷作用下变截面杆结构中应力波的传播特性，与理论公式对比验证了数值精度，然后进一步探讨了舷侧外板结构在遭遇水下爆炸载荷后的应力波传播特性，得到如下结论：

1）当应力波由大截面向小截面传播时，透射波扰动强度大于入射波扰动，这种结构起到“聚波”作用。

2）应力波在经过第1个从小到大截面形式的变化时滤掉了大部分高频信号，当应力波再次经过从小到大截面形式的变化时会进一步滤掉响应信号。

3）在舷侧外板到T型材腹板这种从小到大截面形式变化的结构中，激励产生的低频段结构响应谱值，两者之间相差不大，而外板的高频段谱值远高于T型材腹板中的谱值。当应力波再次经过这种截面形式的变化时，舷侧外板产生的中高频段冲击响应大于T型材腹板中的响应，而其他频段的响应相差不大。

4）在含有2个T型材的舷侧外板中，低频段的冲击响应谱峰值沿着从下往上的方向先升高再下降而高频段的谱峰值则依次下降。

以上结论对研究船舶与海洋工程领域的型材、纵骨、纵桁等变截面结构中应力波传播特性以及后续研究复杂舰船结构的冲击响应规律具有一定的参考意义。