2. 江苏科技大学 海外教育学院,江苏 镇江 212001;
3. 哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001
2. Overseas Education College, Jiangsu University of Science and Technology, Zhenjiang 212001, China;
3. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
海洋结构物的入水砰击是一个复杂的流固耦合问题,海洋结构物在入水过程中会对水有砰击作用,造成水向四周飞溅,同时水又会对海洋结构物产生一定的反作用力。特别是在海洋结构物入水的瞬间,会产生比较大的入水砰击载荷,造成结构变形甚至破坏。因此准确预报海洋结构物的入水砰击载荷以及水弹性力学特性,对工程实践有重要的指导意义。
目前,很多学者对入水问题进行了研究。Zhao和Faltinsen[1]在Wagner方法的基础上,提出了求解二维物体入水砰击问题的边界元数值方法,研究结果表明,在砰击角度较小时得到的结果与Wagner方法的渐近解数值模拟结果相近。李辉[2]基于三维非线性水弹性理论,提出一种求解波浪载荷和船舶运动关系的方法。郑坤等[3]采用SPH方法建立数值水槽,讨论了规则波对水平板砰击过程,采样一种新的评价估计方法得到了砰击时历曲线,且更为准确。吴景健[4]利用Ls-dyna软件,对楔形体模型进行二维和三维数值模拟,计算出结构入水的加速度、砰击压力和应力响应得出结构的加速度以及应力随着结构质量的变化规律。这些结论对砰击载荷的合理预报以及船体结构的设计具有重要意义。王文华[5]采用一种新的CFD方法动态数值模拟了二维楔形结构的自由入水过程。张健[6]对二维刚性楔形体入水砰击问题进行研究。获得气垫效应、倾斜角、入水速度对楔形体入水砰击压力峰值的影响规律,并分析了气垫效应对压力峰值的影响机理。王平[7]基于流体力学模型,通过自定义函数模拟了楔形体的自由入水过程,研究了楔形体在不同周期,位置入水时的影响。
本文主要研究波浪作用下,不同刚度三维楔形体的入水过程。详细介绍本文数值模拟的基本理论,验证研究方法的有效性,数值模拟三维弹性体和刚性体的垂直入水过程,得到楔形体入水的砰击压力和砰击压力持续时间的变化,对比分析弹性体和刚性体入水过程中砰击压力的差异。
1 数值模型 1.1 湍流模型本文采用RANS方程基础上建立起来的基于涡粘性假设的SST
k方程:
| $\displaystyle\frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \nabla \cdot \left( {\rho Uk} \right) = \nabla \cdot \left[ {\left( {\mu + \displaystyle\frac{{{\mu _t}}}{{{\sigma _{k3}}}}} \right)\nabla k} \right] + {P_k} - {\beta '}\rho k\omega\text{,} $ | (1) |
ω方程:
| $ \begin{aligned} \!\!\displaystyle\frac{{\partial (\rho \omega )}}{{\partial t}} + \nabla \cdot \left( {\rho U\omega } \right) &= \nabla \cdot \left[ {\left( {\mu + \displaystyle\frac{{{\mu _t}}}{{{\sigma _{\omega 3}}}}} \right)\nabla \omega } \right] + \left( {1 - {F_1}} \right)\times \\ & 2\rho \displaystyle\frac{1}{{{\sigma _{\omega 2}}\omega }}\nabla k\nabla \omega + {\alpha _3}\displaystyle\frac{\omega }{k}{P_k} - {\beta _3}\rho {\omega ^2}\text{。} \end{aligned} $ | (2) |
楔形体结构砰击入水受到的压力除了跟入水速度有关外,还跟许多非线性因素如飞溅效应等有关。在砰击压力峰值处于不同速度入水的情况下,这些非线性效应的影响程度是不同的。试验研究表明,砰击压力持续时间短且在量值上有显著变化,入水速度的平方基本与结构入水所受到的砰击压力峰值呈线性关系。因为当相对速度超过临界速度时产生可计量的砰击压力,所以根据冲量砰击理论,结构物入水所受到的砰击压力峰值可以写为:
| $P = k{\rho _w}{\rm{v}}_n^2\text{。}$ | (3) |
式中:
当静止水面受到外力作用时,水面离开平衡位置并产生波动。自由液面在重力和惯性力的共同作用下,上下往复运动形成波浪。本文所模拟的波浪为线性小振幅波,对于有限水深,其波面方程为:
| $\eta = \frac{H}{2}\cos \left( {kx - \omega t} \right)\text{,}$ | (4) |
速度势为:
| $\phi = \displaystyle\frac{{gH}}{{2\omega }}\displaystyle\frac{{\cosh (z + d)}}{{\cosh kd}}\sin \left( {kx - \omega t} \right)\text{,}$ | (5) |
波数
| $\frac{{{\omega ^2}}}{g} = k\tanh kd\text{,}$ | (6) |
波长
| $\lambda = \frac{g}{{2{\text{π}} }}{T^2}\tanh \frac{{2{\text{π}} }}{\lambda }d\text{,}$ | (7) |
x方向速度:
| ${u_x} = \displaystyle\frac{{gHK}}{{2\omega }}\displaystyle\frac{{\cosh (z + d)}}{{\cosh kd}}\cos \left( {kx - \omega t} \right)\text{,}$ | (8) |
z方向速度:
| ${u_z} = \displaystyle\frac{{gHK}}{{2\omega }}\displaystyle\frac{{\sinh (z + d)}}{{\cosh kd}}\sin \left( {kx - \omega t} \right)\text{。}$ | (9) |
式中:H为波高;k为波数;
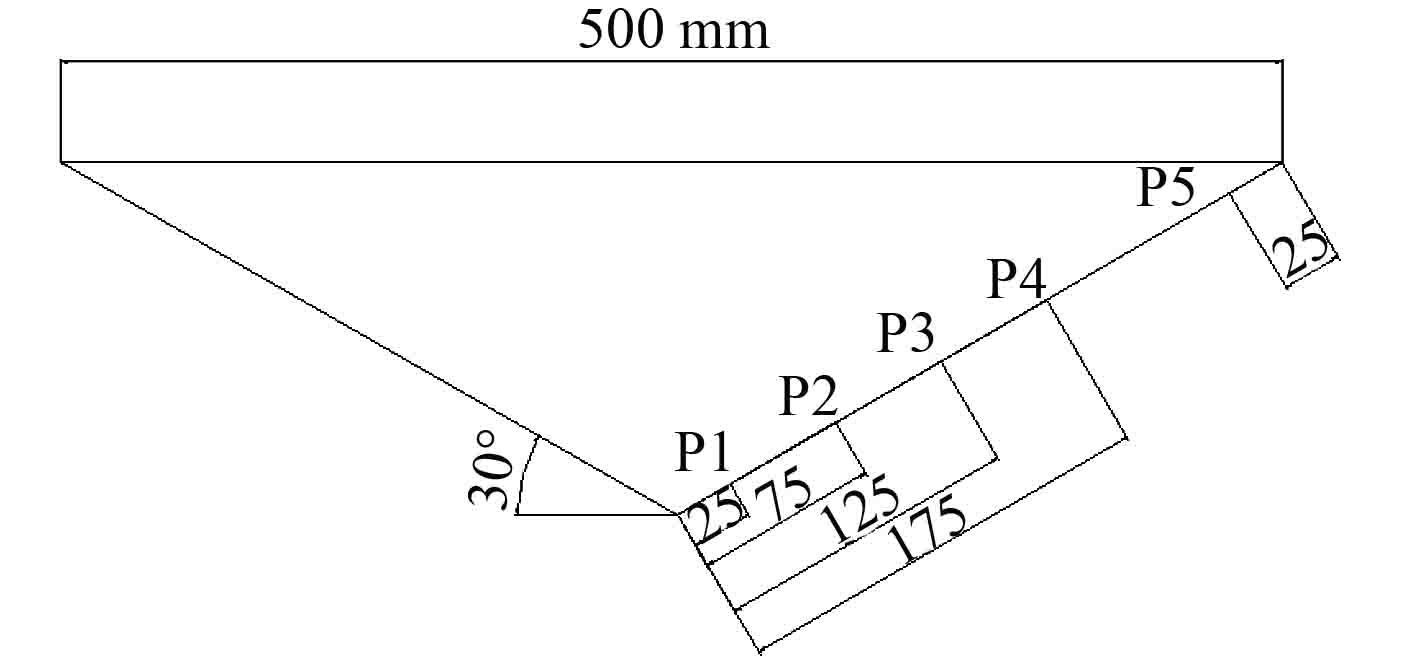
图1为楔形体斜升角45°的三维计算模型示意图,其中监测点选取位置在图2的虚线上,虚线位置处取4个点,且间距相等。

|
图 1 楔形体示意图 Fig. 1 The wedge diagram |

|
图 2 楔形面示意图 Fig. 2 Schematic diagram of wedge′s surface |
表1为波浪概率统计表,汇总了不同波浪周期和波高下波浪的发生概率。从表中可以看出,波高为0.5~2.5 m区间内,波浪参数主要集中介于周期为2.5~8.5 s。
|
|
表 1 波浪概率统计表 Tab.1 Probability statistics of wave |
为了更好地贴合现实情况,波高选取为1 m,水池水深选为5 m,求得周期为3.737 s,具体参数见表2。
|
|
表 2 余弦波参数 Tab.2 The cosine waveparameters |
三维数值水池总长为80 m,宽10 m,高8 m,深5 m,水面以上为空气,消波区长20 m,坐标系原点设置在水池左边界造波区,图3为水池模型示意图。

|
图 3 三维数值水池示意图 Fig. 3 Schematic diagram of the 3-D numerical wave tank |
对于波浪的数值仿真,网格质量在Fluent的数值模拟结果有着至关重要的影响。特别是自由液面处的网格划分直接决定了计算中波浪的精度。网格划分时,在X方向,单个网格尺寸为1/100波长,自由液面上Z方向,网格高度为1/20波幅,远离自由液面处网格按比例系数减少,不妨碍计算。图4为网格划分示意图。

|
图 4 网格划分示意图 Fig. 4 Schematic diagram of the grid |
三维波浪水池左边界YZ面为造波边界Inlet通过利用Fluent软件的二次开发接口UDF (Universal DiscFormat) DEFINE_PROFILE编写速度表达式实现造波条件;在出口端加载UDF附加动量源项来实现消波。右边界YZ面设置为压力Oulet出口,通过UDF语言定义其出口压力函数;上边界XY面设置为压力Pressure入口(即一个标准大气压);底边界wall为无滑移固壁条件;用UDF程序在自由液面的界定处实现实时捕捉水池中液面的位置。
1.4.5 计算参数设置计算模型以静水面为界包括空气和水下2个部分:上方为空气,密度为1.225 kg/m3;下方为水,密度为998.2 kg/m3。流场初始速度为0,参考压力值为101 320 Pa。计算时间步长设置取0.01 s,采用Fluent瞬态求解器进行数值计算,控制方程采用有限体积法进行离散,压力速度耦合方法为PISO(Pressure Implicit with Splitting of Operator),压力插值采用Body Force Weight体积力。
1.5 消波设置在模拟数值波浪水池中,为防止波浪到达水池尾部边界处反射回来造成叠加现象影响模拟结果,需要在水池尾部设置消波区。常用的消波方法主要有设置阻尼区消波法、辐射边界条件法、主动消波法。本文用阻尼消波法,在水池尾部一个波长区间内通过在动量方程中加载UDF程序DEFINE_SOURCE(momentum,c,t,dS,eqn)实现消波。消波区内,动量方程如下:
| $ \begin{aligned} \displaystyle\frac{{\partial w}}{{\partial t}} + u\displaystyle\frac{{\partial w}}{{\partial x}} + v\displaystyle\frac{{\partial w}}{{\partial y}} + w\displaystyle\frac{{\partial w}}{{\partial z}} &= g - \displaystyle\frac{1}{\rho }\displaystyle\frac{{\partial p}}{{\partial z}} + \\ & \upsilon \left( {\displaystyle\frac{{{\partial ^2}w}}{{\partial {x^2}}} + \displaystyle\frac{{{\partial ^2}w}}{{\partial {y^2}}} + \displaystyle\frac{{{\partial ^2}w}}{{\partial {z^2}}}} \right) - C\left( x \right)w\text{,} \end{aligned} $ | (10) |
其中:
| $C\left( x \right) = c\sqrt \lambda {\left( {\displaystyle\frac{{x - {x_0}}}{{{x_L} - {x_0}}}} \right)^2}\rho \text{。}$ | (11) |
式中:
为了能够验证本文模拟楔形体入水数值方法的正确性,使用与文献[8]相一致的几何模型,如图5所示。将文献中的实验结果与在水池中计算楔形体做自由运动入水的砰击压力峰值与速度衰减的结果进行对比。
|
图 5 楔形体图 Fig. 5 The wedge sketch |
对于距离运动区域较远的流域外部,采取压力出口边界条件。通过UDF来进行定义,使边界上的压力得到正确的模拟,其中在流场前部区域采取压力P0=101 320 Pa。对楔形体周围网格进行加密,保证楔形体在空气与流体域中更好地过渡,让流体飞溅区域到达计算结果的精度更高。
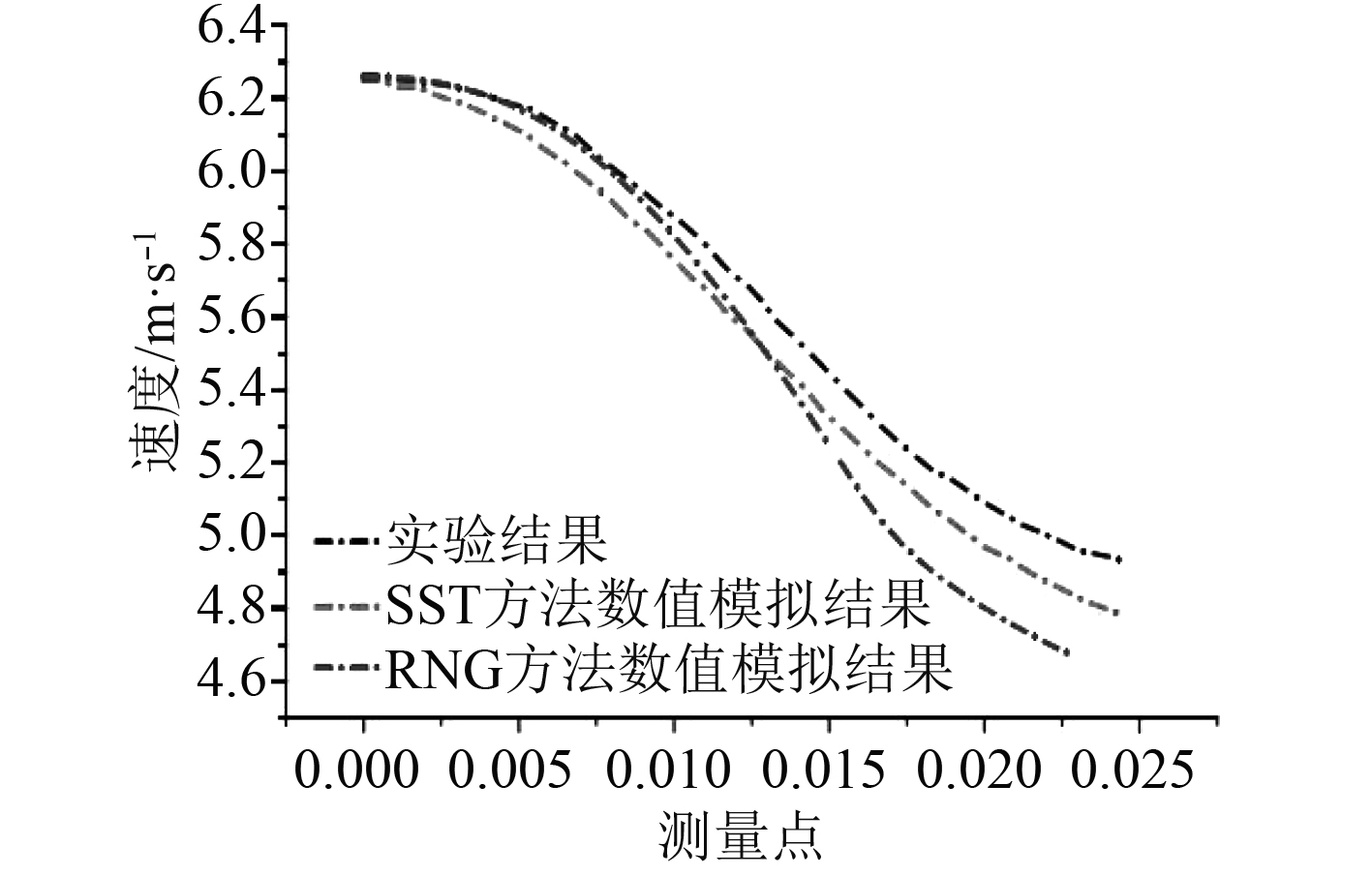
图6为斜升角为30°的楔形体以入水速度为6.27 m/s时分别在RNG
|
图 6 楔形体入水速度变化曲线对比 Fig. 6 Comparison of the curve of water entry velocity of wedge |
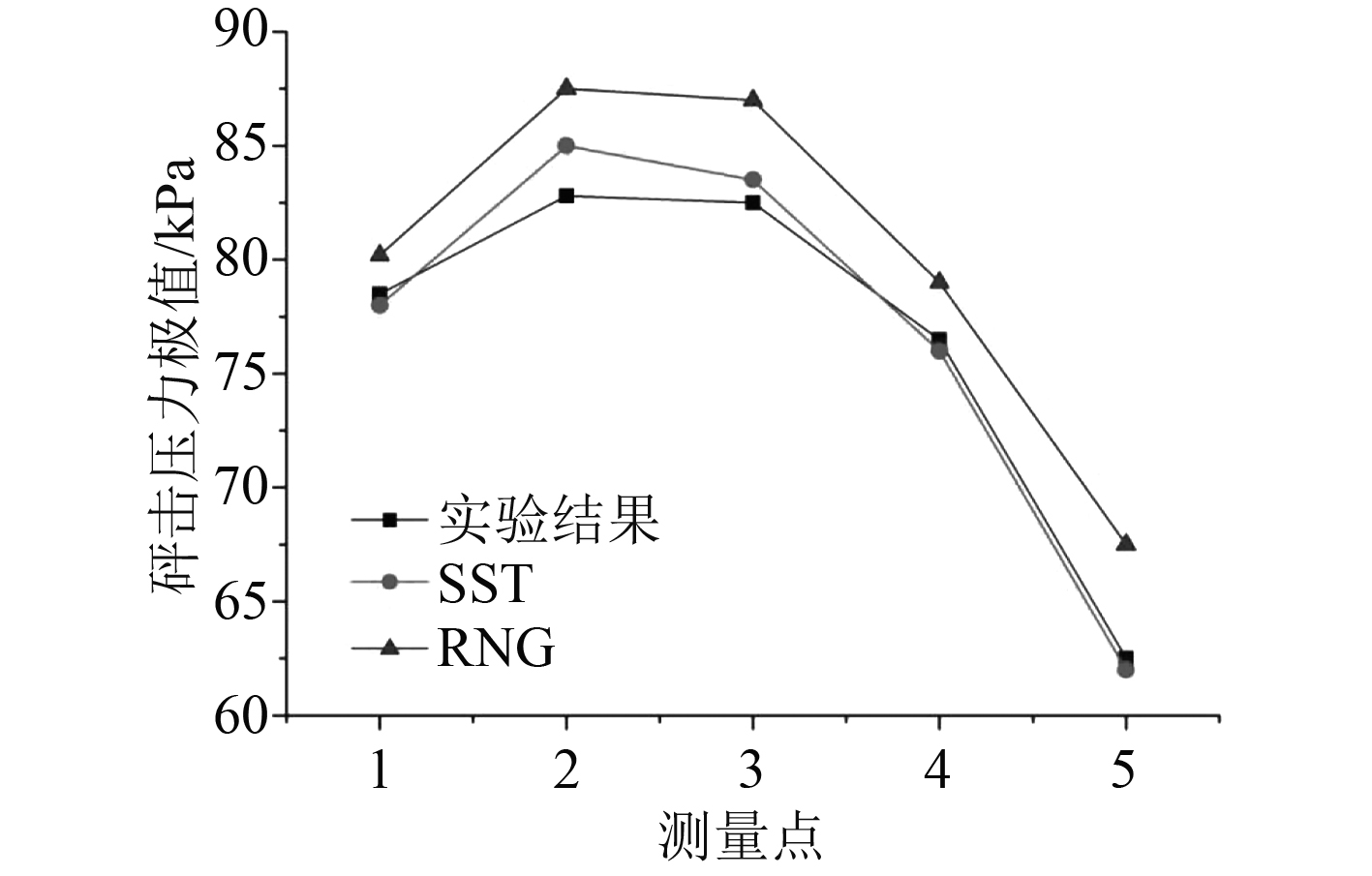
|
图 7 不同湍流模型下各点砰击压力极值 Fig. 7 The extreme slamming pressure of each point under different turbulence models |
表3记录的是三维弹性楔形体入水砰击的数值模拟结果,包括入水的砰击压力峰值和砰击压力持续时间。
|
|
表 3 弹性楔形体入水砰击数值模拟计算结果 Tab.3 Numerical simulation of water slamming in elastic wedge structure |
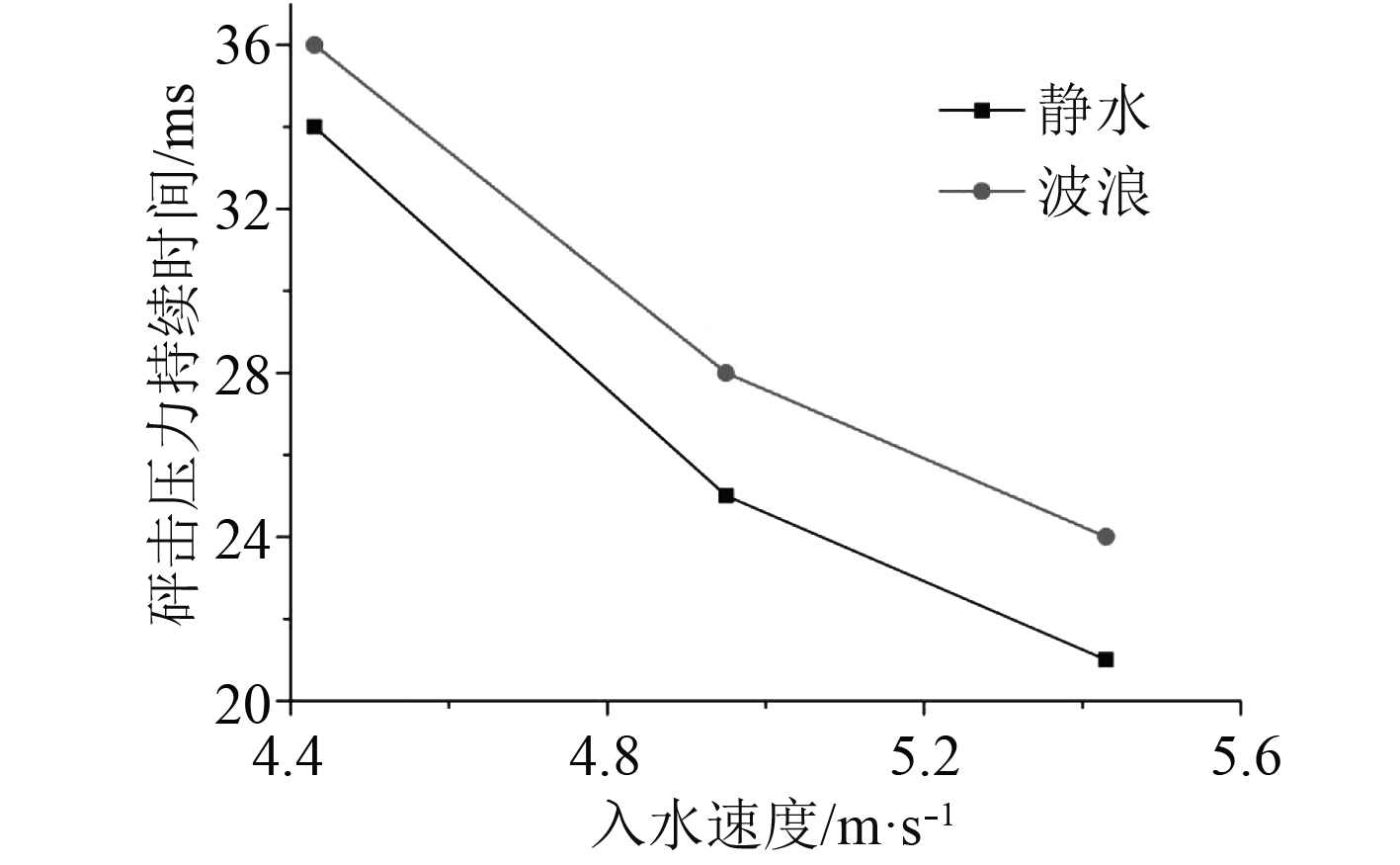
图8为三维弹性楔形体在静水和波浪中入水砰击压力峰值的差异。图9为三维弹性楔形体在静水和波浪中砰击压力峰值持续时间的对比。

|
图 8 弹性楔形体在静水和波浪中砰击压力峰值比较 Fig. 8 Comparison of peak slamming pressure of elastic wedge in still water and waves |
|
图 9 弹性楔形体在静水和波浪中砰击压力峰值持续时间比较 Fig. 9 Comparison of duration of elastic wedge's peak slamming pressure in still waterand waves |
通过以上结果可以发现:
1)不管是砰击压力峰值,还是砰击压力持续时间,波浪值和静水值随入水速度的变化趋势均一致;
2)砰击压力峰值随着入水速度的增加而增加且静水值略大于波浪值;
3)随着入水速度的增加,砰击压力峰值持续时间逐渐减少,且总体静水值小于波浪值。
3.2 刚性体入水砰击压力表4为三维刚性楔形体入水砰击的数值模拟结果,包括不同下落高度与速度的情况下入水的砰击压力峰值和压力持续时间。
|
|
表 4 刚性楔形体结构入水砰击数值模拟计算结果 Tab.4 Numerical simulation results of water entry slamming of rigid wedge-shaped structures |
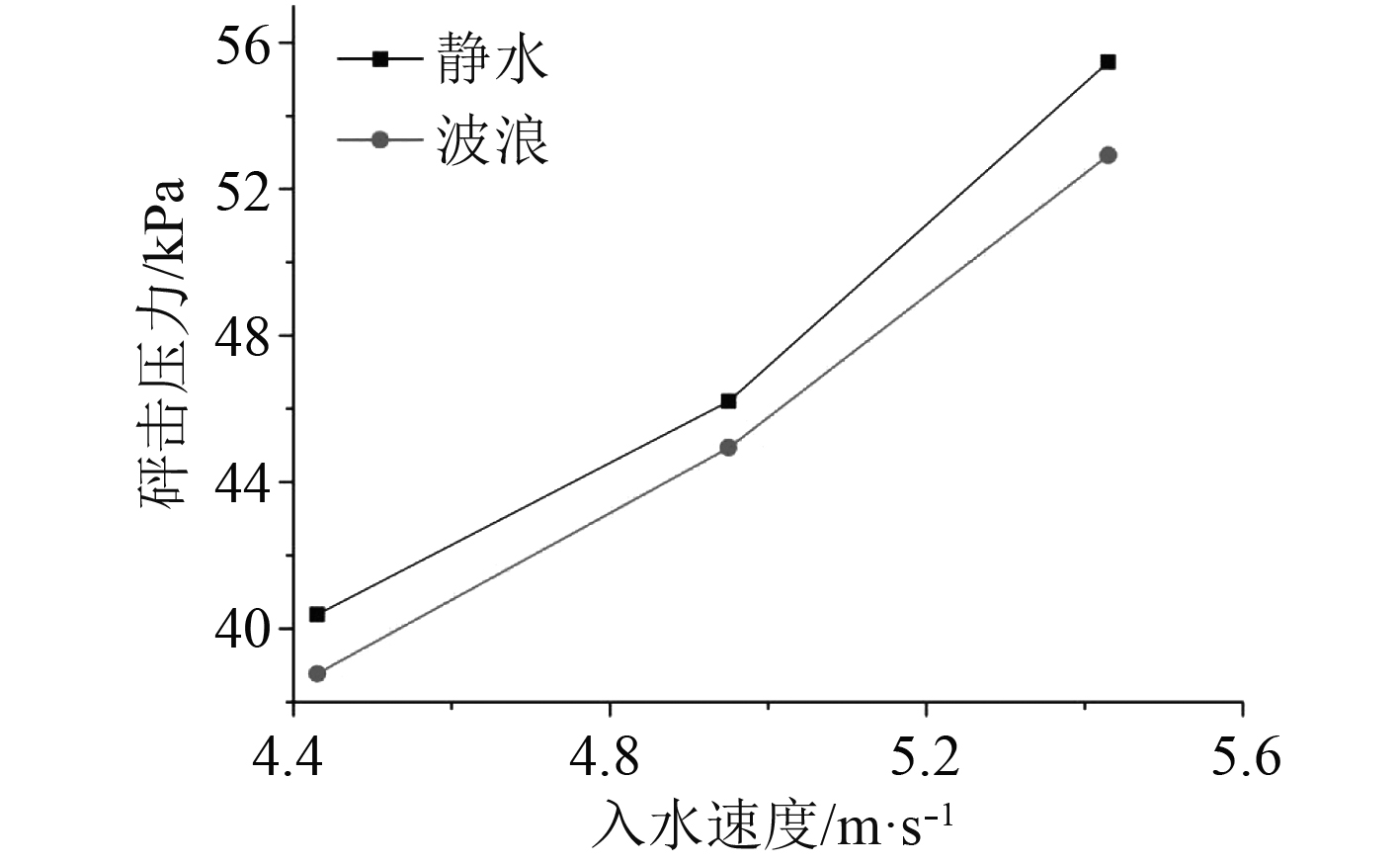
图10为三维刚性楔形体在静水和波浪中入水砰击压力峰值的差异。图11为三维刚性楔形体在静水和波浪中砰击压力峰值持续时间的对比。
|
图 10 刚性楔形体在静水和波浪中砰击压力峰值比较 Fig. 10 Comparison of peak slamming pressure of rigid wedges in still water and waves |

|
图 11 刚性楔形体在静水和波浪中砰击压力峰值持续时间比较 Fig. 11 Comparison of duration of rigid wedge's peak slamming pressure in still water and waves |
根据图10和图11可知,三维刚性体在静水和波浪中,砰击压力和砰击压力持续时间随入水速度的变化趋势与弹性体基本一致,仅在具体数值上有所差异。
3.3 弹性体与刚性体入水砰击压力的对比弹性楔形体在波浪作用下抨击入水的数值模拟中,当楔形体与流体发生砰击作用时,不但流体会对楔形体产生强大的砰击作用力,楔形体的变形响应也会对流场产生巨大影响,因此两者之间存在着强烈的双向流固耦合作用。
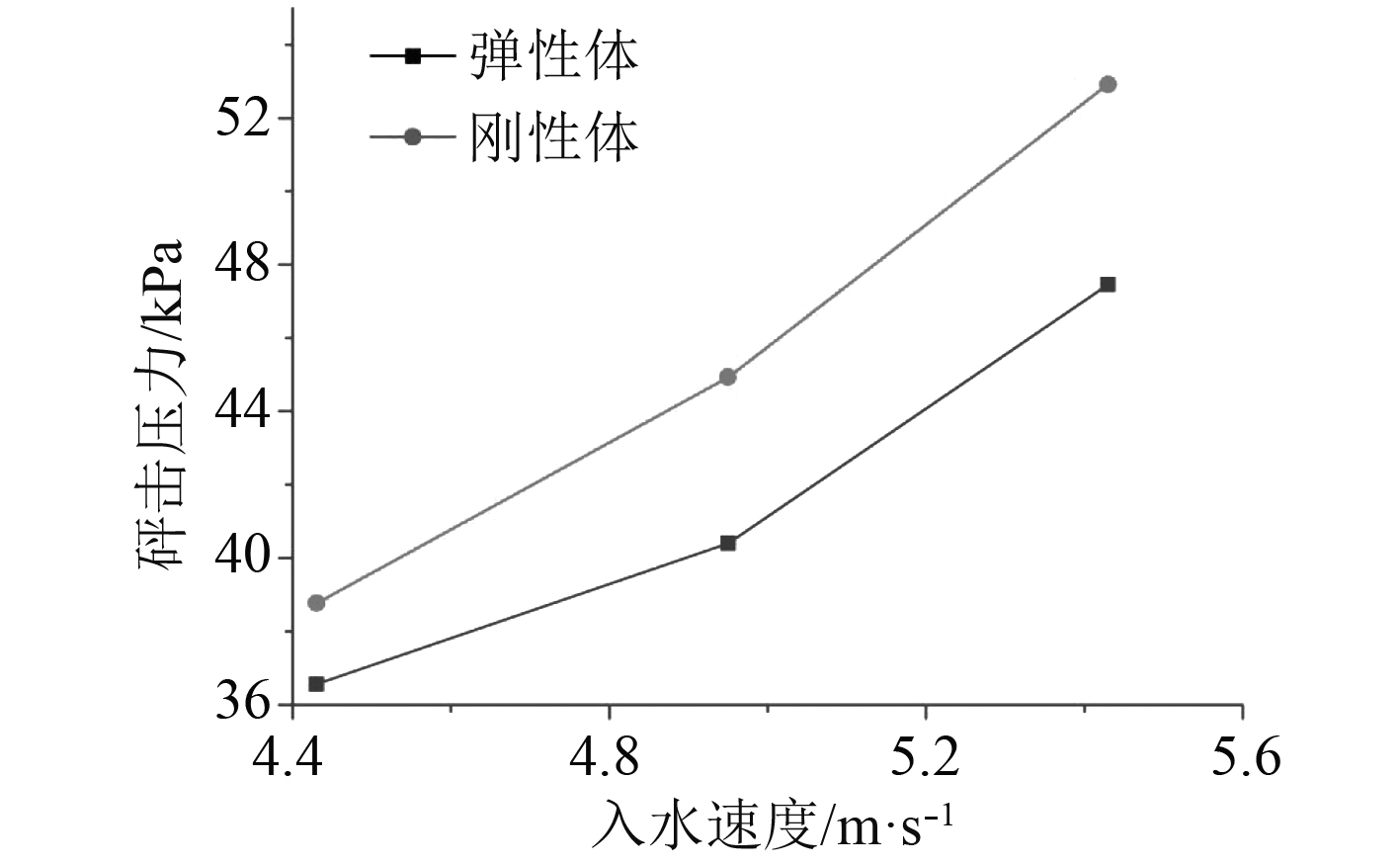
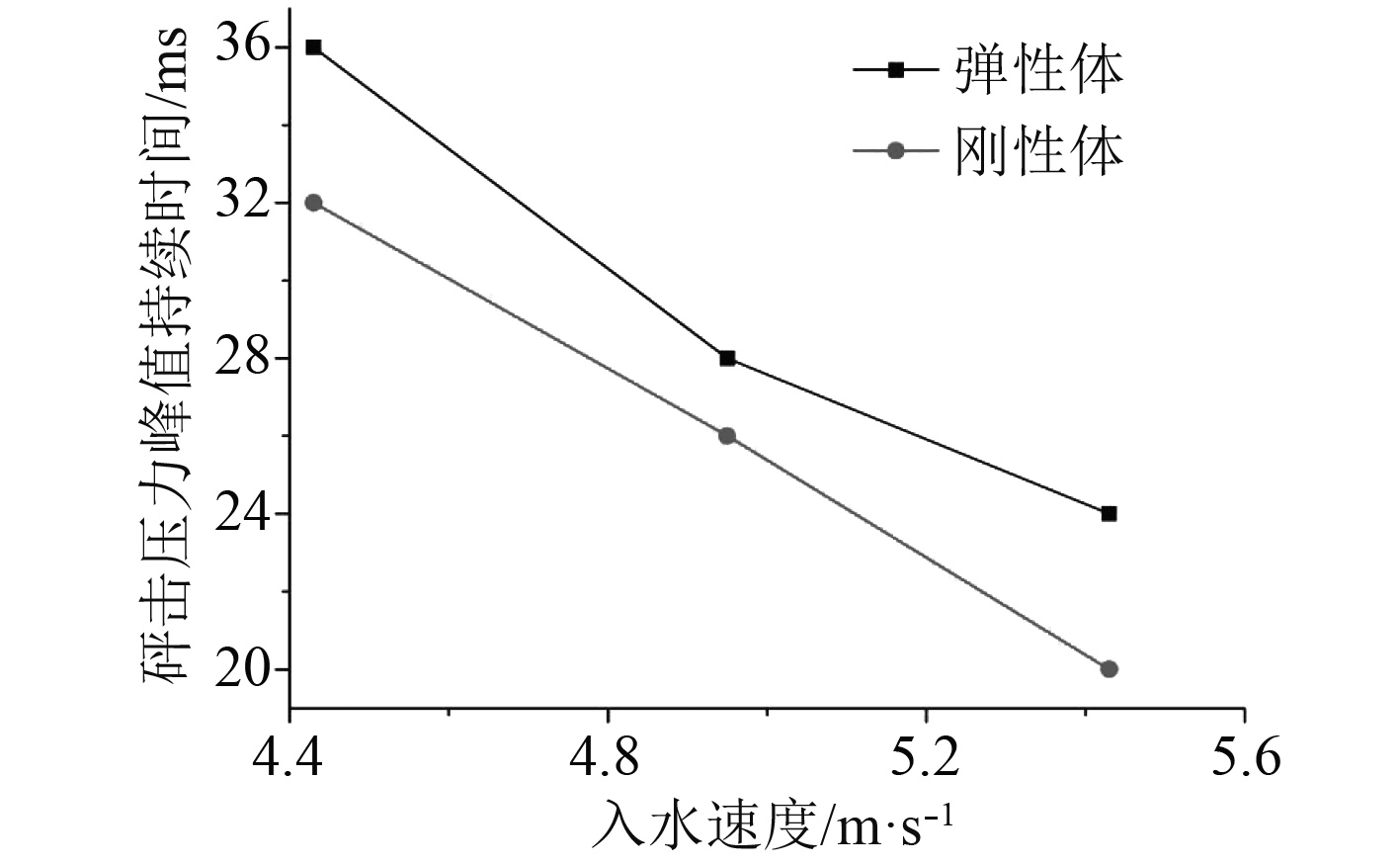
不同刚度的楔形体入水过程会发生不同的弹性变形,从而影响结构入水时所受到的砰击压力。表5为弹性体和刚性体在不同入水速度下,砰击压力峰值和砰击压力持续时间的数值结果。图12为弹性体和刚性体所受到砰击压力峰值的对比,图13为弹性体和刚性体砰击压力峰值持续时间的比较。
|
|
表 5 弹性楔形体与刚性楔形体砰击压力比较 Tab.5 Comparison of slamming force between elastic wedge and rigid wedge |
|
图 12 弹性楔形体和刚性楔形体砰击压力峰值比较 Fig. 12 Comparison of peak slamming pressure between elastic wedge and rigid wedge |
|
图 13 弹性体和刚性体砰击压力峰值持续时间比较 Fig. 13 Comparison of peak duration of slamming pressure between elastic wedge and rigid wedge |
通过本文的研究,可以得出如下结论:
1)在其他条件不发生改变的情况下,结构入水速度的增加,将导致结构与水发生撞击时产生的砰击压力峰值会迅速增大;
2)在其他条件不发生改变的情况下,结构弹性模量的增加,将导致结构与水发生撞击时产生的砰击压力峰值会随之增加,有成线性增加的趋势。这表明当结构的刚度逐渐增强,结构的弹性效应随之减弱,表现为结构在与流体相互作用时产生的变形越来越小即弹性结构的砰击加速度峰值越来越接近刚性结构的砰击砰击压力峰值;
3)刚性结构和弹性结构分别与水发生撞击时,弹性结构受到的砰击压力峰值要小于刚性结构受到的砰击压力峰值,但是无论结构的弹性模量怎么增加,结构与水发生撞击时产生的砰击压力峰值都不会超过结构为刚性材料时的砰击压力峰值。这说明弹性效应的存在会在一定程度上减缓砰击的发生。
| [1] |
ZHAO R, FALTINSEN O. M.. Water entry of two-dimensional bodies[J]. Journal of Fluid Mechanics, 1993, 246: 593-612. DOI:10.1017/S002211209300028X |
| [2] |
李辉. 船舶波浪载荷的三维水弹性分析方法研究[D]. 哈尔滨工程大学, 2009.
|
| [3] |
ZHENG K, SUN Z C, CHEN C P, et al. Numerical simulations of regular wave impact on horizontal plate based on SPH methods[J]. Applied Mechanics and Materials, 2013, 353: 3531-3536. |
| [4] |
吴景健. 加筋板楔形体结构水弹性砰击试验与仿真研究[D]. 天津: 天津大学, 2014.
|
| [5] |
王文华, 黄一, 王言英, 等. 弹性楔形体各状态参数对入水运动性能的影响[J]. 船舶力学, 2014, 18(11): 1320-1330. DOI:10.3969/j.issn.1007-7294.2014.11.007 |
| [6] |
张健, 尤恽, 王珂, 等. 基于气垫效应的二维楔形体入水砰击载荷预报方法研究[J]. 舰船科学技术, 2016, 38(3): 7-12. |
| [7] |
王平, 袁帅, 张宁川, 等. 楔形体在波浪中自由入水的数值模拟[J]. 海洋工程, 2017, 35(5): 42-50. |
| [8] |
任冰, 王永学. 非线性波浪对结构物的砰击作用[J]. 大连理工大学, 1999, 39(4): 562-566. DOI:10.3321/j.issn:1000-8608.1999.04.020 |
 2019, Vol. 41
2019, Vol. 41
