0 引　言

调度是一个历久弥新的重要课题，主要工作内容集中于制定合理的时间表来跟踪多类工作的计划以及实时监控最后期限。在很大程度上，生成和优化工作时间表是所有工业活动的重要组成部分，以丰田创造的Kanban管理、订单制造为代表的生产调度技术，将传统粗放型生产模式提升到现代化精细柔性制造阶段，极大地减少了库存并提高了生产效率^[1]。

对于舰载机而言，调度优化问题关系到作战能力的生成，具有十分重要的价值。在有限空间和时间约束条件下，要实现舰载机的优化调度，最关键的挑战是找到一个兼顾效率、安全性的时间表。长期以来，学者多使用常识性和启发式策略进行调度，出动回收流程本质上可看做排队网络，舰载机在接受不同的作业时，大多遵循先到先得（FCFS）策略，同时由于舰载机的任务差异性，在某些关键过程中又存在着优先级。基于此，郑茂等^[2]根据舰载机出动回收过程中同时具有先到先得（FCFS）、部分舰载机高优先级的特征，在传统闭环排队网络基础上提出了多优先级马尔科夫排队网络的近似算法，获得了舰载机出动回收流程稳态解析解，对于分析航母各航空保障作业站点配置具有重要价值。然而基于排队论的理论模型无法对高度动态、强随机的舰载机作业细节进行深入刻画，特别是随机事件出现时，整个系统的响应会出现“牵一发而动全身”的效果，因此针对随机事件的调度策略是维持舰载机出动回收流程鲁棒性的重要支撑。冯强等^[3] 利用多主体技术（Multi-Agency System）建立了舰载机出动回收流程网络模型，分析了多主体之间的交互协商机制，引入遗传算法和合同网算法，实现了舰载机出动回收流程的动态调度。Michini等^[4]将逆向强化学习算法（IRL）引入到舰载机出动回收调度过程中，对于降落环节和加油环节，分别按照效率优先、安全优先、均衡水平3种服务策略，建立了舰载机出动回收流程模型，利用逆向强化学习实现了随机故障条件下的快速重决策，其调度策略更为贴近真实，为将智能算法引入舰载机调度作业中做出了有益探索。吴宇等^[5] 针对舰载机着舰顺序调度问题，考虑低油量水平舰载机优先着舰，引入蚁群算法实现了着舰顺序的动态调度。李耀宇等^[6]在开展舰载机调度决策过程中，利用逆向强化学习算法，获得了合理的舰载机调度方案生成方法，并结合甲板面推演仿真环境实现了舰载机的作业流程——空间位置联合自主调度。杨炳恒等（2016）^[7] 通过分析舰载机机务勤务保障作业关键流程，提出了一种多机同步保障的资源调度方法，可为航母多机出动甲板保障方案的制订提供决策支持。

上述出动回收调度模型对舰载机出动回收过程做了大幅简化，将舰载机在网络中的转移过程看做泊松流，按照负指数分布确定执行每项任务的时间，未考虑实际舰载机作业中的集中出动、集中回收、波次攻击的情况。从理论上讲，尽管这种基于泊松流的状态转移模型可以得到出动回收流程的稳态解，然而对于高度动态、强随机的舰载机作业而言，稳态平均值无法反映作业峰值数据，而这些峰值数据对于航母作战尤为重要。例如舰载机集中降落后的维护保障，由于短时间内转移至保障站的舰载机众多，远超平均稳态水平，极易发生严重排队情况，而这些现象在稳态解中无法体现。郑茂等^[8]以美国海军高强度演习为研究对象，建立了具有波次特征的出动回收仿真模型，以先到先得（FCFS）为服务策略，实现了贴近真实作战场景的舰载机出动回收流程仿真，特别是对舰载机维修、保障站位的舰载机排队数量进行了统计分析，获取了不同航保设施配置条件下的舰载机排队峰值数据，为航空保障设施配置提供了依据。

本文首先建立了舰载机高强度出动回收流程仿真模型，深入分析各主要舰载机服务站的服务规则，引入基于线性的服务策略模型对服务规则进行数学化表达，最终获得了基于线性策略的舰载机高强度出动回收流程仿真模型，通过与美国海军高强度演习记录数据进行对比，验证了仿真模型的精度可靠。最后对比了2种不同调度策略对于舰载机出动架次率、作业安全性的影响。

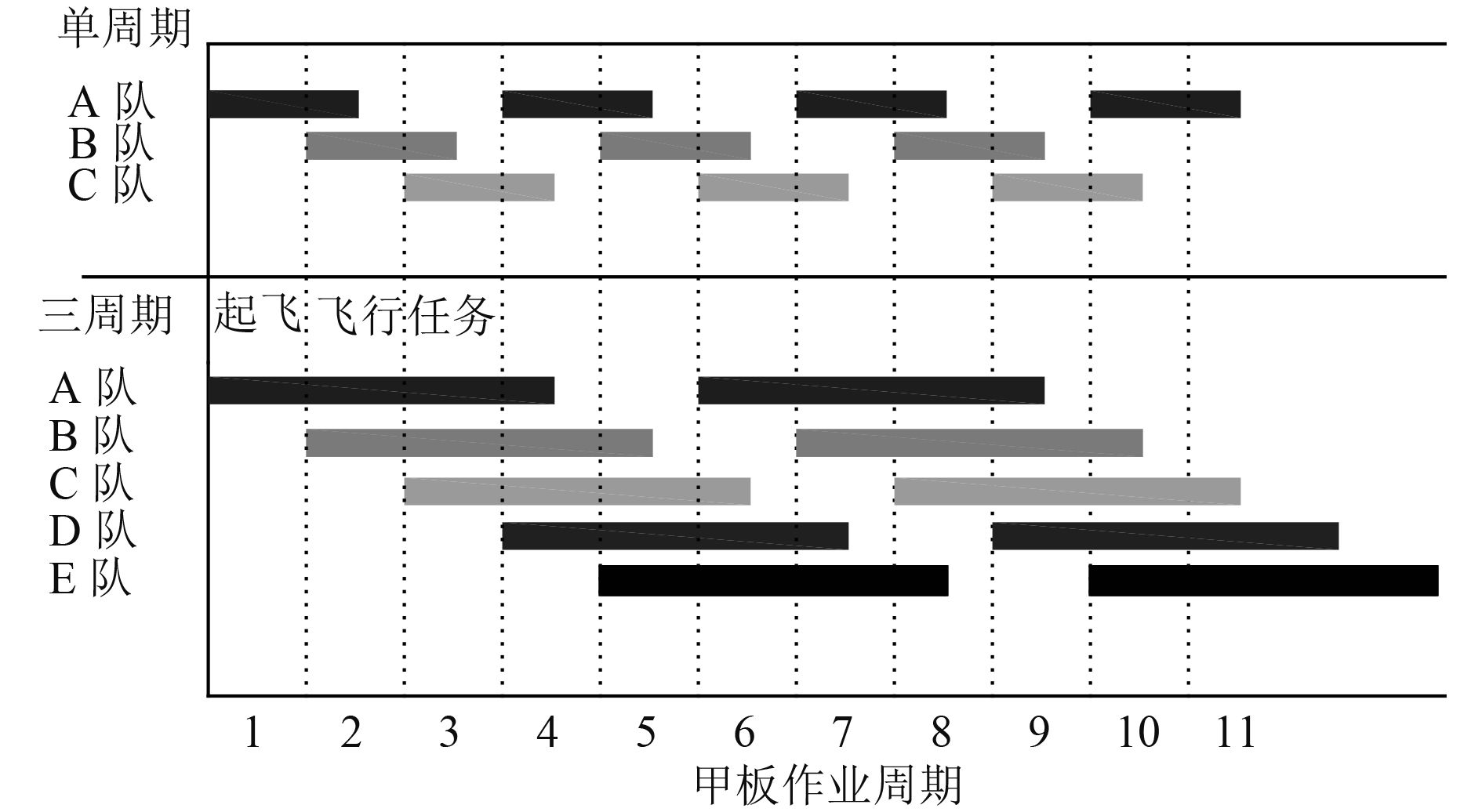
1 舰载机高强度出动回收排队模型的建立 1.1 舰载机高强度出动回收作业特征

舰载机高强度出动回收作业是美国海军为执行多类型作战任务，通过长期作战训练不断摸索创造的，是航母最强作战能力的体现。其特点是航母甲板上的所有工作都按照“甲板作业周期”安排，甲板作业周期时间长度根据任务而定，有1+00（1 h），1+15（1 h 15 min），1+30（1 h 30 min），1+45（1 h 45 min）和2+00（2 h）等多种，每个甲板周期都放飞一批舰载机，之后回收上一批舰载机，甲板面同时还开展对舰载机的维护保养、补给加油等工作，环环相扣、紧密衔接，每天持续放飞和回收舰载机18-24 h，最高出动160架次以上^[9]。对于舰载机而言，又分为单周期、双周期和三周期，执行单周期任务的舰载机在第T周期起飞，第T+1周期着舰，之后在甲板面上进行机务勤务保障作业，完成后再次起飞；执行双周期任务的飞机在第T周期起飞，第T+2周期着舰，完成保障作业后再次起飞；执行三周期的飞机在第T周期起飞，第T+3周期着舰，完成保障后再次起飞，如图1所示。

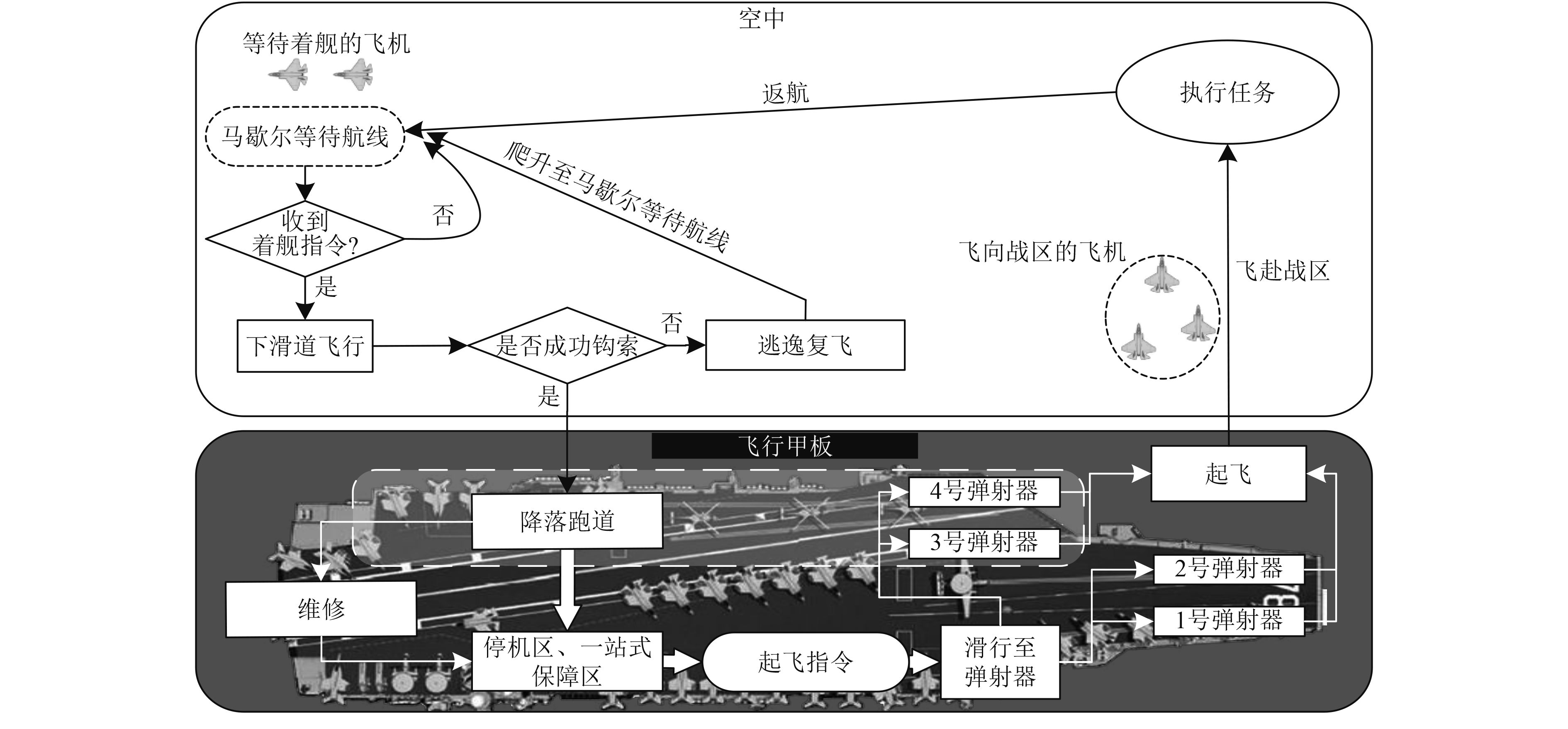
高强度出动回收作业具有分批出动、定时性、非稳态的特征，决定了舰载机在出动回收网络中不可能是泊松流，因而常规求解网络排队的卷积法、均值分析法均无法处理此类复杂排队问题，故本文基于蒙特卡罗法对舰载机高强度出动回收随机过程进行仿真建模。舰载机高强度出动回收作业可看做一个闭环排队网络，每项涉及舰载机的作业都可看作服务站^[7]，舰载机可看作顾客在网络中循环转移。这些作业按逻辑顺序包括：弹射起飞、飞行（含飞赴战区、执行任务、返航）、马歇尔等待航线、下滑道飞行、钩索、逃逸复飞、降落跑道、停机区/一站式保障站位、滑行至弹射器等9个服务站，其中舰载机在作业期间可能会损坏，因此每次降落后会进行故障诊断和维修作业（不进入一站式保障区），维修完成后方可进入一站式保障区进行机务作业。完成保障后的舰载机起动发动机，待下一个甲板作业周期开始时滑行至弹射器起飞，如图2所示。

1.2 仿真数据设定与初始化 1.2.1 航母及作业流程参数设定

以美国最先进的“福特”号航母为研究对象，该航母航空保障设施中最为突出的特点是在舰首中部和右舷的甲板上设置了18个一站式保障站位，舰载机无需重新调度即可完成所有机务勤务保障作业。另外，甲板上所有停机位均可得到加油服务和维修服务。该航母有4台电磁弹射器，一般高强度作业时会使用其中的2～3台。降落区装有3道阻拦索和1道阻拦网。弹射器和阻拦机的临时性检修与舰载机起降穿插进行，互不影响。每项作业的持续时间可通过美国海军统计数据^{[8 – 9]}或数学建模，具体如表1所示。

1.2.2 舰载机参数设定

选择高强度作业中典型的E-2C“鹰眼”预警机和F/A-18舰载战斗机^[10]。其仿真参数参考文献[8–9]中的部分数据，具体如表2所示。

2 舰载机调度策略的建立

航母飞行甲板是一个高度动态和随机的环境，飞机需要不断进行维修、维护、保养、加油，才能维持其长时间稳定可靠的飞行与作战。为确保这些种类复杂、流程繁多的作业顺利进行，航母上每天都会依据当前状态和作战目标，人工排定各项作业的计划进度总表。然而根据美国海军的实际情况，这种人工排定的作业计划进度总表难以完全精确执行，在高强度出动回收作业中更是如此，从而导致各项作业出现不同程度的延误和紊乱，降低了出动架次率。

为了应对这种不确定，往往会采用重新决策的方式，对舰载机的作业进行全盘重新规划。为了精确有效地实现舰载机的调度，需要结合当前舰载机和航母的状态，根据某种规则为航空保障设施选择合适的舰载机开展保障作业。

2.1 舰载机状态参数定义

麻省理工学院的Rajarshi等^[11]提出了基于线性回报函数的策略表达方法，通过计算每架舰载机在每个服务站点的回报函数值，来确定该服务站下一步执行什么任务，按该回报函数值递减排序，从而确定服务顺序。本文中，对于第 $i$ 架舰载机，作业选择最关键的特征值包括：飞机类型、剩余飞行时间、到达服务站点的顺序、舰载机完好性参数。

1）飞机类型参数

飞机类型参数为 $x_{i1}$ ，包括F/A-18型舰载战斗机（ $x_{i1}=1$ ）、E-2C舰载预警机（ $x_{i1}=2$ ）。

2）剩余飞行时间参数

剩余飞行时间参数为 $x_{i2}$ ，即飞机剩余燃油所能支持的飞行时间在所有等待降落舰载机中由小到大的排序，主要用于确定降落顺序，数值越小表示剩余飞行时间越少，因燃油耗尽而坠毁的风险就越大。

3）到达服务站点时间参数

到达服务站点时间顺序参数 $x_{i3}$ ，即到达同一个服务站开始排队的时间先后顺序，数值越小表示到达越早。

4）舰载机完好参数

舰载机完好参数 $x_{i4}$ ，即舰载机能否执行任务的标准， $x_{i4}=1$ 表示舰载机状态良好可以执行任务， $x_{i4} = 2$ 表示舰载机有轻微故障无法执行任务，但可以安全飞行， $x_{i4}= 3$ 表示舰载机有关键故障无法执行任务，可以飞行但需立即降落， $x_{i4}=4$ 表示舰载机有重大故障无法飞行，在飞行阶段发生则坠毁，在甲板上发生则需退出作业，短时间内无法修复。该数值越大表示飞机状态越差。

由此可将所有舰载机的主要状态用矩阵 ${{X}}=\left[ {x_{i1},x_{i2},}\right.$ $ \left.x_{i3}{x_{i4}} \right]\left| \right.{i = } 1,2, \cdots ,N$ 表示， $N$ 为舰载机总架数。

2.2 服务策略参数定义

定义参数 $w_{j1}$ , $w_{j2}$ , $w_{j3}$ , $w_{j4}$ 为第 $j$ 类服务站对应舰载机各特征值的权重，则类型 $j$ 服务站处的策略可以由特征权重向量 ${\bf {W}}=\left. {\left[ {{w_{j1}},{w_{j2}},{w_{j3}},{w_{j4}}} \right]} \right|j = 1,2,...,M$ 来定义， $M$ 为待决策服务站的类型数。

诸多航空保障作业实际上是按照先到先得策略执行的，例如飞行。另外弹射起飞的顺序由提前完成的作战计划所规定，亦无法改变。需要着重关注的是，马歇尔等待航线中的着舰顺序直接关系到舰载机着舰时的剩余油量，若剩余油量过少会造成坠机事故，因此一般会优先让剩余燃油量低的飞机先降落。一站式保障站位数量有限，其服务策略关系到特定舰载机能否准时起飞。飞机加油量会影响一站式保障作业时间，加过多或过少的油都不利于任务的执行。因此本文确定将舰载机的降落顺序、保障顺序、加油量作为策略控制对象，由此定义舰载机线性回报值函数为：

${f_{ij}}\left( {{x_{i1}},{x_{i2}},{x_{i3}},{x_{i4}}} \right) = \sum\limits_{k = 1}^4 {w_{jk} \cdot {x_{ik}}}\text{。} $

(1)

式中： $w_{jk}$ 为第 $j$ 类服务站对应的舰载机第 $k$ 个特征值的权重， ${x_{ik}}$ 为第 $i$ 架舰载机的第 $k$ 个特征值，那么任何一架舰载机在任何一个服务站的回报函数都可以由式（1）计算，写成矩阵形式为：

$ { F }= W \cdot X\text{。}$

(2)

选择在某一服务站回报函数值最大的舰载机开始该服务站的作业，通过这种形式将舰载机的调度规则转换为数学语言，即根据舰载机和整个航空保障作业系统的当前状态来确定下一步工作内容。通过修改策略 $W$ ，就能方便地为每架舰载机选择下一步行动，对于高度复杂、随机环境下的舰载机调度尤为方便。

2.3 调度策略的生成

为实现舰载机出动回收调度，特别是在一些需要基于当前状态做出合理决策的服务站，需要提前依据规则制定策略。舰载机在多数服务站遵循的是先到先得的服务策略，但是在部分服务站会遵循更为复杂的服务策略。下文重点针对降落顺序、保障顺序、加油量分别进行分析。

2.3.1 降落顺序策略

舰载机在降落前，会先抵达以航母为圆心5 nmile直径的圆形等待区，并分层飞行，称为马歇尔等待航线，在飞行过程中会接收降落指令，从而脱离航线进入进近航线，并最终着舰。在马歇尔等待航线，一般先返航的舰载机在马歇尔等待航线中的飞行高度更低，更早降落，然而以安全起见，低燃料水平的飞机优先降落。另外，预警机需要担负空中警戒任务，且由于体积庞大，往往最后降落。因此可确定降落策略机型分量取最大反向值，剩余飞行时间分量和到达顺序分量可取较小反向值，飞机完好性分量取最大正向值，经分析得降落作业策略为：

${w_1} = \left[ {\begin{array}{*{20}{c}} { - 5}&{ - 1}&{ - 1}&5 \end{array}} \right]\text{。}$

(3)

2.3.2 保障顺序策略

甲板上的保障资源有限，在高强度作战时很难确保每架飞机都能及时得到保障服务，因此为了维持作战效能，需要优先保障预警机，然后是战斗机。除此之外，按照先到达保障站先保障的策略进行。故可以确定保障策略机型分量应具有最大正向值，剩余飞行时间分量无作用取0，到达顺序分量取较小反向值，飞机完好性分量取最大反向值。经 分析得保障作业策略为：

${w_2} = \left[ {\begin{array}{*{20}{c}} 5&0&{ - 1}&{ - 5} \end{array}} \right]\text{。}$

(4)

2.3.3 加油量策略

为了维持执行任务所需的飞行时间，根据美国海军规定，着舰时飞机剩余燃油应确保能安全飞行至少20 min，据此可估算2种机型起飞前所需要的加油量，其中F/A-18实际加油量为最大加油量的75%，E-2C为90%，则实际加油量策略为

${w_3} = \left[ {\begin{array}{*{20}{c}} {0.75/{{0.9}^*}}&0&0&0 \end{array}} \right]\text{。}$

(5)

式中，*表示需要根据机型选择实际加油量，实际加油量与机型所对应的任务有关。

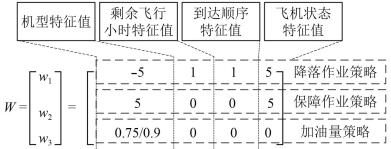
从上文分析可以得出，该排队网络中既有先到先得服务策略，也有优先服务策略，还有按时服务策略，对舰载机的调度并非单纯按照某一种特定“规则”来执行，而是多种规则融合的复杂策略，不同的服务站会根据舰载机的机型、剩余飞行小时、到达顺序、飞机状态等主要特征，选择哪架飞机最先得到服务，合理的策略可提升舰载机出动回收作业的安全性和效率。3种策略可以写成如下形式：

(6)

将策略 $W$ 和飞机特征 $X$ 代入式（2），可求得每架飞机在每个服务站的回报函数值，选择回报函数最大的舰载机开始服务，如式（7）所示，从而实现调度。

$ i = \arg \max \left[ {{f_{ij}}({X_i})} \right]\text{。} $

(7)

3 算例结果 3.1 仿真背景

为尽量贴合美国海军高强度演习，本仿真采用文献[8]中所述的基本状态（Base case）作为仿真背景。航母甲板周期为1+30，每天执行任务18 h，其中F/A-18战斗机执行单周期作业，E-2C执行三周期作业。以式（6）作为基本调度策略，开展仿真研究。

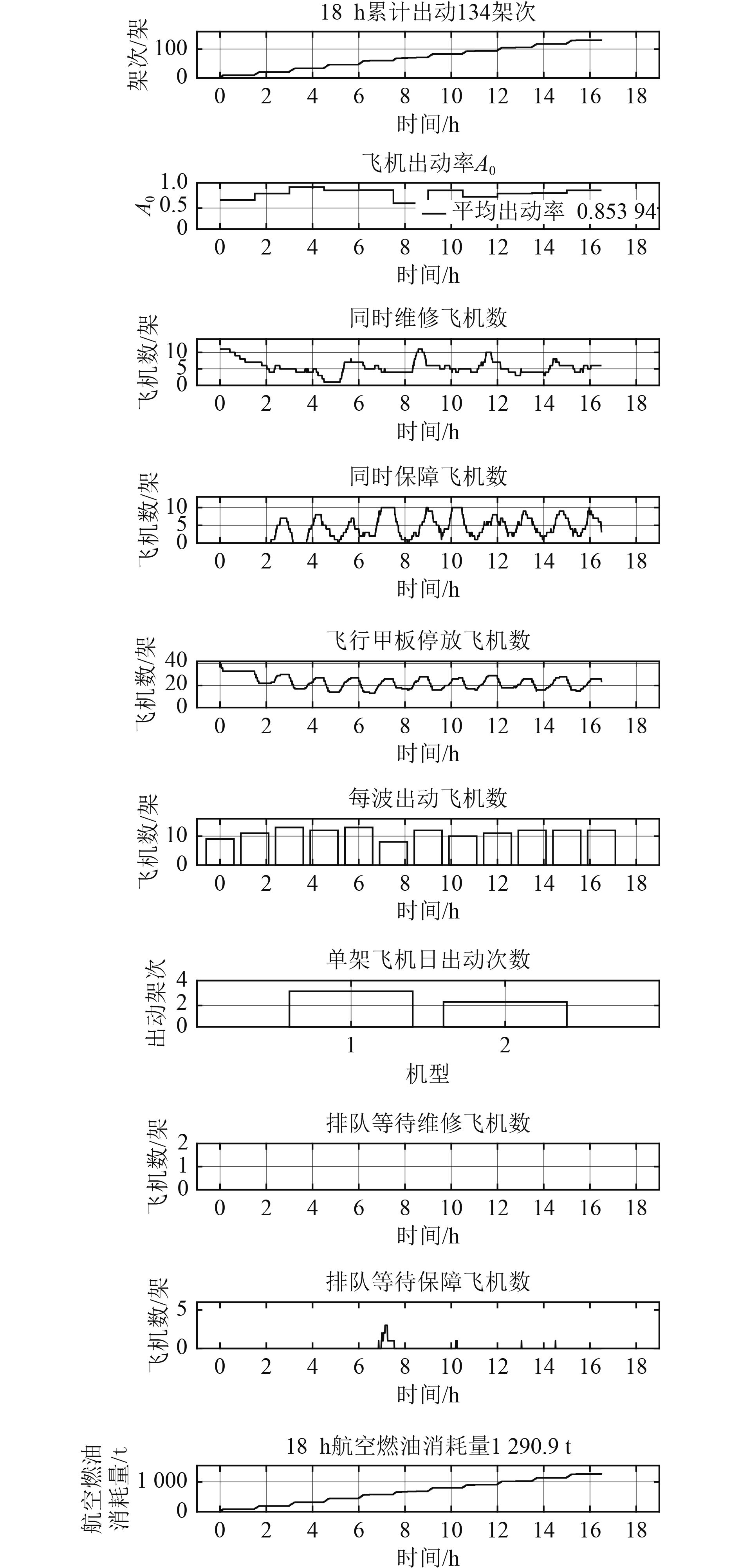
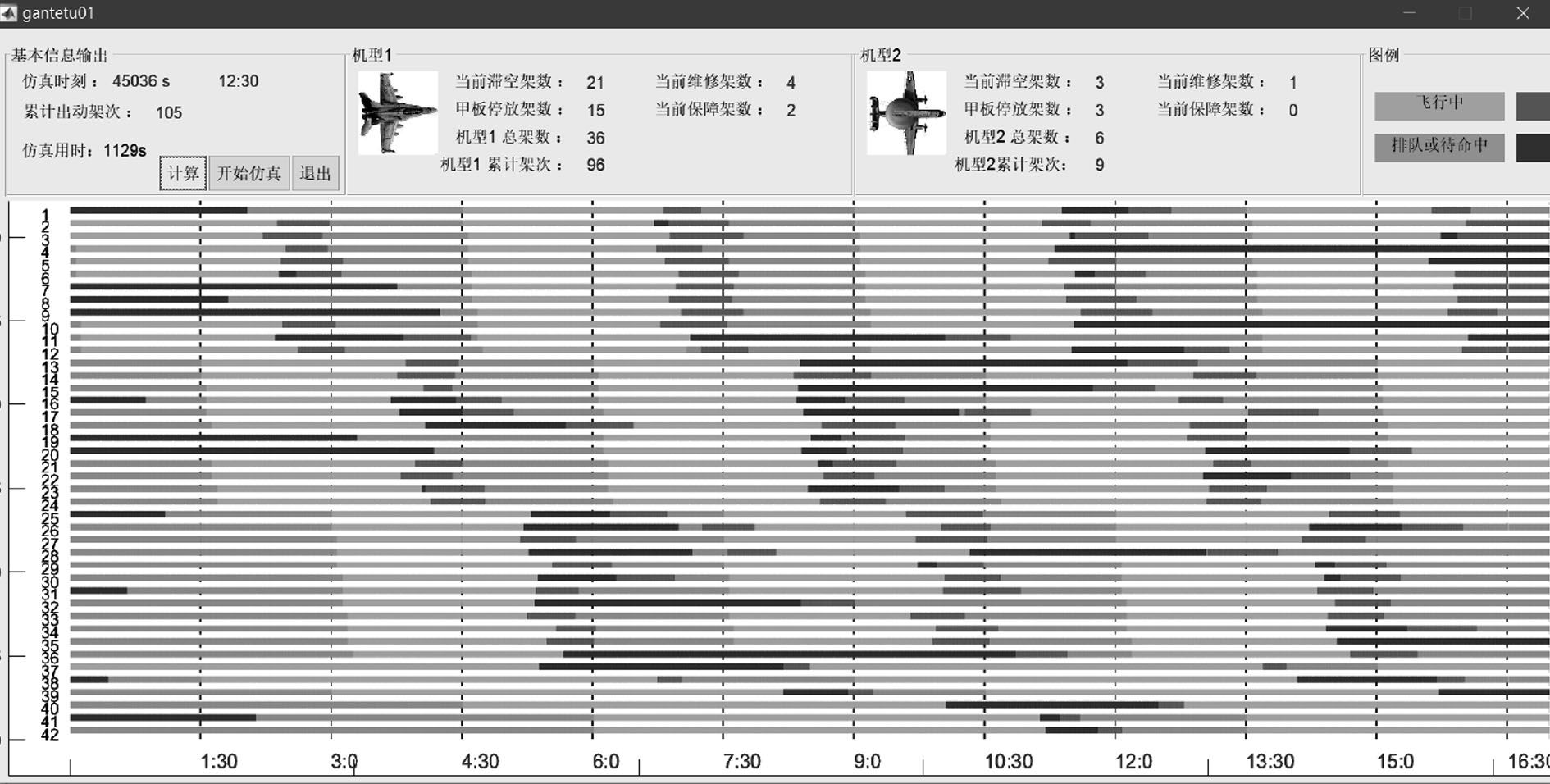
3.2 仿真程序实现

基于Matlab开发了蒙特卡罗仿真程序，用于流程仿真。该仿真模型可输出单日累计出动架次、飞机出动率，以及维修、保障相关数据，同时可统计全天因燃油不足而坠毁飞机数、返航时剩余飞行小时不足20 min飞机数、一站式保障站利用率等信息，如图3所示。为了更直观地了解舰载机的作业调度方案，程序可自动输出高强度作业流程甘特图，如图4所示。

3.3 仿真结果 3.3.1 仿真精度检验

考虑到目前“福特”级航母尚未开展过高强度演习，缺少相关数据用于验证本文的仿真程序。由于“福特”级是在“尼米兹”级的基础上改进而来，其一站式保障概念在“尼米兹”级航母上也部分实现，考虑到本文的仿真原型系统是以“尼米兹”级航母高强度演习为背景开发的，为对“福特”级航母高强度演习进行仿真，针对一站式保障环节做了局部流程调整，因此“福特”级航母在很大程度上与“尼米兹”级航母保持一致。为验证仿真程序的可靠性，选择美国海军1997年高强度演习记录数据作对比。

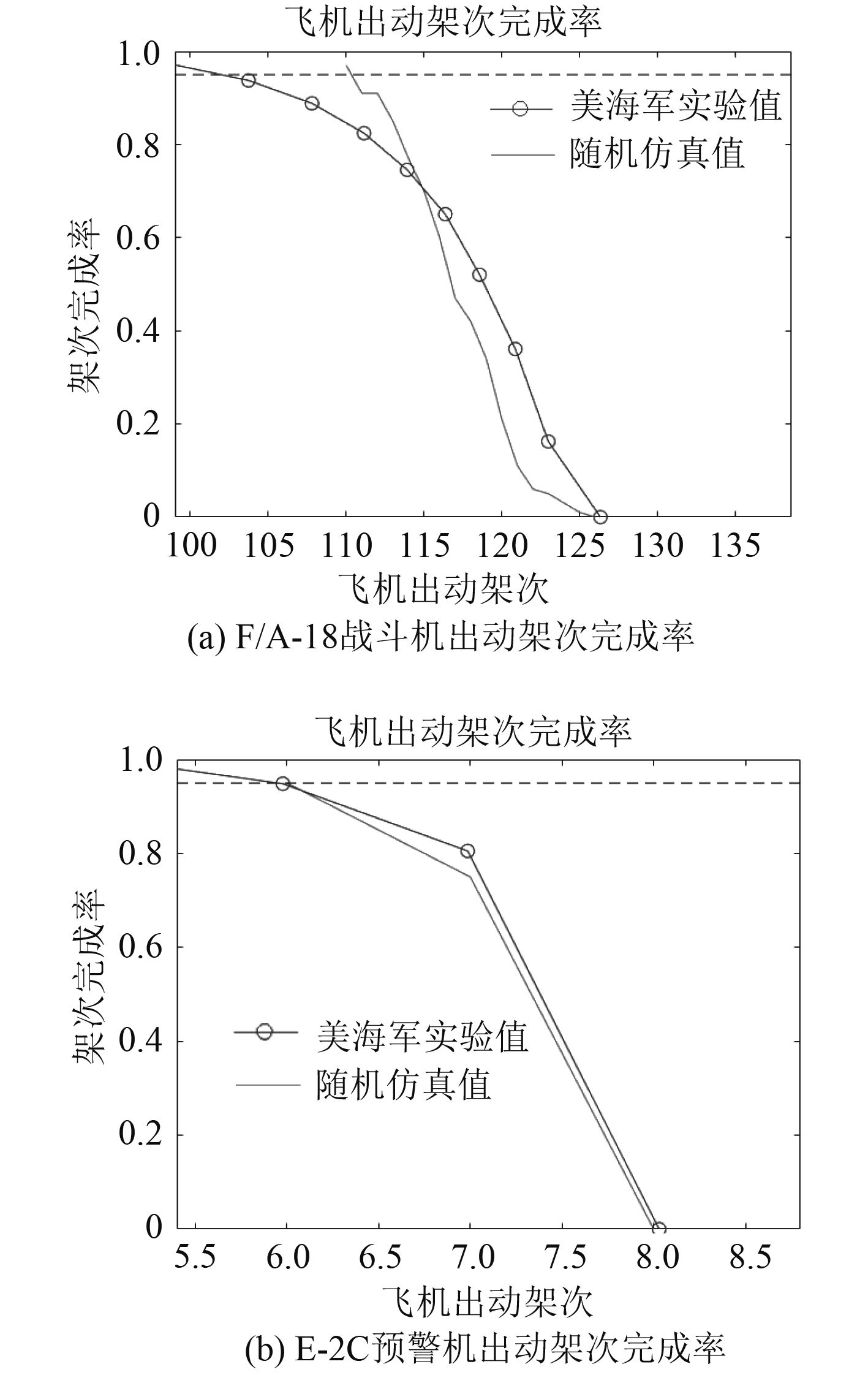
由于蒙特卡罗仿真存在大量随机性，选择出动架次完成率指标进行对比。出动架次完成率的对比不仅是单次仿真的结果比较，而是大量随机仿真结果分布对比，可以更好地说明仿真模型精度情况。通过1 000次随机仿真获取2种机型每天的出动架次，进行统计从而获取出动架次完成概率，如图5所示。横坐标为单日出动架次，纵坐标为出动某一架次舰载机作业所能完成的概率。图5（a）为F/A-18战斗机的出动架次完成率，可见仿真程序与美国海军高强度演习期间记录的F/A-18出动架次完成率较为接近，在95%概率完成架次方面，仿真程序比实际值多8架次左右，原因主要是其他因素导致的出动架次降低，例如天气、人为失误等。图5（b）为E-2C预警机的出动架次完成率，可见仿真程序与实际统计值非常接近，差别不到1架次。主要原因是预警机架数少且优先级高，多数服务会得到优先保障，随机事件带来的排队延误少。

采用基本策略时，平均每日发生舰载机坠毁事故0.011 2次，返航时剩余油量过低的事件平均发生4.174次。

3.3.2 策略调整对比

通过改变策略，可以对舰载机的调度方案进行调整。主要考虑2种策略，分别为追求出动架次率的情况1和追求作业安全性的情况2。

情况1：为追求更高的出动架次率，在着舰环节，采用先到先得的服务策略，即到达马歇尔航线就直接降落，无机型、剩余飞行小时的区别；在保障环节，采用高油量优先的服务策略，优先给油量水平高的飞机提供保障，减少排队时间，从而在相同的时间内保障完更多的飞机；同时合理减少实际加油量以节省保障时间，以提高保障效率。于是情况1策略修改如下：

$ {W_{\text{情况}1}} = \left[ \begin{gathered} {w_1} \\ {w_2} \\ {w_3} \\ \end{gathered} \right]=\left[ {\begin{array}{*{20}{c}} 0&{ 0}&{-1}&0 \\ 0&1&{0}&{ 0} \\ {0.65/0.65}&0&0&0 \end{array}} \right] $

(8)

情况2：为追求更安全的出动回收，对于着舰环节，采用低油量优先的服务策略，剩余飞行小时最小的飞机最先降落；实际加油量均为飞机最大载油量，以尽可能确保飞机燃油充足。于是情况2策略修改如下：

${W_{{\text{情况}2}}} = \left[ \begin{gathered} {w_1} \\ {w_2} \\ {w_3} \\ \end{gathered} \right]=\left[ {\begin{array}{*{20}{c}} 0&{ - 1}&0&0 \\ 5&0&{ - 1}&{ - 5} \\ {1/1}&0&0&0 \end{array}} \right]$

(9)

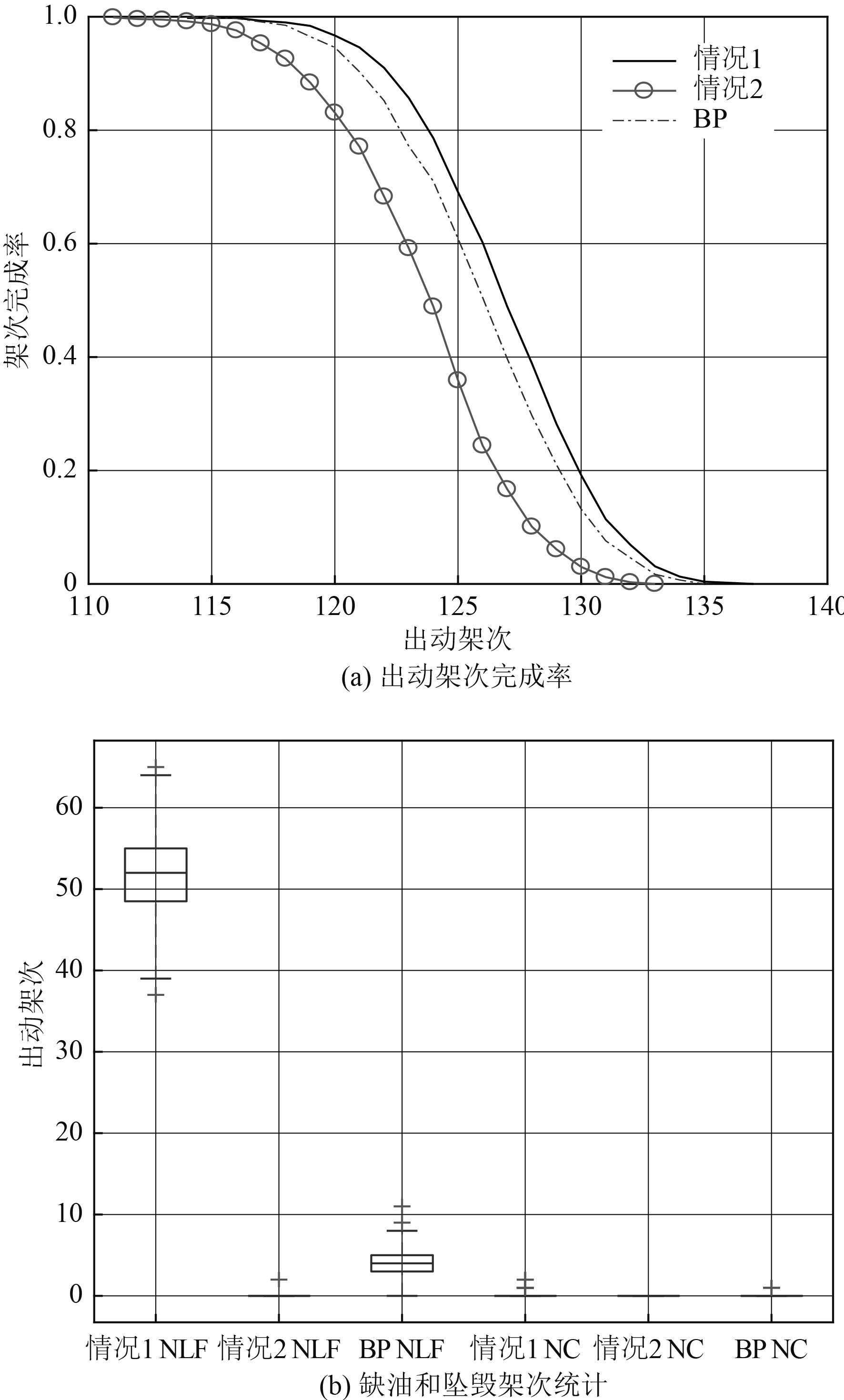
分别将式（8）和式（9）所对应的策略输入到仿真程序中进行1 000次重复推演，结果如图6所示。图6（a）为3种策略控制下2种机型总共出动架次完成率曲线；图6（b）为着舰时剩余飞行时间小于20 min架次、因燃油耗尽而坠毁飞机数统计箱形图。

从图6（a）可看出，基本策略 情况1由于减少了舰载机加油量，在一定程度上节约了保障作业时间，使更多的舰载机得以及时保障完毕，出动架次率相对基本策略（BP）增加约1架次，然而由图6（b）可见，情况1策略飞机降落时，剩余飞行时间小于20 min的情况更多，均值达到51架次，不利于安全作业。图6（a）中情况2由于每次都给舰载机加满油，因此会使部分舰载机在出动时尚未完成保障作业，从而错过起飞时机，出动架次率相对基本策略减少了约2架次。由图6（b）可看出，情况2策略控制下不存在剩余飞行时间少于20 min和因燃油耗尽而坠毁的架次。作为对比，基本策略控制下有约4架次降落时剩余飞行时间少于20 min，因此情况2相对安全性更好。可见策略的变化对出动架次率影响不大，对作业安全性影响大。

分析其原因主要是，舰载机的出动回收作业大部分时间是飞行，通过调整策略可以减少排队时间，但排队时间在整个出动回收流程中的比例较小，故影响有限；飞机加油量会影响剩余飞行时间，对飞行安全十分重要，通过减少实际加油量来节约保障时间，从而在规定时间内保障更多飞机的做法，对提高出动架次率提升十分有限，鉴于此建议舰载机在能满足任务需求的条件下尽可能多加油。

4 结　语

1）基于线性函数的调度策略可以用于舰载机高强度出动回收仿真，对舰载机调度控制有效；

2）与美国海军演习数据的对比显示，本文所述的高强度出动回收仿真程序在基本策略控制下精度良好；

3）控制策略的优化可有效提升作业安全性，对出动架次率的提升不大。