随着舰船技术的发展,舱门因在舰船不同的部位以及不同的应用需求,呈现出了多种舱门机构需求。而有些舱门机构布置空间较紧凑、需满足水密等较高的承载需求,平面连杆虽在目前舱门机构中应用较广泛,但需占用较大的空间尺寸,无法满足设计需求。本文提出将空间RSSR机构应用于舱门机构中,在相同的承载需求条件下,空间RSSR机构相对平面机构需要布置空间较小并能实现较复杂的运动功能需求[1],例如空间RSSR机构能实现非平行旋转轴之间的运动传递,可实现常见的机构不在同一平面内运动转换。
空间RSSR机构被广泛应用于工程机械、农业机械等多个行业。归纳空间机构的研究方法主要为图解法和解析法[1,2]。图解法主要是采用画法几何的方法对空间机构进行设计和分析,由于其采用的是平面作图的方法,无法实现针对运动规律较复杂的空间机构研究,当前主要采用解析法对空间机构进行研究。空间机构解析法主要有方向余弦矩阵法、矢量旋转法和类复向量法等[2 − 3]。
传统采用解析法对空间机构进行研究的计算量较大且复杂,使空间机构在较精密机构中的应用较少。基于当代计算机技术和理论研究方法的发展采用现代设计方法对空间机构进行研究具有重要意义。本文将应用于舰船舱门机构中的空间RSSR机构作为主要研究对象,采用现代设计方法对其结构参数进行设计和分析。
1 空间RSSR机构基本原理空间RSSR机构的具体组成如图1所示,主要由2个球面副和2个转动副组成,运动可由
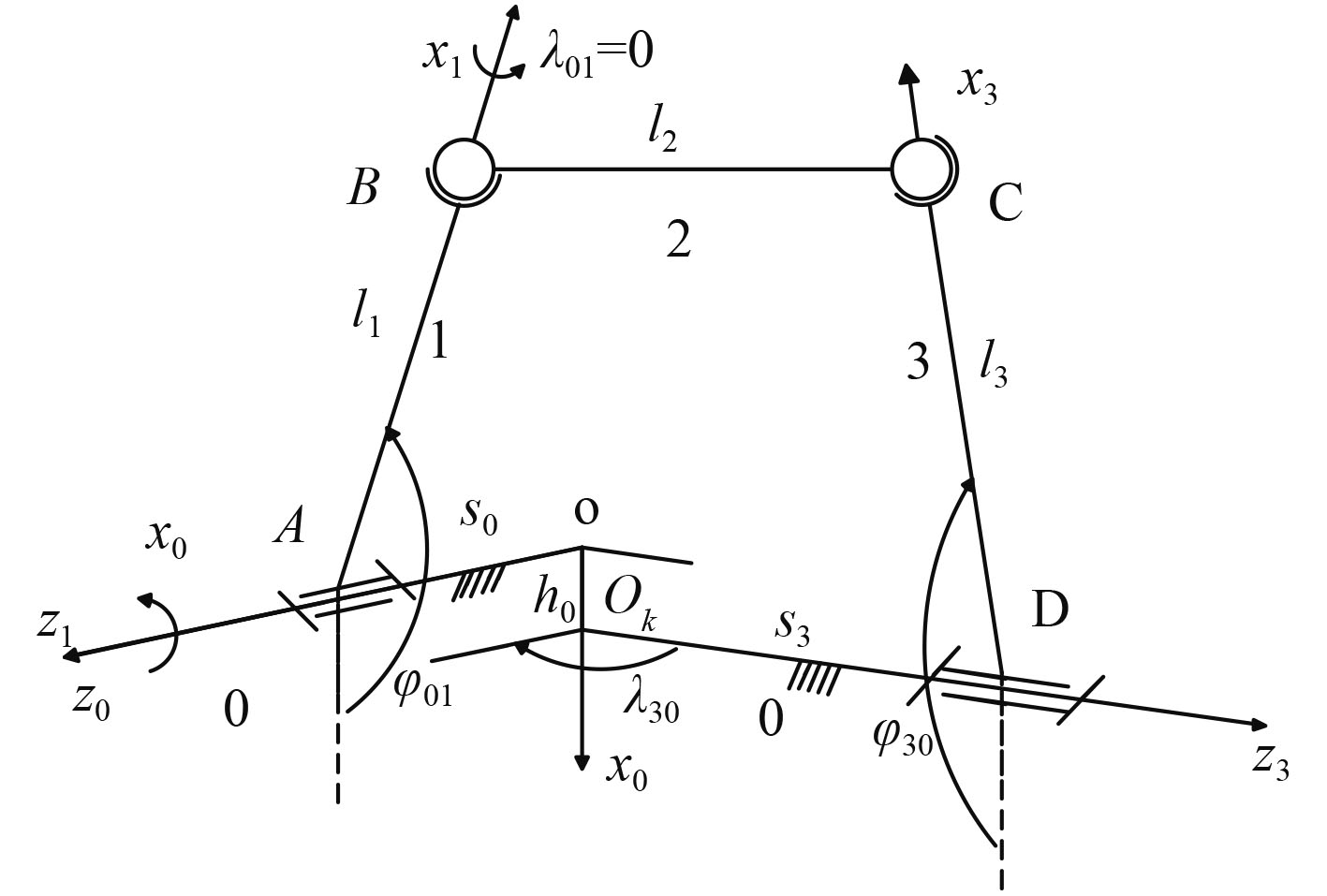
|
图 1 空间RSSR机构组成 Fig. 1 The composition of RSSR mechanism |
将图1中的RSSR机构在
| $ \begin{aligned} & {x_{\text{B}}} = {l_1}\cos {\varphi _{01}}, \\ & {y_{\text{B}}} = {l_1}\sin {\varphi _{01}}, \\ & {z_{\text{B}}} = {s_0}, \\ & {x_{\text{C}}} = {l_3}\cos {\varphi _{03}} + {h_0}, \\ & {y_{\text{C}}} = {l_3}\cos {\lambda _{30}}\sin {\varphi _{03}} + {s_3}\sin {\lambda _{30}}, \\ & {z_{\text{C}}} = - {l_3}\sin {\lambda _{30}}\sin {\varphi _{03}} + {s_3}\cos {\lambda _{30}} \text{。} \end{aligned} $ |
由B,C两点间的杆长
| $ \begin{split} & \left( {{s_0}\sin {\lambda _{30}}/{l_1} - \cos {\lambda _{30}}\sin {\varphi _{01}}} \right)\sin {\varphi _{03}} + \left( {{h_0}/{l_1} - \cos {\varphi _{01}}} \right) \!\!\!\!\!\!\!\!\!\\ & \quad \quad \quad \quad \cos {\varphi _{03}} + \frac{{l_1^2 + l_3^2 + s_0^2 + s_3^2 + h_0^2 - l_2^2}}{{2{l_1}{l_3}}} - \\ &\quad \frac{{{s_3}\sin {\lambda _{30}}\sin {\varphi _{01}} + {h_0}\cos {\varphi _{01}} + {s_0}{s_3}\cos {\lambda _{30}}}}{{{l_3}}} = 0 \text{。}\!\!\!\! \end{split} $ | (1) |
由式(1)可得,空间机构设计需确定参数主要为
空间机构设计时需确定的参数较多且需满足舰船舱门机构的研制需求,选取较为先进的设计算法进行设计。遗传算法(Genetic Algorithm)是1975年由美国密歇根大学的John Holland首先提出的一种模拟生物的自然进化过程的算法[4 – 6],其在解决大规模组合和全局寻优等复杂问题时具有传统方法不具备的优越性,并且鲁棒性强已广泛于优化设计、自动控制、经济预测等多个领域。
2.1 空间RSSR机构的优化设计过程以空间RSSR机构在某舰船舱门机构中的应用为例简述基于遗传优化算法的空间RSSR机构参数的设计过程。
1)设计变量的确定
在一般的设计过程中为计算方便常取
| $X = [{l_1},{l_2},{l_3},{s_0},{s_3}]\text{。}$ | (2) |
2)目标函数的确定
由于舰船舱门机构需承受的载荷较大,且杆件
| $ \begin{aligned} & {v_{{\text{B}}x}} = - \sin ({\varphi _{01}}), \\ & {v_{{\text{B}}y}} = \cos ({\varphi _{01}}), \\ & {v_{{\text{B}}z}} = 0, \\ & {v_{{\text{C}}x}} = - \sin ({\varphi _{03}}), \\ & {v_{{\text{C}}y}} = 0, \\ & {v_{Cz}} = \cos ({\varphi _{03}}) \text{。} \end{aligned} $ | (3) |
设杆件
| $\frac{{\overrightarrow {{F_{12}}} }}{{\left| {\overrightarrow {{F_{12}}} } \right|}} = \frac{{\left[ {{x_{\rm{C}}},{y_{\rm{C}}},{z_{\rm{C}}}} \right] - \left[ {{x_{\rm{B}}},{y_{\rm{B}}},{z_{\rm{B}}}} \right]}}{{{l_2}}}\text{。}$ | (4) |
可得B和C点处的压力角分别为:
| $ \begin{aligned} & {\alpha _1} = {\rm arc}\sin \left( {\left| {\frac{{\overrightarrow {{F_{12}}} }}{{\left| {\overrightarrow {{F_{12}}} } \right|}} \times \overrightarrow {{V_{\rm{B}}}} } \right|} \right) \times 180/{\rm{ {\text{π}}}}\;\text{,}\\ & {\alpha _2} = {\rm arc}\sin \left( {\left| {\frac{{\overrightarrow {{F_{23}}} }}{{\left| {\overrightarrow {{F_{23}}} } \right|}} \times \overrightarrow {{V_{\rm{C}}}} } \right|} \right) \times 180/{\rm{{\text{π}} }}\text{。} \end{aligned} $ |
设定舱门开启的角度为
对于多目标函数求取最优解问题,采用较为常见转化为单目标函数求解。
目前还没有较好的方法用于多目标函数优化问题的求解,一般处理的方法为将其转变为单目标函数的优化问题,即选取一能综合反映各目标函数情况的总体评价函数。处理的方法主要有几何平均法、乘除法、线性加权法、规格化加权法等。本文选取较为简单的线性加权法即
| $f\left( X \right) = \sum\limits_{j = 1}^t {{\omega _j}{f_j}\left( X \right) }(j = 1,2, \cdots t)\text{。}$ | (5) |
式中:
| ${\omega _j} = \frac{1}{{{f_j}({X^*})}} (j = 1,2, \cdots ,t)\text{,}$ | (6) |
可得式(5)也即是本文的目标函数为:
| $ \begin{split} & f = \sum\limits_{j = 1}^{30} {{\omega _j}\left( {\left| {\left| {\left( {{\rm arc}\sin \left( {\left| {\frac{{\overrightarrow {{F_{12}}} }}{{\left| {\overrightarrow {{F_{12}}} } \right|}} \times \overrightarrow {{V_{\rm{B}}}} } \right|} \right) \times 180/ {\text{π}} } \right)\left( j \right)} \right| - 30} \right|} \right. } + \\ & \left. {\left| {\left| {\left( {{\rm arc}\sin \left( {\left| {\frac{{\overrightarrow {{F_{23}}} }}{{\left| {\overrightarrow {{F_{23}}} } \right|}} \times \overrightarrow {{V_{\rm{C}}}} } \right|} \right) \times 180/{\text{π}}} \right)\left( j \right)} \right| - 30} \right|} \right) \text{,} \\ & (j = 1,2, \cdots 30)\text{。} \end{split} $ | (7) |
本文中计算得权系数
3)约束函数的定义
设空间RSSR机构中输入参数为
| ${\varphi _{03}} = 2a\tan \left( {(A + \sqrt {{A^2} + {B^2} - {C^2}} )/(B - C)} \right)\text{。}$ | (8) |
式中:
| $ A = {s_0}\sin {\lambda _{30}}/{l_1} - \cos {\lambda _{30}}\sin {\varphi _{01}}\text{,} $ |
| $ B = {h_0}/{l_1} - \cos {\varphi _{01}}\text{,} $ |
| $ \begin{gathered} C = \frac{{l_1^2 + l_3^2 + s_0^2 + s_3^2 + h_0^2 - l_2^2}}{{2{l_1}{l_3}}} - \\ \frac{{{s_3}\sin {\lambda _{30}}\sin {\varphi _{01}} + {h_0}\cos {\varphi _{01}} + {s_0}{s_3}\cos {\lambda _{30}}}}{{{l_3}}}\text{。} \end{gathered} $ |
要得到各参数解则要求
4)边界条件的定义
基于某舰船结构条件的限制等因素,设定空间RSSR机构中各参数的边界条件为:
| $ \begin{split} & {l_1} = \left[ {80,120} \right],{l_2} = \left[ {120,250} \right],{l_3} = \left[ {90,130} \right] \\ &{s_3} = \left[ {20,150} \right],{s_0} = \left[ {20,200} \right] \text{,} \end{split} $ | (9) |
利用Matlab软件工具箱,对空间机构相关参数进行求解。其中,搜索函数定义为[7]:
| $ \begin{split} &\left[ {{\rm{xf,endPop,beestSols,trace}}} \right] = \\ &\rm{ga}(\rm{bounds},'\rm{RSSR}\_1',\left[ {} \right],\rm{startPop},\left[ {} \right], \\ & '\max \rm{GenTerm}',300, \\ & '\rm{normGeomSelect}',\left[ {0.08} \right], \\ & \left[ {'\rm{arithXover}'} \right],\left[ {2} \right],'\rm{nonUniMutation}', \\ & \left[ {2\;300\;3} \right]) \end{split} $ | (10) |
式中:左侧表示输出结果;等式右侧的
编码和种群生成函数initializega函数的定义为:StartPop=initailizega(80,bounds,'RSSR_1',[])。编辑相应的计算程序,经过300代的繁殖计算得到该空间RSSR机构设计参数的最优解为:
在Matlab软件软件绘制求解最优目标值以及平均值的变化情况如图2所示。
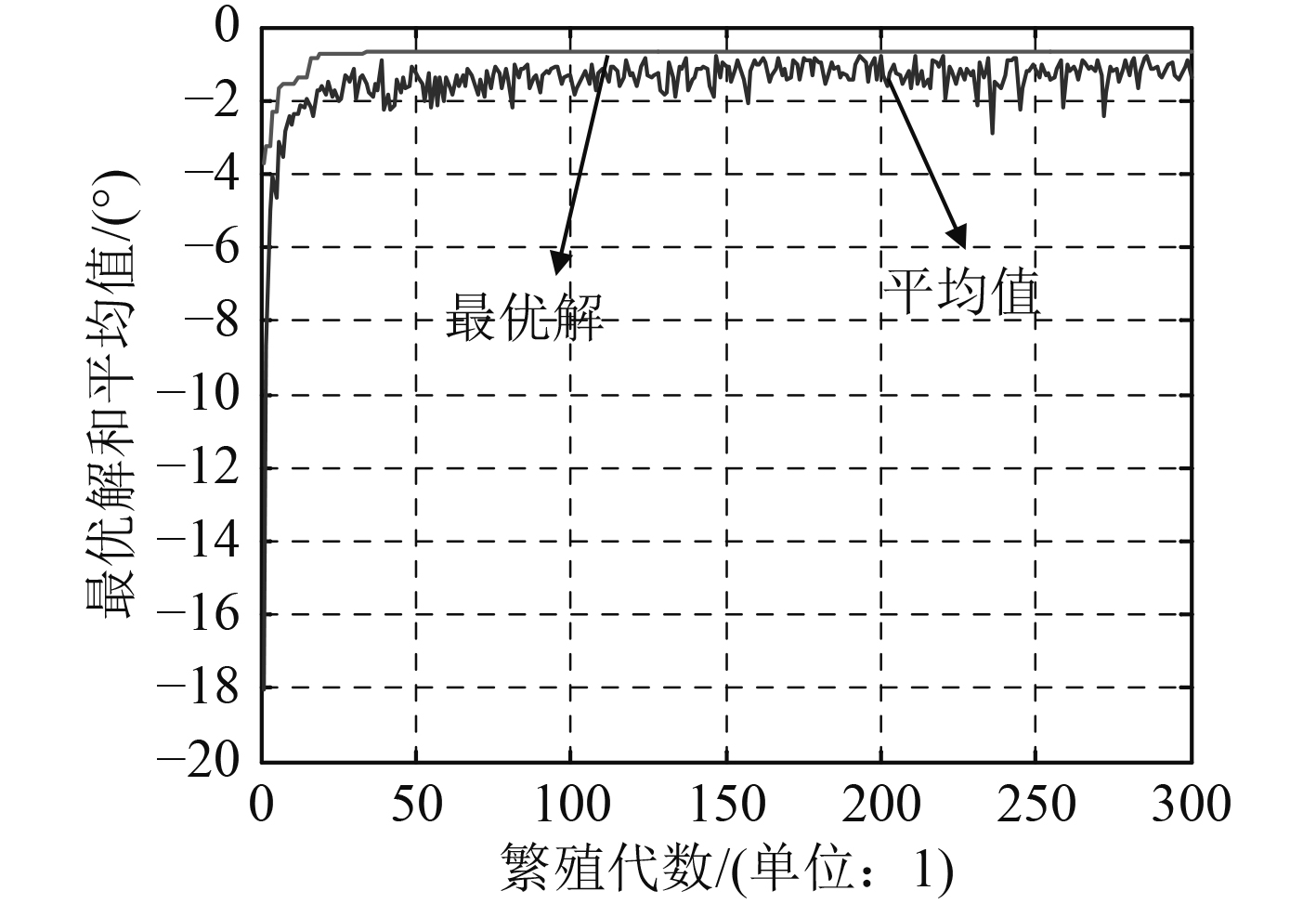
|
图 2 空间RSSR机构目标函数最优解和平均值的变化曲线 Fig. 2 Optimal solution and average value′s varying curve of RSSR mechanism |
依据采用遗传优化算法所得到的应用于某舰船舱门机构中的空间RSSR机构各参数的设计结果,对其正确性进行验证。将各参数的设计结果代入式(10)可得输出参数
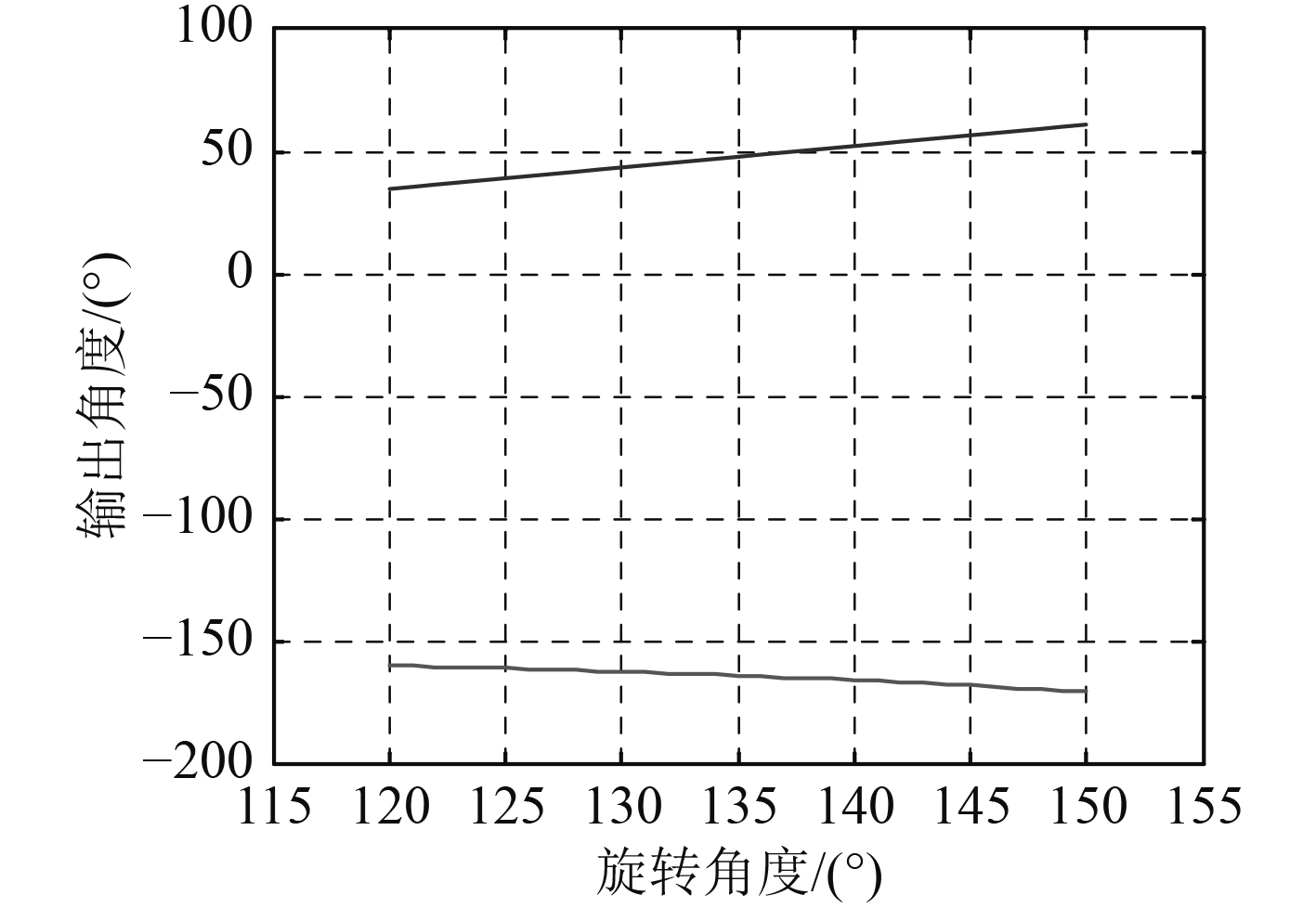
|
图 3
输出参数
|
由图3参考实际的应用情况最终选取
由空间RSSR机构的压力角计算公式,绘制出在工作过程中

|
图 4
|

|
图 5
|
由图4和图5可知在工作过程中压力角
本文提出了将基于遗传优化算法的空间RSSR机构设计应用于舰船舱门机构中的技术方法,并以某舰船舱门为例,通过遗传优化算法成功设计出了应用于该舱门的空间RSSR机构。对设计结果进行分析,设计出的空间RSSR机构具有较好的力传递特性,并且得出了应用该舱门的空间RSSR机构各连杆尺寸,较好满足设计需求。基于遗传优化算法的空间RSSR机构设计将在舰船舱门机构以及其他复杂运行机构需求得到更多应用。
| [1] |
黄锡恺, 郑文纬.机械原理[M]. 上海: 高等教育出版社, 1989: 557–573.
|
| [2] |
周勇, 孙海刚. 某型空间RSSR机构的图 解分析与设计[J]. 北京理工大学学报, 2011, 31(4): 394-397. |
| [3] |
张启先.空间机构的分析与综合[M]. 北京: 机械工业出版社, 1984: 286-361.
|
| [4] |
李权, 莫才颂. 遗传算法在斜齿圆柱齿轮 传动优化设计中的应用[J]. 茂名学院学报, 2004, 14(4): 49-51. DOI:10.3969/j.issn.2095-2562.2004.04.012 |
| [5] |
周明, 孙树栋.遗传算法原理及应用[M]. 北京: 国防工业出版社, 1999: 18-64.
|
| [6] |
王小平, 曹立明. 遗传算法—理论、应用与 软件实现[M]. 西安: 西安交通大学出版社, 2000: 1–16.
|
| [7] |
于玲, 贾春强. Matlab遗传算法工具箱函 数及应用实例[J]. 机械工程师, 2004(11): 27-28. DOI:10.3969/j.issn.1002-2333.2004.11.011 |
 2019, Vol. 41
2019, Vol. 41
