地磁场是地球内部存在的天然磁性现象,在近地空间内,任一位置均存在着地磁场,且大小和方向不同,为地磁匹配定位提供了天然的坐标系,已成为国内外很多学者研究的热点[1 – 2]。地磁匹配定位系统主要由地磁测量模块、匹配运算模块和位置输出模块3部分构成。在地磁测量模块中,由安装在航行载体上的地磁传感器实时测量地磁场数据,经载体运动一段时间后,测量得到一系列地磁特征值序列,对测量的原始数据进行误差补偿处理后,构成实时数据序列图,输送至计算机匹配运算模块;在匹配运算模块中,将实时测量的地磁数据序列与预先存贮在计算机内的区域地磁数据库进行查询匹配,确定载体的具体位置;位置输出模块将载体位置输出给人机界面。地磁匹配定位既可以单独组成导航定位系统,也可以与惯性导航、重力导航等构成组合导航系统,弥补单一导航定位技术的不足及误差,具有自主性强、误差不随时间积累、全天候工作的特点。
地磁匹配定位技术研究的热点主要集中在匹配算法方面[3],关于高精度地磁测量的研究,还缺乏有价值的研究成果。地磁测量属于弱磁测量,由于导航载体均由钢铁构件组成,其本身磁场对安装在载体上的地磁传感器造成的误差较大,必须进行误差补偿处理。本文在分析地磁测量误差补偿模型的基础上,针对载体上多种钢铁构件组成的干扰磁场,提出了采用十二常系数补偿算法消除测量误差,并利用实验数据,对误差补偿效果进行对比分析,提出解决措施,有效提高了地磁测量精度。
1 误差补偿算法地磁测量误差补偿技术主要包括地磁场方位参数的误差补偿和地磁场三分量及总场的误差补偿。
地磁场方位参数主要用于航向导航。磁方位确定实际上就是以地磁场为坐标系,确定载体运动方向,即测量载体运动方向与磁北间的夹角。由于载体磁场的影响,磁场传感器所测的磁方位与真实磁方位存在一定的误差,即罗差。罗差修正问题也就是消除载体磁场对地磁测量影响的问题。为了消除载体对地磁测量精度的影响,主要采取两项措施,一是适当安装传感器使传感器远离载体[4],如测量船测量地磁时,传感器采用拖曳方式,传感器与船体间的距离不小于船长的3倍,该方法虽然能有效地防止船磁效应对地磁测量的影响,但由于海浪的作用往往使被拖曳的磁传感器漂浮不定,难以确定传感器的位置。二是进行误差校正,在测量前后需要进行误差校正试验,最后根据校正试验的结果对测量数据进行校正。罗差修正方法主要有两种,测力法和测自差法[5]。测自差法就是通过实验得出罗差与磁方位的函数关系,在实际修正中,根据磁方位计算罗差。这种方法不需要对地磁测量数据进行校正,直接采用磁方位校正罗差。测力法首先对磁场传感器测量的地磁分量进行校正,再利用校正后的地磁分量计算磁方位。地磁匹配定位技术是需要确定导航载体在空间的具体位置,因此,上述误差修正技术不适合地磁匹配定位。
地磁场三分量及总场用于导航定位。地磁场参数值可以为地磁匹配定位算法提供位置参照坐标系,实现导航定位的目的。
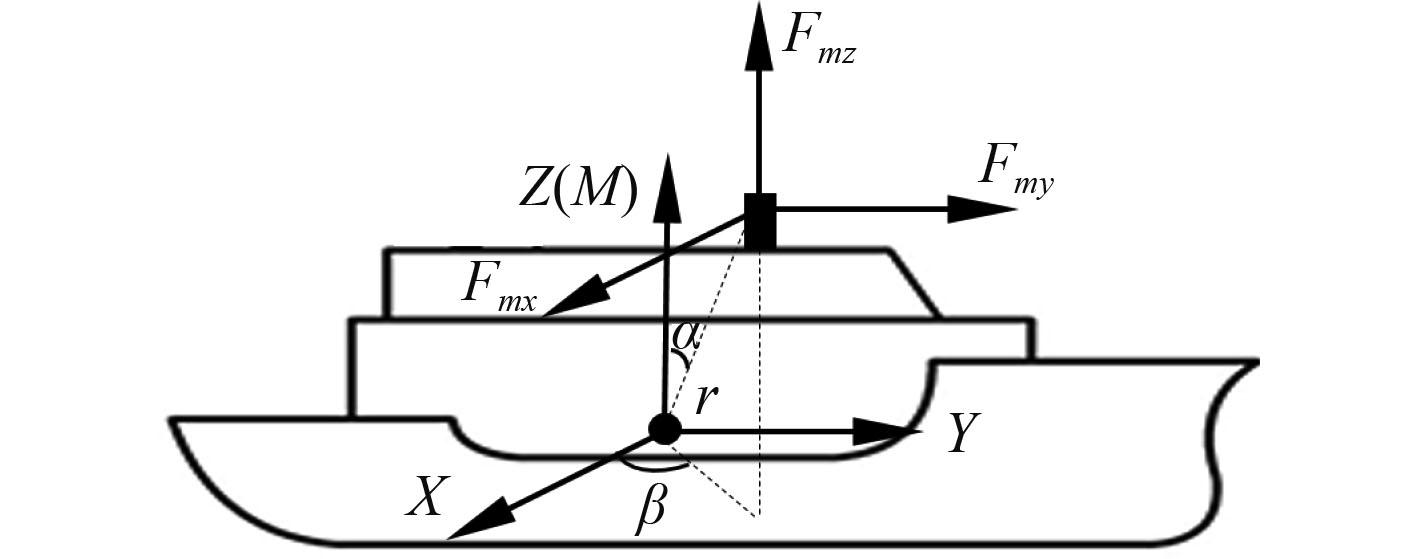
安装在导航载体上的磁传感器,测量值除了地磁场之外,还包含了导航载体感应磁场和固有磁场对地磁测量的误差干扰。如图1所示,地磁测量三分量为:
|
图 1 地磁测量示意图 Fig. 1 Geomagnetic measurement diagram |
| $ {F_{mx}} \!=\! {F_x} \!+\! {F_{ix}} \!+\! {F_{cx}};{F_{my}} \!=\! {F_y} \!+\! {F_{iy}} \!+\! {F_{cy}};{F_{mz}} \!=\!\! {F_z} \!+\! {F_{iz}} \!+\! {F_{cz}}\text{。} $ |
式中:
假设将导航载体产生的干扰磁场等效为一个磁偶极矩M,根据文献[6],磁矩M在传感器所在位置产生的感应磁场三分量为:
| $ {F_{ix}} = (3\mu M/8 {\text{π}} {r^3})\sin 2\alpha \cos \beta \text{,} $ | (1) |
| $ {F_{iv}} = (3\mu M/8 {\text{π}} {r^3})\sin 2\alpha \sin \beta \text{,} $ | (2) |
| $ {F_{iz}} = (\mu M/2 {\text{π}} {r^3})(1 - 1.5{\sin ^2}\alpha )\text。$ | (3) |
基于式(1) ~ 式(3)结论,以及文献[7]中的磁场叠加原理可得:
| $ \begin{split} &\left[ {\begin{array}{*{20}{l}} {{F_{mx}} - {F_{cx}}}\\ {{F_{my}} - {F_{cy}}}\\ {{F_{mz}} - {F_{cz}}} \end{array}} \right] =\\ &\scriptsize\left[ {\begin{array}{*{20}{c}} {\frac{{\mu {\lambda _x}}}{{2 {\text{π}} {r^3}}}(1 - \frac{3}{2}{{\sin }^2}{\alpha _x}) + 1}&{ - \frac{{3\mu {\lambda _y}}}{{8 {\text{π}} {r^3}}}\sin 2{\alpha _y}\sin {\beta _y}}&{\frac{{3\mu {\lambda _z}}}{{8 {\text{π}} {r^3}}}\sin 2{\alpha _z}\cos {\beta _z}}\\ {\frac{{3\mu {\lambda _x}}}{{8 {\text{π}} {r^3}}}\sin 2{\alpha _x}\sin {\beta _x}}&{\frac{{\mu {\lambda _y}}}{{2 {\text{π}} {r^3}}}(1 - \frac{3}{2}{{\sin }^2}{\alpha _y}) + 1}&{\frac{{3\mu {\lambda _z}}}{{8 {\text{π}} {r^3}}}\sin 2{\alpha _z}\sin {\beta _z}}\\ { - \frac{{3\mu {\lambda _x}}}{{8 {\text{π}} {r^3}}}2\sin {\alpha _x}\cos {\beta _x}}&{ - \frac{{3\mu {\lambda _y}}}{{8 {\text{π}} {r^3}}}\sin 2{\alpha _y}\cos {\beta _y}}&{\frac{{\mu {\lambda _z}}}{{2 {\text{π}} {r^3}}}(1 - \frac{3}{2}{{\sin }^2}{\alpha _z}) + 1} \end{array}} \right] \times \!\!\!\!\! \\ & \left[ {\begin{array}{*{20}{l}} {{F_{x'''}}}\\ {{F_{y'''}}}\\ {{F_{z'''}}} \end{array}} \right]\text{。} \end{split} $ | (4) |
式中:
| $ \left[ \begin{array}{l} {F_{mx}} - {F_{cx}}\\ {F_{my}} - {F_{cy}}\\ {F_{mz}} - {F_{cz}} \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {{k_{11}}}&{{k_{12}}}&{{k_{13}}}\\ {{k_{21}}}&{{k_{22}}}&{{k_{23}}}\\ {{k_{31}}}&{{k_{32}}}&{{k_{33}}} \end{array}} \right]\left[ \begin{array}{l} {F_{x'''}}\\ {F_{y'''}}\\ {F_{z'''}} \end{array} \right]\text{。} $ | (5) |
系数矩阵中的9个常系数k11,k12,k13,k21,k22,k23,k31,k32,k33在短时间内不会随着载体的姿态和位置而发生变化。式(5)中有3个独立方程,每个方程有4个常系数,相当于4元方程,因此,至少使载体处于4种方位姿态,并测量各姿态下地磁场三分量,加上载体所在位置地磁背景场和实时
在实验室内,用无磁三轴转台模拟导航载体姿态,采用多种尺寸规格的铁块模拟导航载体磁干扰源,铁块尺寸分别为100×50×30 mm,200×50×20 mm,500×300×1 mm,500×400×1 mm,500×500×1 mm,中心点距离磁力仪的尺寸分别为150 mm,162 mm,175 mm,321 mm,416 mm,磁力仪为FVM400三轴磁通门磁力仪,分辨率为1 nT,如图2所示。

|
图 2 地磁测量误差补偿平台 Fig. 2 Magnetic measurement error compensation platform |
首先,调整无磁转台三轴方位归0,记录下转台不安装铁块时10种不同姿态的地磁场三分量作为地磁背景场。然后,在转台工作面的不同位置安装上钢铁构件作为地磁测量干扰源,调整三轴转台处于上述10种对应的姿态,分别记录下载体在各姿态下磁力仪的三轴分量,实验数据如表1所示,角度单位为度,磁场三分量单位为nT。
|
|
表 1 误差补偿参数数据 Tab.1 Error compensation parameter data |
将实验数据代入式(5)求得12个补偿系数,然后使转台处于表2所示的10种姿态下,按上述实验步骤分别测量安装铁块和未安装铁块时各种姿态下的磁场三分量,并计算10种姿态补偿后的磁场三分量,最后统计10种姿态下磁场总场的实验数据如表2所示,10种姿态补偿后的总场与实际总场的误差均方差为88 nT。实验证明,该模型取得了较好的补偿效果。
|
|
表 2 磁场测量误差分析 Tab.2 Analysis of magnetic measurement error |
通过实验,对比分析导航载体强、弱干扰磁场对地磁测量误差补偿精度的影响。按照上述实验方法,减少工作台上钢铁构件的数量,只保留铁块100×50×30 mm,中心点距离磁力仪的尺寸为150 mm,重新求解12个补偿参数,并对表3中5种姿态下的干扰数据进行误差补偿处理,地磁测量误差补偿前后数据如表3所示。
|
|
表 3 小干扰源误差补偿数据 Tab.3 Small interference source error compensation data |
通过对比表2和表3中校正后的误差可以看出,当导航载体的干扰磁场增大时,校正后误差有所增加,但按误差补偿率来统计:
| $ {f_1} = (\Delta {F_a}/\Delta {F_f}) \times 100\%\text{。} $ | (6) |
表2中误差补偿率的均方差为1.5%,表3中误差补偿率的均方差为2.1%,因此,增大磁干扰时,误差补偿率要优于较小磁干扰时的误差补偿率。
如果按地磁测量误差补偿精度来统计:
| $ {f_2} = (\Delta {F_a}/F)\times100\% {f_1} = (\Delta {F_a}/\Delta {F_f})\times100\%\text{,} $ | (7) |
表2中的误差补偿精度均方差为0.19%,表3中的误差补偿精度均方差为0.01%,两者补偿精度都比较高,较小磁干扰时的误差补偿精度要优于较大磁干扰时的补偿精度。因此,在导航载体上安装磁传感器时,应尽量远离磁性较强的钢铁构件。
4 结 语12常系数法地磁测量误差补偿算法对于导航载体强、弱磁场的干扰均有较高的补偿精度。载体干扰磁场较强时,要优于载体磁场较弱时的地磁测量误差补偿率,在实际应用中,传感器尽量安装在距离钢铁构件较远的位置。
| [1] |
SONG Z G, ZHANG J S, ZHU W Q, et al. The vector matching method in geomagnetic aiding navigation[J]. Sensors, 2016, 16(7): 1120. DOI:10.3390/s16071120 |
| [2] |
NYATEGA C O, LI S X. Study on geomagnetic-matching technology based on ICP algorithm[J]. International Journal of Science & Research, 2015, 4(4): 3258-3261. |
| [3] |
肖晶, 段修生, 齐晓慧. 一种基于概率数据关联的地磁匹配ICCP算法[J]. 中国惯性技术学报, 2018, 26(2): 202-208. XIAO Jing, DUAN Xiu-sheng, QI Xiao-hui. Iterated closest contour point algorithm for geomagnetic matchingbased on probability data association[J]. Journal of Chinese Inertial Technology, 2018, 26(2): 202-208. |
| [4] |
宗发保, 邓瑞辉, 任来平. 一种阵列式海洋磁力测量系统[J]. 海洋测绘, 2015, 35(1): 45-47. ZONG Fa-bao, DENG Rui-hui, REN Lai-ping. A marine magnetometer array system[J]. Hydrographic Surveying And Charting, 2015, 35(1): 45-47. DOI:10.3969/j.issn.1671-3044.2015.01.012 |
| [5] |
马海瑞, 龙飞, 王亦平. 磁罗经自差校正准确性评估软件设计[J]. 计算机测量与控制, 2018, 26(2): 276-279. MA Hai-rui, LONG Fei, WANG Yi-ping. Design of accuracy estimation software for magnetic compass deviation adjustments[J]. Computer Measurement & Control, 2018, 26(2): 276-279. |
| [6] |
任来平, 张启国, 马刚. 水下铁磁体的海面磁场计算模型研究[J]. 海洋测绘, 2004, 24(6): 16-19. REN Lai-ping, ZHANG Qi-guo, MA Gang. Research for calculating magnetic model of underwater ferromagnet field on sea surface[J]. Hydrographic Surveying And Charting, 2004, 24(6): 16-19. DOI:10.3969/j.issn.1671-3044.2004.06.005 |
| [7] |
杨云涛, 石志勇, 关贞珍. 一种基于磁偶极子磁场分布理论的磁场干扰补偿方法[J]. 兵工学报, 2008, 29(12): 1485-1491. YANG Yun-tao, SHI Zhi-yong, GUAN Zhen-zhen. A magnetic disturbance compensation method based on magnetic dipole magnetic field distributing theory[J]. Acta Armamentarii, 2008, 29(12): 1485-1491. DOI:10.3321/j.issn:1000-1093.2008.12.015 |
 2019, Vol. 41
2019, Vol. 41
