2. 中国舰船研究设计中心,湖北 武汉 430064
2. China Ship Development and Design Center, Wuhan 430064, China
在流体力学和声学的探索过程中,钝体绕流问题一直是重要的研究课题之一。钝体指外形为非流线形,当流体流经其表面时会发生流动分离现象的这样一类物体。圆柱及圆柱群绕流现象作为钝体绕流中的经典问题,在自然界中广泛存在,并被大量运用于海洋结构、船舶工程、航空航天、土木、机械等多种工程领域中。当流体流经圆柱类结构物时,在一定流动工况下,会在结构物的后方呈现旋涡脱落的现象。这些旋涡周期性地交替出现,导致结构物在垂直于来流方向上受到周期性变化的作用力,致使结构物产生振动,圆柱后会产生大范围的流动分离和涡脱落的现象,压差导致阻力的增加,同时产生噪声[2]。水下航行器的天线和升降平台等凸出附体在运动均是典型的圆柱绕流水动力噪声问题,这些结构物在水中运动时产生水动力噪声,一方面降低了水下航行器自身的隐蔽性,另一方面降低了航行器内部声学仪器的探测精度,同时影响海洋环境。因此,如何有效地预报和降低圆柱绕流产生的水动力噪声,对推进水下航行器的安静化进程有着重要的意义,已经成为水下航行器研究范畴的重要方向之一。然而,由于雷诺数较高、流态复杂等特点,导致水下圆柱绕流噪声计算困难,随着数值模拟和试验技术的不断进步,CFD技术也得到了很大的进步,激励着众多学者对复杂的圆柱绕流及其噪声问题进行深入探索[3 – 7]。
本文以三维刚性圆柱为研究对象,开展了基于大涡模拟和Lighthill声类比理论的混合数值模拟方法研究,探讨了声场模型参数对计算结果的影响,评估了水下结构水动力噪声的计算精度,为水下航行器的流噪声精准预报提供技术手段。并采用该混合数值模拟方法计算并分析了雷诺数、间距比以及排列方式对水下单圆柱及双圆柱绕流噪声特性的影响,为工程应用提供参考依据。
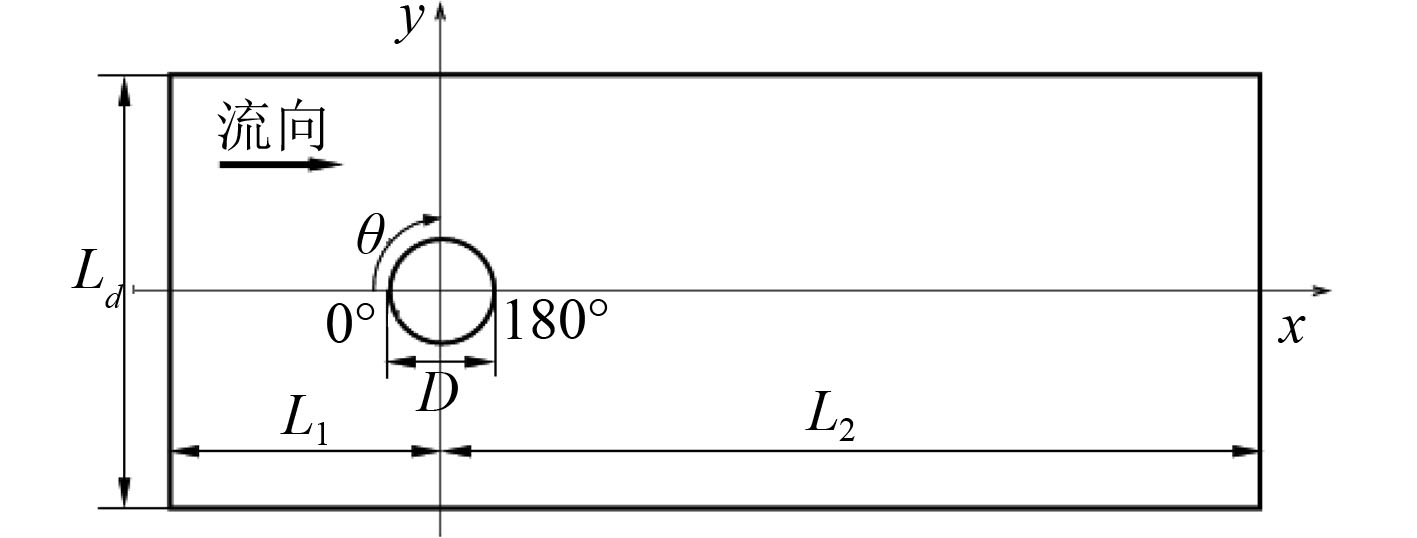
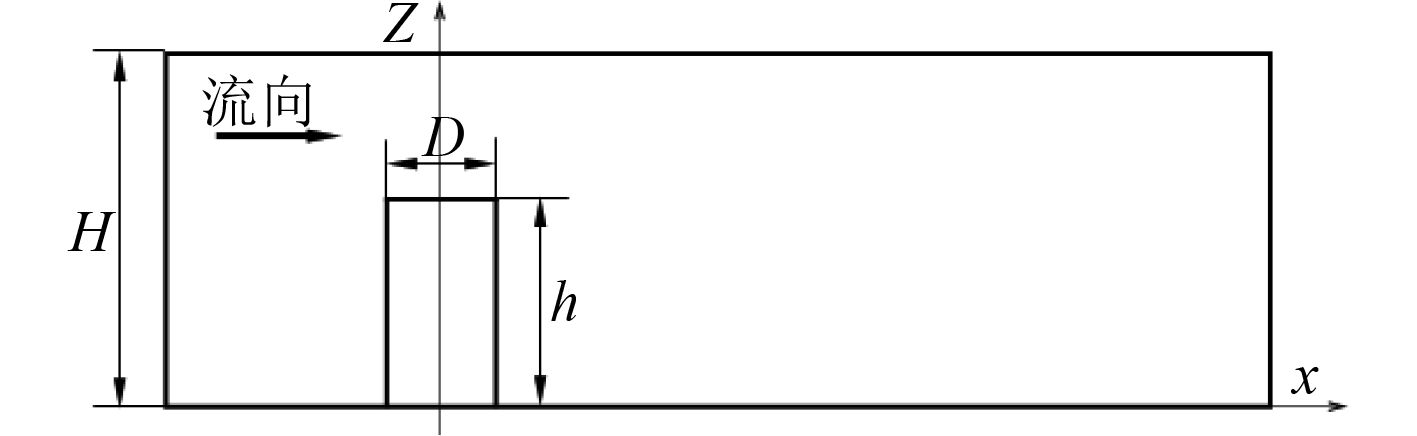
1 圆柱绕流计算模型采用的水下圆柱绕流模型如图1和图2所示,圆柱直径D=80 mm,圆柱高度h=2.5,D=200 mm,来流域长度L1=1.6h,去流域长度L2=6h,宽Ld=2.8h,高H=1.5h。模型坐标系以圆柱圆心在底板的位置为坐标原点,以来流方向为X正方向,径向为Y方向,展向为Z方向,以圆柱的上游驻点为起点,逆时针角度θ为正值。
|
图 1 圆柱绕流几何模型俯视图 Fig. 1 Model of fluid field |
|
图 2 圆柱绕流几何模型主视图 Fig. 2 Model of fluid field |
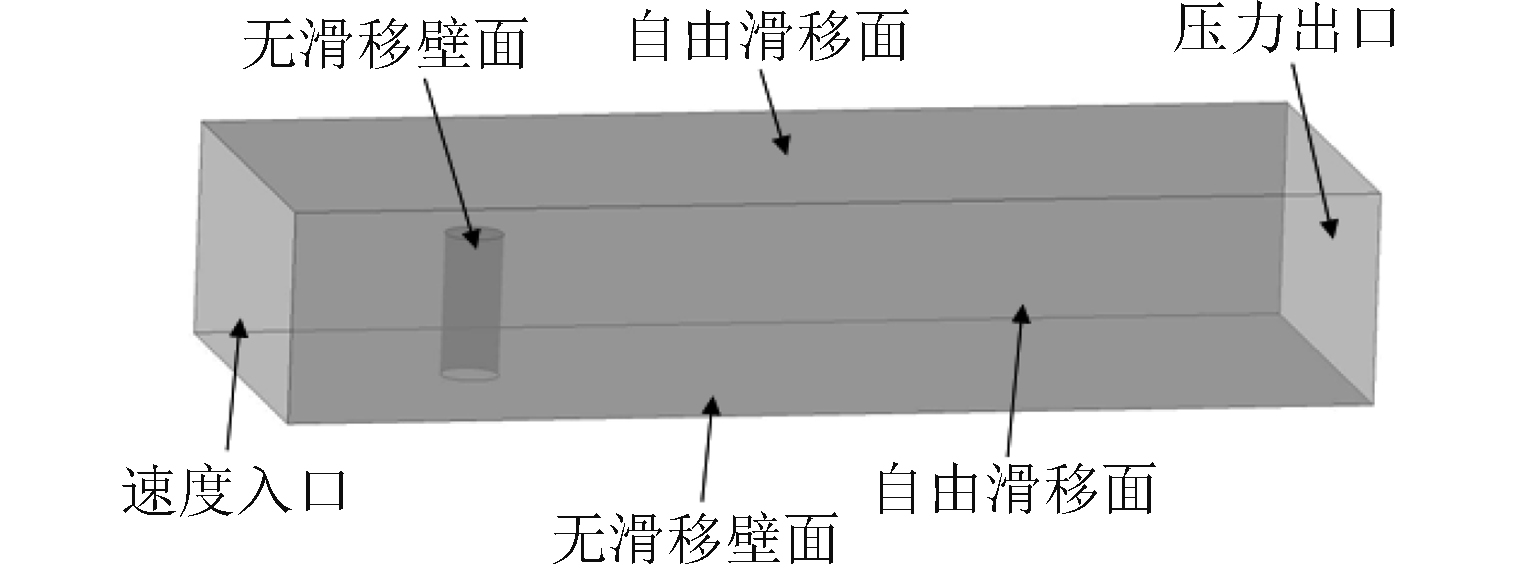
本文以流场速度为已知条件来计算圆柱绕流的流场特性,因此在流场边界条件设置中,流场进口为速度入口,入口速度为0.54 m/s,出口为压力出口,相对压力为0 Pa,圆柱壁面和底部壁面为无滑移壁面,上表面和侧面为自由滑移面,流场计算模型如图3所示。采用专业的商业软件CFX进行三维流场的数值模拟,稳态流场计算采用k-ε模型,基于稳态流场结果的瞬态计算则采用LES湍流模型,其中对流项采用高精度的中心差分格式进行离散,瞬态模式为second order backward euler。流体介质为常温下的水,参考压力为101 325 Pa,流体密度为997 kg/m3。
|
图 3 圆柱绕流流场计算模型 Fig. 3 Calculation model of fluid field |
在声场计算中,声源信息和声学模型是影响计算结果的2个重要因素。在噪声特性分析之前简单探讨了声学模型(网格量、无限元基面、滤波函数)对计算结果的影响,通过对比分析可以得到以下结论:1)3种因素对圆柱绕流声辐射特性均存在一定的影响,其中,滤波函数对计算结果的影响最大,差值比例在10%以上,滤波函数最优厚度在0.1 m左右、无限元基面对声场的影响次之,网格量的影响最小;2)声学计算结果对网格量敏感度低,计算误差在0.5%以内,为了保证计算精度,网格量应控制在10万以上。
综合以上,声场计算模型采取10万网格量以上、无限元基面采用椭球形,减小声源域的截断处理造成的虚假声,在声源域的边界处布置一层余弦波过滤面,采用的滤波函数厚度取0.10 m。
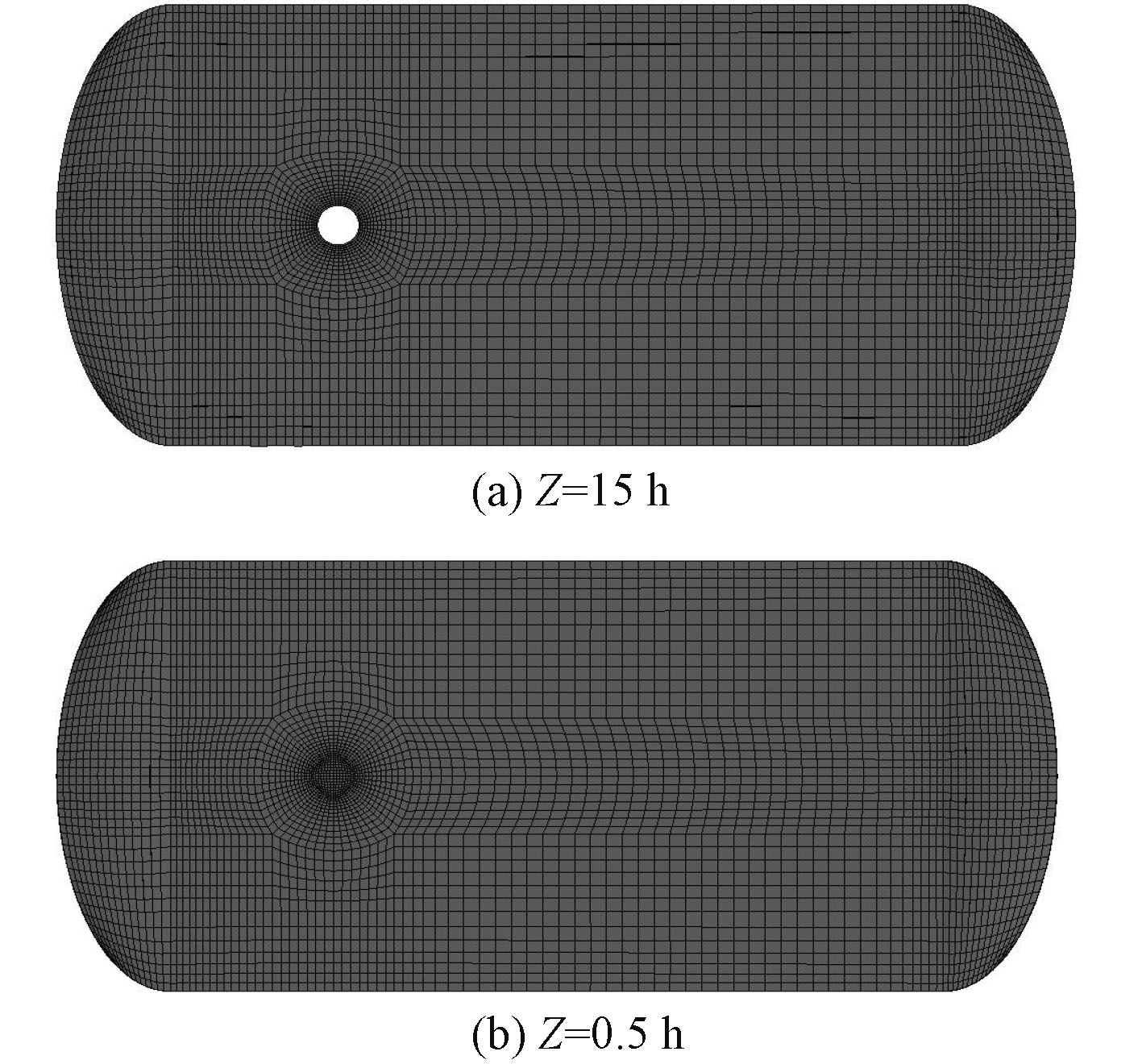
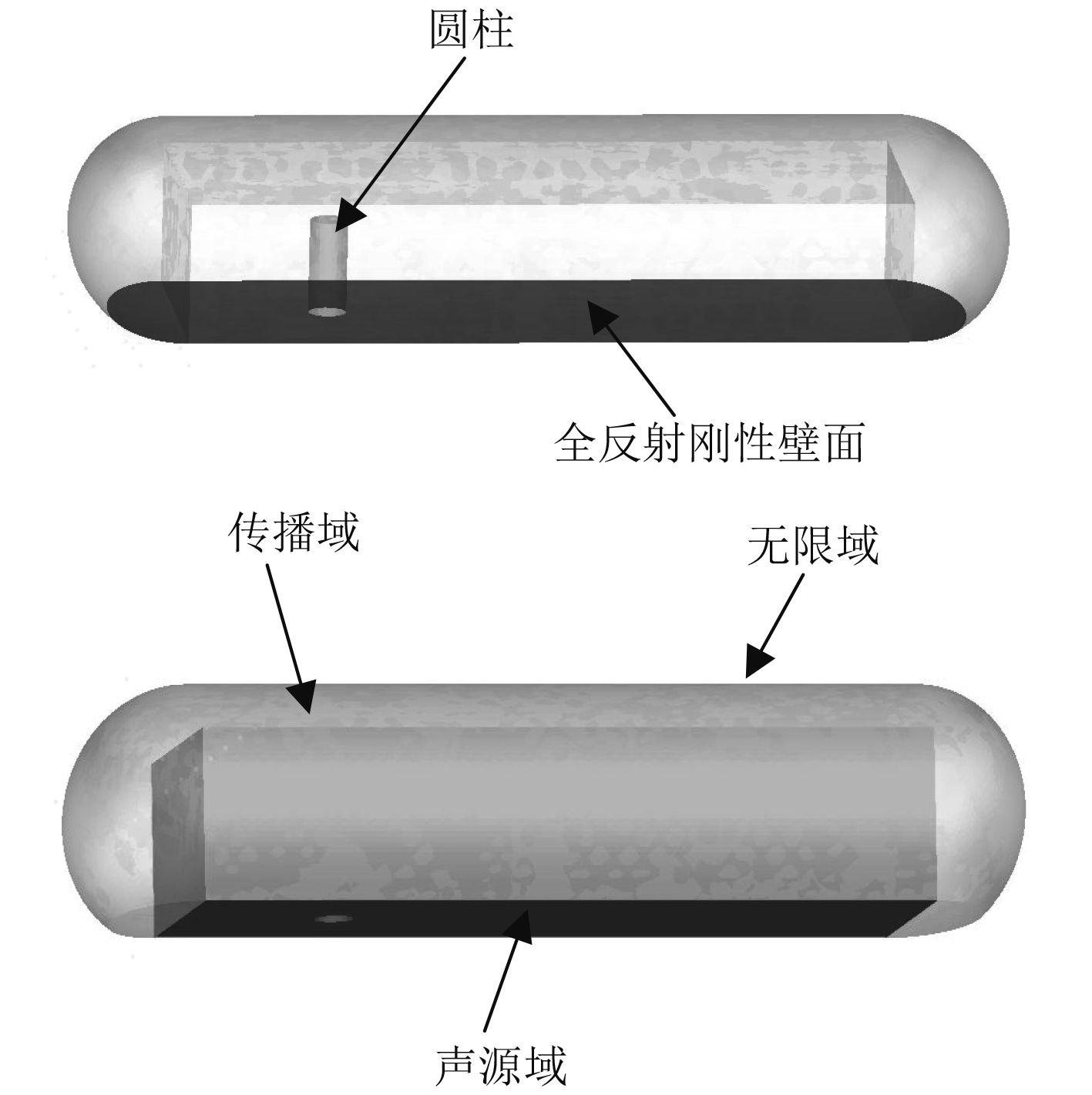
图4和图5分别给出了X-Y截面面和X-Z截面的网格示意图。本文采用ICEM CFD软件划分结构化六面体网格,整个声源域和传播域被划分为94个block,该模型共包含20万个网格节点。在声学计算模型设置中,将整个椭球体声学计算域划分为3个部分:声源域(source domain)、传播域(radiation domain)和无限域(infinite domain)。如图6所示,深色区域为声源域,声源域为流场结果的插值计算区域,即Lighthill声类比计算域。浅色区域为传播域,传播域的外表面为无限元的基面(infinite element),计算阶数设置为10阶,用于模拟无限远处无反射边界。由于有限高圆柱的底部为无滑移固壁,与双圆柱模型不同,噪声在此方向不能无限传播,应设置为全反射刚性壁面(rigid wall),与圆柱壁面的边界条件相同。
|
图 4 模型X-Y面网格示意图 Fig. 4 Mesh of fluid field(X-Y) |

|
图 5 模型X-Z面网格示意图(Y=0) Fig. 5 Mesh of fluid field(X-Z) |
|
图 6 单圆柱绕流声学计算模型 Fig. 6 Acoustics calculation model |
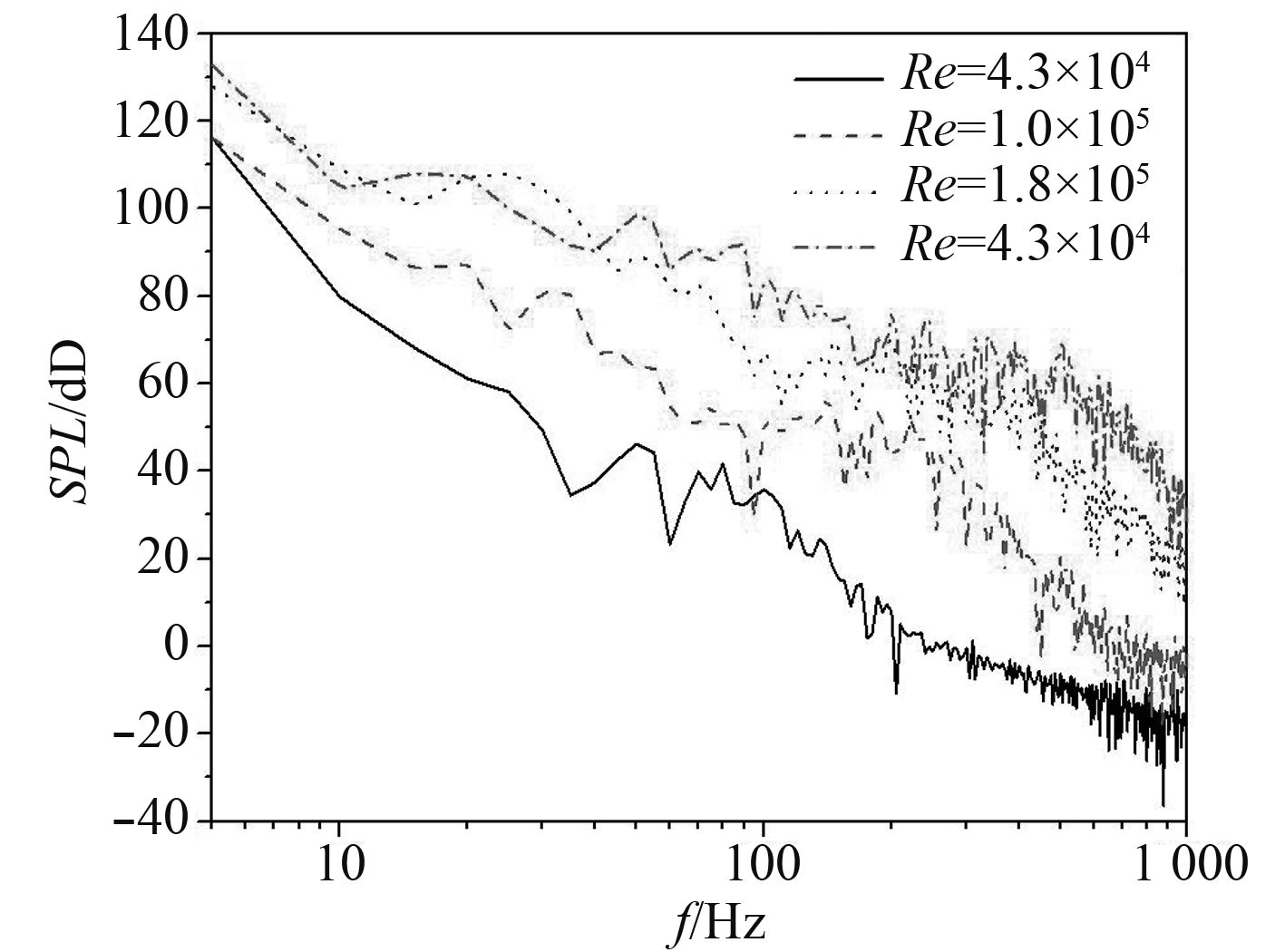
本节以有限高单圆柱为研究对象,采用Lighthill声类比理论对4种雷诺数(Re=4.3×104,Re=1.0×105,Re=1.8×105和Re=2.5×105)下的有限高单圆柱绕流水动力噪声特性进行计算。图7给出了4种不同雷诺数下圆柱绕流噪声频谱曲线,监测点坐标为(–12.5D,0,1.25D)。
|
图 7 不同雷诺数下的声压级图 Fig. 7 SPL with different Reynolds number |
可知,4种不同雷诺数下的声压级随着频率的增加而减小,在全频段内存在明显的声压级差值。Re=1.8×105和Re=2.5×105下的声压级在全频段内均大于0 dB,而Re=4.3×104和Re=1.0×105下的声压级在高频段为负值。另外,4种不同雷诺数下的声压级曲线均没有出现峰值,这是由于声场的声压级分布与流场的振荡规律有关,圆柱绕流的涡脱落频率决定着声压级的峰值频率。圆柱绕流的脱落频率为1.08 Hz,而图中给出的频率范围为5~1 000 Hz,故声压级曲线没有出现峰值。
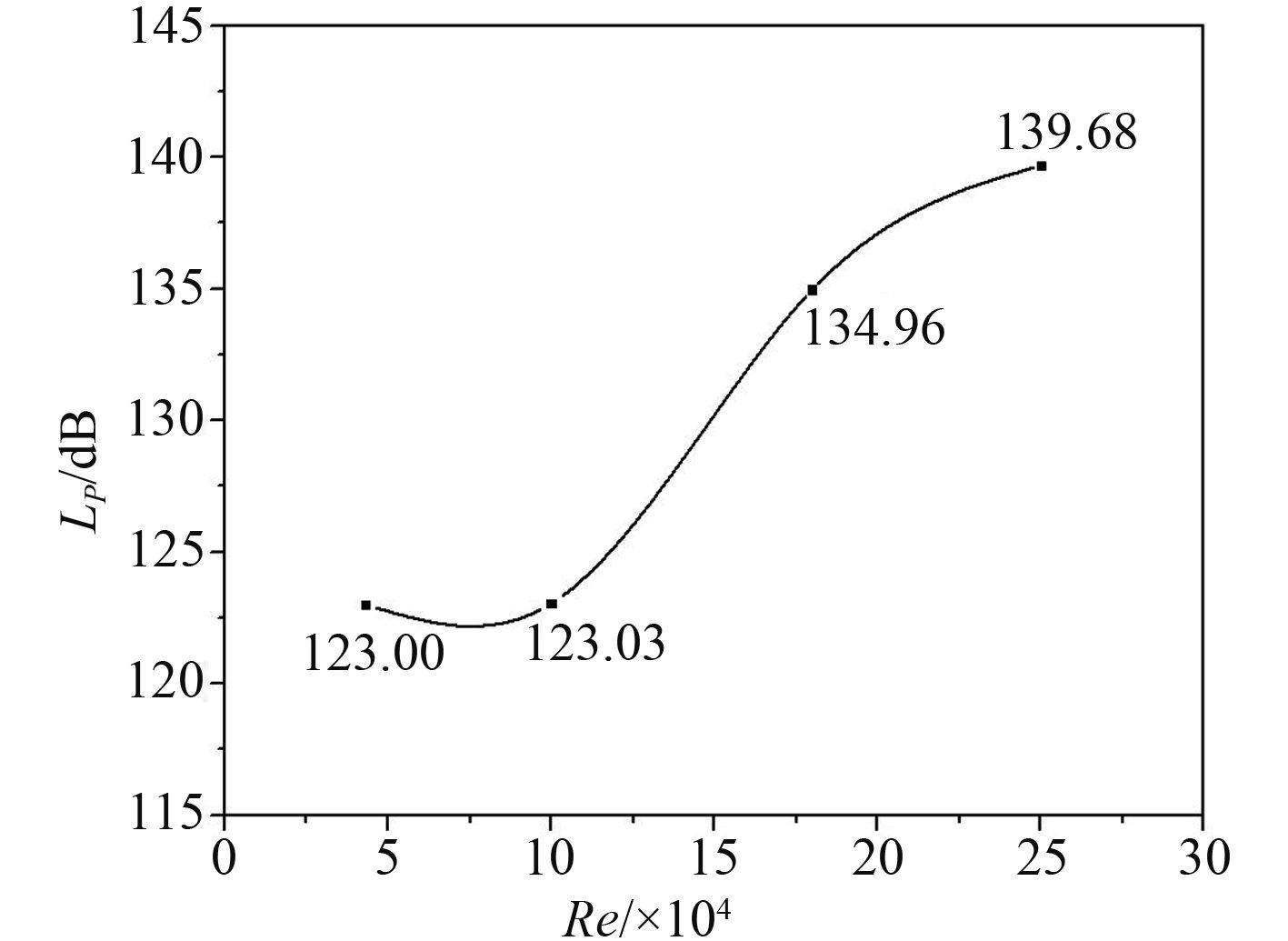
计算出不同雷诺数下测点的声压总级,得到声压总级随雷诺数的变化曲线,如图8所示。可以看出,测点声压总级随着雷诺数的增加呈非线性增加,增加速率由小变大后又减小,不同雷诺数下声压总级差值达到18 dB。Re=4.3×104和Re=1.0×105下测点声压总级大小几乎相等,约为123 dB,说明在该区间内雷诺数变化对噪声的声压总级基本没有影响。在Re=1.8×105时声压总级明显增加,增加值约12 dB,可见雷诺数的影响显著。Re=2.5×105下声压总级持续增加,此时声压总级最大,约为140 dB。该雷诺数处于超临界区,圆柱表面边界层开始转捩为湍流,流动状态变得更加复杂,导致了流噪声变大。
|
图 8 声压总级随雷诺数的变化图 Fig. 8 Lp with different Reynolds number |
对该变化曲线进行拟合,得到声压总级与雷诺数的变化关系如下:
| $ Lp= - 0.0079{x^3} + 0.3627{x^2} - 3.9103x + 133.73{\text{。}} $ |
式中:Lp为监测点的声压总级,dB;x为雷诺数(×104)。
可知,测点的声压总级与雷诺数呈三次方关系,随着雷诺数的增加非线性增加。
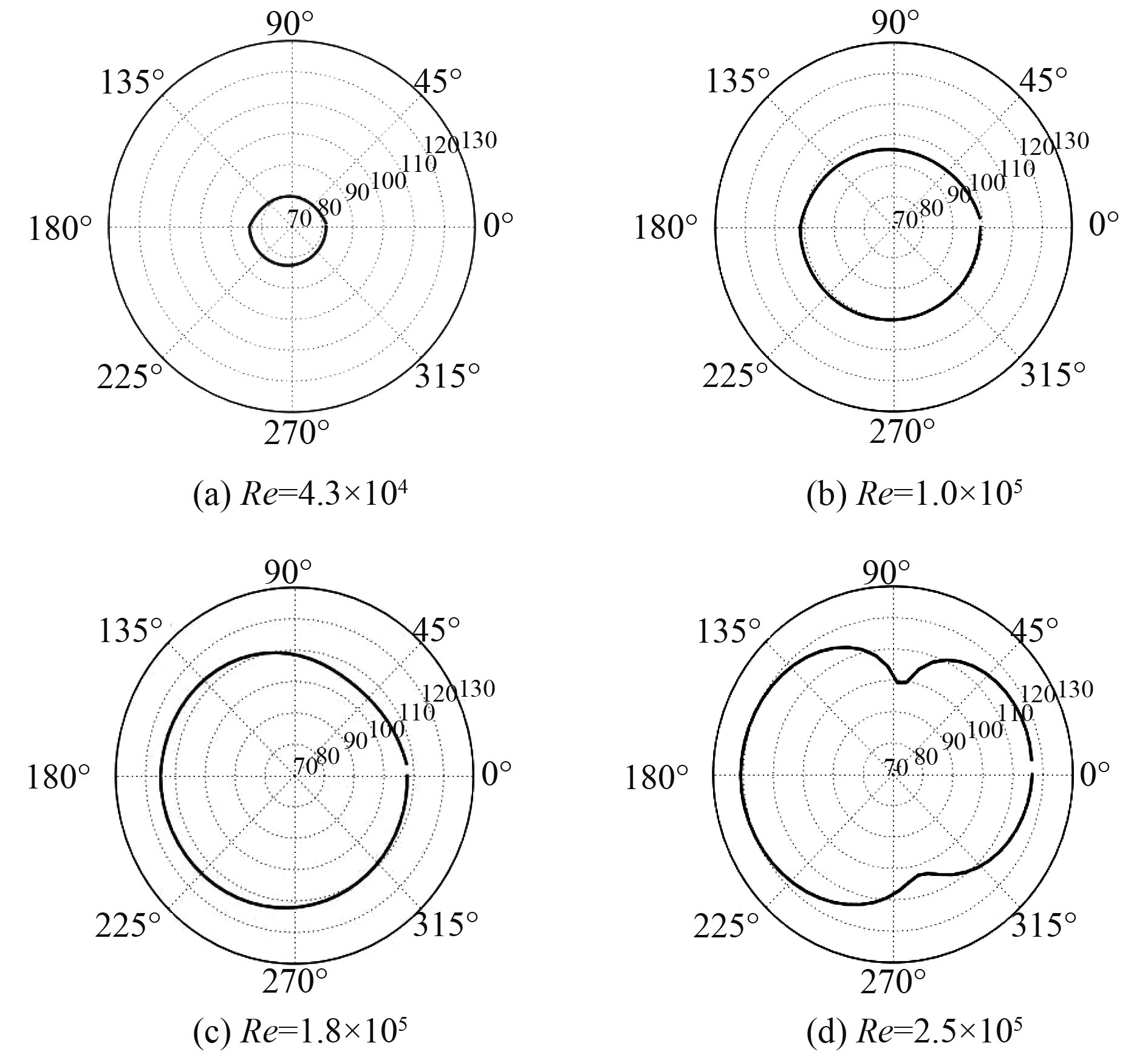
在距离圆柱中心12.5D处沿XY平面和YZ平面创建2个声学监测点组,以获取圆柱流噪声的声学指向性。给出了4种雷诺数下圆柱流噪声声学指向性图,0°~180°为XY平面,180°~360°为YZ平面的。从图中可以看出,当Re=4.3×104、Re=1.0×105和Re=4.3×104时,三者的声学指向性相近,声场分布规律相同,绕圆柱并非完全对称分布。Re=2.5×105下声场的声学指向性与偶极子声源的声学指向性相近,由于圆柱表面的旋涡交替脱落导致瞬态压力脉动,从而形成偶极子声源,此偶极子声源为该雷诺数下圆柱绕流水动力噪声的主要噪声源。在垂直于来流方向的Y轴上辐射噪声达到最大,说明Y轴是偶极子轴。在平行于来流方向的X轴上存在很小的声压级值,由于在垂直于偶极子轴上没有声辐射,说明圆柱绕流脱落涡中的湍流应力产生了噪声,且为四极子声源。
|
图 9 不同雷诺数下的声指向性图 Fig. 9 Acoustical directionality with different Reynolds number |
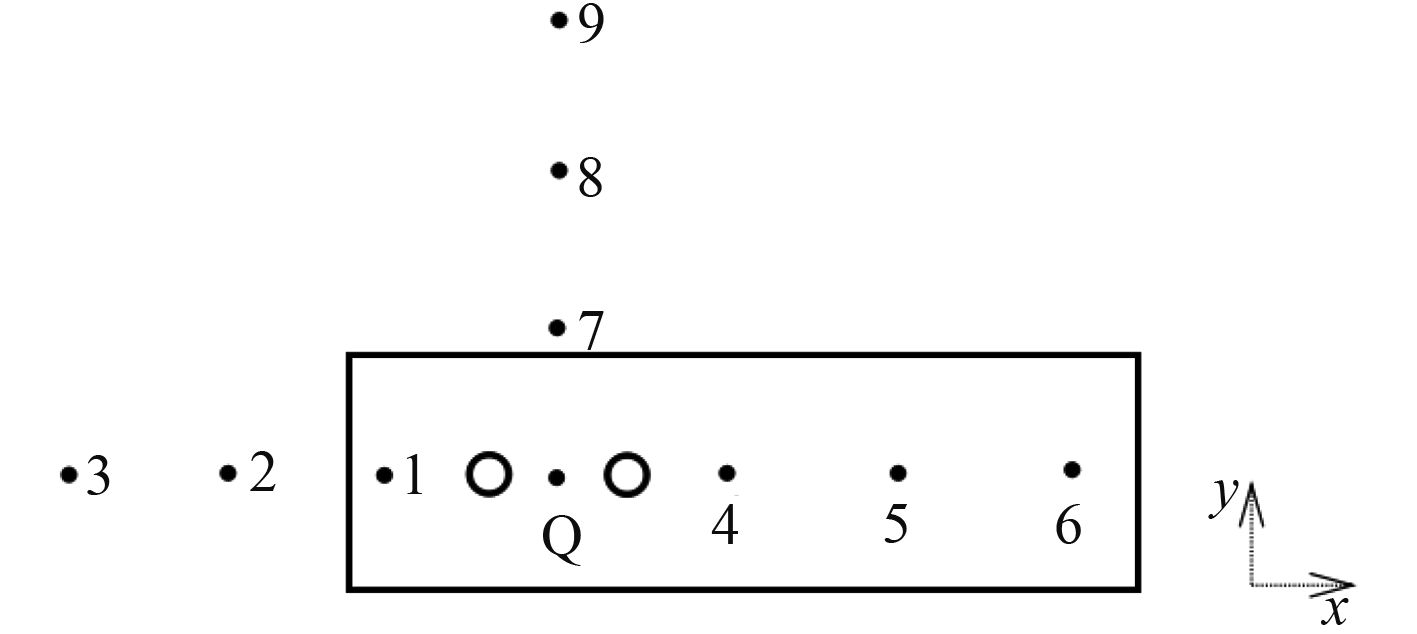
根据圆柱绕流流场和声场的数值模拟方法,在相同雷诺数(Re=2.5×105)、相同直径(D=80 mm)和相同高度(h=2.5D=200 mm)条件下,对不同间距比(L/D=2,3,4和5)下有限高串联圆柱的流噪声进行计算,分析不同间距比对有限高串联圆柱水动力噪声特性的影响。以串联双圆柱的中间位置(0.5L,0,1.25D)为参考点Q,分别在X和Y方向上距离点Q为5D,10D,15D的位置处设置声学监测点1~9,以采集不同位置处的声压信息,如图10所示。
|
图 10 双圆柱模型的声学监测点 Fig. 10 Monitoring points in the model of double cylinders |
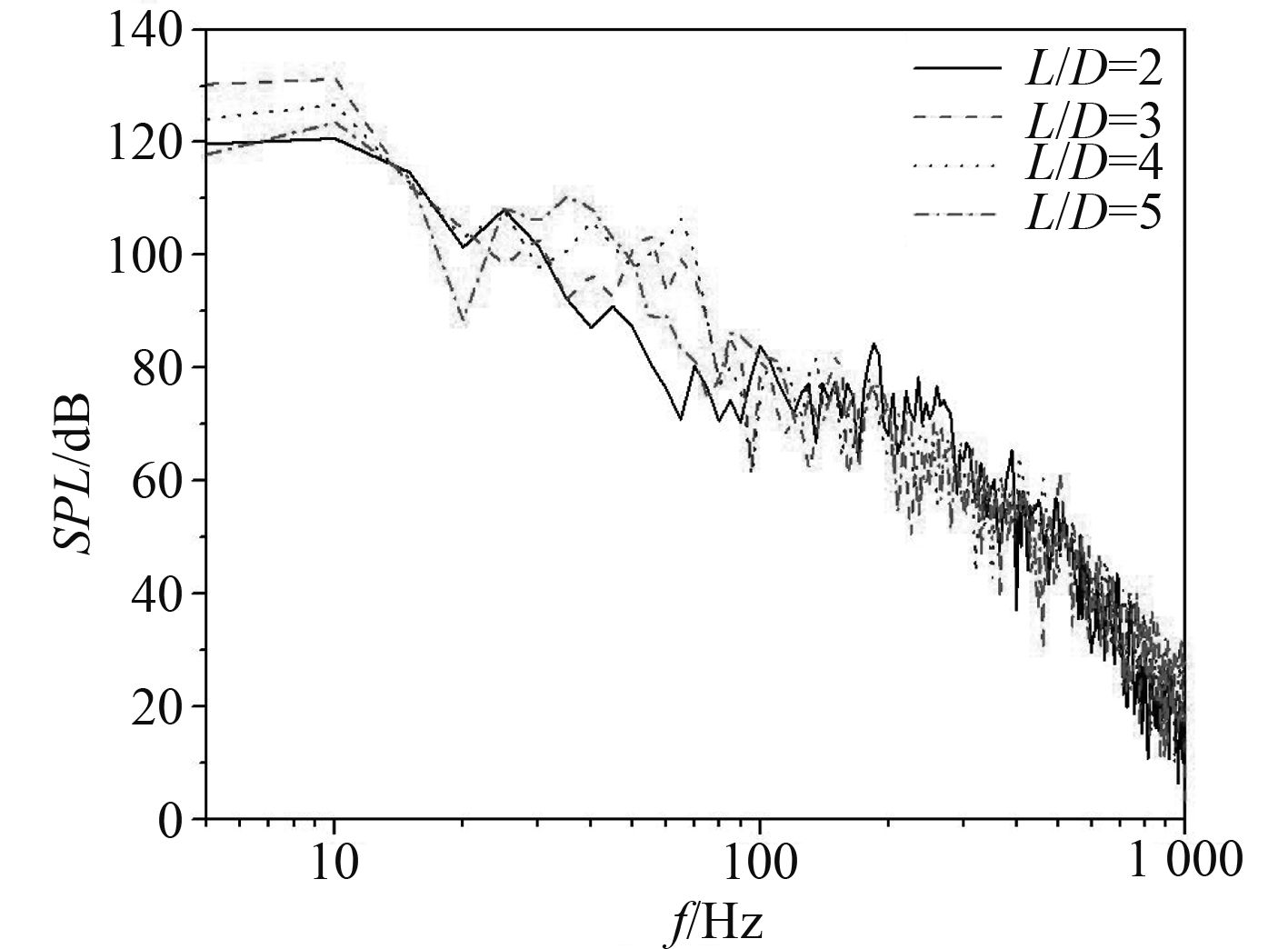
图11给出了4种不同间距比(L/D=2,3,4和5)下监测点9的噪声频域曲线图。由图可知,4种不同间距比下的声压级在频率小于300 Hz时,声压级值及分布规律差别较大,在大于300 Hz频段的声压级分布规律一致,声压级值差异较小。L/D=2下的声压级存在一个较小的峰值,峰值频率为184 Hz,其他间距比下的声压频域曲线均没有出现峰值。
|
图 11 不同间距比下的声压级图 Fig. 11 SPL with different pitch ratio |
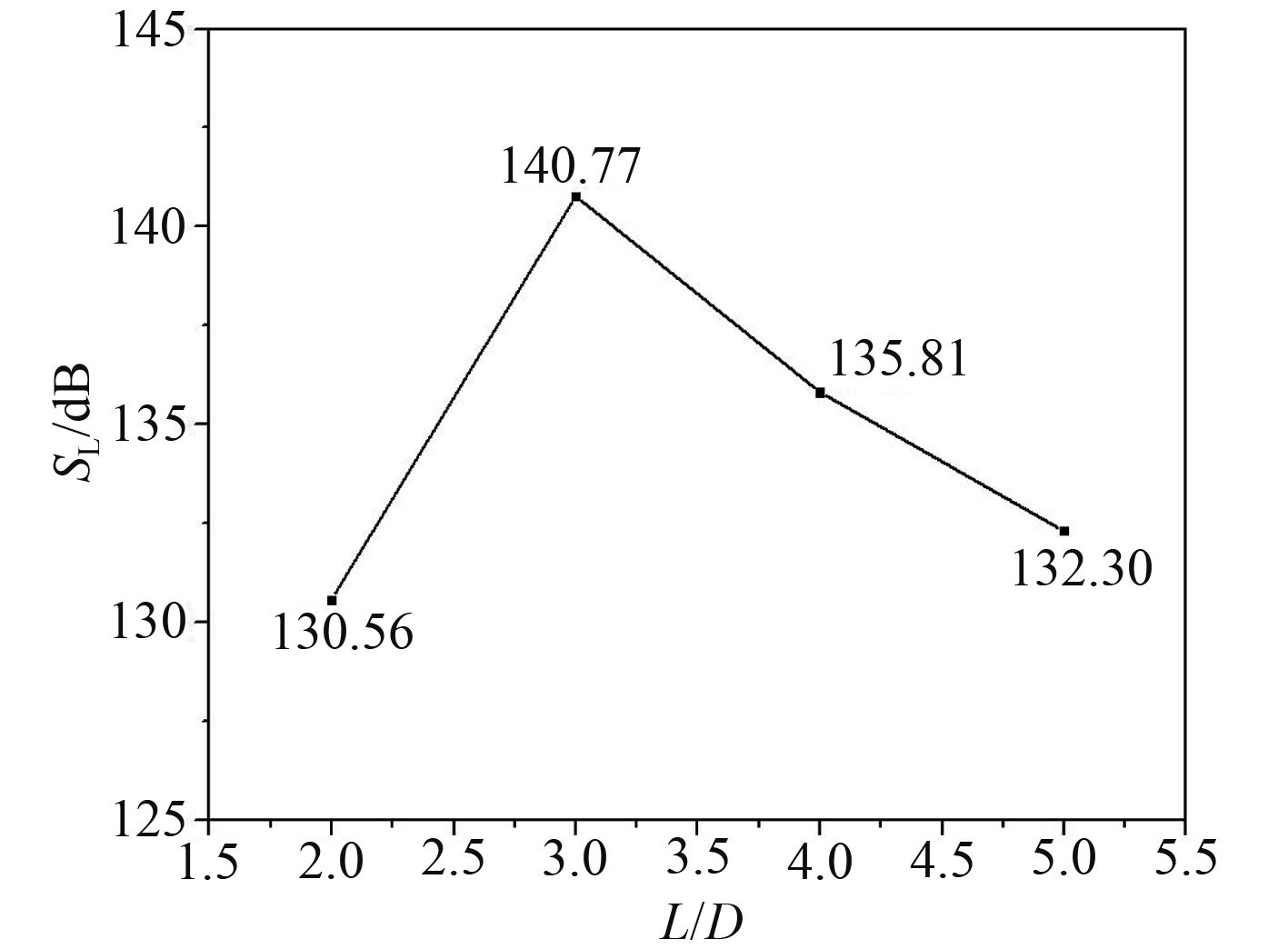
根据公式计算不同间距比下测点9的声压总级,得到声压总级随间距比的变化曲线,如图12所示。声压总级随着间距比的增加先变大后减小,不同间距比下的声压总级差值高达10 dB。间距比为2时声压总级最小,存在临界间距比(L/D=3)使得声压总级最大,最大声压总级为141 dB。可能原因是,L/D=3时从上游圆柱脱落的旋涡在向下游发展的过程中,大部分旋涡撞击下游圆柱并重新附着,对下游圆柱上的旋涡脱落产生影响,导致流噪声变大。从降噪角度考虑,双圆柱的串联设计应当避免出现在临界间距比(L/D=3)附近。
|
图 12 声压总级随间距比的变化曲线 Fig. 12 Lp with different pitch ratio |
为进一步了解有限高串联圆柱绕流噪声的分布规律,采集不同监测点1~9的噪声数据并绘制噪声频域曲线。以L/D=2为例,各监测点的声压级频域曲线如图13所示。可以看出,与参考点Q距离相等的监测点1,7(2,8以及3,9),其噪声的频谱分布规律基本相同,声压级随着频率的增加而减小,随着距离的增加而逐渐变小同时衰减速度变慢。不同之处是,来流方向上测点1,2,3的声压级较垂直于来流方向上相应测点7,8,9的声压级略高,在低频段高出约10 dB。下游区域内测点4,5,6的噪声频域曲线明显与其他方向上的不同,声压级显著增加,同时噪声大小与测点距离没有明显的变化规律,这可能是因为测点4,5,6处于尾流场的湍流区,属于声源域。以上表明,串联双圆柱的辐射噪声存在明显的指向性。

|
图 13 不同监测点的声压级曲线(L/D=2) Fig. 13 SPL of different monitoring points |
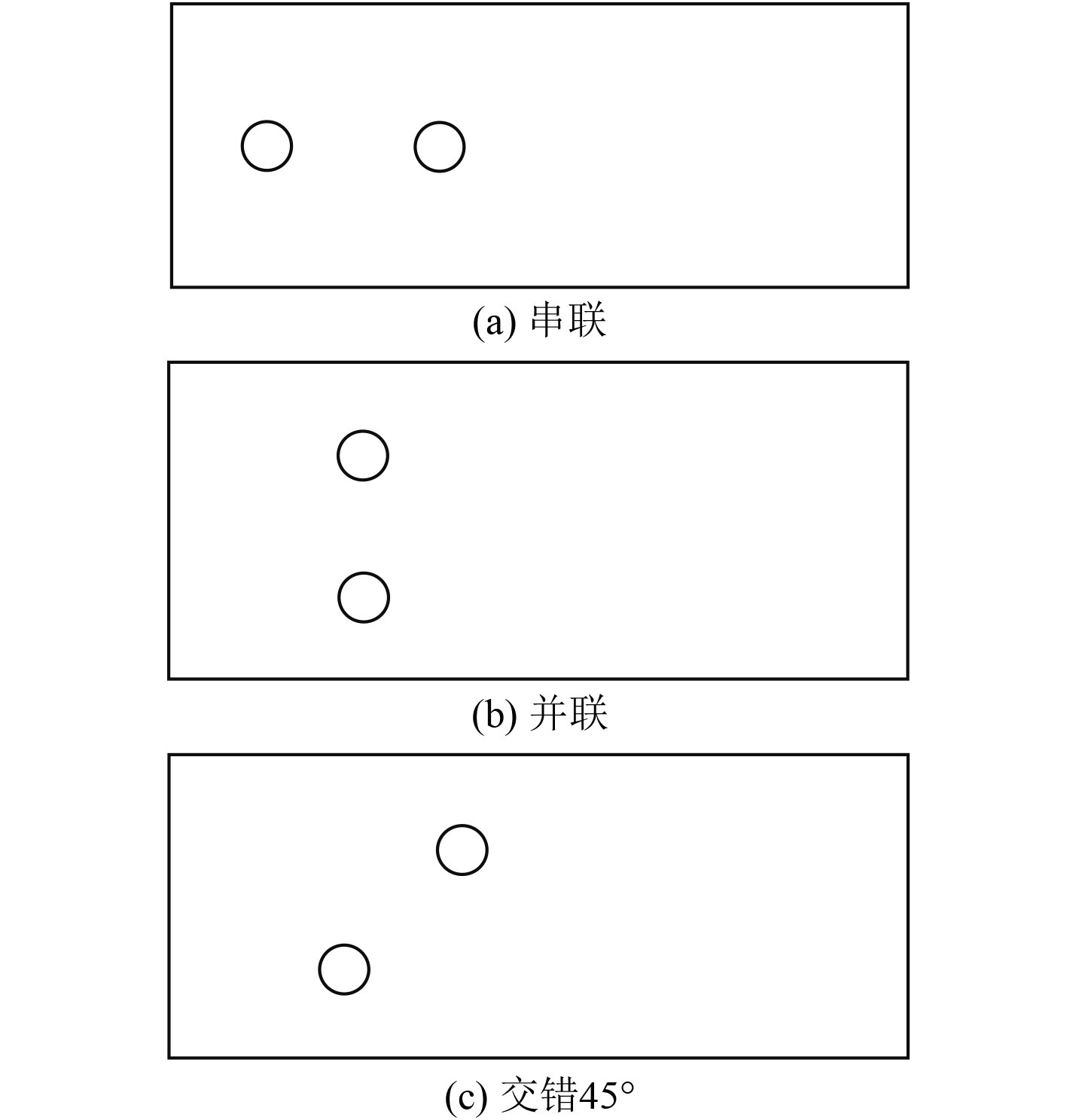
在相同雷诺数(Re=2.5×105)、相同直径(D=80 mm)、相同高度(h=2.5D=200 mm)、相同间距比L/D=3条件下,对不同排列方式(串联、并联和交错45°)下有限高双圆柱的流噪声进行计算,分析双圆柱的不同排列方式对水动力噪声特性的影响。不同排列方式下的双圆柱模型如图14所示。
|
图 14 双圆柱的不同排列方式 Fig. 14 Different arrangement method of double cylinders |
表1给出了不同排列方式下监测点1~3,7~9的声压总级大小。可以看出,在同一种排列方式下,与中间参考点Q的距离越大,测点的声压总级越小;来流方向(X方向)上的声压总级大于垂直于来流方向(Y方向)上的声压总级,具有明显的声学指向性。关于X,Y方向上声压总级的差值,串联方式下高达16 dB,并联方式下约为9 dB,交错45°排列方式下的最大差值约为13 dB。3种排列方式相比,来流方向上串联方式下的噪声最大,交错45°下次之,并联方式下最低,同时串联方式下的噪声随着距离的衰减速度最大。在垂直于来流方向上,靠近声源位置并联方式下的噪声最大,串联方式下最低;然而,在远离声源的位置,串联方式的噪声最大,交错45°方式时最小。以上规律说明,不同排列方式下噪声的衰减速度不同,总体而言,串联方式下的声压总级较高。从双圆柱降噪的角度考虑,应当避免串联的排列方式。
|
|
表 1 不同排列方式下测点声压总级表(L/D=3) Tab.1 Lp of monitoring points with different arrangement method |
基于大涡模拟和Lighthill声类比理论的混合数值模拟方法,通过计算对比得到了相对准确的声学计算模型,计算了不同高雷诺数(Re=4.3×104,Re=1.0×105,Re=1.8×105和Re=2.5×105)、不同间距比(L/D=2,3,4和5)和不同排列方式(串联、并联和交错45°)下的单圆柱及双圆柱绕流水动力噪声特性,分析了雷诺数、间距比以及排列方式对圆柱绕流水动力噪声的影响。研究结果表明:1)雷诺数对水下圆柱绕流噪声特性的影响显著,噪声随着雷诺数的增加而非线性增加,并与雷诺数呈三次方关系;通过减小雷诺数可以有效地降低圆柱绕流的水动力噪声;4种雷诺数下的声辐射场具有很明显地指向性,超临界区雷诺数(Re=2.5×105)下的圆柱绕流水动力噪声的声学指向性与偶极子声源最相似,3个亚临界区雷诺数(Re=4.3×104,Re=1.0×105和Re=1.8×105)下的声学指向性相似。2)随着间距比的增加,双圆柱绕流水动力噪声先增大后减小;4种间距比下,L/D=2时声压总级最小,存在临界间距比(L/D=3)使得噪声最大。3)3种不同排列方式下,来流方向上的双圆柱噪声均大于垂直于来流方向上的噪声,具有明显的声学指向性;三者相比,串联方式的噪声最大。
| [1] |
GOVARDHAN R, WILLIAMSON C H K. Modes of vortex formation and frequency response of a freely vibrating cylinder[J]. Journal of Fluid Mechanics, 2000, 420: 85-130. DOI:10.1017/S0022112000001233 |
| [2] |
YOU D, CHOI H, CHOI M R, et al. Control of flow-induced noise behind a circular cylinder using splitter plates[J]. AIAA Journal, 1998, 36(11): 1961-1967. DOI:10.2514/2.322 |
| [3] |
贲安庆.圆柱绕流的数值模拟及其稳定性研究[D]. 大连: 大连理工大学, 2015.
|
| [4] |
段志强. 低雷诺数下尾部隔板影响圆柱绕流的数值研究 [D]. 重庆: 重庆大学, 2012.
|
| [5] |
方媛媛. 三维圆柱体绕流数值模拟流场选择及网格划分[J]. 水道港口, 2009(1): 70-76. DOI:10.3969/j.issn.1005-8443.2009.01.014 |
| [6] |
张翰钦, 陈明, 孙国仓. 圆柱绕流噪声预报的流场与声场模拟方法对比研究[J]. 噪声与振动控制, 2016, 36(3): 26-31. |
| [7] |
贾晓荷. 单圆柱及双圆柱绕流的大涡模拟[D]. 上海: 上海交通大学, 2008.
|
| [8] |
ZDRAVKOVICH M M. Flow around circular cylinders. Fundamentals, 1997, 1.
|
| [9] |
KALTENBACHER M, ESCOBAR M, BECKER S, et al. Numerical simulation of flow-induced noise using LES/SAS and Lighthill's acoustic analogy[J]. International Journal for Numerical Methods in Fluids, 2010, 63(9): 1103-1122. |
 2019, Vol. 41
2019, Vol. 41

