压缩视频数据在视频通信过程中由于受信道带宽限制、无线信道不稳定性[1]以及IP网络“尽力而为”影响,不可避免地会发生丢包或误码。与此同时,视频编码标准大多采用帧内预测、帧间预测和可变长编码等技术去除视频图像在空域、时域和统计域的冗余度以达到数据压缩的目的[2],这些技术在提高编码效率提升的同时也使得视频数据之间存在较强的关联性。当视频数据发生丢包或误码时,解码错误会在空域或时域迅速扩散,导致解码的视频质量急剧下降。因此,为提高解码的视频质量,需要在解码端采用错误掩盖技术,在不改变编解码结构、不增加传输带宽的情况下,根据视频信号的相关性,对丢包或误码的视频数据进行恢复。
当帧间编码帧发生丢包或误码时,常采用时域错误掩盖算法,即根据视频的运动相关性,估算受损图像块的运动矢量,然后在前续帧中查找图像块替代受损图像块。因此,时域错误掩盖算法的核心在于如何估算受损的运动矢量。时域替换算法[3]是时域错误掩盖最基本的算法,通过假定受损运动矢量为0,直接用前续图像块替代受损图像块,该算法易于实现,但在运动剧烈区域很容易产生错位感。边界匹配算法[4]以候选图像块与相邻图像块的边界像素差值为准则,从候选图像块中选取使得差值最小的图像块作为最佳替代图像块,该算法已被H.264参考软件JM选作时域错误掩盖算法,但对于物体边界处的受损图像块,掩盖时会选择出错误的替代图像块。文献[5]根据相邻图像块运动矢量构造拉格朗日插值多项式,进而根据插值多项式恢复受损图像块的运动矢量。该算法利用了运动的空域相关性,但当受损图像块与相邻区域运动趋势不同时,掩盖效果较差。文献[6]采用时空结合边界匹配法,以保持图像平滑性和结构相似性。文献[7]采用物体检测、边界匹配和参考帧相关图像块的运动矢量来恢复不同尺寸的受损图像。文献[8]首先采用边界匹配算法估算运动矢量,然后通过粒子滤波器对运动矢量进行去噪处理。文献[9]将张量模型引入到视频通信中,提出了基于张量模型的错误掩盖算法。这些算法利用相邻图像块或前续图像块的运动信息对受损图像块的运动矢量进行估算,但存在一个共同的不足,即缺少对运动区域的分析,没有选取与受损图像块运动相关性最强的相邻图像块对受损图像块进行错误掩盖,因此恢复的运动矢量存在一定偏差,解码的视频质量有待提升。
为此,本文根据运动的空域相关性和时域相关性,提出一种基于相关运动矢量外推的错误掩盖算法。对于受损图像块,首先构造经过前续相邻图像块的一阶平面集,然后计算前续图像块与1阶平面集距离,选取使得距离最短的1阶平面所代表的前续相邻图像块为相关最强前续相邻图像块,最后将相关最强前续相邻图像块外推到当前帧,通过外推图像块与受损图像块重叠区域加权估算受损运动矢量,并采用边界匹配算法对运动矢量进行优化,进而恢复受损图像块。
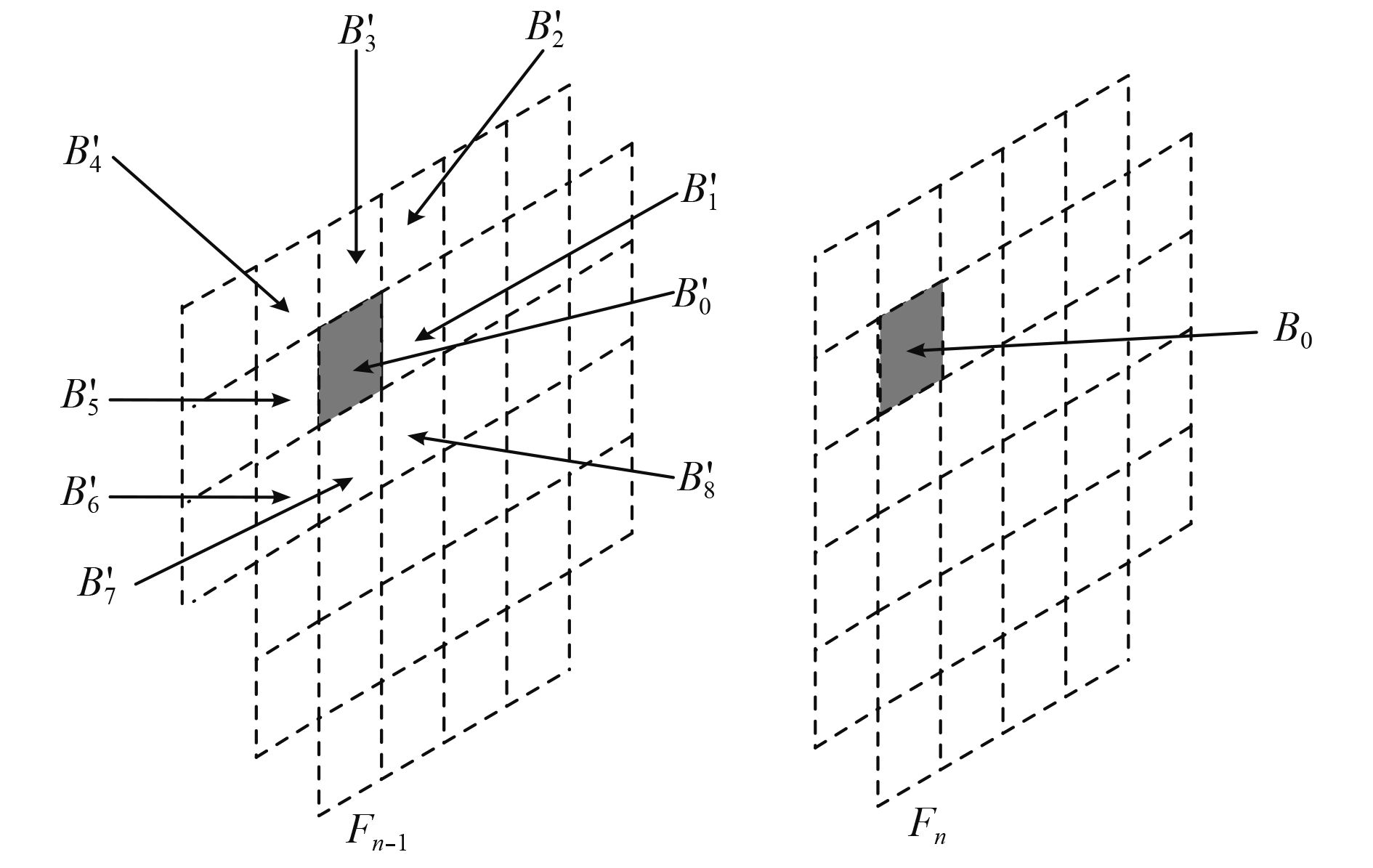
1 相关最强前续相邻图像块确定前续图像块、前续相邻图像块、受损图像块位置关系如图1所示。
|
图 1 图像块位置关系示意图 Fig. 1 Position relation of image blocks |
图中,
以
|
|
表 1 前续相邻图像块横向距离和纵向距离 Tab.1 Lateral and longitudinal distances of previous adjacent image blocks |
将
将
| $S = \{ B_i'B_j'B_k'|i > j > k,(i,j,k) \in \{ 1,2,3,4,5,6,7,8\} \} \text{。}$ | (1) |
式中:通过三点
| $ax + by + cz + d = 0\text{。}$ | (2) |
将
| $\left\{ \begin{gathered} a \times d{s_{x,i}} + b \times d{s_{y,i}} + c \times x_i' + d = 0 \text{,}\\ a \times d{s_{x,j}} + b \times d{s_{y,j}} + c \times x_j' + d = 0 \text{,}\\ a \times d{s_{x,k}} + b \times d{s_{y,k}} + c \times x_k' + d = 0 \text{。}\\ \end{gathered} \right.$ | (3) |
求解方程组,得到:
| $ \left\{ \begin{aligned} & a = (d{s_{y,j}} - d{s_{y,i}}) \times (x_k' - x_i') - (d{s_{y,k}} - d{s_{y,i}}) \times (x_j' - x_i') \text{,}\\ & b = (d{s_{x,k}} - d{s_{x,i}}) \times (x_j' - x_i') - (d{s_{x,j}} - d{s_{x,i}}) \times (x_k' - x_i') \!\!\! \text{,}\\ & c = (d{s_{x,j}} - d{s_{x,i}}) \times (d{s_{y,k}} - d{s_{y,i}}) - (d{s_{x,k}} - d{s_{x,i}}) \times \\ & \quad(d{s_{y,j}} - d{s_{y,i}}) \text{,}\\ &d = - (a \times d{s_{x,i}} + b \times d{s_{y,i}} + c \times x_i')\text{。} \end{aligned} \right. $ | (4) |
求得
求得所有的1阶平面后,通过比较
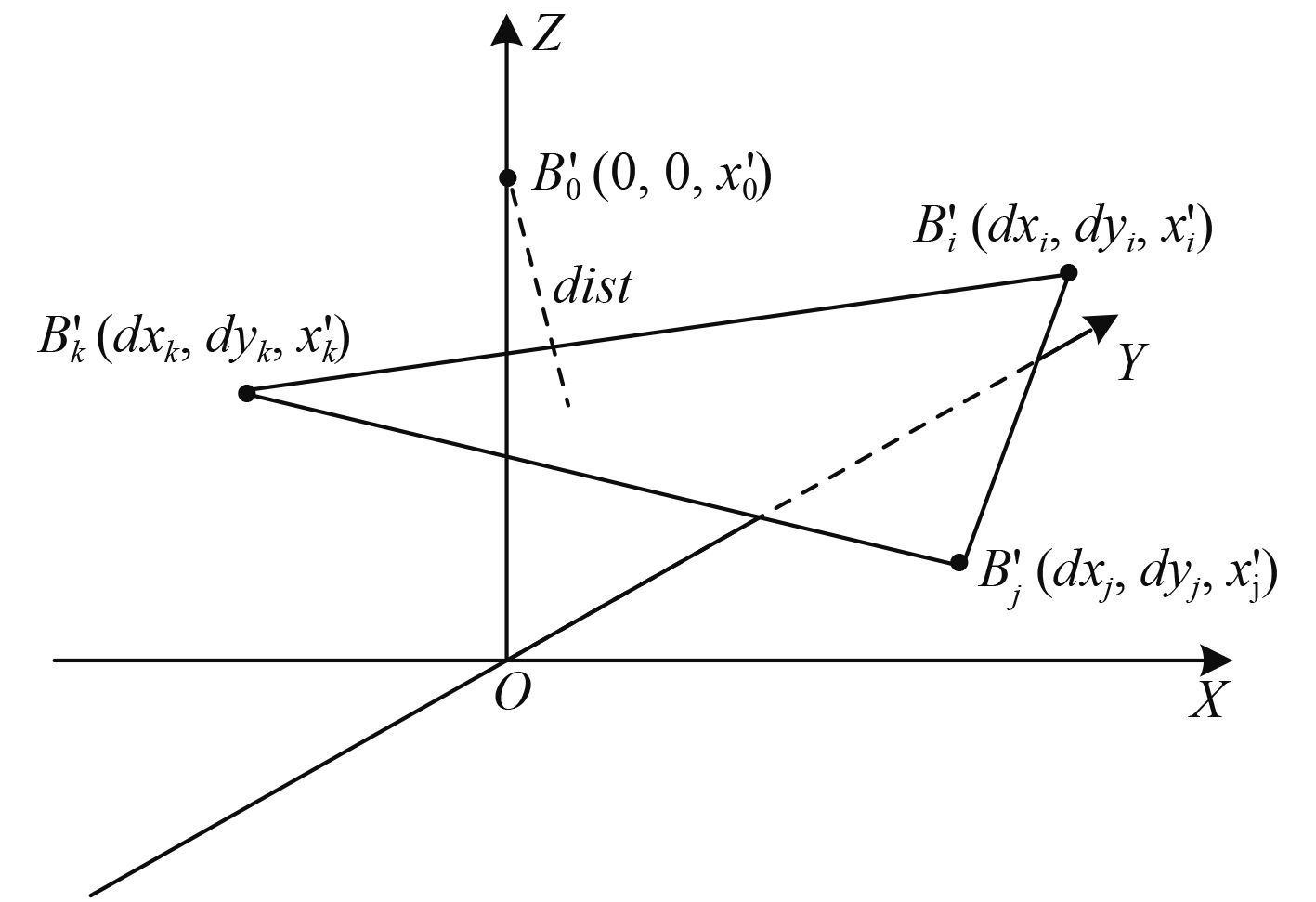
|
图 2 前续图像块与1阶平面距离 Fig. 2 Distance between preceding image blocks and first-order plane |
| ${\rm {dist}}(B_0',B_i'B_j'B_k') = \frac{{\left| {c \times x_0' + d} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\text{。}$ | (5) |
选取使得
| $(B_\alpha ',B_\beta ',B_\delta ') = \mathop {\min \arg }\limits_{i,j,k \in \{ 1\sim 8\} ,i > j > k} \{ dist(B_0',B_i'B_j'B_k')\}\text{。} $ | (6) |
式中:
根据运动的时域相关性可知,相邻视频帧的运动趋势大多具有连续性,即可以将前续相邻图像块的运动矢量根据其运动趋势外推到当前帧中以估算受损图像块的运动矢量。
得到相关最强前续相邻图像块
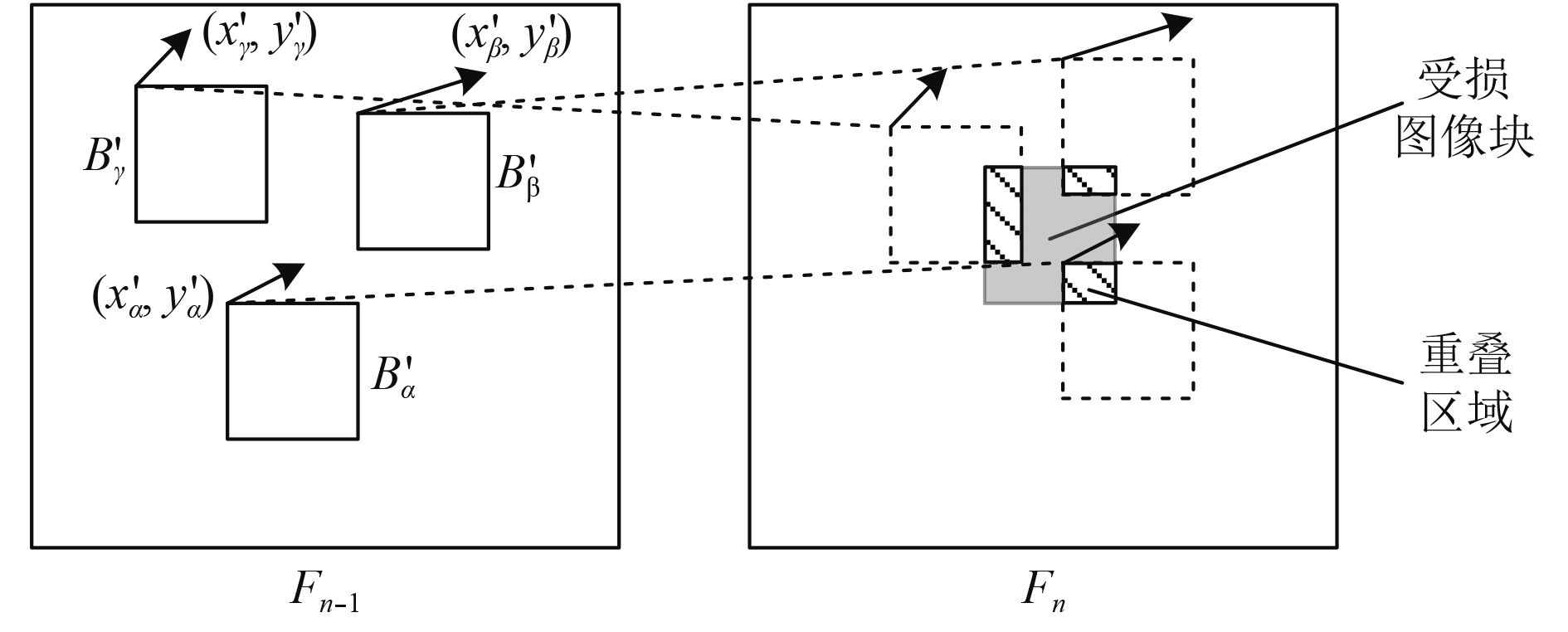
|
图 3 运动矢量外推示意图 Fig. 3 Diagram of motion vector extrapolation |
图中,虚线框为外推图像块。
重叠区域大小反映了前续图像块与受损图像块的运动相关程度:重叠区域越大的前续图像块,越有可能运动到受损图像块的位置。因此,受损图像块的运动矢量可根据外推图像块与受损图像块重叠区域加权得到,即
| $ \!\left\{ \begin{gathered} m{v_x} = \frac{{S(B_\alpha ',{B_0}) \times x_\alpha ' + S(B_\beta ',{B_0}) \times x_\beta ' + S(B_\gamma ',{B_0}) \times x_\gamma '}}{{S(B_\alpha ',{B_0}) + S(B_\beta ',{B_0}) + S(B_\gamma ',{B_0})}}\text{,}\!\!\!\!\!\!\!\!\!\!\! \\ m{v_y} = \frac{{S(B_\alpha ',{B_0}) \times y_\alpha ' + S(B_\beta ',{B_0}) \times y_\beta ' + S(B_\gamma ',{B_0}) \times y_\gamma '}}{{S(B_\alpha ',{B_0}) + S(B_\beta ',{B_0}) + S(B_\gamma ',{B_0})}}\text{。}\!\!\!\!\!\!\!\!\!\!\! \\ \end{gathered} \right. $ | (7) |
式中,
通过上述运动矢量外推方法,初步估算了受损图像块的运动矢量,但在上述运动矢量估算过程中,只考虑了运动的时域相关性,因此恢复的图像块可能存在块边界效应。因此,本文对已初步估算的运动矢量进行优化,在初步估算的运动矢量相邻区域内寻找一个最优边界匹配的运动矢量作为受损图像块最终掩盖的运动矢量。
边界匹配算法以图像块边界亮度失真作为度量,通过计算候选图像块的内部边界像素值与受损图像块的外部边界像素值的亮度差值之和大小衡量边界匹配程度,边界匹配程度越高,则图像块边界差值越小。因此,在已初步估算的运动矢量相邻区域内,查找使得图像块边界差值最小的图像块恢复受损图像块。由于图像块的解码或掩盖的次序为从上至下,从左至右,当对受损图像块进行错误掩盖时,只有其上边界图像块和左边界图像块可用,因此在计算边界差值时,只计算上边界图像块和左边界图像块的差值。最优运动矢量查找过程如图4所示。
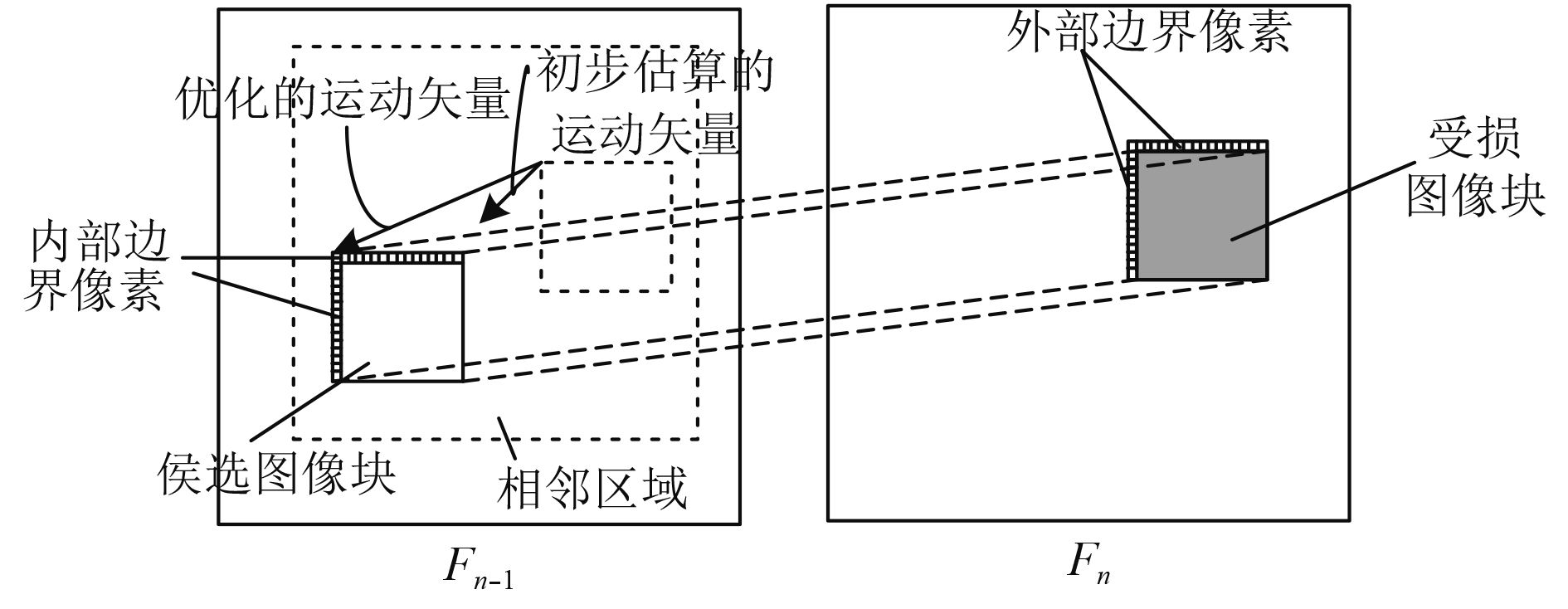
|
图 4 最优运动矢量查找过程示意图 Fig. 4 Searching process for optimal motion vector |
对于
| $ \begin{split} dif{f_{(\Delta x,\Delta y)}} = & \sum\limits_{m = 0}^3 \left| pi{x_n}({x_{start}} + m,{y_{start}} - 1)-\right. \\ & \left. pi{x_{n - 1}}({x_{start}} - \Delta x + m,{y_{start}} - \Delta y) \right| {\rm{ + }} \\ & \sum\limits_{m = 0}^3 \left| pi{x_n}({x_{start}} - 1,{y_{start}} + m)-\right. \\ & \left. pi{x_{n - 1}}({x_{start}} - \Delta x,{y_{start}} - \Delta y + m) \right| \text{。}\\ \end{split} $ | (8) |
式中:
| $ ({x_0},{y_0}) = (\Delta x,\Delta y) = \mathop {\arg \min }\limits_{\begin{array}{*{20}{c}} {\Delta x \in [m{v_x} - \delta ,m{v_x} + \delta ]}\\ {\Delta y \in [m{v_y} - \delta ,m{v_y} + \delta ]} \end{array}\text{。}} dif{f_{(\Delta x,\Delta y)}}\text{,} $ | (9) |
选取QCIF格式的Foreman,Carphone和Suzie序列进行仿真实验。仿真实验采用H.264的参考软件JM[10]作为测试平台,视频序列编码档次为Baseline,关键帧间隔为40,量化参数为26。考虑到运动的空间相关性及运算复杂度,选取
采用时域替换算法、边界匹配算法、拉格朗日算法和本文提出的算法进行比较。视频客观质量通过亮度分量的峰值信噪比(PSNR)进行衡量,实验结果如表2所示。
|
|
表 2 不同掩盖算法的性能比较 Tab.2 Performance comparison of different concealment algorithms |
仿真实验中,Foreman序列人物和镜头均在运动,而且还存在场景的切换;Carphone序列中等速度的运动;Suzie序列运动方向随机。由表2可见,对于不同运动类型的视频序列和不同的数据丢包率,本文算法PSNR均高于时域替换算法、边界匹配算法和拉格朗日算法。相比时域替换算法提高2.3~2.7dB,相比边界匹配算法提高1.3~2dB,相比拉格朗日算法提高0.5~1.1dB,是一种鲁棒性较强的算法。3个测试序列中图像的不同区域具有不同的运动趋势,本文算法分析了相邻图像块运动趋势,并选取运动相关最强相邻图像块进行错误掩盖,从而更好地重建了受损的图像。此外,随着丢失率的增大,更多的受损图像块采用本文算法恢复受损的运动矢量,本文算法的优势更加明显。
从解码视频质量比较各算法的主观视觉效果,图5给出了Foreman序列第82帧解码视频质量。

|
图 5 各算法解码视频主观视觉效果 Fig. 5 Decoded visual effects of various algorithms |
由图可见,时域替换算法解码图像效果较差,在人物眼睛、鼻梁、嘴巴和脖子处存在割裂痕迹;边界匹配算法解码图像在人物鼻梁、脖子处存在错位痕迹;拉格朗日算法解码图像在人物鼻子下方存在切线;本文算法在一定程度上克服了上述不足,解码的视频质量相对较好。
4 结 语本文利用运动空域相关性得到相关最强前续相邻图像块,然后利用运动时域相关性将相关最强前续相邻图像块外推到当前帧,根据外推图像块与受损图像块重叠区域大小估算受损的运动矢量。在此基础上,依据边界匹配算法对估算的运动矢量进行优化,从而完成受损图像块的错误掩盖。仿真结果表明,对于不同运动特征的视频序列和不同的数据丢包率,本文算法相比传统时域错误掩盖算法可获得更高的客观质量和主观视觉效果。
| [1] |
ANDREAS F.M. 无线通信[M]. 北京: 电子工业出版社, 2015.
|
| [2] |
高文, 赵德斌, 马思伟. 数字视频编码技术基础[M]. 北京: 科学出版社, 2018.
|
| [3] |
彭强, 张蕾. 视频传输差错掩盖技术研究现状与发展趋势[J]. 西南交通大学学报, 2009, 44(4): 473-483. DOI:10.3969/j.issn.0258-2724.2009.04.001 |
| [4] |
陈健. 基于H.264的视频差错掩盖算法研究[D]. 成都: 西南交通大学, 2016: 6–7.
|
| [5] |
ZHENG J. H, CHAU L. P. A Motion vector recovery algorithm for digital video using lagrange interpolation[J]. IEEE Transactions on Broadcasting, 2008, 49(4): 383-389. |
| [6] |
姚伟新, 杨丹, 葛愿. H.264/AVC自适应时空域错误隐藏算法[J]. 计算机工程, 2016, 42(2): 261-265. DOI:10.3969/j.issn.1000-3428.2016.02.046 |
| [7] |
YANG S. H, CHANG C, W, CHAN C. C. An Object based error concealment technique for H.264 Coded Video[J]. Multimedia Tools and Applications, 2015, 74(23): 10785-10800. DOI:10.1007/s11042-014-2206-9 |
| [8] |
RADMEHR A, GHASEMI A. Error concealment via particle filter by gaussian mixture modeling of motion vectors for H.264/AVC[J]. Signal, Image and Video Processing, 2016, 10(2): 311-318. DOI:10.1007/s11760-014-0743-3 |
| [9] | |
| [10] |
H.264/AVC Reference Software JM18.0. Available: http://iphome.hhi.de/suehring/tml/download.
|
 2019, Vol. 41
2019, Vol. 41
