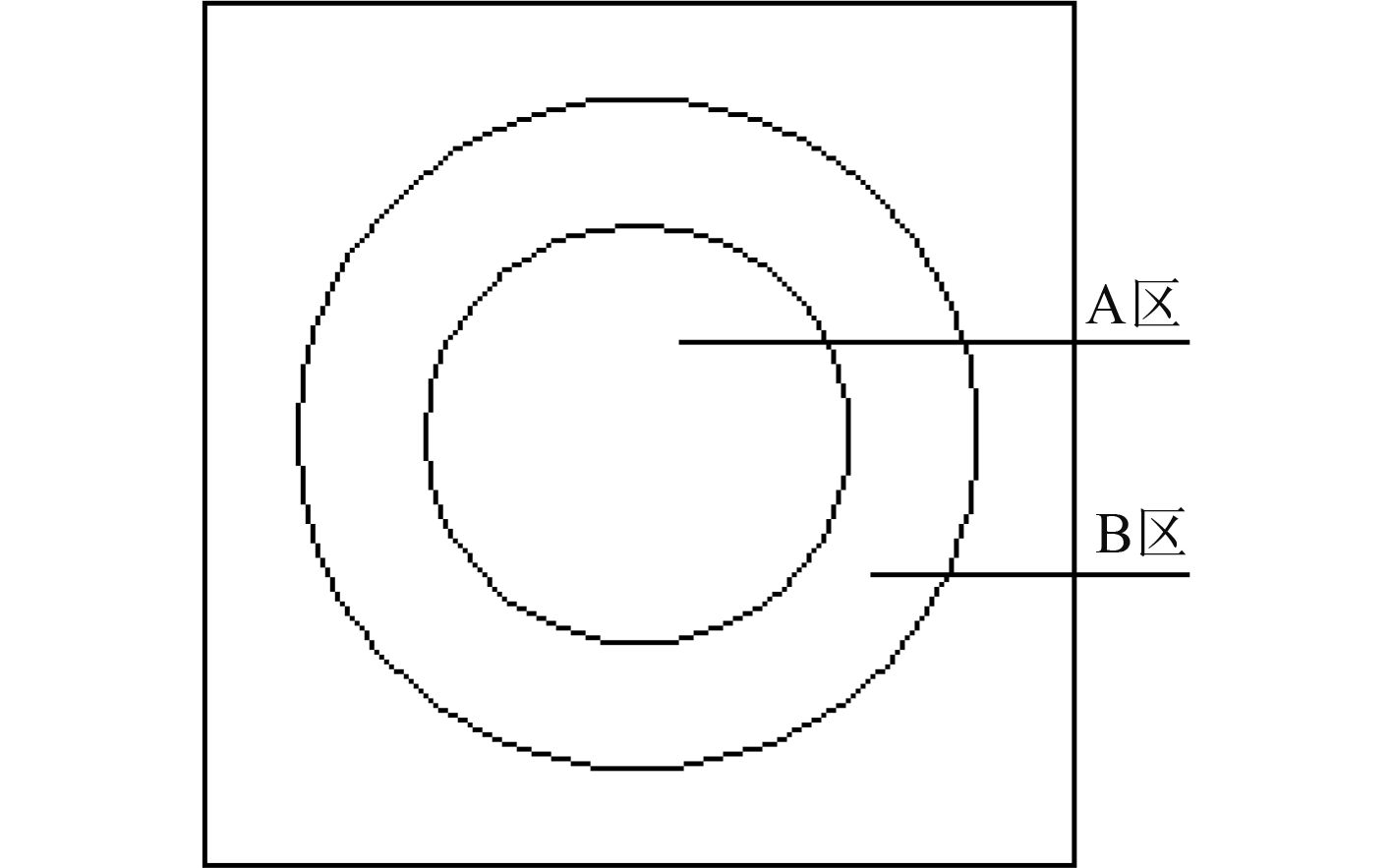
某型发射装置导轨直线度是该装置的关键指标之一,总装过程中,可利用基于PSD的准直激光线位置检测装置对导轨直线度进行校准。由于位置敏感探测器PSD光敏面上电阻率的非均匀性,导致了PSD输出位置标注产生非线性误差[1]。由于制造工艺的不同,PSD的非线性误差大小不同,根据PSD的非线性程度不同,通常把PSD的光敏面人为地划分成A区和B区[2]。如图1所示,A区为中心区,其线性度好,测量误差小;B区为边缘区,其非线性误差较大,测量误差也较大。误差较大不能满足发射装置导轨直线度校准要求,因此需要对准直激光线位置检测装置进行标定来提高测量精度。一般采用硬件补偿或软件方法对PSD的非线性进行校正,来提高测量精度。
|
图 1 PSD的A区和B区 Fig. 1 Regions A and B of PSD |
硬件补偿非线性校正,主要在信号处理部分加入硬件校正环节,该方法电路设计复杂,实现困难且不具有通用性。基于硬件方法的不足,随着现代计算机、微处理器运算速度越来越快,利用软件实现非线性校准受到很多学者的青睐。常用的非线性校准校正方法主要有:查表法、反函数法、曲线拟合法、分段内插法、双一次、双二次插值法及神经网络法[3 – 5]。查表法需要存储大量数据,精度要求越高,查找时间就越长[6]。BP神经网络按照均方差的梯度下降方向收敛,会有局部极小值问题的存在;学习算法的收敛速度慢,且收敛速度与初始权的选择有关;新加入的样本会影响到已选好的样本[7]。
本文根据PSD传感器输出数据的特点,提出利用二元多项式校正PSD的非线性。采用精度远大于待测装置的二维平移台获取被测位置坐标真值,根据PSD位置检测装置输出的坐标位置与二维平移台上读取的标准坐标位置之间的对应关系进行校准,并取得较好的校正效果。
1 多项式校正非线性算法工艺上用于制作PSD材料的非均匀性往往呈现出一种缓慢的梯度变化,PSD表面的电阻率也相应地呈现出了缓慢的梯度变化。因此,整个PSD表面上光斑的位置误差函数
由PSD的原理可知,PSD在x,y方向上的非线性误差是相对独立的,对PSD光敏面上每一点测量值有x方向上的误差值:
| $\Delta x = {E_x}({x_i},{y_j}) = {x_i} - {x_{i0}}\text{,}$ | (1) |
| $\Delta y = {E_y}({x_i},{y_j}) = {y_j} - {y_{j0}}\text{。}$ | (2) |
式中:
二次多项式为:
| $ {{E}_x}({x_i},{y_j}) = a{x^2} + b{y^2} + cxy + dx + ey + f\text{,} $ | (3) |
| ${{E}_y}({x_i},{y_j}) = {a_1}{x^2} + {b_1}{y^2} + {c_1}xy + {d_1}x + {e_1}y + {f_1}\text{;}$ | (4) |
三次多项式为:
| $ \begin{split} {{E}_x}({x_i},{y_j}) = & a{x^3} + b{y^3} + c{x^2}y + dx{y^2} + e{x^2} +\\ & f{y^2} + gxy + hx + iy + k\text{,} \end{split} $ | (5) |
| $ \begin{split} {{E}_y}({x_i},{y_j}) =& {a_1}{x^3} + {b_1}{y^3} + {c_1}{x^2}y + {d_1}x{y^2} +\\ & {e_1}{x^2} + {f_1}{y^2} + {g_1}xy + {h_1}x + {i_1}y + {k_1}\text{;} \end{split} $ | (6) |
四次多项式为:
| $ \begin{split} {{E}_x}({x_i},{y_j}) = a{x^4} + b{y^4} + c{x^3}y + dx{y^3} + e{x^2}{y^2} + f{x^3} + \\ g{y^3} +h{x^2}y + ix{y^2} + j{x^2} + k{y^2} + lxy + mx + ny + p \text{,} \end{split} $ | (7) |
| $ \begin{split} {{E}_y}({x_i},{y_j}) =& {a_1}{x^4} + {b_1}{y^4} + {c_1}{x^3}y + {d_1}x{y^3} + {e_1}{x^2}{y^2} + {f_1}{x^3} + \\ &{g_1}{y^3} + {h_1}{x^2}y + {i_1}x{y^2} + {j_1}{x^2} + {k_1}{y^2} + {l_1}xy +\\ &{m_1}x + {n_1}y + {k_1} \text{。} \end{split} $ | (8) |
多项式拟合主要是其系数的计算,以三次多项式为例说明多项式系数的计算方法。利用测得的n组位置坐标并根据式(1)与式(2)计算出
令
| $ \scriptsize A = \left( {\begin{array}{*{20}{c}} {x_1^3} \!\!\!\!&\!\!\!\! {y_1^3} \!\!\!\!&\!\!\!\! {x_1^2{y_1}} \!\!\!\!&\!\!\!\! {{x_1}y_1^2} \!\!\!\!&\!\!\!\! {x_1^2} \!\!\!\!&\!\!\!\! {y_1^2} \!\!\!\!&\!\!\!\! {{x_1}{y_1}} \!\!\!\!&\!\!\!\! {{x_1}} \!\!\!\!&\!\!\!\! {{y_1}} \!\!\!\!&\!\!\!\! 1 \\ {x_2^3} \!\!\!\!&\!\!\!\! {y_2^3} \!\!\!\!&\!\!\!\! {x_2^2{y_2}} \!\!\!\!&\!\!\!\! {{x_2}y_2^2} \!\!\!\!&\!\!\!\! {x_2^2} \!\!\!\!&\!\!\!\! {y_2^2} \!\!\!\!&\!\!\!\! {{x_2}{y_2}} \!\!\!\!&\!\!\!\! {{x_2}} \!\!\!\!&\!\!\!\! {{y_2}} \!\!\!\!&\!\!\!\! 1 \\ {x_3^3} \!\!\!\!&\!\!\!\! {y_3^3} \!\!\!\!&\!\!\!\! {x_3^2{y_3}} \!\!\!\!&\!\!\!\! {{x_3}y_3^2} \!\!\!\!&\!\!\!\! {x_3^2} \!\!\!\!&\!\!\!\! {y_3^2} \!\!\!\!&\!\!\!\! {{x_3}{y_3}} \!\!\!\!&\!\!\!\! {{x_3}} \!\!\!\!&\!\!\!\! {{y_3}} \!\!\!\!&\!\!\!\! 1 \\ {x_4^3} \!\!\!\!&\!\!\!\! {y_4^3} \!\!\!\!&\!\!\!\! {x_4^2{y_4}} \!\!\!\!&\!\!\!\! {{x_4}y_4^2} \!\!\!\!&\!\!\!\! {x_4^2} \!\!\!\!&\!\!\!\! {y_4^2} \!\!\!\!&\!\!\!\! {{x_4}{y_4}} \!\!\!\!&\!\!\!\! {{x_4}} \!\!\!\!&\!\!\!\! {{y_4}} \!\!\!\!&\!\!\!\! 1 \\ \vdots \!\!\!\!&\!\!\!\! \vdots \!\!\!\!&\!\!\!\! \vdots \!\!\!\!&\!\!\!\! \vdots \!\!\!\!&\!\!\!\! \vdots \!\!\!\!&\!\!\!\! \vdots \!\!\!\!&\!\!\!\! \vdots \!\!\!\!&\!\!\!\! \vdots \!\!\!\!&\!\!\!\! \vdots \!\!\!\!&\!\!\!\! \vdots \\ {x_{n - 1}^3} \!\!\!\!&\!\!\!\! {y_{n - 1}^3} \!\!\!\!&\!\!\!\! {x_{n - 1}^2{y_{n - 1}}} \!\!\!\!&\!\!\!\! {{x_{n - 1}}y_{n - 1}^2} \!\!\!\!&\!\!\!\! {x_{n - 1}^2} \!\!\!\!&\!\!\!\! {y_{n - 1}^2} \!\!\!\!&\!\!\!\! {{x_{n - 1}}{y_{n - 1}}} \!\!\!\!&\!\!\!\! {{x_{n - 1}}} \!\!\!\!&\!\!\!\! {{y_{n - 1}}} \!\!\!\!&\!\!\!\! 1 \\ {x_n^3} \!\!\!\!&\!\!\!\! {y_n^3} \!\!\!\!&\!\!\!\! {x_n^2{y_n}} \!\!\!\!&\!\!\!\! {{x_n}y_n^2} \!\!\!\!&\!\!\!\! {x_n^2} \!\!\!\!&\!\!\!\! {y_n^2} \!\!\!\!&\!\!\!\! {{x_n}{y_n}} \!\!\!\!&\!\!\!\! {{x_n}} \!\!\!\!&\!\!\!\! {{y_n}} \!\!\!\!&\!\!\!\! 1 \end{array}} \right)\text{,} $ |
| $ {B = }\left( {\begin{array}{*{20}{c}} {\Delta {x_1}}&{\Delta {y_1}} \\ {\Delta {x_2}}&{\Delta {y_2}} \\ {\Delta {x_3}}&{\Delta {y_3}} \\ {\Delta {x_4}}&{\Delta {y_4}} \\ \vdots &{} \\ {\Delta {x_{n - 1}}}&{\Delta {y_{n - 1}}} \\ {\Delta {x_n}}&{\Delta {y_n}} \end{array}} \right)\text{,} X = \left( {\begin{array}{*{20}{c}} a&{{a_1}} \\ b&{{b_1}} \\ c&{{c_1}} \\ d&{{d_1}} \\ e&{{e_1}} \\ f&{{f_1}} \\ g&g \end{array}} \right)\text{,} $ |
则可得方程组AX=B,这是一个超静定方程组。利用最小二乘法[8]求解方程组中的系数得:
| ${X = }{\left( {{A^{\rm T}}A} \right)^{ - 1}}{A^{\rm T}}B\text{。}$ | (9) |
把求得的系数代入式(5)与式(6)即可得到测量值与标准值的误差:
| $B = AX\text{。}$ | (10) |
再用测量值减去误差即可计算出PSD实际的输出位置值:
| ${X_R} = {X_{out}} - \Delta x\text{,}$ | (11) |
| ${Y_R} = {Y_{out}} - \Delta y\text{。}$ | (12) |
式中:
利用VC编写程序实现算法,具体程序实验步骤如下:
1)编写打开文件程序,从文件中读取PSD位置检测装置测量的位置坐标,即读取用来校正的原始数据存储在数组中。
2)根据二维平移台测量的数据与PSD输出的位置坐标,利用式(1)与式(2)分别计算出Δx,Δy。
3)利用循环结构计算出每个坐标对应方程的幂次项。
4)利用CMatrix类计算矩阵A与矩阵B,通过矩阵的运算求得矩阵X。
5)利用式(11)与式(12)对每一个位置坐标进行修正,求出修正后的均方差,最后把校正后的结果输出到文件中。
2 二维PSD标定系统二维PSD标定系统由二维平移台、激光发射装置、导轨、待测装置组成。选择标准导轨,利用经纬仪校准其直线度。在导轨的一端把二维平移台垂直固定在标准长导轨上,把激光发射装置固定在二维平移台上。在导轨的另一端固定位置检测装置,并使PSD表面与导轨垂直,从而保证了激光光斑能够垂直打在PSD表面上。
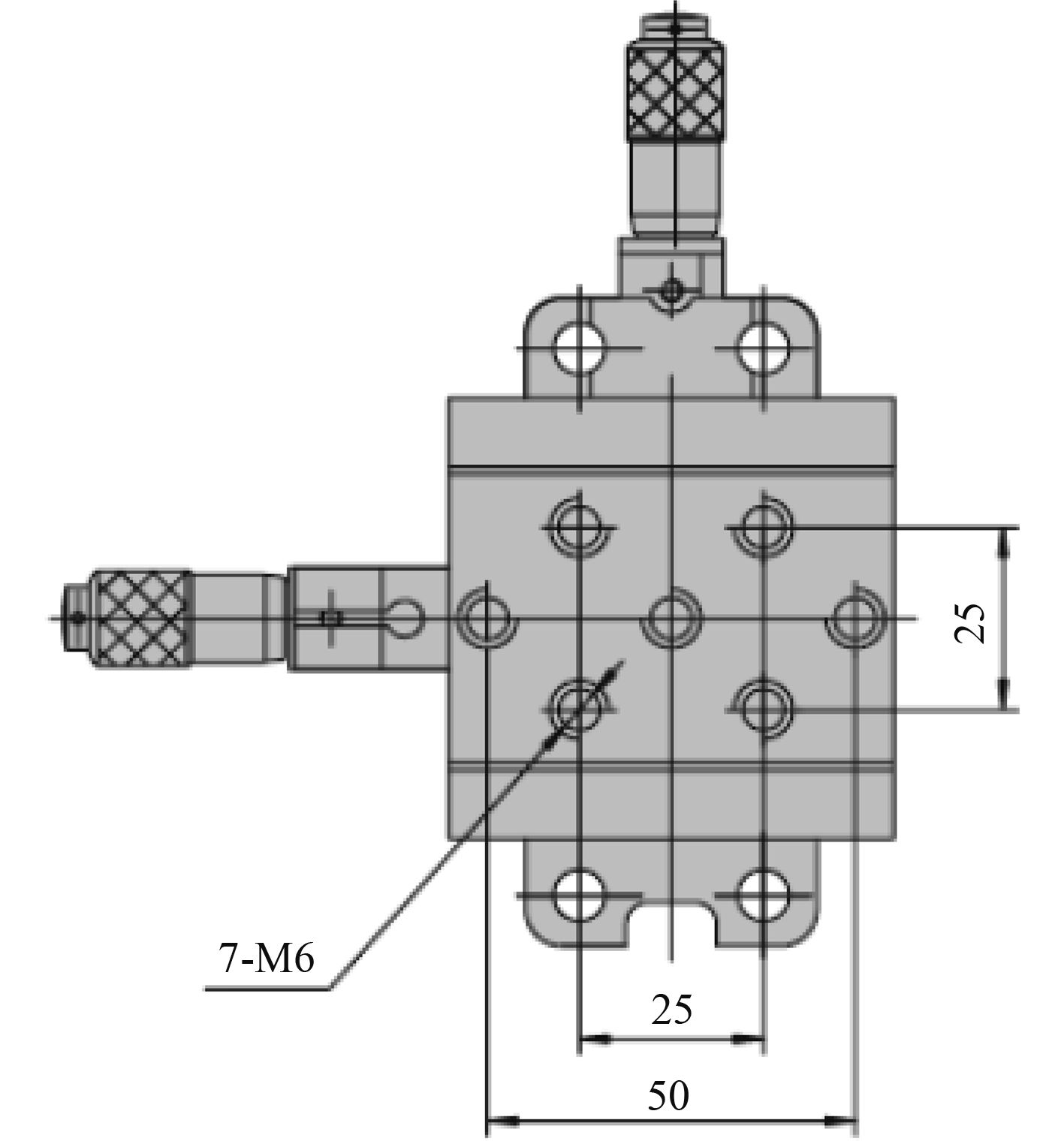
2.1 二维平移台选择标定系统中选择上海正信光学仪器有限公司的二维平移台,其结构设计紧凑,在小的体积内实现两轴平移调整,并且两轴正交精度高,左右手成对设计,两轴的测微头安装在同一个水平面上,方便操作。该平移台行程15 mm,最小刻度0.01 mm,灵敏度0.002 mm,完全能够满足校准本设备0.01 mm的精度要求。其结构图如图2所示。
|
图 2 二维平移台结构图 Fig. 2 Structure diagram of two-dimensional translation table |
在准直激光线位置检测系统中,由于激光具有高亮度、高单色性、高方向性等特点,设计中选用半导体激光器作为光源。半导体激光器是以一定的半导体材料做工作物质而产生受刺激发射作用的器件,其工作原理是通过一定的激励方式,利用半导体物质在能带间跃迁发光,用半导体晶体的解理面形成2个平行反射镜面作为反射镜,组成谐振腔,使光振荡、反馈、产生光的辐射放大,输出激光。
根据二维PSD的频谱响应特性可知PSD对930 nm波长的光响应灵敏度最大,但由于可见光波长范围为350 ~ 770 nm之间,波长930 nm的光为不可见光,考虑到实际测量时的方便性,在实际应用时选用波长630 nm的可见红色激光作为激光源。其光斑直径2 mm,功率5 mW。
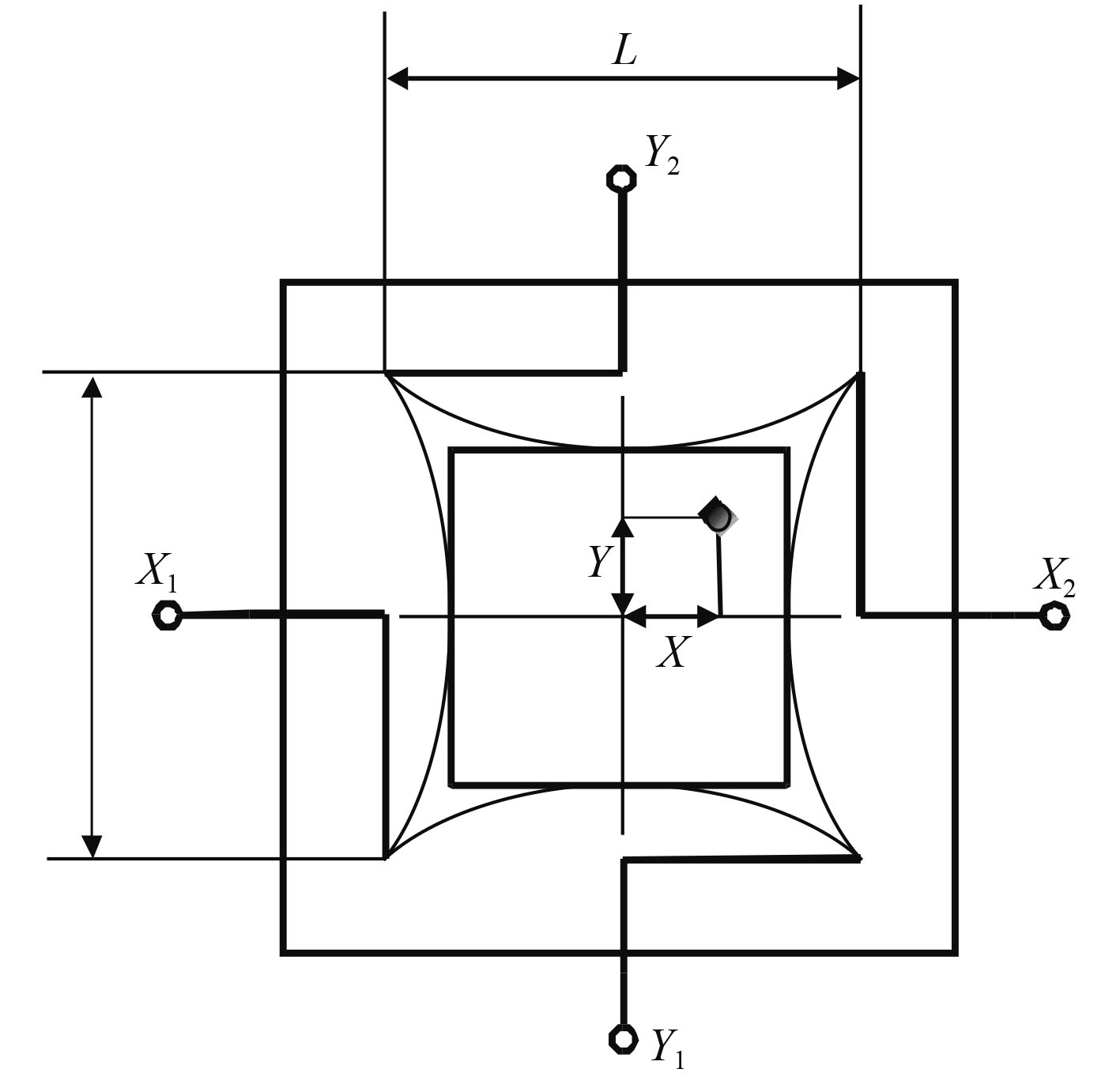
2.3 PSD的选择根据实际测量需求,在所设计的检测装置中采用二维枕型PSD-1515型PSD,该PSD具有位置分辨率高、光谱响应宽、响应速度快、位置和光强同时测量、不受光斑的约束、可靠性高等特点,在工业工程领域得到广泛应用。具体可应用在光学位置和角度的探测、光学遥测系统、位移和振动测量、激光对中和准直、距离测试、人类运动姿态分析等领域。枕型PSD的结构如图3所示。
|
图 3 枕型PSD结构 Fig. 3 Occipital PSD structure |
PSD-1515具体参数:有效光敏区为15 mm*15 mm,分辨率1 μm,响应时间1 μs,响应光谱范围380 ~1 100 nm,反偏电压为6 V。
3 原始数据测量方法1)首先调整二维平移台使得光斑打在PSD中心位置,即令位置检测装置输出坐标为(0,0)位置。
2)移动二维平移台,向左移动3 mm,向下移动3 mm,使得光斑打在PSD左下角,标准位置坐标(–3,–3)。
3)固定二维平移台左右方向位置不动,上下方向移动二维平移台带动激光发射器移动,每移动0.5 mm记录一次测量结果。测量13组数据,即位置坐标为(–3,3)。
4)向右移动二维平移台0.5 mm,然后上下移动二维平移台同样每隔0.5 mm记录一次结果,直到位置坐标为(–2.5,–3)为止。
5)重复上述过程,测量整个PSD平面,直到光斑位置坐标(3,3)时结束,这样可测得169个点坐标。
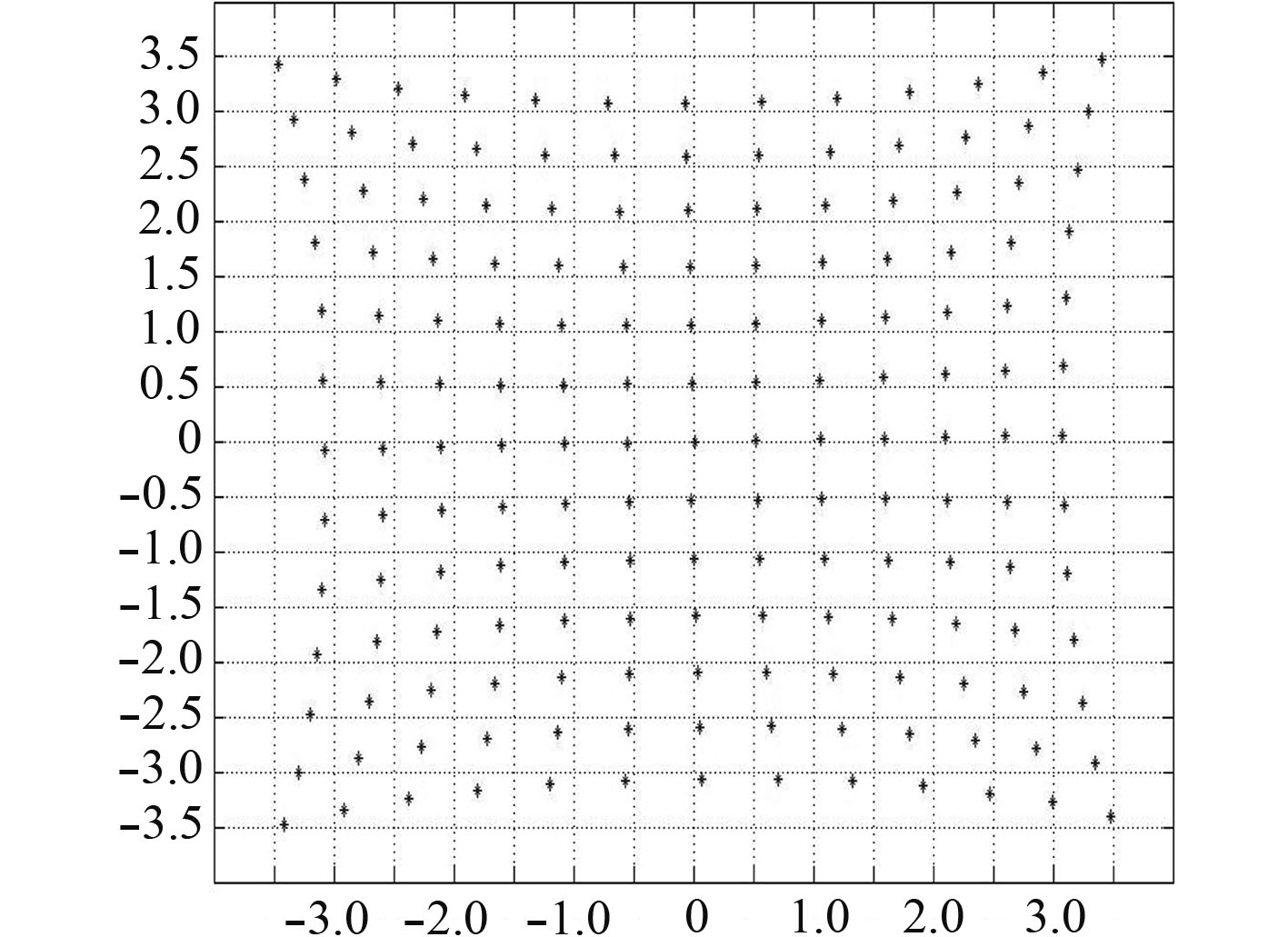
4 非线性校正实验结果分析实验中测得12组数据,利用Matlab画出位置坐标在平面中的点图,每组实验数据都有相似的特点,其中一组数据点图如图4所示。通过点图分析PSD光斑的非线性呈现一定规律:点图分布呈中心对称,四个象限的误差具有相似特性,并且在PSD的中心区域(即坐标为(0,0)位置附近的区域)其误差较小,距离中心区域越大,其非线性越大,测试数据符合PSD的特性,即中心区域的A区线性度好,距离中心区域远的B区线性度差的特点。由于测试数据是每隔0.5 mm的测量结果,其理想位置应该都是坐标虚线的交点处,根据点图分布可看出PSD的非线性呈现平滑的曲线,因此采用多项式拟合。
|
图 4 原始实验数据点图 Fig. 4 Original experimental data point diagram |
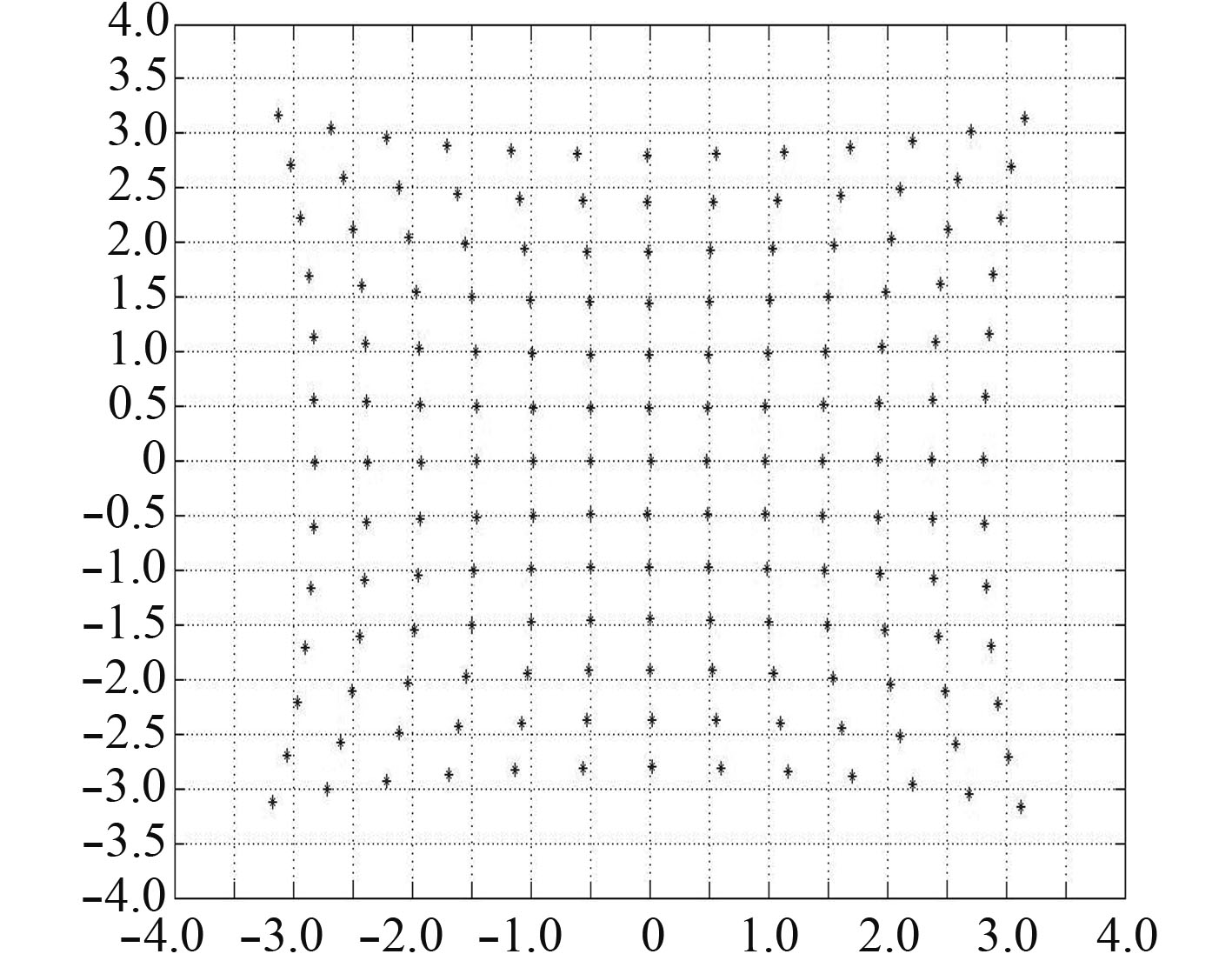
利用二次多项式校正后的数据结果画出的数据点图如图5所示。
|
图 5 二次多项式校正结果 Fig. 5 Quadratic polynomial correction result |
从图4中可看出,利用二次多项式对PSD进行非线性校正其效果不好,非线性误差仍然很大。通过计算可得校正后的均方差x方向均方差为0.093 6,y方向均方差为0.096 2。均方差仍很大,不能满足装置精度要求。
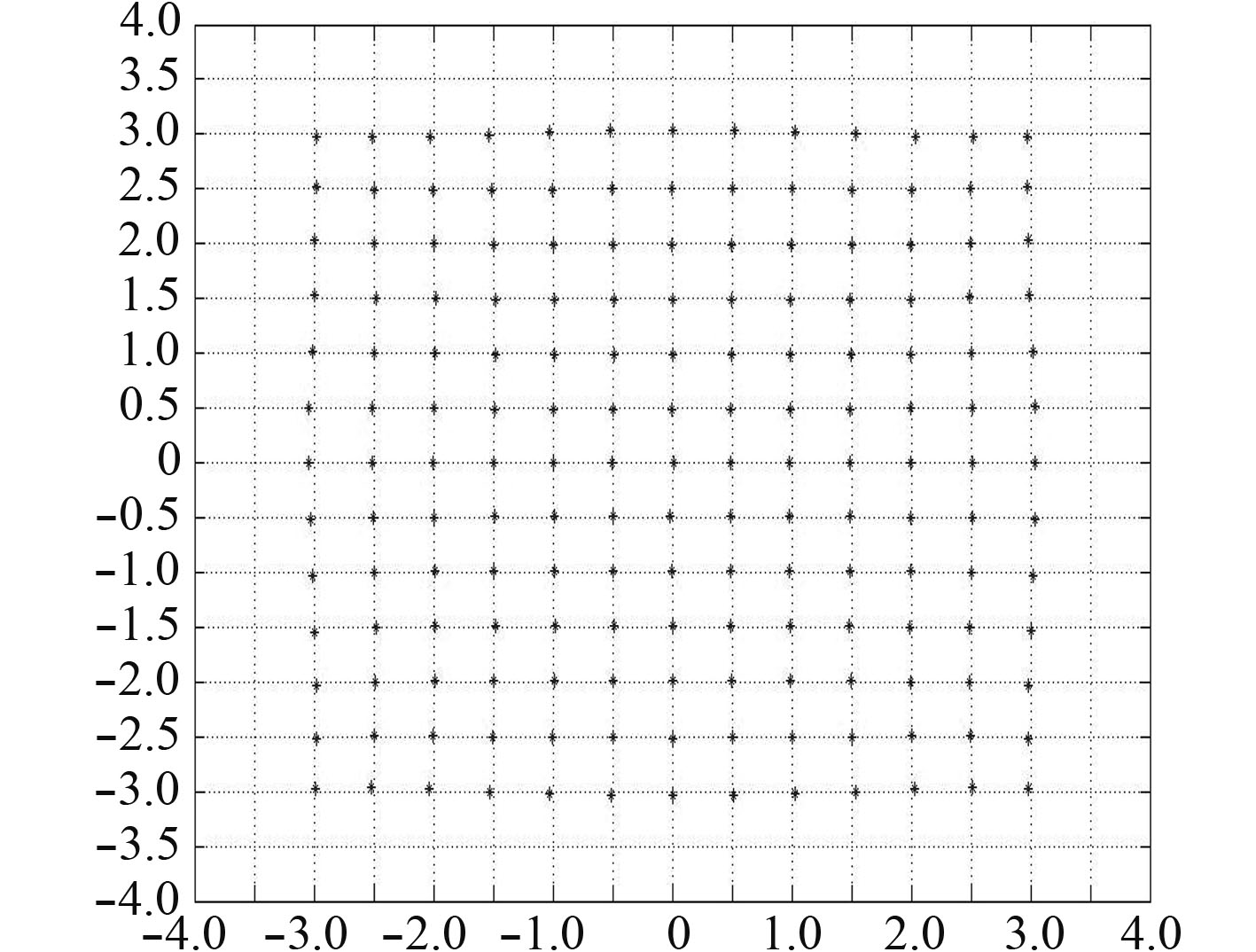
利用三次多项式校正后的数据结果画出的点图如图6所示。从图中可看出校正后的数据其非线性明显得到修正。中心区域的最大误差小于0.01 mm,最外层的校正效果还不是很理想,这符合PSD的特性,即中心区域线性度好,距离中心区域越远其非线性度越大。其校正后均方差分别为:x=0.015 8,y=0.015 5。其均方差已经很小,能够满足装置测量精度要求。
|
图 6 三次多项式校正结果 Fig. 6 Cubic polynomial correction result |
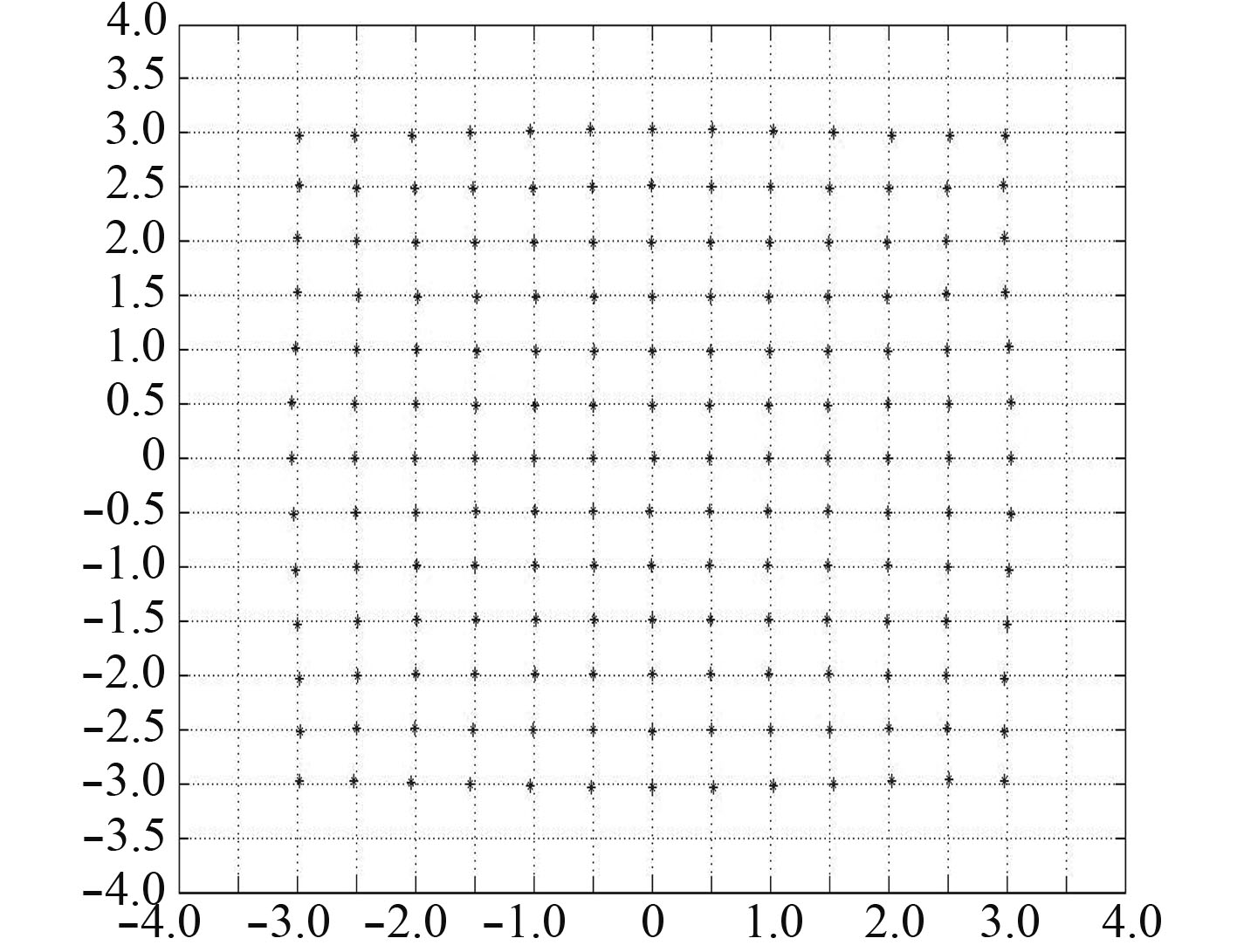
利用四次多项式校正后数据位置点图如图7所示。
|
图 7 四次多项式校正结果 Fig. 7 Quartic polynomial correction result |
从图7可以看出其校正效果较好,比较图6与图7,可得出利用三次多项式与四次多项式校正的结果相似。利用四次多项式校正后的均方差分别为x=0.015 7,y=0.015 4,其均方差与三次校正后的均方差相近,其非线性校正效果没有得到更好的改善。
根据多项式系数分析,x方向偏差校正多项式中x幂次项前的系数较大,因此x方向偏差主要由x坐标值决定,y方向同理。分析四次多项式中四次项前的系数,x方向偏差校正多项式中四次项系数分别为:–0.000 094,–0.000 061,–0.000 052,–0.000 049,–0.000 039,y方向偏差校正多项式中四次项系数分别为:–0.000 041,0.000 001,–0.000 034,0.000 051,–0.000 045,其系数都很小,对非线性校正作用很小。由此可推出高于四次的多项式其校正效果相似,因此,设计中采用三次多项式校正PSD的非线性。
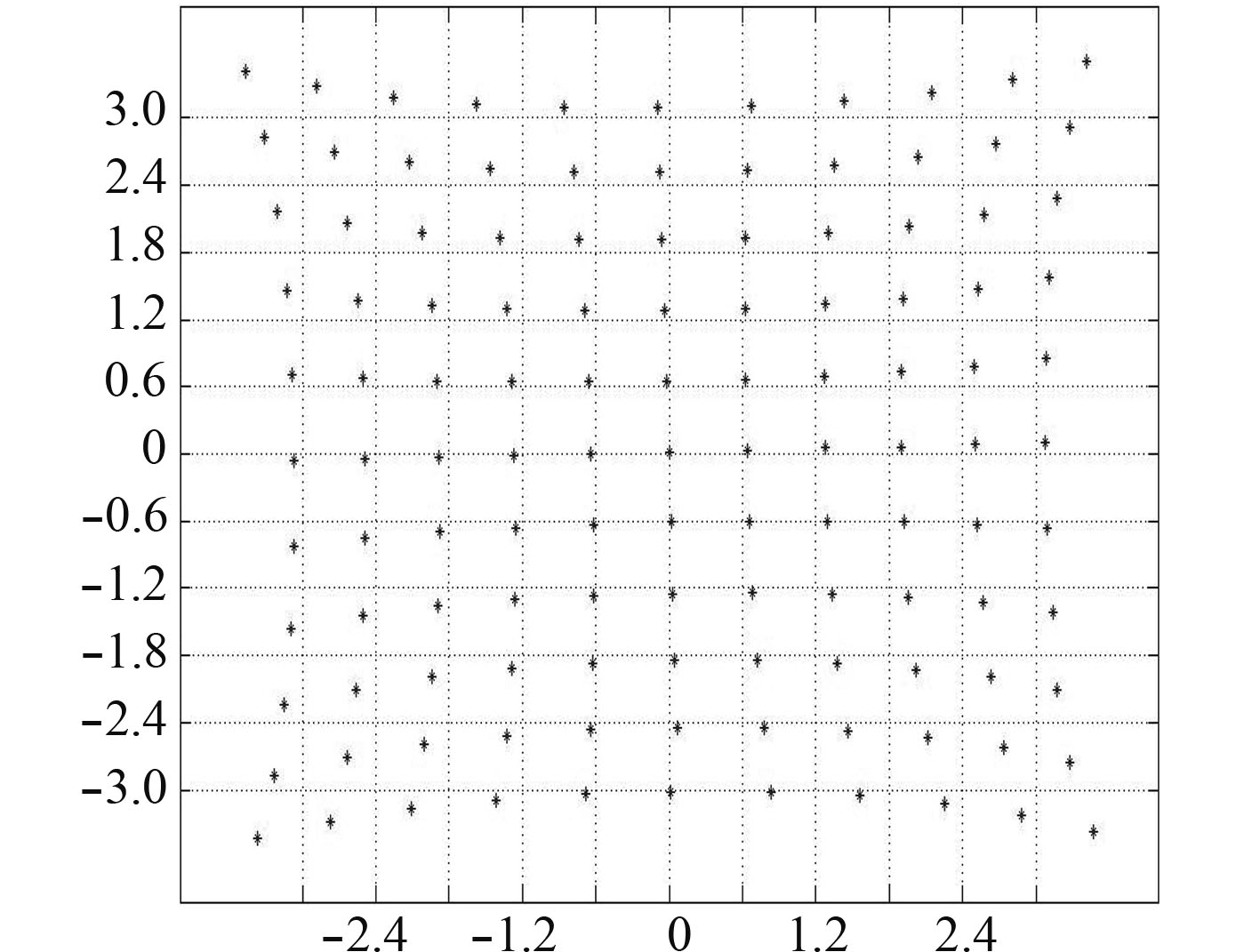
为了验证校正后的效果,在PSD光敏面多个不同位置测量数据进行校正,其中在位置为0,±0.6 mm,±1.2 mm,±1.8 mm,±2.4 mm,±3.0 mm处测得的一组数据如图8所示。
|
图 8 原始数据点图 Fig. 8 Original data point diagram |
利用式(11)与式(12)求出偏差,校正后的结果如图9所示。
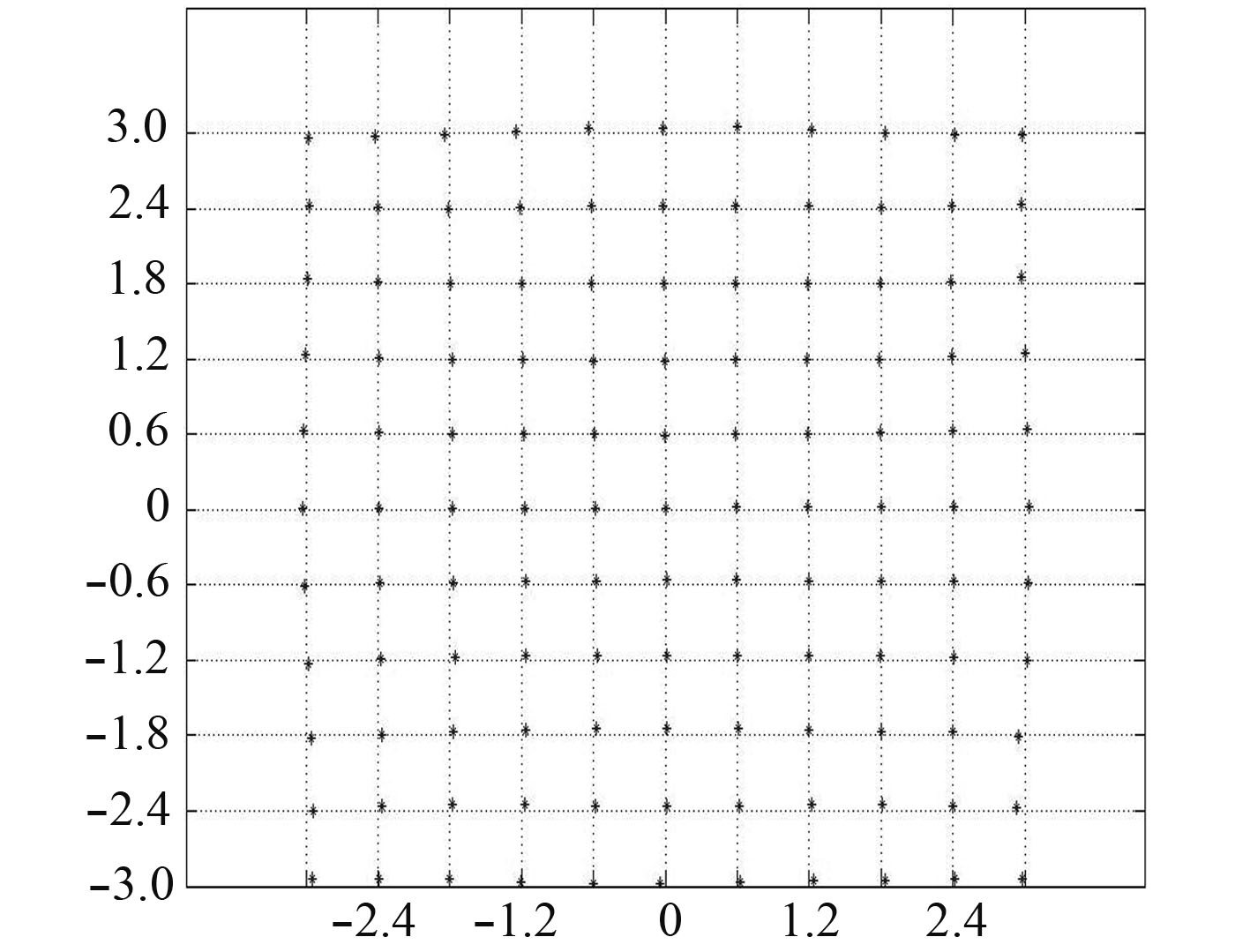
|
图 9 校正后的结果 Fig. 9 Corrected result |
校正后的均方差为:x方向0.018 5,y方向0.011 7。从图9可看出,中心校正结果较好,利用中心区域进行发射装置导轨直线度校准可满足测量要求。
| [1] |
史春玉, 李田泽, 仝其丰, 等. 基于改进共轭梯度算法的二维PSD非线性修正[J]. 山东理工大学学报(自然科学版), 2017(2): 27-30. DOI:10.3969/j.issn.1672-6197.2017.02.006 |
| [2] |
周宝玉, 陈培锋, 朱明珠. 位置敏感探测器非线性误差修正实验研究[J]. 光学仪器, 2005(5): 13-17. |
| [3] |
管炳良, 李星, 王俊. 二维PSD非线性修正技术研究[J]. 仪器仪表学报, 2007(7): 1295-1299. DOI:10.3321/j.issn:0254-3087.2007.07.027 |
| [4] |
谭超. 基于三次样条函数的传感器特性曲面二维插值[J]. 传感器技术, 2005(1): 69-71. DOI:10.3969/j.issn.1000-9787.2005.01.027 |
| [5] |
莫长涛, 陈长征, 张黎丽, 等. 二维PSD非线性修正的神经网络算法的研究[J]. 光电子·激光, 2003(4): 342-344. DOI:10.3321/j.issn:1005-0086.2003.04.003 |
| [6] |
张家田, 董秀莲. 非线性传感器的校正方法[J]. 石油工业技术监督, 2002(6): 27-29. DOI:10.3969/j.issn.1004-1346.2002.06.010 |
| [7] |
牟丽娜, 陈鸿, 陈闽鄂. 基于L-M算法的二维PSD非线性校正[J]. 计量与测试技术, 2006(12): 21-22. DOI:10.3969/j.issn.1004-6941.2006.12.013 |
| [8] |
徐士良. 数值分析与算法[M]. 北京: 机械工业出版社, 2003.266–276.
|
 2019, Vol. 41
2019, Vol. 41
