在船舶管路系统中,各种各样的阀门至关重要,这些阀门装置的作用是对流体的流量、压力及流动方向进行调节和控制以满足系统的要求,但由于其内部流道结构一般相对于管路系统其他结构更为复杂,流噪声问题突出,进而影响管路系统的振动噪声。随着阀门设计、制造技术水平的不断提高,不仅要求其能完成对传输介质的通断,同时对其工作过程中的声学性能要求也越来越高[1]。
目前,流体力学问题,尤其是湍流问题,机理方面的研究进展较为缓慢,加之阀门内部流道结构、边界条件及支配方程的复杂性,直接对其进行解析研究难度较大。随着近些年CFD技术的飞跃式发展,特别是计算速度的大幅提升,使得对流体通道内的声场性能进行仿真分析成为可能。针对阀门内部流场,国内外学者进行过许多研究。其中,刘少刚等[1]采用计算流体力学通用软件Fluent对实际使用中的通海阀内流场分布进行仿真计算,并对其结构进行改进提出了一种新型内流道结构;江山等[2]根据可视化结果分析影响通海阀性能和产生噪声的原因.为通海阀的内流道优化提供理论依据;Ito等[3]用有限差分法对液压锥阀层流流场进行了研究。本文针对不同类型、不同规格阀门,结合相关理论研究,建立流道的几何模型,借助于流体力学通用软件Fluent,进行了阀门声学性能计算与对比分析。
1 仿真方法 1.1 阀门流道建模由于阀门内部流道的复杂性,借助专业的三维建模软件ProE对阀体内部流道进行建模,综合运用了变剖面造型等多项几何建模技术,并去除了部分倒圆角,在兼顾后续网格顺利划分的同时,保证了流道几何尺寸的准确性。
1.2 仿真对象本文选取的数值仿真计算对象如表1所示。
|
|
表 1 各规格阀门计算对象 Tab.1 Valve calculating objects of various specifications |
典型阀门流体通道的几何模型如图1所示。

|
图 1 典型阀门流体通道的几何模型 Fig. 1 Geometric model of typical valve fluid channel |
对于阀门内流体介质,为不可压缩流体。入口处流速约为2.5 m/s,取20 ℃时海水的动力粘度系数为1.005×10–3 Pa·s、海水的密度约为1 025 kg/m3,以最小公称通径DN10阀门计算无量纲雷诺数:
| $ {{R}_{e}}=\frac{vd\rho }{\eta }=\frac{2.5\times 0.01\times 1\;025}{1.005\times {{10}^{-3}}}=25\;498\text{。} $ | (1) |
对于圆形充液管路,Re>2300时内部液体即为湍流流动,因此阀门内流体介质处于湍流状态,计算时需要选择合适的湍流模型。
1.4 基本理论1)RANS控制方程
直角坐标系下,不可压缩牛顿流体连续性方程与RANS方程为:
| $ \frac{\partial \overline{{{u}_{i}}}}{\partial {{x}_{i}}}=0\text{,}\hspace{170pt} $ | (2) |
| $ \rho \frac{\partial \overline{{{u}_{i}}}}{\partial t}+\rho \overline{{{u}_{j}}}\frac{\partial \overline{{{u}_{i}}}}{\partial {{x}_{j}}}=\rho \overline{{{F}_{i}}}-\frac{\partial \overline{p}}{\partial {{x}_{i}}}+\frac{\partial }{\partial {{x}_{j}}}(\mu \frac{\partial \overline{{{u}_{i}}}}{\partial {{x}_{j}}}-\rho \overline{{{{{u}'}}_{i}}{{{{u}'}}_{j}}})\text{。} $ | (3) |
其中:
2)湍流模型
以上的方程组不封闭,需要采用相应的湍流模型。湍流过程的复杂性和工程计算的多层次性决定了湍流模型的多样性,不同的湍流模型有着自己不同的适用范围,主要的湍流模型包括标准k-ε模型、RNG k-ε模型、可实现k-ε模型、标准k-ε模型、大涡模型(LES)等。其中,二方程模型中的标准k-ε模型是在工业应用中被普遍使用的湍流模型,其计算收敛性和精确性都非常符合工程计算的要求,因此在本文中选取标准k-ε模型进行计算。
在标准k-ε模型中,湍流动能k和湍流耗散率ε方程分别为:
| $ \rho \frac{Dk}{Dt}=\frac{\partial }{\partial {{x}_{i}}}\left[ \left( \mu +\frac{{{\mu }_{t}}}{{{\sigma }_{k}}} \right)\frac{\partial k}{\partial {{x}_{i}}} \right]+{{G}_{k}}+{{G}_{b}}-\rho \varepsilon -{{Y}_{M}}\text{,}\hspace{20pt} $ | (4) |
| $ \rho \frac{D\varepsilon }{Dt}\!=\!\frac{\partial }{\partial {{x}_{i}}}\left[ \left( \mu \!+\!\frac{{{\mu }_{t}}}{{{\sigma }_{k}}} \right)\frac{\partial \varepsilon }{\partial {{x}_{i}}} \right]\!+\!{{C}_{1\varepsilon }}\frac{\varepsilon }{k}({{G}_{k}}\!+\!{{C}_{3\varepsilon }}{{G}_{b}})\!-\!{{C}_{2\varepsilon }}\rho \frac{{{\varepsilon }^{2}}}{k}\text{。} $ | (5) |
式中:k为湍动能量;ε为耗散率;Gk表示由于平均速度梯度引起的湍动能产生;Gb是由于浮力影响引起的湍动能产生;YM可压缩湍流脉动膨胀对总的耗散率的影响;σk,C1ε,C2ε,C3ε为常系数;μt为湍流粘性系数,且有:
| $ {{\mu }_{t}}=\rho {{C}_{\mu }}\frac{{{k}^{2}}}{\varepsilon }\text{。} $ | (6) |
为保证来流的稳定性与出口段的充分发展,阀门上下游均延长5DN,在Ansys Workbench中的DS中完成网格划分后导入Fluent进行分析,边界条件设置如下:
1)入口边界。入口设置为速度入口,方向垂直于边界,大小为2.5 m/s;
2)出口边界。出口设置为Outflow边界条件,即自由出流;
3)壁面。流体通道的壁面采用固壁边界条件,即设定为无滑移条件u=v=ω=0,并在近壁面处设置边界层,加密网格。
1.6 计算方法在考虑湍流的许多实际应用中,噪声并不存在清晰的音调,噪声能是在一个宽频带范围呈连续分布的。在这种宽频噪声的条件下,可以从RANS方程计算统计意义上的湍流量,并结合半经验公式和Lighthill气动噪声比拟理论来解决宽频噪声问题,而宽带声源模型中的Proudman噪声能近似公式用于预测流场噪声问题的方法在国内外某些领域已得到一定范围的应用和验证[4 – 6]。
本文利用BNS(broadband noise source)模型进行流场流噪声计算,计算中须在Fluent中设置BNS模型参数,该模型借助统计方法,推导出适用于每个体单元的声功率表达式。
各向同性湍流单位体积中所产生的声能:
| $ {{P}_{A}}=\alpha {{\rho }_{0}}\left( \frac{{{u}^{3}}}{l} \right)\frac{{{u}^{5}}}{\alpha _{0}^{5}}\text{,} $ | (7) |
上式又可写为:
| $ {{P}_{A}}={{\alpha }_{\varepsilon }}{{\rho }_{0}}\varepsilon M_{t}^{5}\text{,} $ | (8) |
声功率级为:
| $ {{L}_{P}}=10\ \lg \left( \frac{{{P}_{A}}}{{{\operatorname{P}}_{ref}}} \right)\text{。} $ | (9) |
式中:u为湍流速度;l为湍流特征尺度;α0为声速度;α为模型常数;
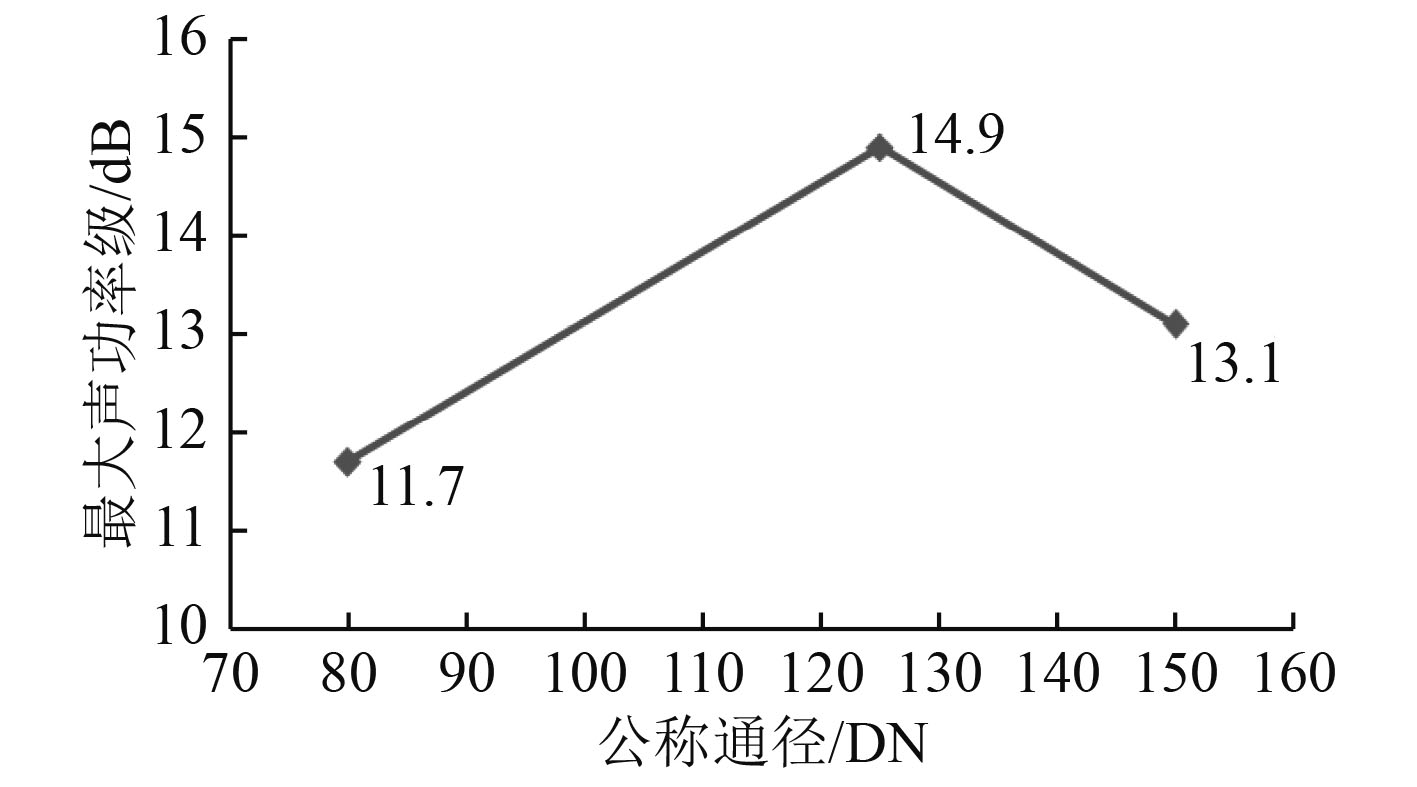
由表2和图2可知,DN80的阀门声学性能较优,DN125的阀门声学性能较差。
|
|
表 2 各公称通径阀门声场计算结果 Tab.2 Summary of calculation results of sound field of nominal size valves |
|
图 2 最大声功率级对比图 Fig. 2 Maximum sound power level contrast diagram |
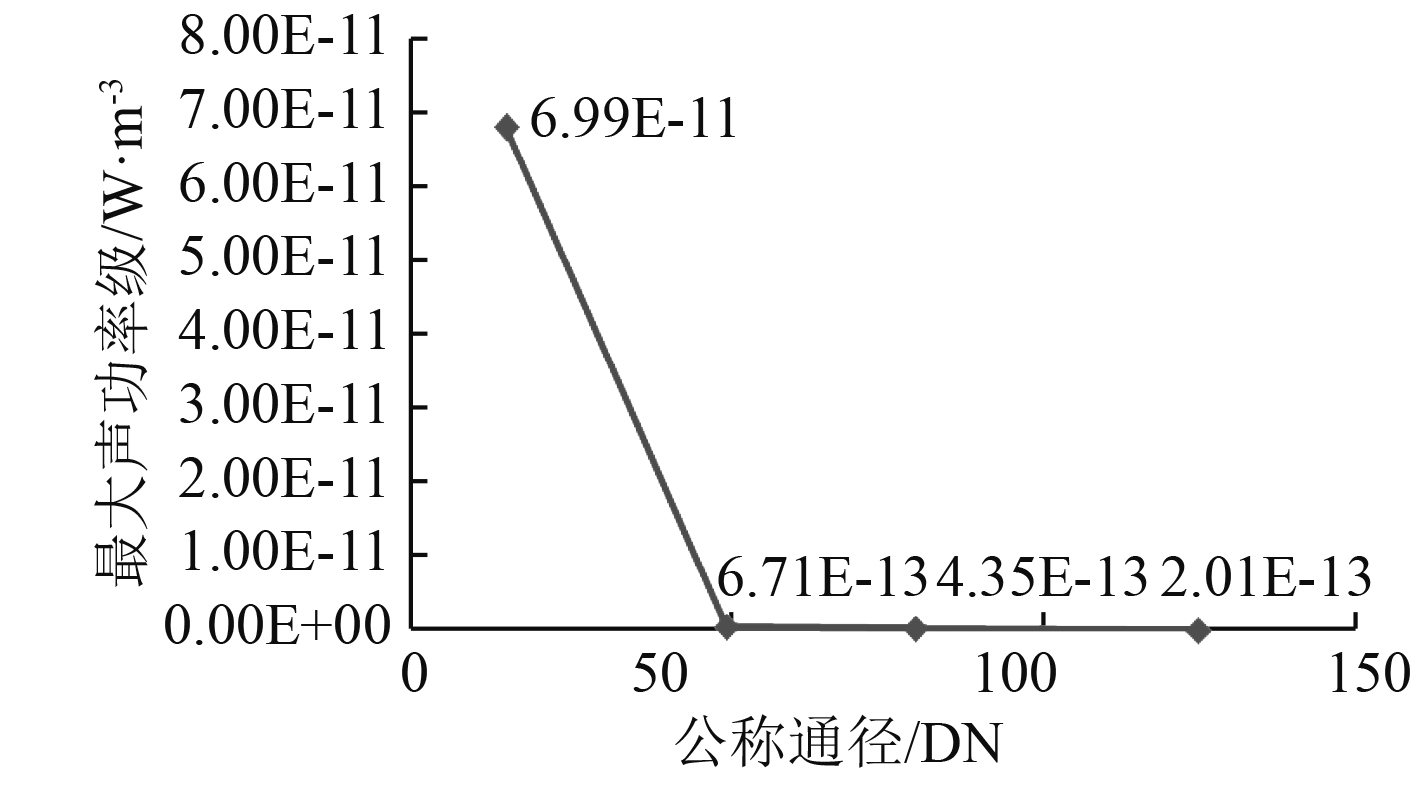
由表3和图3可知,DN125的阀门声学性能较优,DN15的阀门声学性能较差。
|
|
表 3 各公称通径阀门声场计算结果 Tab.3 Summary of calculation results of sound field of nominal size valves |
|
图 3 最大声功率对比图 Fig. 3 Maximum sound power contrast diagram |
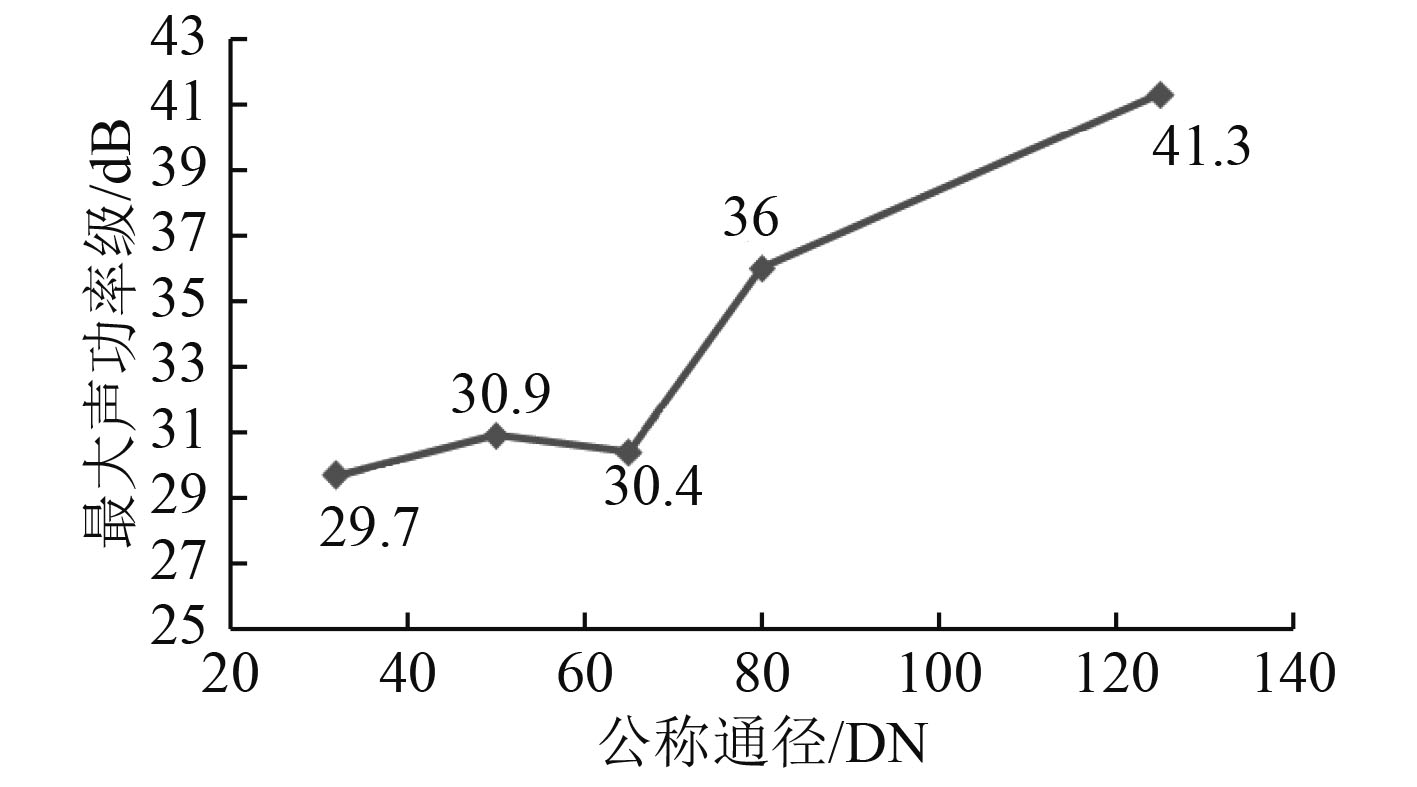
由表4和图4可知,DN32的阀门声学性能较优,DN125的阀门声学性能较差。
|
|
表 4 各公称通径阀门声场计算结果 Tab.4 Summary of calculation results of sound field of nominal size valves |
|
图 4 最大声功率级对比图 Fig. 4 Maximum sound power level contrast diagram |
由表5和图5可知,DN65的阀门声学性能较优,DN125的阀门声学性能较差。
|
|
表 5 各公称通径阀门声场计算结果 Tab.5 Summary of calculation results of sound field of nominal size valves |

|
图 5 最大声功率级对比图 Fig. 5 Maximum sound power level contrast diagram |
由表6和图6可知,DN125的阀门声学性能较优,DN150的阀门声学性能较差。
|
|
表 6 各公称通径阀门声场计算结果 Tab.6 Summary of calculation results of sound field of nominal size valves |

|
图 6 最大声功率级对比图 Fig. 6 Maximum sound power level contrast diagram |
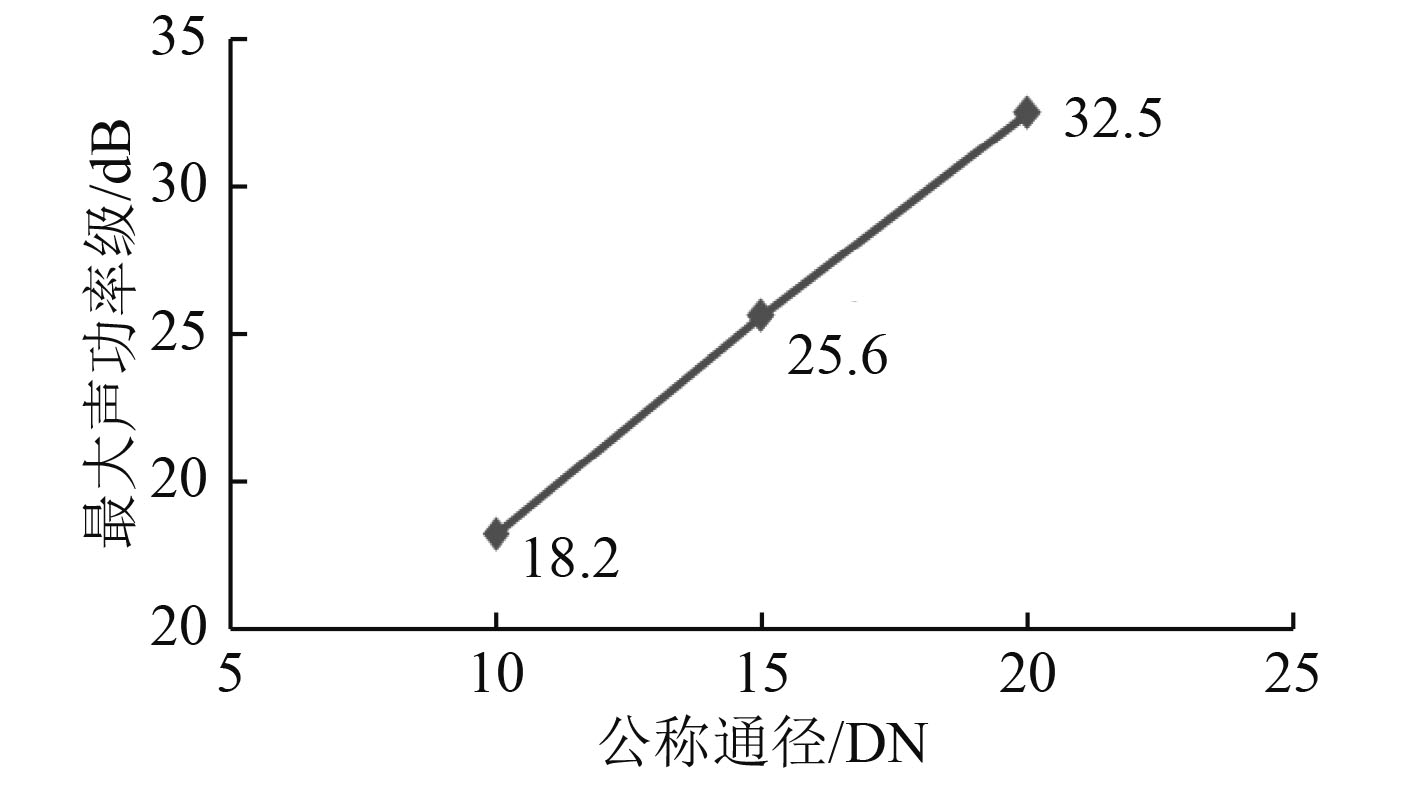
由表7图7可知,DN10的阀门声学性能较优,DN20的阀门声学性能较差。
|
|
表 7 各公称通径阀门声场计算结果 Tab.7 Summary of calculation results of sound field of nominal size valves |
|
图 7 最大声功率级对比图 Fig. 7 Maximum sound power level contrast diagram |
由表8可知,对于公称通径同为DN50的阀门,球阀声学性能较优,截止阀、截止止回阀、节流阀声学性能较差;对于公称通径同为DN80的阀门,球阀声学性能较优,蝶阀、截止止回阀声学性能较差;对于公称通径同为DN125的阀门,球阀声学性能较优,蝶阀、截止阀、截止止回阀声学性能较差。
|
|
表 8 相同公称通径、不同参考标准阀门声场计算结果 Tab.8 Summary of acoustic field calculations of valves with same nominal diameter and different reference standards |
在进行阀门选型时,应综合阀门的使用环境、功能、声学性能等要素进行全面考量,本文针对不同类型、不同公称通径的阀门,利用CFD软件Fluent进行了声场数值模拟,并提取流道内最大声功率级定量比较,得出以下主要结论:
1)球阀相比其他类型阀门声学性能较优。这是由于球阀全开时其内通道是直通的,球阀通道与管路截面积相差不大,介质流过球阀,与流过一段直通的管子类似,流体畅通,不易产生阀门漩涡,从而降低了湍流脉动噪声,建议在阀门选型时优先选用球阀;
2)其他类型阀门如蝶阀、截止阀以及截止止回阀,由于流体通道的复杂多变,压力脉动较大,而流场的剧烈变化是影响阀门声学性能和产生噪声的重要因素,数值仿真计算结果也表明这几类阀门声学性能较差,建议在阀门选型时尽量回避。
| [1] |
刘少刚, 刘海丰, 舒海生, 等. 通海阀内流道优化降低流噪声[J]. 哈尔滨工程大学学报, 2013, 34(4): 511. |
| [2] |
江山, 张京伟, 吴崇健, 等. 通海阀内流场的三维数值模拟[J]. 中国舰船研究, 2009, 4(2): 37. DOI:10.3969/j.issn.1673-3185.2009.02.009 |
| [3] |
ITO K, TAKAHASHI K, INOUE K. Pressure distributions and flow force on the body of a poppet valve[C]// Proceddings of Fourth Bath International, Fluid Power Workshop, Bath: UK, 199l: 123–136.
|
| [4] |
杨博, 傅立敏. 稳态数值模拟在轿车外气动噪声源预测中的应用[J]. 吉林大学学报: 工学版, 2007, 37(5): 1005-1008. |
| [5] |
HORVATH Csaba, VAD Janos. Broadband Noise Source Model Acoustical Investigation on Unskewed and Skewed Axial Flow Fan Cascades[J]. Conference on Modelling Fluid Flow, 2009, 9: 682-689. |
| [6] |
董仁义, 吴崇健. 基于Lilley宽带声源模型的舵叶流噪声数值模拟研究[J]. 船海工程, 2009, 38(5): 24-26. DOI:10.3963/j.issn.1671-7953.2009.05.006 |
 2019, Vol. 41
2019, Vol. 41
