轴系校中是船舶推进轴系安装或检修过程中的重要环节,轴系的校中状态关乎轴系工作的安全性、可靠性与稳定性,校中不良会引起轴承不均匀磨损、减速齿轮啮合不良、轴系振动等问题[1]。轴系校中计算须综合考虑轴系的各性能指标,如轴承负荷、轴段内应力、轴系截面转角等,通过对这些性能参数进行计算分析从而得出最佳的轴系校中方案。目前,关于轴系校中计算方法的研究较多,主要有三弯矩法、传递矩阵法及有限元法,周瑞平[2],李冬梅[3],杨勇等[4]采用三弯矩法对轴系校中进行了分析;张辉等[5]将传递矩阵法与智能微群优化算法相互结合,并运用于轴系校中计算;尤国英等[6]用ALGOR FEAS软件对某试验船舶轴系进行了有限元校中计算。研究表明,三弯矩法对理论基础的要求高且计算过程较为复杂,传递矩阵法的计算精度与通用性略差,有限元法程序实现比较困难、对计算人员素质要求较高,故以上几种方法都存在一定的局限性[7]。
本文基于梁变形微分方程与奇异函数,针对某型船舶推进系统传动轴系校中,推导出了一种更为简洁易懂的轴系校中计算方法,并在直线校中、负荷校中2种不同轴系校中方案下,对实船轴系各状态参数进行了计算分析。结果表明,该方法能满足船舶推进轴系校中的计算精度要求,且可以更为快速准确地表述出轴系的校中状态。
1 校中计算方法研究 1.1 梁变形微分方程在横向外力或轴线平面内外力偶的作用下,轴系会发生弯曲变形,其轴线将变为挠曲线,由高等代数知识可知,挠曲线上任一点的曲率方程为:
| $ \frac{1}{\rho } = \frac{{{{\rm d}^2}w/{\rm d}{x^2}}}{{{{\left[ {1 + {{\left( {\rm d}w/{\rm d}x \right)}^2}} \right]}^{3/2}}}} {\text{。}}$ | (1) |
式中:ρ为曲率;w为挠曲度;x为轴线横坐标。当轴系变形量较小时,轴系截面转角
| $ \frac{1}{\rho } = {{\rm d}^2}w/{\rm d}{x^2}{\text{。}} $ | (2) |
将式(2)与梁变形公式
| $ \frac{{{{\rm d}^2}w}}{{{\rm d}{x^2}}} = \frac{M}{{EI}} {\text{,}}$ | (3) |
又在材料力学中,轴系剪力Q、弯矩M、载荷集度q有如下微分关系[8]:
| $ \frac{{{{\rm d}^2}M}}{{{\rm d}{x^2}}} = \frac{{{\rm d}Q}}{{{\rm d}x}} = q {\text{。}}$ | (4) |
由以上各式可知,只要将轴系承受的复杂外力以载荷集度函数的形式给出,并按次序进行积分运算,就可以求得轴系上各轴向位置的剪力、弯矩、截面转角、挠曲度等状态参数。
1.2 奇异函数奇异函数是指函数本身有不连续点或其导数与积分有不连续点的一类函数,又称麦考利函数或脉冲函数,其基本表达式如下[9]:
| $ F(x) = < x - a{ > ^n} {\text{。}}$ | (5) |
式中:< >常称麦考利括号,当各变量取不同值时,奇异函数有不同的形式,具体定义如下:
| $ \left\{ \begin{array}{l} {\text{当}n \text{≥} 0\text{时}, < x - a{ > ^n} = \left\{ {\begin{array}{*{20}{c}} {{{\left( {x - a} \right)}^n}{\rm{ }}x \text{≥} a}{\text{,}}\\ {0{\rm{ }}x < a}{\text{,}} \end{array}} \right.}\\ {\text{当}n < 0\text{时}, < x - a{ > ^n} = \left\{ {\begin{array}{*{20}{c}} {\infty {\rm{ }}x = a}{\text{,}}\\ {0{\rm{ }}x \ne a}{\text{。}} \end{array}} \right.} \end{array} \right. $ | (6) |
由于奇异函数特有的形式与定义,其在进行微、积分运算时可避免积分常数的求解,这就大大简化了计算的工作量,为快速求解轴系各状态方程提供了可能。奇异函数具体的微、积分形式归纳如下:
| $ \left\{ \begin{array}{l} {\displaystyle\frac{{{\rm d} < x - a{ > ^n}}}{{{\rm d}x}} = \left\{ {\begin{array}{*{20}{c}} {n < x - a{ > ^{n - 1}}}{\text{,}}\\ { < x - a{ > ^{n - 1}}}{\text{,}} \end{array}} \right.{\rm{ }}\begin{array}{*{20}{c}} {n > 0}{\text{,}}\\ {n \text{≤} 0}{\text{,}} \end{array}}\\ {\int { < x - a{ > ^n}{\rm d}x = \left\{ {\begin{array}{*{20}{c}} {\frac{1}{{n + 1}} < x - a{ > ^{n + 1}}}{\text{,}}\\ { < x - a{ > ^{n + 1}}}{\text{,}} \end{array}{\rm{ }}\begin{array}{*{20}{c}} {n > 0}{\text{,}}\\ {n \text{≤} 0}{\text{。}} \end{array}} \right.} } \end{array} \right. $ | (7) |
奇异函数的另一个优点是其对不连续性的表达,只要将轴向各位置的载荷集度函数相互叠加就能把轴系上承受的复杂外力以一个方程式的形式给出,这就避免了对轴系状态方程进行分段积分,进一步提高了运算速度与准确度,且有利于计算机的编程。
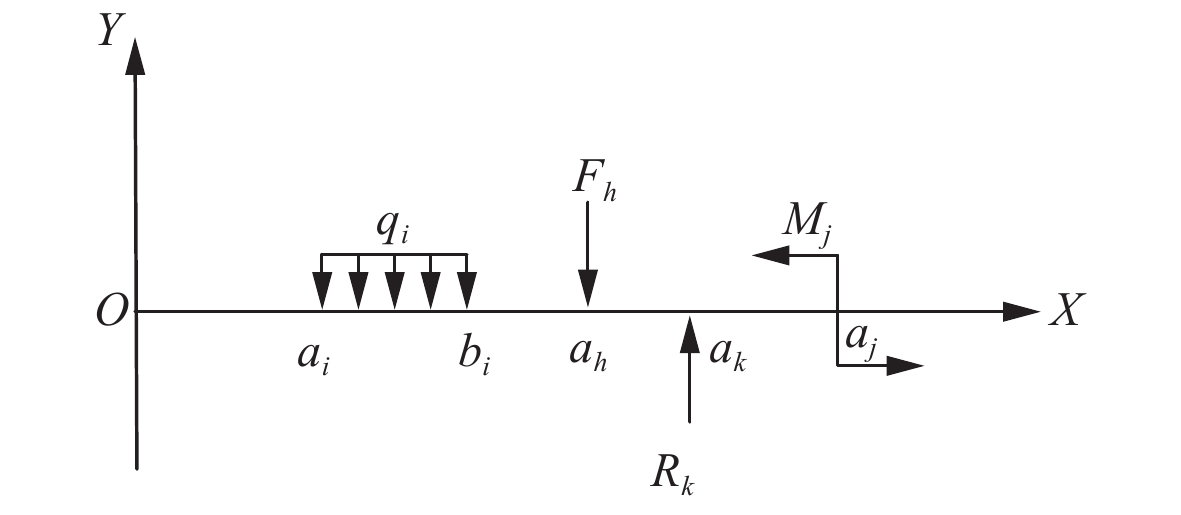
1.3 轴系校中计算方法的推导为使轴系校中计算方法更具通用性,取某一受典型载荷的轴段进行分析,简化后的轴段模型载荷分布如图1所示。以螺旋桨末端为坐标原点建立直角坐标系X0Y,取船首方向为X轴正方向,过原点垂直X轴向上为Y轴正方向。qi为轴系所受均布载荷;Fh为轴系所受集中载荷;Rk为轴承支反力;Mj为轴系所受外力矩;ai,bi分别为均布载荷作用起点与作用终点在X轴上坐标;ah为集中载荷作用点在X轴上的坐标;ak为轴承支反力作用点在X轴上的坐标;aj为外力矩作用点在X轴上的坐标。
|
图 1 简化轴段载荷分布图 Fig. 1 Load distribution of simplified shafting |
基于梁变形微分方程与奇异函数的轴系校中计算模型构建的关键是将各典型载荷用奇异函数的形式表示为轴系载荷集度函数[10]。
1)将作用于[ai,bi]区域的均布载荷qi转化为载荷集度函数为:
| $ {q_i}(x) = {q_i}( < x - {a_i}{ > ^0} - < x - {b_i}{ > ^0}) {\text{;}}$ | (8) |
2)将作用于ah点的集中载荷转化为载荷集度函数为:
| $ {q_h}(x) = {F_h} < x - {a_h}{ > ^{ - 1}} {\text{;}}$ | (9) |
3)作用在ak处的轴承支反力的载荷集度载荷函数为:
| $ {q_k}(x) = {R_k} < x - {a_k}{ > ^{ - 1}} {\text{;}}$ | (10) |
4)将作用于aj点的外力偶转化为载荷集度函数为:
| $ {q_j}(x) = {M_j} < x - {a_j}{ > ^{ - 2}} {\text{。}}$ | (11) |
综合式(8)~式(11),并结合梁弯曲变形叠加原理,可得到轴系的载荷集度函数表达式:
| $ \begin{split} q(x) =& \displaystyle\sum\limits_{i = 1}^n {{q_i}( < x - {a_i}{ > ^0} - < x - {b_i}{ > ^0}) + } \displaystyle\sum\limits_{h = 1}^m {{F_h} < x - {a_h}{ > ^{ - 1}}}+ \\ &\displaystyle\sum\limits_{k = 1}^l {{R_k} < x - {a_k}{ > ^{ - 1}} + } \displaystyle\sum\limits_{j = 1}^o {{M_j} < x - {a_j}{ > ^{ - 2}}}{\text{。}} \quad\quad\;\;\,\,(12) \end{split} $ |
对载荷集度函数依次积分可得到轴系剪力、弯矩、截面转角及挠曲线方程,当q(x)中各项均由奇异函数表达时,在求解轴系剪力与弯矩时为定积分,故可得:
剪力方程
| $ \begin{array}{l} Q(x) = \displaystyle\sum\limits_{i = 1}^n {{q_i}( < x - {a_i}{ > ^1} - < x - {b_i}{ > ^1}) + } \displaystyle\sum\limits_{h = 1}^m {{F_h} < x - {a_h}{ > ^0}} +\\ \qquad\;\;\;\displaystyle\sum\limits_{k = 1}^l {{R_k} < x - {a_k}{ > ^0} + } \displaystyle\sum\limits_{j = 1}^o {{M_j} < x - {a_j}{ > ^{ - 1}}} {\text{;}}\quad\quad\;\;\,\,(13) \end{array} $ |
弯矩方程
| $ \begin{array}{l} M(x) = \displaystyle\sum\limits_{i = 1}^n {\frac{{{q_i}}}{2}( < x - {a_i}{ > ^2} - < x - {b_i}{ > ^2}) + } \displaystyle\sum\limits_{h = 1}^m {{F_h} < x - {a_h}{ > ^1}} + \\ \qquad\;\;\;\;\displaystyle\sum\limits_{k = 1}^l {{R_k} < x - {a_k}{ > ^1} + } \displaystyle\sum\limits_{j = 1}^o {{M_j} < x - {a_j}{ > ^0}} {\text{;}}\quad\quad\;\;\;\;(14) \end{array} $ |
截面转角方程
| $ \begin{array}{l} \displaystyle\frac{{\theta (x)}}{{EI}} = \displaystyle\sum\limits_{i = 1}^n {\frac{{{q_i}}}{6}( < x - {a_i}{ > ^3} - < x - {b_i}{ > ^3}) + } \displaystyle\sum\limits_{h = 1}^m {\frac{{{F_h}}}{2} < x - {a_h}{ > ^2}}+ \\ \qquad\;\;\displaystyle\sum\limits_{k = 1}^l {\frac{{{R_k}}}{2} < x - {a_k}{ > ^2} + } \displaystyle\sum\limits_{j = 1}^o {{M_j} < x - {a_j}{ > ^1} + C} {\text{;}}\quad\;\;(15) \end{array} $ |
挠曲线方程
| $ \begin{array}{l} \displaystyle\frac{{Y(x)}}{{EI}} \!=\! \displaystyle\sum\limits_{i = 1}^n {\frac{{{q_i}}}{{24}}( < x \!-\! {a_i}{ > ^4} - < x - {b_i}{ > ^4}) \!+\! } \displaystyle\sum\limits_{h = 1}^m {\frac{{{F_h}}}{6} < x \!-\! {a_h}{ > ^3}}\!+\! \\ \qquad\;\;\displaystyle\sum\limits_{k = 1}^l {\frac{{{R_k}}}{6} < x \!-\! {a_k}{ > ^3} \!+\! }\displaystyle \sum\limits_{j = 1}^o {\frac{{{M_j}}}{2} < x \!-\! {a_j}{ > ^2} \!+\! C} x \!+\! D{\text{。}}\;(16) \end{array} $ |
式中:C,D为可由边界条件确定的积分常数。
轴系校中实质是轴承标高的改变,采用不同轴系校中方案,各轴承支撑处的轴线挠曲度也不同,已知某特定校中方案下各轴承支点处的轴承标高为Y(xi),结合轴系静力平衡条件:1)力平衡条件
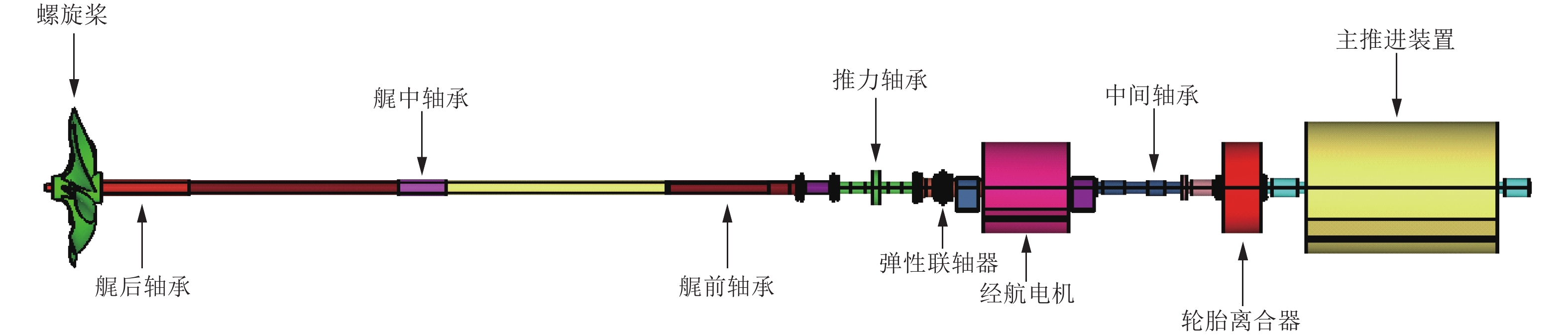
以某型船舶主推进轴系为例,依据轴系简化基本原则[3]与以上校中计算方法,构建其校中计算模型。该船舶推进轴系结构如图2所示,轴系总长为20.270 0 m,由首至尾依次为主推进装置、轮胎离合器、中间轴承、经航电机、弹性联轴器、推力轴承、尾前轴承、尾中轴承、尾后轴承、螺旋桨。整个轴系为中空结构,内径为0.120 0 m,尾轴轴段外径为0.270 0 m,推力轴段与中间轴段外径均为240.0 mm,螺旋桨质量为3 940 kg,推力盘质量为686.5 kg,弹性联轴器质量为426 kg,轮胎离合器质量为3 000 kg,轴系材料密度为7 800 kg/m3,弹性模量为2.1E11 N/ m3。
|
图 2 某船舶推进轴系结构示意图 Fig. 2 The schematic diagram of ship propulsion shafting |
在对推进轴系开展校中计算前,需要对轴系各结构要素进行合理简化,如轴段的自重、轴系上作用的载荷、外力及支反力的作用点、推力盘、轮胎离合器等,以确保理论计算结果与轴系实际校中后的状态在一定的精度要求范围内相吻合。
对以上主推进轴系作简化如下:
1)轴段自重的简化
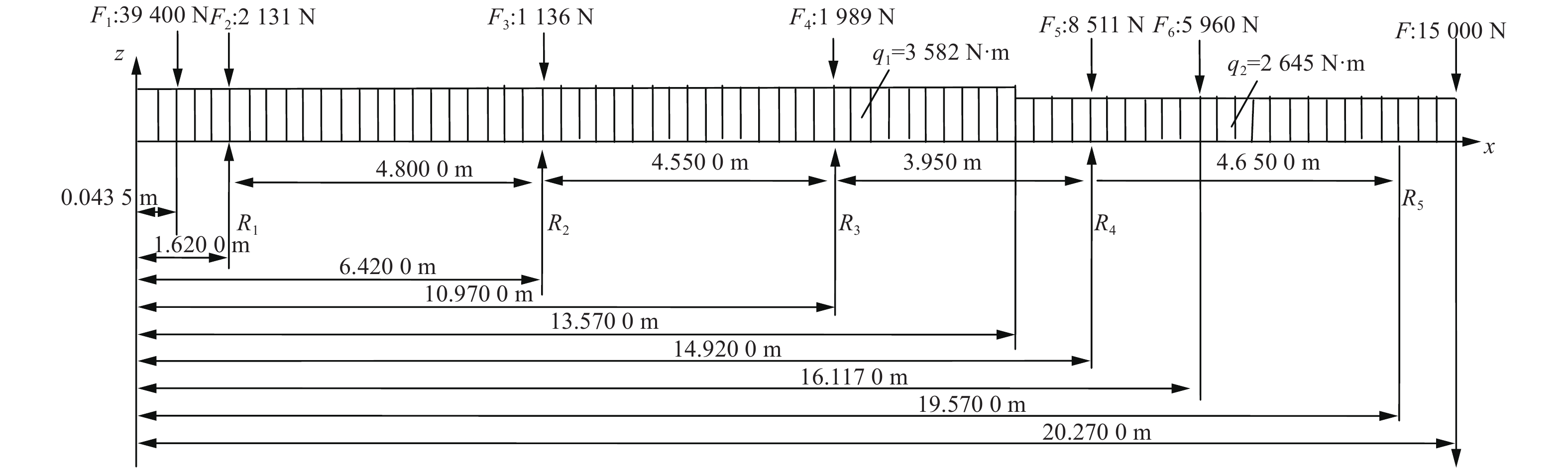
在推进系统中,轴段以连续质量的形式作用于各轴承上,因而对模型进行处理时,将其视为均布载荷,由于与轴承接触处的轴径比相邻轴段稍大,将轴径与同长度相邻轴段质量差简化为集中载荷,并作用于各轴承上。该轴系尾轴与中间轴、推力轴外径不一致,故需进行分段加载。根据以上轴系直径与材料参数,可求得各轴段质量及轴承接触处轴径与同长度相邻轴段质量差,采用均布载荷与集中载荷分别将它们加载于轴系如图3所示。图中q1为尾轴轴段自重简化后的均布载荷;q2为推力轴及中间轴自重简化后的均布载荷;F2,F3,F4分别为尾后轴承,尾中轴承,尾前轴承处轴径与同长度相邻轴段质量差简化后的集中载荷。
|
图 3 某船舶推进轴系载荷分布图 Fig. 3 Load distribution of ship propulsion shafting |
2)载荷的简化
作用在轴系上的载荷,如螺旋桨、推力盘、弹性联轴器、轮胎离合器等均作为施加在轴上的集中载荷处理(见图3),图中F1为螺旋桨质量简化后的集中载荷,F5为推力盘质量及船体通过推力盘作用在轴系上的力简化后的集中载荷,F6为弹性联轴器质量及经航电机通过弹性联轴器作用在轴段上的力简化后的集中载荷,F7为轮胎离合器质量简化后的集中载荷。
3)轴承支点的简化
除尾后轴承外,其它各轴承支点位置均取轴承长度中点。对于不同材料的尾轴后轴承,其支点位置的选取方式也不同,常以支点距轴承衬套后端面的距离S取推荐值来确定支点位置(其中B为轴衬长度、D为尾轴后轴承孔直径):
| $ \left\{ \begin{array}{l} \text{对铁梨木轴承}:S = (1/4\sim1/3)B\text{或}S = (1\sim1.4)D\text{,}\\ \text{对白合金轴承}:S = (1/7\sim1/3)B\text{或}S = (0.3\sim0.7)D\text{。} \end{array} \right. $ |
在该计算模型中S取0.3B。简化结果见图3。R1,R2,R3,R4,R5分别为尾后轴承、尾中轴承、尾前轴承、推力轴承、中间轴承载荷及其作用点位置。
4)轴的简化
校中计算时将轴系视为放置在刚性铰链支座上的连续梁,在建立物理模型时对轴的有关部分作如下简化:
①轴系中每个轴承都视为梁的一个实支座;
②轴系尾端悬伸于尾轴后轴承外,作自由端处理;
③轴系通过轮胎离合器与主机主轴相连,计算模型首端取到轮胎离合器从动部分,且作自由端处理;
④阶梯轴系各段刚度差小于30%时,轴系抗弯刚度可视为常数,故只要在以上轴系模型简化时对轴段自重进行合理简化,可将整个轴系看作等刚度均匀轴。
2.2 校中计算模型的构建由以上实船推进轴系载荷分布图,结合式(8)~式(16)可列出该轴系总的载荷集度、剪力、转矩、截面转角及挠曲线方程。又已知该船舶轴系直线校中及负荷校中2种校中方案下各轴承标高数据如表1所示。表中轴系各轴承由尾至首依次编号为1#~5#轴承,其中直线校中时各轴承标高都恒定为0,负荷校中时2#与3#轴承标高的改变主要是为了使各轴承负荷在标高改变后都处于规定的范围内,这是经反复校中优化计算后得到的结果。将这2组数据代入轴系挠曲线方程,分别可列出由5个轴承支点处挠曲线方程综合所构成的线性方程组,结合轴系固有的2个静力平衡条件,可以求得2种校中方案下的各轴承载荷R1~R5与积分常数C,D。将各轴承载荷回代入轴系剪力、弯矩、截面转角方程,即可得到该船舶轴系任一轴向位置的状态参数。
|
|
表 1 轴承标高表(mm) Tab.1 Height of bearings (mm) |
根据上述某型船舶主推进轴系校中模型,对该船轴系直线校中、负荷校中2种校中方案进行校中计算。其中各轴承载荷计算结果如表2所示。由表中可以看出,直线校中状态下,该轴系1#轴承载荷较其它轴承载荷明显偏大,这是由于轴系尾部悬臂安装着重且大的螺旋桨,同时这也使得2#轴承的载荷偏小,在轴系运转时存在脱空的可能。负荷校中状态下,1#轴承载荷有所改善,2#轴承的载荷则明显加大,整个轴系轴承负荷分配更为均匀。
|
|
表 2 校中计算轴承负荷结果对比表 Tab.2 Comparison of bearing load in alignment calculation |
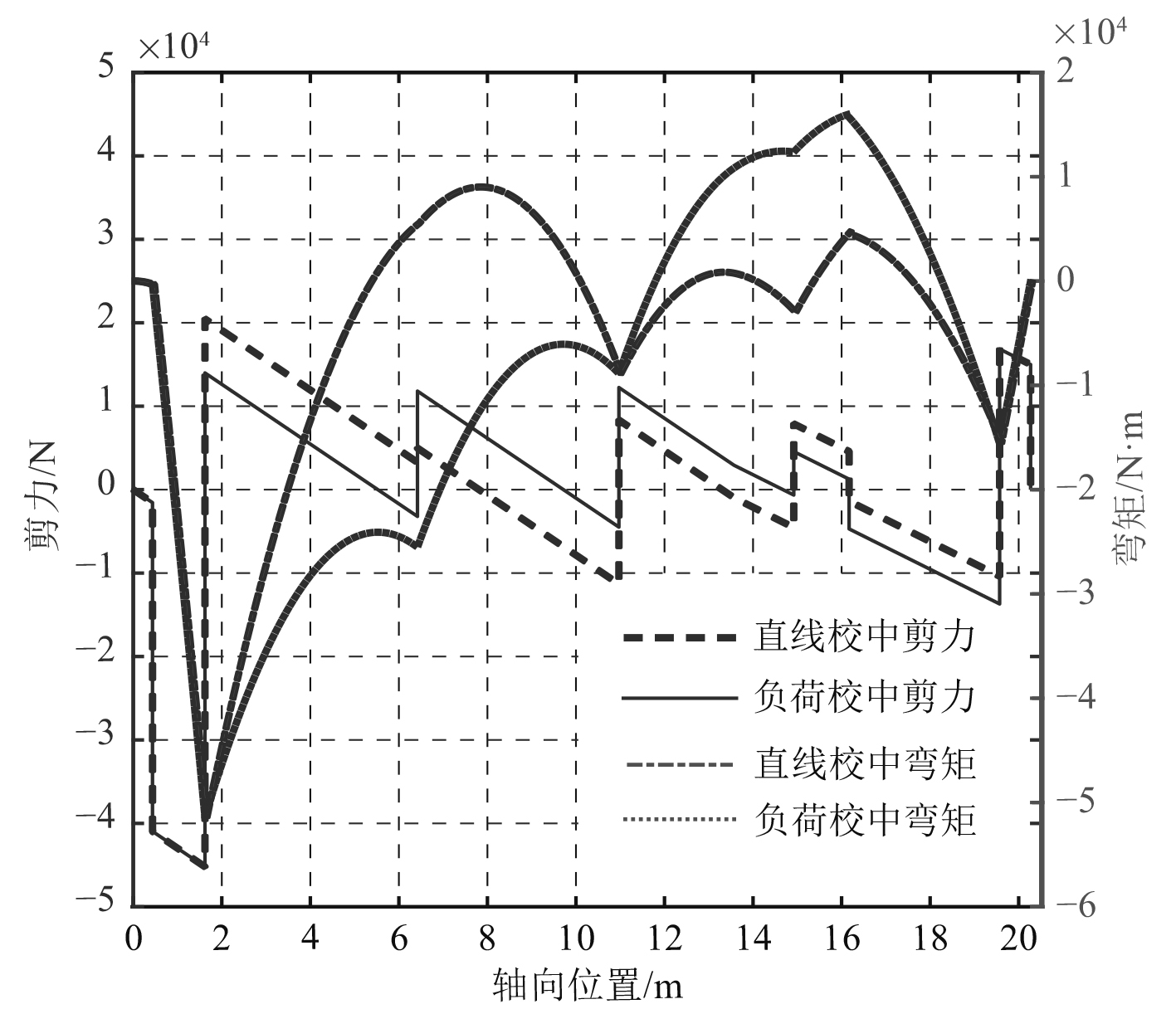
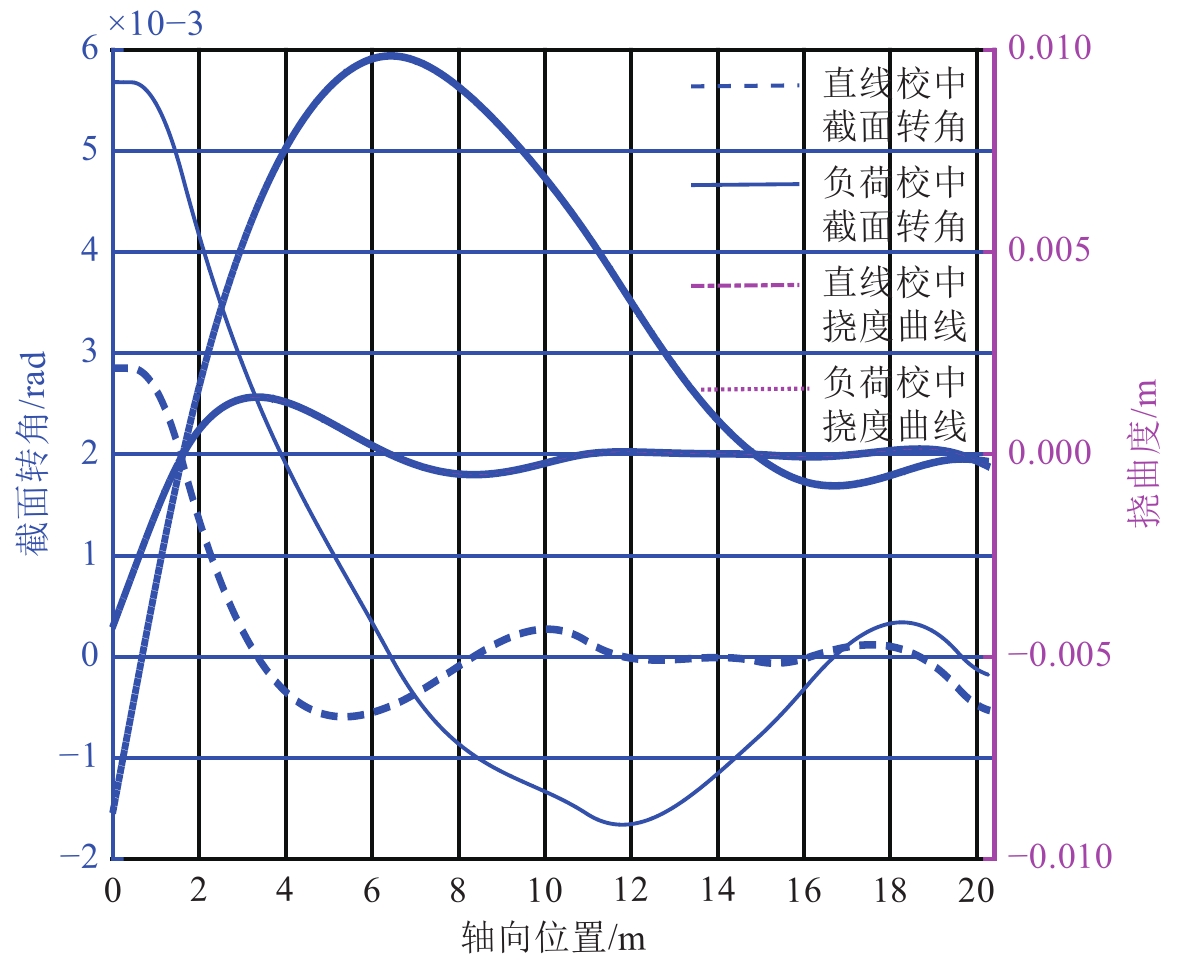
在此基础上进一步计算了2种不同校中方案下,轴系轴向位置各点的剪力、弯矩、截面转角及挠曲度,计算结果如图4和图5所示。由图4可知,2种不同校中方案下,轴系总的剪力与弯矩改变较少,只是在部分轴段有所不同,剪力与弯矩改变量最大位置都位于尾中间轴承附近,最大改变量分别为0.6829×104N与3.1044×104N·m。由图5可知,校中方案改变对轴系截面转角影响较大,负荷校中后,轴系的截面转角曲线更陡,截面转角变化率较直线校中时变大;工程规范中要求轴系校中后,尾后轴承处轴段截面转角不应大于3.5×10–4rad,否则需对后轴承进行斜镗孔处理[11]。在这2种校中方案下,后轴承处的轴段截面转角均大于该数值,故需对尾后轴承进行斜镗孔。挠度曲线直观地反映出轴系校中后轴系静态条件下轴向位置各处的变形量,2种校中方案下,尾轴轴段都存在不同程度的“中拱”现象,负荷校中时,“中拱”的峰值变大且向船首方向移动,整个轴系的变形比直线校中时为更明显。
|
图 4 轴系剪力与弯矩图 Fig. 4 Shear force and bending moment of shafting |
|
图 5 轴系截面转角与挠曲度图 Fig. 5 Sectional angle deflection of shafting |
以上计算结果表明,运用本文推导出的计算方法能快速有效地求解轴系在不同校中方案下的各状态参数。直线校中、负荷校中2种不同校中方案下,负荷校中状态时各轴承负荷分布更为合理;校中方案的改变对轴系所受剪力、弯矩影响相对较小,但各轴段截面转角及轴系挠度有明显变化,这是由于轴系截面转角与挠度是载荷集度函数的高次积分。
本文基于梁变形微分方程与奇异函数推导出的校中计算方法能较好地适应船舶推进轴系校中计算的要求,为实船轴系校中方案的选取与评估提供了理论参考。
| [1] |
刘玉君, 张生俊, 汪骥. 考虑工艺要求的船舶推进轴系校中改进算法研究[J]. 中国造船, 2017, 58(2): 138-144. LIU Yu-jun, ZHANG Sheng-jun, WANG Ji. Research on improved algorithm of ship alignment with consideration of technical requirements[J]. Shipbuiding of China, 2017, 58(2): 138-144. DOI:10.3969/j.issn.1000-4882.2017.02.015 |
| [2] |
周瑞平. 超大型船舶推进轴系校中理论研究[D]. 武汉: 武汉理工大学, 2005. ZHOU Rui-ping. The theoretic studies on the proplusion shafting alignment of ultra-large vessels[D]. Wuhan:Wuhan University of Technology, 2005. |
| [3] |
李冬梅. 船舶轴系动态校中三弯矩方程的应用[J]. 舰船科学技术, 2017, 39(8): 73-75. LI Dong-mei. The application of three moment equation in dynamic alignment of ship shafting[J]. Ship Science and Technology, 2017, 39(8): 73-75. |
| [4] |
YANG Yong, TANG Wen-yong, CHE Chi-dong. Shafting alignment based on improved three-moment method with hydrodynamic simulation for twin propulsion systems[J]. Journal of Ship Mechanics, 2013, 17(9): 1038-1052. |
| [5] |
张辉, 陈嘉伟, 封海宝. 船舶轴系校中计算中优化算法的应用[J]. 船舶工程, 2017, 39: 41-42+87. ZHANG Hui, CHEN Jia-wei, FENG Hai-bao. Optimization algorithm application on marine shafting alignment calculation[J]. Ship Engineering[J], 2017, 39: 41-42+87. |
| [6] |
尤国英, 杜尚林, 顾忠明, 等. 有限元法用于船舶轴系校中计算[J]. 舰船科学技术, 2009, 31(8): 60-62+66. YOU Guo-ying, DU Shang-ming, GUI Xiao-chun, et al. Application of FEM in ship shafting alignment[J]. Ship Science and Technology, 2009, 31(8): 60-62+66. |
| [7] |
冷坳坳. 舰船推进轴系校中技术研究[D]. 武汉:武汉理工大学, 2015. LENG Ao-ao. Research on the proplusion shaft alignment technology for warships[D]. Wuhan:Wuhan University of Technology, 2015. |
| [8] |
金蓉. 工程力学[M]. 大连:大连海事大学出版社, 2012.
|
| [9] |
徐斌. 高层建筑分析奇异函数法[M]. 北京: 科学出版社, 2009.
|
| [10] |
FALSONE G. The use of generalised function in the discontinuous beam bending differential equations[J]. Int.J.Engng Ed, 2002, 18(3): 337-344. |
| [11] |
CB/Z 338-2005, 船舶推进轴系校中[S].
|
 2019, Vol. 41
2019, Vol. 41
