受海洋环境影响,船舶结构易出现裂缝、涂层破裂和腐蚀等缺陷性损伤,影响运输效率,因此提高船舶缺陷检测性能具有重要意义。目前,船舶结构缺陷检测主要依赖人工,而人工检测易受外界环境干扰。为模拟人的视觉特点,学者们提出了视觉显著性算法,利用视觉注意机制提取图像中最容易引起注意的部分,在工业检测领域广泛应用。
针对船舶结构的缺陷检测问题,李瑛[1]利用最小二乘支持向量机逐级分类的方式对船体表面缺陷进行检测,检测效率较高;Oullette等[2]提出使用遗传算法进化方法训练权重和模拟卷积神经网络对裂缝进行检测,实验表明检测精确率有所提升,但需要进一步优化滤波器的大小和数量以及下采样的数量,减少计算时间,提升稳定性;Eich等[3]通过对机器人设定外部定位系统及管理系统,可检测出船舶结构缺陷,但需借助机器人和微型飞行器,成本较高;Bonnín-Pascual等[4 – 5]提出船舶结构裂缝和腐蚀的检测算法,检测效率与采集图像的距离有关,并且需要根据缺陷图像特征调整参数,适应性较差。
本文提出采用自适应全变分模型替代FT算法中高斯滤波器来弱化背景特征表达,并引入H分量来增强船舶缺陷特征的显著度,获取区域显著图;通过SMD算法捕捉船舶图像的结构信息以提取船舶缺陷区域,获得结构显著图;使用自适应融合算法将两类显著图融合,生成综合显著图。
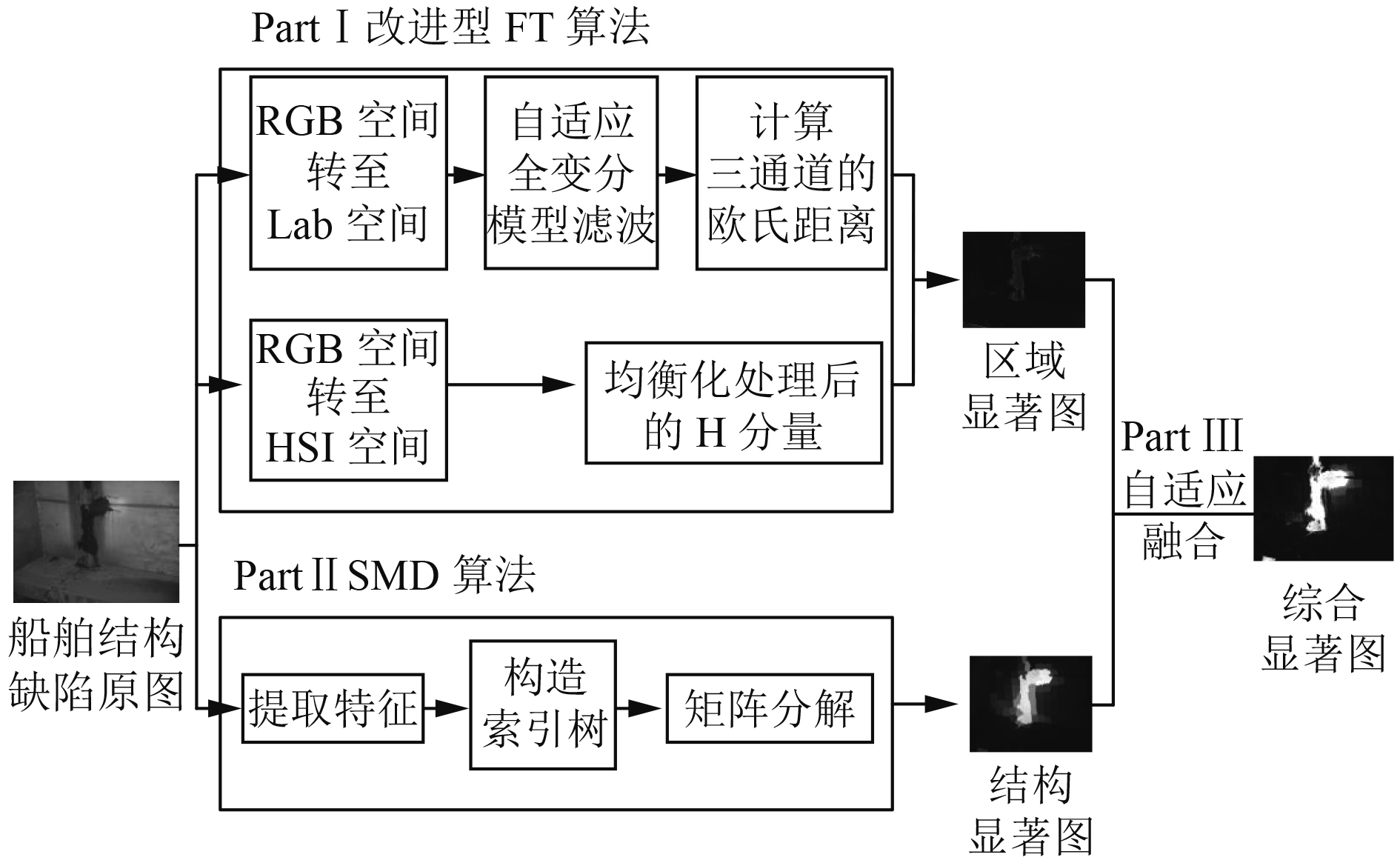
1 船舶结构缺陷检测算法船舶结构缺陷图像检测的对象主要包括裂缝、涂层破裂和腐蚀等缺陷,基于视觉显著性的船舶结构缺陷检测算法流程框图如图1所示。
|
图 1 船舶结构缺陷检测算法流程框图 Fig. 1 Ship structure defect detection algorithm flow chart |
频率调谐(FT)算法[6]基本思路为:采用经人工经验选取的高斯滤波器对图像滤波;将滤波后的图像从RGB空间转到Lab空间;计算图像u在像素点(i,j)处的显著值。计算式为:
| $ {{S}_{0}}\left( i,j \right)=\left\| {{ u}_{\mu }}-{{u}_{\omega hc}}\left( i,j \right) \right\|\text{。}$ | (1) |
式中:uμ为各特征分量算术平均值矩阵;uωhc(i,j)为高斯滤波后的图像;||·||为二范数。
FT算法理论简单,检测效果良好,将其应用于船舶结构缺陷检测中,存在2点不足之处:根据人工经验选取的高斯滤波器的模板尺度较单一;FT算法要求缺陷与背景区域存在一定的对比性。针对不足之处,对FT算法进行改进如下:
1)对于高斯滤波器模板尺寸选取问题,提出采用自适应全变分模型[7]替代高斯滤波器。该模型根据图像边缘或纹理信息丰富的区域的梯度值高于平坦区域的特性,对图像分块处理,将船舶结构缺陷图像划分为边缘区域和平坦区域,并自适应选择去噪模型。对于边缘区域,使用边缘性较强的L1范数的各向异性的全变分模型,反之,使用L2范数的各向同性的全变分模型。该模型的增广拉格朗日函数为:
| $ \begin{split}{{L}_{A}}\left( {{w}_{ij}},u,\lambda \right)=&\sum\limits_{i,j=1}^{n}{\left\| {{w}_{ij}} \right\|+\sum\limits_{i,j=1}^{n}{\frac{\beta }{2}\left\| {{D}_{ij}}u-{{w}_{ij}} \right\|_{2}^{2}}}+\\ &\frac{\lambda }{2}\left\| u-f \right\|_{2}^{2}\text{。} \end{split}$ | (2) |
式中:wij为辅助变量;β为惩罚项系数;Diju∈R2为图像中像素(i,j)在水平和垂直方向的一阶有限差分;u为原图像;f为观测图像;λ为正则化参数。
求解模型的最优解与求解增广拉格朗日函数的最小化问题是等价的。采用交替迭代法求解LA(wij,u,λ)函数的最小化问题,即求解w子问题和u子问题。设定u为定值,从式(2)的前两项分离出wij,即w子问题,通过紧缩算子(shrinkage)快速求解最优值。计算式为:
| $\begin{split} w_{ij}^{k+1}=& {\rm {shrinkage}}\left( {{D}_{ij}}{{u}^{k}},\beta \right)=\\ &\max \left\{ \left\| {{D}_{ij}}{{u}^{k}} \right\|-\frac{1}{\beta },0 \right\}\times \frac{{{D}_{ij}}{{u}^{k}}}{\left\| {{D}_{ij}}{{u}^{k}} \right\|}\text{。} \end{split}$ | (3) |
从式(2)的后两项分离出u,即u子问题。通过紧缩算子法求得
| $\left( \sum\limits_{i,j}{D_{ij}^{T}{{D}_{ij}}}+\frac{\lambda }{\beta }{{K}^{\rm {T}}}K \right){{u}^{k}}=\sum\limits_{i,j}{D_{ij}^{T}w_{ij}^{k+1}}+\frac{\lambda }{\beta }{{K}^{\rm {T}}}f\text{。}$ | (4) |
式中:KTK表示块循环。
2)针对FT算法对亮度低及背景颜色差异较小的缺陷区域不敏感的问题,将HSI颜色空间中H分量融入船舶结构缺陷特征表达,增强图像局部颜色的对比度,便于捕获船舶结构缺陷区域与背景之间的细微差异。融合式为:
| ${{S}_{1}}\left( i,j \right)=\sqrt{H\left( i,j \right){{S}_{0}}\left( i,j \right)}\text{。}$ | (5) |
式中:H(i,j)为该像素点的均衡化色调;S0(i,j)为该像素点的频率调谐显著值;S1(i,j)表示每一个像素点(i,j)的区域显著值。
1.2 结构显著性算法通过结构化矩阵分解(SMD)算法[8]将图像的特征矩阵N分解为低秩矩阵L和稀疏矩阵M,获取船舶缺陷图像结构信息。使用矩阵L表示缺陷图像背景部分,并采用核范数作为凸松弛的方法对矩阵L进行低秩正则化处理,获得内部结构。反之,用矩阵M表示船舶缺陷图像中缺陷区域,生成矩阵M的过程即提取船舶结构缺陷区域的过程。利用树型结构稀疏诱导范数来模拟图像块之间的空间邻接性和特征相似性,从而通过结构稀疏正则化算法将缺陷区域完整地分离出来。计算方法如下:
| $\mathop {\min }\limits_{L,M} \psi \left( { L} \right) + \alpha \varOmega \left( { M} \right) + \mu \Theta \left( {{ L},{ M}} \right)\begin{array}{*{20}{c}} {}\!\!&\!\!{{\rm s}.{\rm t}.}\!\!&\!\!{{ N} = { L} + { M}}\text{,}\!\!\!\!\! \end{array}$ | (6) |
| $ \psi \left( { L} \right) = rank\left( { L} \right) = {\left\| { L} \right\|_ * } + \varepsilon\text{,} \hspace{95pt}$ | (7) |
| $\varOmega \left( { M} \right) = \sum\limits_{i = 1}^d {\sum\limits_{j = 1}^{{n_i}} {\nu _j^i} } {\left\| {{{ M}_{G_j^i}}} \right\|_p}\text{。} \hspace{95pt}$ | (8) |
式中:N为特征矩阵;L为低秩矩阵;M为稀疏矩阵;ψ(L)表示低秩约束;Ω(M)表示结构化稀疏约束;Θ(L,M)是拉普拉斯正则化项;α和μ是权衡参数;
同时,为扩大低秩矩阵L和稀疏矩阵M的子空间的距离,增强背景和缺陷区域的差异性,使用拉普拉斯正则化算法对特征矩阵N处理:
| $\Theta \left( {{ L},{ M}} \right) = \frac{1}{2}\sum\limits_{i,j = 1}^K {\left\| {{{ M}_i} - {{ M}_j}} \right\|} _2^2{n_{i,j}}\text{。} $ | (9) |
式中:Mi为M的第i列;ni,j为亲和度矩阵的第(i,j)项。
对于式(8)计算得到的结构化稀疏矩阵M,根据式(10)计算显著值,生成结构显著图S2如下式:
| $Sal\left( {{P_i}} \right) = {\left\| {{{ M}_i}} \right\|_1}\text{。}$ | (10) |
式中:Pi为第i个图像块。
1.3 自适应融合算法将2种算法融合可更好地发挥每种算法的特性,完整地提取船舶缺陷区域,获得更好的检测结果。因此,根据区域显著图和结构显著图之间的相关性,采用自适应权值融合算法获取综合显著图S3,计算式为:
| ${S_3}\left( {i,j} \right) = {\omega _1}{S_1}\left( {i,j} \right) + \left( {1 - {\omega _1}} \right){S_2}\left( {i,j} \right)\text{,}$ | (11) |
| $ {\omega _1} = \frac{{\sum\limits_{i,j} {{S_2}\left( {i,j} \right)} }}{{\sum\limits_{i,j} {{S_1}\left( {i,j} \right)} + \sum\limits_{i,j} {{S_1}\left( {i,j} \right)} }}\text{。} \hspace{42pt}$ | (12) |
式中:S1(i,j),S2(i,j)和S3(i,j)分别为船舶缺陷图像中某一像素点的区域显著值,结构显著值和综合显著值;ω1为融合权值。
2 实验结果与分析实验数据为Balearic Islands大学[5]提供的船舶结构缺陷图像数据集,从中选取200幅图像作为实验样本。为全面评价本文算法(Ours),在相同实验条件下,将本文算法与Itti[9],LC[10],SR[11],FT[6]和SMD[8]五种视觉显著算法进行比较。
2.1 船舶结构缺陷检测对比实验对船舶表面两处涂层破裂的检测效果如图2所示,图2(a)为船舱拐角处的裂缝原图像,非缺陷区域置于图像前方,并含有浅白色管道、部分区域光线较强的墙壁以及显著度较高的孔洞,易对检测结果造成干扰。从图2(b)~图2(f)可以看出,Itti算法和SMD算法能够将裂缝分离出来,但缺乏完整性;SR算法检测失败;LC和FT算法能够保留完整的裂缝轮廓,且显著图清晰,但将管道和孔洞也标为缺陷区域;本文算法能够检测并准确标注裂缝区域,更接近于图2(h)所示的缺陷真实情况,但受到孔洞部分的干扰,造成底部孔洞边缘区域的误检。

|
图 2 不同显著性算法检测结果对比 Fig. 2 Comparison of test results of different saliency algorithms |
为对检测算法性能进行评估,采用精确率-召回率(P-R)和F值作为评价指标。P-R值和F值越大,表示算法性能越好,表达式为:
| $P = \frac{{TP}}{{TP + FP}},R = \frac{{TP}}{{TP + FN}},F = \frac{{\left( {1 + {\beta ^2}} \right) \times P \times R}}{{{\beta ^2} \times P + R}}\text{。}$ | (13) |
式中:TP为正确检测样本数;FP为误检样本数;FN代表漏检样本数;根据应用F-measure的文献[7]建议,设置β2=0.3。
对200幅实验图像计算6种检测算法的平均精确率、平均召回率以及F值,结果如表1所示。可知,本文算法的检测平均精确率和平均召回率以及F值分别达到86.48%,75.05%和0.84,均高于5种对比算法。造成这种现象的主要是在检测船舶结构缺陷时,Itti算法和SR算法将缺陷区域的信息也去除了,最终生成的显著图无法包含完整的船舶缺陷区域信息,导致检测结果较差;LC算法则将背景信息提取为缺陷区域,召回率达到66.72%,精确率和F值较低;FT算法和SMD算法的检测精确率较高,但均低于本文算法,分别低了13.83%和10.91%,2种算法的召回率和F值较低,算法的整体检测性能较弱。
|
|
表 1 使用不同算法进行缺陷检测的结果比较 Tab.1 Comparison of results using different algorithms for defect detection |
为解决当前船舶缺陷检测算法存在的问题,提出了多特征融合的船舶缺陷检测算法。实验结果表明,本文算法可较好描述船舶缺陷区域形状和边界,从而构建较为有效的视觉显著图,凸显缺陷区域。相比于其他显著性算法,所提算法更适用于对船舶结构缺陷的检测,具有较好的检测性能。今后将进一步优化算法,增强缺陷区域的显著度,提高检测精确率。
| [1] |
李瑛. 船体表面缺陷检测系统研究[J]. 舰船科学技术, 2016(24): 109-111. LI Ying. Research on hull surface defect detection system[J]. Ship Science and Technology, 2016(24): 109-111. |
| [2] |
OULLETTE R, BROWNE M, HIRASAWA K. Genetic algorithm optimization of a convolutional neural network for autonomous crack detection[M]. Evolutionary Computation, 2004: 516–521.
|
| [3] |
EICH M, BONNINPASCUAL F, GARCIAFIDALGO E, et al. A robot application to marine vessel inspection[J]. Journal of Field Robotics, 2014, 31(2): 319-341. DOI:10.1002/rob.2014.31.issue-2 |
| [4] |
BONNíN-PASCUAL F, ORTIZ A. Detection of Cracks and Corrosion for Automated Vessels Visual Inspection[J]. Integrated Pest Management Reviews, 2010, 3(2): 111-120. |
| [5] |
BONNIN-PASCUAL F, ORTIZ A. Corrosion Detection for Automated Visual Inspection[M]. Austria: In Tech, 2014: 619–632.
|
| [6] |
ACHANTA R, HEMAMI S, ESTRADA F, et al. Frequency-tuned salient region detection[C]. Conference on Computer Vision and Parttern recognition, 2009: 1597–1604.
|
| [7] |
PAN Jinquan, CHEN Shuner, FENG Yuanhua, et. al. Method of Image Block Denoising Based on Adaptive Total Variation[J]. International Journal of Computer Techniques, 2016, 4(3): 174-179. |
| [8] |
PENG H, LI B, LING H, et al. Salient Object Detection via Structured Matrix Decomposition[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2017, 39(4): 818-832. |
| [9] |
ITTI L, KOCH C. Computational modelling of visual attention[J]. Nature Reviews Neuroscience, 2001, 2(3): 194-203. DOI:10.1038/35058500 |
| [10] |
ZHAI Y, SHAH M. Visual Attention detection in video sequences using spatiotemporal cues[C]. New York: Proceedings of the14th Annual ACM International Conference on Multimedia, 2006: 815–824.
|
| [11] |
HOU X, ZHANG L. Saliency Detection: A spectral residual approach[C]. Minneapolis: 2007 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2007), 2007: 1–8.
|
 2019, Vol. 41
2019, Vol. 41
