2. 哈尔滨工程大学,机电工程学院,黑龙江 哈尔滨 150001;
3. 哈尔滨工程大学,船舶工程学院,黑龙江 哈尔滨 150001
2. Harbin Engineering University, College of Mechanical and Electrical Engineering, Harbin 150001, China;
3. Harbin Engineering University, Marine Engineering College, Harbin 150001, China
在军事领域或者舰船工业领域,分析了解外在冲击信号特点,提高舰船抗冲击能力,提高舰船的抗击打能力和生命力,一直是研究的热点问题。本文旨在从外在爆炸冲击出发,研究外在冲击激励产生的冲击波波形、冲击波脉宽、冲击波峰值等不同冲击波载荷,通过模态分析计算、归类分析等方法,得出冲击波载荷特征对冲击响应谱影响的一些基本规律,希望对于该领域研究有些帮助。
1 冲击谱理论与物理模型 1.1 冲击谱理论目前国内外船舶领域规范中的冲击环境都是以冲击谱作为恒准,可见冲击谱是研究爆炸冲击的重要指标。将冲击源施加于一系列线性、单自由度无质量弹簧振子时,将各自单自由度振子的响应运动中的最大响应值,作为对应于系统固有频率的函数而绘制的曲线,即称为冲击响应谱,简称冲击谱。根据定义,用图1来解释冲击谱形成过程。结构受到冲击后,若想得到其上一点处冲击响应谱,假设一固有频率为
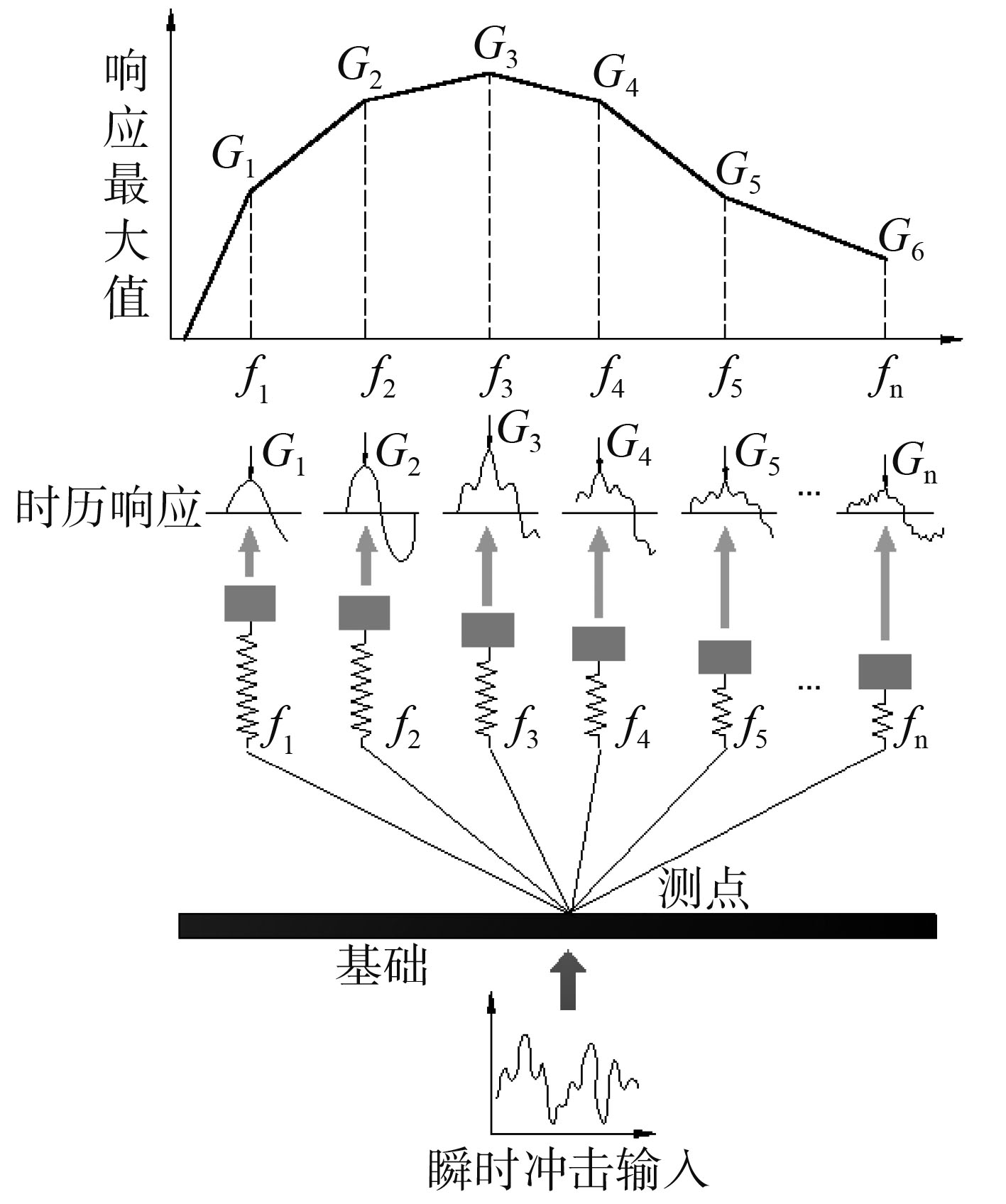
|
图 1 冲击谱形成原理 Fig. 1 Principle of shock spectrum formation |
响应是指位移、速度、加速度,冲击谱中所指的最大响应要结合工程需要来确定。振子相当于实际工程中考核的设备,决定设备是否损坏的往往是设备相对于结构的距离变化及速度大小,所以更关心的是振子的相对位移及相对速度,而不是其绝对位移和绝对速度,因此位移谱值取自相对位移,速度谱值取自相对速度。而振子的绝对加速度反映了弹簧力的大小,即工程中设备安装位置的拉压力大小,其相对加速度没有明显的力学意义,因此加速度谱值取自振子绝对加速度,下面具体介绍谱值的计算方法。
已知结构受到冲击后,其上一点加速度响应时历曲线为
| $m\ddot x(t) + k\left[ {x(t) - {x_0}(t)} \right] = 0\text{。}$ | (1) |
式中:
| $y(t) = x(t) - {x_0}(t)\text{。}$ | (2) |
将式(2)代入式(1)得到振子相对运动与结构响应之间的关系:
| $\ddot y(t) + {\omega ^2}y(t) = - {\ddot x_0}(t)\text{。}$ | (3) |
式中:
| $y(t) = - \frac{1}{\omega }\int_0^t {{{\ddot x}_0}(\tau )\sin \omega \left( {t - \tau } \right){\rm d}\tau }\text{,} $ | (4) |
其中
由式(1)可得:
| $\ddot x(t) = - {\omega ^2}y\left( t \right)\text{,}$ | (5) |
即振子绝对加速度为:
| $\ddot x(t) = \omega \int_0^t {{{\ddot x}_0}(\tau )\sin \omega \left( {t - \tau } \right){\rm d}\tau } \text{。}$ | (6) |
针对一个固定的
把式(4)进行一次微分得相对速度:
| $\dot y(t) = - \int_0^t {{{\ddot x}_0}(\tau )\cos \omega \left( {t - \tau } \right){\rm d}\tau } \text{,}$ | (7) |
参考相对位移与绝对加速度形式,工程上为了方便定义了伪速度:
| ${\dot y_p}(t) = \int_0^t {{{\ddot x}_0}(\tau )\sin \omega \left( {t - \tau } \right){\rm d}\tau } \text{,}$ | (8) |
从形式上,其与相对位移和绝对加速度各差一个
| ${\dot y_p}(t) = - \omega y\left( t \right) = \frac{1}{\omega }\ddot x\left( t \right)\text{。}$ | (9) |
工程上,积分时间不会达到无限大,往往只计算有限固定时间内的积分,具体冲击谱与积分时间的关系下节讨论。考虑以下不等式:
| $ \begin{split} &\left| {\int_0^t {{{\ddot x}_0}(\tau )cos\omega \left( {t - \tau } \right)d\tau } - \int_0^t {{{\ddot x}_0}(\tau )sin\omega \left( {t - \tau } \right){\rm d}\tau } } \right|=\\ & \;\;\;\;\left| \left. {\frac{1}{\omega }[{{\ddot x}_0}(\tau )\cos (\omega \tau - \omega t + \frac{{\text{π}} }{4})} \right|_0^t\right. - \\ &\;\;\;\;\left.\int_0^t {{{\dddot x}_0}(\tau )\cos (\omega \tau - \omega t + \frac{{\text{π}} }{4}){\rm d}\tau ]} \right| \leqslant \\ &\;\;\;\;\frac{1}{\omega }\left[ {\frac{{\sqrt 2 }}{2}\left| {{{\ddot x}_0}(t)} \right| + \left| {{{\ddot x}_0}(0)} \right| + \int_0^t {\left| {{{\dddot x}_0}(\tau )} \right|{\rm d}\tau } } \right] \text{。} \end{split} $ | (10) |
式中:
| $\frac{1}{\omega }\left[ {\frac{{\sqrt 2 }}{2}\left| {{{\ddot x}_0}(t)} \right| + \left| {{{\ddot x}_0}(0)} \right| + \int_0^t {\left| {{{\dddot x}_0}(\tau )} \right|{\rm d}\tau } } \right]\xrightarrow[{\omega \to \infty }]{}0\text{,}$ | (11) |
即当
| $\int_0^t {{{\ddot x}_0}(\tau )cos\omega \left( {t - \tau } \right){\rm d}\tau } \underset {\omega \to \infty } \leftrightarrows \int_0^t {{{\ddot x}_0}(\tau )\sin\omega \left( {t - \tau } \right){\rm d}\tau } \text{。}$ | (12) |
此时伪速度和振子相对在数值上是等价的,可以用伪速度代替相对速度,只在
用式(4)、式(8)和式(6)即可由给定的结构加速度响应直接求出冲击谱的谱位移、谱速度和谱加速度。把3个谱值作为关于
| $\log V\left( \omega \right) = \log \omega + \log D\left( \omega \right)\text{,}$ | (13) |
| $\log V\left( \omega \right) = - \log \omega + \log A\left( \omega \right)\text{。}$ | (14) |
由式(13)、式(14)可以看出,按对数坐标绘制出伪速度谱,则过一点处伪速度值做45°斜线在纵坐标轴上的截距即为该点频率所对应的谱位移对数值。过一点处伪速度值做-45°斜线在纵坐标轴上的截距即为该点频率所对应的谱加速度对数值,如图2所示。
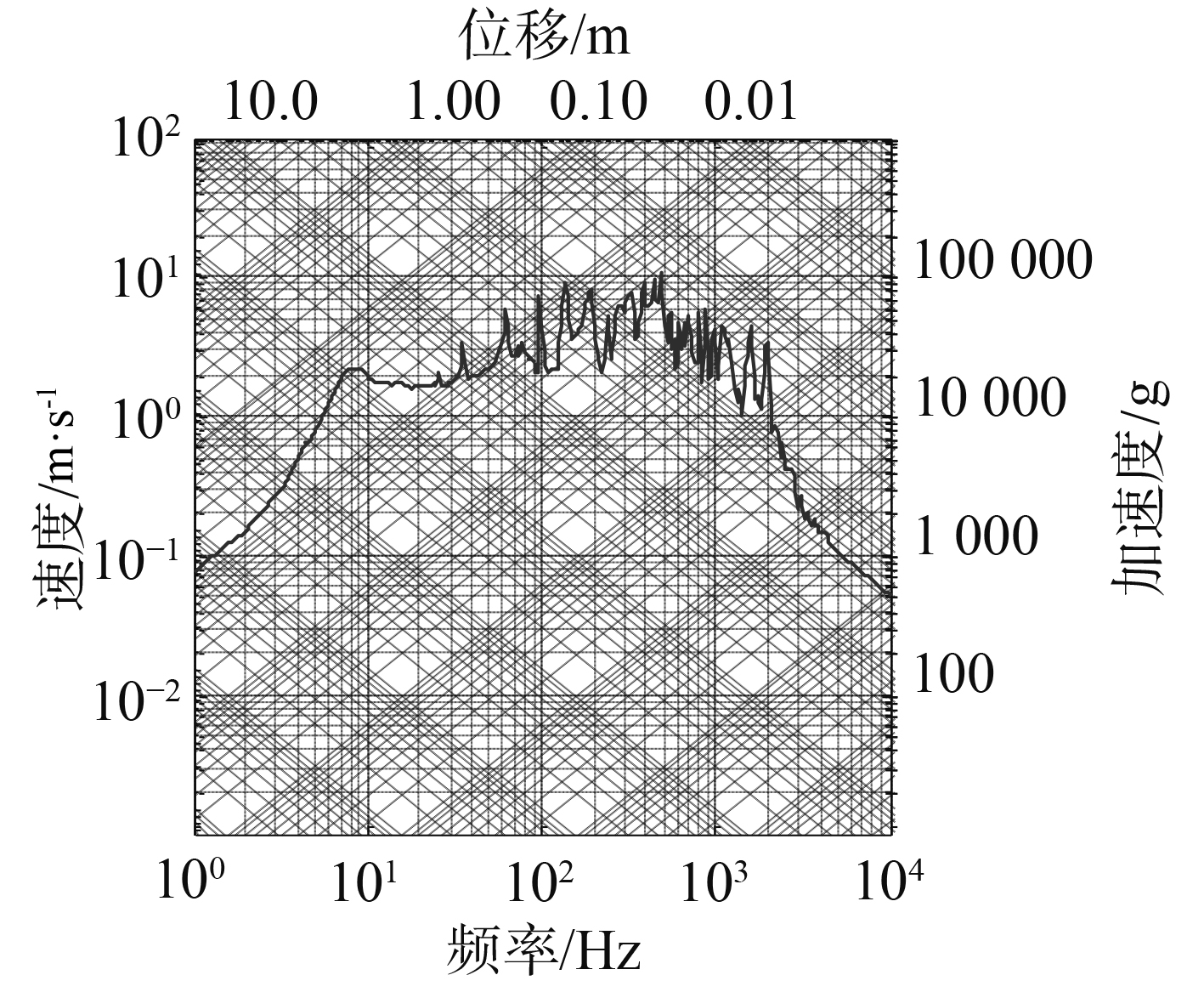
|
图 2 四参数冲击谱 Fig. 2 Four parametric shock spectrum |
根据任意一点伪速度谱值即可得到该点频率处位移谱值和加速度谱值。为了方便将位移谱值和加速度谱值坐标线画在图像的上方和右方,这样即可直接读出一点处的3个谱值,图2即称为冲击谱。观察到,冲击谱低频段位移谱值趋于定值,高频段加速度谱值趋于定值。
2 计算结构与分析 2.1 输入载荷特征对典型加筋板冲击响应的影响 2.1.1 工况设置对固定加筋板施加不同载荷,对比分析冲击谱的差异即可得出输入载荷对冲击谱特性的影响规律。载荷采用集中力载荷作用在加筋板中心,实际计算时,为避免中心节点受力过于集中导致网格畸变过大,把集中力等效为面载荷作用在加筋板中心4个单元面上,作用在有加强筋的一侧。本章载荷大小均指等效节点力的大小,载荷具体设置20个工况。
|
|
表 1 各工况载荷参数 Tab.1 Load parameters for each working condition |
前1~5工况为不同脉宽相同峰值的矩形波。6~10工况为不同脉宽相同峰值的半正弦波,分别与1~5工况一一对应,保证具有相同脉宽和冲量,仅波形不同。11~15工况为不同脉宽相同峰值的后峰锯齿波,分别与1~5、6~10工况一一对应,保证具有相同脉宽和冲量,仅波形不同。16~20工况与1~5工况一一对应,具有相同脉宽和波形,仅峰值不同。
2.1.2 冲击波波形对冲击响应影响研究将前15个工况按相同脉宽不同波形分为5组,各组冲击谱对比曲线如图3所示。
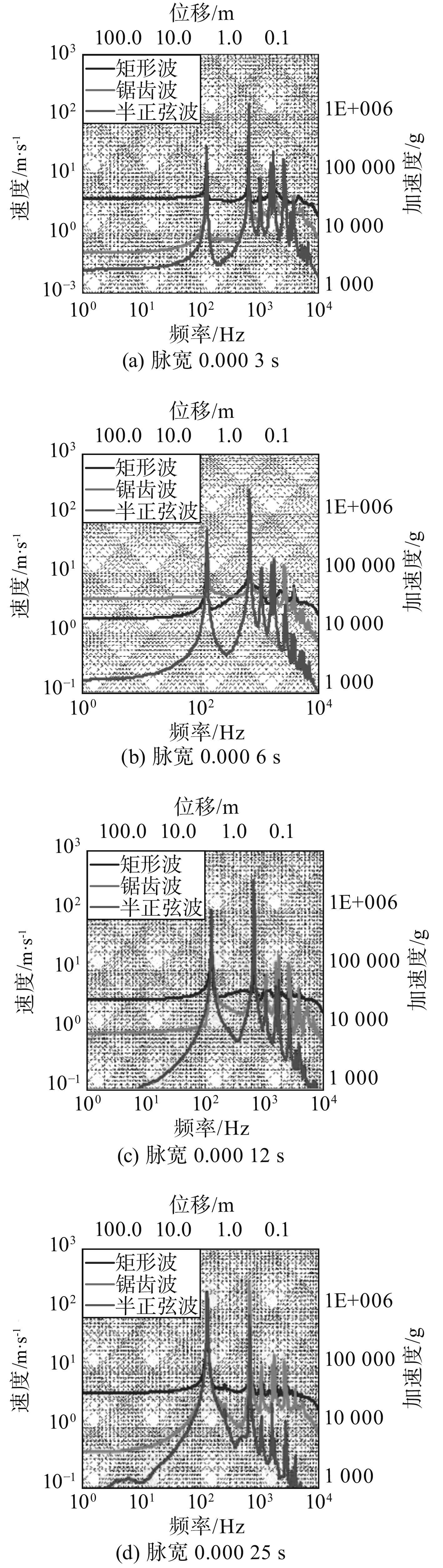
|
图 3 各脉宽3种波形冲击谱对比图 Fig. 3 Comparisons of shock spectra of three kinds of waveforms with different pulse widths |
可以看出,相同冲量和脉宽、不同波形的冲击谱呈现一致的规律,各峰值频率相近,都具有2个较高的峰值,这2个峰值高度相近。此外矩形波和后峰锯齿波对应冲击谱整体比较相近,所有峰值相近,半正弦波在谱值上整体较前二者较小,峰值频率接近但高度较小。
2.1.3 冲击波脉宽对冲击响应影响研究将前15个工况按相同波形不同脉宽分为3组,各组冲击谱对比曲线如图4所示。
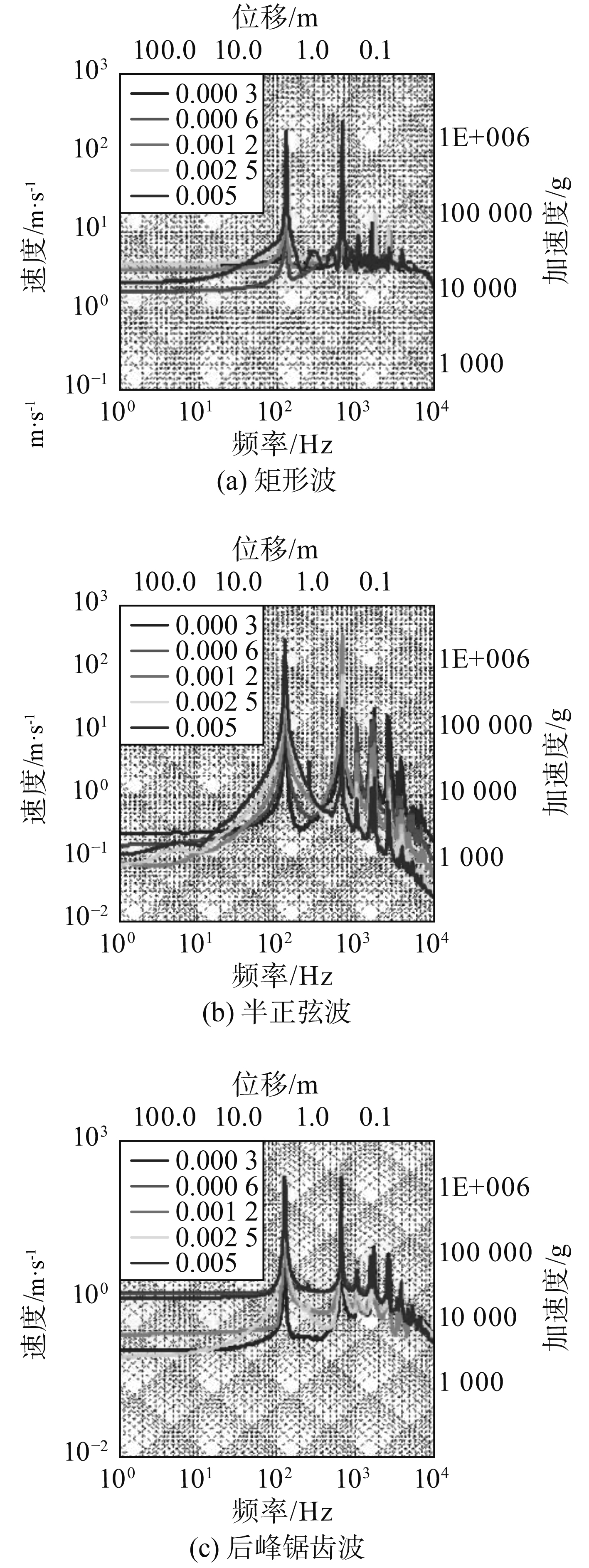
|
图 4 各波形5种脉宽冲击谱对比图 Fig. 4 Comparisons of five pulse width impulse spectra for each waveform |
可以看出,相同波形、峰值不同脉宽的冲击谱呈现一致的规律,各峰值频率相近,都具有2个较高的峰值。对于第1峰值,随着脉宽变大,峰值高度不断变大。对于第2峰值,脉宽为0.001 2时峰值达到最大然后又会减小。第1峰值对应固有周期为0.007 8s,第2峰值对应固有周期为0.001 5s,可以认为当脉宽接近峰值对应固有周期的时候峰值高度最大。
2.1.4 冲击波峰值对冲击响应影响研究对比工况1~工况5和工况15~工况20的矩形波,按照相同脉宽、不同峰值分为5组,各组冲击谱对比图如图5所示。
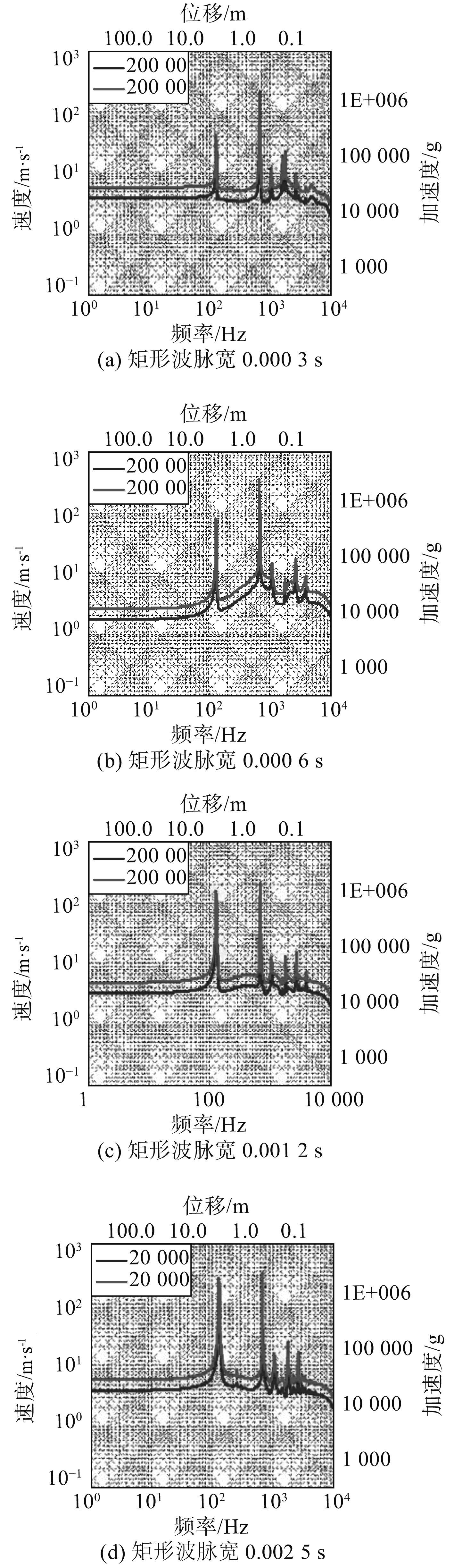
|
图 5 矩形波各脉宽不同峰值冲击谱对比图 Fig. 5 Comparisons of different peak impulse spectra of rectangular wave with different pulse widths |
可以看出相同脉宽、不同峰值的2个矩形波形成的冲击谱在形状上十分相近,每个峰值一一对应,只是峰值较高的矩形波对应的冲击谱峰值较大。将前2个最高峰值及位于1 072 Hz处的第3个较高峰处值谱速度进行对比,如表2~表4所示。
|
|
表 2 不同峰值矩形波冲击谱第1峰值谱速度对比 Tab.2 Comparison of first peak spectral velocities of shock spectra of rectangular waves with different peak values |
|
|
表 3 不同峰值矩形波冲击谱第2峰值谱速度对比 Tab.3 Comparison of second peak spectral velocities of shock spectra of rectangular waves with different peak values |
|
|
表 4 不同峰值矩形波冲击谱1 072 Hz处峰值谱速度对比 Tab.4 Comparison of peak spectral velocities at 1072 Hz for different peak rectangular wave shock spectra |
由表可以看出,各脉宽矩形波前3个峰值处的谱速度值比例都近似为1.5,而峰值频率相同,所以对应谱位移、谱加速度比值均为1.5,即与冲击波峰值比值30 000/20 000相同。在弹性阶段板的响应与外力的大小呈现严格的线性关系。冲击谱的谱值代表响应的最大值,在结构的弹性范围内其与外载荷的幅值也会呈现明显的线性关系。因此弹性阶段相同脉宽冲击波的峰值对冲击谱值的影响是线性的,但不影响冲击谱形状,只能使冲击谱做上下平移。
3 结 语1)外载荷不会影响冲击谱峰值频率,只能影响冲击谱峰值高度。冲击谱峰值频率对应着加筋板的某阶模态,即主振型,结构主振型与外载荷形式无关。
2)波形对冲击谱特性的影响与脉宽有关,当外载荷脉宽与结构峰值对应固有周期之比很小(约小于0.25)时,可认为波形对冲击谱峰值高度无影响。随着脉宽增大,波形的影响越来越大。
| [1] |
邢天虎等. 力学环境试验技术[M]. 西安.西北工业大学出版社, 2003.
|
| [2] |
宁建国. 爆炸与冲击力学[M]. 北京. 国防工业出版社. 2010.
|
| [3] |
王军, 等. 中型浮动冲击平台结构设计研究[J]. 振动与冲击, 2014(7). |
| [4] |
都军民, 等. 冲击响应谱在冲击试验中应用研究[J]. 舰船科学技术, 2007(29SL). |
| [5] |
任昌, 潘宏侠. 基于冲击信号的冲击响应谱研究[J]. 火炮发射与控制学报, 2010(3). DOI:10.3969/j.issn.1673-6524.2010.03.006 |
| [6] |
李伟森, 张冬冬. 冲击响应谱分析[J]. 绿色质量工程, 2008(05). |
| [7] |
华师韩, 等. 冲击响应谱计算相关参数选择的研究[J]. 遥测遥控, 2005(11). |
 2019, Vol. 41
2019, Vol. 41
