0 引　言

舰船由于风、浪、流等的作用产生六自由度运动，并会随干扰因素的增强而加剧其运动，且表现出越强的随机性与非线性。严重的船舶运动会对海上作业、设备与人员安全等造成较大影响。利用舰船运动与包络的极短期预报技术，可以有效缓解这部分影响。将预报出的横摇运动趋势作为前馈信号，添加至减摇控制系统，则可实现前馈加反馈的复合控制，增强减摇效果；对航母运动姿态进行极短期预报，则可优化舰载机起降时机，减少事故发生；也可对舰船海上补给、舰船在风浪中转向时机的优选做出指导等^{[1 – 3]}。

国内外对舰船运动姿态的极短期预报进行了大量研究，许多国家投入巨资进行理论分析、数字仿真、模型试验和实船分析，取得了许多有价值的成果，部分已应用于实际。美国海军系统中心夏威夷实验室I R Yumor在1981年采用ARX模型预报航母运动，可有效预报2～4 s^[4]；英国伦敦大学的D R Broome等在1994年将仪器安装在某护卫舰上，采用ARMA模型进行预报，对于相对平稳的数据可预报10 s内横摇运动^[5]。国内的哈尔滨工程大学及中国船舶科学研究中心等单位也展开过深入研究，在预报理论及方法上取得了很大进展，在仿真研究方面有较多成果，在船模试验数据的基础上也有部分研究，在实船运动数据基础上的分析以及实际应用方面仍少有文献记载。国内基于模型运动数据的极短期预报分析表明，采用自适应AR模型可有效预报6～9 s，采用首前波法预报时间较长，可达15 s左右，但该方法需同步预知首前波及舰船运动时历，测量设备较复杂^{[6 – 10]}。

本文根据某实船航行过程中采集的运动数据对船舶运动和包络进行了预报分析。预报方法采用当前最流行且最方便计算与使用的时间序列法。考虑到实船运动在随机海浪作用下的非线性以及混沌特性，预报模型采用非线性的2阶自适应Volterra级数模型。模型参数采用收敛速度快、计算简单且精度较高的最小二乘(RLS)算法。

1 实船运动与包络极短期预报的应用设计

海面上的波浪常常以群的形式出现，各个振幅与周期相近的波构成一个波群。这种大大小小不同的波群表现出了波浪的低频特性。由波群诱导的船舶运动也具有低频特性。舰船的运动包络包裹了运动的所有过程，表现了这些群的缓慢变化趋势。对这些低频运动趋势的实时预报，即为船舶运动包络的实时预测。

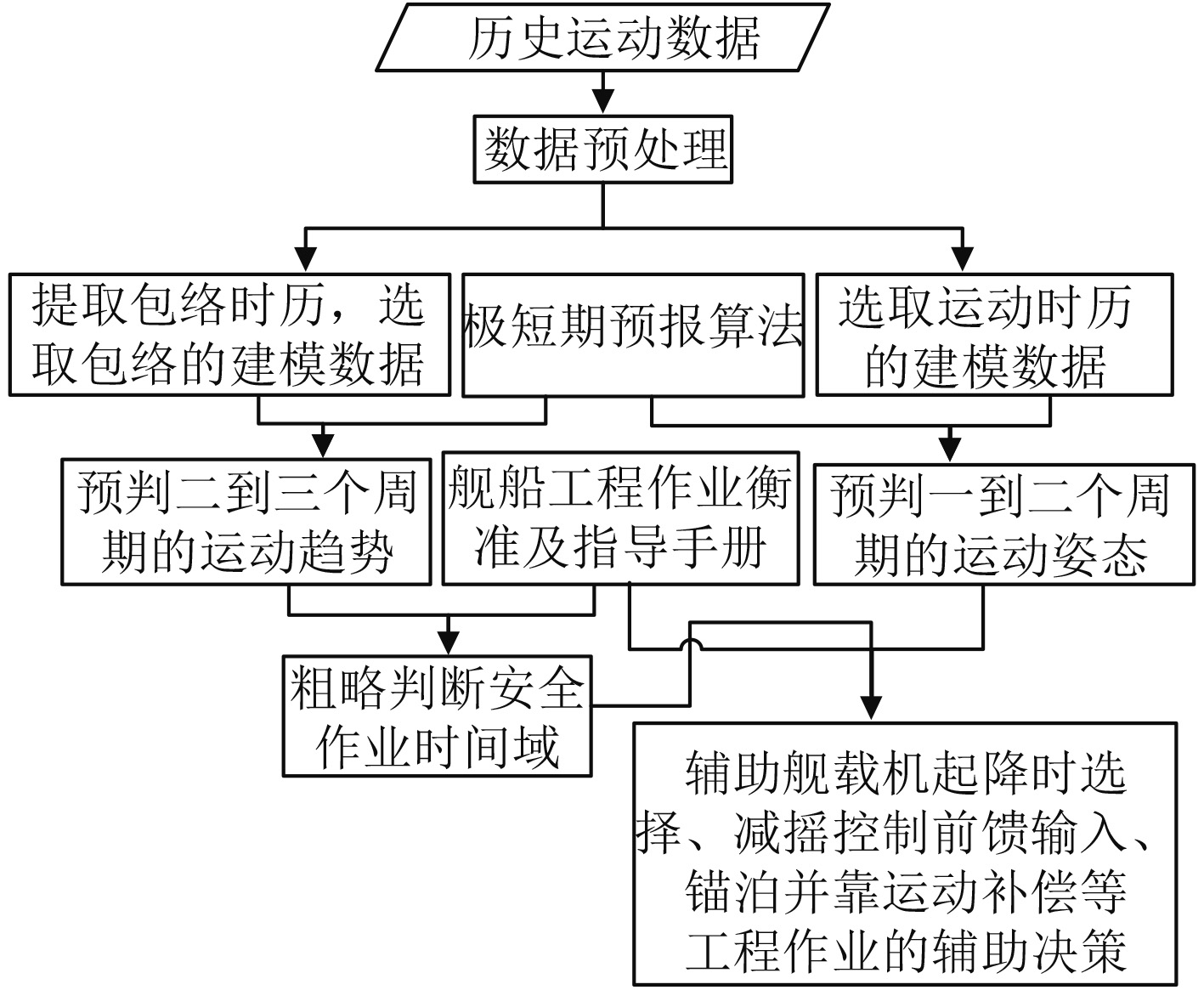
通过极短期预报方法对未来2～3个周期的包络趋势进行预报，可以粗略预判较长时间内的运动范围，结合相关工程作业衡准对安全作业时间域给出建议。通过对未来1～2个周期的运动姿态进行精细预报，可以实时预判下一周期的运动姿态，结合安全作业时间域对舰载机起降、减摇控制、锚泊并靠等给出具体的起降或补偿建议。具体的应用设计如图1所示。

2 实船运动与包络极短期预报方法

通过时间序列法对舰船运动和包络进行实时预报可分为4步：首先对运动时历数据进行预处理，然后分别建立运动和包络的预报模型，再估计各自模型的参数与阶，最后利用辨识完成的模型对运动和包络进行预报。实际中大量的非线性系统可用Volterra级数^[6]表征，考虑到船舶运动的随机性与非线性，本文运用Volterra级数展开式来构造舰船运动和包络的非线性预测模型。

2.1 数据预处理

利用2阶自适应Volterra级数模型对舰船运动和包络进行实时预报，需要预先做好以下3步：1）运动时间序列零均值化，得到近似的零均值平稳时间序列；2）选取适宜的建模数据量 ，即体现出信息的完整性又避免不必要的计算；3）通过运动时历提取出包络的时间序列。

数据零均值化采用以下公式：

$ x(t) = {x_0}(t) - {\bar x_0} {\text{。}}$

(1)

其中： ${\bar x_0}$ 为样本时间序列 $\left\{ {{x_0}(t)} \right\}$ 的均值； $\left\{ {x(t)} \right\}$ 为零均值化后可用于建立预报模型的数据。需要注意的是，模型预报结束时需加上 ${\bar x_0}$ ，经还原得出实际信号的预报值。

建模数据量 $N$ 的选取，通过模型参数向量的范数 ${\left\| \varphi \right\|_2}$ 来判定。模型成功辨识后，各参数分量趋于平稳，参数向量的范数 ${\left\| \varphi \right\|_2}$ 也达到平稳状态，因此， ${\left\| \varphi \right\|_2}$ 也能说明算法的收敛速度。

针对包络时间序列的获取，本文提出以下方法：首先提取滤波后运动数据的峰谷值；然后去除峰（谷）值过大或过小的点，使包络时历曲线较为光顺，提高预报精度；最后对选取的峰（谷）包络点进行等间距插值，得到等时间间隔的包络离散序列。

2.2 二阶自适应Volterra级数模型

针对船舶运动和包络的时间序列，假设该非线性离散系统的输入为 $x(t)(t = 1,2, \cdots ,N)$ ， $X(t) = [x(t),x(t - 1),$ $ \cdots ,x(t - N + 1)]$ ，输出为 $\hat x(t + 1)$ 。考虑到多级展开式的计算难度，取Volterra级数展开式的2阶截断求和形式^[6]来表示该系统，表达形式如下：

$ \begin{split} \hat x(t + 1) =& {h_0} + \displaystyle\sum\limits_{{m_1} = 0}^{m - 1} {{h_{{m_1}}}} (t)x(t - m) + \\ & \displaystyle\sum\limits_{{m_1} = 0}^{m - 1} {\displaystyle\sum\limits_{{m_2} = 0}^{m - 1} {{h_{{m_1},{m_2}}}} } (t)x(t - {m_1})x(t - {m_2}) {\text{。}} \end{split} $

(2)

式中： $N$ 为建模数据个数； $m$ 为滤波器长度； ${h_{{m_1},{m_2}, \ldots ,{m_p}}}(t)$ 为 $p$ 阶Volterra核。

定义二阶Volterra级数滤波器的状态扩展的输入矢量为：

$\begin{split} U(t) =& [1,x(t),x(t - 1), \cdots ,x(t - m + 1), \\ &{x^2}(t),x(t)x(t - 1), \cdots ,{x^2}(t - m + 1)]^{\rm T} {\text{。}} \end{split} $

(3)

系数向量为：

$\begin{split} H(t) =& [{h_0},{h_0}(t),{h_1}(t), \cdots , \\ &{h_{0,0}}(t),{h_{0,1}}(t), \cdots ,{h_{m - 1,m - 1}}(t){]^{\rm T}} {\text{。}} \end{split} $

(4)

则二阶Volterra级数滤波器状态扩展后的系数总个数为 $p = 1 + m + m(m + 1)/2$ 。

由式（1）～式（3）可得， $\hat x(t + 1)$ 可表示为：

$\hat x(t + 1) = {H^{\rm T}}(t)U(t){\text{。}}$

2.3 基于RLS算法的Volterra级数滤波器的核估计

关于Volterra级数的核估计有多种算法，常用的有最小均方算法（LMS）、递推最小二乘算法（RLS）、Kalman滤波算法等。考虑到RLS算法计算复杂度低、收敛速度快等优点，本文采用该方法估计Volterra级数核。依次令 $t = m, \cdots ,N - 1$ ，则可得基于RLS算法的Volterra级数核估计^[6]的递推算法如下：

$\begin{gathered} \hat H(t + 1) = \hat H(t) + K(t + 1)[x(t + 1) - {U^{\rm T}}(t + 1)\hat H(t)] \end{gathered} {\text{，}}$

(5)

$K(t + 1) = \frac{{{\varPhi _t}U(t + 1)}}{{1 + {U^{\rm T}}(t + 1){\varPhi _t}U(t + 1)}}{\text{，}}$

(6)

${\varPhi _{t + 1}} = {\varPhi _t} -{ K}(t + 1){U^{\rm T}}(t + 1){\varPhi _t}{\text{。}}$

(7)

其中： ${ K }(t + 1)$ 为时变增益矩阵； ${\varPhi _t}$ 与 $\hat H(t)$ 的初始值可以设置为

$\left\{ {\begin{array}{*{20}{c}} {{\varPhi _m} = I \times {{10}^4}}{\text{，}} \\ {\hat H(m) = 0} {\text{。}} \end{array}} \right.$

2.4 Volterra级数模型多步预测

未来 $l$ 步的预测值^[6]为：

$l = 1$ 时

$\begin{split} \hat x(t + l) =& {{\hat h}_0} + \sum\limits_{{m_1} = 0}^{m - 1} {{{\hat h}_{{m_1}}}} (t)x(t - m)+ \\ & \sum\limits_{{m_1} = 0}^{m - 1} {\sum\limits_{{m_2} = 0}^{m - 1} {{{\hat h}_{{m_1},{m_2}}}} } (t)x(t - {m_1})x(t - {m_2}) {\text{；}} \end{split} $

(8)

$1< l \leqslant m$ 时，令

$\begin{split} {U_1}(t) =& [1,\hat x(t + l - 1),\hat x(t + l - 2), \cdots ,\hat x(t + 1), \\ &x(t), \cdots ,x(t + l - m){]^{\rm T}}, \end{split} $

则

$\hat x(t + l) = {\hat H^T}(t){U_1}(t){\text{；}}$

(9)

$l > m$ 时，令

${U_2}(t) = {[1,\hat x(t + l - 1),\hat x(t + l - 2), \cdots ,\hat x(t + l - m)]^{\rm T}}{\text{，}}$

则

$\hat x(t + l) = {\hat H^{\rm T}}(t){U_2}(t){\text{。}}$

(10)

3 实船运动和包络预报实例分析

船舶在海面上顶浪或顺浪航行时主要产生纵摇和垂荡运动，横浪航行时主要产生横摇运动。尾斜浪和首斜浪航行时产生的纵向运动与横向运动都比较明显。剧烈的横摇、纵摇和垂荡运动会对船舶的适居性、航行使用性、安全性等产生极为不利的影响。本文以某实船运动数据为基础，应用上述方法对运动与包络进行预报。预报模型的建立采用300个历史运动时历，采样间隔为0.35 s，对于包络向前预报40步，对于运动向前预报20步。

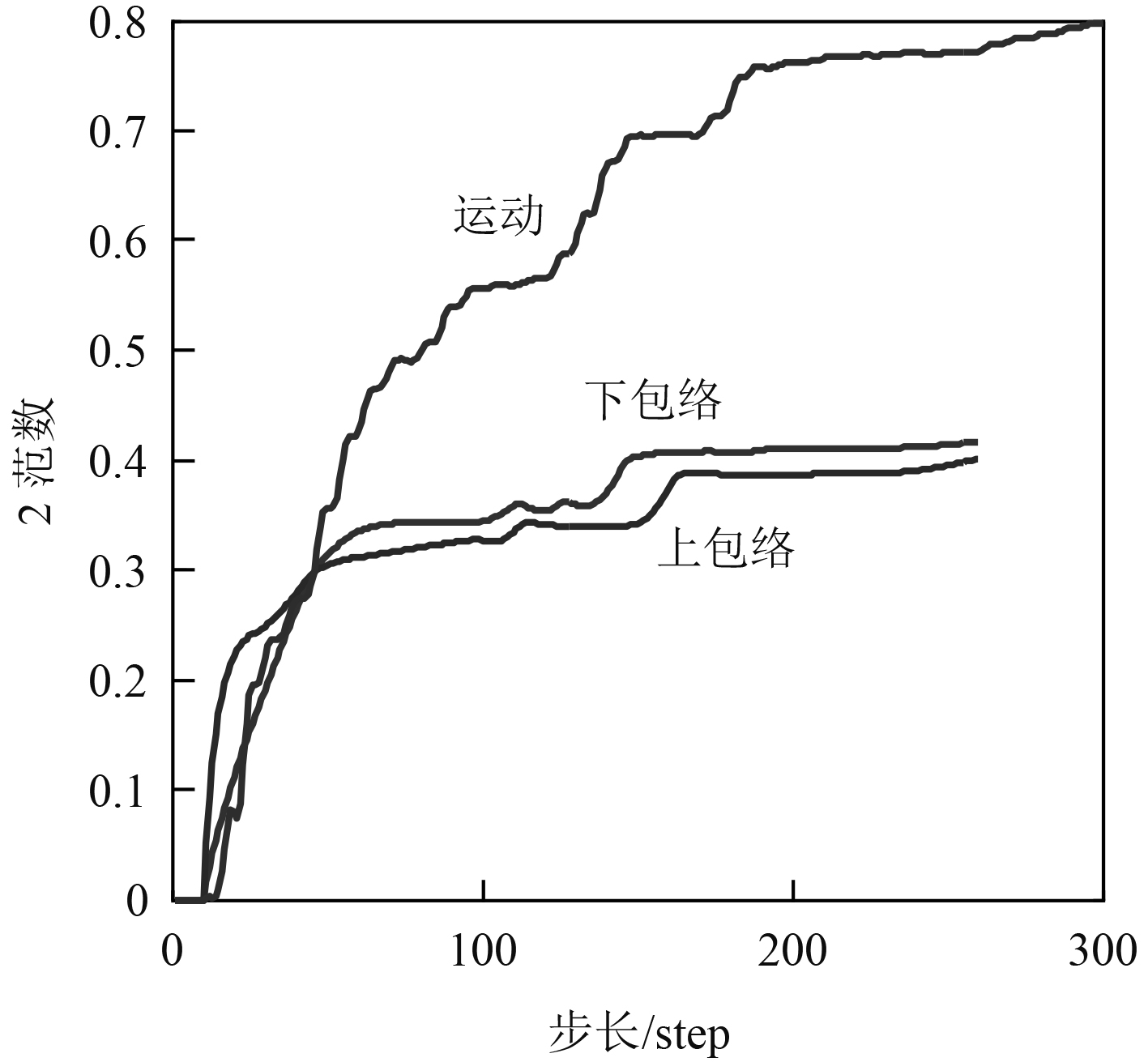
图2显示了舰船在4级海况下，以20 kn航速顶浪航行时，对升沉时历的运动和包络建模过程中，模型参数向量的2-范数变化过程。由图可知，建模数据量达到180个左右时，参数向量的2-范数趋于稳定，表明模型参数收敛。由此可见，本文选取300个数据建立预报模型即能体现信息完整性，又能成功辨识模型。

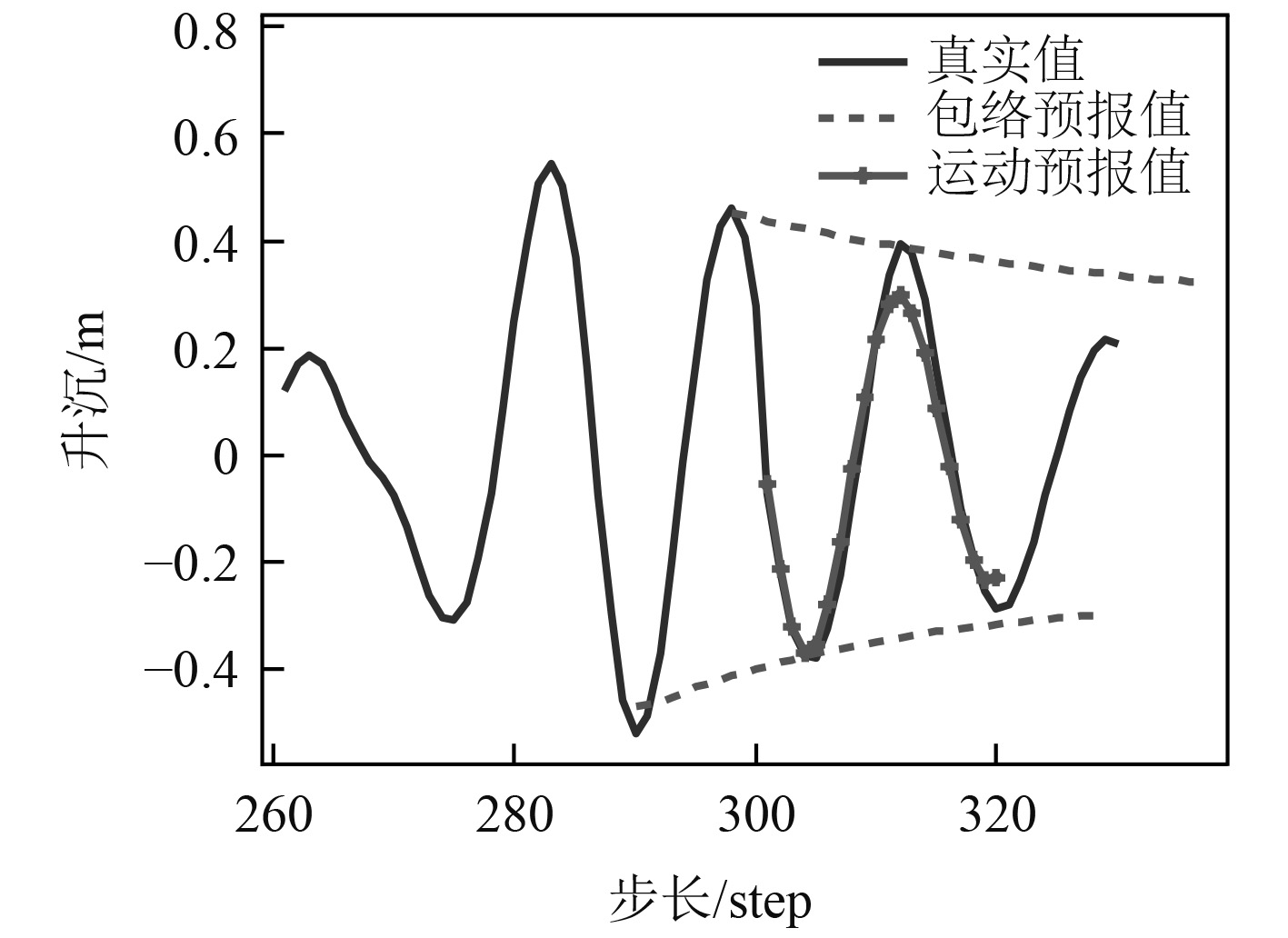
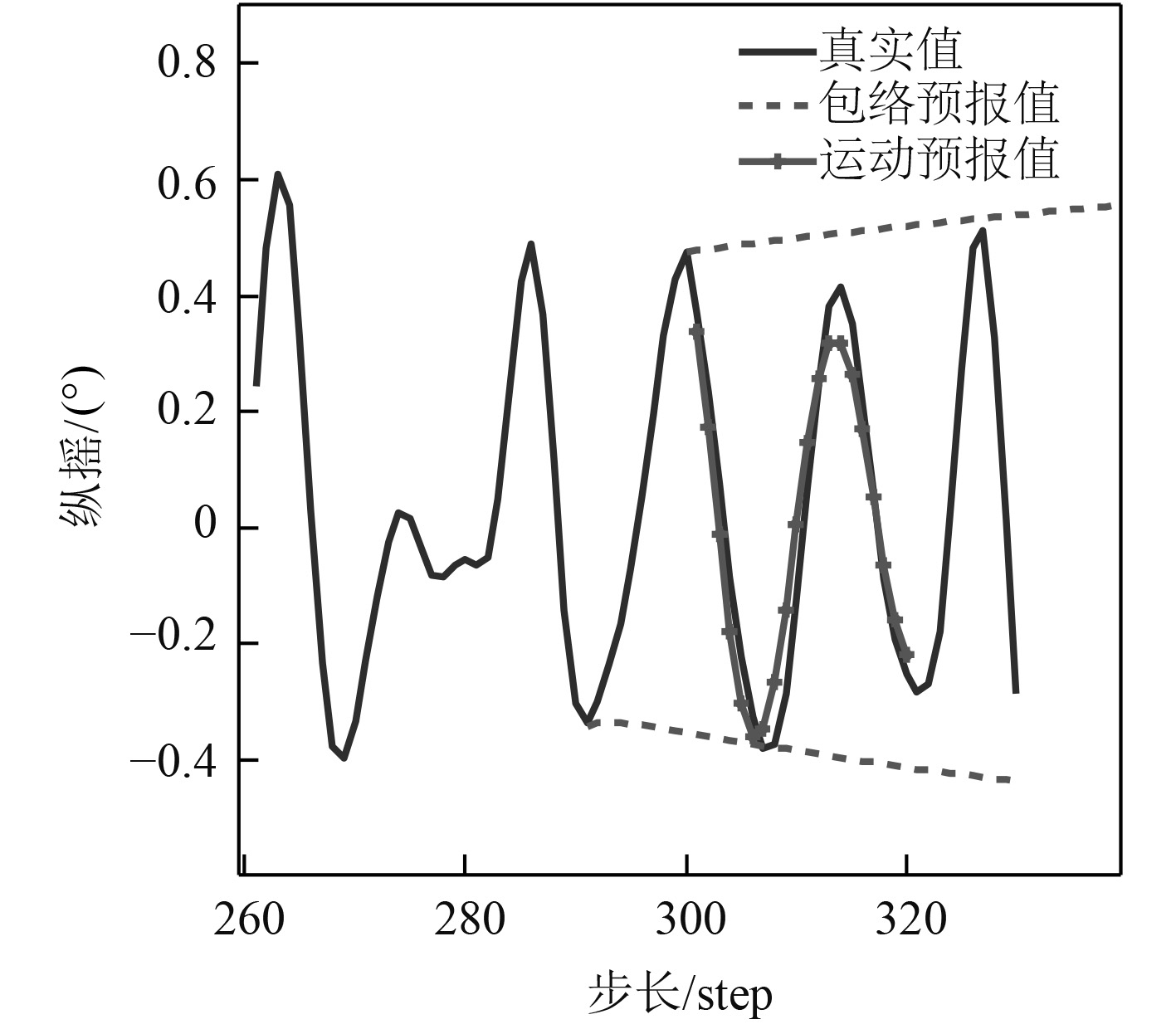
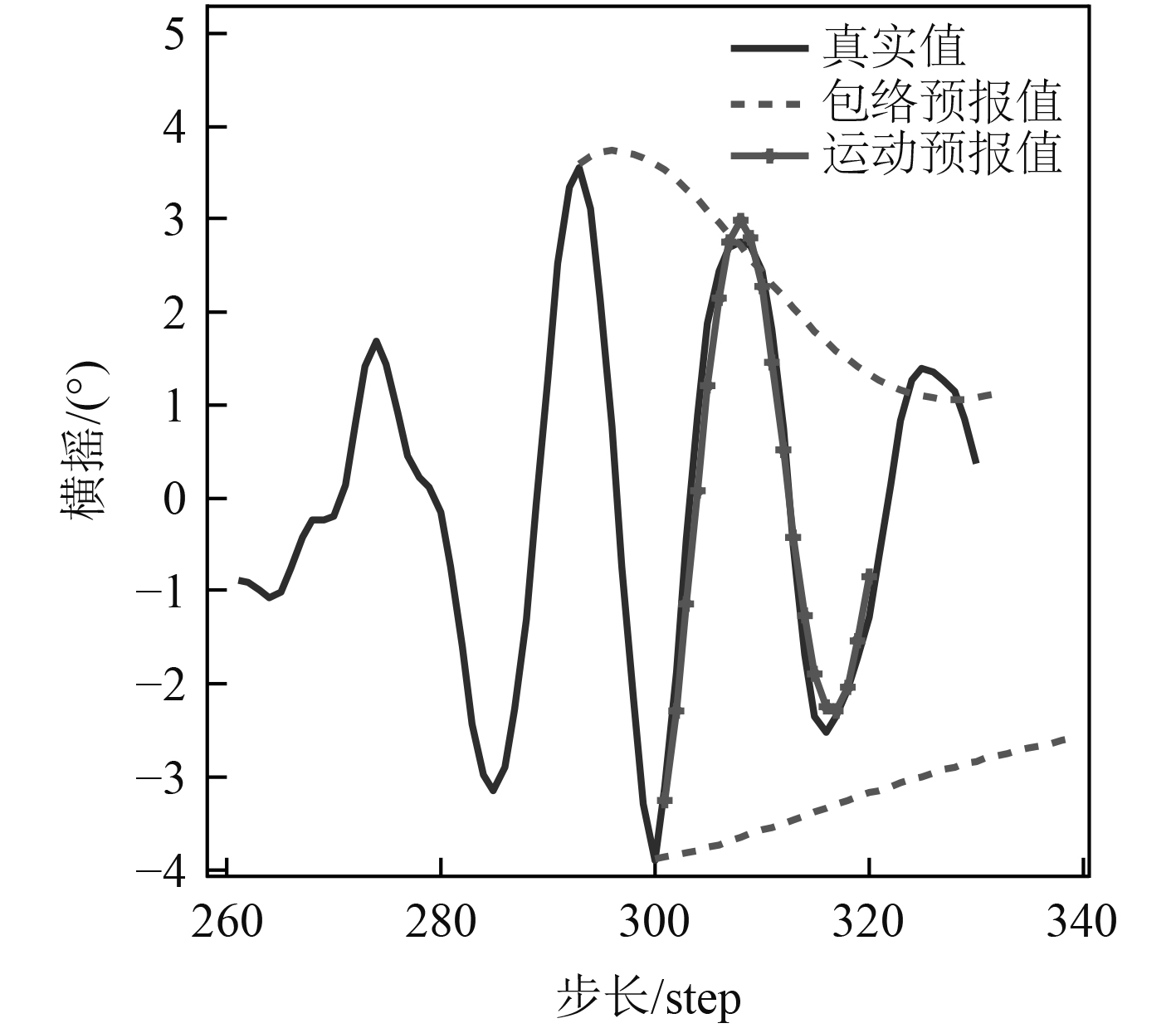
图3～图5分别为某舰船在4级海况下，以20 kn航速，顶浪升沉、顶浪纵摇和首斜浪横摇的运动与包络预报算例。表1为3个算例的预报误差情况。由图及表1可知，运动和包络预报均能有效预报出舰船的运动趋势，有时包络预报比运动预报更能反映运动趋势的幅值范围；随预报步长的增加，包络和运动预报的精度均下降。因此，可以将包络与运动的预报相结合，共同为舰载机起降、减摇控制等工程作业提供辅助意见。

为了分析二阶自适应Volterra级数模型的预报性能，分别对不同工况，采用300个时段的数据多次建立预报模型，统计其预报精度。每次的预报精度 $\eta $ 以式（11）衡量，300次预报的统计精度 $E\left( \eta \right)$ 以这300次的精度期望表示。预报统计结果如表2所示。

$\eta = \frac{{\sum\limits_{t = N + 1}^{N + l} {\left\{ {\left[ {\hat x(t) - \bar {\hat x}(t)} \right]\left[ {x(t) - \bar x(t)} \right]} \right\}} }}{{(n - 1){\sigma _{\hat x}}{\sigma _x}}}{\text{。}}$

(11)

其中： $l$ 为预报数据个数； $x(t)$ ， $\bar x(t)$ 分别为预报区的真实值及其期望； $\hat x(t)$ ， $\bar {\hat x}(t)$ 分别为预报值及其期望； ${\sigma _x}$ ， ${\sigma _{\hat x}}$ 分别为预报时区内的真实值及预报值的标准差。 $\eta $ 表示预报精度，越接近1，表明预报序列与真实序列拟合度越高。

由表2可知，对于纵摇和升沉运动，向前预报10步的精度高于85%，向前预报20步的精度高于70%；该舰船以15 kn或20 kn航速航行时，运动预报的精度没有明显的变化；横摇运动的预报精度相对较低，向前预报10步的精度只有73%左右，可能的原因是横摇运动随机性比纵摇及升沉明显，且横摇信号的测量中混入了较多的杂乱信号。

4 结　语

舰船运动和包络的实时预报可以为舰载机起降、船舶减摇等提供辅助指导意见。本文根据某实船运动数据，建立二阶自适应Volterra级数模型，分析了舰船运动和包络的极短期预报情况，得出以下结论：

1）二阶自适应Volterra级数模型可以用来辨识船舶运动系统，RLS算法可以有效估计Volterra级数模型的核，收敛速度快；

2）包络预报可以预判未来2～3个周期的运动范围，可以将运动与包络的预报相结合，共同为舰船工程作业提供辅助意见；

3）升沉与纵摇的预报效果较好，横摇预报效果有待提高。对于该船，15 kn与20 kn航速下的运动预报效果并没有明显的变化；

4）针对文中实船数据，采用二阶自适应Volterra级数模型，升沉与纵摇的有效预报时长5～7 s，横摇有效预报约4 s。如果需要预报更长时间，可以考虑提高测量精度，滤掉运动信号中的杂波信号，或采用首前波法将波浪作为前馈添加至模型中。