潜艇的操纵性和隐身性是潜艇生命力最主要的2个部分,尾操纵面的结构形式对这两方面性能有着重要影响。潜艇的尾操纵面大多由舵与稳定翼两部分构成,一般在设计舵时并不会对艇体以及稳定翼的影响进行充分的评估。近些年来,计算机性能不断提高、水动力计算软件功能越来越强大,为小型关键附体的水动力研究提供了可能。STAR-CCM+在水动力分析上有很大优势,其生成的非结构化网格在相同数量上甚至可以与结构化网格相比拟,大大节省了划分结构化网格所需的时间。SUBOFF潜艇模型试验数据充足,利用STAR-CCM+对其不同工况下尾操纵面的水动力进行分析,可以更好的认识艇体与稳定翼对舵水动力性能的影响,为优化潜艇舵翼的水动力布局提高潜艇操纵性以及隐身性打下坚实基础。
1 敞水舵水动力分析敞水舵的计算分析以及计算方法的准确性验证是开展系列研究的基础和前提。
1.1 研究对象研究对象为实验数据完备的NACA0018小展弦比翼型,模型为矩形舵,其参数如表1所示。
|
|
表 1 矩形舵模型的主参数 Tab.1 The main parameters of rectangular rudder model |
计算域设置为圆柱形状,计算域的大小综合考虑壁面流场干扰和计算量问题,将外域直径设计为矩形舵弦长的4倍,速度入口到导边的距离设置为弦长的5倍,对计算影响较大的尾流设置出口到舵随边距离为弦长的7倍。
1.2 棱柱层网格研究第1层棱柱层厚度对壁面y+的影响较大[1],壁面y+直接影响到计算结果的准确性。为此,对棱柱层网格进行计算分析:
| $ {y^ + } = 0.172\frac{{\Delta y}}{L}{{ {Re}} ^{0.9}}\text{。} $ |
式中:
由于舵相比于艇体较小,同样来流速度下,舵位置雷诺数不会太高,取Re=1.95x105,base size=0.7 m。棱柱层厚度0.01 m,层数10层。
从计算结果图1可以看出,当base size=0.7 m控制Prism Layer sketching(PLS)=1.05/1.10时,计算结果与实验值吻合较好,再减小该值对计算结果的影响不大。相反如果增加增长因子,计算精度、准确性下降,原因在于,此时雷诺数较小,近壁面位置边界层较厚,当采用壁面函数时,棱柱层的划分要合理分布在边界层厚度范围使得可以较好地模拟流动。此时壁面y+值在30~150之间。
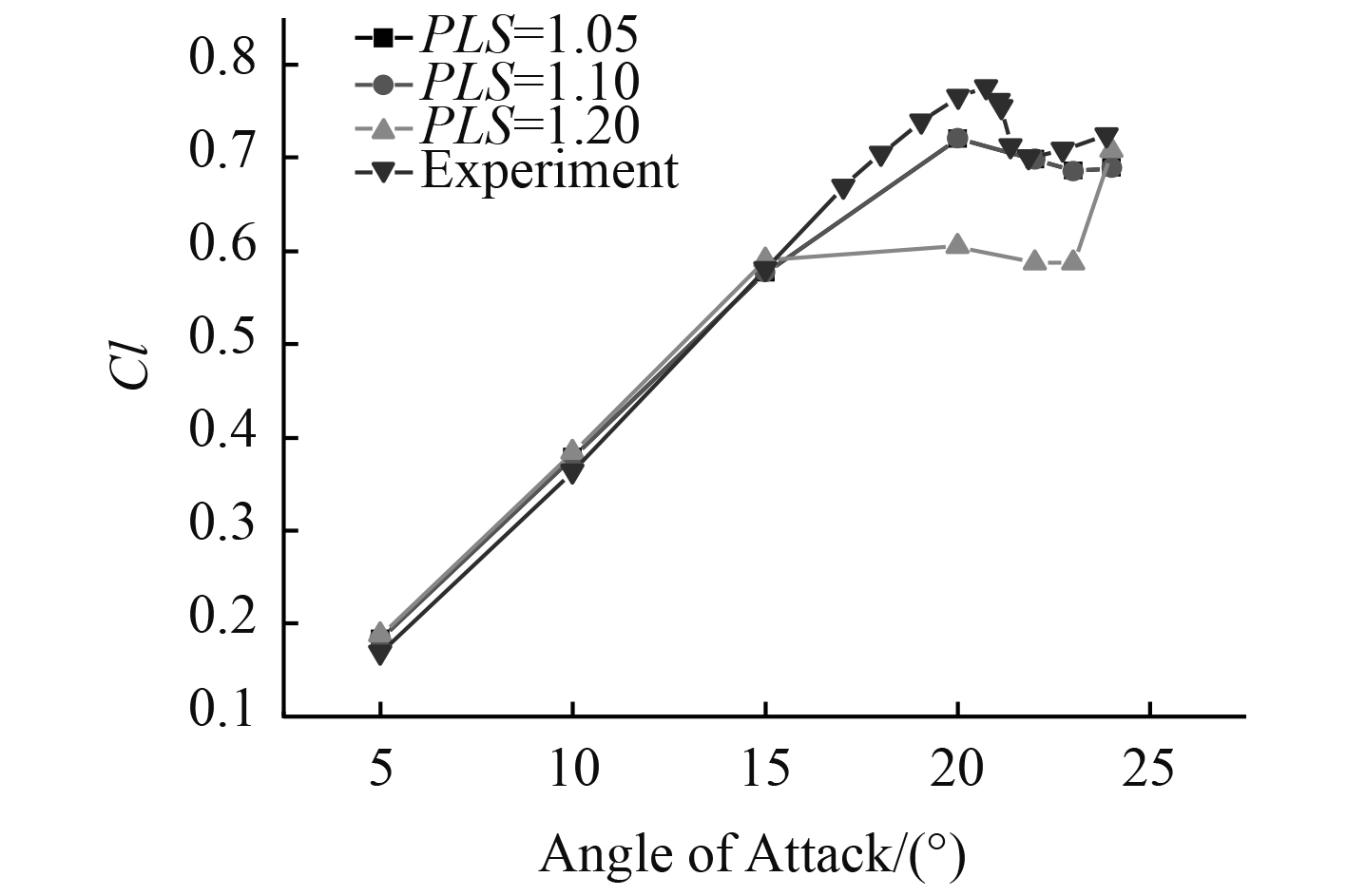
|
图 1 不同增长因子下升力系数的数值结果与试验值 Fig. 1 Experimental and numerical value of lift coefficients based on different PLS |
设置Prism Layer sketching=1.05,对网格离散进行分析。再分别取base size为0.4 m,0.6 m,1.0 m进行研究。计算结果如图2所示。

|
图 2 不同基础尺寸下升力系数数值 Fig. 2 Numerical value of lift coefficients based on different base size |
从计算结果可以看出网格数量增多,会使得未失速时的计算更准确;网格数目过小导致整体计算结果的下降,计算也就失去了意义。
1.3 物理模型研究前面对NACA0018的计算利用的是定常的SST
为了获得更好的模拟精度以及对运动情况进行研究,有必要研究一下
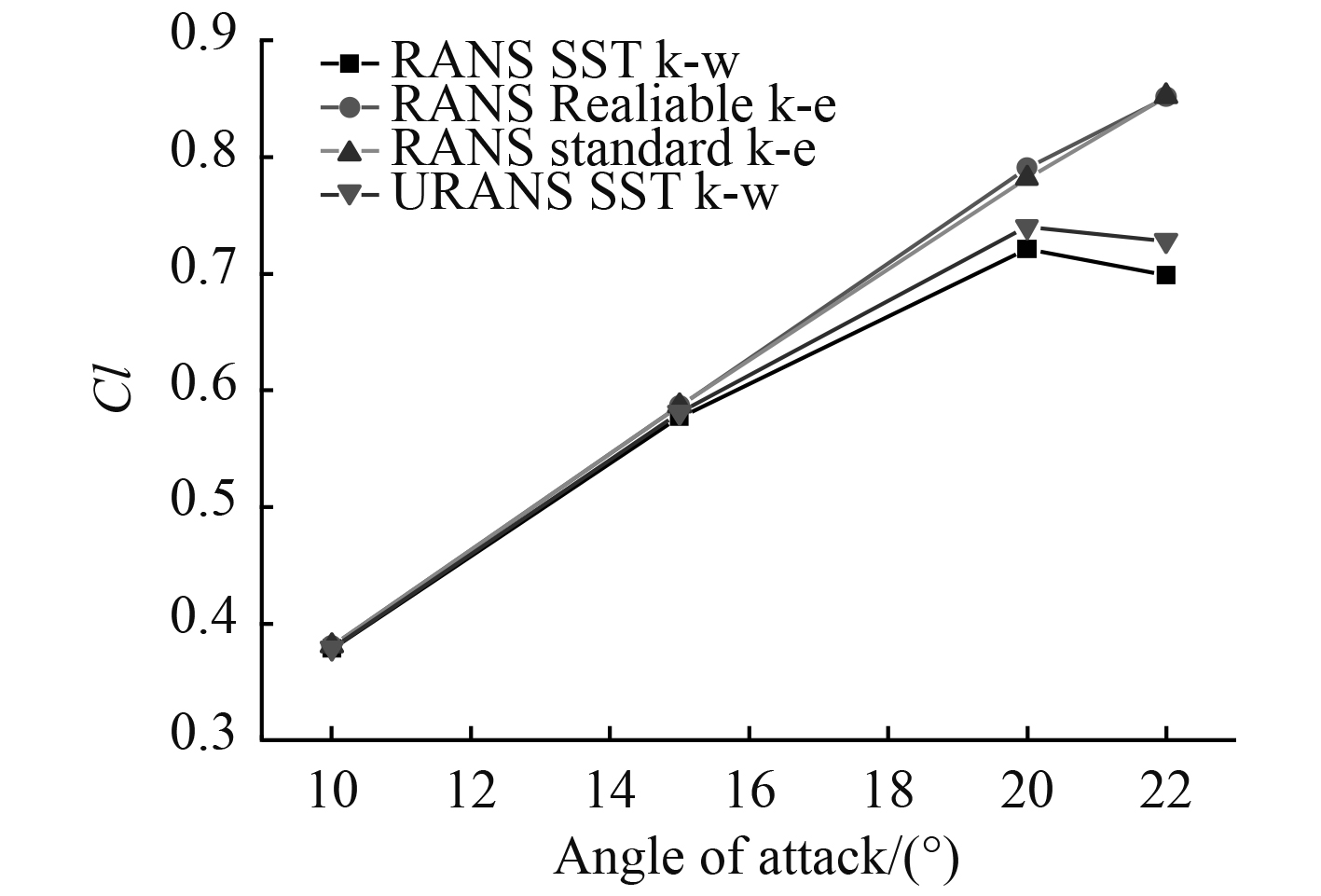
|
图 3 不同湍流模型下升力系数的数值 Fig. 3 Numerical value of lift coefficients based on different turbulence models |
对比分析可以看出,非定常方法、定常方法都可以获得较好的精度,非定常方法计算精度更高。但同样条件下,在计算未失速舵角的水动力时,
计算模型利用SUBOFF Config 1 Fully Appended的水平操纵面。特征长度取为沿艇长方向的最大舵宽0.2 m。可以得知,对舵来说Re=7.51E105。
仿照NACA0018的计算域以及网格划分形式。该操纵面的网格以及局部棱柱层划分状况如图4~图5所示。

|
图 4 舵叶面网格 Fig. 4 The rudder blade grid |

|
图 5 舵附近棱柱层网格 Fig. 5 Prism layers grid around the rudder |
对比分析不同舵角下SUBOFF单独舵的水动力性能和艇后舵的水动力性能对于认识艇体伴流对舵的影响具有重要意义。控制绝大部分y+都控制在30~150之间。图6展示了2种物理模型下计算结果的对比。
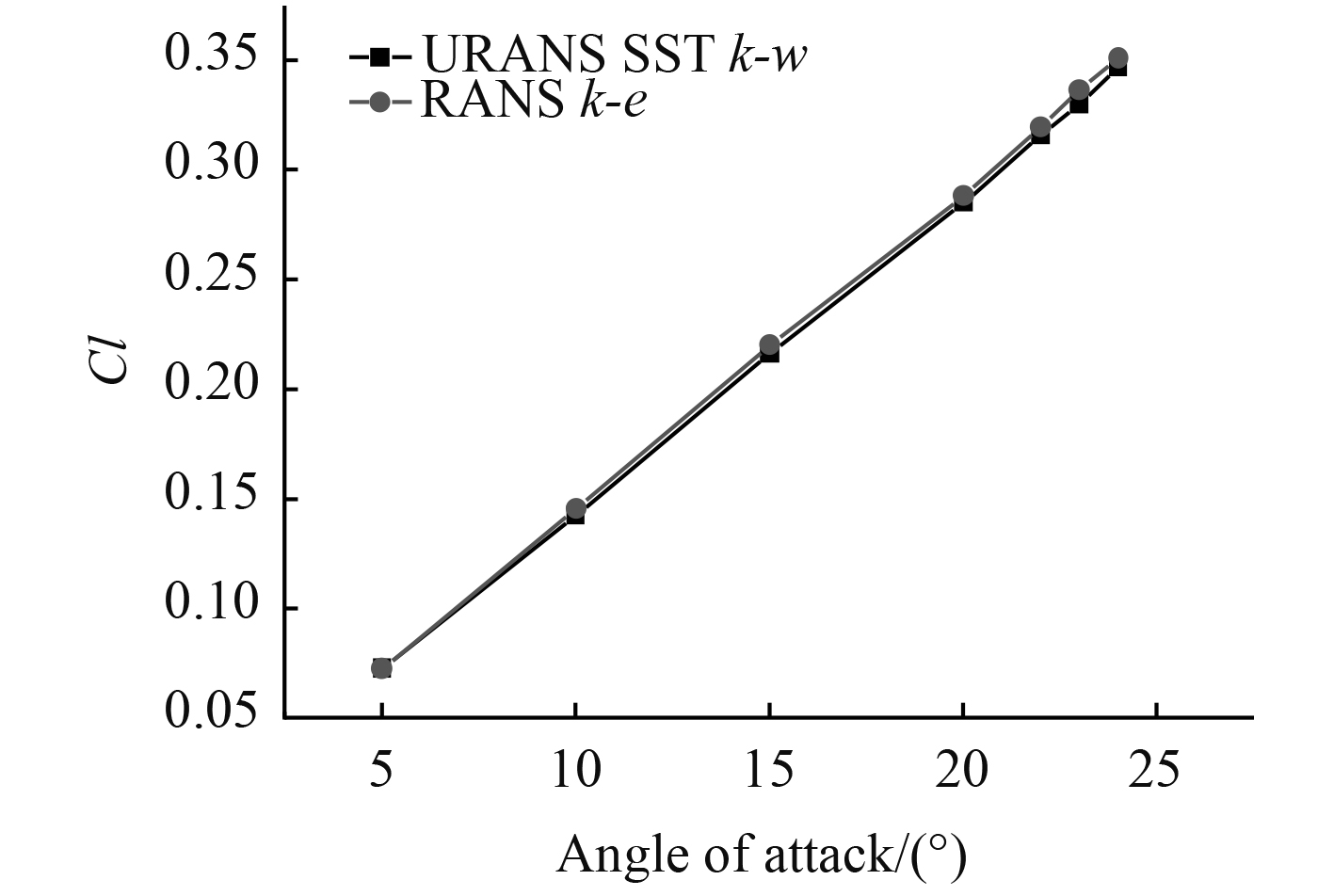
|
图 6 不同湍流模型下升力系数的数值 Fig. 6 Numerical value of lift coefficients based on different turbulence models |
试验表明当雷诺数大于1.2×105时,仅失速角随着雷诺数增加而增大,未失速范围的舵升阻力系数不变[3]。相比于NACA0018,除了翼型的差异外,雷诺数增大使得SUBOFF舵失速角后移,在所关心的舵角范围内,不会出现失速现象。分析计算结果也可以看出,利用非定常
计算模型利用SUBOFF Config 1 Fully Appended模型。根据流体力学中自由表面水质点的运动理论,可知,自由表面水质点的运动深度方向上衰减的很快,当深度达到1/2兴波波长时,可以忽略自由表面兴波的影响。当潜艇的航行深度大于1/2艇长时,可以认为不受自由面兴波的影响[4]。所以文中以深水中的潜艇为研究对象,可以不计兴波。
SUBOFF的实验研究表明,艇体的无因次水动力系数随着雷诺数改变而变化,但当雷诺数达到1×107~1.5×107时,可以忽略雷诺数影响和尺度效应。计算时来流速度选为3.343 9 m/s,Re=1.6×107。
网格划分考虑因素基本同上,为确保计算的准确性,对小部件、曲率较大的位置采用面控制加密。计算域以及网格划分结果如图7和图8所示。

|
图 7 计算域几何 Fig. 7 Geometry of computation domain |

|
图 8 艇体表面及域剖面网格 Fig. 8 Mesh for submarine and cross-sections of computation domain |
对SUBOFF Config 1 Fully Appended模型在初始来流为3.343 9 m/s直航时,在打不同舵角下的航行状况进行数值模拟。
由表2可知,阻力数值模拟的相对误差在3.7%以内,可以达到较好的精度。
|
|
表 2 不同水平舵舵角下阻力系数 Tab.2 Effect of sternplane angle on drag coefficient |
从速度分布图9可以看出,考虑艇体伴流的速度分布相比于敞水舵下降很多。利用有拱度的茹可夫斯基升力公式分析可知,舵升力的下降正比于速度的平方;相当平板理论表示摩擦阻力与速度的平方成正比,经验表明摩擦阻力约与速度的1.83次方成比例。
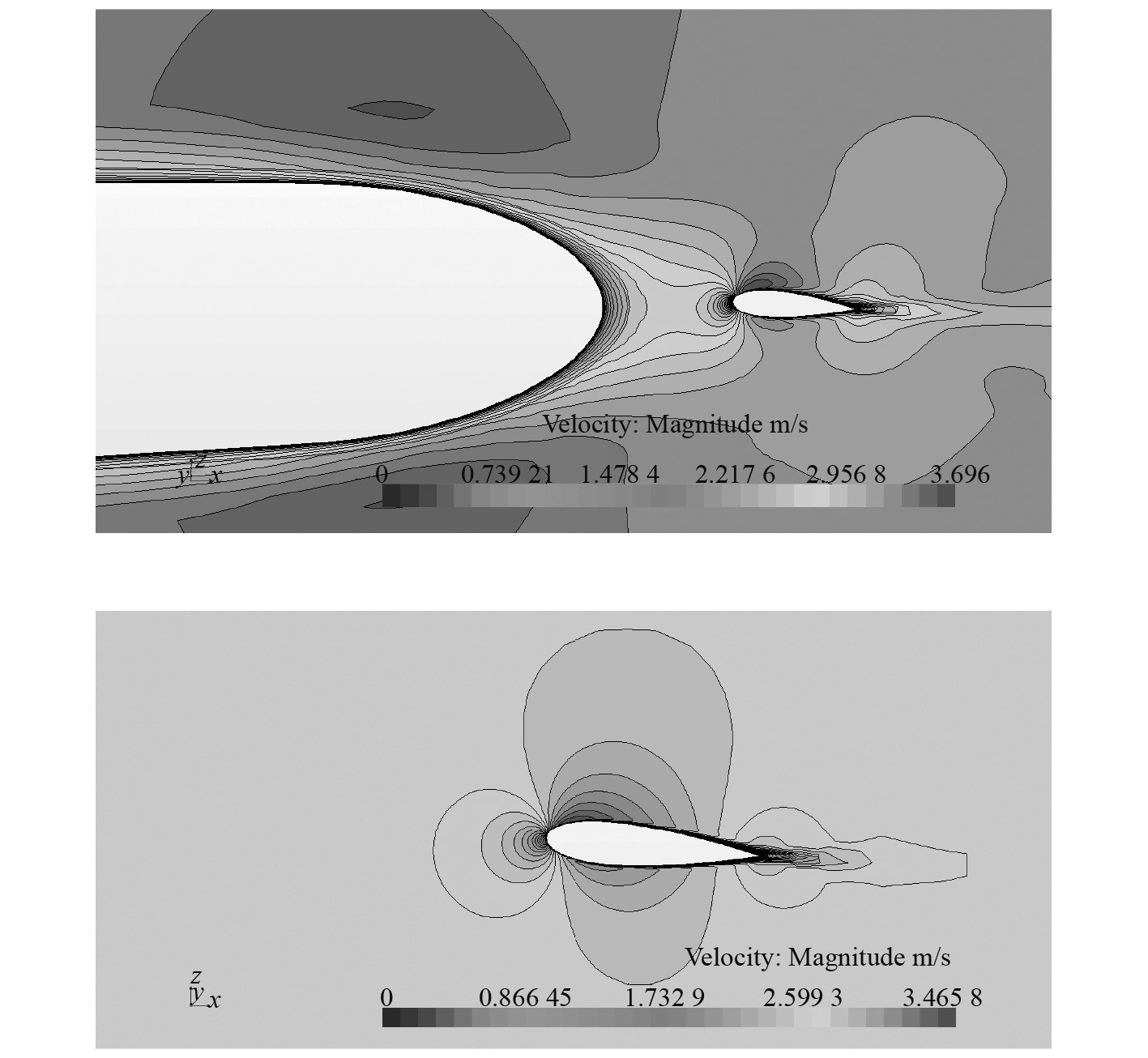
|
图 9 一纵剖面处速度大小 Fig. 9 Velocity magnitude at one longitudinal profile |
表3展示了不同舵角下,敞水舵与艇后舵前缘驻点处的最大速度以及用理论、经验估计的艇后舵相比于敞水舵升阻性能变化百分数。
|
|
表 3 考虑艇体伴流时舵升力变化 Tab.3 Effect of angle of attack on the difference on sternplane considering submarine wake |
艇后舵水动力性能的改变是潜艇伴流引起的,艇体的存在使得流场与敞水舵相比变得不再均匀。实际潜艇的舵与稳定翼一起构成潜艇的操纵面,稳定翼的存在就会对舵产生类似艇体流场的影响。图10~图13展示了压力状况,图14~图15展示了涡强分布状况。

|
图 10 直航打舵10°迎流面压力云图 Fig. 10 The pressure cloud picture of one sternplane′s upstream face, 10°sternplane angle |
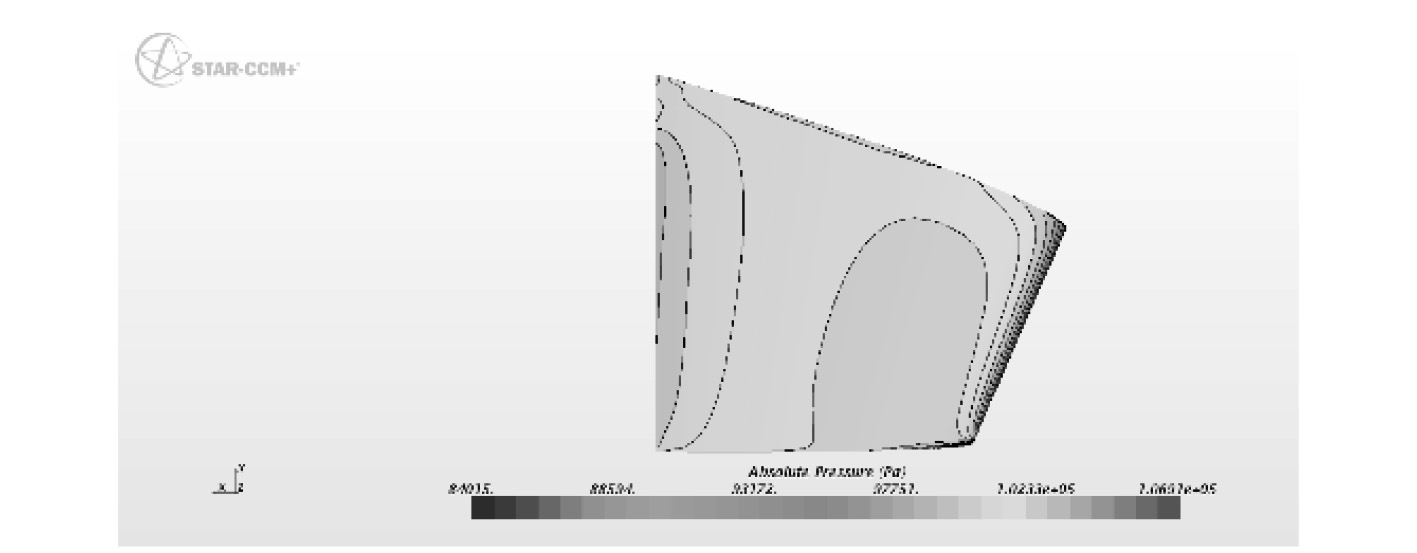
|
图 11 敞水舵10°迎流面压力云图 Fig. 11 The pressure cloud picture of one sternplane′s downstream face, 10°sternplane angle, open-water |

|
图 12 直航打舵10°背流面压力云图 Fig. 12 The pressure cloud picture of one sternplane′s downstream face, 10°sternplane angle |

|
图 13 敞水舵10°背流面压力云图 Fig. 13 The pressure cloud picture of one sternplane′s downstream face, 10°sternplane angle, open-water |
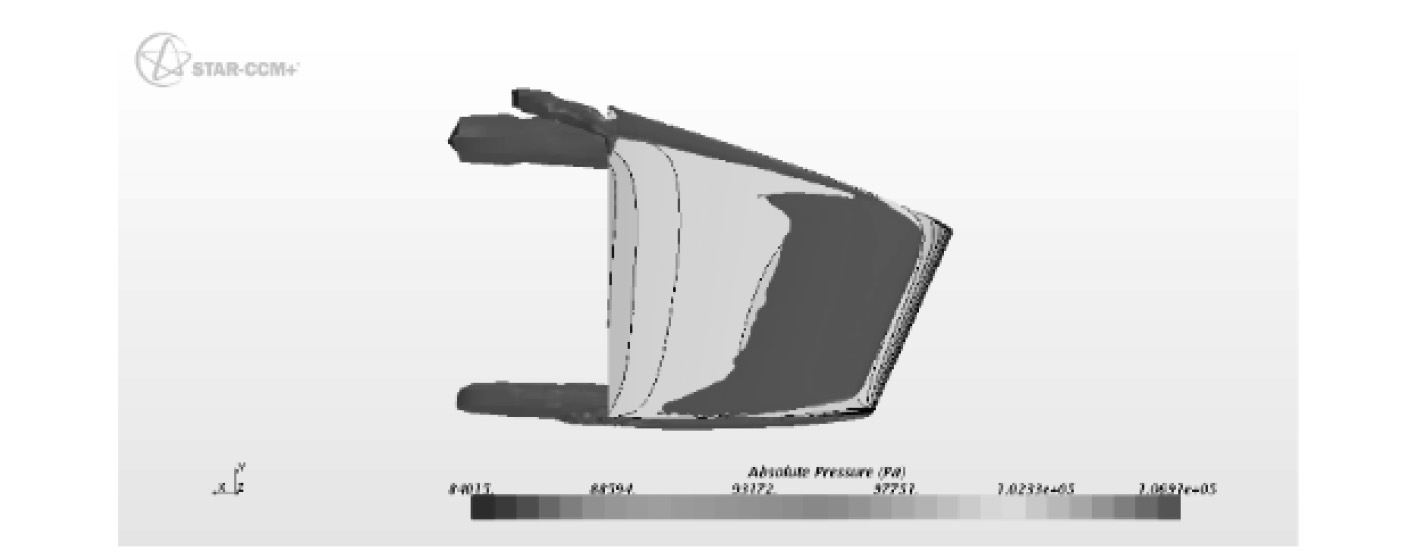
|
图 14 敞水舵10°迎流面涡强(Q-criterion) Fig. 14 The vortex magnitude of one sternplane′s upstream face, 10°sternplane angle, open-water |
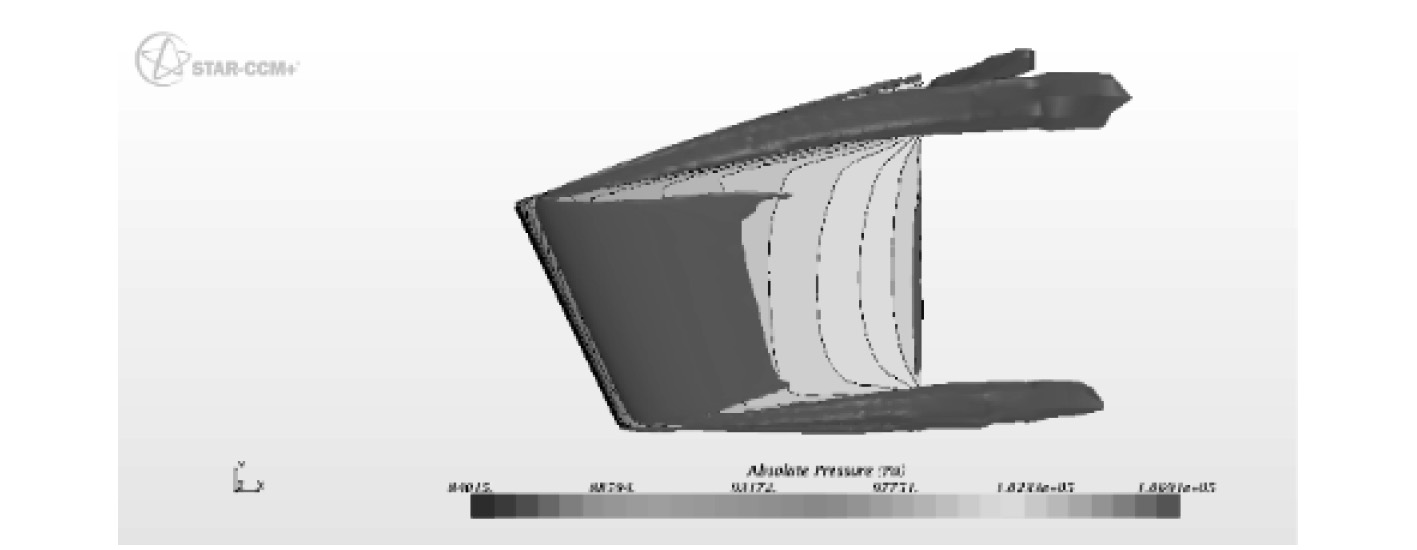
|
图 15 敞水舵10°背流面涡强(Q-criterion) Fig. 15 The vortex magnitude of one sternplane′s downstream face, 10°sternplane angle, open-water |
斜航是潜艇操纵的一种典型工况,对于分析艇体的水动力具有重要意义。基于全附体潜艇模型对潜艇在0°~18°斜航工况进行模拟,斜航冲角间隔2°,采取“攻角扫掠”的方式进行模拟,如图16和图17所示。将数值模拟的结果同泰勒水池的实验值[5]以及风洞试验[6]的实验值进行分析比较, 泰勒水池DTRC Uncertainty=20%。同时风洞试验为了更贴近实尺度时的流动,对潜艇的围壳上布置了两排激流丝的状况也进行了实验。布置的激流丝,使得附体附近湍流度增加。有无激流丝的风洞试验效果趋势一样,但数值结果有一定差异,如图18所示。
|
图 16 垂向力 Fig. 16 Normal force |
|
图 17 纵倾力矩 Fig. 17 Pitching moment |
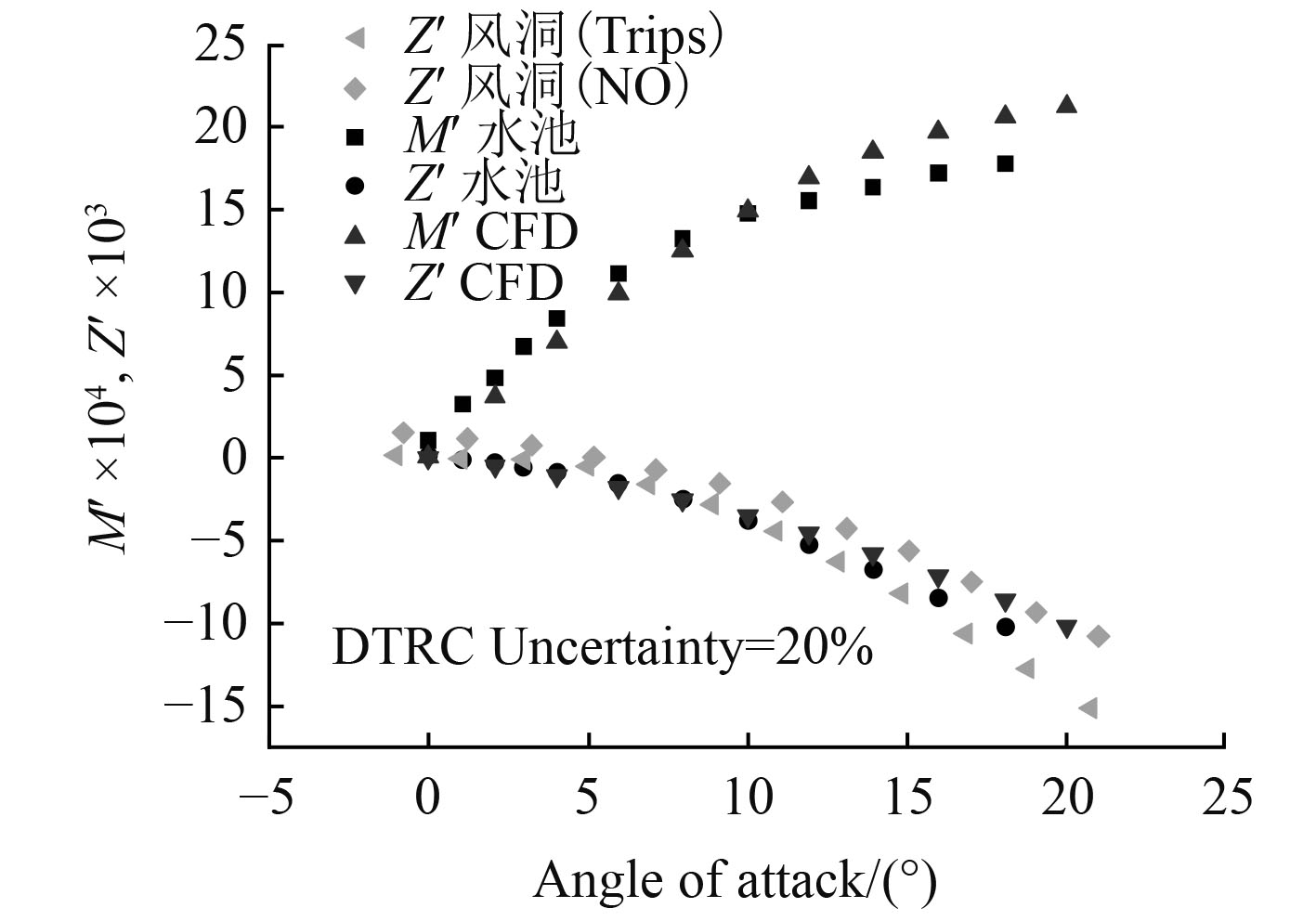
|
图 18 垂向力和力矩随攻角变化 Fig. 18 Effect of angle of attack on the normal force and pitching moment |
比较可见,数值模拟的结果同实验值吻合较好,验证了数值模拟方法的精度。当冲角较大(12°左右),数值模拟的结果尽管落在实验区间,但从力矩系数可以看出模拟精度已经开始表现出下滑趋势。
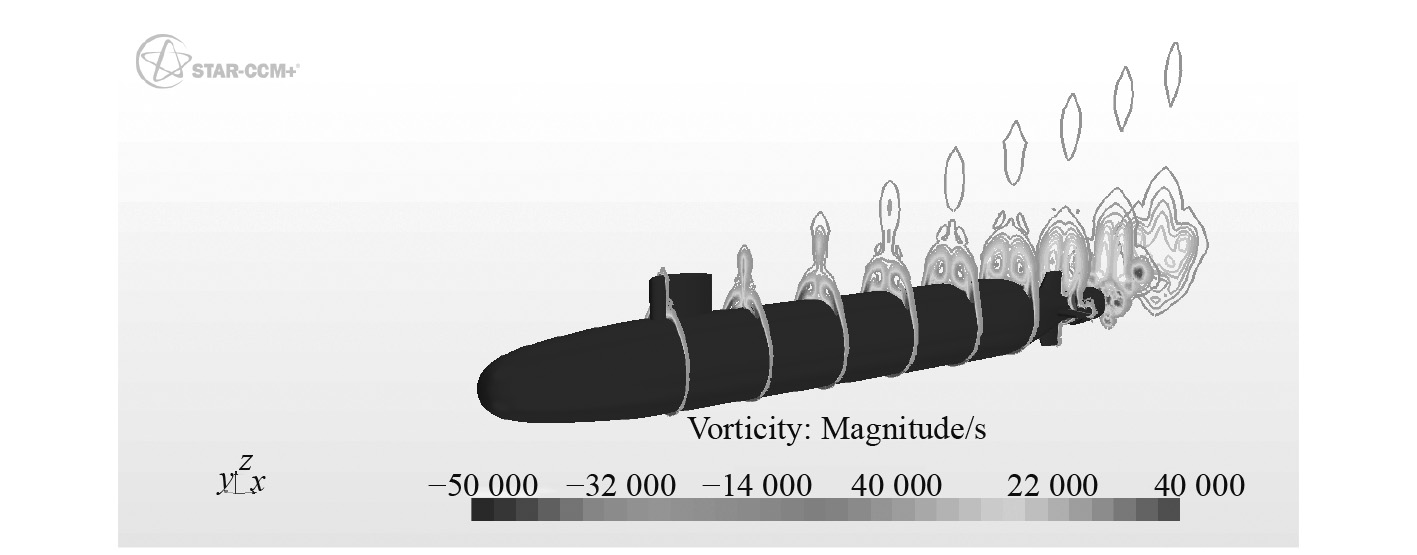
通过艇体各剖面附近的涡量图19~图21可以看出,模拟潜艇斜航,当冲角达到10°时,艇体的背风面就已经出现了流动分离,冲角达到20°时,流动分离已经比较严重,出现了涡的脱落,应用RANS方法目前无法捕捉分离涡系的演化过程[7],模拟失真。
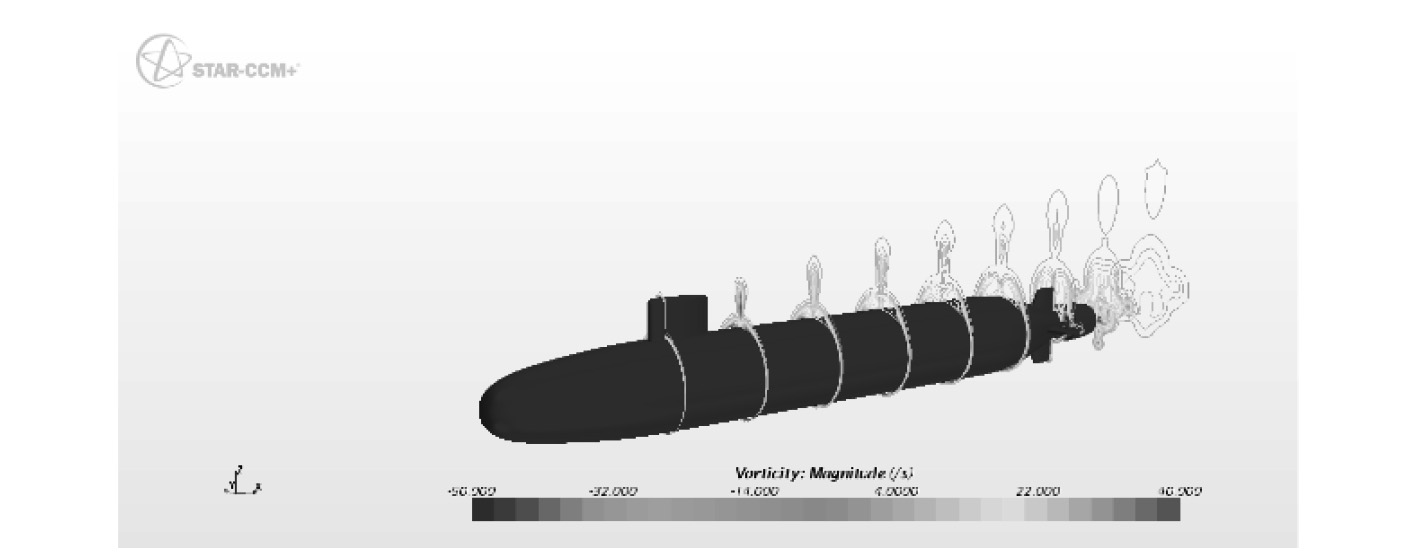
|
图 19 冲角10°斜航艇体各站涡量分布 Fig. 19 Contours of vorticity magnitude at nine axial station, 10°angle of attack, pitchup |
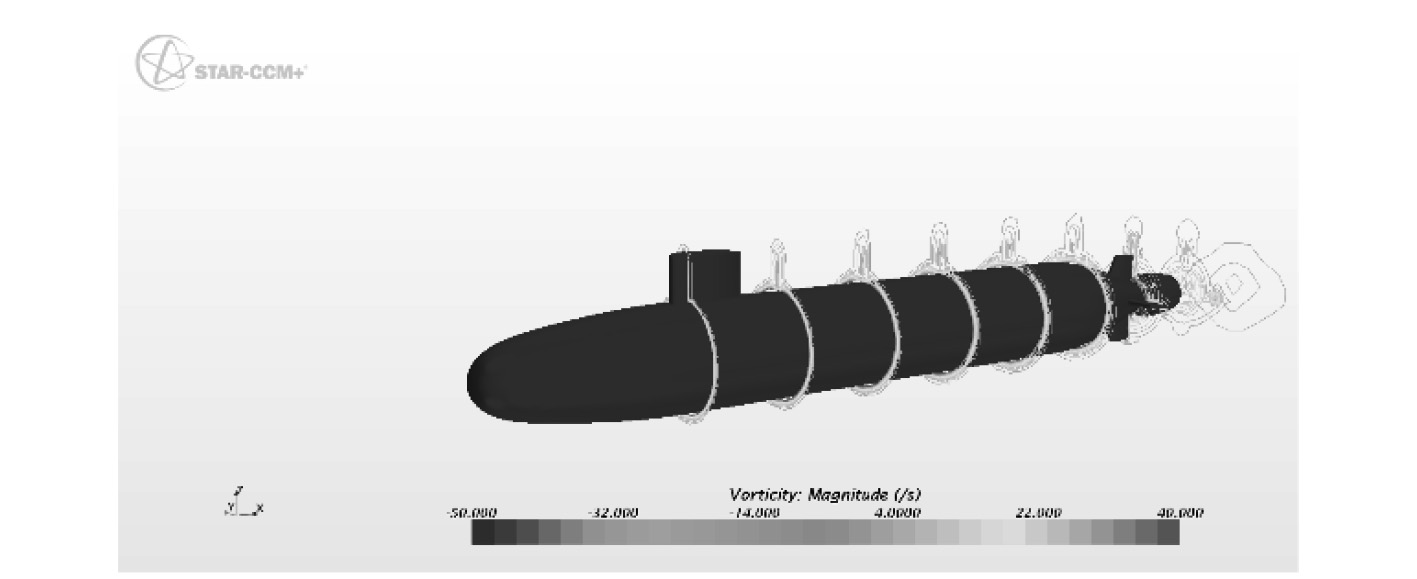
|
图 20 舵角10°直航艇体各站涡量分布 Fig. 20 Contours of vorticity magnitude at nine axial station, 10°sternplane angle |
|
图 21 冲角20°斜航艇体各站涡量分布 Fig. 21 Contours of vorticity magnitude at nine axial station, 20°angle of attack, pitchup |
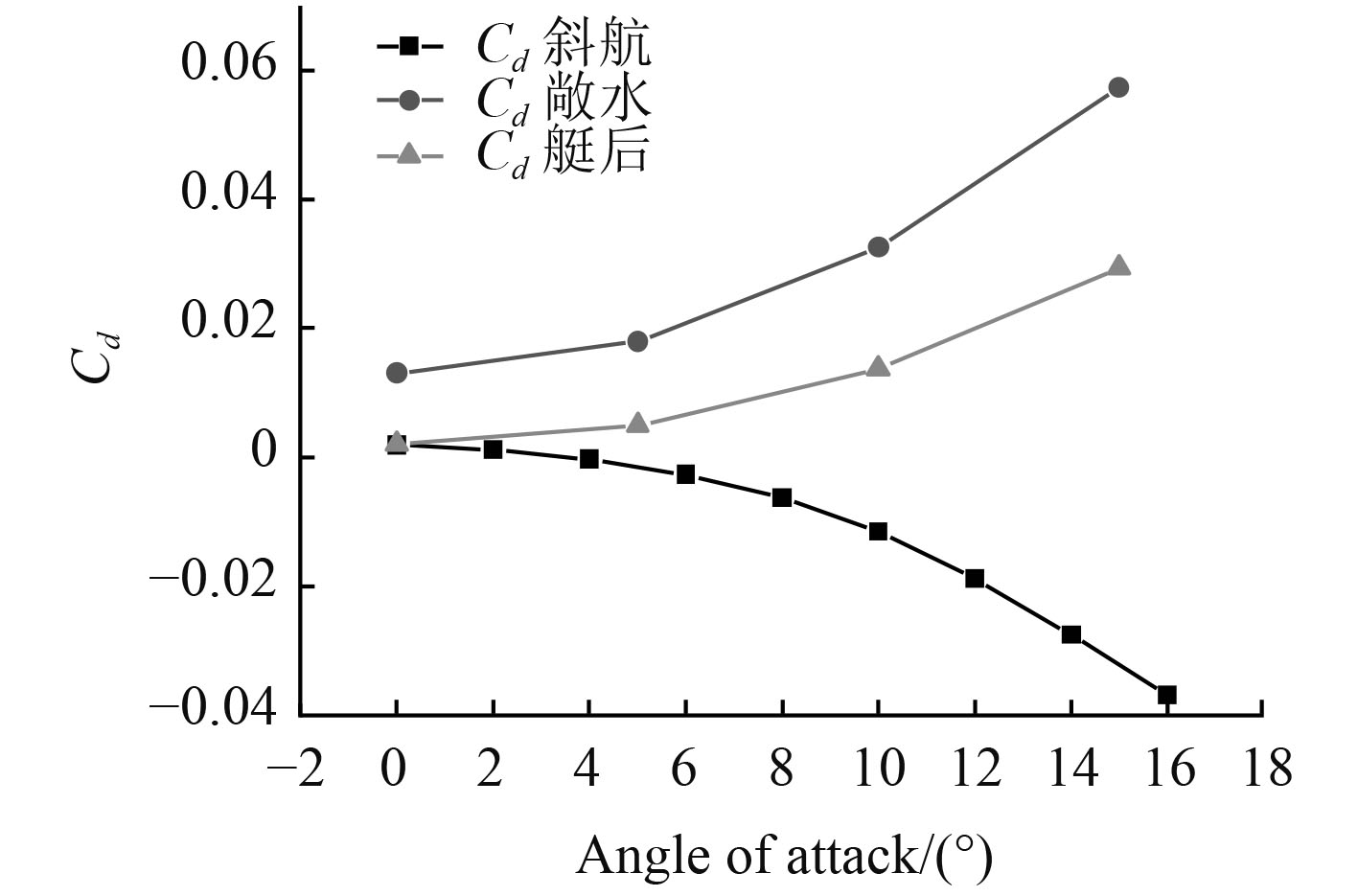
潜艇直航打舵与零舵角斜航,在速度入口的速度与舵形成的攻角相同的情况下,舵的水动力却有很大差异。直航工况下,潜艇附体涡系的变化较为平缓,不会形成大范围的涡系脱离以致大幅改变舵附近流场的流动。但在斜航工况下,随着冲角的增大,潜艇背流面涡系发展、脱离速度加快,舵附近的特性相比于敞水以及直航状况差异明显。对潜艇舵的水动力系数进行分析,如图22~图25所示。

|
图 22 舵升力系数随攻角变化 Fig. 22 Effect of angle of attack on lift coefficient for one sternplane |
|
图 23 舵总阻力系数随攻角变化 Fig. 23 Effect of angle of attack on drag coefficient for one sternplane |

|
图 24 舵粘压阻力系数随攻角变化 Fig. 24 Effect of angle of attack on viscous pressure resistance coefficient for one sternplane |

|
图 25 舵摩擦阻力系数随攻角变化 Fig. 25 Effect of angle of attack on friction resistance coefficient for one sternplane |
由于艇体的存在,无论是直航或是斜航,舵的升力系数下降的都较为明显,这会使得潜艇对操舵的敏感性变差,于潜艇的快速机动性极为不利,降低了潜艇的生命力。特别地,当舵的前端有稳定翼存在时,会造成相似的影响。通过研究可以发现伴流场会对舵的阻力系数产生积极的影响,尤其是粘压阻力,但舵的面积与整艇相比很小,其阻力只占了较小的一部分。在进行优化设计时,可以视研究所关注的问题,平衡二者之间的关系。
5 结果分析从数据分析可知,艇体存在时,舵由于受到艇体流场的干扰,实际的水动力效果有所下降。下降的原因直观上分析是艇体的作用使得舵附近的流场场均匀度下降、舵速度环量变小,这种速度场改变引起的升力以及阻力变化符合理论的定性分析。进一步研究,可以了解流场改变的原因在于潜艇在不同航行状况下,主艇体以及其附体(如指挥台围壳)形成的涡系干扰。通过数值模拟将这种不利影响定性更定量地展现出来,为后续研究工作奠定了基础。
6 结 语从简单翼型舵的敞水性能分析入手,通过研究网格、物理模型对计算结果的影响,确定了物理模型以及网格划分时应该主要控制的参数。并对全附体的SUBOFF在直航打舵及斜航状态做了数值模拟,得出以下结论:
1)壁面y+对计算结果的影响较大,应用
2)对比敞水舵、潜艇直航打舵及斜航时舵的水动力性能,针对关心的艇体干扰问题,得出了由于艇体的干扰舵升力性能下降很大的结论;
3)实际潜艇尾操纵面由舵与稳定翼两部分构成,稳定翼的存在会对舵的水动力性能产生类似艇体伴流场的影响,通过研究指明了改善艇体、舵和稳定翼结构布局的重要性;
4)通过对涡量的可视化研究,可以发现涡流较强的位置就是舵升力性能变差的位置,要想降低涡激振动以及噪声,流场的精确控制必不可少,这将催生对传统潜艇附体结构的改进研究热潮。
| [1] |
ANSYS AF. 14.0 Theory Guide[J]. ANSYS inc, 2011.
|
| [2] |
THOMAS P D, MIDDLECOFFEE J. F.. Direct Control of the Grid Point Distribution in Meshes Generated by Ellipitic Equations[J]. AIAA Journal, 1980, 18: 652-656. DOI:10.2514/3.50801 |
| [3] |
陆惠生, 朱文蔚, 费乃振, 等. 敞水舵的试验研究[J]. 上海交通大学学报, 1981(2): 001. LU Hui-sheng, ZHU Wen-wei, FEI Nai-zhen, et al. Experiment study on open rudders[J]. Journal of ShanghaiJiaotong University, 1981(2): 001. |
| [4] |
苏玉民, 庞永杰. 潜艇原理[M]. 哈尔滨: 哈尔滨工程大学出版社, 2013.
|
| [5] |
GROVES N C, HUANG T T, CHANG M S, et al. Geometric characteristics of DARPA (defense advanced research projects agency) SUBOFF models (DTRC Model Numbers 5470 and 5471)[J]. Geometric Characteristics of Darpa Suboff Models, 1989. |
| [6] |
WHITFIELD C C. Steady and unsteady force and moment data on a DARPA2 submarine[J]. Virginia Tech, 1999. |
| [7] |
BREUER M, JOVICIC N, MAZAEV K. Comparison of DES, RANS, and LES for the separated flow around a flat plate at highincidence[J]. International Journal for Numerical Methods in Fluids, 2003, 41(4): 357-388. DOI:10.1002/(ISSN)1097-0363 |
 2019, Vol. 41
2019, Vol. 41
