船舶结构轻量化技术是指在满足强度、刚度等相关规范约束条件下,借助数学方法和计算机编程,对船舶设计参数进行优化,使结构重量减轻的一种技术。国内外学者常用的船舶结构优化算法有ASA算法、MIGA算法、PSO算法、遗传算法等启发式算法,以及基于代理模型的优化算法。其中,本文采用的ASA算法是在传统的模拟退火法和模拟淬火过程的基础上提出的,用以解决具有多峰和非光滑性的高难度非线性优化问题,收敛速度快,能够以较小成本获得最优解[1];MIGA算法是在传统遗传算法基础上建立的一种基于群体分组的并行性遗传算法,可保证进化过程中优化解的多样性,抑制早熟现象的发生[2];PSO算法是在鸟类捕食行为研究的基础上提出的一种智能优化算法,具有收敛快,全局寻优能力强等优点[3 – 4]。
船舶结构轻量化后,虽仍满足规范等相关约束要求,但其安全水平降低程度尚未明确,当下轻量化船舶仍未有相关安全评估衡准,因此本文主要从安全水平角度出发,基于RBF神经网络近似模型,采用当下的主流优化算法ASA算法、MIGA算法、PSO算法对油船舱段进行轻量化设计,通过计算舱段极限强度及其可靠性,提出失效概率折减率μ,对比分析了不同优化算法对船舶可靠性的影响。
1 油船舱段轻量化 1.1 混合轻量化策略由于油船货舱舱段仿真计算时间较长,优化问题具有明显的非线性和不确定性,因此本文以油船货舱舱段重量最轻为优化目标,选择基于“参数化建模—试验设计—近似模型—全局优化—验证分析”的混合轻量化策略搜索全局最优解。
1)参数化建模
在设计阶段由于需要反复调整各设计变量的形状、尺寸,因此本文利用PCL语言,结合Patran的session文件,编制油船舱段参数化建模程序。
2)构建基于优化拉丁试验设计的RBF近似模型
采用优化拉丁试验设计在初始设计点周围的设计空间选取样本点作为训练集和测试集,在训练集的基础上构建RBF神经网络[5]近似模型,用近似模型替代结构有限元分析,获得设计点的响应值。测试集为模型精度不足时补充的样本点,精度要求为预测响应值与实际响应值误差小于1%。
3)在近似模型的基础上进行全局优化
本文采用ASA算法、MIGA算法、PSO算法3种现代智能优化算法进行优化,以获得近似模型的局部最优解。
4)近似模型最优解的验证
为检验近似模型的精度,将近似模型的优化结果代入有限元模型中进行核算,进一步判断是否满足约束条件。若误差较大,则需要增加新的样本点,在验证后的最优解周围设计空间再次建立新的局部近似模型,直到获得满足设计目标的最优解。
1.2 油船舱段轻量化实例以一艘16 800吨成品油船中部舱段为优化对象,建立起(1/2+1+1/2)的油船中部舱段结构有限元模型。该油船船长142.5 m,型宽23 m,型深12.6 m,设计吃水8.8 m,航速13 kn。选取连续的板材厚度和纵向骨材的截面型号为设计变量,共设置17个板材厚度设计变量,6个纵向骨材截面型号设计变量。每种板材变化的范围是ti0±2 mm(ti0为板材的初始厚度,取整)。将骨材按照剖面模数从小到大排序进行编号,编号设置为连续整数,每种骨材以编号作为设计变量,取值范围为xi0±2(xi0为骨材的初始型号),设计变量所处的位置如图1所示。

|
图 1 设计变量所处的位置 Fig. 1 Location of design parameters |
根据规范[6]中的相关规定设置载荷及边界条件,选取满载航行工况,约束条件为板的中面应力和梁的轴向应力小于规范[6]中规定的许用应力,共得到6个约束条件:
| ${g_i}(x) = {\sigma _i} - {\sigma _{ei}} \text{≤} 0\;\;(i = 1,2,3,4,5,6){\text{。}} $ | (1) |
式中:σ1(x)~σ6(x)分别为计算所得第1~6个区域[6]的应力。
优化目标为油船货舱舱段的质量mall最小,其表达式为:
| $ \min \displaystyle\sum {{m_{all}}} (x){\text{。}} $ | (2) |
为得到近似模型本次优化采集了700个样本点,采用交叉验证法,将点分为20组,每组35个测试点,用于近似模型误差分析与改进,最终所得近似模型所求响应值的R-squared值在0.9以上,拟合程度较好。采用ASA算法、MIGA算法、PSO算法3种智能优化算法进行全局搜索,得到了轻量化设计方案,对3种优化算法的结果进行分析:
|
|
表 1 不同优化算法下的轻量化油船舱段设计结果 Tab.1 Comparation between results of different optimizations |
1)优化效率
基于RBF神经网络近似模型进行全局优化探索,生成近似模型需要约3 h,取得优化结果约2 min,若直接利用优化算法则需要运算10 h以上,因此基于RBF神经网络近似模型进行优化效率高,方便工程计算。
2)验证分析
为验证近似模型的精度,将优化结果代入有限元模型中进行核算,由MSC.Natran计算分析后发现各个约束以及目标函数的预测值与实际值相差不到1%。以ASA算法为例,图2给出的有限元分析结果表明,优化后等效应力、轴向应力等满足设计规范要求,表明了本文优化策略的有效性。
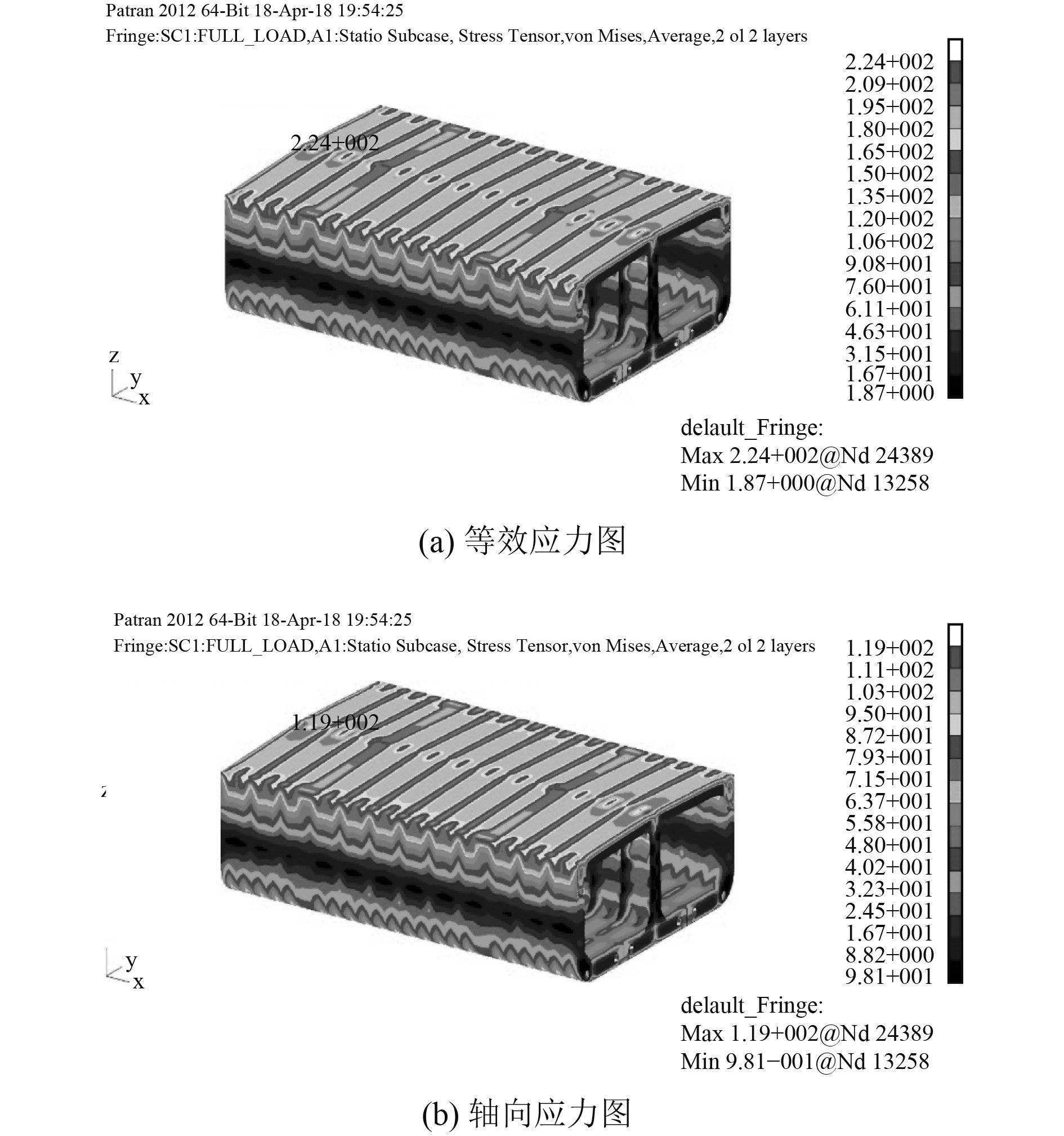
|
图 2 ASA算法下的舱段应力云图 Fig. 2 Stress nephograms of ASA algorithm |
3)轻量化程度
ASA算法、MIGA算法、PSO算法优化后的舱段质量分别较初始方案下降了4.01%,3.05%,2.62%,ASA算法的减重效果最好,相较初始方案减重28.4 t。这3种优化方法均为启发式算法,通过对自然过程的数学模拟来寻找全局最优解,其优化方向与算法自身的适应规则有关,在局部某一或几步是随机的,但总体具有趋向性,导致其追寻的最优解不同。
2 优化后舱段的可靠性分析模型 2.1 极限状态方程考虑船体在总纵弯曲下的极限状态,船体承受的静水弯矩和波浪弯矩超过自身的极限承载能力时船体崩溃。兼顾模型本身的不确定性、载荷组合等因素对方程的影响,船体极限状态方程表达如下:
| $ Z = {X_u}{M_u} - {X_w}{M_w} - {X_s}{M_s} {\text{。}}$ | (3) |
式中:Mu为船体极限强度;Xu为与极限强度有关的不确定性参数;Mw为波浪弯矩;Xw为与波浪弯矩相关的不确定参数;Ms为静水弯矩;Xs为与静水弯矩有关的不确定参数。分析可靠性时假定所有参数和弯矩都是相互独立的。
2.2 极限强度的非线性有限元求解根据已有的轻量化设计资料,采用Abaqus软件建立船舶平行中体部分1/2+1+1/2的舱段有限元模型。整个模型采用右手坐标系,x轴向船首为正向,y轴向左舷为正向,z轴竖直向上为正向。模型横向范围为左舷到右舷,垂向范围为船底到货舱甲板。整体尺寸约为33.6 m×22 m×11.1 m,网格尺寸为700~735 mm,全部网格数约为2.9万,节点数约为1.5万。选取模型前后端面中和轴与中纵剖面的交点作为参考点,前后端面施加刚体约束并与参考点关联,对两端面的参考点施加角位移载荷M1和M2,以此来模拟模型的“中拱”和“中垂”状态。
采用Abaqus动态显式算法[7]计算舱段模型的极限强度,该算法不需要进行平衡迭代,稳定性较好,适用于大型复杂结构的准静态分析。实际计算时,在模型两端施加随时间变化的强迫转角位移,并输出端面弯矩反力,整个计算历程中船体经历了由完好至崩溃的过程,端面弯矩反力的极值即为船体的极限强度。纵向弯曲是船体破坏的主要形式,故本文中船舶的极限强度是抵抗总纵弯曲的能力,计算时以纵向转角为控制量,保证遵循静态准则法,在200步将纵向转角增大为0.02 rad。
2.3 随机模型考虑完整情况下的船体极限强度均满足对数正态分布[8],其均值为非线性有限元计算值,板厚、屈服强度和弹性模量的变异系数按文献[9]选取,根据Rosenbluth法计算得到极限强度的变异系数为0.12。
静水载荷是货物分布和重量、浮力等的函数,随着货物装载及燃油消耗情况的变化静水弯矩也发生变化并呈现出随机特征,其长期分布可以用正态分布进行拟合。根据挪威船级社规范计算静水弯矩设计值,其最大值的累积概率分布中垂状态时服从Rayleigh分布,中拱状态时常用指数分布表示,采用基本极值理论可以估算指定寿命周期T内静水弯矩极值的均值和标准差[10]。
波浪载荷包括垂向弯矩、水平弯矩、扭矩、水动压力以及上浪砰击等引起的瞬时载荷。最重要的波浪载荷是垂向波浪弯矩,它对总纵极限强度有决定性的影响。垂向波浪弯矩可以简化认为服从Rayleigh分布,根据极值理论确定波浪弯矩的均值和方差[11]。
用不确定性参数修正随机模型与真实模型之间的差,认为各不确定性参数是随机变量且服从正态分布,其统计特征见表2[12]。
|
|
表 2 不确定性参数统计特征 Tab.2 Characteristics of uncertain parameter |
假定船舶设计服役周期为20年,采用一阶二次矩法,借助Matlab编程计算,计算服役20年,船体在中拱、中垂情况下的可靠性、失效概率,如表3所示。为直观、量化地反映船舶的风险变化程度,基于可靠性计算结果,定义失效概率折减率μ为:
|
|
表 3 轻量化方案的可靠性和失效概率分析 Tab.3 Reliability and failure probability of each optimization design |
| $\mu = \frac{{\Delta {P_f}}}{{\Delta m}} {\text{。}} $ | (4) |
式中:
油船舱段质量减轻后,船体极限强度可靠性下降了约3%~5%,其中ASA算法方案的船体中拱极限强度可靠性下降最高达到–5.06%,失效概率增大至为初始方案的2.27倍;中垂极限强度可靠性较初始方案下降了–4.72%,失效概率增大至初始方案的2.39倍。若预设初始海况危险化,ASA算法方案若以约2.27倍的概率发生失效,结构可靠性难以保证。而不论是中垂还是中拱情况,PSO算法下的失效概率折减率μ都为三者中最小,表明减重单位舱段重量的情况下其失效概率增加的最少,也即轻量化后的船体失效的可能性增加最小。虽然MIGA算法与PSO算法的舱段质量减轻百分比仅相差0.43%,但MIGA算法的失效概率折减率相比PSO算法增大了32.7%(中拱)、58.6%(中垂),即减重单位舱段重量失效概率显著增加。
4 结 语以一艘16 800吨成品油船中部整体舱段为例,制定了“参数化建模—试验设计—近似模型—全局优化—验证分析”的混合轻量化策略,利用PATRAN的PCL语言建立了具有一道纵舱壁且水平撑杆在侧边液舱的油船舱段优化模型;基于ISIGHT平台,采用优化拉丁方进行试验设计选择样本点,构建了RBF神经网络近似模型;分别采用多种智能优化算法进行了油船舱段结构的轻量化设计;之后,利用Abaqus非线性有限元法计算轻量化舱段的极限强度,通过建立极限状态方程,而求得轻量化方案下的船体失效概率,得到了风险量化数据;为直观、量化地反映船舶的风险变化程度,提出了失效概率折减率μ。
1)混合轻量化策略适用于油船舱段结构,且通过构建RBF神经网络近似模型进行优化可极大提高工程计算效率,在较短时间内给工程优化提供参考意见;
2)不论是在中拱还是中垂情况下,PSO-RBF算法下的失效概率折减率μ均为三者最小,即减重单位舱段重量,船体梁的失效概率增加最小,由轻量化引起的风险值最小;
3)若以油船舱段质量最轻为目标函数,ASA-RBF算法在该模型上减重效果更好,结果显示重量减轻4.1%,为油船舱段的轻量化设计提供了参考。
| [1] |
INGBER L. Adaptive simulated annealing (ASA): Lessons learned[J]. 2000, 25(1): 33–54.
|
| [2] |
丁泉惠, 王森, 黄修长, 等. 基于有限元法和多岛遗传算法的飞轮结构参数优化设计[J]. 噪声与振动控制, 2016, 36(2): 56-60. |
| [3] |
KENNEDY J, EBERHART R. Particle swarm optimization[A]. Perth, Australia, 1995: 1942–1948.
|
| [4] |
EBERHART R, KENNEDY J. A new optimizer using particle swarm theory[A]. Nagoya, Japan, 1995: 39–43.
|
| [5] |
卢金娜. 基于优化算法的径向基神经网络模型的改进及应用[D]. 太原: 中北大学, 2015.
|
| [6] |
中国船级社. 油船结构直接计算分析指南[M]. 北京: 人民交通出版社, 2003.
|
| [7] |
庄茁, 由小川, 廖剑晖. 基于ABAQUS的有限元分析和应用[M]. 北京: 清华大学出版社, 2009.
|
| [8] |
HUSSEIN A W, GUEDES S C. Reliability and residual strength of double hull tankers designed according to the new iacs common structural rules[J]. Ocean Engineering, 2009, 36(17): 1446-1459. |
| [9] |
祁恩荣, 崔维成. 损伤船舶极限强度可靠性分析[C]// 船舶力学学术会议暨船舶力学创刊十周年纪念学术会议. 2007.
|
| [10] |
江晓俐. 基于船舶总纵极限强度的可靠性研究[D]. 武汉: 武汉理工大学, 2005.
|
| [11] |
WIRSCHING P H, FERENSIC J, THAYAMBALLI A. Reliability with respect to ultimate strength of a corroding ship hull[J]. Marine Structures, 1997, 10(7): 501-518. DOI:10.1016/S0951-8339(97)00009-9 |
| [12] |
段明昕. 船体极限强度及其可靠性研究[D]. 大连: 大连理工大学, 2011.
|
 2019, Vol. 41
2019, Vol. 41
