2. 江南造船(集团)有限责任公司,上海 201913
2. Jiangnan Shipyard(Group) Co.,Ltd., Shanghai 201913, China
在焊接过程中,由于集中的瞬时热输入,会在结构中产生相当大的残余应力。焊接残余应力的存在会对结构的动力学特性产生影响,继而影响其声辐射特性。隐蔽性是潜艇的生命线,其噪声水平直接关系着战斗力。作为一种大型焊接结构,在潜艇建造过程中,会在壳体焊缝附近产生大量的焊接残余应力。残余应力的存在会改变潜艇的声辐射特性,研究焊接残余应力对结构声辐射特性的影响对于提高潜艇的隐蔽性具有重要意义。
环肋圆柱壳是潜艇的简化结构形式,对于其振动声辐射问题的研究,已经取得大量的成果。缪宇跃等[1]考虑了海面和吸声海底的声反射作用,分析了圆柱壳在浅海中的声辐射特性。陈清坤等[2]将舱壁等价为线力,研究了流场中带压载及舱壁的有限长环肋圆柱壳振动与声辐射特性。张聪等[3]推导了双层加筋圆柱壳舷间实肋板和托板的反力表达式,并对不同连接方式的双层加筋圆柱壳的声辐射特性进行比较。Loock等[4]通过数值仿真和试验的方法对水中浸没状态圆柱壳低频声辐射相应进行了研究,并对2种方法得到的结果进行对比。Guo等[5]研究了有限浸深有限长圆柱壳远场声辐射的解析求解方法。邓博文等[6]分析了不同模型及不同载荷形式对单层圆柱壳声振特性的影响。陈美霞等[7]应用Flügge壳体方程,研究了不同激励力对流场中敷设阻尼材料的有限长双层圆柱壳的声辐射特性的影响。刘佩等[8]分析了在有限深水域中潜深对水下圆柱壳振动声辐射特性的影响。Farshidianfar等[9]研究了应用不同的壳体理论对圆柱壳的自由振动进行了分析,并对结果进行了对比。Zhao等[10]对谐波集中力激励的正交各向异性复合材料圆柱壳的振动声辐射问题进行了研究,得到了声辐射解析解。
焊接残余应力是一种典型的非均匀分布预应力。李良碧等[11]对环肋圆柱壳结构的焊接残余应力进行了数值模拟。一些学者研究了含焊接残余应力的圆柱壳振动与声辐射问题。Liu等[12]使用解析方法研究了焊接残余应力对圆柱壳自由振动的影响。Yang等[13]考虑流固耦合的作用,研究了焊接残余应力对水下圆柱壳自由振动的影响。陈炉云等[14]分析了局部预应力对结构动力学特性的影响。
综上所述,从理论和试验上都已经证明了焊接残余应力对于结构动力学特性的影响。但是,对于焊接残余应力对结构声辐射特性的影响研究较少。本文建立了环肋圆柱壳模型,较为系统地分析了残余应力大小和焊缝类型对于其声辐射特性的影响。
1 含预应力的圆柱壳振动-声辐射方程在焊接过程中,焊区材料会产生塑性变形。焊接完成后,由于塑性应变的存在,会改变结构的刚度,继而影响结构的振动声辐射特性。根据Flügge壳体理论,设壳体中面半径为
| ${u} = {[{u_x}\;\;{u_\theta }\;\;{u_r}]^{{\rm T}}}{\text{。}}$ | (1) |
式中:
假设流场为理想流体静止流场,忽略声振动耦合关系,则在结构域
| $\int_{{{\varOmega }_{s}}} {\delta { \varepsilon }^{{\rm T}}} {{D\varepsilon }}{{\rm d}}{\varOmega _{s}} + \int_{{{\varOmega }_{s}}} {\delta {{u}^{{\rm T}}}} \rho {{{\ddot u}\varepsilon }}{{\rm d}}{\varOmega _{s}} - \int_{{{\varOmega }_{s}}} {\delta {{u}^{{\rm T}}}} {{F}}{{\rm d}}{\varOmega _{s}}{{ = }}0{\text{。}}$ | (2) |
式中:
将式(2)进行结构离散,并建立相应的局部坐标系,定义结构位移变量为:
| ${{u}}(x,\theta ,r,t) = {[{{N}_{{s}}}{\bar{ u}_x}\;\;{{N}_{{s}}}{\bar{ u}_\theta }\;\;{{N}_{{s}}}{\bar{ u}_r}]^{{\rm T}}} = { N}{\bar{ u}}{\text{,}}$ | (3) |
式中:
| ${{N}}{{ = }}\left[ {\begin{array}{*{20}{c}} {{{N}_{{s}}}}&{{0}}&{{0}} \\ {{0}}&{{{N}_{{s}}}}&{{0}} \\ {{0}}&{{0}}&{{{N}_{{s}}}} \end{array}} \right]{\text{,}}$ |
忽略阻尼的影响,结构的动力响应微分方程可表达为:
| ${{m}_s}{\bar{\ddot { u}}} + {{k}_{{s}}}{\bar{ u}}+ { F} =0{\text{。}}$ | (4) |
式中:
圆柱壳结构在流场中振动将引起向外声辐射,声压方程
| ${{\nabla }^2}{p}(x,\theta ,r,t) + {k^2}{p}(x,\theta ,r,t) = 0{\text{,}}$ | (5) |
| ${\left. {\frac{{{\partial ^2}{{u}_r}}}{{\partial {t^2}}} = - \frac{1}{{{\rho _f}}}\frac{{\partial {p}(x,\theta ,r,t)}}{{\partial {r}}}} \right|_{r = R}}{\text{。}}\hspace{15pt}$ | (6) |
式中:
对于连续振动结构体,其声辐射功率为:
| $P = \frac{1}{2}{Re} \int_{{\varOmega _s}} {{{p}_f}} {v}_n^*{{\rm d}}{\varOmega _s}{\text{。}}$ | (7) |
式中:
如将结构的声辐射面进行离散,此时声辐射功率等于
| $P = \frac{1}{2}{Re} \sum\limits_{j = 1}^{{N_e}} {\int_{{\varOmega _{s,e}}} {{{p}_{f,j}}} {v}_{n,j}^*{{\rm d}}{\varOmega _s}}{\text{。}} $ | (8) |
式中:
根据结构表面声压与节速度的形函数关系,单元
| ${P_j} = \frac{1}{2}{Re} \int_{{\varOmega _{s,e}}} {{{p}_j}^{{\rm T}}} {N}{{N}^{{\rm T}}}{v}_{n,j}^*{{\rm d}}{\varOmega _{s,j}}{\text{。}}$ | (9) |
式中:
选用1个两端简支的环肋圆柱壳模型进行计算分析如图1所示。模型基本参数为:长度
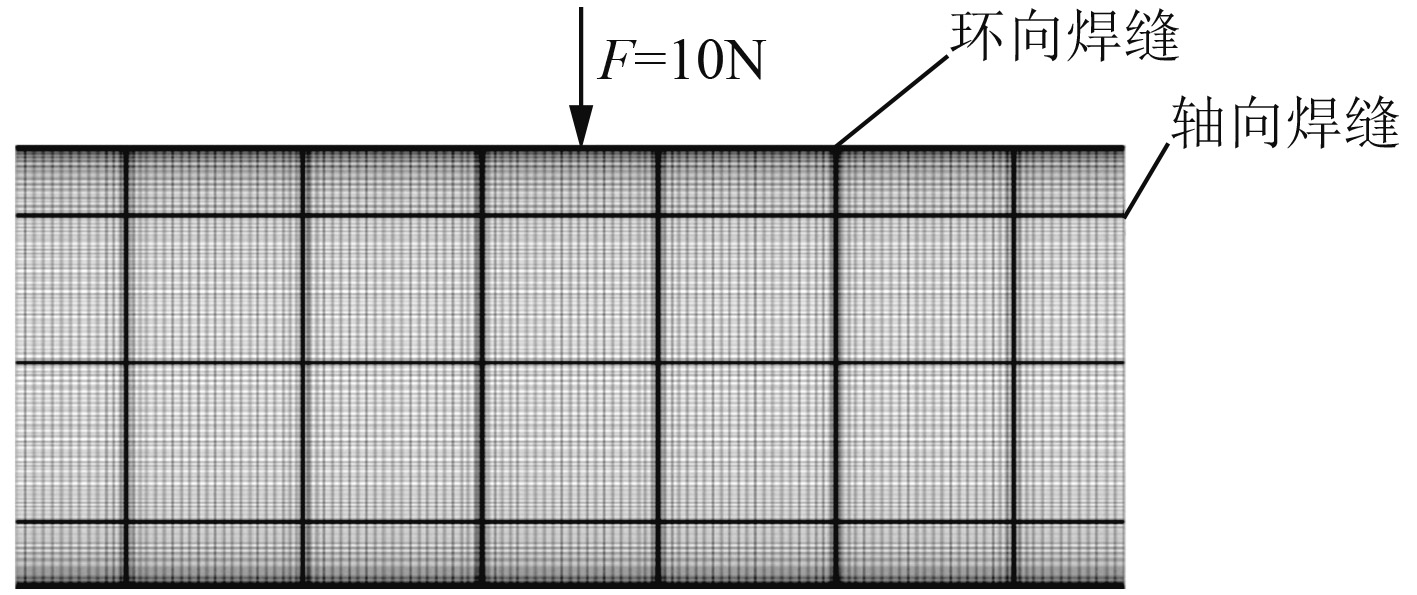
|
图 1 环肋圆柱壳模型 Fig. 1 Model of ring-stiffened cylindrical shell |
参考文献[15]的实测结果,本文在焊缝处施加初始焊接残余应力,在靠近焊缝处施加拉应力,远离焊缝处施加压应力,残余应力的分布如表1和表2所示。
|
|
表 1 环向焊缝残余应力分布 Tab.1 The distribution of welding residual stress of circumferential weld |
|
|
表 2 轴向焊缝残余应力分布 Tab.2 The distribution of welding residual stress of axial weld |
本文在有限元软件中施加初始焊接残余应力,图2为应力加载之后的模型。

|
图 2 含焊接残余应力有限元模型 Fig. 2 Finite element model with welding residual stress |
本文使用有限元软件进行结构频率响应计算,计算频率段为2~500 Hz,计算步长为2 Hz。将频率响应计算结果导入声学计算软件中,应用声边界元法开展结构的声辐射特性数值计算。声媒介为水,流体密度
图3给出了结构含焊接残余应力和无焊接残余应力的声辐射功率对比。从图中可以看出,残余应力的存在改变了结构的声辐射特性,在低频段(2~250 Hz)二者声辐射功率差别不大,在75 Hz,150 Hz,200 Hz附近有残余应力的声功率极值点要大于无残余应力的情况。在高频段(250~500 Hz)残余应力对结构的声辐射功率产生了较大影响,在300 Hz,350 Hz,400 Hz,450 Hz和500 Hz附近含残余应力的结构声辐射功率幅值要大于无残余应力结构。残余应力的存在使声辐射功率极值的频率产生了偏移。在432 Hz处,无残余应力的结构声辐射功率达到了最大值,但在此频率下含残余应力的结构声辐射功率较小。
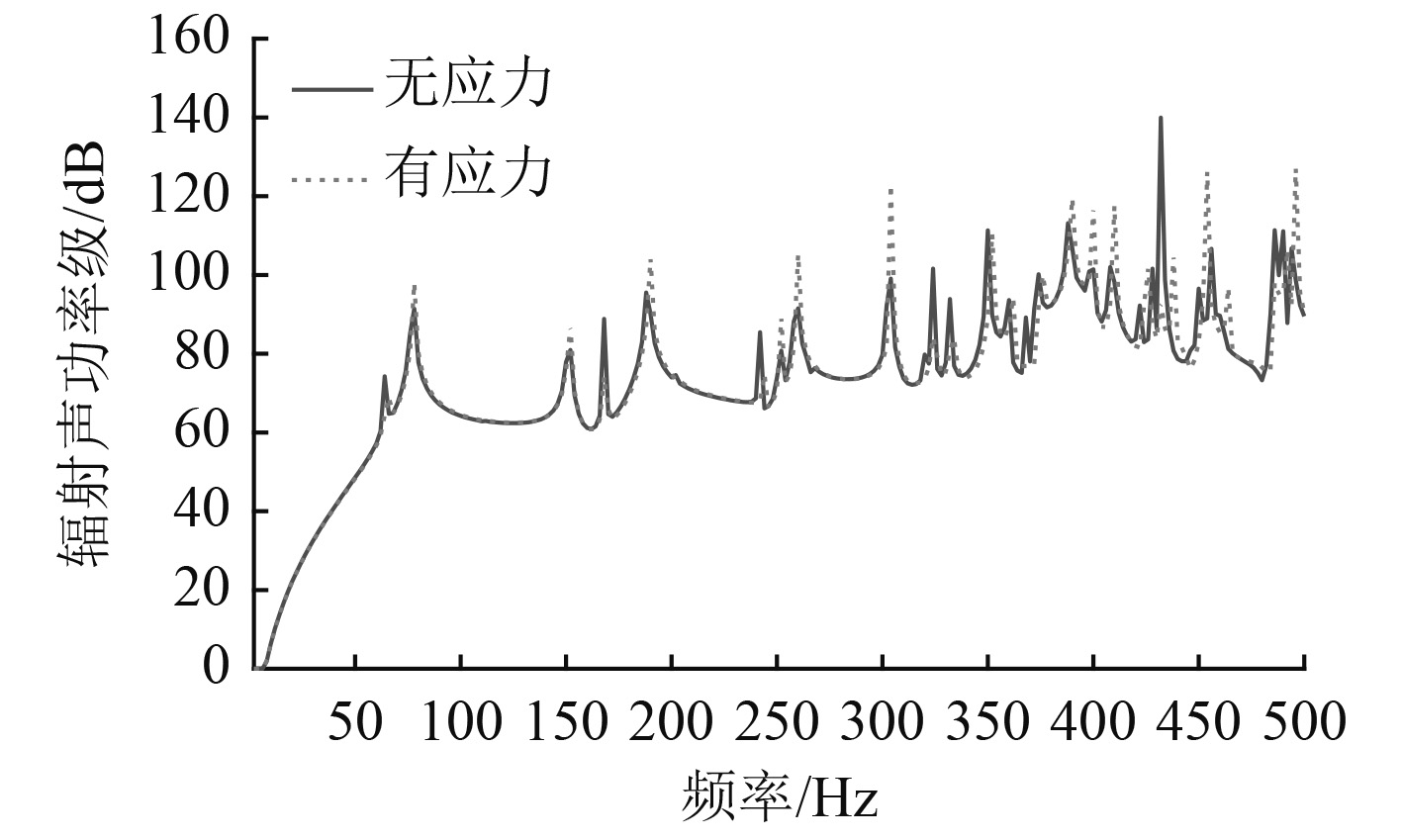
|
图 3 结构声辐射功率对比 Fig. 3 Comparison of structural acoustic radiation power |
为进一步研究焊接残余应力对结构声辐射特性的影响,本文定义声场平面为通过圆柱壳中部且与其轴向垂直的面,进行结构声辐射指向性分析。本文选取计算频率范围的中间频率250 Hz为典型频率,对结构的声辐射指向性进行研究,计算结果如图4所示。从图中可以看出,在本算例中,焊接残余应力在一些方向上对结构的声辐射指向性产生了一定影响,改变了声辐射特性。

|
图 4 结构声辐射指向性对比 Fig. 4 Comparison of structural acoustic radiation directivity |
本文对初始残余应力进行变换,将各应力大小乘以一个幅值参数n,将变换后的应力加载到模型中,以此研究焊接残余应力幅值对结构声辐射特性的影响。在本文研究中,幅值参数分别取0.4,0.6,0.8,1.0,1.2,1.4,图5所示为各参数条件下结构声辐射功率计算结果。
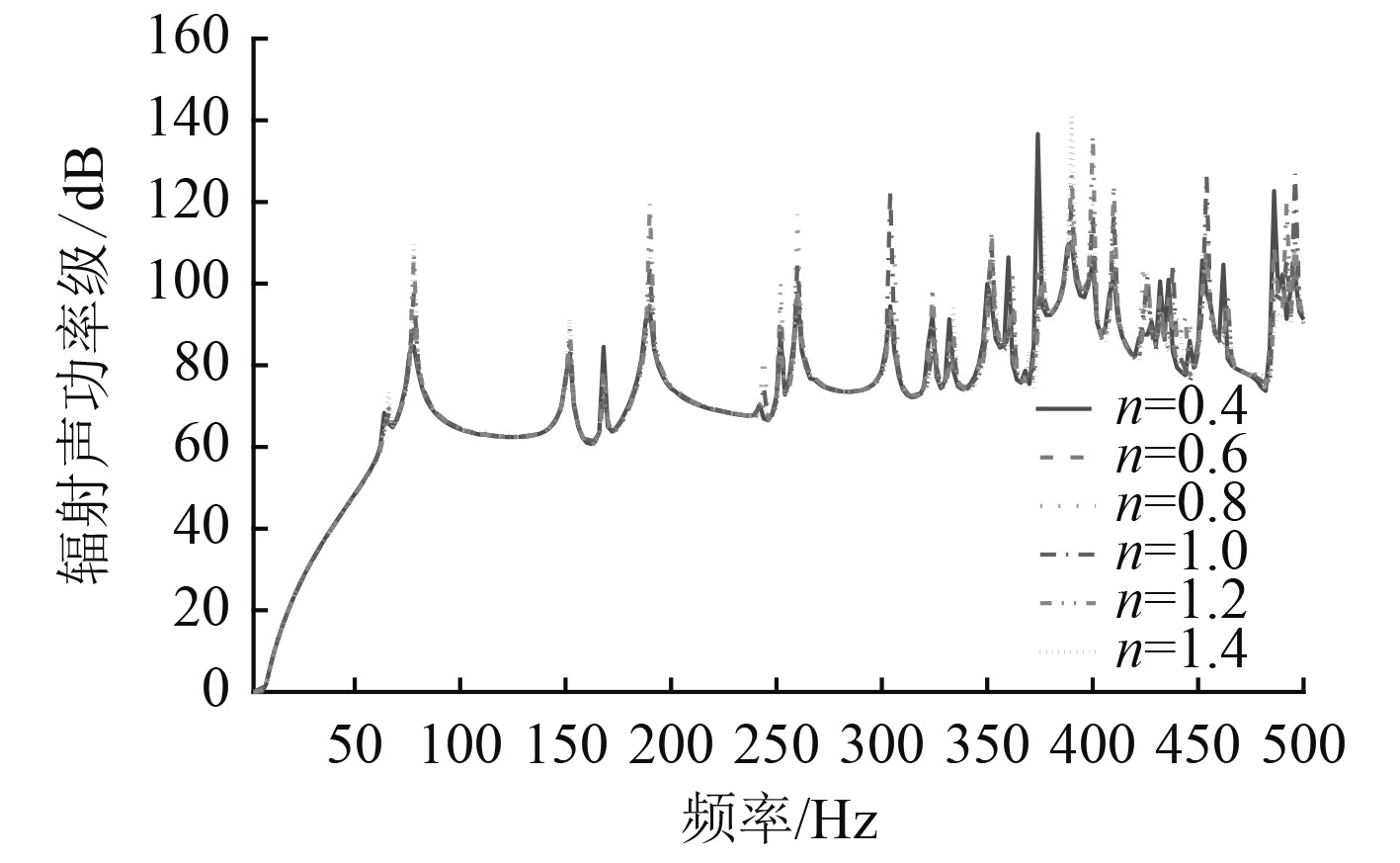
|
图 5 不同应力幅值下结构声辐射功率 Fig. 5 Structural acoustic radiation power of different stress amplitude |
从图5可以看出,焊接残余应力幅值的变化主要影响结构最大声辐射功率值,这是由于残余应力的存在改变了结构的刚度,不同的残余应力幅值对结构预应力区的刚度矩阵的改变情况不同。在本算例中,各频率辐射声功率极值会出现在不同的幅值参数取值时。例如,在200 Hz附近,幅值参数取1.2时辐射声功率达到最大。在375 Hz附近,声功率最大值为幅值参数取0.4时。
图6为结构在250 Hz时不同残余应力幅值下的声辐射指向性。由图中可以看出,在本算例中,残余应力的幅值对结构声辐射指向性的影响不是非常明显,只在某些方向上产生了一些影响。
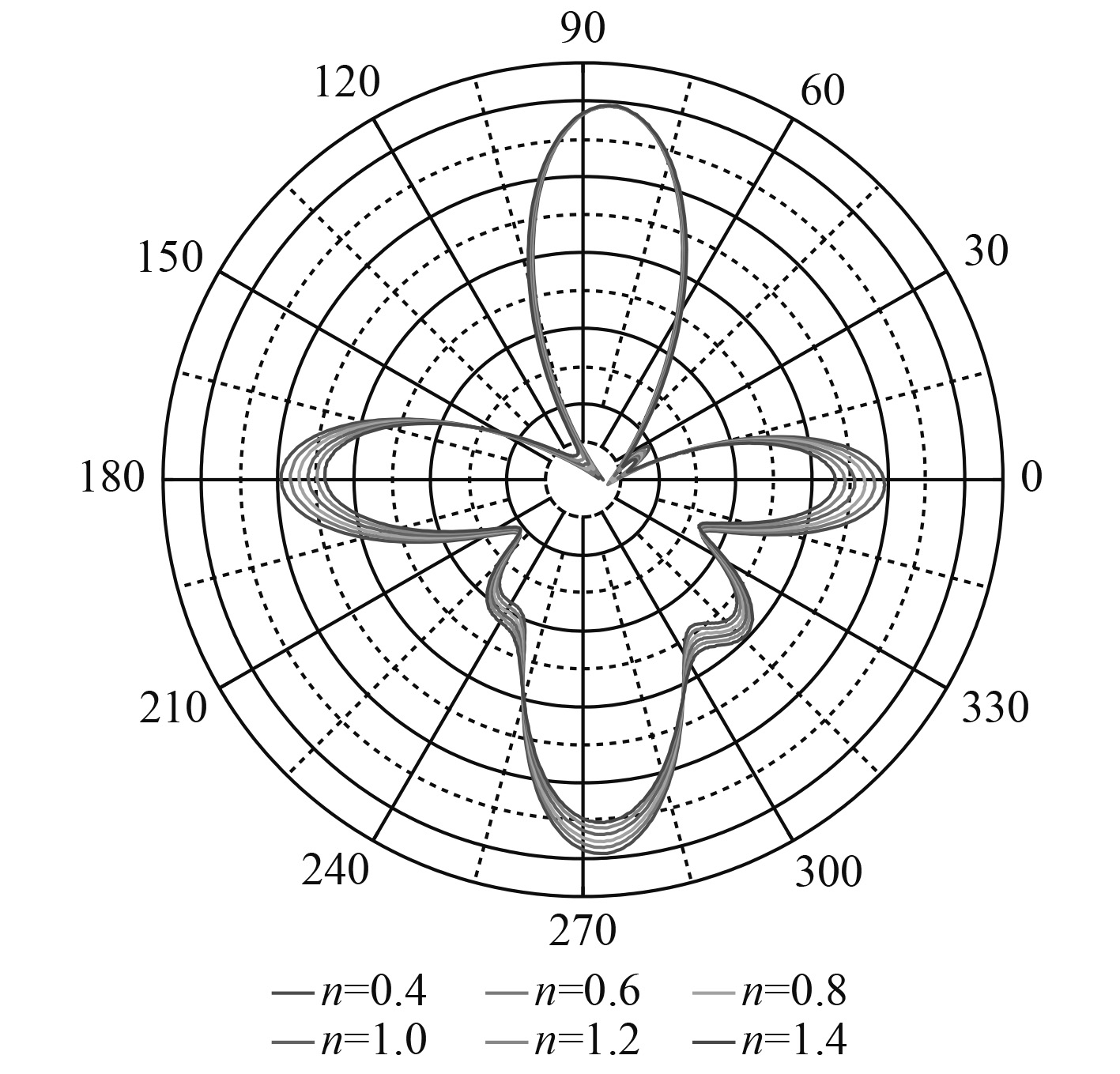
|
图 6 不同应力幅值下结构声辐射指向性 Fig. 6 Structural acoustic radiation directivity of different stress amplitude |
在环肋圆柱壳结构中,主要含有环向和轴向2种焊缝类型,为研究焊缝类型对结构声辐射特性的影响,本文分别对环向和轴向焊缝残余应力进行变化,计算结构声辐射响应。在研究环向焊缝的影响时,保持轴向焊缝应力大小不变,将环向焊缝应力大小分别乘以参数k,将变化应力加载到结构中进行计算。在研究轴向焊缝的影响时,保持环向焊缝应力大小不变,将轴向应力大小分别乘以参数l,将变化应力加载到结构中进行计算。在本文研究中,参数k和l分别取0.4,0.6,0.8,1.0,1.2和1.4。声辐射功率计算结果如图7和图8所示。

|
图 7 不同环向焊缝应力下结构声辐射功率 Fig. 7 Structural acoustic radiation power of different stress of circumferential weld |
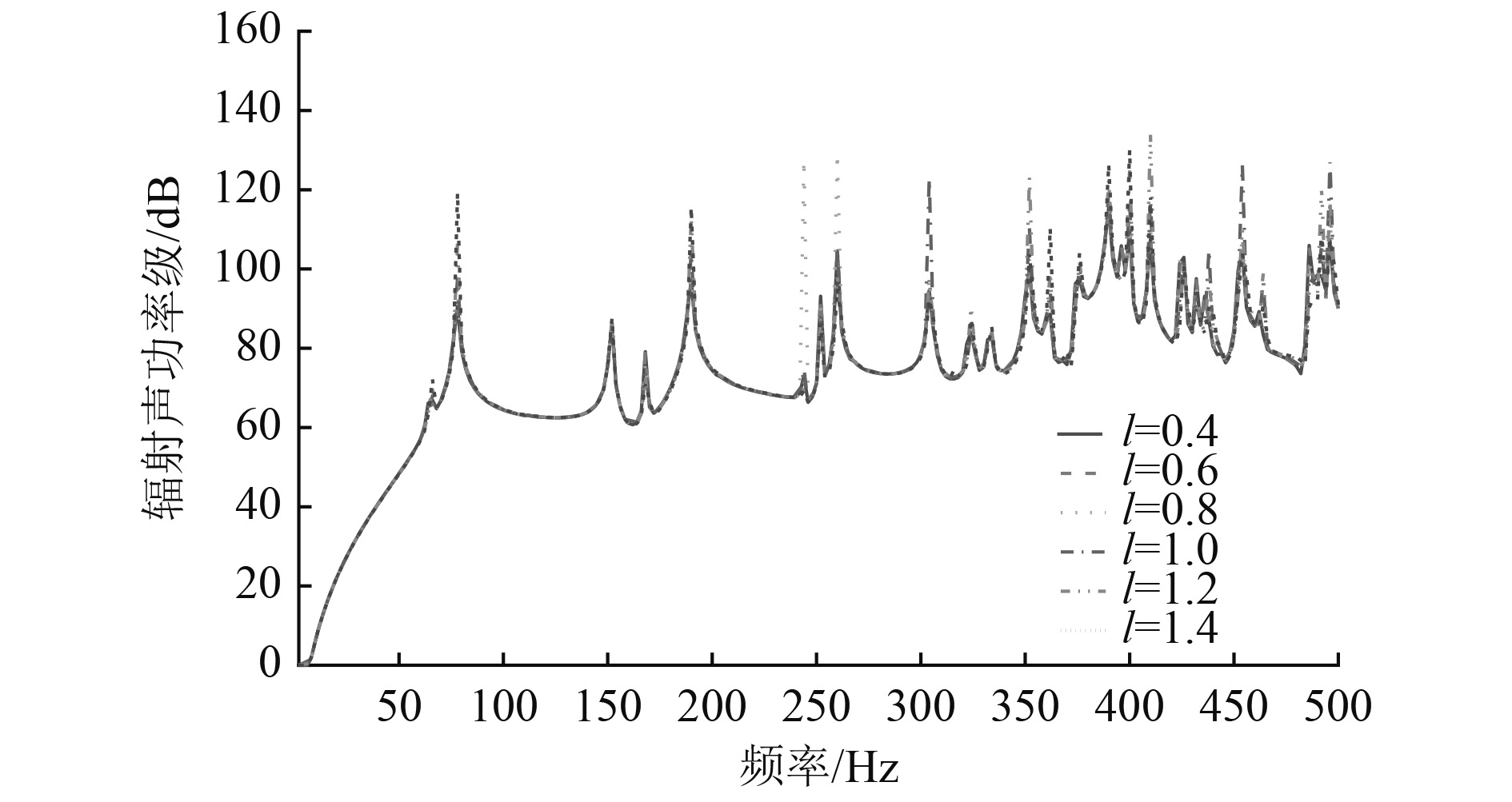
|
图 8 不同轴向焊缝应力下结构声辐射功率 Fig. 8 Structural acoustic radiation power of different stress of axial weld |
从图7可以看出,在低频段(2~250 Hz),环向焊缝应力大小对结构声辐射功率影响较小。在高频段(250~500 Hz),环向焊缝应力大小的变化使结构声辐射功率极值产生了较大影响。当参数k取0.4时,在350 Hz附近结构声辐射功率取得最大值。
从图8可以看出,纵向焊缝应力大小的变化同样改变了结构声辐射功率极值。在250 Hz附近,参数l=0.8时,结构声辐射功率取得2个较大极值点。在400 Hz附近,参数l=1.2时,结构声辐射功率取得最大值。
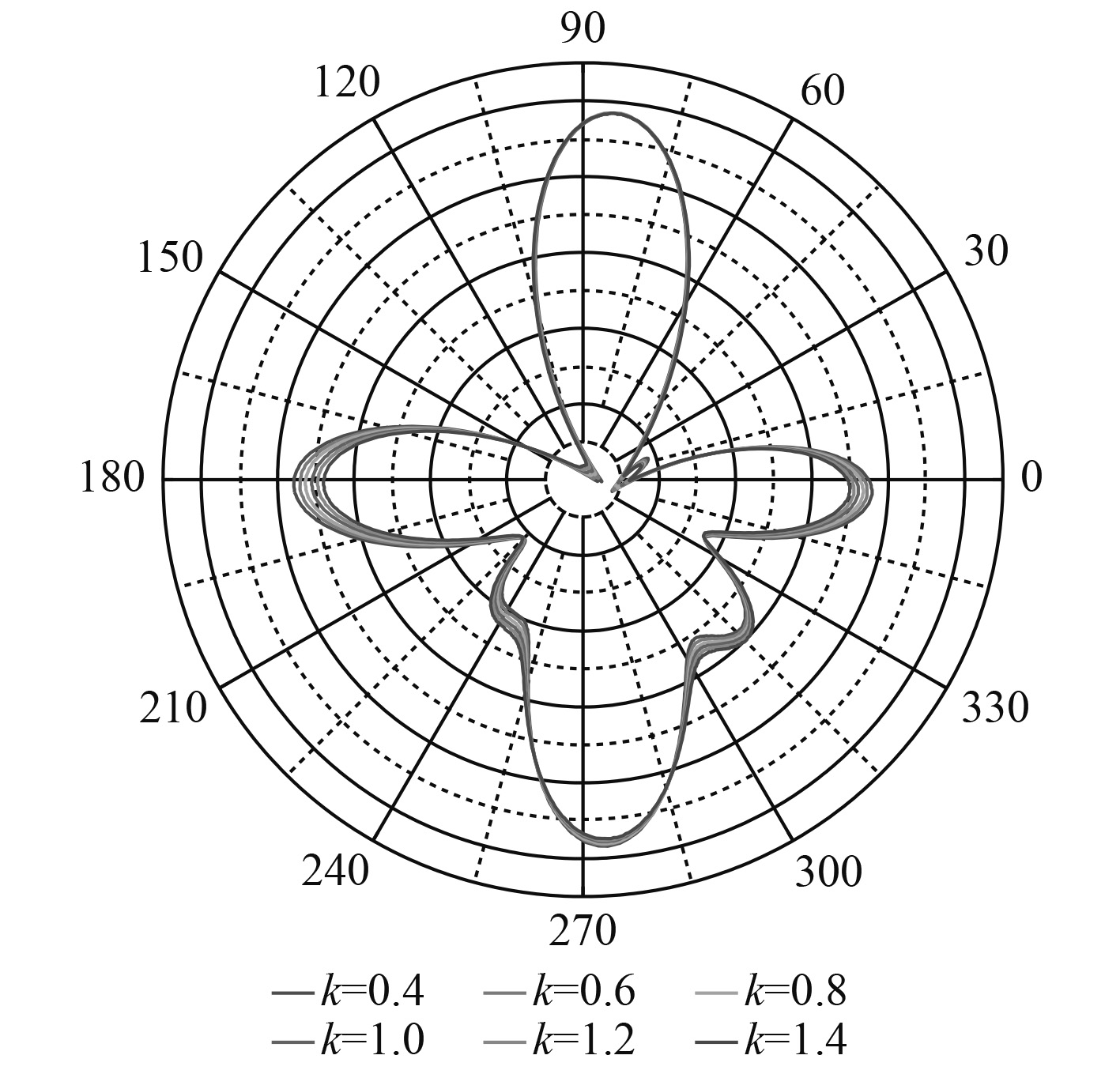
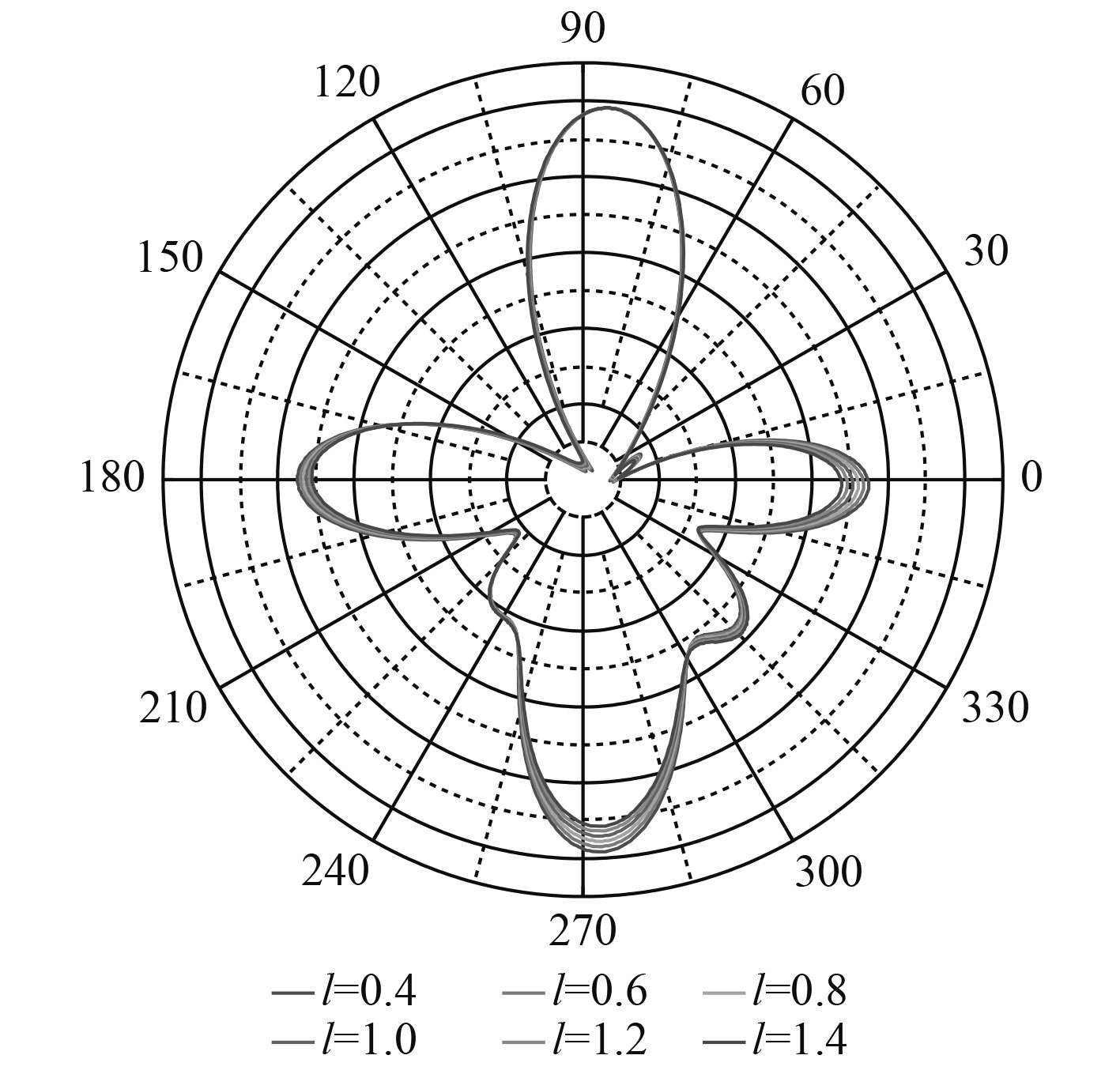
图9和图10分别给出了环向和轴向焊缝应力变化时在250 Hz下结构声辐射指向性的变化情况。可以看出,焊缝应力的变化对结构声辐射指向性的影响较小,声辐射指向性图形状相近。
|
图 9 不同环向焊缝应力下声辐射指向性 Fig. 9 Structural acoustic radiation directivity of different stress of circumferential weld |
|
图 10 不同轴向焊缝应力下声辐射指向性 Fig. 10 Structural acoustic radiation directivity of different stress of axial weld |
本文以环肋圆柱壳为对象,通过数值计算,以声辐射功率和声辐射指向性为代表,研究了焊接残余应力对结构声辐射特性的影响,得到以下结论:
1)焊接残余应力的存在改变了结构的刚度,继而改变了结构的动力学特性,影响了结构的声辐射特性。
2)焊接残余应力的幅值的变化主要影响结构最大声辐射功率值,并且会使声辐射功率极值的频率产生偏移。各频率辐射声功率极值会出现在不同的幅值参数取值时。焊接残余应力幅值的变化会对结构声辐射指向性产生一定的影响。
3)在低频段,环向焊缝应力大小对结构声辐射功率影响较小。在高频段,环向焊缝应力大小的变化改变了结构声辐射功率极值。轴向焊缝应力大小的变化会对结构声辐射功率的极值和最大值产生影响。环向和轴向焊缝应力大小的变化对结构声辐射指向性的影响较小。
| [1] |
缪宇跃, 李天匀, 朱翔, 等. 浅海中圆柱壳的声辐射特性分析[J]. 哈尔滨工程大学学报, 2017, 38(5): 719-726. MIAO Yu-yue, LI Tian-yun, ZHU Xiang, et al. Research on the acoustical radiation characteristics of cylindrical shells in ashallow sea[J]. Journal of Harbin Engineering University, 2017, 38(5): 719-726. |
| [2] |
陈清坤, 陈美霞, 和卫平, 等. 舱壁与压载对流场中有限长圆柱壳声辐射影响[J]. 舰船科学技术, 2010, 32(11): 21-25. CHEN Qing-kun, CHEN Mei-xia, HE Wei-ping, et al. Impact of bulkhead and ballast on acoustic radiation of submerged finite cylindrical shell[J]. Ship Science and Technology, 2010, 32(11): 21-25. |
| [3] |
张聪, 陈美霞, 高菊, 等. 双层加筋圆柱壳在不同舷间连接形式下的声辐射性能分析[J]. 固体力学学报, 2011, 32(5): 465-474. ZHANG Cong, CHEN Mei-xia, GAO Ju, et al. Analysis of sound radiation of double stiffened shells connected by different structures[J]. Chinese Journal of Solid Mechanics, 2011, 32(5): 465-474. |
| [4] |
LOOCK J V D, DÉCULTOT D, LÉON F, et al. Acoustic radiation of a submerged cylindrical shell in low frequency[J]. Journal of the Acoustical Society of America, 2013, 133(1): EL26. DOI:10.1121/1.4769398 |
| [5] |
GUO W, LI T, ZHU X, et al. Vibration and acoustic radiation of a finite cylindrical shell submerged at finite depth from the free surface[J]. Journal of Sound and Vibration, 2017, 393: 338-352. DOI:10.1016/j.jsv.2017.01.003 |
| [6] |
邓博文, 朱翔, 李天匀, 等. 不同模型及不同载荷形式对单层圆柱壳声振特性的影响分析[J]. 舰船科学技术, 2015, 37(12): 13-17. DENG Bo-wen, ZHU Xiang, LI Tian-yun, et al. Effects of different models and driving forces on vibroacoustic characteristic of single cylinder shell[J]. Ship Science and Technology, 2015, 37(12): 13-17. DOI:10.3404/j.issn.1672-7649.2015.12.003 |
| [7] |
陈美霞, 骆东平, 王祖华, 等. 激励力对双层圆柱壳声辐射性能的影响[J]. 船舶力学, 2005, 9(2): 124-130. CHEN Mei-xia, LUO Dong-ping, WANG Zu-hua, et al. Effect of driving forces property on characteristics of sound radiation from finite double cylindrical shell[J]. Journal of Ship Mechanics, 2005, 9(2): 124-130. DOI:10.3969/j.issn.1007-7294.2005.02.018 |
| [8] |
刘佩, 刘书文, 黎胜. 潜深对水下圆柱壳振动声辐射特性的影响[J]. 舰船科学技术, 2014, 36(5): 36-41. LIU Pei, LIU Shu-wen, LI Sheng. The effect of immersion depth of submerged cylindrical shell on vibro-acoustic characteristics[J]. Ship Science and Technology, 2014, 36(5): 36-41. DOI:10.3404/j.issn.1672-7649.2014.05.008 |
| [9] |
FARSHIDIANFAR A, OLIAZADEH P. Free vibration analysis of circular cylindrical shells: comparison of different shell theories[J]. International Journal of Mechanics and Applications, 2012, 2(5): 74-80. DOI:10.5923/j.mechanics.20120205.04 |
| [10] |
ZHAO X, GENG Q, LI Y. Vibration and acoustic response of an orthotropic composite laminated plate in a hygroscopic environment[J]. Journal of the Acoustical Society of America, 2013, 133(3): 1433-42. DOI:10.1121/1.4790353 |
| [11] |
李良碧, 万正权, 王自力, 等. 环肋圆柱壳结构焊接残余应力和变形的数值模拟[J]. 焊接技术, 2011, 40(3): 9-12. LI Liang, WAN Zheng-quan, WANG Zi-li, et al. Numerical simulation on welding residual stresses and deformation of ring-stiffened circular cylindrical shell[J]. Welding Technology, 2011, 40(3): 9-12. DOI:10.3969/j.issn.1002-025X.2011.03.003 |
| [12] |
LIU Y, CHEN L. The effect of weld residual stress on the free vibrational characteristics of cylindrical shell through the analytical method[J]. Journal of Vibroengineering, 2016, 18(1): 334-349. |
| [13] |
YANG N, CHEN L, YI H, et al. The effect of welding residual stress on the free vibration of underwater cylindrical shell[J]. Journal of Vibroengineering, 2016, 18(4). |
| [14] |
陈炉云, 李磊鑫, 张裕芳. 含局部预应力的圆柱壳结构声辐射特性分析[J]. 上海交通大学学报, 2014, 48(8): 1084-1089. CHEN Lu-yun, LI Lei-xin, ZHANG Yu-fang. Characteristics analysis of structural-acoustic of cylindrical shell with prestress in local areas[J]. Journal of Shanghai Jiao Tong University, 2014, 48(8): 1084-1089. |
| [15] |
洪江波, 杜仲民, 侯海量, 等. 大型耐压壳环焊缝焊接残余应力实验研究[J]. 船舶工程, 2006, 28(5): 14-18. HONG Jiang-bo, DU Zhong-min, HOU Hai-liang. Experimental study of residual stress in girth weld of large pressure hull[J]. Ship Engineering, 2006, 28(5): 14-18. DOI:10.3969/j.issn.1000-6982.2006.05.016 |
 2019, Vol. 41
2019, Vol. 41
