0 引言

随着世界科学研究进程的飞速发展，舰船朝着高智能化、高集成化、高模块化发展，舰船综合电力中压直流系统势必成为未来重点攻克目标^{[1 – 2]}。采用中压直流配电不仅具有高压交流配电的优点，而且还可以减少安装空间、降低传输损坏、提高电网容量及效率等特点。目前国内外对中压直流电力系统的研究尚处于试验阶段，仍有许多核心问题亟待解决^[3]。舰船综合电力中压直流电网与大容量陆地电网相比，属于孤立电网，其容量较小，具有供电距离短、电网间耦合性强、工作环境恶劣、且终端负载的切换易引起电网稳定性恶化等特点，易引发电压凹陷、畸变、电流涌浪、尖峰等不良现象。因此为提高舰船综合电力系统稳定性，满足负载频繁变化并改善电网电能质量，各国先后对综合电力系统进行多方面深入研究，如改进电网控制策略、配电网分层保护、输电布局改进设计、电制电压等级设计，采用新型电力电子设备或装载先进储能系统等以提高综合电力系统整体运行性能。美国舰船综合电力系统已明确将大容量集成化的飞轮储能设备应用于对大功率重要负载供电，用以抑制电压波动^[4]。结合国家能源发展战略，采用具有储能密度高、瞬时功率大、充电时间短、能量转换效率高、使用寿命长、绿色无污染等优点的飞轮储能系统（Flywheel energy storage system，FESS）作为不间断UPS电源能够增强综合电力中压直流系统在各种工况过渡下的稳定性，同时还能够降低电网功率突变对燃气轮机造成的冲击影响。

本文为探究飞轮储能充放电模式切换的动态特性以及对直流电网电压稳定性的影响，对大功率飞轮储能充放电系统进行建模仿真。采用飞轮永磁同步电机转速外环、电流内环的充电模式和直流电压外环、电流内环的放电模式的双闭环控制策略；最后通过仿真验证了飞轮储能充放电模式切换的动态特性以及中压直流母线电压的变化特性。

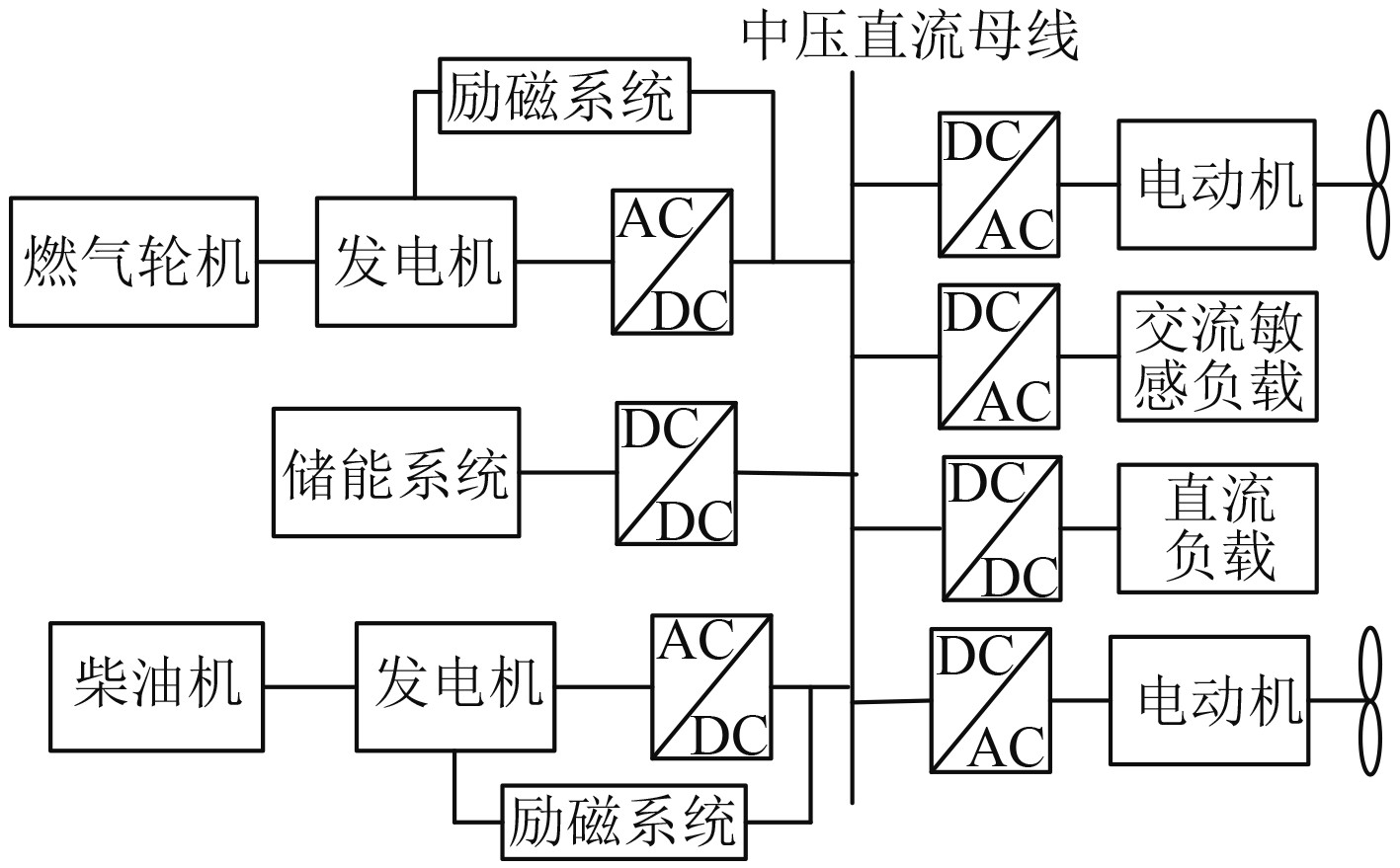
1 中压直流电网

图1为舰船中压直流配电系统结构的一种设计方案。原动机带动发电机发出的交流电经AC/DC变换器转变成中压直流电网，在近用电终端再通过高功率DC/DC变换器或DC/AC变换器将直流电转变成所需的电压等级供给设备使用^[5]。系统不仅引入了大量阻感性电力电子设备，同时还包含了各种典型组成部分，这造成中压直流配电系统会出现不同于交流配电网络的一些特性：

1）舰船负载多属于动态特性差别较大的感性负载，同时舰船常运行在多种运行工况，使得直流母线电压幅值会出现凹陷现象，因此直流配电系统对稳定控制的时间常数要求极高，动态响应速度严格，系统存在较强的刚性非线性问题。

2）直流配电系统存在大量复杂结构的电力电子装置与多级电力电子设备装置的级联问题，输入输出阻抗不匹配极易造成系统失稳。

3）直流配电系统短路电流较大且不存在自然过零点，传统断路器分断困难，给直流配电保护技术提出严峻考验。

4）直流配电系统故障类型及数量较多，目前监测技术尚不成熟，导致对于高功率变流器的拓扑结构及其控制、接地方式、负载模型等均处于研究阶段，系统具体特性深入分析仍需完善。

针对中压直流配电系统容易出现的电压凹陷问题，若通过复杂且技术难度大的系统稳定性保护控制来解决，成本较高。于是可通过潜力大的飞轮储能技术对中压直流母线电压进行补偿，抑制电压凹陷程度，提高系统稳定性。

2 飞轮储能系统充放电控制

PMSM基于dq坐标系下的数学模型表达如下^{[6 – 7]}：

$\left\{ \begin{gathered} {u_{fd}} = {R_{fs}}{i_{fd}} + p{\psi _{fd}} - {\psi _{fd}}{\omega _f}\text{，} \\ {u_{fq}} = {R_{fs}}{i_{fq}} + p{\psi _{fq}} + {\psi _{fd}}{\omega _f}\text{，} \\ \end{gathered} \right.\hspace{28pt}$

(1)

$\left\{ \begin{array}{l} {\psi _{fd}} = {L_{fd}}{i_{fd}} + {\psi _f}\text{，}\\ {\psi _{fd}} = {L_{fq}}{i_{fq}}\text{，} \end{array} \right.\hspace{63pt}$

(2)

${T_{em}} = \frac{3}{2}{P_n}[{\psi _f}{i_{fq}} +({L_{fd}} - {L_{fq}}){i_{fd}}i{}_{fq}]\text{，}$

(3)

$\Delta W = \frac{1}{2}J(\omega _{\max }^2 - \omega _{\min }^2)\text{，}\hspace{55pt}$

(4)

忽略损耗，有

$ {P_e} = \frac{{{\rm d}W}}{{{\rm d}t}} = J{\omega _f}\frac{{{\rm d}{\omega _f}}}{{{\rm d}t}} = {T_{em}}{\omega _f}\text{。} $

(5)

式中： ${i_{fd}} $ ， $ {i_{fq}} $ ， $ {u_{fd}} $ ， $ {u_{fq}} $ 为飞轮电机dq轴分量； $ {R_{fs}} $ 为电机定子电阻； $ {\psi _{fd}} $ ， $ {\psi _{fq}} $ 为永磁体dq轴分量； ${L_{fd}}$ ， ${L_{fq}}$ 为定子电感dq轴分量； $ {\omega _f} $ 为电机同步角速度； $ {\psi _f} $ 为气隙磁通； $ p $ 为微分算子； $ p_n $ 为极对数； ${T_{em}}$ 为电磁转矩； $J $ 为电机转动惯量； $ W $ 为飞轮储存能量。

飞轮运行在3种工作模式：一是从电网吸收能量增加转速的充电过程；二是消耗较小能量保持转速稳定的保持过程；三是降低转速向电网输入能量的放电过程。放电时，由于飞轮电机的转速下降导致发出的交流测电压的频率与幅值均随之降低，且由式（3）、式（5）知要使飞轮恒功率放电，必然要增加制动转矩 $ T_{em}^ * $ ，即主要增大电磁分量参考值 $ i_{fq}^ * $ （ ${L_{fd}} - {L_{fq}}$ 值很小可忽略），同时根据能量守恒定律，飞轮放出的能量可表述为；

$ \begin{split} &\int\nolimits_0^t {{P_e}} (t)dt = J[{\omega _f}{(t)^2} - {\omega _f}{(0)^2}]/2 =\\ &\int\nolimits_0^t {{P_i}} (t)dt + C[U_{dc}^2(t) - U_{dc}^2(0)]/2 + \int\nolimits_0^t {\frac{{{U_{dc}}{{(t)}^2}}}{{{R_L}}}} {\rm {d}}t\text{，}\\ &{P_e} = {T_{em}}{\omega _f} = {U_{dc}}{i_L} + C{U_{dc}}\frac{{{\rm {d}}{U_{dc}}}}{{{\rm {d}}t}} =\\ &\frac{3}{2}({u_{fd}}{i_{fd}} + {u_{fq}}{i_{fq}})\text{。} \end{split} $

(6)

式中： $ {P_\varepsilon }\left( {\rm{t}} \right) $ 为飞轮电机电磁功率； $ {P_i}\left( {\rm{t}} \right) $ 转换到交流侧的平均功率；C为直流侧电容； $ {R_L} $ 为直流侧电阻； ${\omega _f}\left( 0 \right) $ ， $ {\omega _f}\left( {\rm{t}} \right)$ 分别表示电机减速开始及减速后角速度。

将式（3）进一步分解，可得

$ {T_{em}} = \frac{3}{4}{P_n}{i_{fq}}\left[\sqrt {\psi _f^2 + 4{{({L_{fd}} - {L_{fq}})}^2}i_{fq}^2} + {\psi _f}\right]\text{。} $

(7)

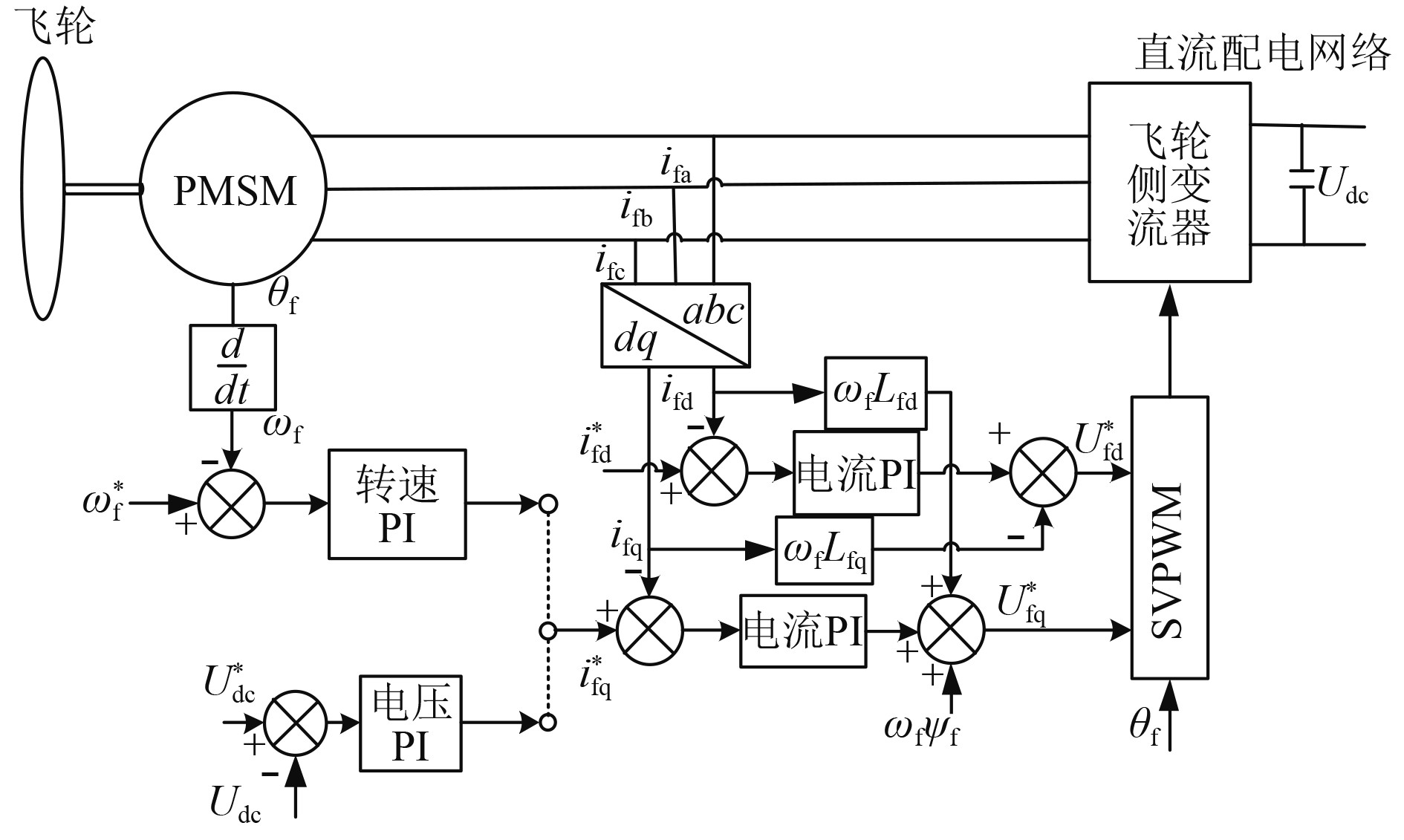
稳态时，直流侧电容总吸收能量为零，故而飞轮所发出的能量将最终都输送进电网，图2为飞轮充放电并网控制框图。但在飞轮放电过程中存在一个问题，在保持恒电压放电时，增大放电功率会导致直流电压下降或剧烈波动，不能保持恒定，进而会影响直流电网的供电品质，故而采用文献[8]所提出的综合优化弱磁控制策略以实现大功率放电下的电压恒定。

直轴电流 $i_{fd}^*$ 与飞轮转速 $ \omega $ 、输出功率 $p_{out}^ * $ 间的关系^[8]如下：

$i_{fd}^* = - |\frac{{p_{{\rm {out}}}^*}}{{{p_{\max }}}}|({\varepsilon _1}\omega + \xi)\text{。}$

(8)

式中： $ {\varepsilon _1} $ ， $ \xi $ 为电机转速的弱磁系数。

3 飞轮充放电模式切换仿真分析

为探究飞轮充放电模式切换特性响应，按图2建立飞轮储能充放电仿真模型，仿真参数如下：

f = 50 Hz，U_dc =3 500 V；

飞轮参数：额定功率 ${p_n} = 600\;{\rm{kW}}$ ；

恒定放电功率为 ${p_f} = 700\;{\rm{kW}}$ ；

电机定子电阻 ${R_s} = 2.192\;\Omega $ ；

电感 ${L_{\rm{d}}} = 3.9e - 3H,{L_q} = 3.708e - 3H $ ；

永磁体磁链 ${\psi _{ff}} = 0.4\;475\;{\rm{Wb}}$ ；

极对数p = 2；

运行转速n = 18 000 r/min；

$ {J_{fm}} = 1.4\;{\rm{kg}} \cdot {{\rm{m}}^2} $ 。

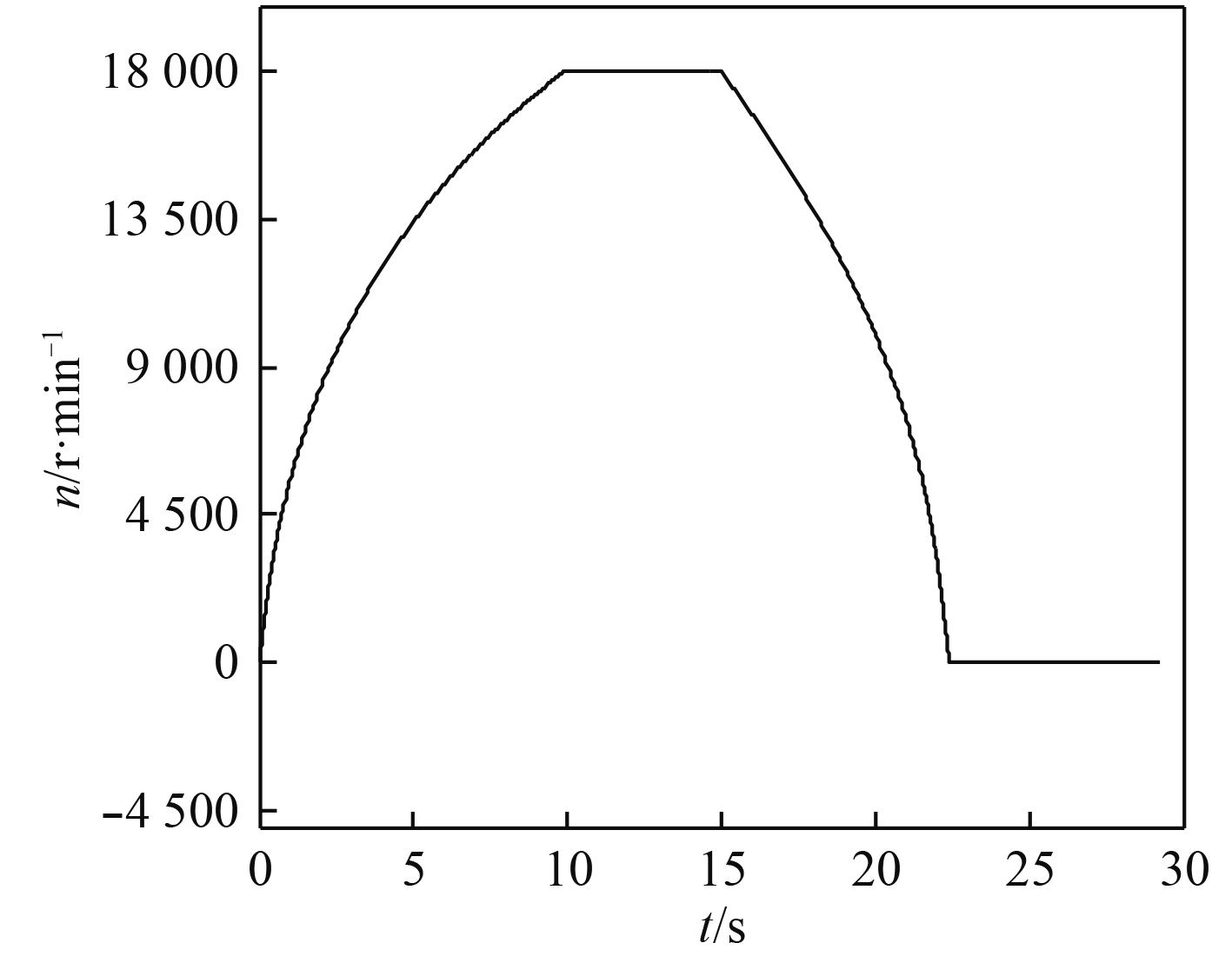
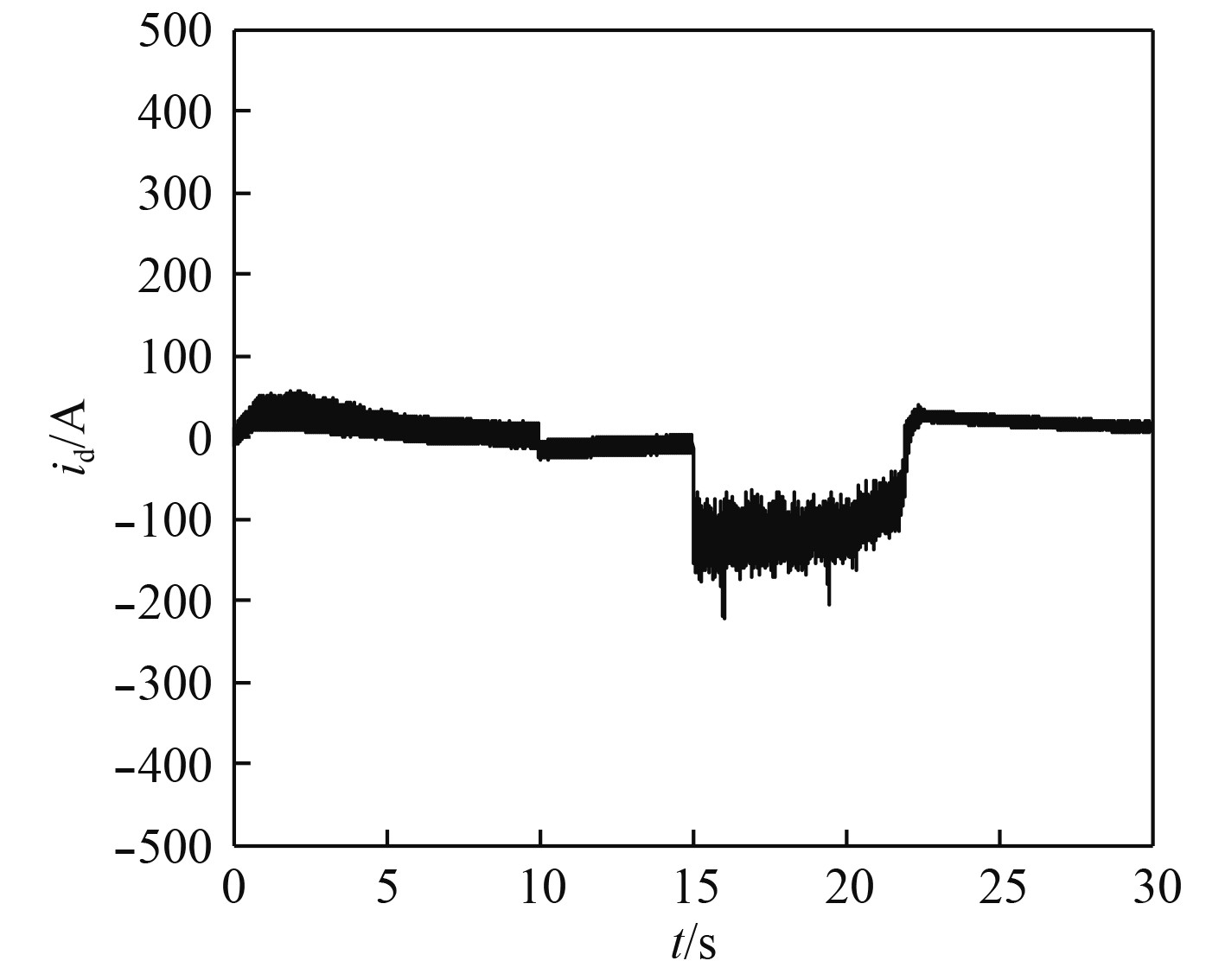
控制模块中共有4个PI控制器，外环转速PI₁与电压PI₂采用典Ⅱ型系统设计以增加抗扰性能，内环电流PI₃与PI₄采用典Ⅰ型系统设计可以提高电流的快速无误差跟踪性能，具有参数如表1所示，其充放电模式切换过程仿真波形如图3所示。充放电过程飞转功率曲线如图4所示，电机q轴电流曲线如图5所示，电机d轴电流曲线如图6所示。

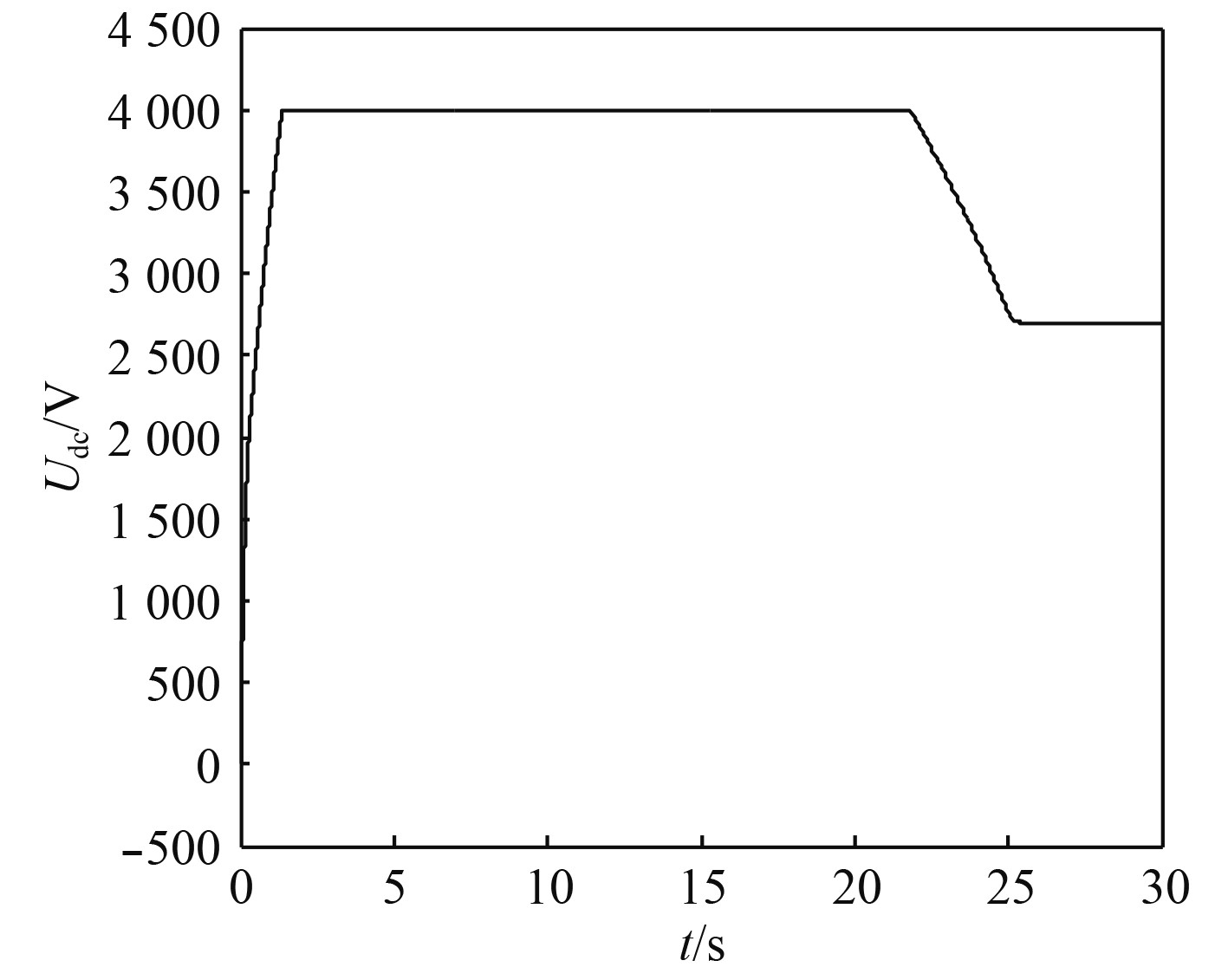
可知，10 s前对飞轮进行充电，在15 s时进行恒功率减速释能，控制输出直流电压，同时为了寻找飞轮储能放电下的最低临界转速，暂令电机转速降低至零时，迅速由“电压外环–电流内环”切换成“转速外环–电流内环”控制，将转速控制为零以保证电机不反转，以保证电机安全稳定运行，根据仿真波形再最终确定最低临界转速。由图4电机功率曲线可知，飞轮装置能够按照指令以恒定700 kW功率进行放电，在21.9 s时放电功率开始迅速降低，不能保持恒定放电，此时转速降低至约1 750 r/min，因此，可把1 750 r/min作为飞轮装置能够恒定700 kW放电下的最低转速值，小于该转速时放电功率将降低。同时放电模式下的直流母线电压如图7所示，能够快速跟随给定稳定在4 000 V，在21.5 s时直流电压不能跟随给定值而开始降低，电压控制环失效，由于直流侧储能电容的存在，直流电压得以维持在2 700 V左右，此时转速约为1 900 r/min，则此时可认为此转速是维持输出直流电压恒定的最低转速值。综上，将飞轮放电最低转速设置为1 900 r/min，能够实现放电过程中输出直流电压恒定与功率恒定。放电过程中电磁转矩与转速方向相反以降低转速进行放电，其变化趋势与 ${i_q}$ 一致，电流在放电过程中 ${i_d}$ 存在较大波动但最终仍稳定在零参考值（见图8），满足控制要求，放电状态下电机定子三相电流仍保持正弦状态，电能品质较高。

4 结论

本文建立了匹配中压直流电网用以增强电网稳定性的大功率飞轮储能系统并网仿真模型，探究飞轮储能充放电模式切换的重要参数特性以及对直流母线电压稳定性的增强效果。仿真分析结果表明：所建立的模型是正确的，飞轮充放电模式切换能够快速跟随指令，运行稳定、效率品质高，飞轮储能系统放电能够对电网进行功率补偿，可减缓直流母线电压的跌落程度，增强直流电网稳定性，为进一步全面实现综合电力推进奠定基础。