在某大型船舶中,柴油机的曲轴和中间轴直接链接,缺少了减速齿轮箱的隔振作用[1],柴油机燃烧工况的变化会对推进轴系的扭转振动造成很大影响,不稳定的燃烧情况可能会引起轴系中心线的偏离,从而引起轴承的振动和磨损,更严重的会造成轴系断裂。因此柴油机燃烧工况的变化对推进轴系扭振影响研究的意义显著。
在国内外学者对轴系扭振影响因素的研究中,多数集中在轴承、轴系转速和算法上[2 – 5],对柴油机燃烧变化的情况考虑较少,而对轴系扭振测量点的确定更少。因此以1艘集装箱船的推进轴系为研究对象,运用有限元技术对轴系进行建模与仿真研究,获得推进轴系的固有频率和振动扭矩,经过分析来确定轴系扭转振动的参考点。在不同的燃烧情况下,计算轴系扭振的情况及规律。
1 理论方程 1.1 气缸燃烧计算理论将缸内气体的流动看作为三维粘性可压缩气体的湍流运动,湍流运动的模型为K-e模型[6]。湍流动能的
1)湍流动能
| $ \begin{split} \rho \frac{{\partial k}}{{\partial t}} + \rho \frac{{{U_j}\partial k}}{{\partial {x_j}}} =& \frac{{ - \overline {{u_i}{u_j}} \partial {U_i}}}{{\partial {x_j}}} - \frac{{{g_i}{C_\mu }\rho {k^2}\partial \rho }}{{\varepsilon {\sigma _p}\partial {x_i}}} - \\ & \varepsilon + \frac{\partial }{{\partial {x_j}}}\left( {\mu + \frac{{{C_\mu }\rho {k^2}\partial k}}{{{\sigma _k}\varepsilon \partial {x_j}}}} \right)\text{,} \end{split} $ | (1) |
2)湍流能量耗散
| $ \begin{split} \rho \frac{{D\varepsilon }}{{\partial t}} =& \left( {{C_{s1}}P - \frac{{{C_{s3}}{C_\mu }\rho {g_i}{k^2}\partial \rho }}{{{\sigma _p}\varepsilon \partial {x_i}}} + \frac{{{C_{s4}}k\partial {U_K}}}{{\partial {x_k}}} -}\right. \\ & {{C_{s2}}\varepsilon } \bigg)\frac{\varepsilon }{k} + \frac{{\partial {C_\mu }\rho {k^2}\partial \varepsilon }}{{\partial {x_j}{\partial _s}\varepsilon \partial {x_j}}}\text{。} \end{split} $ | (2) |
式中:
轴系的扭转振动的计算方法分为自由扭转振动和强迫扭转振动。
1)自由扭振
在推进轴系的当量系统中,质量点为k的自由扭振公式如下[7]:
| $ {J_k}{\ddot \varphi _k} + {k_{k - 1,k}}({\varphi _k} - {\varphi _{k - 1}}) + {k_{k,k + 1}}({\varphi _k} - {\varphi _{k + 1}}) = 0\text{。} $ | (3) |
式中:
2)强迫扭振
对于具有阻尼的n个质量点的扭振直链式推进系统,质量点为k的强迫振动公式为:
| $ \begin{split} & {J_k}{{\ddot \varphi }_k} + {c_k}{{\dot \varphi }_k} + {c_{k - 1,k}}({{\dot \varphi }_k} - {{\dot \varphi }_{k - 1}}) +\\ & {c_{k,k + 1}}({{\dot \varphi }_k} - {{\dot \varphi }_{k + 1}}) + {k_{k - 1,k}}({\varphi _k} - {\varphi _{k - 1}}) + \\ & {k_{k,k + 1}}({\varphi _k} - {\varphi _{k + 1}}) = {M_k}{\rm{sin}}(\omega t + {\varepsilon _k})\text{。} \end{split} $ | (4) |
式中:
因此整个轴系的强迫扭振微分方程为:
| $ { J} {\ddot \varphi } + { C} {\dot \varphi } + { K} {\dot \varphi } = {{M^*}} {e^{i\varepsilon t}}\text{。} $ | (5) |
式中:
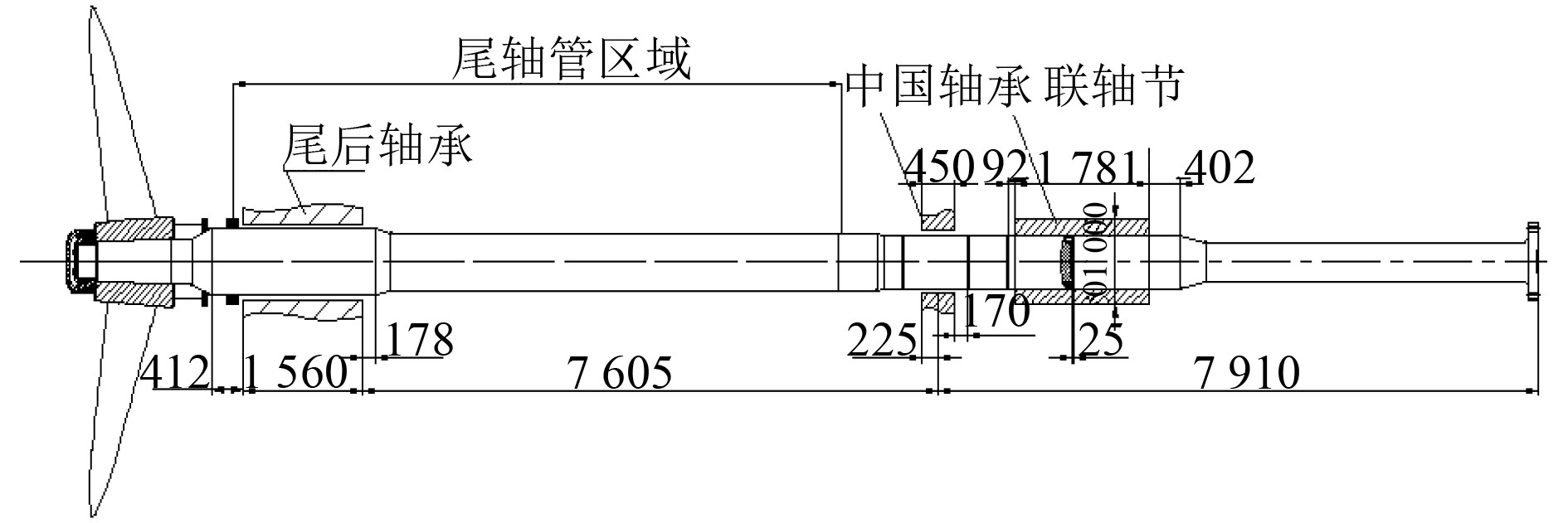
选择4250TEU集装箱船推进系统为仿真对象,该船主机型号为6S50MC-C,推进轴系的结构如图1所示。
|
图 1 推进系统的结构图(mm) Fig. 1 Structure diagram of propulsion system (mm) |
其主要部件如下,
1)轴系:轴系全长19 427 mm(不含主机),由螺旋桨轴13 310 mm和中间轴6 117 mm组成。
2)轴承:轴系(含主机)共有9个轴承:尾轴轴承(1个)、中间轴承(1个)、推力轴承(1个),曲轴轴承(6个)。轴承弹性刚度均为4.6×109N·m–1。
3)柴油机、螺旋桨和推进轴系尺寸参数如表1所示。
|
|
表 1 6S50MC-C主机的参数 Tab.1 Parameters of 6S50MC-C diesel engine |
根据以上提供的推进系统参数,将对轴系的固有频率和扭振情况进行建模计算,并且对振动情况进行分析和规律的总结。
3 对实例进行计算 3.1 轴系柔性体的建立根据推进系统各个部件的参数,建立推进系统的三维模型如图2所示。

|
图 2 推进系统的三维模型 Fig. 2 3D model of propulsion system |
在多体动力学软件中设置轴系的物性参数[8, 9],得到推进系统的多刚体模型。利用有限元软件将多刚体模型生成包含轴系材料参数和模态等信息的模态中性(MNF)文件,对轴系进行柔性化处理。选用三维四面体来对柔性体进行网格划分,单元数为2 666 580,节点数为10 219 632,划分结果如图3所示。

|
图 3 轴系的有限元模型 Fig. 3 Finite element model of shafting |
在有限元软件中,绘制轴系的中心线,并将推进系统的各个部件标注质量号,曲轴的自由端质量号为1,以此类推,螺旋桨的质量号为12。对推进系统进行模态分析,输出质量号对应下的振动扭转角和扭矩,分析并确定可以代表轴系强迫扭振计算结果的测量点。
因为轴系的实际转速较低,对轴系影响较深的共振频率相对较低,所以提取轴系前6阶的自由振动频率如表2所示。
|
|
表 2 固有频率表 Tab.2 Natural frequency table |
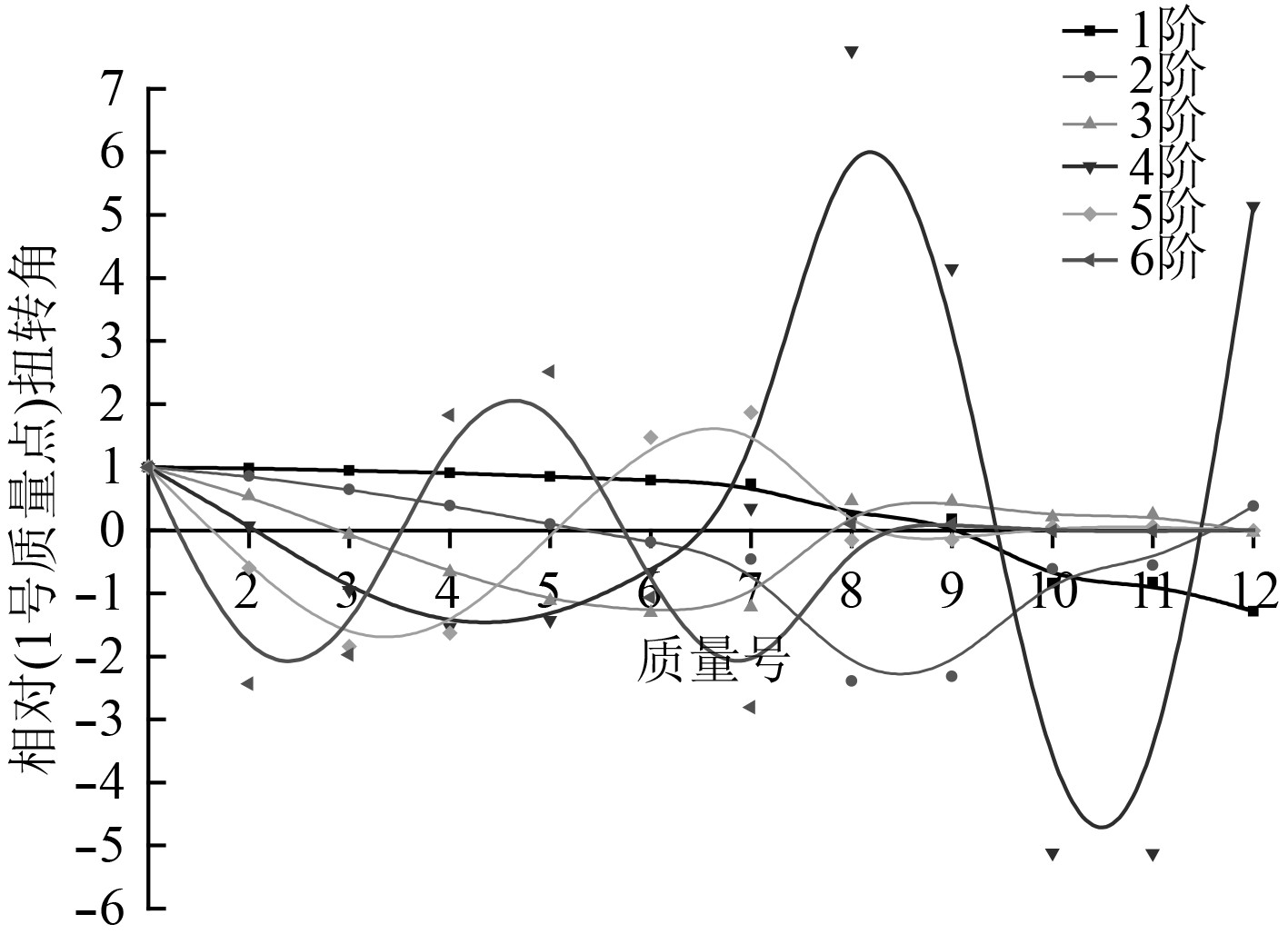
将每一质量段相对于质量点1的扭转振幅整理成如图6所示的振型图。
|
图 4 轴系前6阶自由扭振振型图 Fig. 4 Free torsional vibration modes of the first 6 orders of shafting |
|
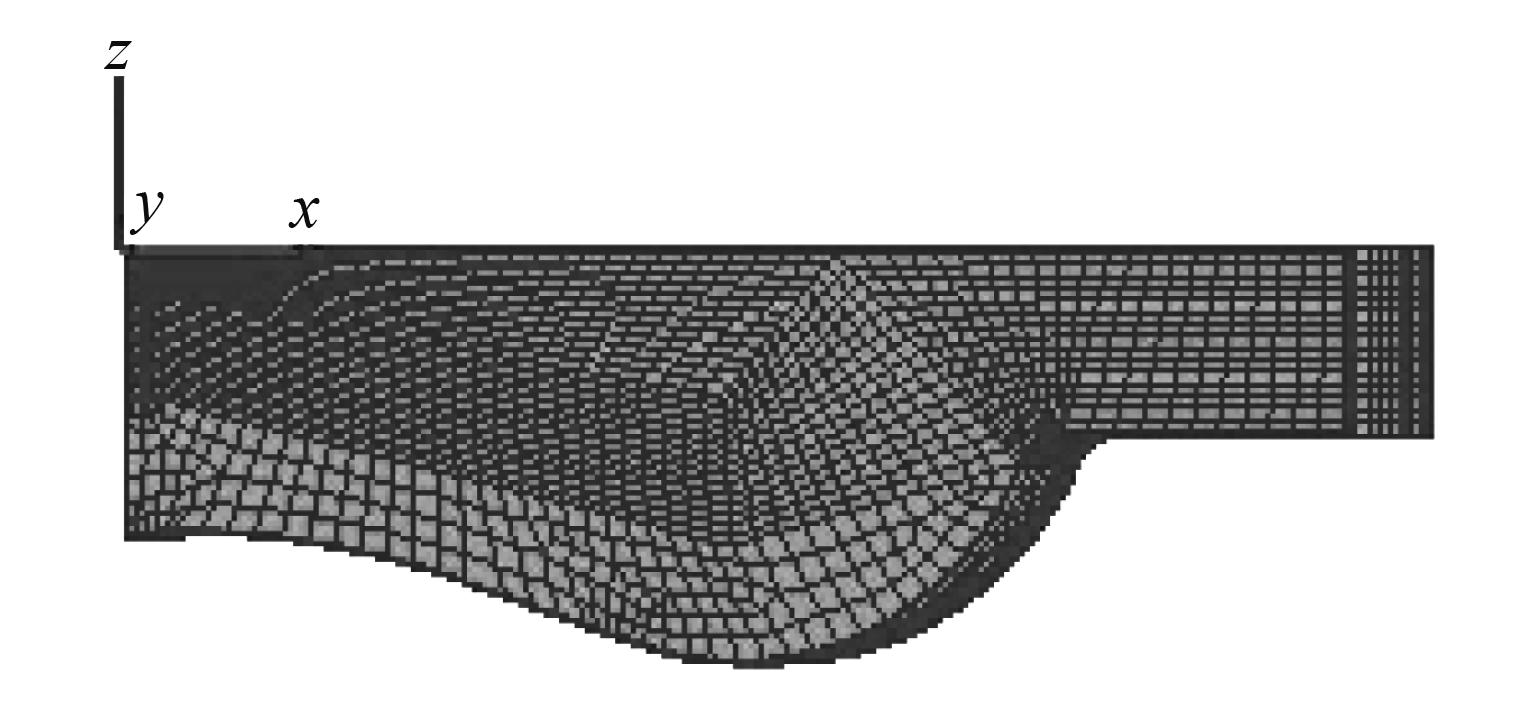
图 6 压缩上止点时燃烧室体网格 Fig. 6 The body grid of the combustion chamber when the TDC compressed. |
可以看出,当频率阶次为1时,推进系统的振幅变化较平缓,尾轴螺旋桨处的相对扭转角最大,最大相对扭转角为–1.3;当频率阶次为2时,6#缸和飞轮的轴承处扭转变形较大,6号缸最大相对扭转角为–2.4;当频率阶次为3,5和6时,中间轴和尾轴振幅较小,变化较平缓;当频率阶次为4时,扭转振幅变化幅度较大,最大振幅发生在曲轴6#缸位置处,相对扭转角为7.6,比较危险;在低频率阶次的振动情况下,曲轴的振幅比中间轴和尾轴的较大,并且曲轴扭转角的最大的位置基本上是发生在输出端,每条线有几个相对扭转角为0的点就为几阶振动。
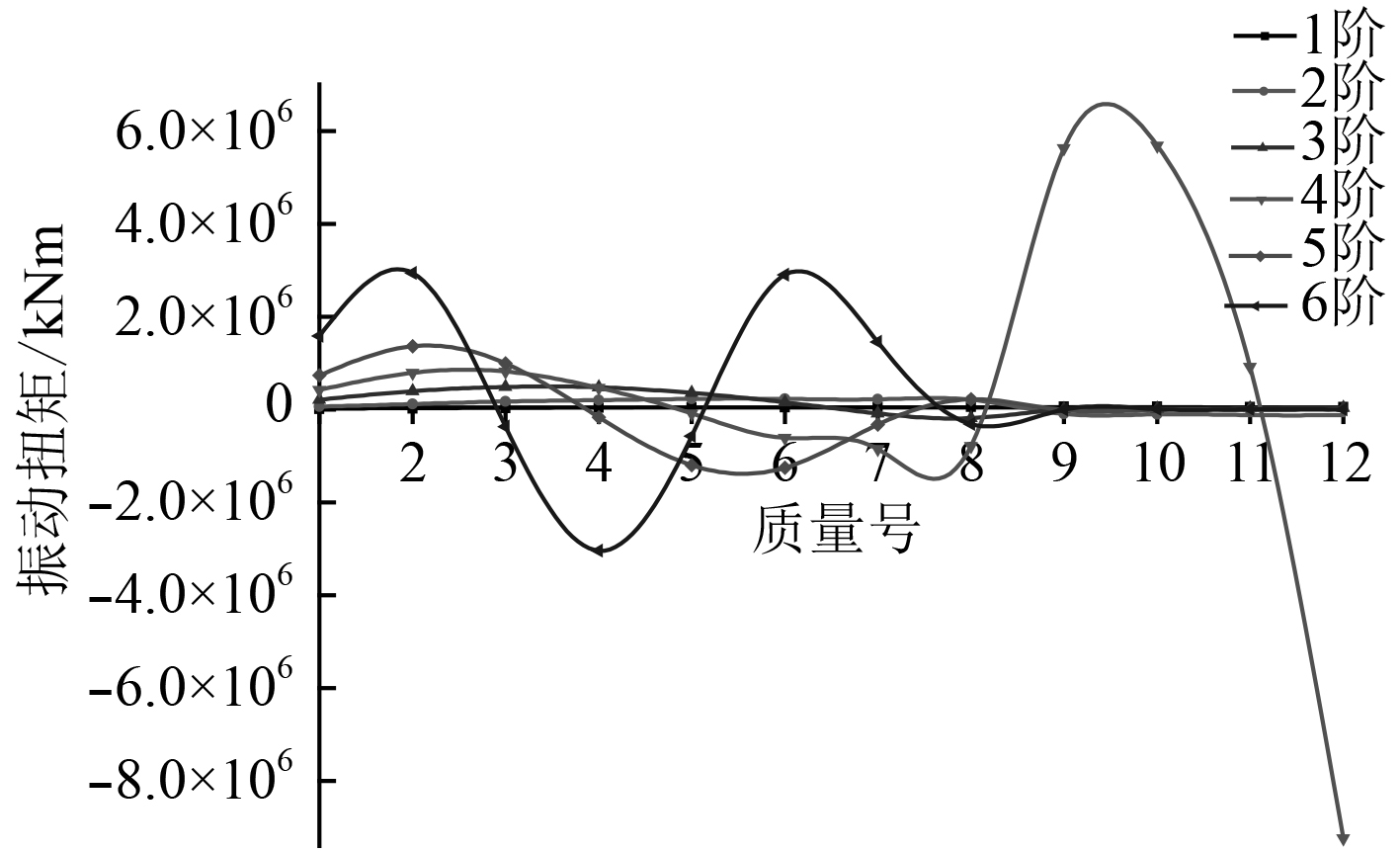
现将从主机自由端到螺旋桨处各个轴系质量段的前6阶振动扭矩绘制成如图5所示。
|
图 5 轴系前6阶自由振动扭矩图 Fig. 5 The first 6 orders free vibration torque diagram of shafting |
轴系振动扭矩的变化幅度随着共振频率的增加而增大;第4阶振动的扭矩相对异常,中间轴和尾轴的扭矩非常大;在第5和第6阶频率阶次下,曲轴的振动扭矩相对较大。
轴系各质量段的振动扭矩大小不同,为了更好地分析研究,需要确定有代表性和振幅最大的质量号为轴系扭振的输出点。推进轴系的第1阶临界转速为410 r/min,而柴油机的额定输出转速为127 r/min,轴系的额定转速低于第1阶的临界转速。结合轴系第1阶的自由扭振的振型图和扭矩图,尾轴中螺旋桨处的相对扭转角和扭矩最大。因此为了研究柴油机燃烧工况对轴系扭振的影响,选择尾轴螺旋桨处作为扭振计算的测量输出点。
3.3 正常燃烧工况对轴系扭振的影响根据6S50MC-C型号柴油机的参数,建立燃烧室压缩上止点的三维模型,运用FIRE燃烧软件来模拟气缸的正常燃烧压力。为了防止FIRE软件计算时产生发散效应,设置柴油机气缸内压力和温度均匀(初始压力为3.82×105 Pa,温度为310 K,设燃烧室壁面温度为593 K)。燃烧室的有限元网格划分如图6所示。
二冲程柴油机的曲轴在旋转360℃A的过程中,每个气缸都完成了压缩和做功2个冲程,选择某气缸的输出压力曲线为分析对象。计算模型选择湍流模型
|
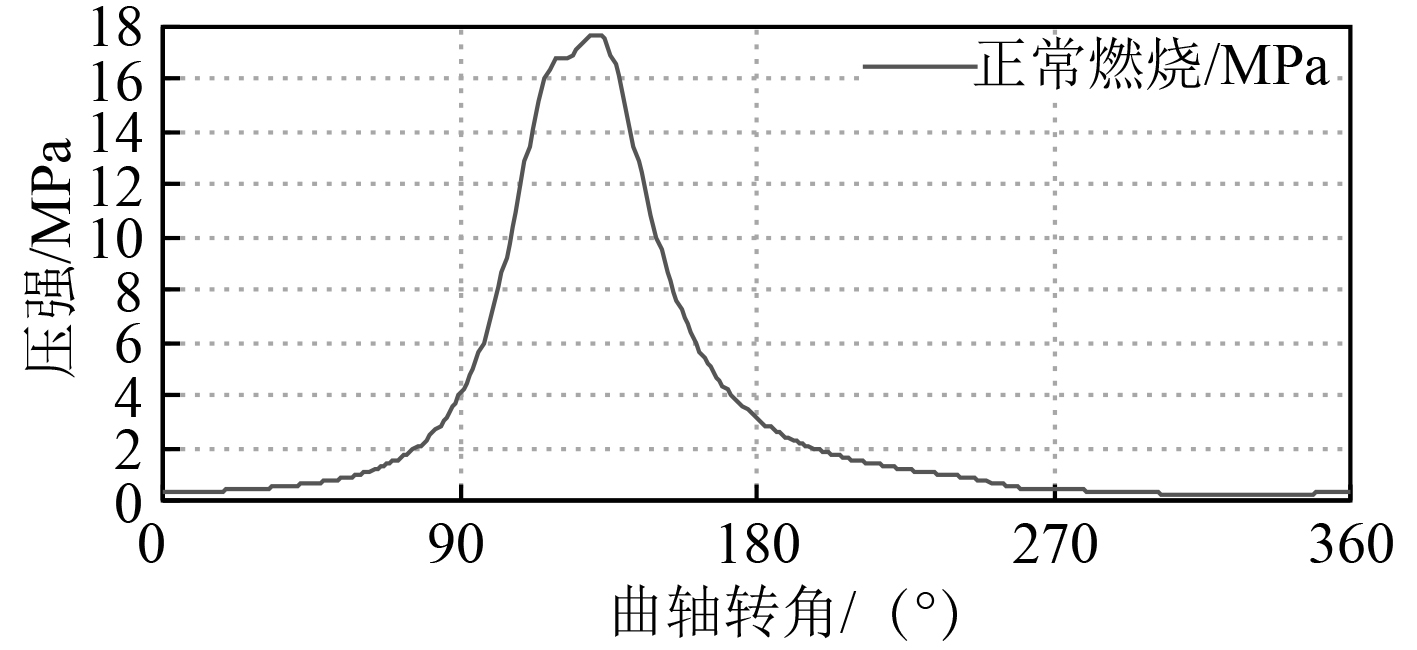
图 7 正常燃烧的压力图 Fig. 7 Pressure diagram of normal combustion |
从正常燃烧的压力图可以发现,在喷油之后的1℃A~5℃A内,气缸内的压力为平稳状态,这一时间段为滞燃期,此时的燃油气体主要进行一系列发火前的准备,燃烧还不够充分,燃烧氧化反应的放热量基本等于物理准备的吸热量,所以气缸内的压力基本处于平稳状态。
在多体动力学软件中,将推进轴系与轴承之间的旋转副上建立铰接副,利用曲线拟合技术,将正常燃烧压力值按气缸发火顺序依次施加在相应的曲轴上,设置发动机以恒定转速127 r·min–1运行,计算得到尾轴最大扭转振幅为5.98×10–3 rad,可以看出,此时的推进轴系振动扭转角非常小。
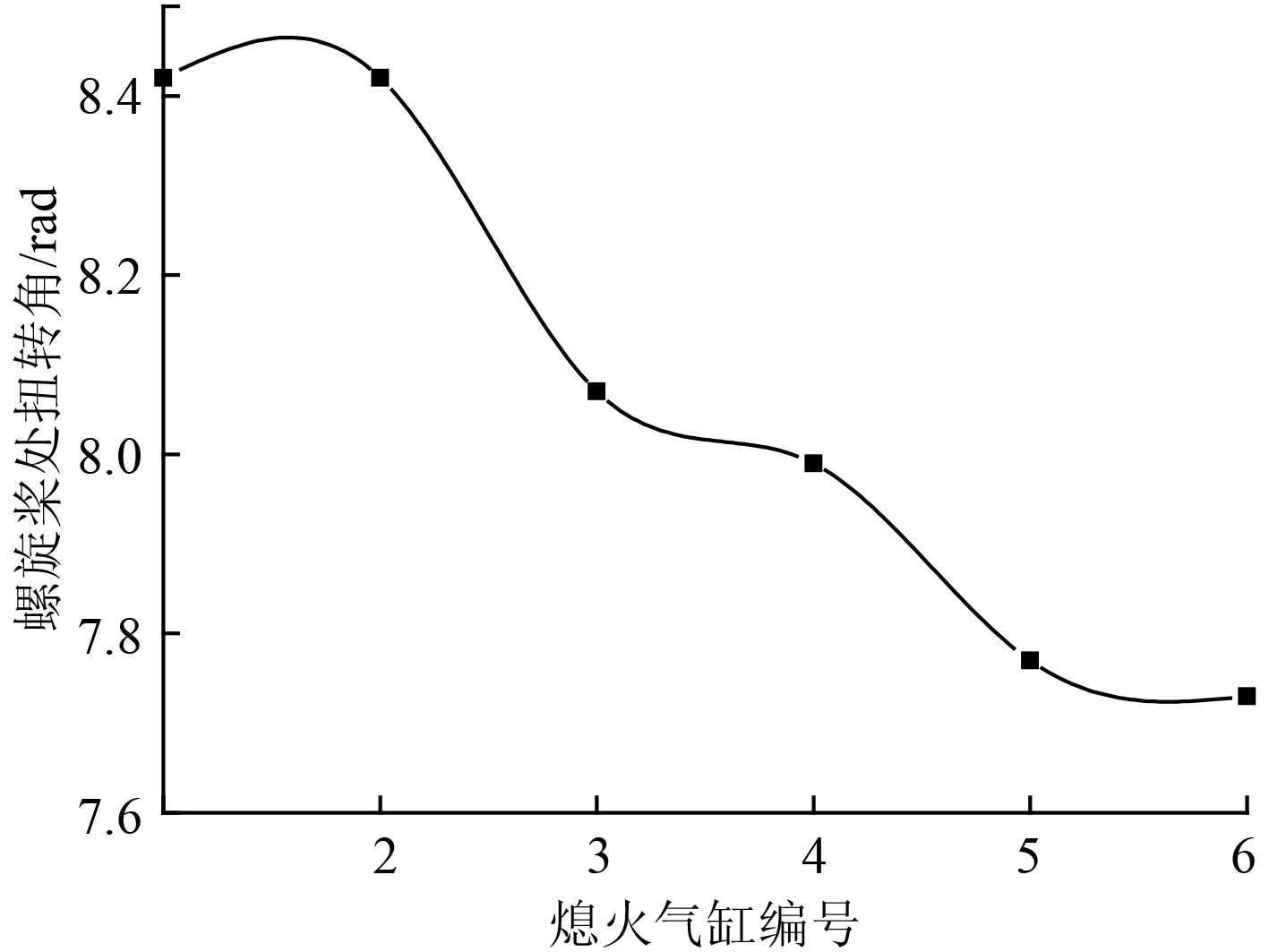
3.4 气缸熄火对轴系扭振的影响船舶航行遇到气缸熄火时,为了维持柴油机的运行,机组人员一般会拆除该气缸的活塞,此时柴油机的运行会对轴系的振动造成不利影响。为了计算该影响的程度和规律,在有限元软件中,依次将各个气缸熄火处理(将活塞拆除),计算各个熄火气缸对应的螺旋桨处扭转角的最大值,输出尾轴螺旋桨处扭振振幅曲线,如图8所示。
|
图 8 单缸熄火对轴系扭振的影响 Fig. 8 The influence of single cylinder extinction on torsional vibration of shafting |
可知,柴油机在单缸熄火的情况下,轴系螺旋桨处的最大扭转角度基本上都在8°左右,随着熄火气缸编号的增大,轴系螺旋桨处的最大扭转振幅逐渐降低,减小的幅度在0.5°之内。
4 结 语通过对比分析柴油机的正常燃烧和单缸熄火对轴系扭振影响的结果,得到如下规律:
1)在低频率阶次的振动情况下,曲轴的振幅比中间轴和尾轴的大,并且扭转角最大的位置基本上发生在曲轴的输出端。每条相对扭转振幅线有几个0点就为几阶振动。
2)尾轴中螺旋桨处的相对扭转角和扭矩在低频率低转速的振动状态下最大。为了研究柴油机燃烧工况对轴系扭振的影响,尾轴螺旋桨处扭振振幅的测量值具有代表性。
3)在柴油机正常燃烧情况下,推进轴系的扭转振幅非常小。在柴油机单缸熄火情况下,熄火气缸越接近曲轴的输出端,轴系螺旋桨处的最大扭转角度越小,但是降低的幅度小。
| [1] |
田哲, 张聪, 严新平. 计入船体变形激励的大型船舶推进轴系振动性能研究[J]. 船舶力学, 2015, 19(11): 1368-1376. TIAN Zhe, ZHANG Cong, YAN Xin-ping. Vibration characteristic study of large vessel’s shaft system taking into account the ship hull deformation excitations[J]. Journal of Ship Mechanics, 2015, 19(11): 1368-1376. DOI:10.3969/j.issn.1007-7294.2015.11.010 |
| [2] |
朱军超, 朱汉华, 严新平. 尾轴承有效接触长度对轴系振动的影响[J]. 润滑与密封, 2012(2): 25-28. ZHU Jun-chao, ZHU Han-hua, YAN Xin-ping. The Effet of the Effective Contact Length of Stern Tube Bearing on Shaft Vibration[J]. Lubrication Engineering, 2012(2): 25-28. DOI:10.3969/j.issn.0254-0150.2012.02.007 |
| [3] |
朱汉华, 严新平, 刘正林. 转速对油膜刚度与螺旋桨轴振动影响研究[J]. 船海工程, 2007(4): 83-85. ZHU Han-hua, YAN Xin-ping, LIU Zheng-lin. Research on the influence of rotation speed upon rigidity of lubricant oil film and vibration of propeller shaft[J]. Ship and Ocean Engineering, 2007(4): 83-85. DOI:10.3963/j.issn.1671-7953.2007.04.026 |
| [4] |
ERKAEV N V, NAGAITSEVA N A. Mathematical model of the unsteady motion of a shaft in a hy drodynamic plain bearing[J]. Journal of Applied Mechanics and Technical Physics, 2003(5): 699-707. |
| [5] |
KIM W H.. Vibration analysis of a shafting system for a marine diesel generator set including dynamic characteristics between shell and housing of generator bearing[J]. 10th International Conference on Vibrations in Rotating Machinery, 2012(2): 69-78. |
| [6] |
潘剑锋, 卢青波, 王谦. 柴油机燃烧过程的数值模拟及燃烧室改进[J]. 江苏大学学报, 2012, 33(4): 390-395. PAN Jian-feng, LU Qing-bo, WANG Qian. Numerical simulation for combustion process of diesel engine and improvement of combustion chamber[J]. Journal of Jiansu University, 2012, 33(4): 390-395. DOI:10.3969/j.issn.1671-7775.2012.04.004 |
| [7] |
周瑞平, 杨建国, 张升平. 船舶推进轴系扭转振动应用软件开发研究[J]. 武汉理工大学学报, 2003, 25(3): 69-72. ZHOU Rui-ping, YANG Jian-guo, ZHANG Sheng-ping. Software development of marine shaft torsional vibration on martrix VB[J]. Journal of Wuhan University of Technology, 2003, 25(3): 69-72. DOI:10.3321/j.issn:1671-4431.2003.03.021 |
| [8] |
李婷云, 林少芬. 船舶柴油机曲轴三维实体动力学仿真[J]. 舰船科学技术, 2012, 34(6): 41-44. LI Ting-yun, LIN Shao-fen. 3-D entity dynamics simulation of marine diesel engine crankshaft[J]. Ship Science and Technology, 2012, 34(6): 41-44. DOI:10.3404/j.issn.1672-7649.2012.06.009 |
| [9] |
谈微中, 张聪, 田哲. 大型船舶推进轴系扭振特性仿真和试验[J]. 舰船科学技术, 2015, 37(1): 45-49. TAN Wei-zhong, ZHANG Cong, TIAN Zhe. Research on the characteristics of torsional vibration of large-scale ship propulsion shafting[J]. Ship Science and Technology, 2015, 37(1): 45-49. DOI:10.3404/j.issn.1672-7649.2015.01.009 |
 2019, Vol. 41
2019, Vol. 41
