管路作为各类系统的重要组成部分,担负着连接设备、传输介质的作用,具有空间走向复杂、介质压力和载荷状态多样等特点,一方面管路传输介质过程中产生的变形及应力,会威胁系统的完整性及功能实现;另一方面,对舰船而言,随着双层隔振、浮筏等减振装置的广泛应用[1 – 3],设备通过基座传递的振动噪声大幅降低,系统管路的振动噪声问题则日益突出,成为影响舰船隐蔽性的关键因素[4]。
对于系统管路的振动噪声问题,最直接的处理方法是在管路上间隔设置支撑结构,一方面支承管路传输介质产生的应力,另一方面有效隔离振动噪声沿管路的传递[4]。
目前,舰船上常用的管路支撑结构,要么固定可靠性差、隔振效果不佳,要么占用空间大、安装工艺复杂;针对这一情况,研制了一种集成式管路弹性支吊架,适用于舰船狭窄环境下的管路隔振设计。本文基于研制的集成式管路弹性支吊架物理模型,在建立集成式管路弹性支吊架有限元模型的基础上,提出集成式管路弹性支吊架的动力学特性计算方法,并对支吊架的动力学特性进行分析,可为后续管路弹性支吊架的动力学特性分析与应用提供技术支撑。
1 集成式管路弹性支吊架动力学模型与计算方法针对舰船常用管路规格设计的集成式管路弹性支吊架结构模型,基于有限单元法,建立集成式管路弹性支吊架动力学计算模型如图1所示。为保证计算精度,模型保留了全部关键细节,如圆角、倒角等,并对关键部位网格进行加密处理。支吊架有限元模型采用六面体结构网格,网格扭曲段控制较好。网格总数230 770,其中橡胶件采用C3D8H杂交单元,金属件采用C3D8I单元。

|
图 1 集成式管路弹性支吊架有限元模型 Fig. 1 FEM model of integrated elasticity bracket of pipe |
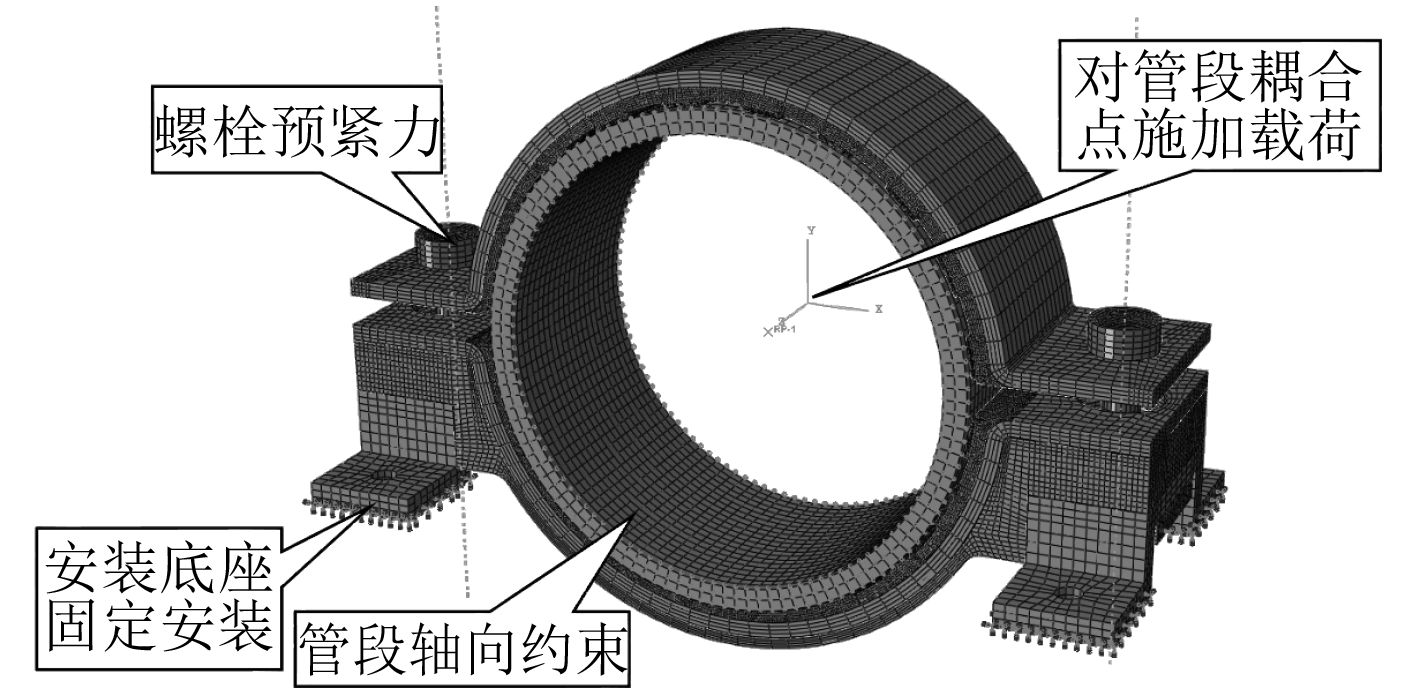
为了保证金属件与橡胶件无相对位移,金属件与橡胶件为绑定约束;为了约束管段轴向变形,管段与管段中心点为耦合刚体约束;安装底座为固定安装约束。在支吊架强度、刚度及模态分析时,先施加螺栓预紧力,再对中间管段施加垂向载荷。支吊架边界条件设置如图2所示。
|
图 2 集成式管路弹性支吊架边界条件设置 Fig. 2 Boundary conditions of integrated elasticity bracket of pipe |
集成式管路弹性支吊架主要是橡胶材料和金属的混合结构,其具有几何非线性(大的形变)、材料非线性(大的应变,塑性、蠕变)、边界非线性(边界开裂、缩颈、细化)的特点[5]。这种混合结构的材料属性对减振元器件的刚度、固有频率等有重要的影响。因此,在数值计算时,必须选择能够与这种结构相适应的有限元模型。
常用的对橡胶力学性能的描述方法主要分为两类:一类是认为橡胶是连续介质的现象学描述;另一类是基于热力学统计的描述方法。目前为止,基于热力学统计理论的本构模型常用的有Arruda-Boyce形式模型、Vander Waals形式模型[6],基于连续介质力学理论较成熟的本构模型有多项式形式模型(包含减缩多项式、Mooney-Rivlin模型、Neo-Hookean模型、Yeoh模型等)和Ogden形式模型[7]。本文利用Abaqus[8 – 9]进行数值计算时拟采用Mooney-Rivlin模型的本构关系[10 – 11]对集成式管路弹性支吊架的动力学特性进行研究,即
| $ U = {C_{10}}({\bar I_1} - 3) + {C_{01}}({\bar I_2} - 3) + \frac{1}{{{D_1}}}{\left( {J - 1} \right)^2}\text{。} $ |
在材料的精确参数未知时往往采用Mooney-Rivlin这种超弹模型。该模型应用于小到中等应变时可较好模拟材料的力学特性[12 – 15]。
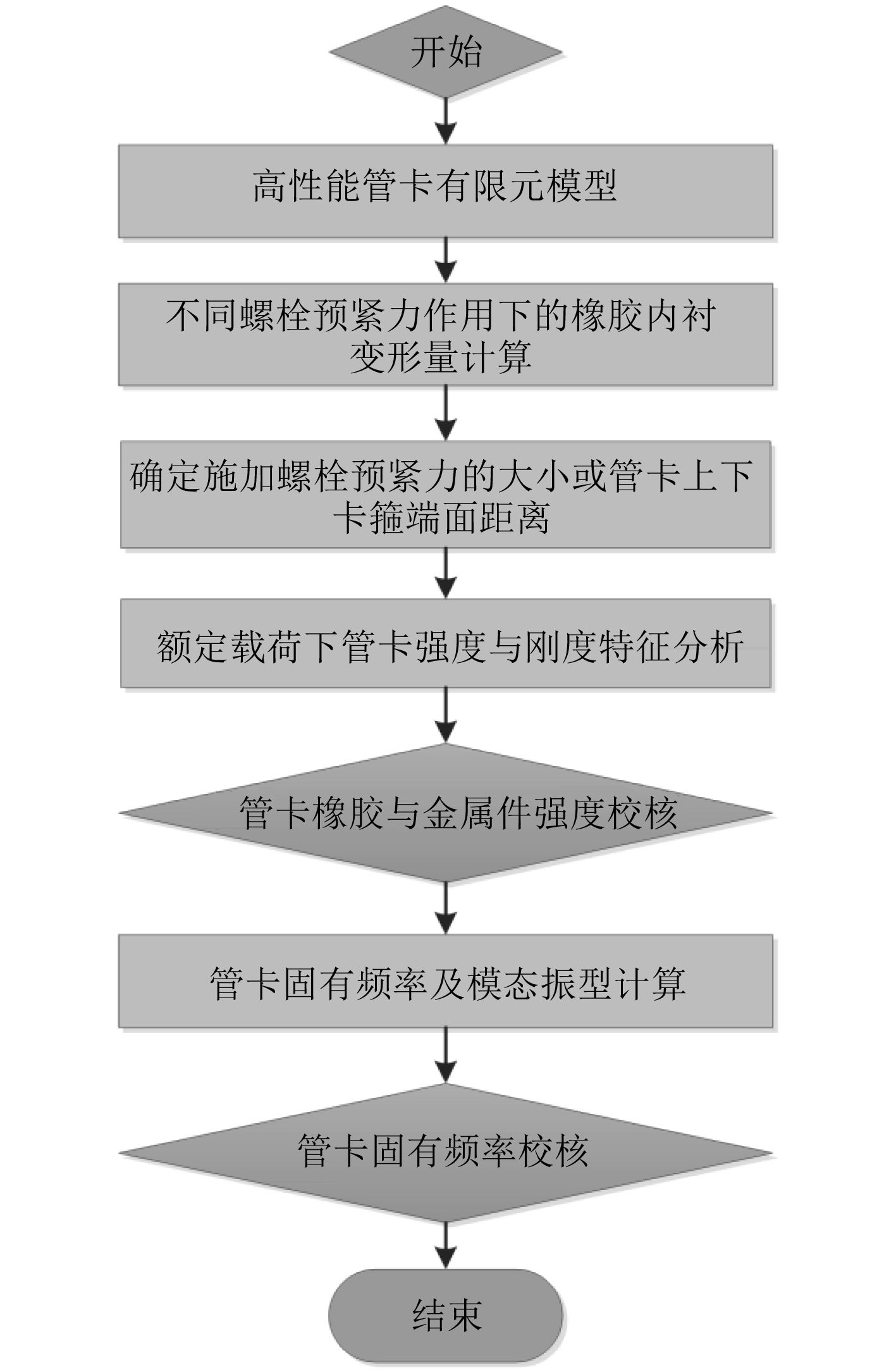
集成式管路弹性支吊架动力学特性计算流程如图3所示。
|
图 3 支吊架动力学特性数值计算方法 Fig. 3 Calculation method for dynamical characteristics |
1)根据支吊架结构方案及材料参数,建立支吊架有限元模型;考虑到支吊架实际应用时,上下卡箍通过螺栓紧固后,卡箍间须保证一定间隙,上下衬垫与管路接触部位设计成齿槽状,部分变形后确保支吊架沿管路轴向锁紧,衬垫变形量过小,支吊架会沿管路轴向串动,无法锁紧管路;衬垫变形量过大,则完全压死,影响支吊架隔振效果,即衬垫变形量对支吊架安装及隔振效果有重要影响,因此计算不同螺栓预紧力作用下上下衬垫的变形量,确定合理的螺栓预紧力及衬垫变形量。
2)在施加合理螺栓预紧力基础上,开展额定载荷作用下支吊架的强度、刚度特性分析,校核支吊架橡胶件、金属件强度。
3)开展支吊架振动模态计算,给出支吊架前几阶固有频率及对应模态振型。
2 集成式管路弹性支吊架动力特性计算结果分析 2.1 螺栓预紧力计算上下衬垫变形量(螺栓预紧力)对支吊架安装及隔振效果有重要影响,因此设置相关位移输出点如图4所示。其中,上衬垫变形量=|S1–S2|,下衬垫变形量=|S3–S4|,上下卡箍端面间隙=|S5–S6|。

|
图 4 位移输出点示意图 Fig. 4 Sketch map of displacement output points |
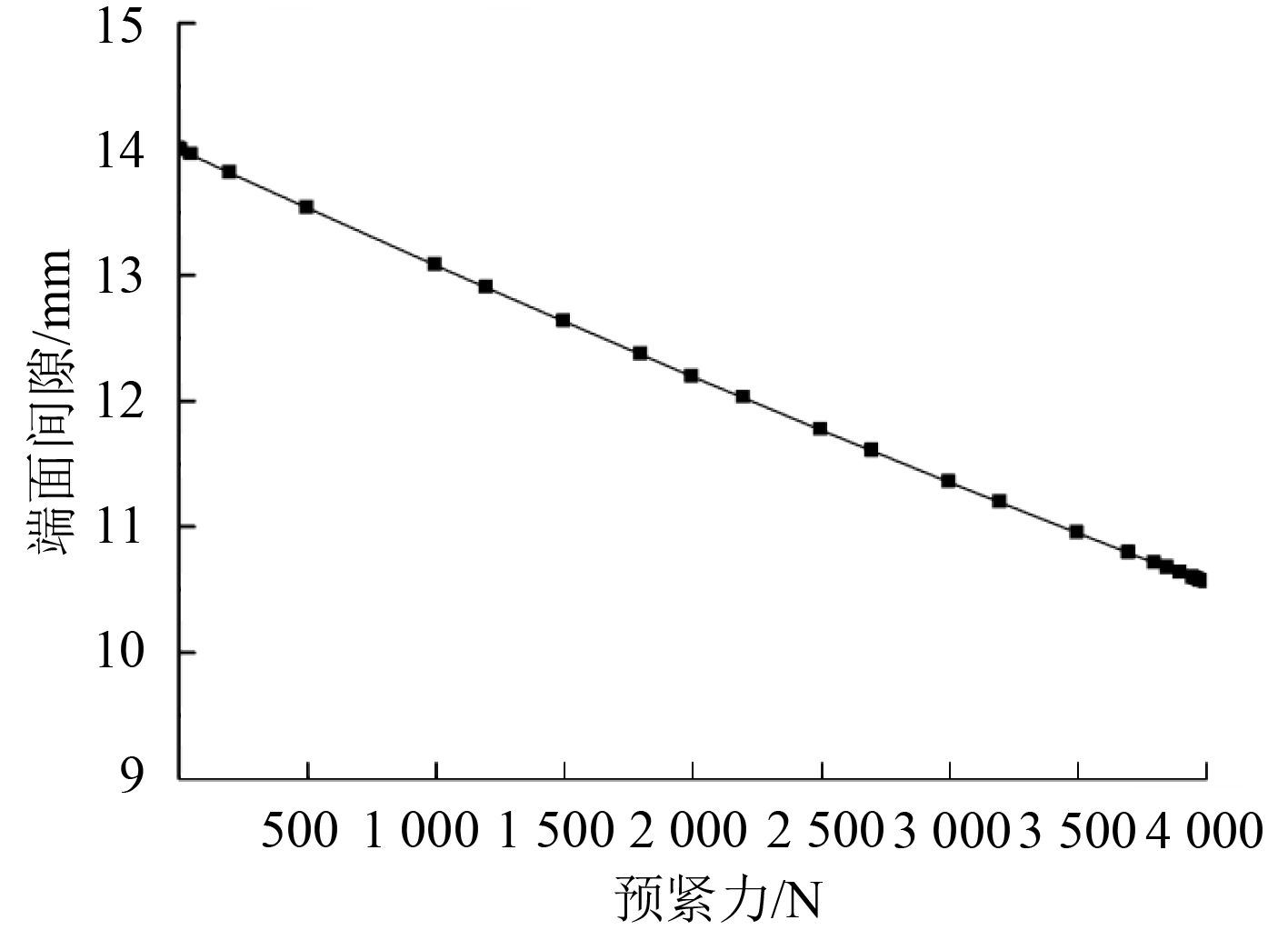
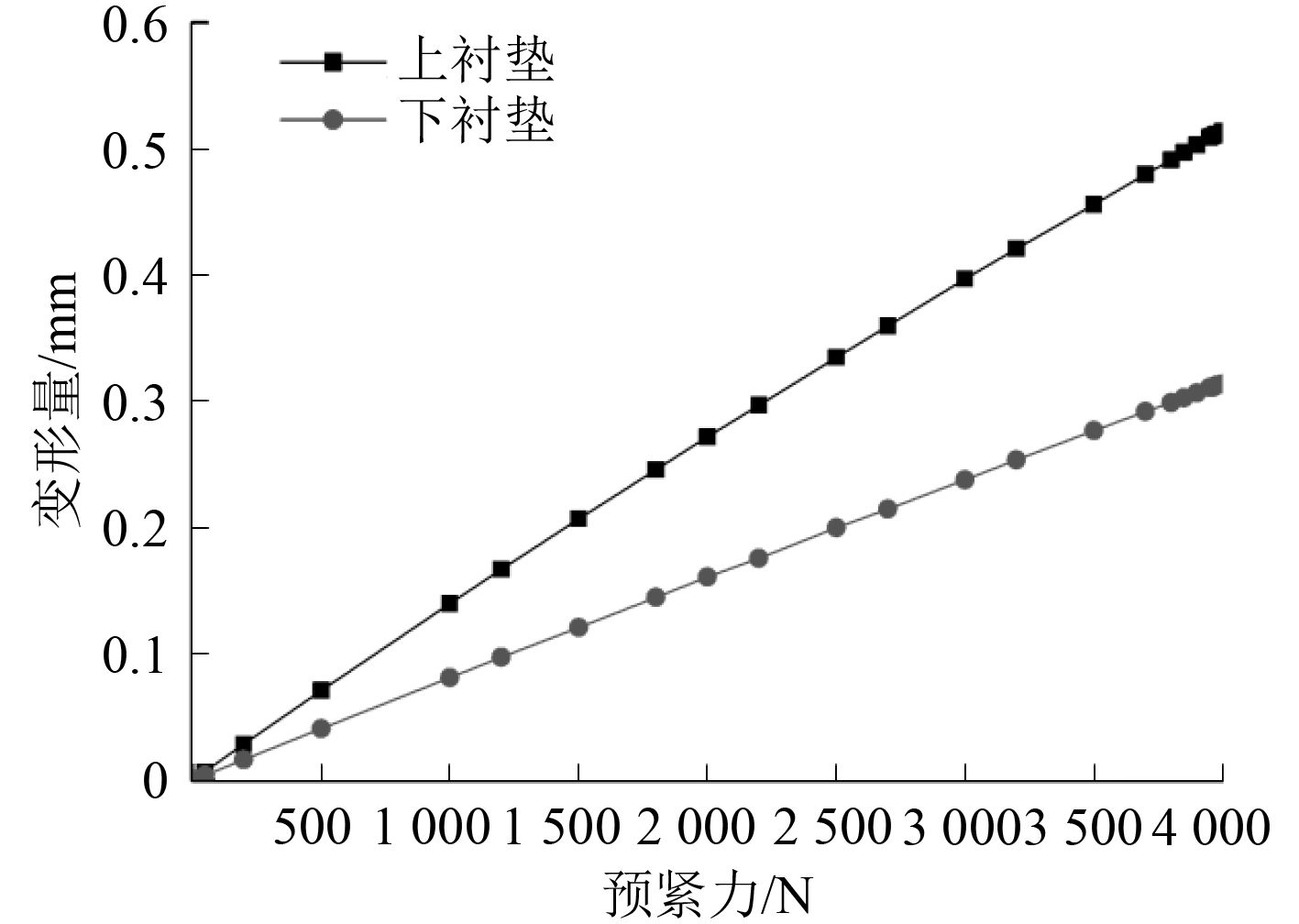
1#~4#位移输出点位移、上下衬垫变形量、上下卡箍端面间隙随螺栓预紧力变化曲线如图5~图7所示。可以看出,橡胶衬垫变形量、卡箍端面间隙均随螺栓预紧力近似线弹性变化,即变形量与预紧力加载呈近似线性关系。

|
图 5 输出点位移随螺栓预紧力变化曲线 Fig. 5 Change curve of output points displacement along with bolt force |
|
图 7 卡箍端面间隙随螺栓预紧力变化曲线 Fig. 7 Change curve of bracket side clearance along with bolt force |
集成式管路弹性支吊架实际应用中,需满足以下要求:1)支吊架锁紧管路,避免沿管路轴向串动;2)衬垫不得压死,保证支吊架隔振效果较好。因此,橡胶衬垫须处于线弹性可满足上述要求。
卡箍端面间隙取12.0 mm±0.5 mm(螺栓预紧力1 800~2 700 N)时,上衬垫变形量0.25~0.36 mm,下衬垫变形量0.15~0.22 mm,均小于衬垫齿槽深度2.5 mm,即支吊架可在确保管路轴向紧固的同时具有较好的隔振效果。
|
图 6 衬垫变形量随螺栓预紧力变化曲线 Fig. 6 Change curve of gasket distortion along with bolt force |
螺栓预紧力取2 000 N,通过计算获得支吊架应力、应变分布如图8和图9所示。

|
图 8 螺栓预紧力作用下支吊架应力分布云图 Fig. 8 Stress distribution of pipe bracket under bolt force |

|
图 9 螺栓预紧力作用下支吊架应变分布云图 Fig. 9 Strain distribution of pipe bracket under bolt force |
可以看出,最大应力170.7 MPa,出现在螺栓上;最大应变0.499 3,出现在橡胶垫上。因此,在螺栓预紧力作用下,集成式管路弹性支吊架最大应力与应变均小于屈服强度与极限压缩应变,满足强度设计要求。
2.3 额定载荷作用下支吊架强度、刚度特性分析在螺栓预紧力(2 000 N)基础上,施加垂向额定载荷(3 200 N)作用,集成式管路弹性支吊架应力、应变分布结果如图10和图11所示。

|
图 10 额定载荷作用下支吊架应力分布云图 Fig. 10 Stress distribution of pipe bracket under rating force |

|
图 11 额定载荷作用下支吊架应变分布云图 Fig. 11 Strain distribution of pipe bracket under rating force |
可以看出,最大应力181.3 MPa,出现在下卡箍上;最大应变0.718 9,出现在下衬垫齿槽边缘。因此,在垂向额定载荷作用下,支吊架最大应力小于屈服强度,最大应变小于极限压缩应变0.8,满足强度设计要求。
在螺栓预紧力(2 000 N)基础上,支吊架垂向刚度随垂向载荷变化曲线如图12所示。由于橡胶块的影响,支吊架垂向刚度随垂向载荷近似呈线性递增趋势;3 200 N垂向额定载荷加载,支吊架垂向静刚度为1.81×106 N/m。

|
图 12 支吊架垂向刚度随载荷变化曲线 Fig. 12 Change curve of uprightness stiffness of pipe bracket along with uprightness force |
支吊架在螺栓预紧力2 000 N及垂向额定载荷3 200 N(考虑管段重量320 kg)作用下的模态计算结果如图13及表1所示。

|
图 13 支吊架前3阶模态振型 Fig. 13 The first three order modal shapes of pipe bracket |
|
|
表 1 支吊架固有频率及振型 Tab.1 Natural frequency and its modal shapes |
可以看出,在螺栓预紧力及垂向额定载荷作用下,支吊架前3阶固有频率依次为12.1 Hz,13.4 Hz,15.8 Hz,其中第1阶模态振型沿垂向平动。
3 集成式管路弹性支吊架动力学特性计算方法实验验证在试验室建立集成管路弹性支吊架动力学特性验证实验台架如图14所示。支吊架下端通过马脚与刚性基础连接,上端紧固一段管路,管段左右两端对称悬挂160 kg压载铁,实现垂向加载3 200 N。

|
图 14 支吊架动力学特性试验台架 Fig. 14 Test-bed of pipe bracket for dynamical characteristic research |
支吊架共布置8个三向振动测点(8×3个测试通道),分别对支吊架进行轴向、横向、垂向锤击激励,测试结果如图15及表2所示。

|
图 15 固有频率相干性分析结果 Fig. 15 Results of pertinence analysis for natural frequency |
|
|
表 2 支吊架固有频率测试结果 Tab.2 Test results of natural frequency and its modal shapes of pipe bracket |
可以看出,垂向额定载荷3 200 N作用下,集成式管路弹性支吊架垂向固有频率12.5 Hz。
针对上述验证试验台架模型,建立了相应的数值计算模型。利用本文提出的集成式管路弹性支吊架动力学特性计算方法,开展了动力学特性数值计算,数值计算模型及加载方式如图16所示,计算结果见表3及图17。

|
图 16 试验台架仿真模型及加载方式 Fig. 16 Numerical calculation model of test-bed and load fashion |
|
|
表 3 支吊架试验台架的数值计算与试验测试结果对比 Tab.3 Result contrast between numerical calculation and test of pipe bracket |
|
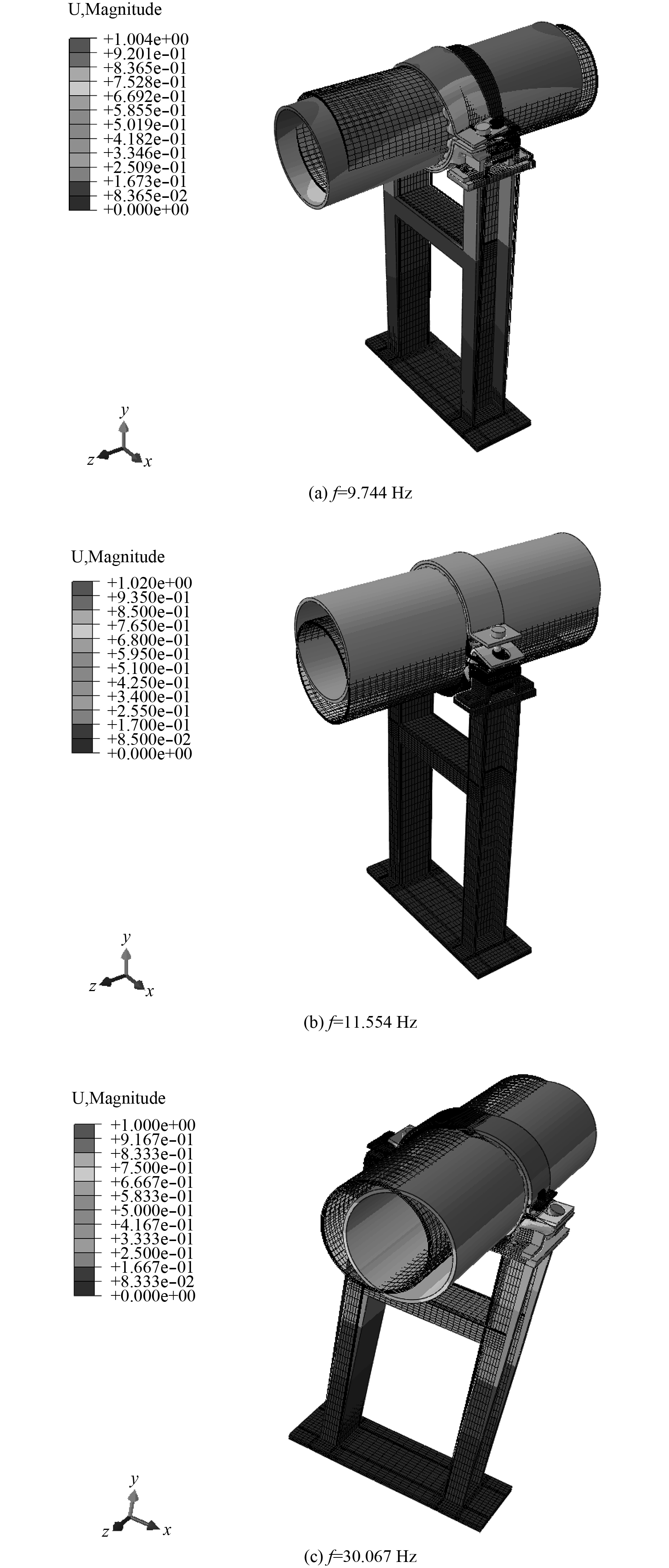
图 17 试验台架振型仿真结果 Fig. 17 Numerical calculation results of test-bed modal shapes |
可以看出,试验台架沿管路轴向弯曲振动频率f=9.744 Hz;支吊架垂向振动频率f=11.554 Hz;试验台架沿管路横向弯曲振动频率f=30.067 Hz。试验获得的支吊架垂向固有频率12.5 Hz,与数值计算结果11.554 Hz的误差在10%以内,进一步验证了本文提出的集成式管路弹性支吊架动力学特性计算方法有效性及支吊架动力学特性计算结果的准确性。
4 结 语本文在建立集成式管路弹性支吊架有限元模型的基础上,利用提出的数值计算方法,开展支吊架的有限元分析,给出不同螺栓预紧力作用下管卡橡胶内衬的变形量,确定了集成式管路弹性支吊架应用中施加螺栓预紧力的大小或上下卡箍端面的距离。在此基础上,开展支吊架额定载荷作用下的强度、刚度特性与固有频率分析,给出支吊架额定载荷下的强度与刚度特性的计算结果,以及支吊架的前3阶固有频率及对应的模态振型。最后,通过台架试验验证了本文提出的集成式管路弹性支吊架动力学特性计算方法有效性及计算结果的准确性。主要结论如下:
1)上下卡箍端面安装间隙为12.0±0.5 mm(初始间隙为14 mm)或施加的螺栓预紧力在1 800~2 700 N范围内,支吊架可在确保管路轴向紧固的同时具有较好的隔振效果。
2)在垂向额定载荷3.2 kN加载作用下,支吊架的垂向刚度值为1.81×106 N/m,最大应力与最大应变值分别为181.3 MPa,0.719,满足强度设计要求。
3)高性能管卡的1阶固有频率12.1 Hz以及其对应的模态振型满足支吊架固有频率的设计要求。
| [1] |
艾歲, 金良安, 等. 舰船隔振技术现状及研究展望[J]. 造船技术, 2015, 1: 4-8. DOI:10.3969/j.issn.1000-3878.2015.01.002 |
| [2] |
马永涛, 周炎, 张泉南, 等. 浮筏隔振系统的一种新隔振效果建模方法[J]. 振动与冲击, 2009, 28(7): 28-32. DOI:10.3969/j.issn.1000-3835.2009.07.006 |
| [3] |
李增光. 浮筏及双层隔振装置隔振性能计算与分析[J]. 噪声与振动控制, 2015, 35(6): 65-68. |
| [4] |
蒋学武, 朱石坚. 舰船管路橡胶减振器的应用[J]. 海军工程大学学报, 2000, 4: 90-94. DOI:10.3969/j.issn.1009-3486.2000.02.021 |
| [5] |
户原春彦. 防振橡胶及其应用[M]. 北京: 中国铁道出版社, 1982: 2–3, 109.
|
| [6] |
SEIBERT D J, SCHOCHE N. Direct comparison of some recent rubber elasticity models[J]. Rubber Chemistry and Technology, 2000, 73: 366-384. DOI:10.5254/1.3547597 |
| [7] |
上官文斌, 吕振华. 汽车动力总成橡胶隔振器弹性特性的有限元分析[J]. 内燃机工程, 2003, 24(6): 1-3. DOI:10.3969/j.issn.1000-0925.2003.06.001 |
| [8] |
石亦平, 周玉蓉. Abaqus有限元分析实例详解[M]. 北京: 机械工业出版社, 2006.
|
| [9] |
曹金凤, 石亦平. Abaqus有限元分析常见问题解答[M]. 北京: 机械工业出版社, 2009.
|
| [10] |
赵建才, 李堑, 姚振强. 橡胶悬置元件结构参数优化设计方法[J]. 振动与冲击, 2008, 27(1): 16-18. DOI:10.3969/j.issn.1000-3835.2008.01.004 |
| [11] |
王小莉. 复杂结构型式橡胶减振元件静刚度计算方法[J]. 噪声与振动控制, 2010, 12(6): 51-54. DOI:10.3969/j.issn.1006-1355.2010.06.012 |
| [12] |
王伯平, 翟敬宇, 等. 橡胶减振元件加速寿命试验的仿真研究[J]. 机电工程, 2013, 30(4): 399-402. |
| [13] |
才建军. 汽车发动机液压悬置的动特性仿真与试验研究[D]. 沈阳: 东北大学机械工程与自动化学院, 2007.
|
| [14] |
祖景平, 钱英莉, 周华樟. ABAQUS6.6基础教程与实例详解[M]. 北京: 中国水利水电出版社, 2008.
|
| [15] |
洪欢欢, 吴茂敏, 陈建, 等. 基于油锯减振的转换桥方法研究[J]. 轻工机械, 2011, 29(4): 11-16. DOI:10.3969/j.issn.1005-2895.2011.04.004 |
 2019, Vol. 41
2019, Vol. 41
