2. 国防大学 军事管理学院,北京 100091
2. School of Military Management, PLA National Defense University, Beijing 100091, China
无人水下航行器(UUV)能够有效降低海上作业风险、提高作业效率,已广泛应用于水下目标搜索和海洋环境调查[1]。为了进一步提高水下搜索的工作效率、可靠性和灵活性,采用多种类型UUV组成异构集群协作系统是未来主要发展趋势。在执行水下探测任务的集群UUV系统中,根据功能定位不同,可以分为探测型UUV(SVs)、识别型UUV(CVs)、导航型UUV(NVs)等。SVs搭载侧扫声呐、前视声呐、合成孔径声呐等对水下目标进行快速大范围搜索、定位,基于已获取的水下图像,通过目标辅助检测/识别技术(CAD/CAC)自动实现图像中疑似目标(OI)的标示[2],并将OI信息发送给系统中各CV。CVs根据OI位置分布情况进行实时在线分配,使用高分辨率识别声呐、水下光学摄像机等近距离对MLO进行识别,确认是否为搜寻目标。集群UUV系统多目标任务分配的主要目的是将SV发现的目标分配给CVs,使得识别目标的总代价(航程、时间等)最小。
目前无人系统任务分配方法可分为分布式和集中式2种。分布式任务分配方法主要采用基于市场的协商拍卖机制[3]。如果待分配的目标任务只有一个,可以使用传统的合同网由无人系统根据各自局部信息对目标分别投标竞争择优;但对于多个目标的情况,由于目标和无人系统之间存在复杂的组合关系(对n个目标,每个无人系统都存在
UUV通常采用电池作为能源[9],航程相对较短,与任务分配的均衡性相比,能源消耗是否满足任务需要,是实际使用中更为关注的因素;此外,已有研究工作主要是在固定条件下静态分析,没有考虑系统异常、能源不足等实际条件动态变化的问题。根据水下目标搜索任务的特点,提出一种基于分层聚类拍卖的集群UUV系统多目标任务分配方法(Hierarchical clustering auction-based multiple objects allocation approach,HCAMOA),采用基于最小生成树(Minimum Spanning Tree,MST)的层次化目标分组聚类方法,改进k-均值聚类分组存在的问题,提出2种水下目标任务分配模式模型,研究了相应的任务分配方法;针对故障或能源不足等异常情况,提出了任务调整机制。
1 基于聚类拍卖的集群UUV系统多目标任务分配方法 1.1 任务描述及模型SVs对海区搜索,由n艘CVs组成的UUV集群V={V1,···,Vn }对探测到的OI进行识别。CV当前需要执行的任务集合称为任务序列(符号TV),第c艘CV长度为k的当前任务序列表示为TVc={tvc1,···,tvck}(tvci∩tvcj=Ø,i,j∈{1,···,k}, i≠j,c∈{1,···,n})。当SVs检测到m个新目标NT={t1,···,tm}后,向CVs广播。CVs接到任务,各自从当前位置P={P1,···,Pn }出发依次访问任务序列中的OI位置。任务分配的目标是满足规定的约束条件下,使CVs的总航程最短。水下多目标识别任务分配有2种模式:
1)异步分配模式(Asynchronous Allocation Mode,AAM)
当SV发布目标信息时,CVs各自的任务序列TVc与新目标NT一起构成任务集合T=TV1∪...∪TVn∪NT。该模式需将系统所有待识别的OI重新分配给CVs,优点是可以实现全局优化,但计算量相对较大。为避免频繁的重新分配任务,SVs应在完成一定海域面积的探测任务工作后发布目标信息。异步分配模式数学模型为:
| $\begin{align} & \ TC=\min \sum\limits_{i\in T\bigcup P,j\in T}{{{c}_{ij}}{{x}_{ij}}}\text{,}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \\ & {\rm s.t.} \\ & \left\{ \begin{array}{*{35}{l}} \displaystyle\sum\limits_{i\in T\bigcup P}{{{x}_{ij}}}{=}1\text{,}\ \ \ \ \ \ \ \ \ \forall {\rm{j}}\in T\text{,}\ \ \ \ \ \ \ \ \ \ \ \ \ (2)\\ \ \displaystyle\sum\limits_{j\in T}{{{x}_{ij}}\leqslant 1}\text{,}\ \ \ \ \ \ \ \ \ \forall i\in T\bigcup P\text{,}\,\ \ \ \ \ \ \ \ \ (3)\\ \displaystyle\sum\limits_{i\in T\bigcup P,j\in T}{{{x}_{ij}}}\le \left| Q \right|{-}1\text{,}\ \ \forall Q\subseteq T\ \left| Q \right|\geqslant 2\text{。}\ \ \ \ \ (4)\\ \end{array} \right. \\ \end{align} $ |
式中:i和j为位置下标,表示UUV或目标位置;cij表示从位置i到位置j的航程;xij为0-1变量,1表示从位置i到j存在路径,0表示没有;TC表示总航程。
式(2)表示对任意一个目标t∈T,都有且只有一次访问。式(3)表示CV不能同时访问多个目标。式(4)表示访问路径是无环的。
2)同步分配模式(Synchronous Allocation Mode,SAM)
该模式只分配新发现的目标集合NT,因此任务分配的计算量相对较小。对于任一Vc∈V,其任务序列TVc与分配给Vc的新目标集NTc(NTc∈NT,NT1∪···∪NTn=NT,NTi∩NTj=Ø,i,j∈{1,···,k}, i≠j)组合成新的任务序列ntvc。相对异步分配模式,虽然不能实现全局优化,但实时性相对较好,在任务过程中,SVs能够不断的将新发现的目标分配给CVs识别,适用于小数量多批次分配目标的场合。同步分配模式数学模型为:
| $ \begin{align} & TC=\min \ \displaystyle\sum\limits_{c\in V}{\rm{pat}{{\rm{h}}_{c}}}\text{,}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \\ & {\rm s.t.} \\ & \left\{ \begin{array}{*{35}{l}} pat{{h}_{c}}=\displaystyle\sum\limits_{i\in nt{{v}_{\rm{c}}}\bigcup {{p}_{c}},\rm{j}\in T}{{{c}_{ij}}{{x}_{ij}}\text{,}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6)\ } \\ \displaystyle\sum\limits_{i\in nt{{v}_{c}}\bigcup {{p}_{c}}}{{{x}_{ij}}} {=}1\ \ \ \forall {\rm{j}}\in nt{{v}_{c}}\text{,}\,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (7) \\ \displaystyle\sum\limits_{j\in nt{{v}_{c}}}{{{x}_{ij}}\leqslant 1}\text{,}\ \ \ \ \forall i\in nt{{v}_{c}}\bigcup {{p}_{c}}\text{,}\ \ \ \ \ \ \ \ \ (8) \\ \displaystyle\sum\limits_{i\in nt{{v}_{c}}\bigcup {{p}_{c}}}{{{x}_{ij}}}\leqslant \left| Q \right|{-}1\ \ \forall Q\subseteq nt{{v}_{c}}\ \left| {\rm Q} \right|\geqslant 2 \text{。}\ \ \ \ \ (9) \\ \end{array} \right. \\ \end{align} $ |
式中:pathc为第c艘UUV的访问路径航程,其余符号定义和公式意义参见上文中的相关说明。
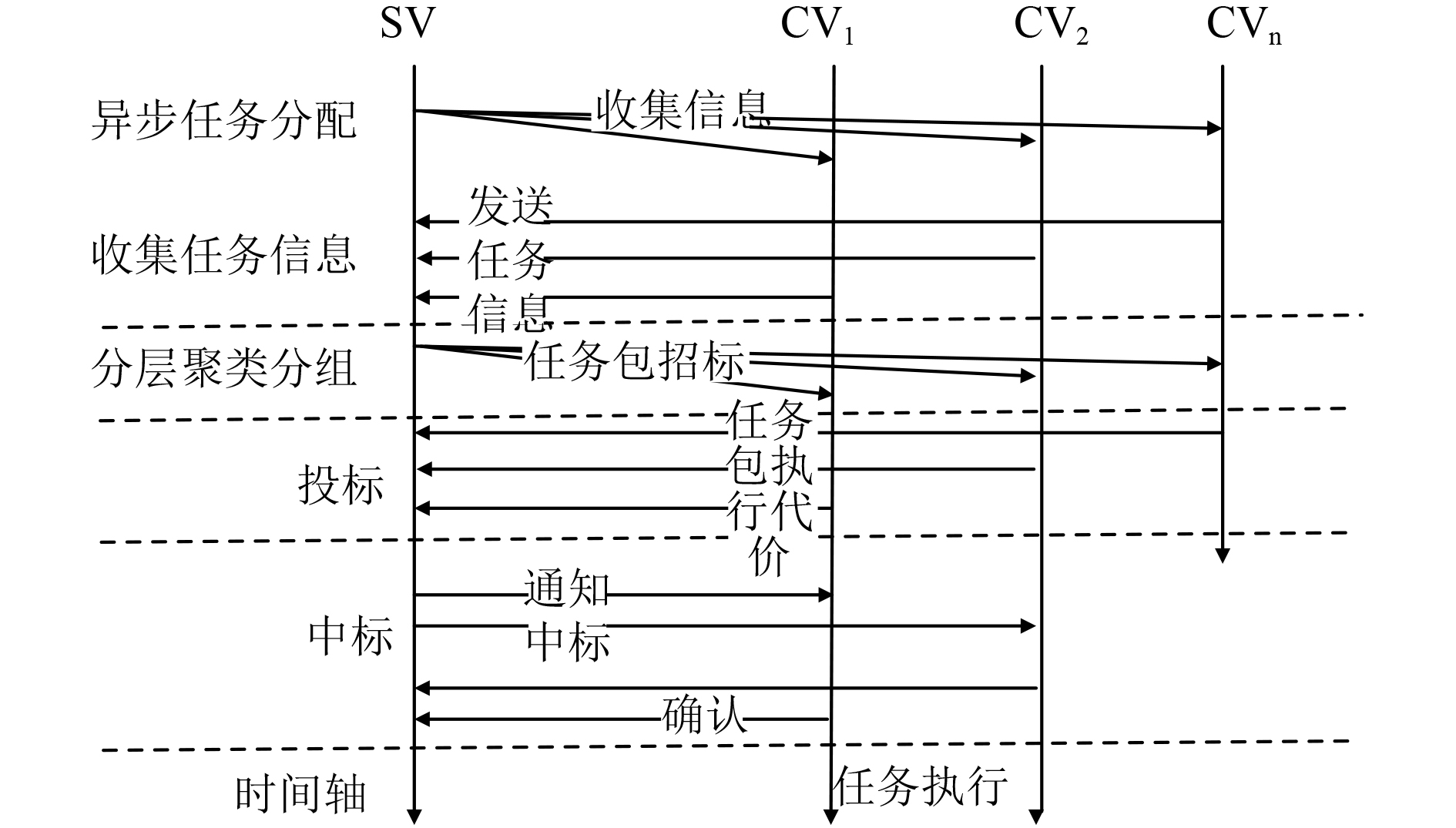
1.2 HCAMOA方法流程 1.2.1 工作流程HCAMOA方法采用基于市场的拍卖机制,基本流程见图1所示。在AAM模式下,SV首先收集所有CVs的位置和任务信息,生成目标集合T;在SAM/AAM模式下,对T进行分层聚类分组,将T分成d个任务包,任务包集合为TP={ tp1,···,tpd}(对任一tpi∈TP,tpi⊆T)。分组完成后,SV发布TP拍卖信息,CVs根据任务分配模式对TP各任务包计算执行代价NC,进行投标。SV收到投标信息后,计算最优的任务组合方式,通知CVs中标情况以及相应的任务包。最后CVs接收中标信息并确认。
|
图 1 HCAMOA方法处理流程 Fig. 1 Procedure of HCAMOA method |
分层聚类将所有目标点自底而上逐层分类,算法1分为聚类和分组2个步骤。
1)聚类
最小生成树能够构建目标集合中连接各点的极小连通子图,是求解旅行商问题一种启发式方法[10],因此基于MST对水下目标点集合进行聚类分组。
定义1:2个目标点集合T1、T2之间距离D,为以T1∪T2为节点所构成连通图的MST权值,即D=MST(T1∪T2)。
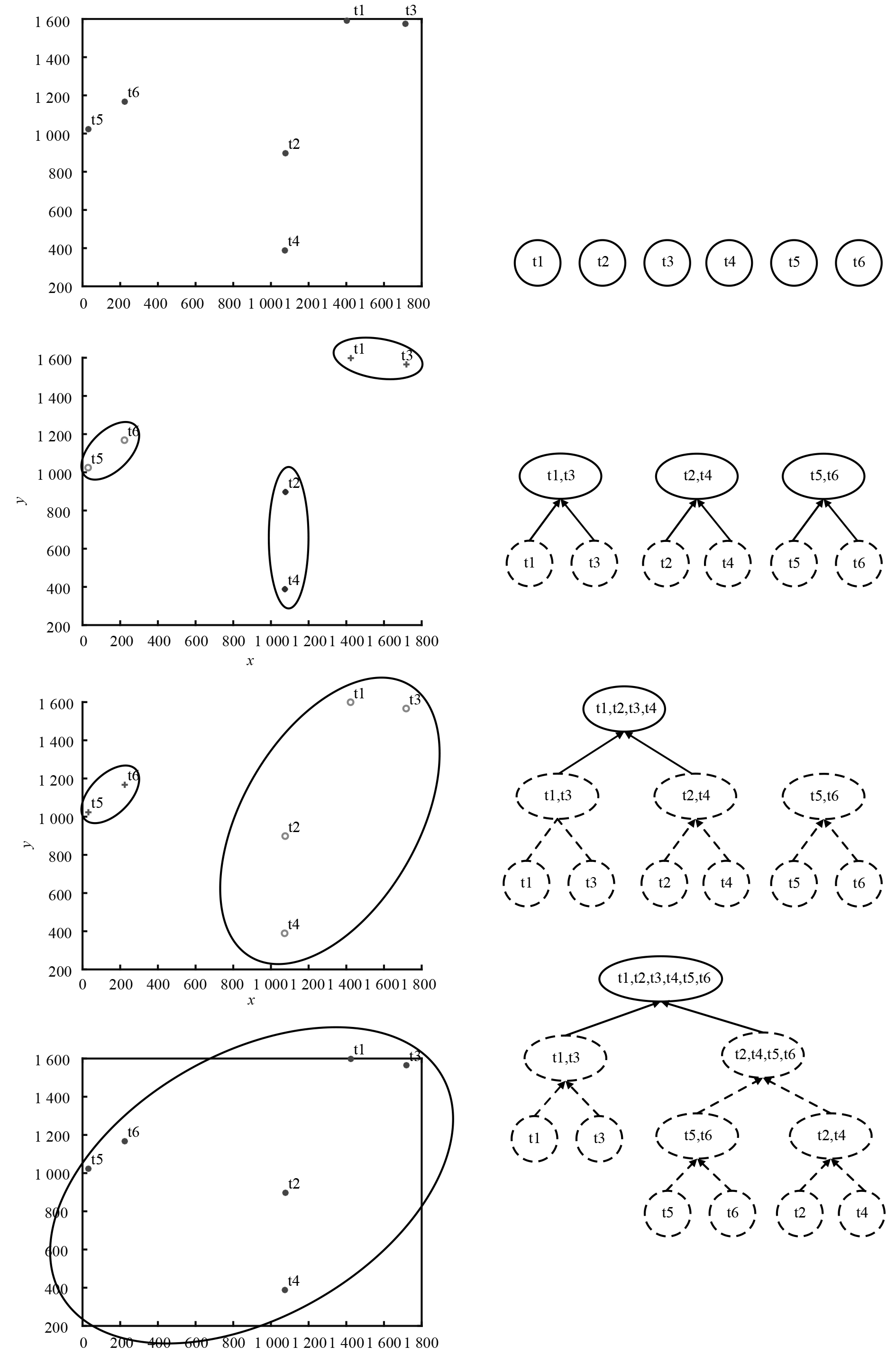
聚类过程示例如图2所示。图中左半部分为目标点分布,右半部分为对应的聚类过程,将6个目标划为5种分类:{t1,···,t6},{t1,t3},{t2,t4},{t5,t6},{t1,t2,t3,t4},最终形成二叉树结构的聚类树。
|
图 2 基于最小生成树的聚类过程示例 Fig. 2 Demonstration of clustering process based on minimum spanning tree |
|
图 3 聚类分组过程示例 Fig. 3 Demonstration of clustering process |
2)分组
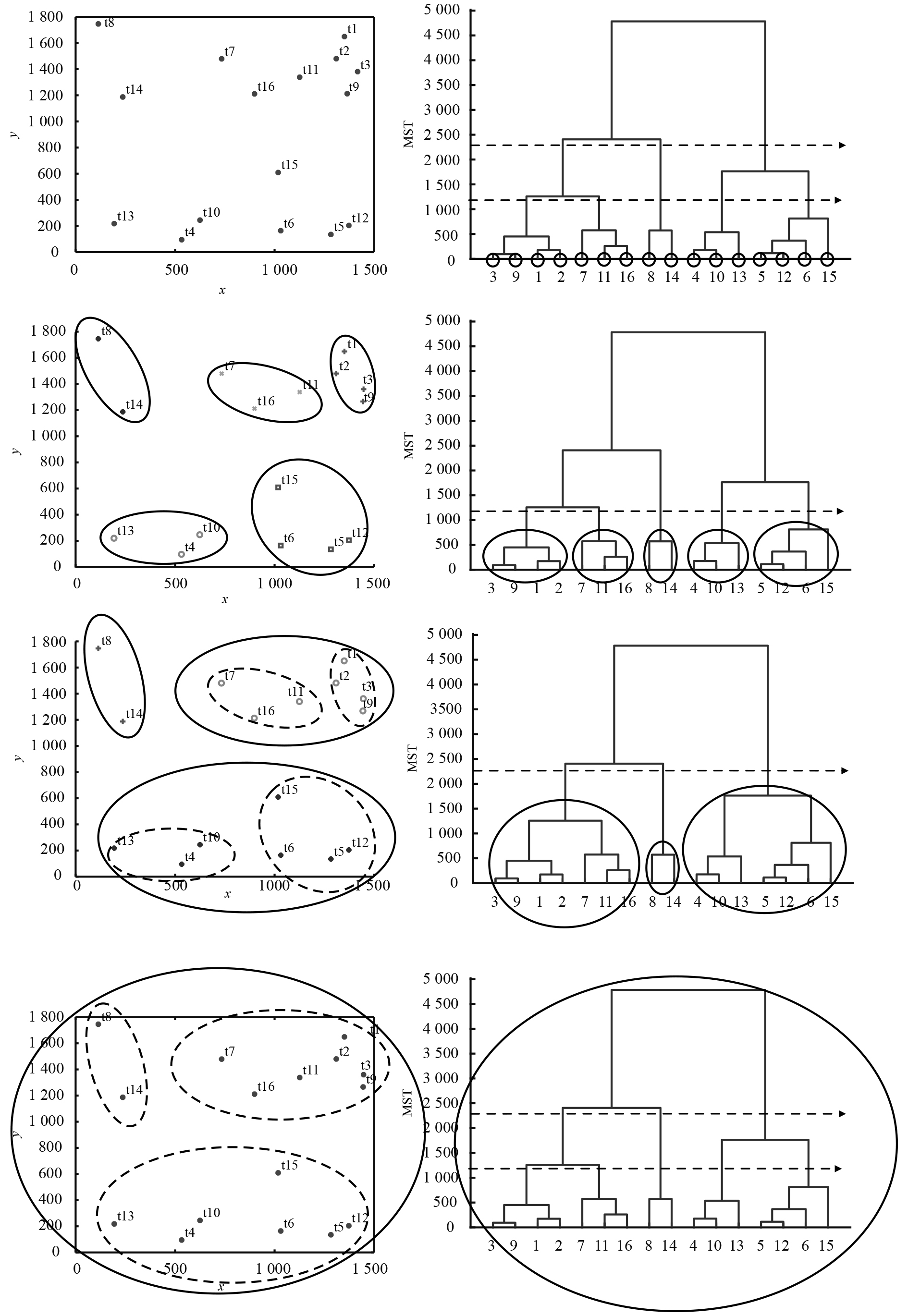
设定若干门限值,根据聚类结果将目标集分组为任务包TP,每个门限值决定一个分组的层级。门限值的设定可以根据分类情况,按最大MST权值(即MST(T)值)的比例确定(如分为50%,25%两个档)。对16个目标分组过程示例如图4所示,图中左半部分为目标点平面分布,右半部分为聚类树以及对应的任务包分组情况,聚类树中的虚线分别表示2个MST权值门限,按不同的门限对聚类结果进行分组,第1个门限1 195将11个分类划为5组,第2个门限2 391将11个分类划为3组,加上16个目标,以及所有目标组成的任务包,共计25个任务包(图中右半部分圈内所示)。TP之间组成树形结构。
|
图 4 目标及CVs初始位置分布 Fig. 4 Distribution of target and CVs initial locations |
CVs分别对各任务包计算执行代价NC(即航程,第i艘CV的NCcvi={NCtp1,...,NCtpd})。NC有2种计算方法:基于MST的快速启发式算法(Fast Heuristic Algorithm Based on MST,H-MST)和基于遗传算法的开放式单旅行商求解模型(Open Traveling Salesman Problem based on GA,GA-OTSP)[11]。H-MST以MST权值替代航程作为执行代价的估计值,计算速度相对较快;GA-OTSP以CV当前位置点为起点,计算遍历任务包中各目标位置的最小航程,且不返回起点,使用遗传算法不一定能得到最优解,但有限时间内可以获得相对较优的方案。在2种任务分配模式下,计算执行代价的位置点集合有所不同:SAM模式时,位置点集合为任务包、CV任务序列和CV当前位置点的并集;而AAM模式时,位置点集合不包括CV的任务序列。GA-OTSP方法可以准确计算航程,当CV剩余航程不足以完成某个任务包tpi时,则在投标信息中加入tpi的投标失败标识,不参与tpi的投标。
1.2.4 中标SV接收到CVs的投标信息后,根据NC的大小,对TP进行择优中标操作。从TP树形结构最底层的叶子节点开始,自底而上逐层比较。
1.2.5 系统异常情况的任务处理机制引发异常情况问题的主要原因包括:受环境等条件影响,导致CV实际能耗大于预计值,如避障、逆流航行等情况,导致剩余能源不足以完成所分配的任务;CV系统发生故障退出,无法完成其后续的任务;快速启发式方法H-MST只是实现了对执行代价的估计值,与实际航程有一定出入,可能发生剩余能源不足的问题。发生异常情况导致后续任务执行失败,需对任务进行再分配。任务再分配可以等效为集群UUV系统处理新的目标识别任务,因此任务分配过程同HCAMOA流程,只是发起者为能源不足的CV。采用AAM模式时,CVs的所有任务均参与重新分配;SAM模式时,只对CVs任务序列进行局部调整。按异常事件的性质,分为2种情况。
情况1:CV不能完成后续任务。CV发生故障或剩余能源不足退出任务时,需要将所担负的所有后续任务分配给其他CVs。
情况2:CV剩余能源能完成部分后续任务。将不能完成的任务分配给其他CVs。
2 仿真实验1)异步分配模式
3艘CV,10个目标,采用MST作为执行代价。初始条件如表1和表2所示。
|
|
表 1 目标点的分布情况 Tab.1 Distribution of target locations |
|
|
表 2 CVs当前位置以及初始任务位置分布情况 Tab.2 Distribution of CVs and their initial tasks locations |
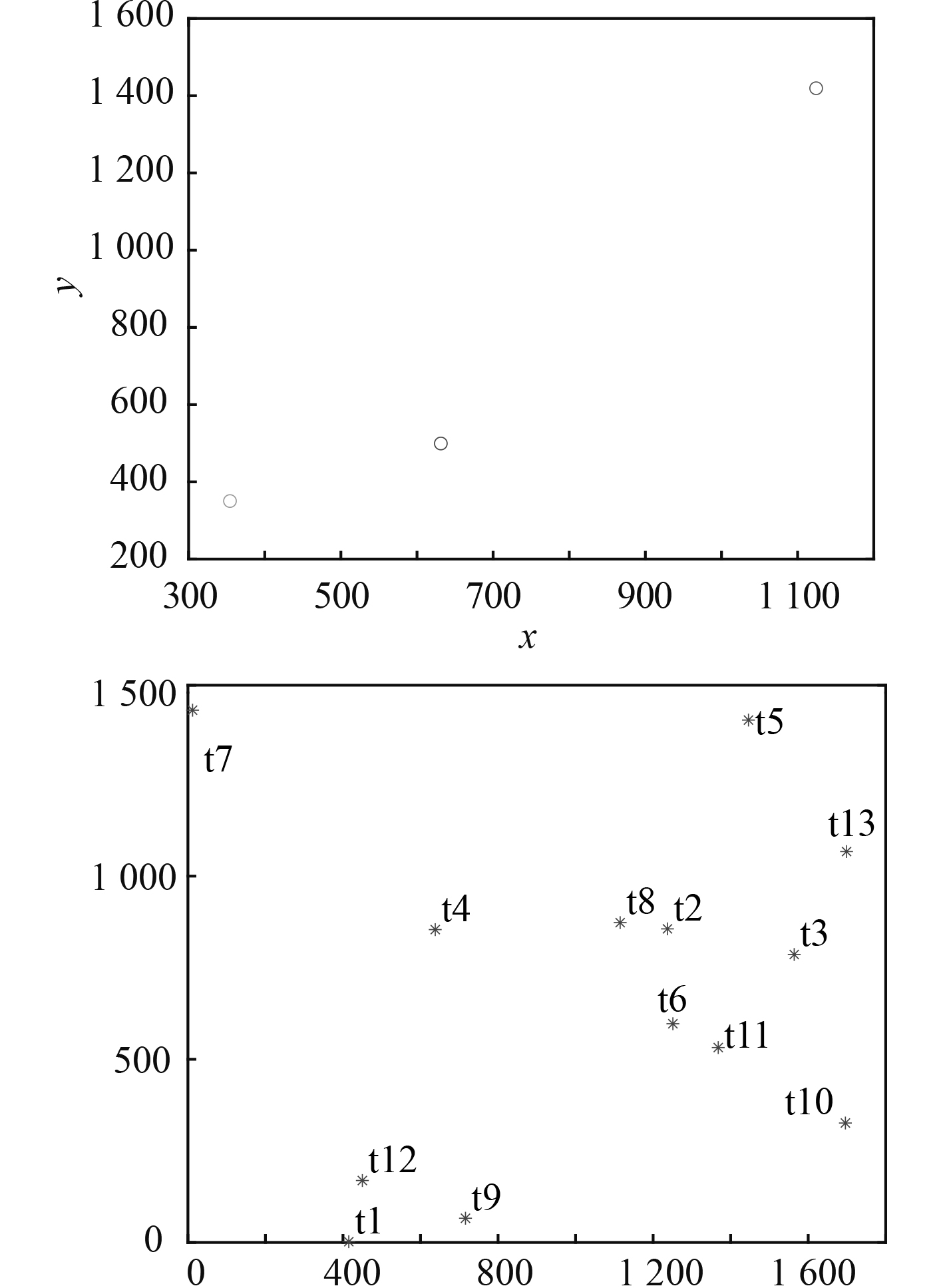
在初始阶段,每艘CV任务序列中各有一个待完成的目标识别任务。在AAM模式下,上述目标均参与分组,共计13个目标,如图4所示。聚类和分组结果如图5所示。
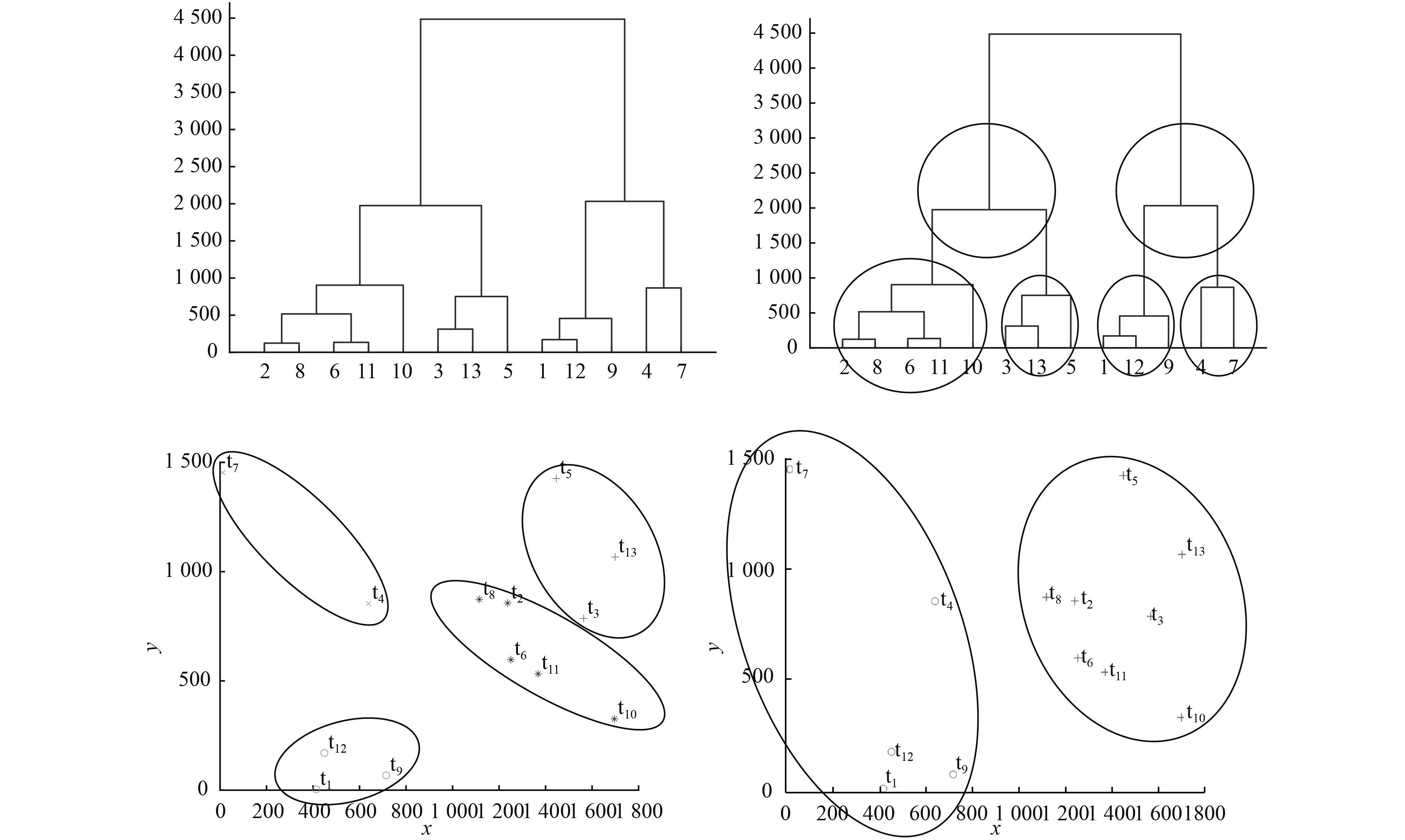
|
图 5 聚类和分组结果 Fig. 5 Results of clustering and grouping |
12个目标共分为2档20个任务包。CVs对各任务包最小MST代价投标结果如表3所示(任务包编号为树形结构自底而上顺序排列)。
|
|
表 3 各任务包最小代价 Tab.3 The minimum cost for each task package |
根据算法3,最终中标结果如表4所示。
|
|
表 4 中标结果 Tab.4 The bidding results |
2)同步分配模式
3艘CV,4个目标,采用TSP作为执行代价。初始条件如表5和表6所示。
|
|
表 5 目标点的分布情况 Tab.5 Distribution of target locations |
|
|
表 6 CVs当前位置以及初始任务位置分布情况 Tab.6 Distribution of CVs and their initial tasks locations |
4个目标共分为2档10个任务包。CVs对各任务包最小TSP代价投标结果如表7所示。
|
|
表 7 各任务包最小TSP代价投标结果 Tab.7 The minimum TSP cost of each task package and bidding results |
最终中标结果如表8所示。
|
|
表 8 中标结果 Tab.8 The bidding results |
发生异常情况时,需将不能完成的任务进行再分配,分配的基本流程和方法同上。上述2个仿真实例运行时间分别为0.89 s和87.8 s(仿真平台Matlab2016b,运行环境为Intel core i5 1.6 GHz,8G RAM)。尽管实例2分配的目标数量较少,但采用计算量较大的TSP算法,运行时间大幅增加。因此,在对实时性要求较高,或目标较多的情况下,适合使用快速启发式H-MST算法。
3 结 语作业效率和可靠性是集群UUV协同执行任务关注的主要问题。针对水下多目标识别任务的特点,提出了2种任务分配模式,AAM模式本质上是全局任务重分配方法,适合大量目标分阶段分配,而SAM模式是对CVs任务进行局部增量式的调整,适合少量目标的多批次任务分配情况。提出2种任务模式的优化模型及拍卖分配方法,能够在保证系统可靠运行的条件下,提高运行效率(总航程最短)。针对现有多任务分组研究工作的不足,提出了基于分层聚类的分组方法,改进了K均值聚类分组方法存在的问题。仿真结果表明,HCAMOA方法能够有效解决集群UUV水下多目标任务分配问题。该方法也可应用于其他无人系统同类型任务分配领域。后续主要工作是进一步开展同时考虑任务时间、航程、任务负载率等多目标优化问题。
| [1] |
ZHANG F, MARANI G, SMITH R N, et al. Future trends in marine robotics[J]. Robotics & Automation Magazine IEEE, 2015, 22(1): 14-122. |
| [2] |
WILLIAMS D P. Fast target detection in synthetic aperture sonar imagery: a new algorithm and large-scale performance analysis[J]. IEEE Journal of Oceanic Engineering, 2015, 40(1): 71-92. DOI:10.1109/JOE.2013.2294532 |
| [3] |
CHEIKHROUHOU O, KOUBÂA A, BENNACEUR H. Move and improve: A distributed multi-robot coordination approach for multiple depots multiple travelling salesmen problem[C]//In: IEEE International Conference on Autonomous Robot Systems and Competitions, 2014: 28–35.
|
| [4] |
DENG Y. Task allocation and path planning for acoustic networks of AUVs[D]. Boca Raton Florida: Flodrida Atlantic University The college of engineering and computer science, 2010: 25–42.
|
| [5] |
TRIGUI S, KOUBÂA A, CHEIKHROUHOU O, et al. A clustering market-based approach for multi-robot emergency response applications[C]//International Conference on Autonomous Robot Systems and Competitions, 2016: 137–143.
|
| [6] |
ELANGO M, NACHIAPPAN S, TIWARI M K. Balancing task allocation in multi-robot systems using K -means clustering and auction based mechanisms[J]. Expert Systems with Applications, 2011, 38(6): 6486-6491. DOI:10.1016/j.eswa.2010.11.097 |
| [7] |
ASSAF M, NDIAYE M. Solving an open path multiple depot multiple traveling salesman problem after transformation[C]//International Conference on Modeling, Simulation, and Applied Optimization, 2017: 1–4.
|
| [8] |
WANG X, LIU D, HOU M. A novel method for multiple depot and open paths, Multiple Traveling Salesmen Problem[C]//IEEE International Symposium on Applied Machine Intelligence and Informatics, 2013: 187–192.
|
| [9] |
李亮, 邹金顺. 国外水下无人系统技术发展现状与趋势浅析[J]. 舰船科学技术, 2017, 39(12A): 6-9. |
| [10] |
LINHARES A, SWAMY C. Improved algorithms for MST and Metric-TSP Interdiction[J]. arXiv preprint arXiv: 1706. 00034, 2017.
|
| [11] |
LIU S. A Powerful Genetic Algorithm for Traveling Salesman Problem[J]. arXiv preprint arXiv: 1402. 4699, 2014.
|
 2019, Vol. 41
2019, Vol. 41
