为避免欠驱动UUV在低速状态下可能出现的“反常操舵”(即出现逆速)现象[1],或者为了加强欠驱动UUV纵平面的控制舵效,部分UUV在总体设计上会同时布置尾水平舵和首水平舵。对于同时配置首、尾水平舵的UUV而言,纵平面控制通常有3种操舵模式,即首尾分时单独操舵、首尾相对操舵和首尾平行操舵。首尾分时单独操舵模式中,不工作的舵面在零位上可起到稳定鳍的效果,也可以作为纵平面的备份执行机构,提高控制的可靠性。后2种操舵模式为首尾舵联合控制,控制过程涉及首、尾舵产生的升力与操纵力矩的交叉耦合关系,二者具有截然不同的控制效果。
首尾相对操舵模式中,其有效的控制输入为叠加后的操纵力矩,直接控制目标是UUV俯仰角。其原理是利用UUV攻角产生的升力与力矩实现纵平面机动控制。其优点是可获得较大的(即首尾舵叠加的)纵倾控制力矩,纵平面机动性较好,应用较为广泛。但由于爬潜过程中攻角较大,在某些对UUV纵倾姿态平衡性存在特殊要求的任务中,该模式难以满足需求。
首尾平行操舵模式中,其有效的控制输入为叠加后的舵面升力,直接控制目标是UUV深度。其原理是利用首尾舵面产生的升力实现纵平面机动控制,优点是爬潜过程不依赖于攻角,故可获得极小攻角或近似零攻角的爬潜控制。不足是低航速下舵面产生的升力有限,导致UUV纵平面机动性较差。对于纵平面运动中对平衡性要求较高而对机动性要求不高的UUV而言,首尾平行操舵模式是较合适的选择。
首尾平行操舵的控制难点是首尾舵角的动态匹配。为了实现极小攻角的爬潜控制,必须确保稳态下UUV受到的纵倾力矩的矢量和近似为0,以及受扰时能及时补偿扰动的影响。由于UUV数学模型存在误差、作用在舵面的流体阻力为非线性、首尾舵效动态比例关系不易精确获取等原因,采用常规PID控制器很难获得良好的控制效果。尤其在受扰动条件下,常规PID控制器的适应性并不理想。文献[2]描述了首尾相对操舵模式和首尾平行操舵模式的特点,并对首尾相对操舵模式进行分析和仿真,但未对首尾平行操舵模式进行深入研究。
模糊控制是智能控制的一个重要分支。模糊控制把人类自然语言表述的控制策略,通过模糊集合和模糊逻辑推理转化成数学函数,用计算机予以实现。最大的特点是不需要知道控制对象的数学模型,只需要积累对被控对象进行控制的操作经验[3]。对UUV而言,在不能建立精确数学模型的条件下,其控制规则仍然明确,且具有丰富的工程经验可借鉴。
利用模糊控制技术和UUV控制系统的上述特点,本文设计一种尾舵采用PID控制器实现深度控制、首舵采用基于模糊PID的前馈-反馈复合控制器实现姿态调整的UUV首尾平行操舵混合控制器,实现了欠驱动UUV小攻角稳定爬潜控制,可以避免常规PID控制器因模型误差以及由外界扰动引起的性能下降。
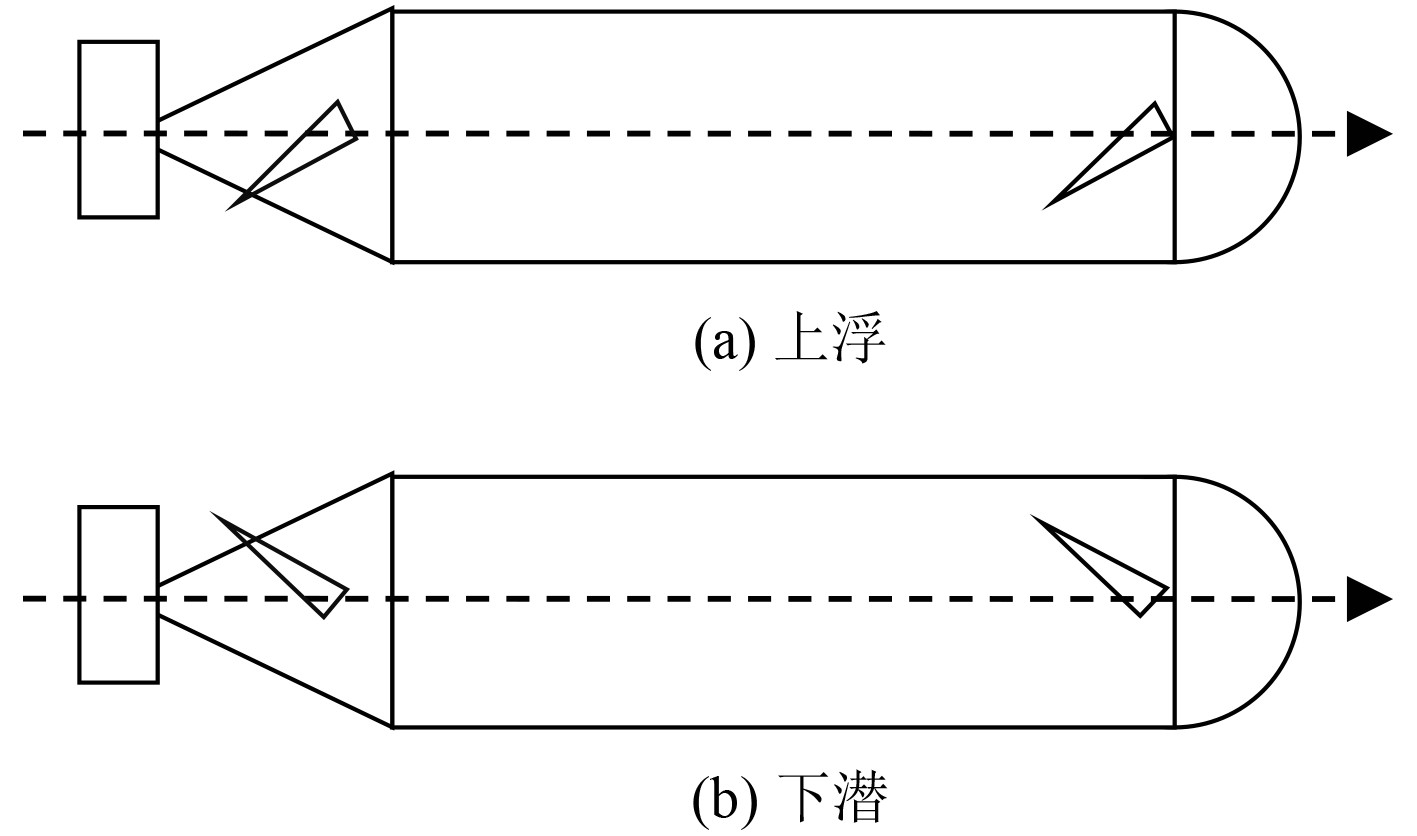
1 UUV首尾平行操舵特性与数学模型 1.1 首尾平行操舵控制特性分析UUV首尾平行操舵模式,即上爬时首尾同时操下舵,下潜时首尾同时操上舵,首尾舵方向始终保持一致(但角度通常不一致),如图1所示。
|
图 1 艏艉平行操舵模式示意 Fig. 1 Example of the paralleled steering mode |
首尾平行操舵模式中,首舵后沿与尾舵后沿的偏转方向始终相同,操舵时产生的升力方向也相同。由于UUV浮心在首、尾舵之间,操舵时首、尾舵引起的纵倾力矩则方向相反。可见,首尾平行操舵模式中,首舵和尾舵产生的升力具有叠加的效应,而首舵和尾舵产生的纵倾力矩则具有抵消的效应。因此,采用该操舵模式,可直接由舵面产生一定的升力或下压力,并且可减小甚至消除操舵时产生的纵倾力矩。在总体布局和流体设计合理的前提下,采用该操舵模式并设计合适的控制系统,在小浮力或零浮力状态下可有效减小UUV爬潜时的攻角,甚至实现水平姿态爬潜控制[2]。
1.2 首尾平行操舵数学模型UUV完整的空间运动方程组为包含6个动力学方程和9个运动学方程的微分方程组,由于本文只分析纵平面运动,故可简化为只包含8个方程的纵向运动方程组[6]。以纵轴正向为x轴、天向为y轴、右舷向为z轴作为载体坐标系,建立某UUV的纵平面运动方程组如下:
| $ \begin{array}{l} \left(m + {\lambda _{11}}\right)\dot u - m{Y_G}\dot r - m\left(vr + {X_G}{r^2}\right) = T - \Delta G\sin \theta + \displaystyle\frac{1}{2}\rho V_T^2S\ \\ \left({C_X}\left(0\right) + C_X^{{\alpha ^2}}{\alpha ^2} + C_X^{{r^2}}r{'^2} + C_X^{{\delta _e}^2}{\delta _e}^2 + C_X^{{\delta _b}^2}{\delta _b}^2 + C_X^{\alpha r}\alpha r'\right)\text{,} \end{array} $ |
| $ \begin{array}{l} \left( {m + {\lambda _{22}}} \right)\dot v + \left( {m{X_G} + {\lambda _{26}}} \right)\dot r - m\left( {ur + {Y_G}{r^2}} \right) = - \\ \Delta G\cos \theta + \displaystyle\frac{1}{2}\rho V_T^2S\left( {C_Y^\alpha \alpha + C_Y^{\alpha \prime }|\alpha | + C_Y^{{\alpha ^2}}{\alpha ^2} + } \right.\\ \left.C_Y^r{r^\prime } + C_Y^{{\delta _e}}{\delta _e} + C_Y^{{\delta _s}}{\delta _b} + C_Y^{\alpha |\alpha |}\alpha |\alpha | + C_Y^{r|r|}{r^\prime }\left| {{r^\prime }} \right| + C_Y^{\alpha |r|}\alpha \left| {{r^\prime }} \right|\right)\text{,} \end{array} $ |
| $ \begin{array}{l} \left( {{J_z} + {\lambda _{66}}} \right)\dot r - m{Y_G}\dot u + \left( {m{X_G} + {\lambda _{26}}} \right)\dot v + \\ \left( {m{X_G}ur + m{Y_G}vr} \right) = mg\left( {{Y_G}\sin \theta - {X_G}\cos \theta } \right) + \\ \displaystyle\frac{1}{2}\rho V_T^2SL\left( {C_N^\alpha \alpha + C_N^r{r^\prime } + } C_N^\delta {\delta _e} + C_N^{{\delta _b}}{\delta _b} + C_N^{\alpha |\alpha |}\alpha |\alpha | +\right.\\ \left. C_N^{r|\gamma |}r'|r'| C_N^{|\alpha |\gamma }|\alpha |r' + C_N^{|\alpha |}|\alpha | + C_N^{{\alpha ^2}}{\alpha ^2}\right)\text{,} \end{array} $ |
| $ \dot{\theta}=r\text{,} $ |
| $ {\dot X_e} = u\cos \theta - v\sin \theta \text{,} $ |
| $ {\dot Y_e} = u\sin \theta + v\cos \theta \cos \phi\text{,} $ |
| $ {V_T} = \sqrt {{u^2} + {v^2}} \text{,} $ |
| $ \alpha = {\rm arctg}( - \displaystyle\frac{v}{u})\text{。} $ |
式中:
方程中尤其需要注意首尾舵
由于模型误差的存在,不可能精确获得首尾舵在所有航态下的操纵力矩比例关系,因此在控制系统设计时,无法用单一控制器兼顾首尾舵的输出。且UUV航行中受到不确定的外界扰动,首尾舵采用同一控制器也无法实现抗扰动的需求。
在本文讨论的某UUV上,从流体动力特性看,首舵舵效优于尾舵舵效。因此本文在设计控制器时,将尾舵设计为定深控制器而将首舵设计为姿态调节控制器。设计中,对深度通道而言,可以将尾舵看作是“主动舵”,而将首舵看作是“从动舵”。尾舵控制器的输入量包括目标深度Ya、当前深度Y以及深度变化率dY/dt。该控制器中,输入量简单、变化过程平缓,小攻角条件下模型近似于线性系统,采用常规PID控制器即可获得较好的控制性能。
首舵调姿控制器中,输入量包括姿态角θ及其变化率ω,控制器根据姿态变化情况输出首舵角db,实现UUV姿态调节。仿真发现,采用常规PID控制器时,控制效果较差,俯仰角θ存在明显的震荡。主要原因是尾舵控制通道和首舵控制通道都存在明显的时延与惯性环节,采用单纯的反馈控制无法实现对姿态扰动的提前检测与补偿。
事实上,当首尾舵独立控制时,对首舵控制器而言可将尾舵输出看作是一个扰动量,而且是可精确观测的扰动。同时,首尾舵双通道的存在使得系统在结构上满足不变性要求(小姿态下近似满足),即当UUV受到干扰即尾舵角de作用时,被控变量θ不受扰动影响。因此可以通过增加前馈控制器,使干扰信号de经前馈控制器至被控变量θ的动态特性(首舵控制通道)尽量复制干扰通道(尾舵控制通道)的动态特性,但符号相反(即纵倾控制力矩相互抵消),以实现对干扰信号的补偿。这里,从控制器输出到首尾舵响应的动态过程完全一致(硬件设计相同),UUV对首尾舵输出的响应过程则可以通过调节舵角比例关系做到大体上一致。引入前馈控制后,首舵控制器就可设计为前馈-反馈复合控制器,前馈控制器用来消除主要扰动量的影响(即尾舵引起的姿态扰动),反馈控制器用来消除前馈控制器不精确和其他干扰所产生的影响。
为克服前馈控制器误差和外界干扰的不确定性和非线性以及UUV数学模型本身存在误差带来的问题,本文采用模糊PID控制器实现首舵的反馈控制。
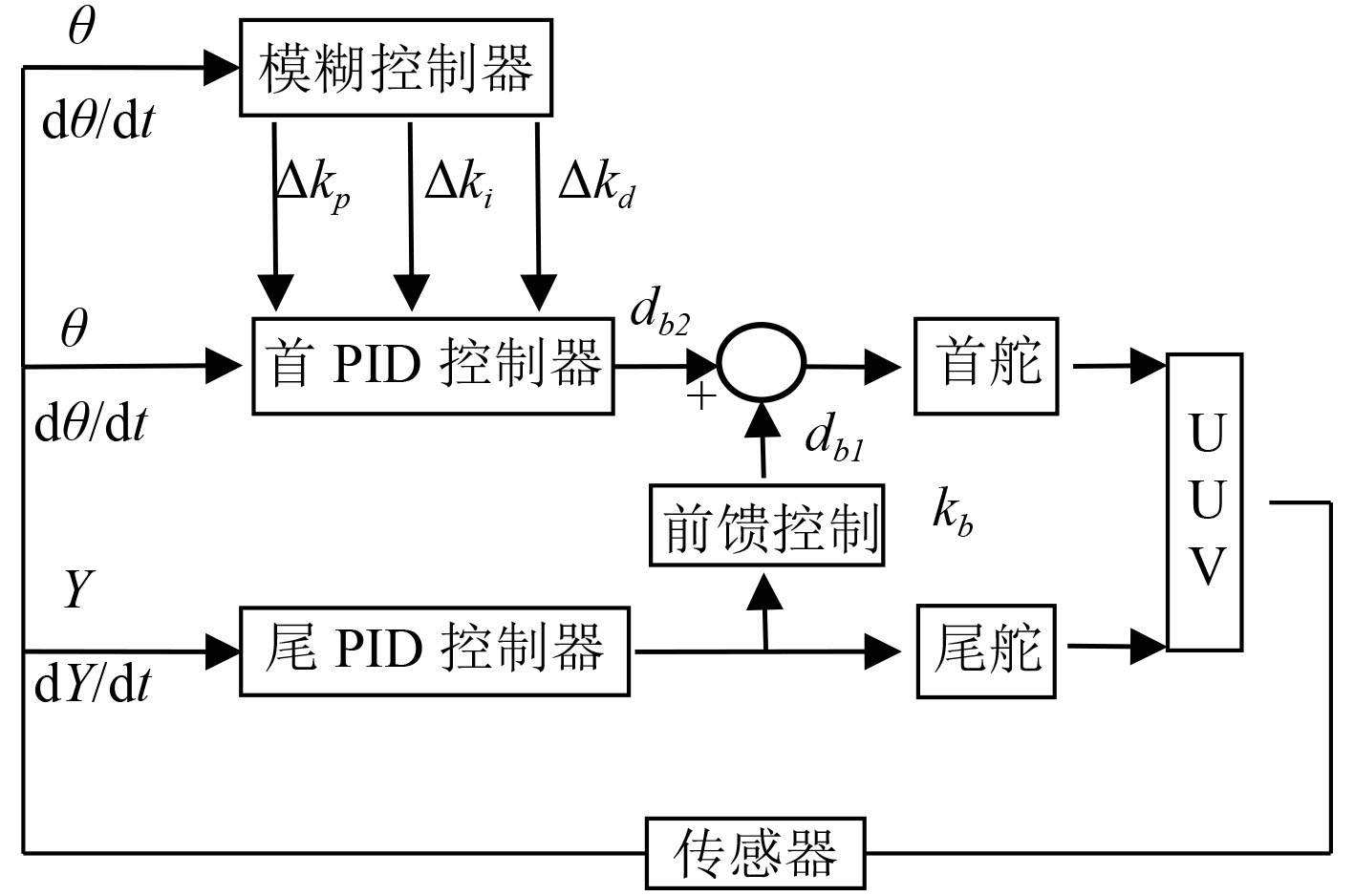
本文设计的首尾平行操舵控制系统框图如图2所示。该系统为混合控制器,包括1个尾舵控制器和1个首舵控制器。尾舵控制器为一PID控制器,用于深度控制。首舵控制器为前馈-反馈复合控制器,实现姿态调节。其中前馈控制器以尾舵控制器的输出作为输入,反馈控制器采用模糊PID控制器。
|
图 2 UUV首尾平行操舵混合控制器 Fig. 2 Hybrid controller of Paralleled steering mode |
在前馈控制器中,最关键的问题是确定输入信号的放大系数kb。本文采用的kb为通过水动力导数计算获得的首舵和尾舵的纵倾力矩系数的比值。由于首尾舵的水动力导数本身为近似计算值或流体试验结果的拟合值,加上航行过程中还受到外界扰动,因此没有必要也没有足够的样本对kb再次动态拟合,故取常数。
必须指出的是,在首尾平行操舵模式中,尾舵控制器的输出极性与尾舵单独控制以及首尾相对操舵模式中的极性相反。另外,极限情况下,如受到强烈扰动导致UUV俯仰角过大,使得图2中db2绝对值大于db1且二者符号相反时,混合控制器会短时等效于相对操舵控制,此时可获得最大的操纵力矩以克服扰动影响。
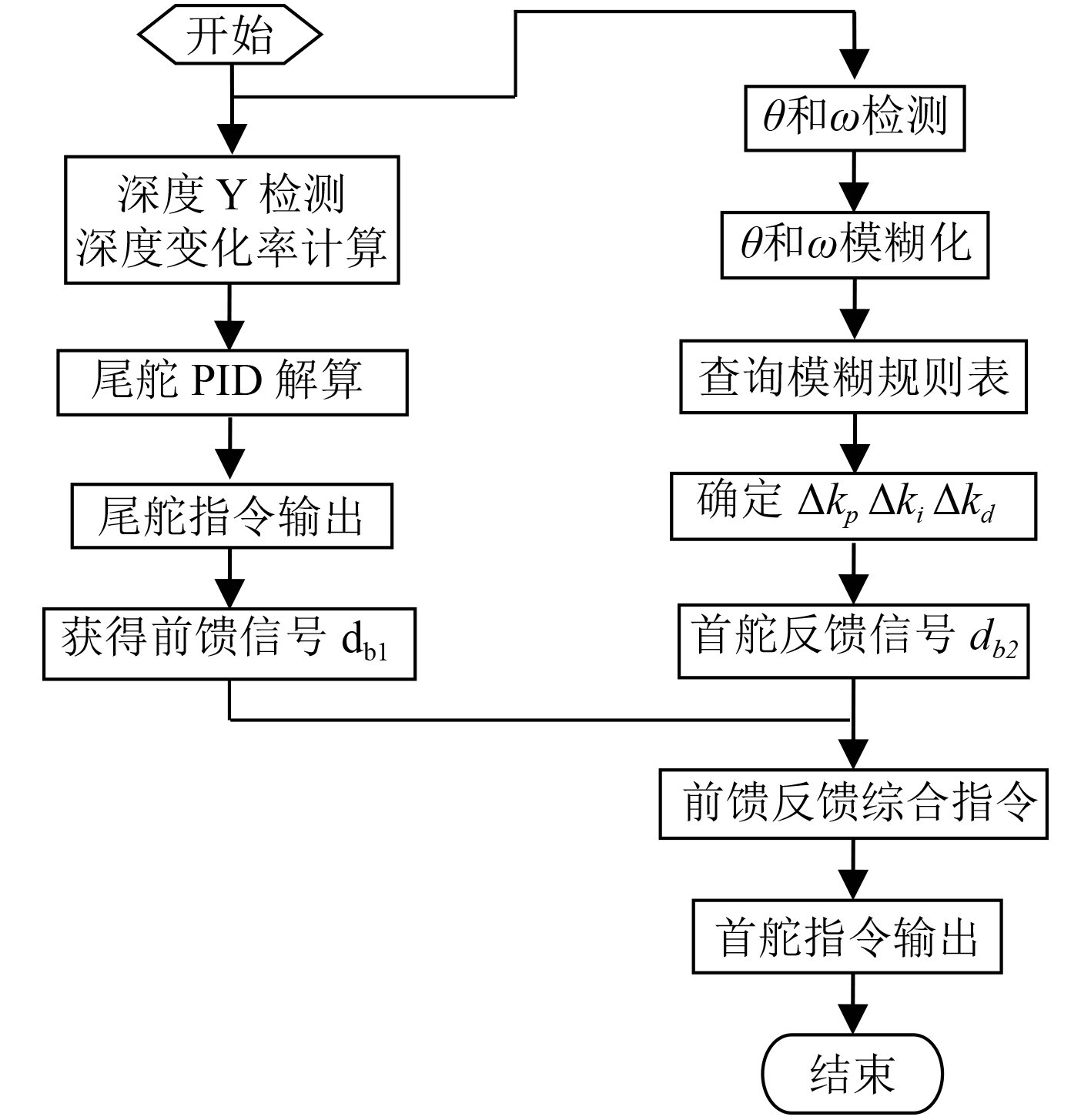
混合控制器的算法流程如图3所示。
|
图 3 混合控制器算法流程 Fig. 3 Algorithm flow of the hybrid controller |
首舵控制器的反馈控制通道中,采用模糊PID控制器实现对姿态偏差的补偿,以解决前馈控制器不精确、模型本身误差以及外界扰动造成的性能降低问题。
模糊控制器采用2输入3输出结构,输入为UUV俯仰角θ和俯仰角速度ω,输出为3个控制参数的修正量Δkp,Δki,和Δkd。利用3个参数的修正量对3个参数的初始值kp0,ki0和kd0分别进行修正,即获得基于参数模糊自适应的PID控制器的最终参数kp,ki和kd[4 – 5]。
根据经验,将模糊变量θ,ω,Δkp,Δki,Δkd的模糊子集均取为7个,其模糊论域用模糊数均表示为{–3,–2,–1,0,1,2,3},模糊子集名称依次为负大(NB)、负中(NM)、负小(NS)、零(ZO)、正小(PS)、正中(PM)、正大(PB)。简单起见,模糊子集的隶属函数均取为等腰三角形函数。采用Mamdani法进行模糊推理,采用面积中心法进行反模糊化。
根据文献[3-5]总结的调节PID控制器3个参数的模糊规则,并结合工程经验,按照俯仰角θ和俯仰角速度ω的变化情况,本文设计的修正PID控制器3个参数的模糊规则如表1~表3所示。
|
|
表 1 调节Δkp的模糊规则 Tab.1 Fuzzy rule for Δkp |
|
|
表 2 调节Δki的模糊规则 Tab.2 Fuzzy rule for Δki |
|
|
表 3 调节Δkd的模糊规则 Tab.3 Fuzzy rule for Δkd |
利用Matlab软件的Simulink工具建立首尾平行操舵混合控制系统仿真框图如图4所示。为验证混合控制器的性能,采用1.2节建立的数学模型,对UUV控制阶跃响应性能进行仿真,并与常规PID控制器(尾舵和首舵控制均采用PID控制器)的性能进行对比。

|
图 4 混合PID控制系统仿真框图 Fig. 4 Simulation block diagram of the hybrid PID control system |
仿真时,取采样时间Δt=0.05 s,仿真时间t为200 s。UUV初始姿态角、初始舵角、初始深度均设为0,航速设为4 kn。首舵模糊PID控制器3个参数初始值为kp=20,ki=0.6,kd=12。UUV设定为零浮力。阶跃响应仿真时,目标深度10 m,仿真时间第10 s时发出阶跃指令。
为比较本文设计的模糊PID控制器与常规PID对模型的依赖性,在仿真模型中引入误差的条件下再次进行仿真对比。
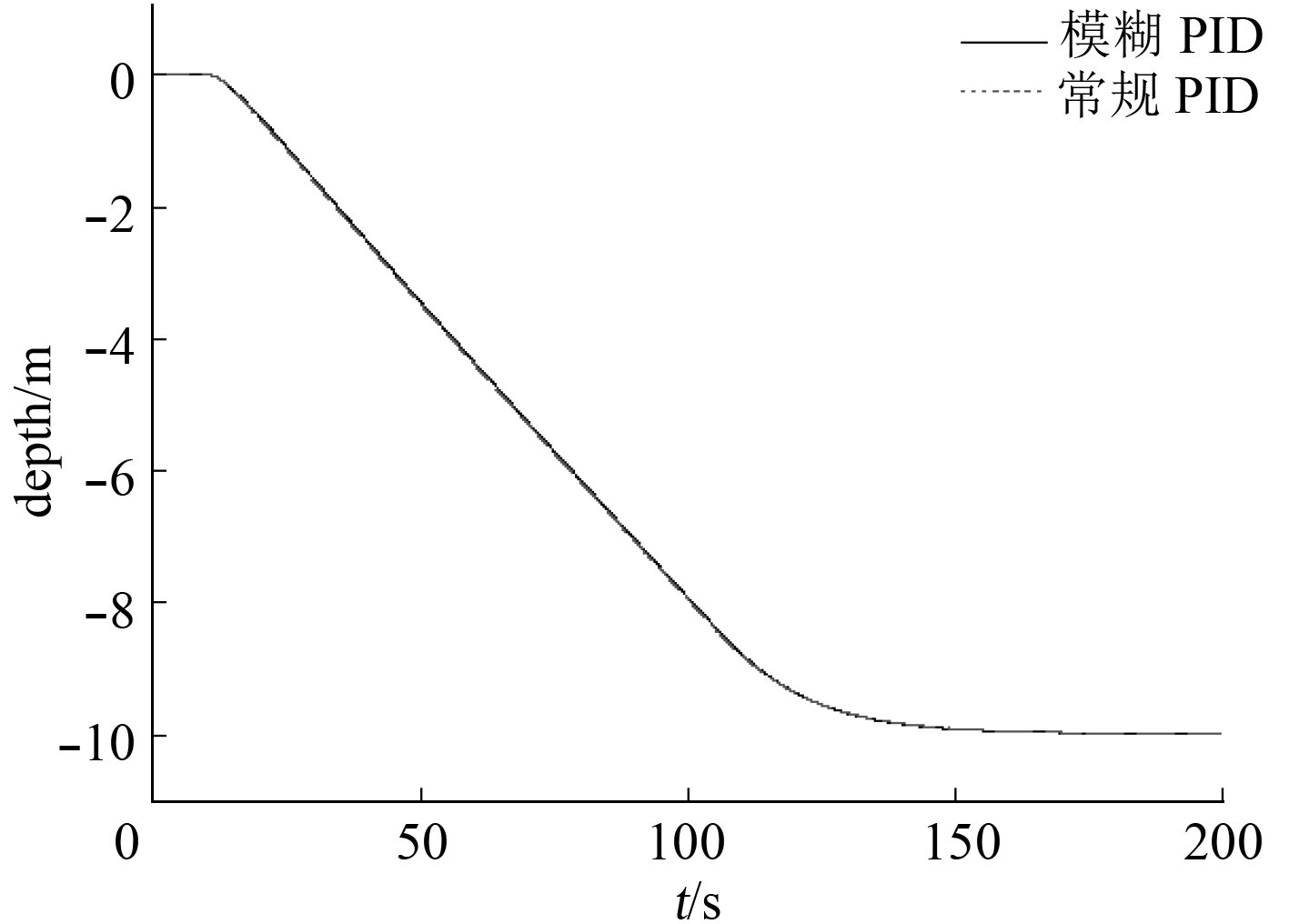
3.2 仿真结果与分析阶跃响应深度控制仿真曲线如图5所示。可以看出,2种控制器的深度响应曲线基本重合,深度控制平稳无超调,稳态无差,且深度变化非常缓慢,天向速度Vy不超过0.1 m/s(见图6)。可见首尾平行操舵模式适用于对纵平面机动性要求较低的UUV,或者是作为首尾相对操舵模式的补充,仅在对姿态平衡性有特殊要求的场合采用。
|
图 5 深度控制响应曲线 Fig. 5 Depth response curve |
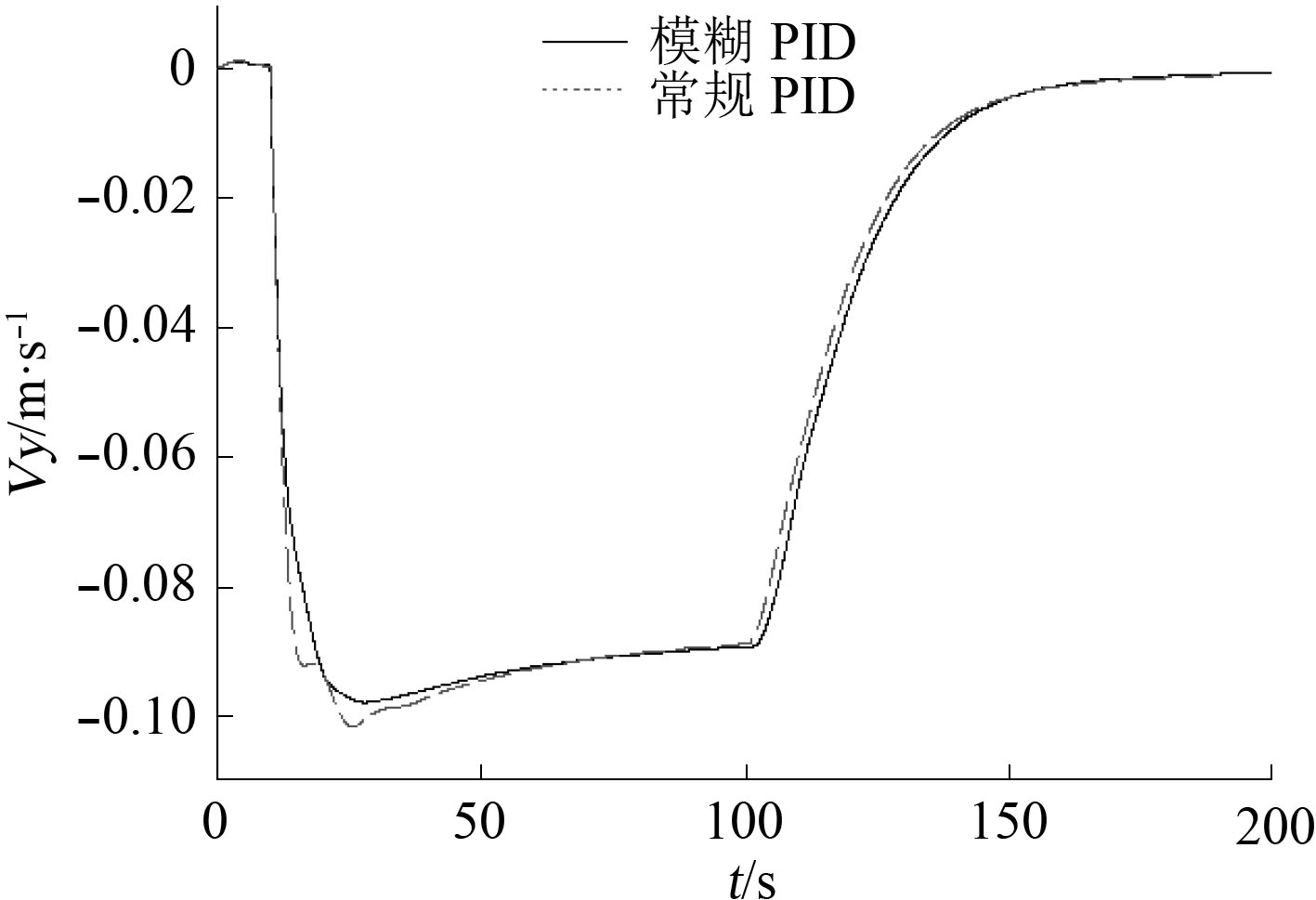
|
图 6 天向速度响应曲线 Fig. 6 Up velocity response curve |
阶跃响应俯仰角控制仿真曲线如图7所示。可知,2种控制器的阶跃响应均实现了微小攻角的爬潜控制。相同条件下,常规PID控制器最大俯仰角约–0.55°,经过一个较明显的震荡周期才进入稳态;模糊PID控制器最大俯仰角约–0.35°,震荡幅值明显减小且更快进入稳态。
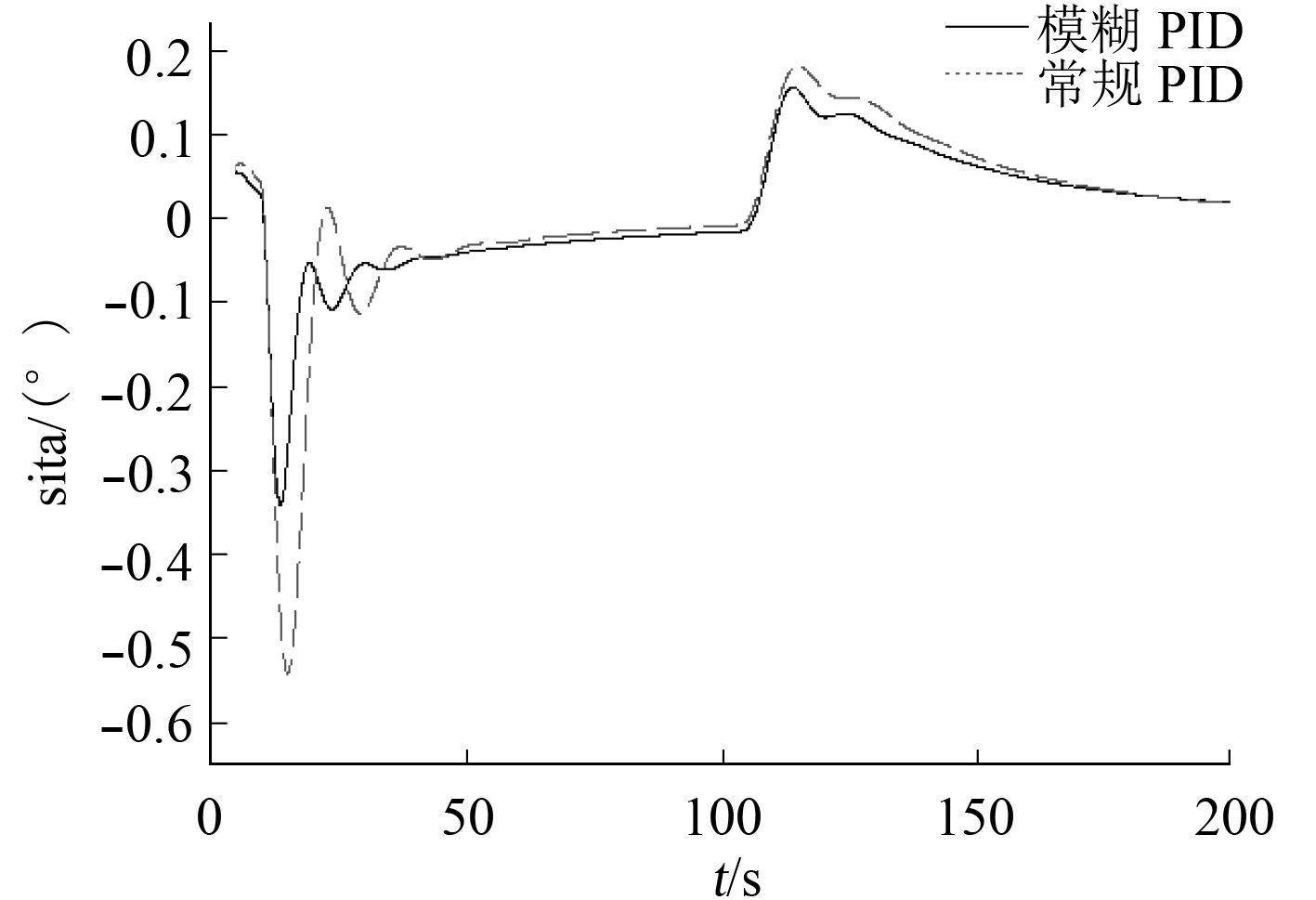
|
图 7 俯仰角响应曲线 Fig. 7 Pitch response curve |
阶跃响应首舵角指令仿真曲线如图8所示。可见,在爬潜的初始阶段,模糊PID控制器的舵角曲线在相位上较常规PID控制器有明显的前移,故对UUV姿态扰动有更好的抑制效果。
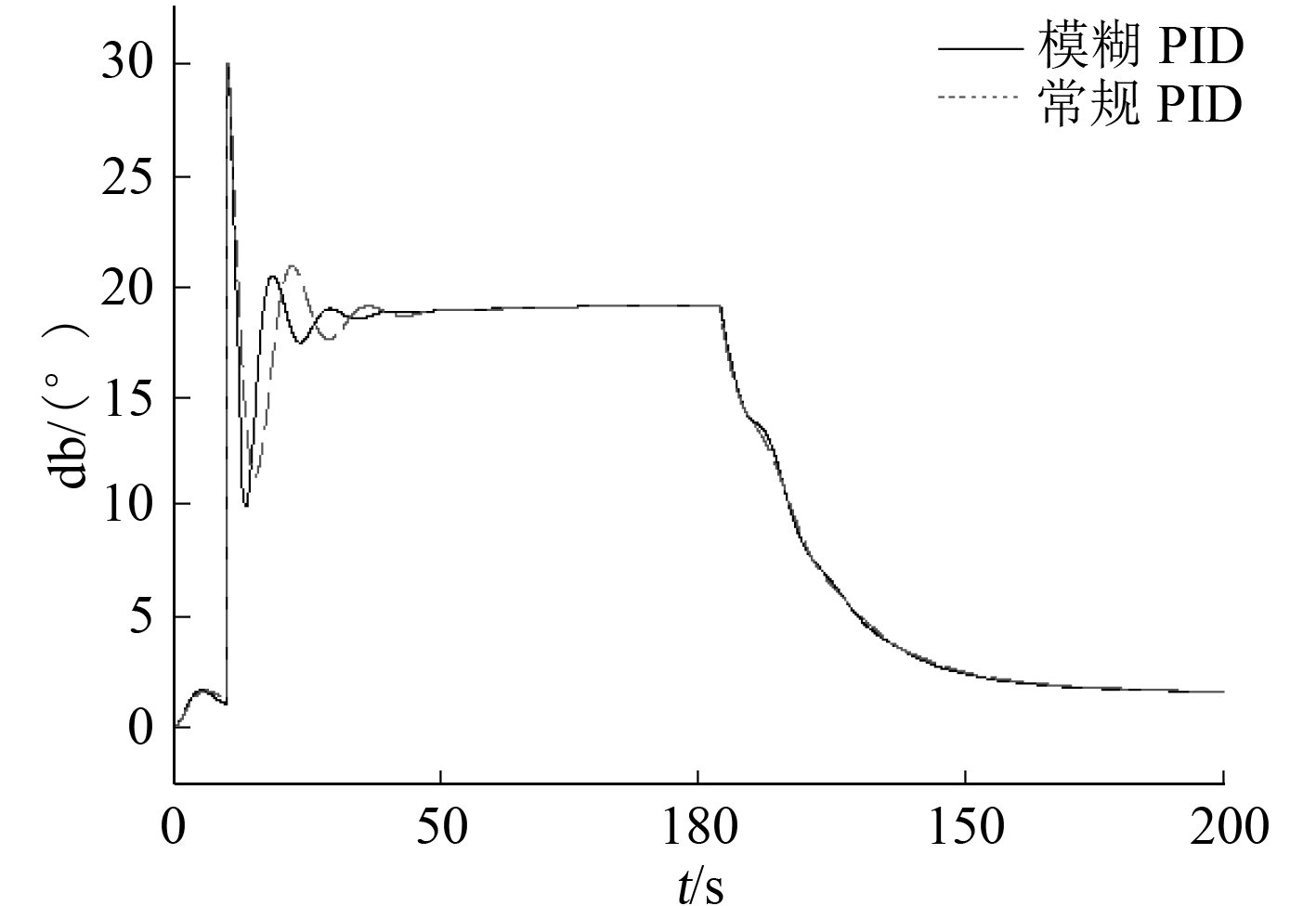
|
图 8 首舵角响应曲线 Fig. 8 bow rudder response curve |
引入模型误差后的俯仰角响应曲线如图9所示。可知,常规PID控制器的最大俯仰角超过–0.9°,而模糊PID控制器的最大俯仰角不到–0.5°。对比图7可知,模糊PID控制器对模型依赖性明显弱于常规PID控制器。
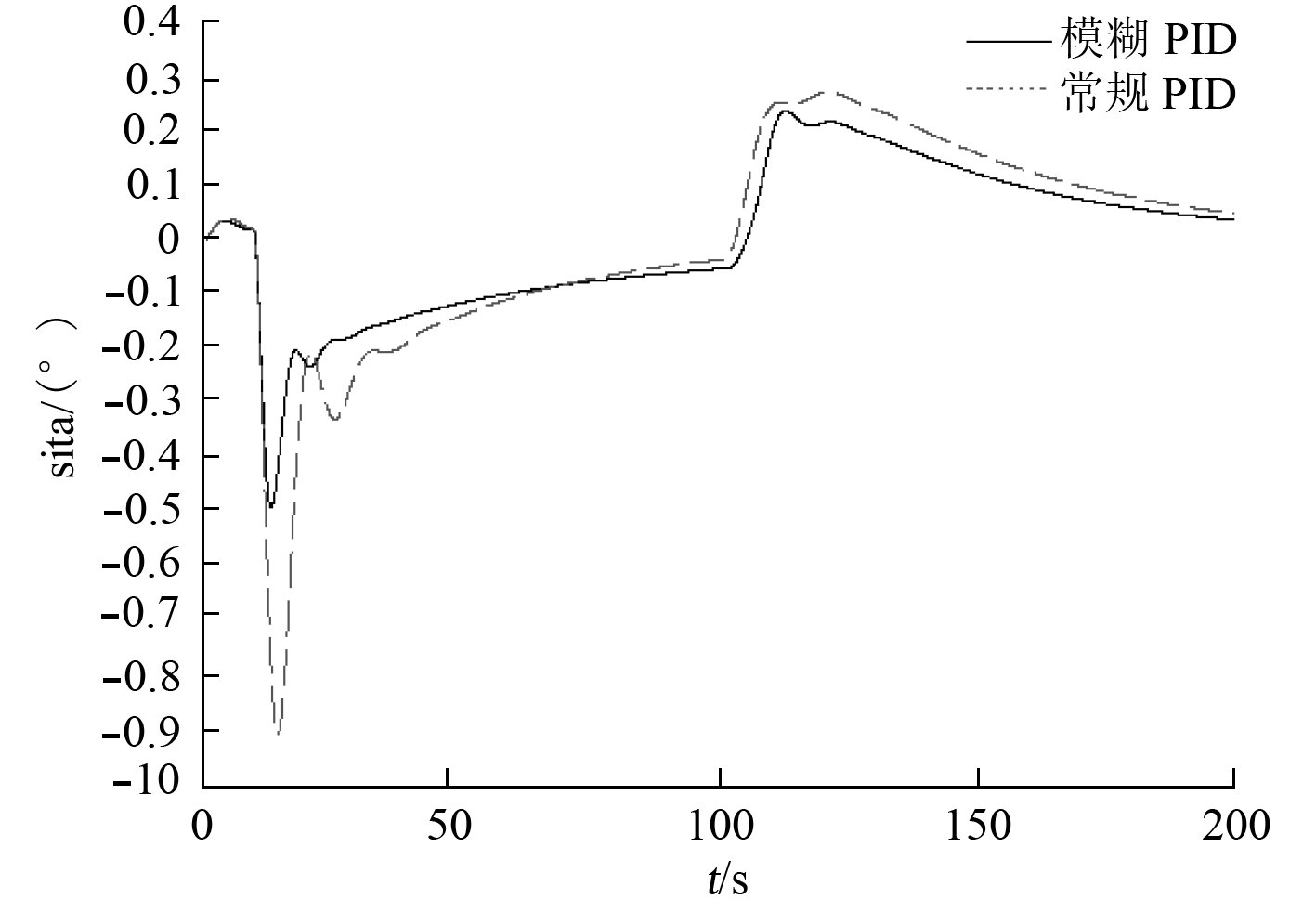
|
图 9 模型误差时的俯仰角响应曲线 Fig. 9 Pitch response curve under model error |
从总体仿真结果看,本文设计的欠驱动UUV首尾平行操舵混合控制器可实现小攻角稳定爬潜控制,且首舵通道采用模糊PID控制器后的性能要优于常规PID控制器。
4 结 语针对某些对姿态有特殊要求的欠驱动UUV,本文设计了首尾平行操舵混合控制器,尾舵通过常规PID控制器实现深度控制,首舵通过基于模糊PID的前馈-反馈复合控制器实现姿态调整。模糊控制器采用Mamdani型控制器,模糊变量的模糊子集均取为7个,隶属函数采用等腰三角形函数。仿真结果表明,本文设计的混合控制系统可实现微小攻角的爬潜控制,控制稳定性好、精度高,具有较好的鲁棒性。
| [1] |
苏玉民, 庞永杰. 潜艇原理[M]. 哈尔滨: 哈尔滨工程大学出版社, 2005.
|
| [2] |
龚时华, 赵先进, 刘明. 低速水下航行器纵平面运动艏艉舵联合控制技术初探[J]. 鱼雷发射技术, 2011, 116(2): 1-5. |
| [3] |
石辛民, 郝整清. 模糊控制及其Matlab仿真[M]. 北京: 清华大学出版社, 2008.
|
| [4] |
刘金琨. 先进PID控制MATLAB仿真(第三版)[M]. 北京: 电子工业出版社, 2014.
|
| [5] |
卢海洋, 林平. 基于模糊PID控制的UUV定深控制系统设计[J]. 重庆理工大学学报(自然科学), 2011, 25(6): 1016-1025. |
| [6] |
李天森. 鱼雷操纵性[M]. 北京: 国防工业出版社, 1999
|
 2019, Vol. 41
2019, Vol. 41
