2. 国防科技大学 装备综合保障技术重点实验室,湖南 长沙 410073
2. Laboratory of Science and Technology on Integrated Logistics Support, National University of Defense Technology, Changsha 410073, China
低频噪声由于传播距离远、透声能力强,会对人们的日常生活以及身体健康造成严重的干扰和影响,因而降噪需求突出。隔声处理是控制低频噪声的有效方法之一。传统的隔声材料在低频段的隔声性能需要遵循质量密度定律,即面密度决定隔声材料的隔声量。增加隔声材料面密度才能提高低频隔声量,由此带来隔声材料重量增加的问题,这也使得传统隔声材料应用受限。因此,探索轻质条件下的低频噪声的隔离技术具有重要的意义。近年来,“声子晶体局域共振板”概念的提出为实现轻质条件下的低频隔声提供了新的理论基础和技术途径。
2011年,法国Oudich等[1]研究了声子晶体板,通过理论分析验证减振特性。随后,国防科技大学机电工程学院肖勇等[2]对集成局域共振单元的薄板结构开展了隔声特性研究,分析了全频带的隔声特性,指出局域共振单元可以打破质量密度定律。辛锋先等[3 – 4]系统研究了简支边界及固支边界型薄板的隔声特性及振动特性。本文通过在简支边界条件的基础上,薄板上集成局域共振单元,采用模态形函数[5],从而求解基板位移,计算得到其隔声量。
据此,本文将以典型的轻质板和局域共振单元为研究对象,开展隔声计算方法、参数分析及实验设计,系统研究并完善局域共振声子晶体板的理论预报方法,加深对其低频隔声机理及特性的认识,并为其在低频降噪工程中的应用设计提供指导,最后通过大量实验验证了声子晶体板的低频隔声特性。本文对边界条件下的薄板隔声理论以及对低频隔声应用转化具有重要的参考意义。
1 数值求解及验证 1.1 模型求解声子晶体薄板由基板和共振单元组成(见图1),基板的弯曲位移可以表示为w(x,y,t),在声场作用下,则动力学响应方程为:

|
图 1 声子晶体板结构示意图 Fig. 1 Schematic of simply supporte locally resonant plate |
| $ \begin{split} & D{\nabla ^4}w + {\rho _s}h\frac{{{\partial ^2}w}}{{\partial {t^2}}} = {{i}}\omega {\rho _0}({\varPhi _1} - {\varPhi _2}) +\\ & \sum\limits_{j = 1}^N {{F_j}\delta (x - {x_j})\delta (y - {y_j})}\text{,} \end{split} $ | (1) |
对斜入射的平面波,其声压速度势为:
| ${\varPhi _1} = {\varPhi _{{{inc}}}} + {\varPhi _{{{ref}}}}\text{,}$ | (2) |
| $ \begin{split} & {\varPhi _{{{inc}}}} = {\varPhi _{{I}}}{e^{ - {{i}}({k_x}x + {k_y}y + {k_z}z - \omega t)}} \text{,} \\ & {\varPhi _{{{ref}}}} = {\varPhi _{{R}}}{e^{ - {{i}}( - {k_x}x - {k_y}y - {k_z}z - \omega t)}} \text{,} \end{split} $ | (3) |
简支边界下板的横向位移可以写为:
| $w(x,y,t) = \sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{\varPsi _{mn}}} } (x,y){p_{mn}}(t)\text{。}$ | (4) |
式中
| $ {\varPsi _{mn}}(x,y) = \sin \left(\frac{{m{\text{π}} x}}{{Lx}}\right)\sin \left(\frac{{n{\text{π}} y}}{{Ly}}\right)\text{,} $ | (5) |
| ${p_{mn}}(t) = {\alpha _{mn}}{e^{{{i}}\omega t}}\text{。}$ | (6) |
式中:αmn为基板弯曲位移的每阶模态系数;ω为角频率。
将基板两侧的声场用基板的位移势函数表示,则基板两侧声场势函数可以表示为[6]:
| $ \begin{split} {\varPhi _1} =& \sum\limits_m^\infty {\sum\limits_n^\infty {{I_{mn}}{\varPsi _{mn}}(x,y){e^{ - {{i}}({k_z}z - \omega t)}}} } + \\ &\sum\limits_m^\infty {\sum\limits_n^\infty {{\beta _{mn}}{\varPsi _{mn}}(x,y){e^{ - {{i}}( - {k_z}z - \omega t)}}} } \text{,} \end{split} $ | (7) |
| ${\varPhi _2} = \sum\limits_m^\infty {\sum\limits_n^\infty {{\xi _{mn}}{\varPsi _{mn}}(x,y){e^{ - {{i}}({k_z}z - \omega t)}}} }\text{。} $ | (8) |
将式(1)化简,方程两边乘以模态函数
得到由MN个方程组成的有限大代数方程组,写成矩阵形式:
| $ \begin{split} &\left\{ {{{\left[ {{{{M}}_{rs}}} \right]}_{MN \times MN}} - \sum\limits_j^N {{{\left[ {{{{R}}_j}} \right]}_{MN \times MN}}} } \right\}{\left\{ {{{{a}}_{rs}}} \right\}_{MN \times 1}} = \\ &{\left\{ {{{{F}}_{rs}}} \right\}_{MN \times 1}}\text{,} \end{split} $ | (9) |
式中相关推导及方程表达式可参考文献[7]。通过式(9)求得每一阶模态系数αrs,再代入式(4),可以求得基板的位移、速度和声压速度势。
1.2 结果分析及验证数值计算时,声波垂直入射(θ=0,φ=0),Lx=Ly=0.06 m,h=0.000 5 m,Nx=Ny=1,fobj=610 Hz,μ=0.2。铝板参数:ρs=2 700 kg/m3,E=70 GPa,υ=0.3,η=0.005,ρ0=2 700 kg/m3,c0=343 m/s,ФI=1 Pa。
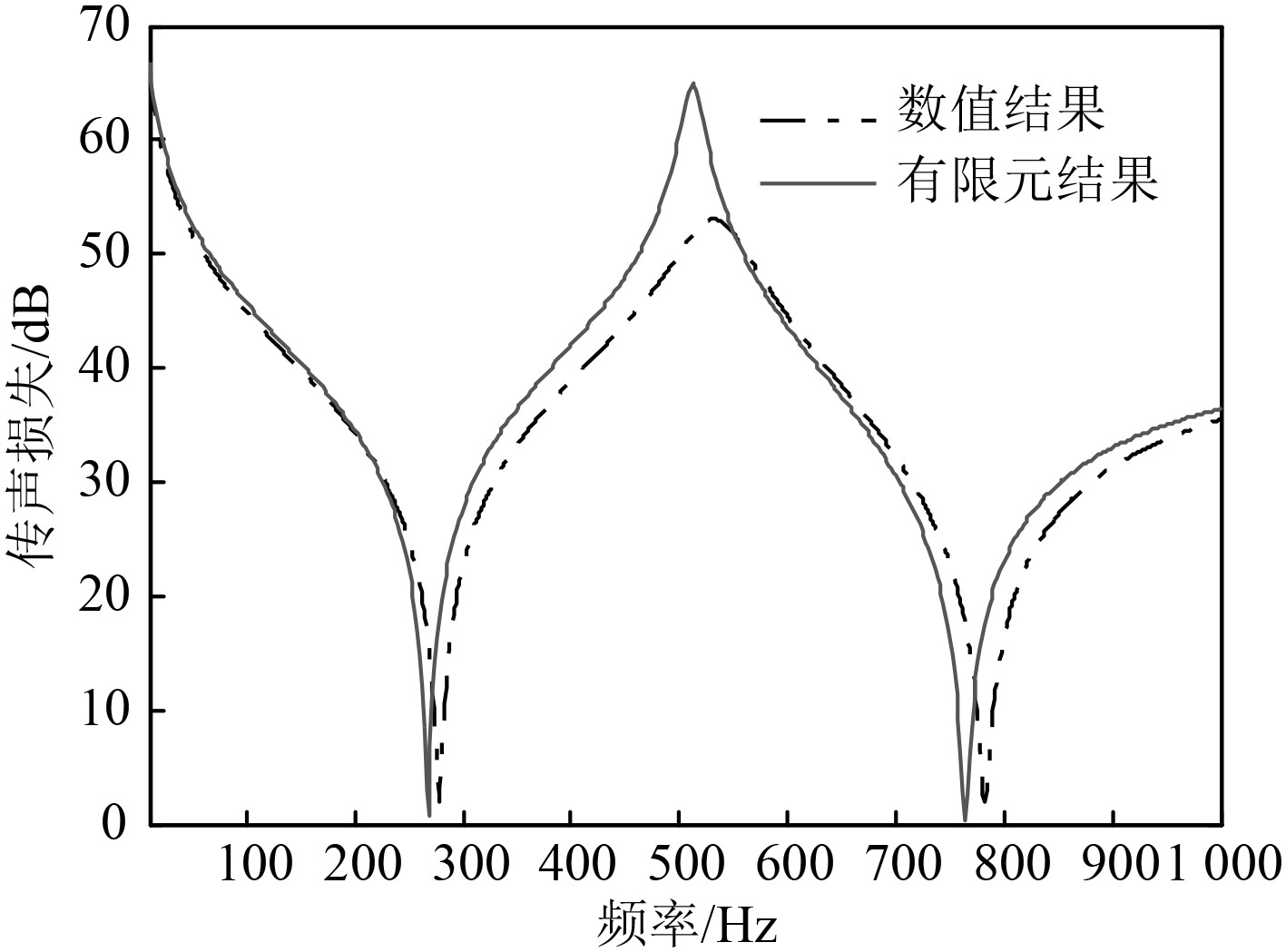
根据收敛理论,如果给定的数值结果在某一频率下收敛,那么针对该算例的结果可以根据收敛特性,判断出对于低于该给定频率的所有数值计算结果都收敛[8]。图2所示结果表明:计算频率低于10 kHz时,当指标M和N大于10时,传声损失结果收敛。由图3可知,有限元计算曲线与数值结果预测曲线基本一致,都能准确地预测隔声峰值和谷值。

|
图 2 传声损失的收敛性(f=10 kHz) Fig. 2 The convergence for STL (f=10 kHz) |
|
图 3 结果对比(μ=0.20,fobj=610 Hz) Fig. 3 Results comparison (μ=0.20,fobj=610 Hz) |
数值计算时,Lx=Ly=0.06 m,h=0.001 m,μ=0.2,fobj=300 Hz。由图4可知,振子固有频率处板的传声损失峰随着振子数目N的增大而在逐渐增大,一定程度后趋于收敛。考虑到波在板中的弯曲波波数[9]

|
图 4 不同振子数N下的传声损失 Fig. 4 STL under different number of local resonators |
| ${k_f} = {\left( {\frac{{{\rho _s}h{\omega ^2}}}{D}} \right)^{\frac{1}{4}}}\text{,}$ | (10) |
结合式(10)可知,当Nx=Ny=3时,计算算例中的弯曲波长约等于局域振子之间的间隔Δx;当Nx=Ny=6时,弯曲波的半个波长等于局域振子之间的间隔Δx;当Nx=Ny=12时,弯曲波的1/4波长等于局域振子之间的间隔Δx;当Nx=Ny=24时,弯曲波的1/8波长等于局域振子之间的间隔Δx。
根据弯曲波的波长与局域振子之间的间隔的相关关系,可判断:当振子之间的间隔减小,声子晶体板的隔声峰将向设计的固有频率靠近,隔声峰数值大小进一步趋于收敛,在此基础上再继续减小振子之间的间隔,峰值处隔声性能趋于稳定(Nx=Ny=30)。综上可知,如果固定基板的参数和振子的附加质量,在某一振子共振频率下,通过选择合适的振子数目,可以得到理想频率处的隔声性能。
2.2 实验测试实际应用中,主要关心材料的隔声量大小,隔声量越大,意味着材料的隔声性能越好。为此,需要在一个标准统一的环境中,采取标准统一的测量方法进行测量,这样才能使结果具有实际意义。
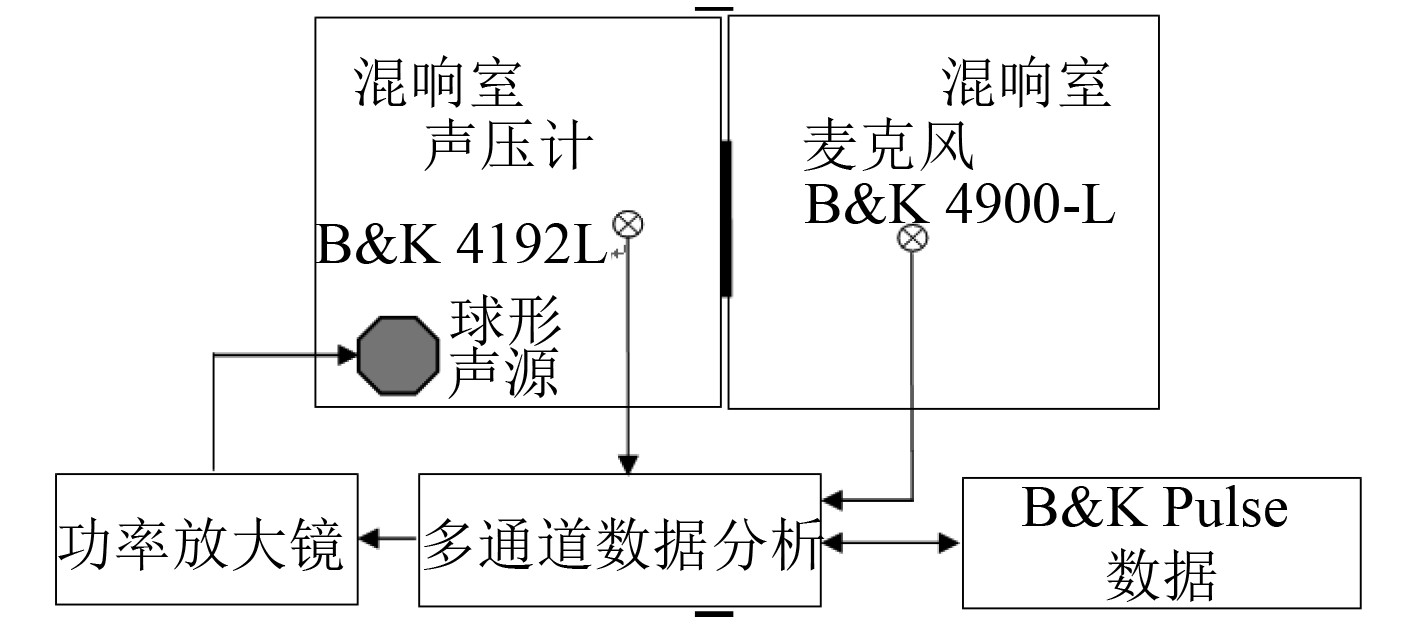
隔声实验室包括发声室和接受室,如图5所示均由混响室构成,测试样件安装在2个混响室的中间。其中球形声源采用白噪声激励,通过多通道的实验测试系统来分析实验数据。本文的局域共振结构参考文献[10]中的梁片结构,将梁片共振频率设计到300 Hz附近,具体的声子晶体板样件如图6所示。

|
图 6 声子晶体板样件 Fig. 6 Experimental specimen of locally resonant phononic plate |
|
图 5 隔声实验示意图 Fig. 5 Schematic of sound transmission test |
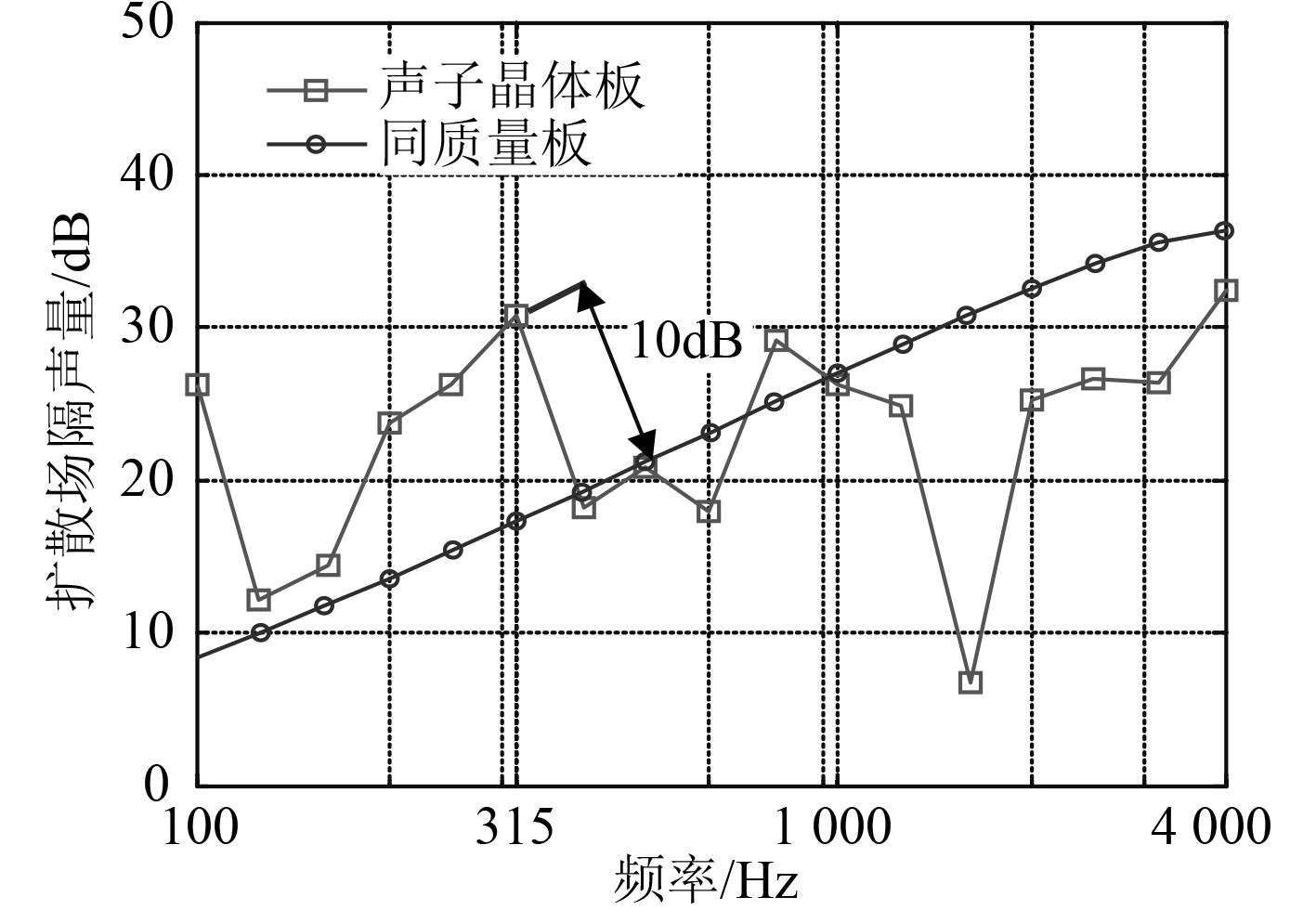
实验测试按照GB/T 19889.3-2005的测试方法,测试结果如图7所示。可知,在设计低频处(约315 Hz)声子晶体板的隔声量比同质量板高10 dB,实验再一次验证了2.1节中的低频隔声特性。
|
图 7 实验测试结果 Fig. 7 Measured frequency response function of STL |
本文基于系统研究了简支边界条件下声子晶体薄板的低频隔声特性。通过引入有限元仿真计算,验证了数值结果的有效性,进一步分析了振子数目对声子晶体板的隔声性能影响规律。最后通过大样实验验证了声子晶体板得低频隔声特性。研究表明:通过调节振子数目、振子共振频率,可以实现声子晶体板在设计频率处的低频隔声性能,无限制的增多数目并不能带来预期的效益,隔声峰数值收敛条件下的振子数目为最佳。声子晶体低频隔声薄板的设计理念为轻质薄板隔声设计提供了一种有效、实用的方法。总之,结合本文方法,根据实际板结构的边界约束条件,可以开展针对性设计,自主调节声子晶体板结构参数,实现板结构的轻质低频隔声。
| [1] |
OUDICH M, SENESI M, ASSOUAR B M, et al. Experimental evidence of locally resonant sonic band gap in two-dimentionalphononic stubbed plates[J]. Physics Review B, 2011, 84(16): 165163. |
| [2] |
XIAO Y, WEN J, WEN X. Sound transmission loss of metamaterial-based thin plates with multiple subwavelength arrays of attached resonators[J]. Journal of Sound and Vibration, 2012, 331(2012): 5408-5423. |
| [3] |
XIN F, LU T. Analytical and experimental investigation on transmission loss of simply supported double panels: Implication of boundary effects[J]. Journal of Vibration and Acoustics, 2009, 124(3): 1506-1517. |
| [4] |
XIN F, LU T. Sound transmission through simply supported finite double-panel partitions with enclosed air cavity[J]. Journal of Vibration and Acoustics, 2010, 132: (011008-1). |
| [5] |
KOPMAZ O, TELLI S. Free vibration of rectangular plate carrying a distributed mass[J]. Journal of Sound and Vibration, 2002, 251(1): 39-57. DOI:10.1006/jsvi.2001.3977 |
| [6] |
BERANEK L L. Noise and vibration control[M]. Washington DC: Institute of Noise Control Engineering, 1988: 442–444.
|
| [7] |
张若军, 肖勇, 温激鸿, 等. 四边固支局域共振型板的低频隔声特性研究[J]. 振动工程学报, 2016, 29(5): 906-912. |
| [8] |
LEE J H, KIM J. Analysis of sound transmission through periodically stiffened panels by space-harmonic expansion method[J]. Journal of Sound and Vibration, 2002, 251(2): 349-366. DOI:10.1006/jsvi.2001.4008 |
| [9] |
MIGUEL C, JUNGER, DAVID F. Sound, structures and their interaction[M]. Seconded.London,England: 1Massachusetts Institute of Technology, 1986: 210–211.
|
| [10] |
吴健, 白晓春, 肖勇. 一种多频局域共振型声子晶体板的带隙与减振特性[J]. 物理学报, 2016(5): 905-912. |
 2019, Vol. 41
2019, Vol. 41
