随着全球变暖和北极冰层逐渐减少,冰区航行船舶开始引起人们的更多关注。与传统航线相比,北极航线将大大缩减航程,节能减排并降低航运成本[1]。据有关方面预测,到2020年,北极东北航道的过境货运量将增至5000万吨。未来随着北极航道的逐步发展,大量货物将通过该航线运输,这将催生更多的极地船舶订单。目前国外对冰区/极地航行船有大量设计和研究经验,而我国对极地船舶的设计和研究还处于起步阶段[2]。
国内外已有较多学者对船体冰区加强结构的承载能力展开研究。Kwon等[3]基于弹性理论研究在船-冰相互作用工况下LNG船的结构强度。ABS的WANG等[4]根据FSICR规范研究了在冰载荷作用下冰带舷侧结构的强度和刚度,重点研究舷侧外板和肋骨的塑性变形以及舷侧纵桁的屈曲强度。Dolny等[5]分析了不同骨架型式船舶在冰压下的结构强度,结果表明纵骨架式船舶的结构强度优于混合架式和横骨架式。徐栋[6]通过引入塑性方程并结合极限载荷准则,提出了冰载荷作用下船体板强度校核的快速方法。
极地运输船因其载荷环境的特殊性,满足冰区加强要求必然带来船体结构重量的大幅增加,但同时载重量和运营经济性的指标又必须兼顾考虑。如何平衡二者之间的内在矛盾,在确保冰带结构安全的同时,尽量缩减结构重量以降低建造/营运成本,是此类船型结构设计的重中之重。
本文以中国船舶及海洋工程设计研究院(MARIC)正在研发的某20 000吨级PC5级极地多用途运输船为研究对象,基于规范设计载荷及相应计算工况要求,集成Isight/Nastran,对货舱区中部冰带舷侧骨架系统进行优化设计。通过多方案的优化与对比分析,得出适用目标船型的冰带骨架系统设计方案,在保证结构安全的前提下,实现了相应区域船体冰带结构的适度减重设计,对相关船型开发工作起到了有力的支撑作用,所采用优化思路、流程及所得出结论也可供同类型船设计参考。
1 舷侧冰带结构校核 1.1 有限元模型基于目标船型结构设计,建立由舷侧外板、内壳纵舱壁、肋板、平台甲板、舷侧肋骨和舷侧纵桁组成的冰带结构计算模型。肋距800 mm,每1/2肋距设一冰带肋骨,肋骨尺寸为HP300x13DH36;强框间距设为2 400 mm;平台甲板间设置一道冰带纵桁,纵桁尺寸为T600x18/150x25DH36。
模型范围为沿船长方向取货舱区的平行中体(模型长度为19.2 m),船宽方向从外板至内壳板,吃水方向从内底板至最顶端,如图1所示。其中肋骨的腹板、纵桁腹板与面板以及其他板均采用2D-Shell单元模拟,肋骨面板和其他次要骨材采用1D-Beam单元模拟,网格单元大小为200×200 mm。冰带构件腐蚀余量依据IACS URI2相关规定扣除,冰带加强结构局部模型见图2。

|
图 1 货舱区舷侧结构有限元模型 Fig. 1 The FEM model of side structure in cargo tank area |

|
图 2 冰带结构局部模型 Fig. 2 The local FEM model of ice structure |
边界条件为沿船长方向2个边界处的肋板以及内底板采用简支约束,只约束线位移,不约束转动位移。
1.2 冰载荷计算概述目前用于计算冰载荷的方法可分为五类:理论分析法、模型实验法、经验公式估算法、数值仿真法以及实船测量法[7]。到目前为止,还没有一种公认的冰载荷计算方法。若要精确研究冰载荷以及船体在冰压作用下的响应,需准确模拟多种冰的相关特性,例如冰的压溃失效模型、冰的材料特性、船-冰相互作用等。
本文采用经验公式估算法计算冰载荷,即参考Lloyd’s Register入级规范Part8,Cha.2,Sec.10,部分(即IACS URI2)关于多年冰海域航行船舶船体结构加强的要求[8]。其中冰载荷采用虚拟载荷板的方式施加,即施加一定宽度bnb和高度wnb以及设计压力Panb的载荷板,其计算公式如下:
1)总压力
| $ {F_{nb}} = 0.36{C_C} \cdot {D_F}\; {\rm{MN}} \text{,} $ |
式中:CC为压溃失效船级因子;DF为船舶排水量因子,当DF≤CDI时,DF=D0.64;当DF>CDI时,
2)线载荷
| $ {Q_{nb}} = 0.639{\left( {{F_{nb}}} \right)^{0.61}} \cdot {C_D}\;{\rm{MN/m}}\text{。} $ |
式中,CD为载荷板尺寸船级因子。
货舱区设计载荷板的宽度wnb和高度bnb的尺寸如下:
| $ \begin{array}{l} {w_{nb}} = {F_{nb}}/{Q_{nb}}\left( m \right);\\ {b_{nb}} = {w_{nb}}/3.6\left( m \right)\text{。} \end{array} $ |
设计载荷板范围平均压力Panb按下式确定:
| $ P{a_{nb}} = F/\left( {b \cdot w} \right)\;{\rm{MPa} }\text{。} $ |
船体区因子AF反映了对应区域预期承受载荷的相对大小,货舱区冰带区域的设计压力应为:
| $ P = P{a_{nb}} \times AF\text{。} $ |
具体的设计冰载荷通过IACS URI2定义的各浮冰碰擦载荷特征参数逐步确定。规范定义碰擦载荷特征的参数反映在船级因子之中,本船船级为PC5级,实取船体计算因子见表1,计算载荷板参数见表2。
|
|
表 1 冰载荷计算因子 Tab.1 Calculation factor of ice load |
|
|
表 2 载荷板参数 Tab.2 Parameter of load panel |
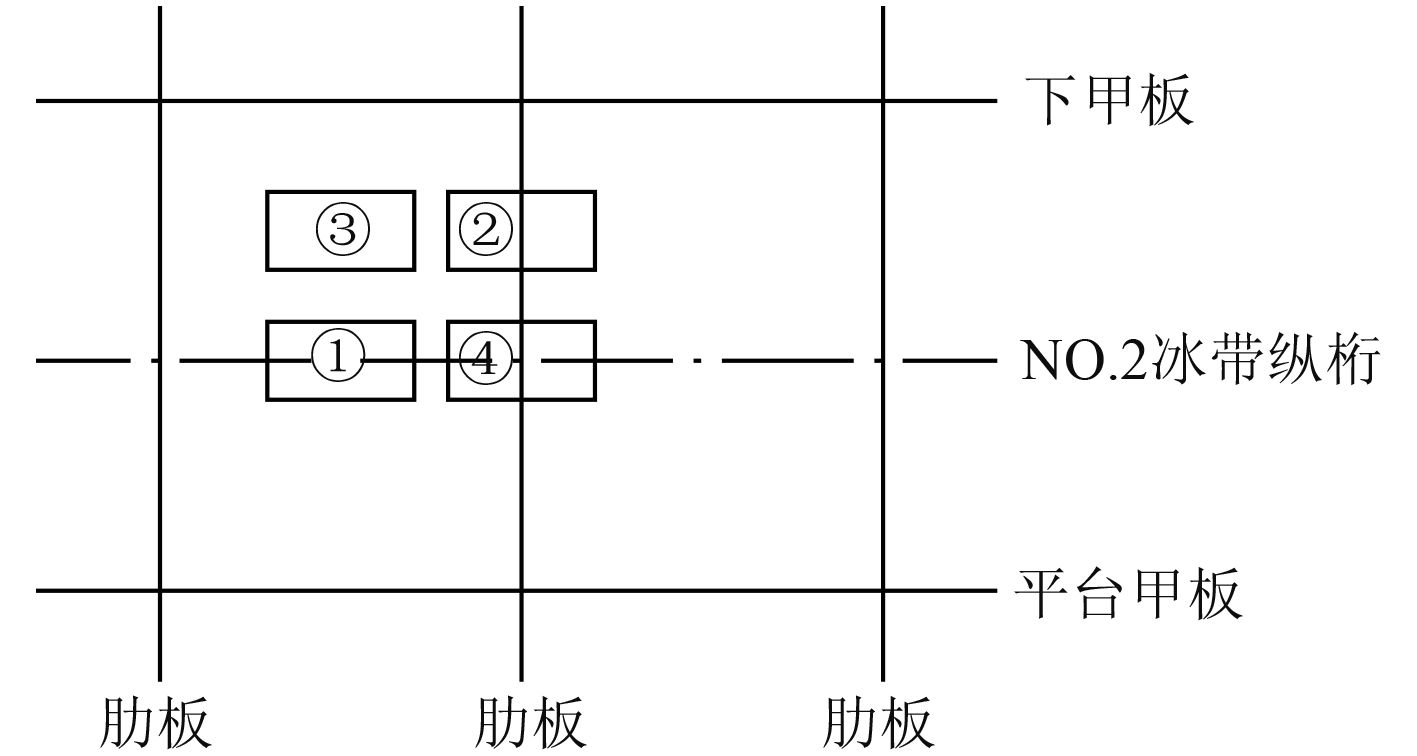
为全面校核舷侧冰带结构主要构件的强度,选取4种工况,即将载荷板施加在4个典型的作用位置上,包括纵桁跨中(LC1)、肋板跨中(LC2)、板格中心(LC3)以及纵横强构件交叉处(LC4),施加位置示意参见图3。
|
图 3 货舱区冰载荷加载示意图 Fig. 3 Scheme of ice load acting on cargo tank area |
本节计算工作目的是校核冰载荷作用下舷侧冰带结构局部强度。因考察区域冰带结构位于船体梁的中和轴附近,总纵应力成分占比较小,与局部冰载相比为一小量,故实际计算过程中总纵影响忽略不计。
考虑到实船项目的应用性与安全性,本计算基于弹性设计的理念,应力衡准参照某PC3级实船项目,各工况下,构件的许用应力不大于材料屈服极限的0.85倍。AH32/DH32钢屈服极限为315 MPa,AH36/DH36钢屈服极限为355 MPa。
1.4 分析结果在冰载荷作用下,4种典型工况的计算结果,包括最大合成应力以及最大变形如表3所示。
|
|
表 3 四种典型工况的应力与变形结果 Tab.3 The stress and deformation results of four typical condition |
由于工况LC3冰载荷作用在外板板格中央,该处主要由骨架系统弱构件,即冰带肋骨传递冰压,故整体变形量相对最大,为9.37 mm;而工况LC4 冰载荷作用在纵桁与肋板的交界处,通过交叉强构件传递冰压,故变形量最小,为6.93 mm;工况LC1冰载荷作用在纵桁跨中,纵桁为主要承载构件,纵桁端部出现应力集中,最大应力为229 MPa。
所有工况均小于许用应力301 MPa,即便不考虑利用材料的塑性应变强化,在弹性限范围内还存在25%左右的强度储备。结构强度裕量较大,故有必要对该区域冰带结构进行优化设计。
2 多方案优化设计 2.1 优化问题描述针对货舱区舷侧骨架系统布置特点,设定四型骨架系统布置初选方案,分别为平台间设置一道冰带纵桁(强框间距3 200)、两道纵桁(强框间距3 200)、一道纵桁(强框间距2 400)和两道纵桁(强框间距2 400)。针对上述布置方案分别进行优化,得到各方案的对应尺度最优解,再进一步对比分析得出相对最优解。
舷侧冰带结构主要包括舷侧纵桁、冰带肋骨、平台板、肋板(强框)以及舷侧外板。其中外板由IACS URI2横骨架式板厚要求计算决定、冰带肋骨的尺寸主要受限于规范关于有效剪切面积和剖面模数的要求,均不可基于有限元计算结果进行尺寸折减;而肋板和平台板需满足冰压作用下的屈曲要求、深舱构件尺度要求及最小板厚要求,在骨材间距、外载(冰载及深舱压头)一定的前提下,实际已无优化空间。
根据有限元计算验证,可知初选方案冰带肋骨强度储备较为富裕,但系基于规范要求不可折减。其中方案2和方案4设有2道冰带纵桁,跨距减小,故冰带肋骨尺寸可减小至HP280x12AH36。而外板、平台板、内壳纵舱壁等均按照规范要求取定值。
故本文拟选取舷侧冰带纵桁尺度为优化对象,设计变量选取纵桁腹板高度hw,板厚tw以及面板宽度bf、板厚tf。基于Isight优化软件,采用多岛遗传算法(MIGA, Multi-Island Genetic Algorithm),自动调用Patran和Nastran软件,进行模型前后处理及计算校核;反复迭代,搜索寻优,得出相对最优解。
2.2 约束条件1)强度约束
结构最大合成应力不超过许用应力:
| $ \sigma \text{≤} \left[ \sigma \right]\text{。} $ |
式中,[σ]为材料的许用应力
2)屈曲约束
根据ICAS URI2,为了防止在冰压作用下腹板和面板发生局部屈曲,需满足以下约束要求:
| $ \begin{array}{l} \frac{{{h_w}}}{{{t_{wn}}}} \text{≤} \displaystyle\frac{{805}}{{\sqrt {{\sigma _y}} }}\text{,}\\ \frac{{{b_f}}}{{{t_{fn}}}} \text{≤} \displaystyle\frac{{310}}{{\sqrt {{\sigma _y}} }}\text{。} \end{array} $ |
式中:twn为腹板净厚度;tfn为面板净厚度,即扣除腐蚀余量后的厚度,根据规范,腐蚀余量取2.0 mm;σy为钢材的许用应力。
3)其他约束
根据CCS规范和施工要求,腹板高度需满足:
| $ {h_w} \text{≥} 1.6\left( {{h_1} + R} \right)\text{,} $ |
式中:h1为舷侧肋骨高度;R=35 mm为贯穿孔半径。
腹板和面板的面积比应满足:
| $ \frac{{{h_w}\cdot{t_w}}}{{{b_f}\cdot{t_f}}} \text{≥} 1.5\text{。} $ |
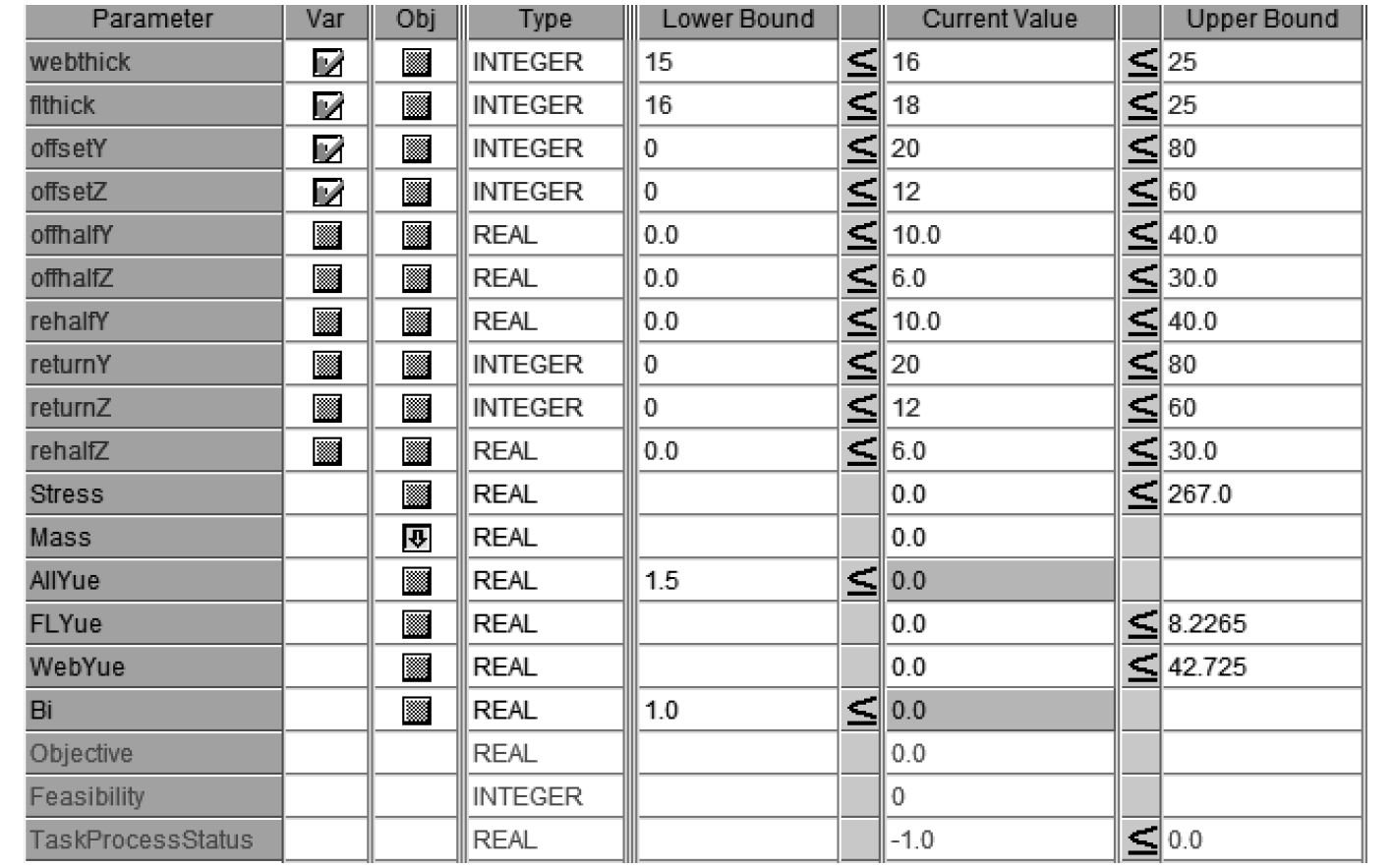
结构优化的目标通常是在一定的约束条件下求解具有最小重量的结构,获得相对最优解。本文以中部冰带骨架系统结构重量最轻为优化目标,各优化参数类型、上下限等参见图4。
|
图 4 优化参数与约束条件 Fig. 4 Parameter and constraints for optimization |
考虑到船厂实际施工/定位方便,实际优化后的冰带纵桁腹板高度取10的倍数,面板宽度取5的倍数,板厚取为整数。
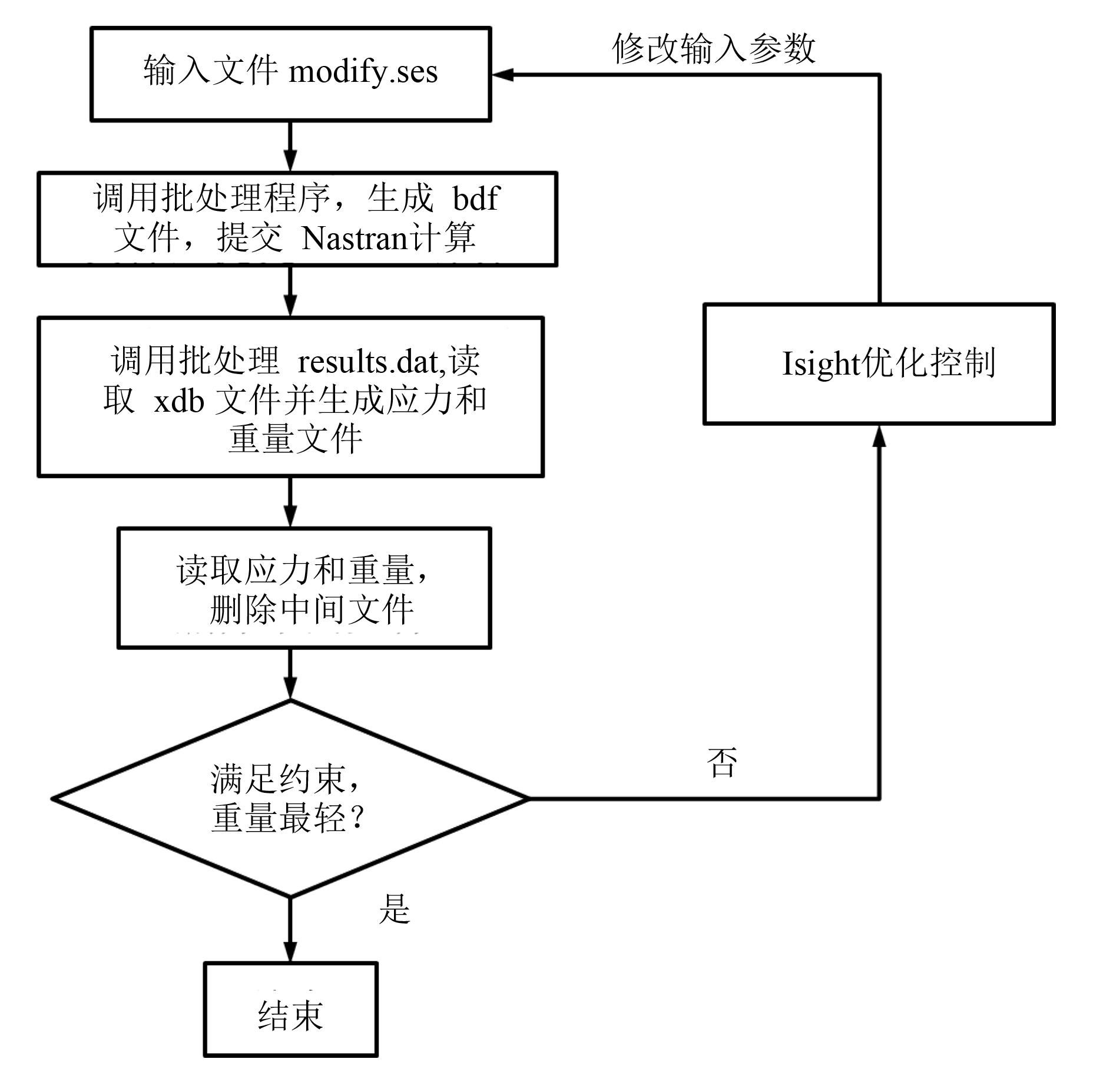
3 优化算法的实现 3.1 优化计算流程简述编写包含修改上述优化参数的输入文件,Isight解析该文件,每次迭代前先修改文件中的输入参数。由批处理命令调用Patran软件输入文件并自动生成计算模型文件,随后提交Nastran计算;通过批处理文件调用Patran读取计算结果文件并提取最大合成应力和相应模型重量;Isight自动解析文件中的应力和重量数据,并删除中间结果文件。Isight分析结果是否满足约束且重量最轻,并重复以上过程进行迭代优化,整个优化流程如图5所示。
|
图 5 优化流程图 Fig. 5 The optimization flow chart |
本文优化采用的多岛遗传算法(MIGA)是在传统遗传算法基础上建立的一种基于群体分组的并行性遗传算法[9]。MIGA将一个大的种群分成若干个子种群(这些子群称之为“岛”),对每个子群中的个体进行传统遗传算法操作(选择、杂交、变异操作)。并且各个“岛屿”间以一定的时间间隔进行“迁移”操作,使各个“岛屿”间进行信息交换,然后继续按照传统遗传算法演化。该算法保证了优化过程中优化解的多样性,从而有效抑制了早熟现象发生,更容易找到全局最优解。图6为多岛遗传算法的流程图。

|
图 6 多岛遗传算法 Fig. 6 Multi-island genetic algorithm |
通过Isight/Nastran程序,不断修改纵桁腹板与面板的尺寸进行有限元校核计算,反复迭代,搜索寻优,使骨架系统在应力满足所设定许用应力衡准的前提下,重量尽可能轻。如图7所示,截取一段在Isight迭代优化过程中各参数的变化情况。

|
图 7 Isight优化过程各参数的变化图 Fig. 7 The variation for various parameters in Isight optimization |
分别建立四型骨架系统布置方案的有限元模型以及优化模型。Isight优化后各方案的最大合成应力云图如图8所示,优化结果汇总如表4所示。

|
图 8 优化后各方案的最大合成应力云图 Fig. 8 The maximum combination stress of each optimization cases |
|
|
表 4 舷侧冰带结构多方案优化对比 Tab.4 The comparison of various optimization cases for ice side structures |
方案1相比原始设计方案,未改变结构布置形式,仅优化了舷侧纵桁的尺寸,优化后的纵桁为T560x16/90x18DH32,优化后骨架系统重量仅减轻1.7%。最大合成应力为263.8 MPa,钢级可从原来的H36钢降档为H32钢,实现了材质选型优化。
方案2相比原始设计方案,增加了一道冰带纵桁,肋骨尺寸可减至HP280x12,优化后舷侧纵桁尺寸为T530x15/90x16DH32。由于增加一道纵桁带来的结构重量增加与结构优化后节省的重量相互抵消,重量几乎没有改变。但是与方案1类似,钢级可选用H32钢,可略减小钢材成本,但相应增加了装配及焊接工作量。总体上看,该方案得不偿失。基于当前船型尺度及较低的冰级(PC5),采用较小的强框间距、加密冰带纵桁的方案适用性不佳。但在首尾冰压相对较大且空间受限区域,尤其是针对PC3及以上高冰级,该思路不失为一种有效解决方案。
方案3采用3 200 mm的强框间距,经过优化后骨架系统减重8.1%,最大应力从229 MPa提升至299.6 MPa,应力增加30%,充分利用了结构的强度储备。本船货舱区总长度约100 m,方案3的优化结果可节省钢材~50 t。这主要归功于方案3强框间距的增加而减少了边舱肋板数量,但同时又不致引起桁材尺度的过度增加,在降低钢材用量的同时,又减小了船厂装配/焊接工作量,可谓一举两得。
方案4采用3 200 mm的强框间距,并增加一道纵桁,肋骨尺寸为HP280x12,优化后舷侧纵桁尺寸为T550x16/140x18DH32。优化后重量减轻6.1%,同时钢材也可采用H32钢,相比原始设计方案施工量几乎没有增加,但是整个货舱区可节省钢材37 t,且减小钢材成本。
综合考虑结构减重、材质以及施工量3个因素,各方案对比如表5所示。
|
|
表 5 各优化方案对比 Tab.5 The comparison between various optimization cases |
因钢级变化(H32,H36)对建造成本影响相对较小,故基于目标船型尺度、冰级而言,方案3(强框间距3 200 mm、单纵桁方案)相对最优。
5 总结与展望本文以中国船舶及海洋工程设计研究院(MARIC)研发的某20 000吨级PC5级极地多用途运输船为目标船型,针对冰载作用下中部舷侧冰带骨架系统进行分级优化设计。通过采用多岛遗传算法(MIGA)分别对四型骨架系统布置方案进行优化,综合评估得出适用于目标船型的相对最优方案,即强框间距3 200 mm、平台间设置单冰带纵桁方案。本文所得出结论有力地指导了目标船型结构设计工作,所总结得出的优化思路、解决途径可进一步扩展应用至高等级极地船型。
本文当前优化工作的主要约束条件系基于弹性准则计算冰载作用下船体结构的局部强度。而实际冰-船作用工况极为复杂,船舶和浮冰之间的碰撞/二次反射碰撞往往会产生局部高应力,此时需进行非线性有限元分析,考虑材料的塑性变形以研究在冰载荷作用下结构的极限强度[10]。另外,对于高冰区等级(PC2、PC3)的极地航行船/破冰船,其冰带结构在规范冰载作用下的响应往往超过材料的弹性限。因此,基于弹塑性理论对极地船型冰带结构进行优化是后续研究的重要发展方向。
| [1] |
吴刚, 张东江. 极地船舶技术最新动向[J]. 中国船检, 2015(3): 97-101. DOI:10.3969/j.issn.1009-2005.2015.03.026 |
| [2] |
张健, 韩文栋. 极地破冰船技术现状及我国发展对策[J]. 中国水运(下半月), 2016, 16(5): 47-50. |
| [3] |
KWON J, JEON B, KIM J, et al. Structural integrity assessment of cargo containmentsystems in arctic LNG carriers under ice loads[C]// Arctic Shipping Conference, 2008, St. Petersburg, Russia.
|
| [4] |
WANG G, BASU R, CHAVDA D, et al. Rationalization of design ofside structure of ice strengthened tankers[C]// International Journal of Offshore andPolar Engineering, 2005, 15(3): 210–219.
|
| [5] |
DOLNY J, LIU S, WON D, et al. Structural integrity assessment for a Polar Class arctictanker under ice loads[C]// ICETECH. 2010, Alaska, USA.
|
| [6] |
徐栋, 载荷作用下极区船舶强度校核研究[D]. 上海: 上海交通大学, 2014.
|
| [7] |
田喜民, 邹早建, 纪均, 等. 冰区航行船舶冰载荷研究发展综述(英文)[J]. 船舶力学, 2015, 19(3): 337-348. DOI:10.3969/j.issn.1007-7294.2015.03.011 |
| [8] |
Lloyd’s Register Rules and Regulations, 2015, 7.
|
| [9] |
丁泉惠, 王森, 黄修长, 等. 基于有限元法和多岛遗传算法的飞轮结构参数优化设计[J]. 噪声与振动控制, 2016, 36(2): 56-60. |
| [10] |
徐栋, 刘俊, 刘杜文. 冰载荷作用下极区船舶极限载荷准则研究(英文)[J]. 船舶力学, 2014, 18(3): 280-290. DOI:10.3969/j.issn.1007-7294.2014.03.007 |
 2019, Vol. 41
2019, Vol. 41
