2. 武汉理工大学,湖北 武汉 430063
2. Wuhan University of Technology, Wuhan 430063, China
槽道船是20世纪70年代末期由英国Cougar公司研制出的一种高性能艇型。槽道船的主要特征是主船体底部有一条对称于纵中剖面并纵向贯通首尾的槽道。槽道将船体分成左右2个片体,它具有双体船的诸多优点,如甲板面积大、快速性优良、稳性好、抗漂性能好等[1 – 3]。不少学者对该类船型进行研究,例如,邓爱民[4]利用我国船舶标准化委员会制定的稳性计算程序,简单修改源程序,采用组合船的方法,计算该船型的大倾角稳性;Morteza等[5]对槽道型高速滑行艇船型的自动生成进行研究;高扬[6]则完成了对M型高速槽道滑行艇的概念设计工作,而槽道船结构强度方面的研究相对较少。
对于含大开口的槽道船,受到静浮力和波浪载荷的联合作用,槽道的存在也使得结构扭转受力较为复杂。采用铝合金建造的船舶虽然能够使结构具有重量轻、耐腐蚀等优点,但其许用结构应力要比钢制船小,使得船体在外载荷作用下更易于达到许用应力值,也更易出现结构安全问题。因此,对含大开口的槽道型铝合金船进行结构强度计算分析有必要。
本文以某含大开口的槽道型铝合金船为研究对象,首先建立水动力模型,对该船进行水动力分析。然后采用设计波法构造等效设计波,作用于船体结构,并对全船进行结构强度计算及分析。
1 水动力分析某船长23 m,型宽7 m,型深2.7 m,吃水0.995 m,满载排水量58.89 t,主甲板上有一个约10 m×5 m大开口,其典型横剖面如图1所示。全船结构均采用铝合金材料,杨氏模量E=70×109 Pa,泊松比μ=0.33,密度ρ=2.7×10–9 t/mm3 。

|
图 1 典型横剖面图 Fig. 1 Typical cross section |
本文应用SESAM软件系统的WADAM模块来计算船舶主要载荷参数在单位波幅作用下的响应。湿表面模型和质量模型构成了水动力计算模型,通过调整船舶重心使水动力计算模型的排水量和首尾吃水与实船装载状态一致,水动力计算模型如图2所示。

|
图 2 湿表面模型 Fig. 2 Model of wet surface area |
根据《海上高速船入级与建造规范》[7]中4.8.1的要求,应校核总纵强度。而对于各类双体船,不论其尺度,都应校核总横强度和扭转强度。考虑到槽道型船的特殊性,本文也对总横强度和扭转强度进行校核计算。因此计算时分别选取中横剖面的弯矩(总纵弯矩)、中纵剖面的弯矩(总横弯矩)、中横剖面的扭矩(纵向扭矩)、中纵剖面的扭矩(横向扭矩)作为主要控制载荷参数。
在进行水动力分析时,波浪的频率范围按波长与船长比范围的0.2~3选取[8],步长取0.1,共29个。浪向角选取了0°,15°,30°,45°,60°,75°,90°,105°,120°,135°,150°,165°和180°共13个浪向角,并认为长期预报时这13个浪向角的波浪作用在船体上的概率相等。
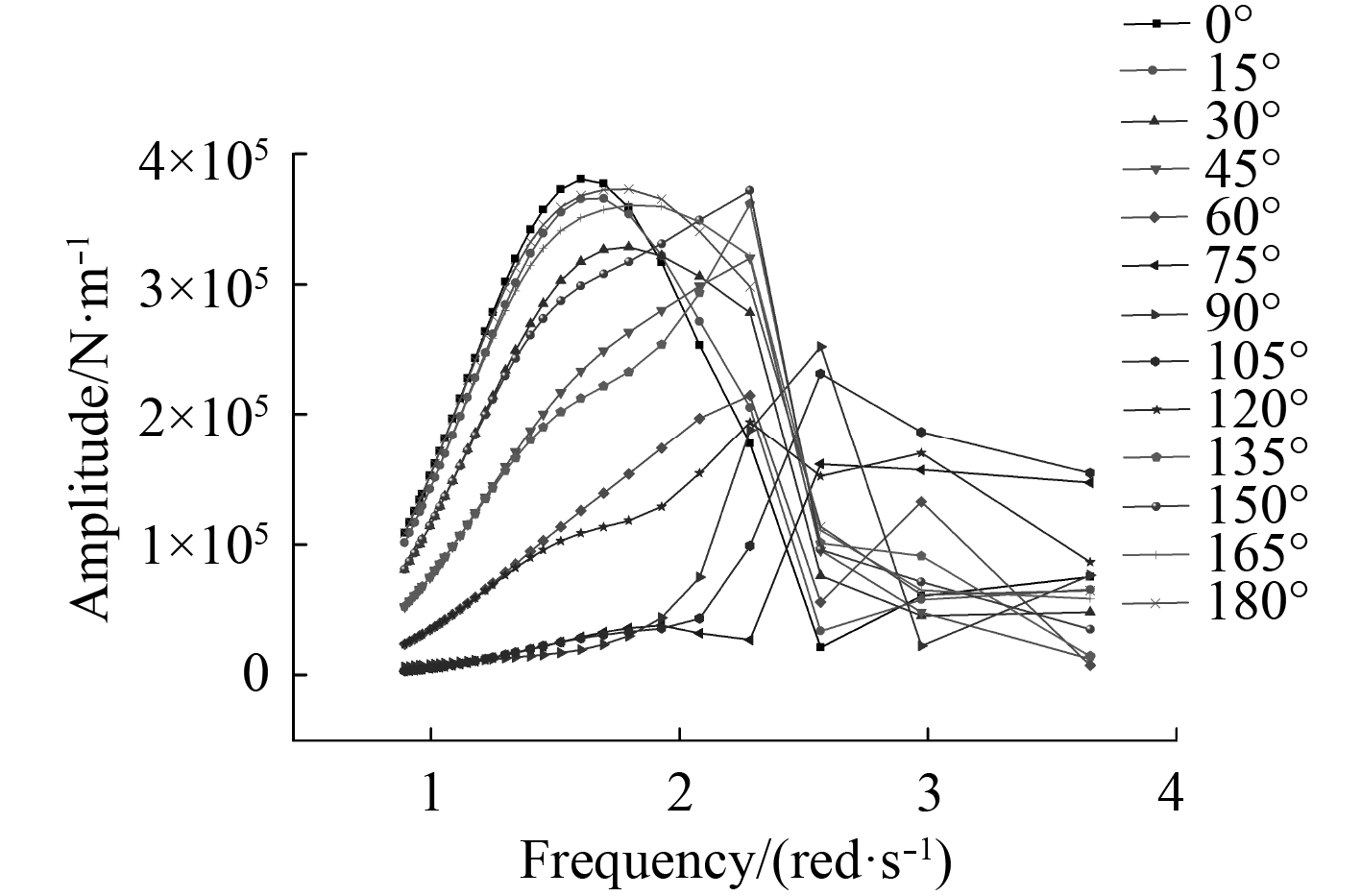
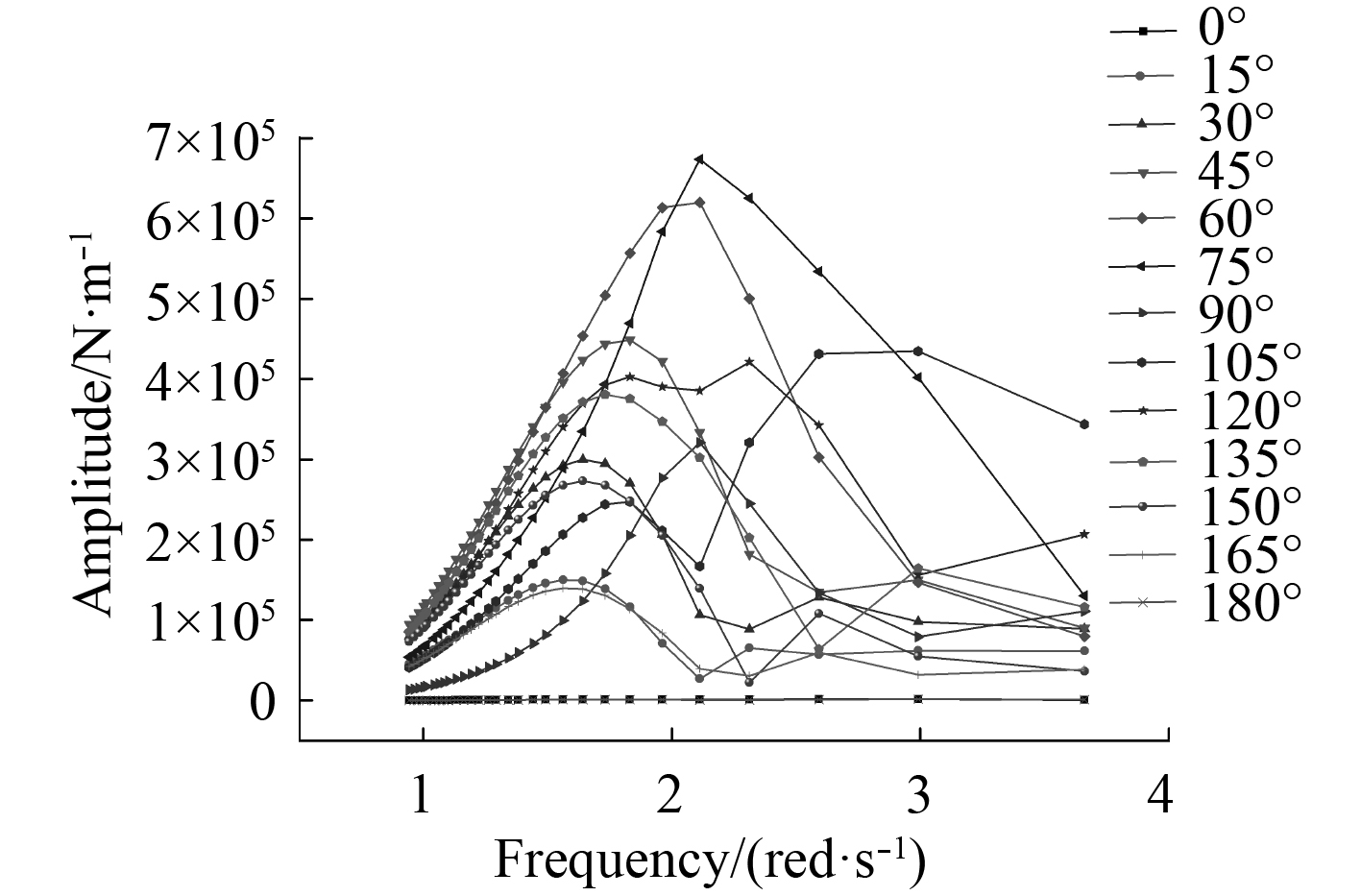
水动力分析得到主要控制载荷参数在单位波高、不同频率、不同浪向角情况下的响应,分别如图3~图6所示。主要载荷参数出现最大值时对应的波浪参数和响应值如表1所示。可以看出,中横剖面弯矩最大值出现在迎浪(0°),中纵剖面弯矩的最大值出现在横浪(90°),与实际情况较为相符。
|
图 3 总纵弯矩响应 Fig. 3 Response of the longitudinal bending moment |

|
图 4 总横弯矩响应 Fig. 4 Response of the transverse moment |

|
图 5 纵向扭矩响应 Fig. 5 Response of the longitudinal torque |
|
图 6 横向扭矩响应 Fig. 6 Response of the transverse torque |
|
|
表 1 主要参数极值下的波浪参数及响应值 Tab.1 Wave parameters and response values when main parameter at extreme point |
根据单位波高下的响应值,结合波浪散布图和功率谱函数,对主要载荷参数进行长期预报。该船主要航行区域为沿海航区,因此采用中国沿海海域波浪散布图。功率谱函数采用P-M谱,即
| $\begin{align} S\left(\omega ,{H_{1/3}},{T_z},\theta \right) = \left\{ \begin{array}{l} \displaystyle\frac{2}{\text{π}}124{H_{1/3}}{T_z}^{ - 4}{\omega ^{ - 5}}\text{,}\\ \exp \left( - \displaystyle\frac{{496}}{{{T_z}^4{\omega ^4}}}\right){\cos ^2}\theta ,\left| \theta \right| \text{≤} \displaystyle\frac{\text{π}}{2}\text{,}\\ {\rm{0,\theta \text{为其他值}}}\text{。} \end{array} \right. \end{align}$ |
式中:ω为波浪圆频率,rad/s;H1/3为有义波高,m;Tz为波浪跨零周期,s;
预报结果如表2所示。其中,通常规定船舶一生遭遇的波浪载荷循环次数n=10–8,按全船设计寿命25年确定重现周期,约与10–8概率水平相对应[9],因此采用直接计算结果中超越概率10–8下预报值列于表2中。
|
|
表 2 满载状态下主要载荷参数长期预报值(kN·m) Tab.2 Long term prediction value of main load parameters under full load condition (kN·m) |
同时,根据《海上高速船入级与建造规范》中4.8节总强度中所提供的公式计算船舶高速航行状态下的波浪引起的总纵弯矩、总横弯矩、横向扭矩及纵向扭矩,计算结果亦列于表2中。通过对比不难看出,规范计算得到的载荷值要比直接计算大很多,这是因为规范考虑了高速冲击的影响。
根据设计波法的思想[8],本文等效设计波的浪向为主要载荷参数的频率响应函数最大值出现时的浪向,等效设计波的波长由频率响应函数达到最大值时的频率确定,等效设计波的波幅由载荷参数在高速航行状态下的规范计算值和频率响应函数的峰值来确定。这样确定能使船舶产生相同弯矩、扭矩的等效设计波,把相对应的设计波载荷施加到船上,通过有限元直接计算得到船舶强度校核结果,并对结果进行分析。
|
|
表 3 等效设计波特征参数 Tab.3 The characteristic parameters of the equivalent design wave |
建立整个主船体范围内的三维全船结构有限元模型,所有船体主要构件,如强框架、甲板室和舷侧结构、首尾结构、机舱结构、横舱壁等都包括在模型内。船舶结构主要由板材和骨架两类构件组成,因此有限元模型中的结构单元的类型主要为板壳单元、梁单元及杆单元等。
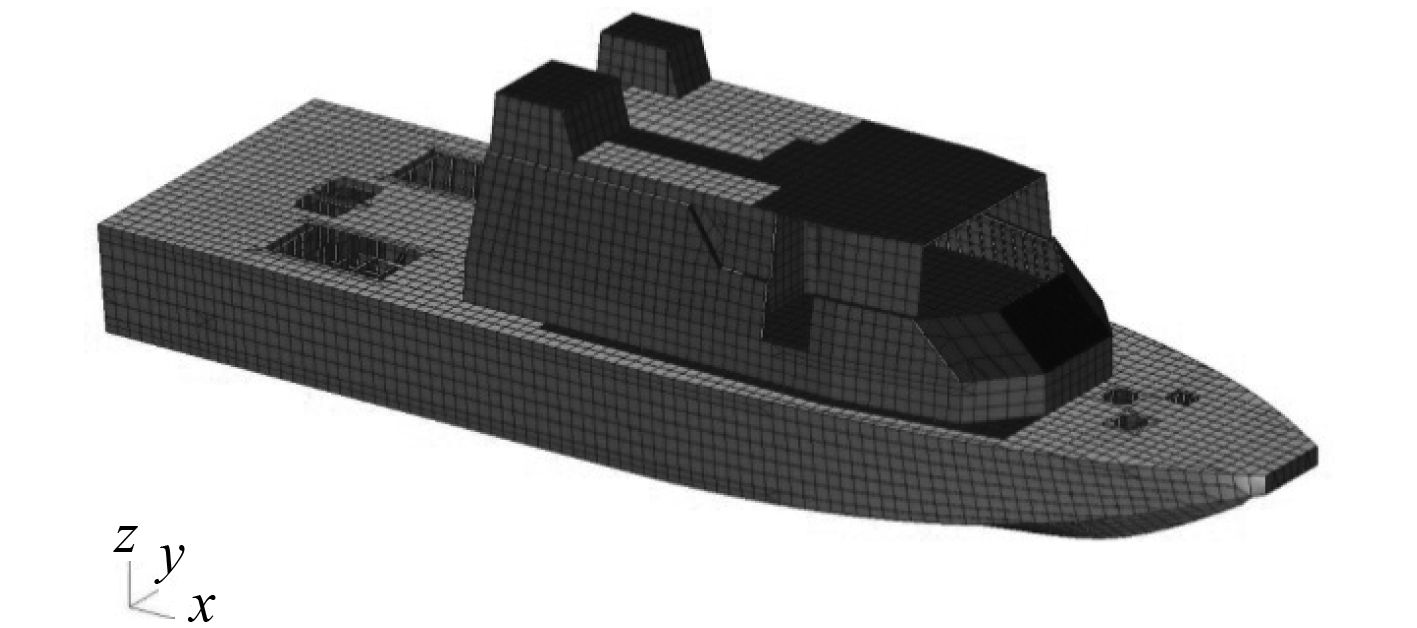
船长方向网格大小为肋距的一半,船宽及型深方向为纵骨间距,有限元模型网格尽可能遵从结构的实际骨材排列方式,以表示出骨材之间的板格的实际几何形状。选择的板单元长宽比应不超过3,在可能产生高应力或高应力梯度的区域,板单元的长宽比应尽可能接近1。整船结构有限元模型如图7所示。模型中共15 253个节点、28 455个单元(其中四边形板单元15 945个,三角形单元921个,梁单元11 589个)。
|
图 7 整船结构有限元模型 Fig. 7 Finite element model of the ship |
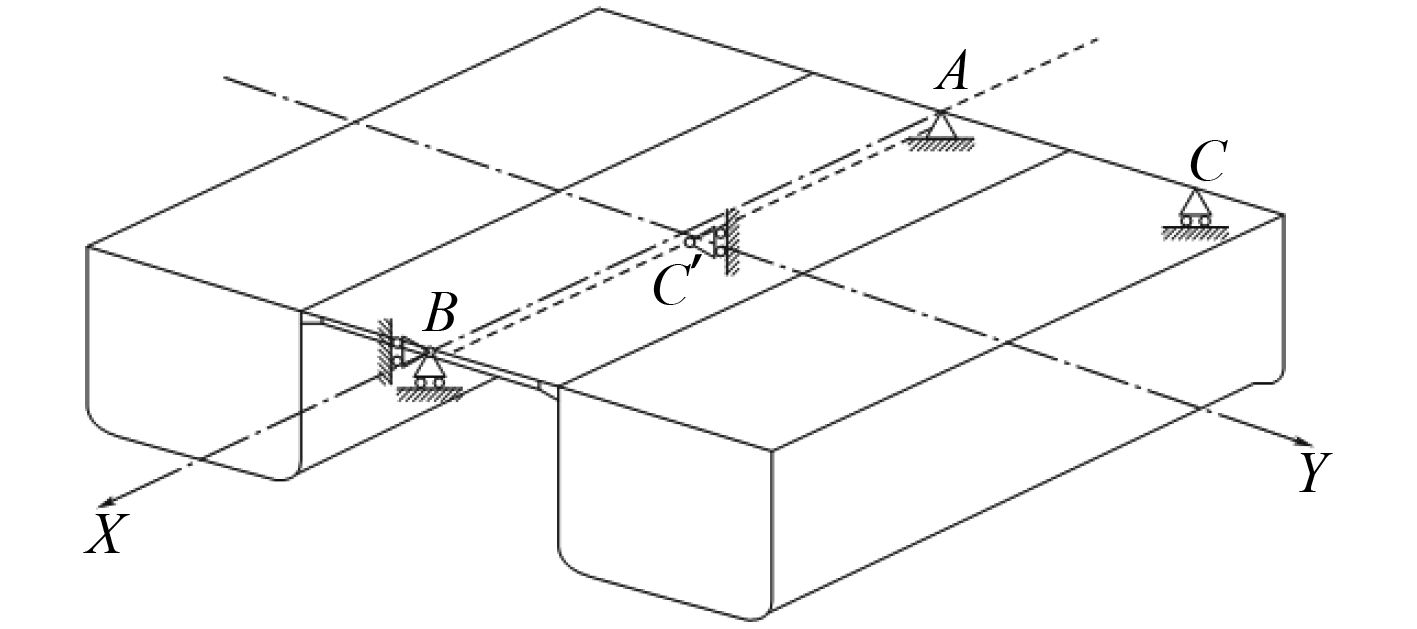
本船船体结构中所有板材及骨材均为铝合金材料,共使用3种型号铝合金材料,分别为5 083,6 082,5 059,并对单元进行赋属性。为了消除刚体位移,在船体的相应节点施加适当的线位移约束。模型约束示意图如图8所示[8]。
|
图 8 模型约束示意图 Fig. 8 Schematic diagram of model constraint |
根据确定的设计波参数,采用SESAM软件系统中的SESTRA子模块对整船结构的应力和变形进行计算,然后再用后处理模块XTRACT对结构应力和变形等计算结果进行显示和分析。
3 结果分析根据《海上高速船入级与建造规范》中的要求,总强度计算的板单元许用应力为0.75倍的焊后屈服强度,许用剪应力为0.41倍焊后屈服强度;梁和杆单元的许用正应力为0.73倍的焊后屈服强度。
经计算,可以得到各个工况下船体结构的应力云图, 船体结构应力最大值及出现的位置如表4所示。其中,总纵弯曲下全船板单元应力云图和梁单元应力云图分别如图9和图10所示。
|
|
表 4 直接计算结果(MPa) Tab.4 The results of direct calculation (MPa) |

|
图 9 总纵弯曲下全船板单元应力云图 Fig. 9 Stress cloud chart of shell elements under longitudinal bending |
|
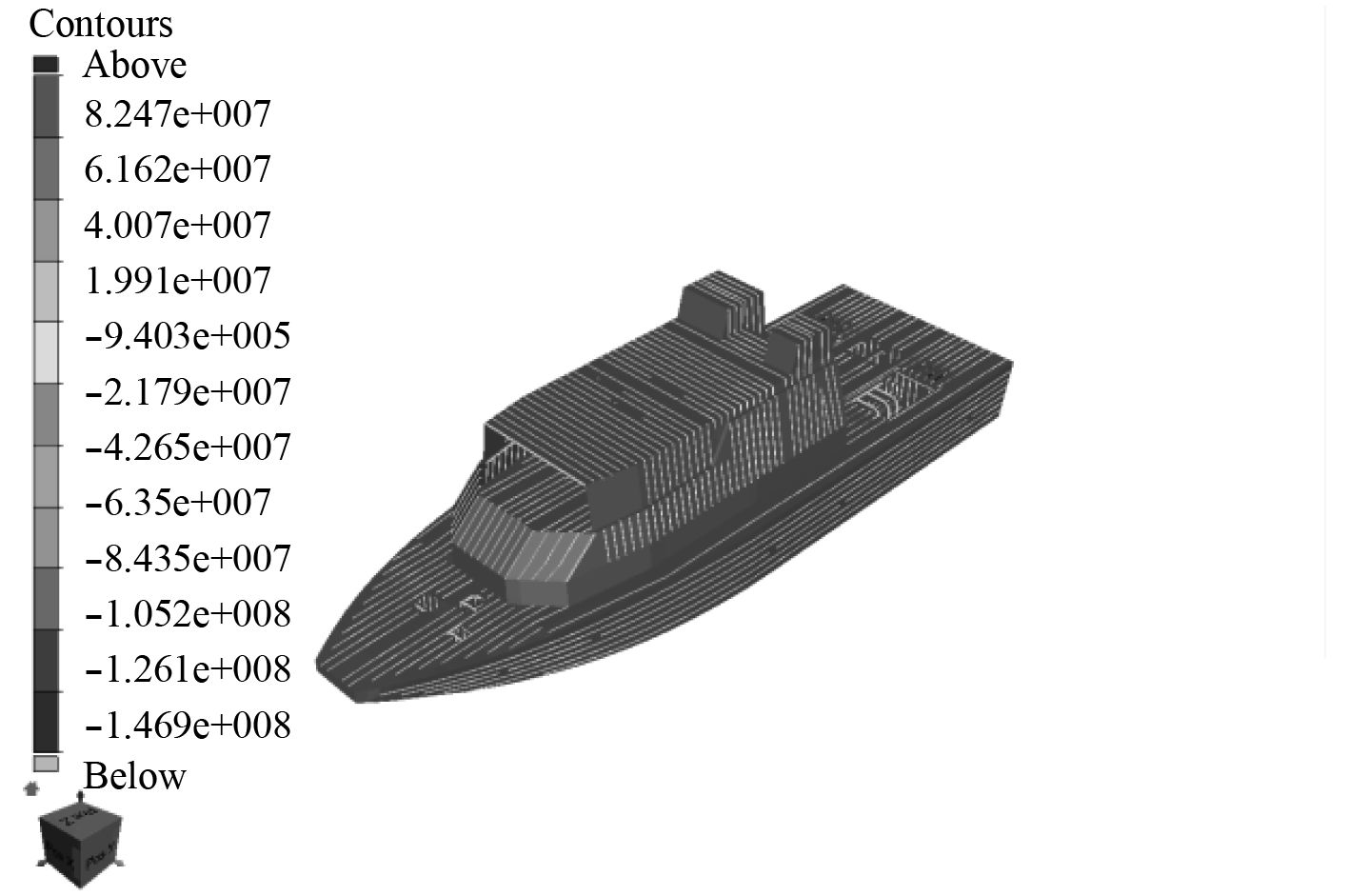
图 10 总纵弯曲下全船梁单元应力云图 Fig. 10 Stress cloud chart of beam elements under longitudinal bending |
从表中结果可以看出,各种工况下,整船板单元等效应力、剪切应力和全船梁单元应力均满足规范对许用应力的要求。
在校核的各工况下,整船应力最大值都发生在主甲板开口角隅处,这是因为该角隅位于主甲板,离中和轴位置较远,其受船体中拱中垂影响较大。而且,主甲板上开口较多,构成开口群,结构不连续,应力集中现象较为明显。因此,虽然开口角隅处应力满足规范要求,但在船体设计制造过程中该处结构应予以关注,必要情况下可做加厚处理。
此外,对比各种工况的计算结果看出,在校核的4个工况下,船舶处于总纵弯曲的设计波下其结构计算所得应力最大,总横弯曲工况下校核结果次之,横扭工况下校核结果最小。波浪冲击力较大,导致总纵弯矩大,从而总纵弯矩下的应力较大;而槽道的存在,使得总横弯矩引起的结构应力较大。扭转载荷下的应力较小,而一般双体船遭受比较大扭转力矩的作用[1],扭转引起的应力较大,这在一定程度上说明槽道船与一般双体船仍有一定的区别。
4 结 语本文以某含大开口的槽道型铝合金船为研究对象,通过水动力分析构造等效设计波,建立全船有限元模型并进行结构强度计算。通过计算,得到如下结论:
1)该槽道型铝合金船在总纵弯矩、总横弯矩、纵向扭矩、横向扭矩的载荷下,全船结构应力小于许用应力值,结构强度满足规范要求。
2)在各工况下,全船应力最大值总出现在主甲板的开口角隅处,且部分应力值接近许用应力值。这是因为主甲板上多处开口构成开口群,应力集中明显,而铝合金船材料的许用应力值较小,因而主甲板上的开口角隅值得关注,必要时需做加强处理。这同时也说明对含大开口的船进行总强度校核非常有必要,与《海上高速船入级与建造规范》中的规定一致。
3)在校核的4个工况下,船舶处于总纵弯曲的设计波下时结构应力最大,总横弯曲工况下的结果次之,横扭工况下的结果最小。这是因为波浪冲击力较大,导致总纵弯矩大,从而总纵弯矩下的应力较大,而槽道的存在,使得总横弯矩引起的结构应力较大。扭矩下的应力较小,表明槽道型船与一般双体船存在一定差别。
| [1] |
郑杰, 谢伟, 骆伟, 等. 穿浪双体船横向强度与扭转强度的有限元计算[J]. 中国舰船研究, 2010, 5(1): 14-18. DOI:10.3969/j.issn.1673-3185.2010.01.004 |
| [2] |
任慧龙, 张清越, 江雪云, 等. 大型小水线面双体船结构强度有限元分析研究[J]. 舰船科学技术, 2015, 37(8): 1-6. DOI:10.3404/j.issn.1672-7649.2015.08.001 |
| [3] |
杨平, 黄乐华. 双体船结构的直接计算分析[J]. 船海工程, 2006, 35(5): 4-7. DOI:10.3963/j.issn.1671-7953.2006.05.002 |
| [4] |
邓爱民. 高性能槽道滑行艇的大倾角稳性计算[J]. 船海工程, 1998(1): 11-12. |
| [5] |
MORTEZA GHASSABZADEH, HASSAN GHASSEMI. Automatic generation of the planning tunnel high speed craft hull form[J]. Journal of Marine Science and Application, 2012. |
| [6] |
高扬. M型高速槽道滑行艇概念设计[D]. 哈尔滨: 哈尔滨工程大学, 2012.
|
| [7] |
中国船级社. 海上高速船入级与建造规范[M]. 北京: 人民交通出版社, 2015.
|
| [8] |
中国船级社. 钢质海船入级与建造规范[M]. 北京: 人民交通出版社, 2005.
|
| [9] |
胡毓仁, 陈伯真. 船舶及海洋工程结构疲劳可靠性分析[M]. 北京: 人民交通出版社, 1996.
|
 2019, Vol. 41
2019, Vol. 41
