0 引　言

随着各国对海洋资源竞争日益激烈，无人水下航行器作为一种海洋开发的重要装备，已成为各国研究机构重要的研究项目。水下无人航行器的广泛应用对于充分利用自然资源，发展国民经济具有十分重要的现实意义，水下无人航行器可以用于科学考察、资源勘探、深海探测、打捞沉船、旅游探险等。在军事上，水下无人航行器可有效执行探测感知、监视侦察、探雷灭雷以及攻击敌舰艇等任务，越来越成为各国水下重要力量。当前水下无人航行器的种类很多，其中遥控式水下航行器（ROV）、无人无缆水下航行器（UUV）、自主式水下航行器（AUV）是3类最重要的水下无人航行器。

由于无人水下航行器（UUV）自身体积小、控制能力弱的特点和水下工作环境恶劣的影响，导致它的机动性、自持力、感知能力和通信能力等较弱，因此必须借助搭载平台（水面舰船、潜艇或海底空间站等）才能发挥其更好的作用。搭载平台回收UUV一直都是技术难题。通常将UUV回收方式分为水面回收和水下回收^[1]2种。水面回收易受海情的影响，而且在执行军事任务时易暴露，而水下回收在水下完成整个对接回收过程，相对于水面回收更隐蔽和安全。水下回收同时可以分为静平台回收和动平台（潜艇为搭载平台）回收。水下动平台回收UUV主要有鱼雷发射管方式、弹道导弹发射管方式、背驼方式和坞载方式^{[2 – 3]}4种。背驼式指在搭载平台（一般是搭载平台背部）安装UUV回收装置，搭载平台在预定航路上处于等速、定深、直航的运动状态，UUV自主按照设定的路径航行靠近，并通过智能自动控制完成与搭载平台对接回收的过程。这种方式在搭载平台与UUV都处于运动状态下完成。背驼方式分为直接驼载和间接驼载，直接驼载指将UUV直接暴露于海水中，间接驼载指将UUV放置在一个专用的耐压装置里，不与海水直接接触^{[4 – 6]}。

UUV回收路径规划是实现搭载平台对UUV回收的重要前提，要求在水下复杂环境下，根据搭载平台的预定航道和运动状态，按照一定的准则，寻找一条从当前状态（包括位置和姿态）到达对接状态的路径。回收路径规划与通常所说的UUV路径规划有很大不同。通常的UUV路径规划是在具有障碍物的环境内，按照一定的评价标准，寻找一条从起始状态到达目标状态的无碰路径^{[7 – 8]}。因此，面向双动平台对接的UUV水下路径规划需要根据搭载平台的运动特征和回收控制要求生成合适的路径。本文基于直接驼载式回收，首先分析水下双动平台对接的整体过程与要求，根据水下双动平台的UUV回收特点，建立水下动平台与UUV回收过程模型，将回收过程分为跟随段、调整段、对接段和回收段；然后根据调整段、对接段的水下导引控制特性，提出UUV对接路径基准轨迹生成模型，建立UUV回收过程调整段、对接段的航路点生成方法，并采用三次插值对航路点进行平滑，生成水下动平台与无人航行器的对接路径，通过案例仿真计算分析，表明提出方法的有效性。

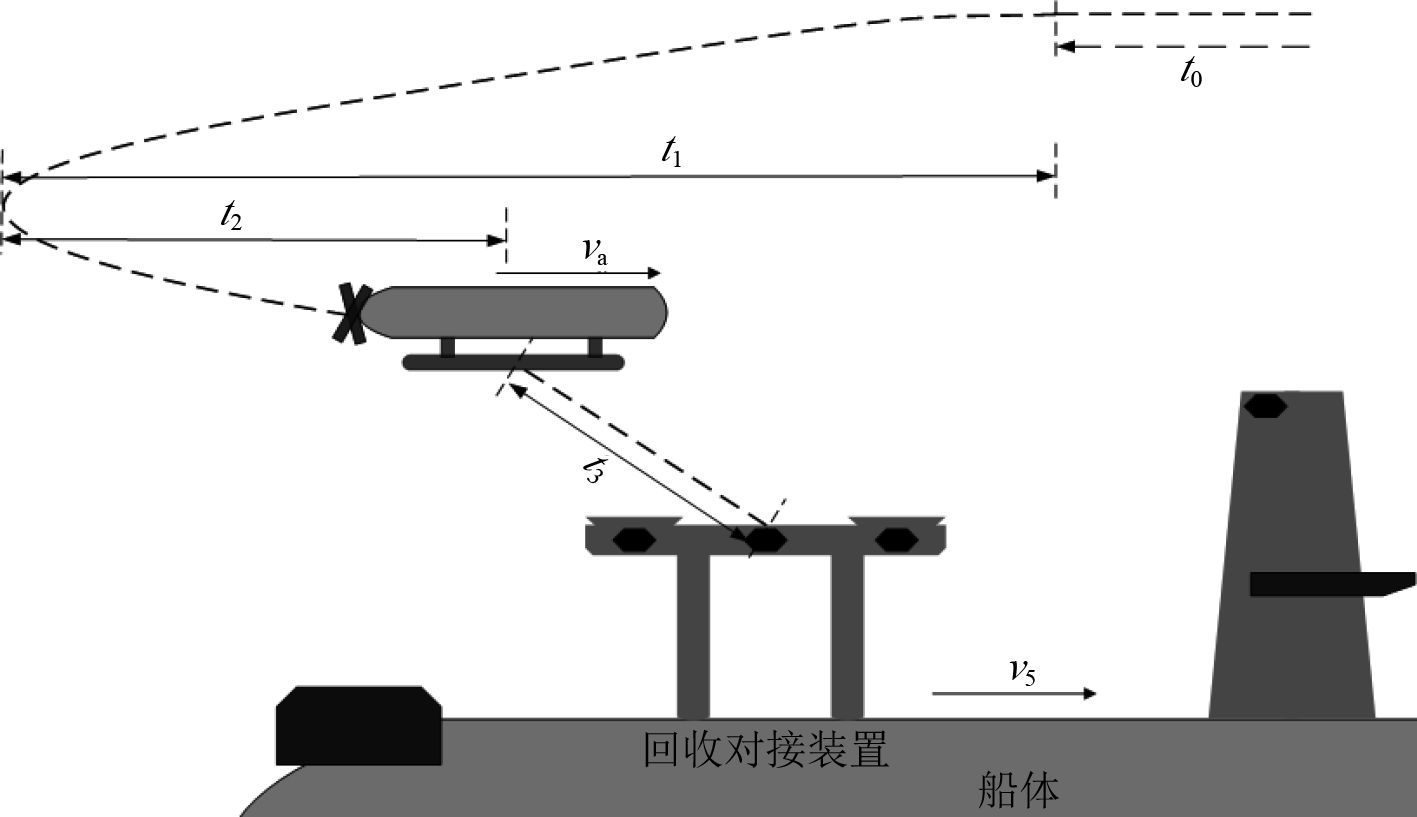
1 基于动平台的UUV回收过程模型

考虑到UUV回收过程中的对接方便性和避碰设计要求，在运动搭载平台后背部设置回收装置，运动搭载平台和UUV共同配合完成回收装置与UUV的精准对接。在回收过程中，UUV航行到距离搭载平台一定范围内时，可通过声光通信、引导系统与搭载平台回收装置实现定位、对接、固定。UUV回收到搭载平台的过程是2个运动平台由远到近直至对接为一体的过程。因此水下动平台与UUV对接过程模型分为跟随段、调整段、对接段和回收段4个阶段（见图1）。

1）跟随段（t₀）是UUV和搭载平台自主航行到汇合区内，UUV稳定跟踪搭载平台的过程。汇合区位置坐标和汇合时间的确定有2种方式，一种是按UUV释放前既定任务规划方案，UUV和搭载平台在指定时间到达指定地点；另一种方式是UUV提前完成作业任务，或搭载平台临时改变作业任务，采用水声通信方式通知UUV在指定时间到达指定地点。到达汇合区后，UUV与搭载平台间通过水声通信建立联系，UUV按照一定的速度和航向稳定跟踪搭载平台，准备进入调整段。

2）调整段（t₁）是UUV自主调整自身姿态和运动状态，形成在搭载平台上方尾随其同向同垂直面航行的过程。在此过程中，搭载平台保持低速、定深、定向的航行工况，UUV利用短基线测量与搭载平台回收装置间的相对距离、角度差、深度差、速度差等，自主控制运动速度和方向航行到搭载平台后上部，并逐渐靠近搭载平台的回收装置，到达视觉导引定位系统的有效工作范围内。

3）对接段（t₂）是UUV自主控制速度、航向和深度下降并靠近回收装置的过程。在此过程中，采用短基线或光学导引定位系统^[8]，通过UUV与回收装置高精度实时定位，调整UUV首向与母艇首向保持一致，同时在垂向上缩小与回收装置的相对距离，实现UUV与回收装置相对静止的运动，并获得2个平台的准确姿态，也就是2个具有三维水下空间的相对位置关系。

4）回收段（t₃）是指利用视觉或光学定位系统在近距离内实现UUV与搭载平台回收装置完成回收与固定的过程。在此过程中，利用光学定位系统引导UUV精确对接，此时UUV首向速度与母艇首向速度保持一致，UUV自主控制垂向速度并克服海流和搭载平台周围水流的影响，做下沉运动，直至UUV与回收装置实现连接与固定，整个对接回收过程结束。

在跟随段UUV的路径规划具有通常所说的路径规划一致的特点，而在回收段主要是实现UUV与回收装置实现连接与固定，并不需要进行复杂路径规划，更多的需要进行下降速度姿态控制和避碰控制。因此，本文重点对调整段和对接段的路径生成进行分析和研究。

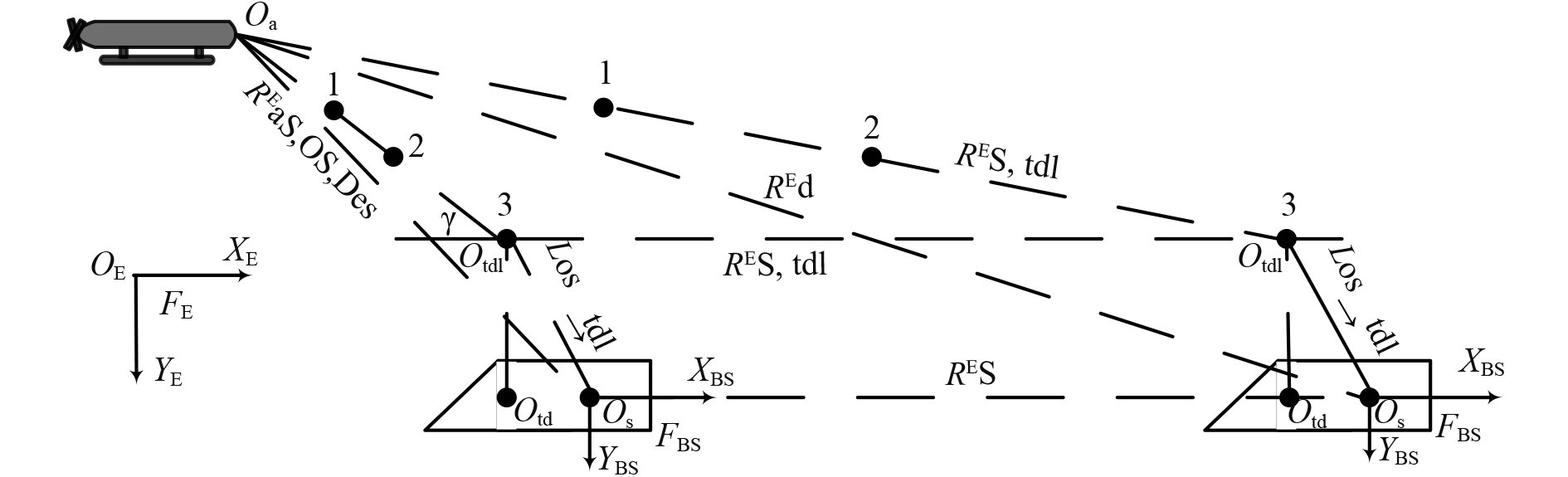
2 UUV对接路径基准轨迹生成模型

要生成回收调整段和对接段的航行路径，首先需要建立UUV航路的基准轨迹^[9]。图2给出了UUV对接路径基准轨迹的生成过程。首先建立UUV在以 ${O_S}$ 为原点的搭载平台坐标系（ ${F_{BS}}$ ）中的相对运动基准轨迹 $R_{aS,OS,Des}^{BS}$ ，然后通过 $L_{B0}^E$ 方向余弦建立在 ${F_{ES}}$ 坐标系中的基准轨迹 $R_{aS,OS,Des}^E$ ，此时有 $R_{aS,OS,Des}^E$ = $L_{B0}^E \cdot R_{aS,OS,Des}^{BS}$ 。该轨迹与搭载平台是固定连接关系（即随搭载平台运动而移动）。然后通过UUV下降段的终点 ${O_{t{ d}1}}$ 与 ${O_S}$ 的斜矩矢量 ${L_{OS \to td1}}({X_{TD}}, {Y_{TD}}, {Z_{TD}})$ ，将 $R_{aS,OS,Des}^E$ 平移至 ${O_{t{d}1}}$ 点上，从而形成了 $R_{aS,t{d}1,Des}^E$ 的期望轨迹。从图上可以看出 ${O_{t{d}1}}$ 点在搭载平台坐标系 ${F_{BS}}$ 中固定，并且其在 ${X_{BS}}$ 轴坐标与 ${O_{td}}$ 相同。同时，由于搭载平台相对于 ${F_E}$ 作等速直航的牵连运动 $R_S^E$ ，与搭载平台固定连接的点 ${O_{t{d}1}}$ 也作相应的等速直航牵连运动 $R_{S,t{d}1}^E$ ，因此可以得到UUV在坐标系 ${F_E}$ 中的基准轨迹 $R_{a,t{d}1}^E$ 为：

$ R_{a,t{d}1}^E = R_{aS,t{d}1,Des}^E + R_{S,t{d}1}^E\text{。} $

图2中 $R_{aS,t{\rm d}1,Des}^E$ 轨迹中的3个航路点构成一条直线，则该航线与搭载平台航行方向构成 $\gamma $ 的对接回收角。

3 UUV对接路径生成与平滑过程

为了对UUV进行对接回收，应首先根据UUV当前在搭载平台坐标系 ${F_{BS}}$ 的空间位置、速度、航向设定对接回收航路点，然后通过航路（对接段）终点 ${O_{t{d}1}}$ 与 ${O_S}$ 的斜矩矢量 ${L_{OS\xrightarrow{{}}t{d}1}}({X_{TD}}, {Y_{TD}}, {Z_{TD}})$ ，将航路点平移至 ${O_{t{d}1}}$ 点上，通过三次插值法将航路点拟合成一条平滑的对接路径。

根据UUV的对接回收过程，UUV首先要以一个较快的速度到达航路起始位置，为了控制航向与对接回收航线一致，UUV必须控制航向进行转弯。在回收时，必须同时控制速度使其缓慢减小，高度沿航线下降，并保持运动姿态稳定。最终对接回收时，必须使UUV的航行方向与搭载平台航行方向一致，即UUV位于搭载平台后上方附近的一固定点，如图2所示的航路点3。为此需要生成到达该点的航路点。

3.1 航路点的生成方法

航路点是UUV在水下航行时必须经过的点有序集合，这些点的连接即组成UUV的路径轨迹。

每个航路点在 ${F_{Etd}}$ 坐标系中可表达为 $({x_n}, {y_n}, {z_n})$ ，其中 $k = 1,2,\cdots,n$ ，因此航路点集由如下组成：

$Upt.poi = \{({x_0}, {y_0}, {z_0}),({x_1}, {y_1}, {z_1}),\cdots,({x_n}, {y_n}, {z_n})\}\text{，} $

同时在UUV经过航路点上还具有确定的运动特征，例如速度、航向等，定义为：

$Upt.speed = \{ {V_0}, {V_1}, \cdots,{V_n}\} \text{，}$

$Upt.course = \{ {\psi _0}, {\psi _1}, \cdots,{\psi _n}\}\text{。} $

这就要求UUV必须以速度 ${V_i}$ 和航向 ${\psi _i}$ 通过航路点 $({x_i}, {y_i}, {z_i})$ 。航路点集合的生成过程必须符合UUV航行特性（如转弯半径、航速等）和UUV对接回收过程（如纵横摇等姿态控制）的要求，主要包括以下几个方面：

1）完成对接回收要求

UUV从起始点（调整段开始） $({x_0}, {y_0}, {z_0})$ 航行到路径终点（对接段结束） $({x_n}, {y_n}, {z_n})$ 必须通过 $({x_i}, {y_i}, {z_i})$ 。

2）考虑水下复杂环境因素

选择航路点避开复杂海流的影响，以保证UUV航行与回收过程的安全。

3）障碍回避

由于UUV对接回收过程中，控制精度要求高，必须选择在没有障碍物的海区进行，以保证对接回收的安全。

4）UUV航路满足可实现性要求

所生成的航路点在水下空间上可到达可实现。当UUV航行到下一个航路点时满足UUV航速和转弯半径的限制。

5）航路点生成要求UUV以可行的航行路线到达规定的物理位置

这需要在水中给出可实现的航路点，并采用样条插值进行平滑，从而形成连续的航行轨迹。如果UUV回收过程中保持一定的速度，则需考虑在此速度下的最小转弯半径，以便给出精确优化的回收期望航行轨迹。

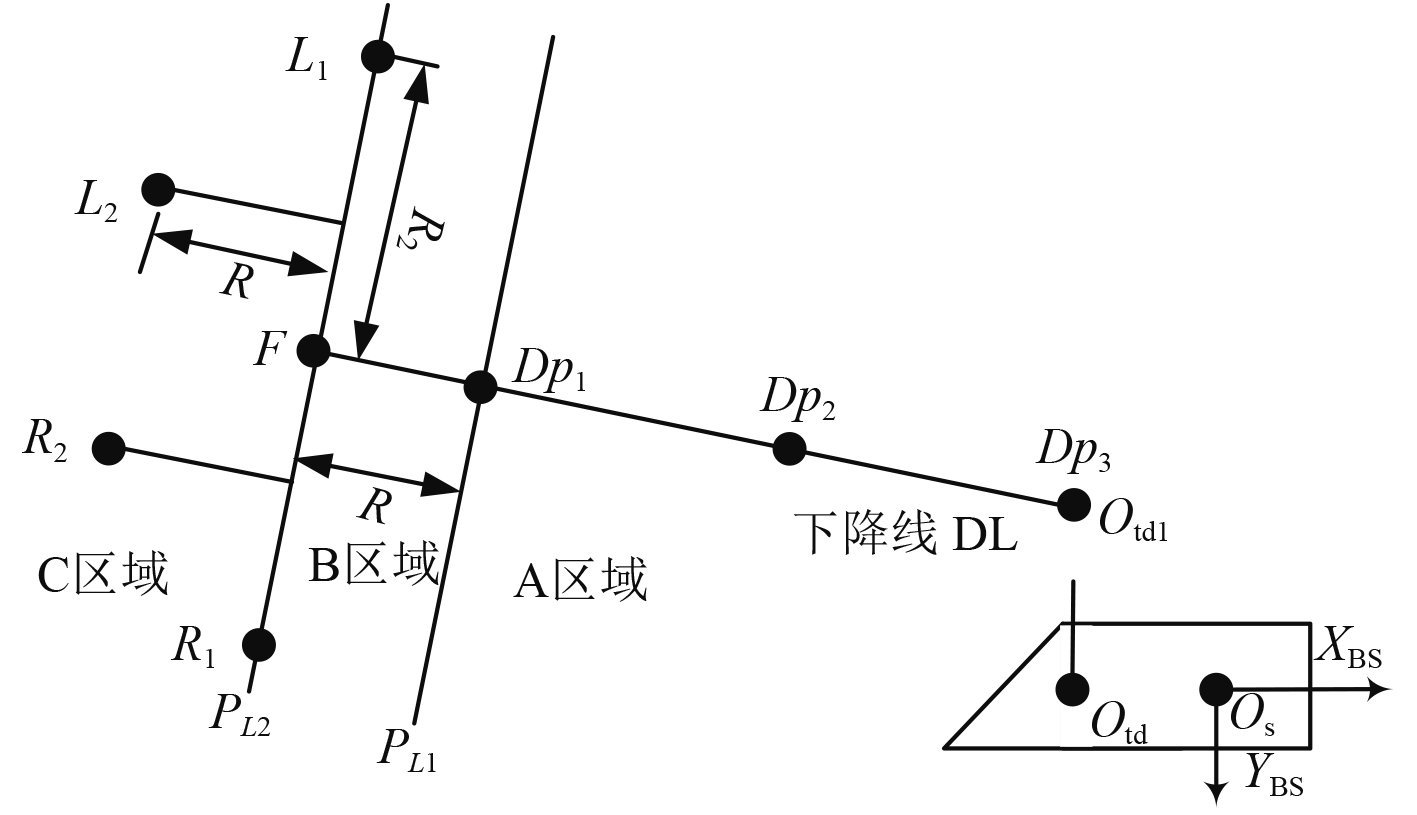
综合上述回收过程的要求和限制，根据UUV回收时所处的位置，航路点的生成可按照3种情况划分（见图3）。点D_p1，D_p2与D_p3为与搭载平台固定连接的航路点，也就是说这3点在搭载平台 ${F_{BS}}$ 坐标系下根据回收时UUV的速度、海流情况、搭载平台航行状态固定。这3点连成的直线就成为UUV靠近搭载平台的下降线DL，下降线DL与X轴形成的1个固定的回收角 $\gamma $ 以便在对接过程中UUV和回收装置的精确控制，P_L1经过点D_p1并与DL垂直，P_L2与P_L1相互平行。UUV在回收过程的航行中必须先经过D_p1点，然后沿着D_p2与D_p3这2个点航行，从而形成UUV对接航路的后部分。考虑UUV对接回收时的航速和转弯半径，根据UUV回收时刻当前坐标，将UUV初始位置区分为A，B，C三个区域。UUV回收时初始点位于不同的区域，则生成航路点也有所差别。

UUV回收时初始点位于A区，除了由D_p1，D_p2与D_p3组成的3个航路点以外，还需要至少生成另外3个航路点。这3个航路点位于下降线的哪边，取决于UUV此时的航向。UUV此刻航向如果在 $\gamma $ ～ $\gamma + {180^\circ}$ 之间，则取R₁，R₂和F作为3个航路点，与下降线的另外3个航路点构成预期航行轨迹；UUV此刻航向如果在 $0^\circ $ ～ $\gamma $ 以及 $\gamma + 180^\circ $ ～ $360^\circ$ 之间，则取L₁，L₂和F作为3个航路点，与下降线的另外3个航路点构成预期航行轨迹。

UUV对接回收时初始点位于B区，此时航路点生成需要增加“R”这段辅助距离，即将辅助线P_L2往后移动“R”长度。然后按照A区情况同样设置另外3个航路点，UUV能顺利到达下降线的航路点。

UUV回收时初始点位于C区（见图3），只要在下降线前增加1个航路点F，并设置在距离D_L1为“R”的下降线DL的延长线上，这样UUV经过航路点F后，就能顺利进入下降线。

3.2 航路点的平滑方法

从物理层面上说，UUV的路径应该是1条光滑的曲线，而将航路点通过直线连接生成的折线，因此可以采用插值函数的方法将其拟合成1条光滑的曲线。为在平滑拟合过程中不会产生病态的结果，本文采用了三次插值对UUV对接回收航路点进行平滑。

三次插值是一种UUV在接近和离开航路点时的速度和加速度保持相等的插值方法^[10]，因此，采用三次插值能确保在拟合各个航路点的速度和加速度不会产生跳变。在对航路点进行插值拟合过程中，需要寻找合适的三次多项式，以拟合生成每2个航路点之间的曲线，同时要求通过每个航路点处曲线的斜率和曲率连续，这样可以确定2个航路点之间唯一的三次多项式。

根据三次插值的原理，UUV应该经过的位置设定为 $({x_d}(\theta),{y_d}(\theta),{z_d}(\theta))$ 则有：

$\left\{ {\begin{array}{*{20}{c}} {{x_d}(\theta)= {a_3}{\theta ^3} + {a_2}{\theta ^2} + {a_1}\theta + {a_0}} \text{，}\\ {{y_d}(\theta)= {b_3}{\theta ^3} + {b_2}{\theta ^2} + {b_1}\theta + {b_0}} \text{，}\\ {{z_d}(\theta)= {c_3}{\theta ^3} + {c_2}{\theta ^2} + {c_1}\theta + {c_0}} \text{。} \end{array}} \right.$

其中， $\theta $ 为UUV回收航路轨迹的变量。

航路轨迹变量 $\theta $ 是航路点的编号，如果航路点编号为2，则对应的航路变量为 $\theta = 1$ 。因此航路轨迹变量无量纲，如果航路点集的个数为n，则有 $0 \leqslant \theta \leqslant n - 1$ 。对上式中的每一个 $\theta $ ，都存在一组这样 ${a_0}\sim {a_3}, {b_0}\sim {b_3}, {c_0}\sim$ $ {c_3}$ 的参数与之对应，对上式进行求导，可得：

$\begin{split} & {{x}^{'}}d(\theta )=\frac{{\rm d}x{\rm d}(\theta )}{{\rm d}\theta }=3a3{{\theta }^{2}}+2a2\theta +a1 \text{，}\\ & {{y}^{'}}d(\theta )=\frac{{\rm d}y{\rm d}(\theta )}{{\rm d}\theta }=3b3{{\theta }^{2}}+2b2\theta +b1 \text{，}\\ & {{z}^{'}}d(\theta )=\frac{{\rm d}z{\rm d}(\theta )}{{\rm d}\theta }=3c3{{\theta }^{2}}+2c2\theta +c1 \text{。} \end{split} $

通过UUV回收航路点（ ${x_{k - 1}}, {y_{k - 1}}, {z_{k - 1}}$ ）的轨迹需要满足下式的要求：

$\begin{split} & {x_d}({\theta _{k - 1}})= {x_{k - 1}}\text{，} \\ & {x_d}({\theta _k})= {x_k}\text{，} \\ & {y_d}({\theta _{k - 1}})= {y_{k - 1}}\text{，} \\ & {y_d}({\theta _k})= {y_k}\text{，} \\ & {z_d}({\theta _{k - 1}})= {z_{k - 1}}\text{，} \\ & {z_d}({\theta _k})= {z_k}\text{。} \end{split} $

其中， $k = 1,2,\cdots,n$ 。从航路轨迹平滑度的要求情况上看，即要求通过每个航路点处曲线的斜率和曲率必须连续，则有：

$\begin{gathered} \begin{align} & \underset{\theta \to \theta _{k}^{-}}{\mathop{\lim }}\,x_{d}^{'}({{\theta }_{k}})=\underset{\theta \to \theta _{k}^{+}}{\mathop{\lim }}\,x_{d}^{'}({{\theta }_{k}}) \text{，}\\ & \underset{\theta \to \theta _{k}^{-}}{\mathop{\lim }}\,y_{d}^{'}({{\theta }_{k}})=\underset{\theta \to \theta _{k}^{+}}{\mathop{\lim }}\,y_{d}^{'}({{\theta }_{k}}) \text{，}\\ & \underset{\theta \to \theta _{k}^{-}}{\mathop{\lim }}\,z_{d}^{'}({{\theta }_{k}})=\underset{\theta \to \theta _{k}^{+}}{\mathop{\lim }}\,z_{d}^{'}({{\theta }_{k}}) \text{，}\\ & \underset{\theta \to \theta _{k}^{-}}{\mathop{\lim }}\,x_{d}^{''}({{\theta }_{k}})=\underset{\theta \to \theta _{k}^{+}}{\mathop{\lim }}\,x_{d}^{''}({{\theta }_{k}}) \text{，}\\ & \underset{\theta \to \theta _{k}^{-}}{\mathop{\lim }}\,y_{d}^{''}({{\theta }_{k}})=\underset{\theta \to \theta _{k}^{+}}{\mathop{\lim }}\,y_{d}^{''}({{\theta }_{k}}) \text{，}\\ & \underset{\theta \to \theta _{k}^{-}}{\mathop{\lim }}\,y_{d}^{''}({{\theta }_{k}})=\underset{\theta \to \theta _{k}^{+}}{\mathop{\lim }}\,y_{d}^{''}({{\theta }_{k}}) \text{。}\\ \end{align} \end{gathered} $

根据上述方程，如果航路轨迹上有 $n$ 个航路点，则 $0 \leqslant \theta \leqslant n - 1$ ，因此一共有12（n–1）个未知数，若确定了UUV对接回收过程航路终点的速度或加速度，构成12（n–1）个约束，通过求解就可以得出相应的参数，并得到3（n–1）个三次多项式，从而能够拟合插值出相应的平滑曲线。

4 案例分析

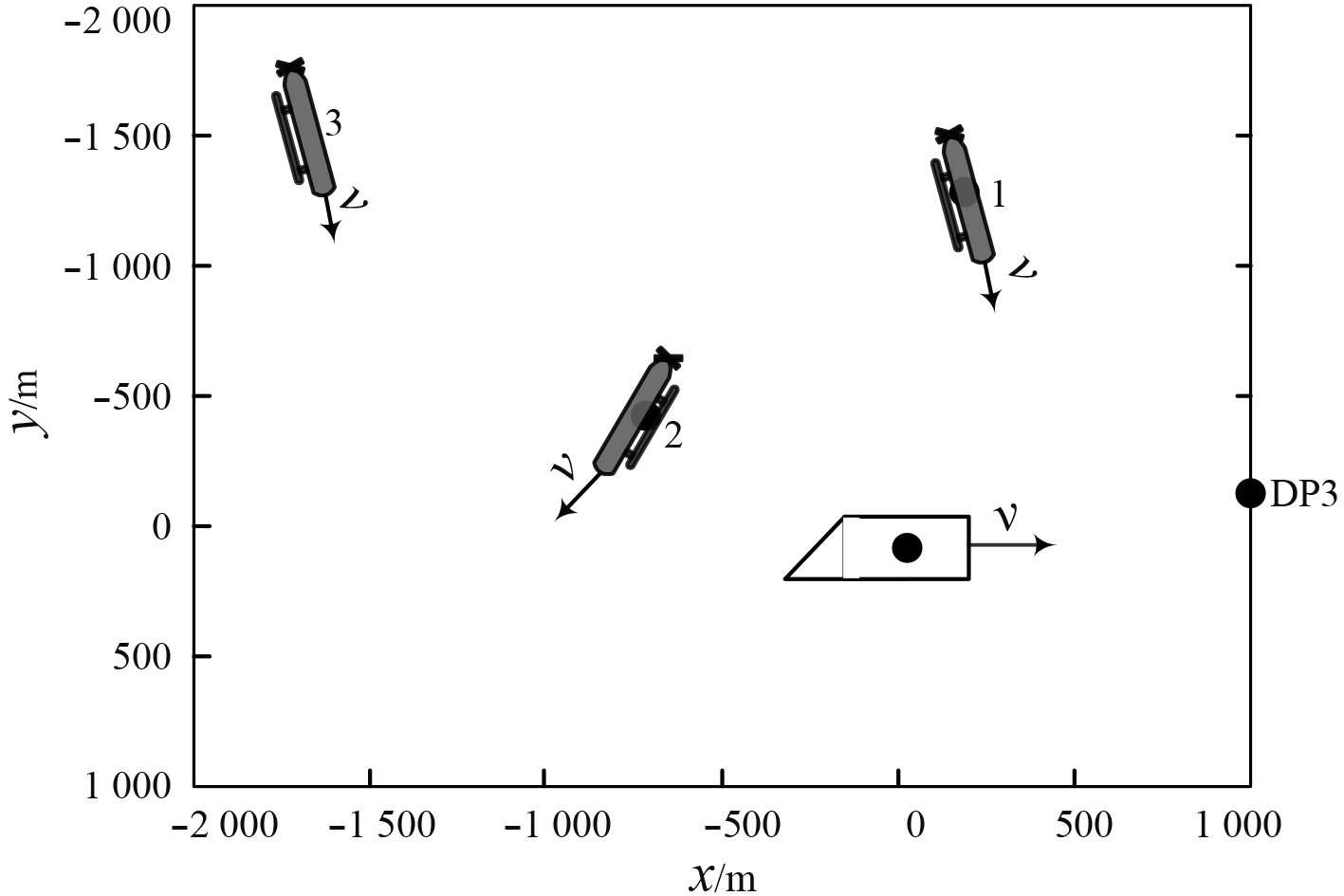
为了验证水下搭载平台与UUV对接路径生成方法的有效性，进行案例的仿真计算。在 $FBS$ 坐标系下UUV的初始点如图4所示，分别为（150，–1 450，50），（–450，–350，50）和（–1 600，–1 500，50），UUV的最小转弯半径为50 m，假设D_p3为路径终点。通过仿真生成14个航路点（见表1）。

在生成航路点的基础上，采用三次样本插值对UUV回收航路点进行平滑，可以得到如图5的3条航路基准轨迹。

需要注意的是，从计算分析结果上看，路径1和路径2的航路点数为8个，而路径3的航路点数为6个，实事上为了实现对接路径的平滑，为每条路径初始参考点，分别为航路点4、航路点11和航路点14。同时利用航路点插值成的参考航线在第1段，如路径1的航路点1、航路点4之间的航线会存在一些不协调，考虑到UUV在这一段航行时，是处于准备接入调整段，而航路点1、航路点4所连线段的方向为初始航向，可以将航路点1、航路点2之间的插值曲线用航路点1、航路点2连线所代替，UUV位于此段时处于进入调整段的缓冲阶段。

5 结　语

水下无人航行器（UUV）协同搭载平台作业已经成为海洋工程领域的一种越来越普遍的作业方式，安全可靠的回收成为UUV使用过程中的关键环节，而水下回收在水下完成整个回收过程，相对于水面回收更隐蔽和安全，然而由于水下回收UUV受到海洋环境的影响，同时受到回收平台运动的限制，视觉和光学作用受限，水下双动平台的对接回收难度很大，而UUV对接路径规划是实现搭载平台与UUV精确对接的基础。本文从回收过程中实现UUV精确航行靠近搭载平台回收装置的角度，提出了水下动平台对UUV回收的对接路径生成方法，通过分析双动平台下回收航路规划的特点，在设定搭载平台水下等速、定深、直航情况下，给出了UUV回收对接航路点生成过程，同时根据UUV航速、转弯半径等限制，提出了采用三次插值对航路点进行平滑，为实现水下双动平台对接回收提供技术支持。

　　水下动平台回收UUV是一个非常复杂的过程，不仅仅需要进行路径规划，而且需要对2个平台进行六自由度的姿态控制、精确对接交会等。在下一步研究工作一方面需要充分考虑海流、能见度、定位误差等条件下优化完善路径生成方法；另一方面，需要对水下双动平台对接过程的六自由度姿态控制、水下对接精确定位控制、水下对接避碰控制等方面开展深入研究。