2. 招商局重工(江苏)有限公司, 江苏 南通 226100
2. China Merchants Heavy Industries (Jiangsu) Co., Ltd., Nantong 226100, China
随着极地资源的开采,冰区航行的船舶数量与日俱增,但随之而来的是屡见不鲜的冰区船舶事故,其中以船-冰碰撞事故最为常见。为了提高船舶在冰区航行时的安全性和船舶结构可靠性,船舶工程师在设计阶段需要将船舶与冰区浮冰、冰山等撞击事故考虑在内,目前主流方法是利用非线性有限元软件对船-冰撞击过程进行数值模拟以达到预估和校核的目的。
在数值模拟中,海冰与船舶接触并互相作用过程的应力状态非常复杂,传统的计算中只考虑海冰单轴强度的准则,在冰力计算时会得到误差较大的结果,船-冰碰撞中海冰力学行为的失效准则非常重要。近年,在二维各向同性连续介质力学基础上,先后建立了线粘性、弹塑性、粘塑性和粘弹塑性等一系列海冰动力学本构模型,能更好地呈现海冰的力学行为和海冰失效。为合理解释在船-冰碰撞过程中海冰在高压区表面的融化现象,Gagnon[1]提出泡沫材料模拟海冰本构模型;为充分考虑高应变率下的海冰力学行为,Derradji-Aouat[2]提出了适合碰撞问题研究的海冰失效准则。
考虑船体板架承受侧向冰载荷作用,开展了结构遭受局部冰块作用的试验以及仿真研究[3]。徐栋[4]按照极限能量机理计算冰载荷,并使用极限载荷来校核极区船舶冰载荷作用下的结构安全性。对于船冰碰撞结构的极限强度,目前还未见相关文献。本文提出适用于碰撞问题研究的线弹性Derradji-Aouat海冰本构模型,并嵌入Ls-dyna程序,生成新的求解器。在此基础上,对船冰碰撞后结构强度影响进行研究,完善冰区规范,为冰区船舶结构的设计提供参考。
1 冰材料本构模型已有的研究表明,粘塑性、弹塑性和粘弹塑性海冰本构模型不适用于模拟船冰碰撞问题中的小尺寸海冰。为了更好地描述船舶与小型冰山碰撞过程中冰山冰所经历的复杂变形和应力状态的变化,Derradji-Aouat[5]在不同的应变率、不同的应力(0.1~85 MPa)和不同的温度(–1 ℃~–45 ℃)下,进行了约300组冰山冰和淡水冰的三轴试验,并通过分析试验数据得到淡水冰和冰山冰存在统一的各向同性三维失效准则—多表面失效海冰本构模型。
除了准确的失效准则外,合理的海冰破坏模式同样重要。Derradji-Aouat[6]指出,在冰块高速冲击过程中(应变率>10–3s–1),冰块表现为具有脆性破坏模式的线弹性模型。虽然线弹性模型的应力应变可逆性与实际海冰力学性质不符,但在小尺寸海冰问题的仿真中,海冰单元容易失效删除,可以不考虑线弹性模型回弹特征的情况下保留其脆性破坏模式。
在线弹性模型的基础上,结合各向同性三维失效准则,提出了基于线弹性的多表面失效海冰本构模型。
1.1 海冰材料的二次开发Ls-dyna作为主流的非线性有限元程序,其用户自定义本构模型二次开发很完善,Ls-dyna提供完备的自定义材料接口。对于本文自定义的冰材料本构模型而言,主要运用变量sig(6),eps(6),hsv(*)和cm(*),应力更新算法采用Ls-dyna欧拉子步法。编译过程如步骤1~步骤5所示。
步骤1:计算剪切模量:
步骤2:计算静水压力(增量):
步骤3:计算静水总应力,定义一个历史变量hisv(2),hisv(2)=hisv(2)−P。
步骤4:计算应力(
| $ \begin{aligned} & {\sigma _{11}}={\sigma _{11}}^* + P + G \times \left({\varepsilon _{11}} - \frac{{{\varepsilon _{11}} + {\varepsilon _{22}} + {\varepsilon _{33}}}}{3}\right)\text{,}\\ & {\sigma _{22}}={\sigma _{22}}^* + P + G \times \left({\varepsilon _{22}} - \frac{{{\varepsilon _{11}} + {\varepsilon _{22}} + {\varepsilon _{33}}}}{3}\right)\text{,}\\ & {\sigma _{33}}={\sigma _{33}}^* + P + G \times \left({\varepsilon _{33}} - \frac{{{\varepsilon _{11}} + {\varepsilon _{22}} + {\varepsilon _{33}}}}{3}\right)\text{,}\\ & {\sigma _{12}}={\sigma _{12}}^* + G \times {\varepsilon _{12}}\text{,}\\ & {\sigma _{23}}={\sigma _{23}}^* + G \times {\varepsilon _{23}}\text{,}\\ & {\sigma _{31}}={\sigma _{31}}^* + G \times {\varepsilon _{31}}\text{。} \end{aligned} $ |
步骤5:参照Derradji-Aouat研究并建立的三维失效准则公式,以应力为衡准定义各向同性三维失效准则。
将上述过程编写成Fortran语句,并将其编入Ls-dyna.LIB文件包接口文件中,生成含有本文所定义的基于线弹性海冰多表面失效本构模型的新求解器。
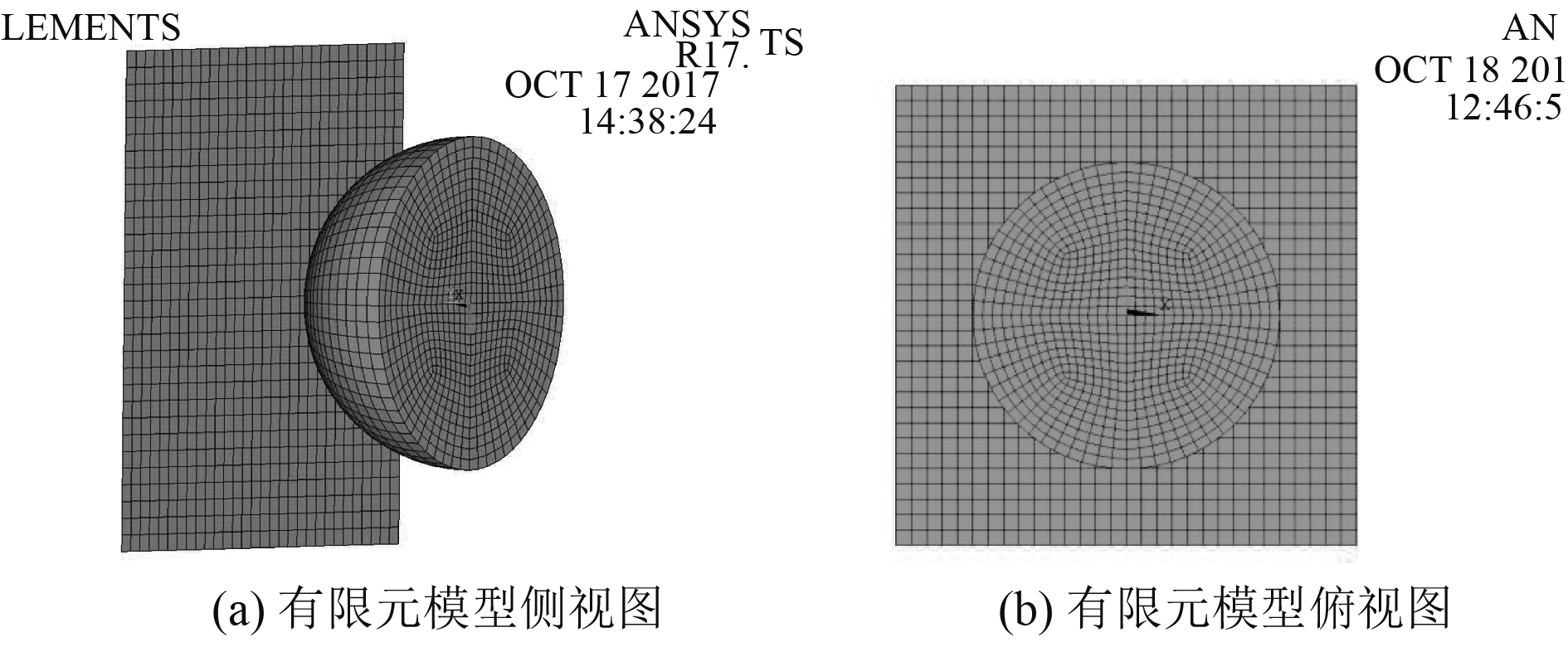
1.2 海冰材料本构模型验证 1.2.1 ISO规范对比分析为了验证所编写的本构模型程序的正确性,本文通过球形冰-钢板碰撞仿真和ISO规范中的压强-面积曲线对比分析。球形冰半径为1 m,以1 m/s的速度撞击钢板,为了便于与国际规范中的冰体压强-面积公式做对比,钢板取30 mm厚并施加全约束。有限元模型如图1所示。
|
图 1 球形冰-钢板撞击算例有限元模型 Fig. 1 Finite element model of spherical ice-plate collision |
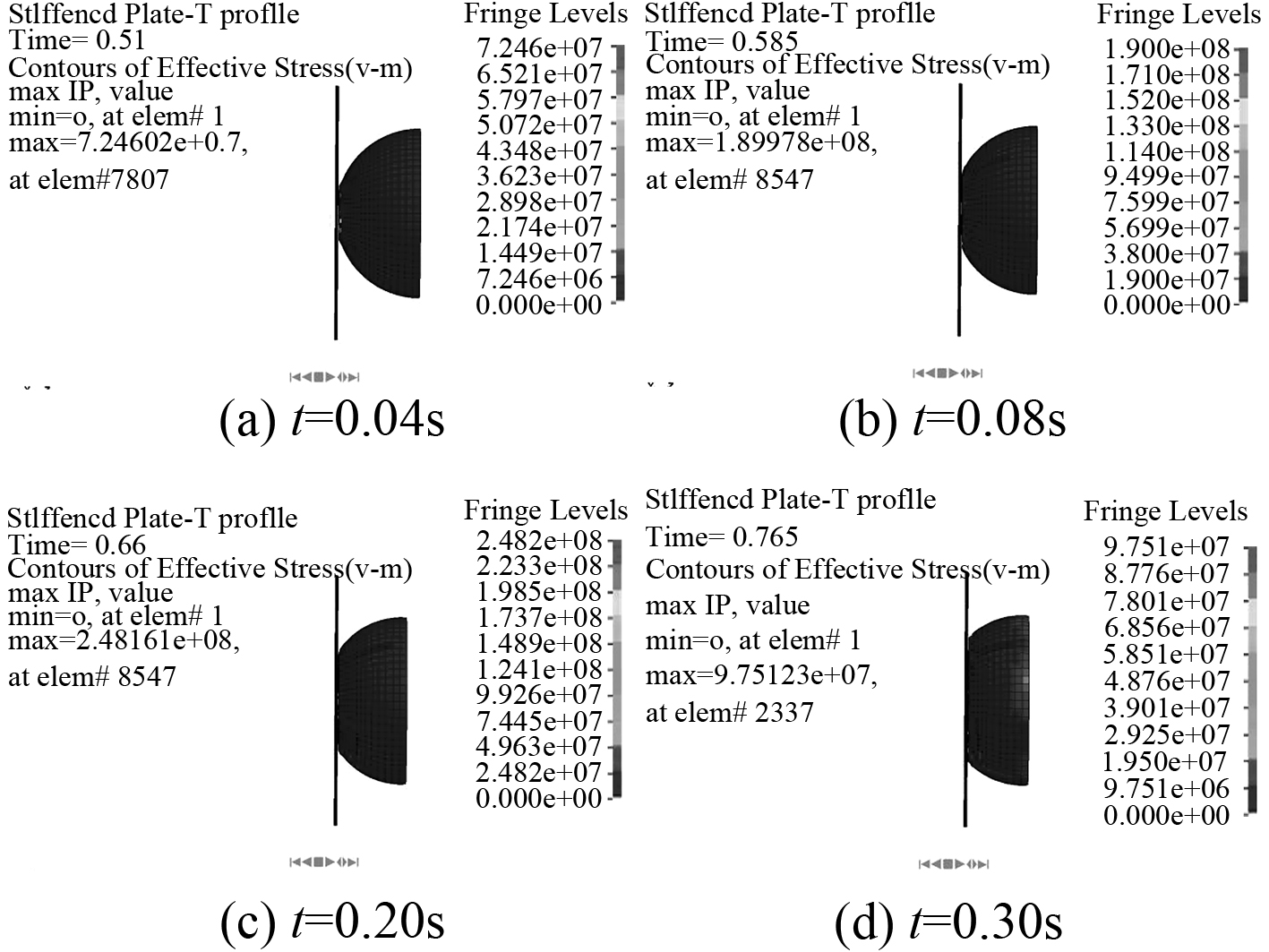
图2为球形冰撞击钢板过程中的应力云图,可以看出冰体的失效变形模式与实际情况相似,不同时刻下产生的压力差异较大。
|
图 2 球形冰撞击钢板过程应力图 Fig. 2 Stress in the process of spherical ice impact steel plate |
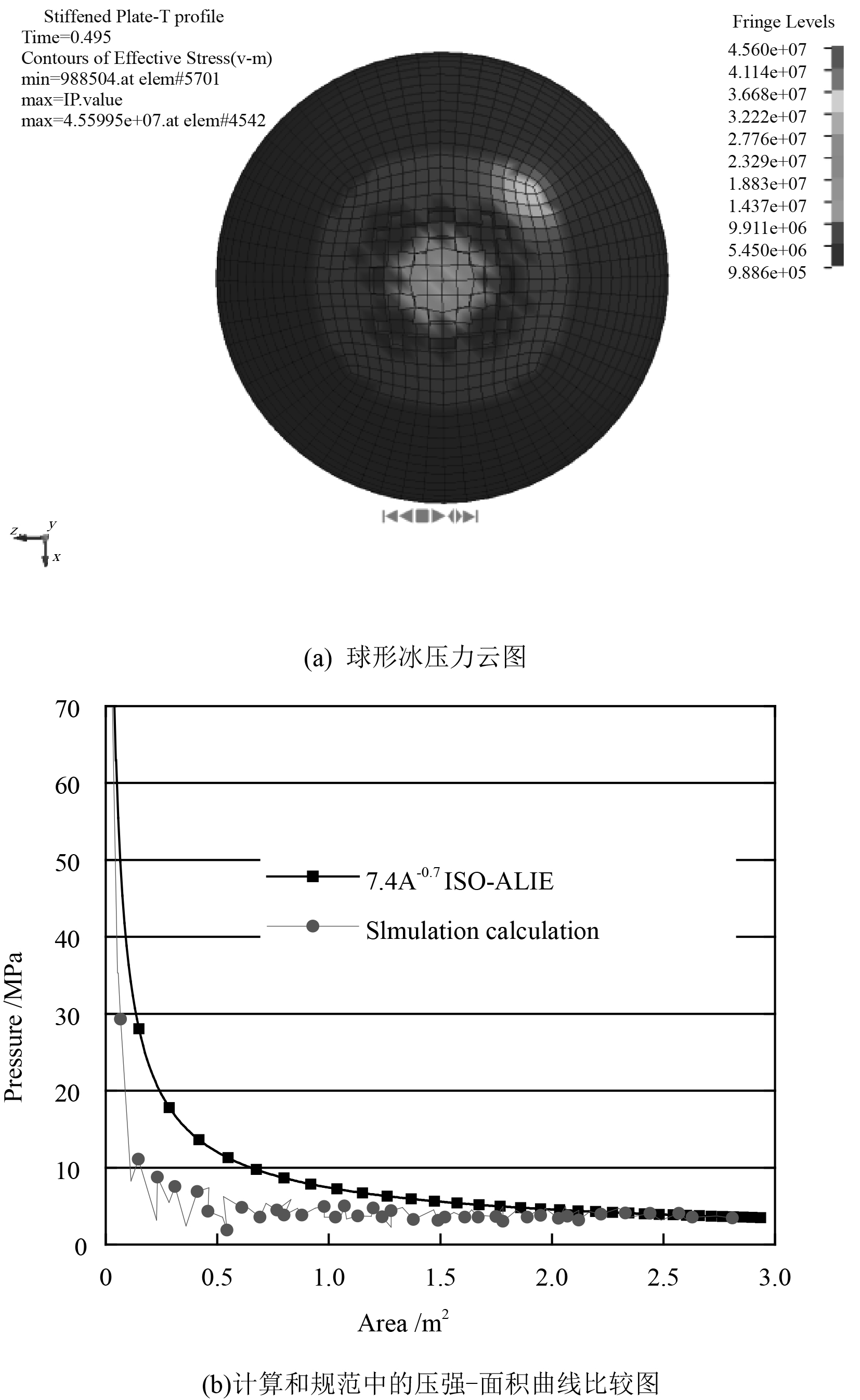
通过球形冰撞击时间和速度,求得撞击面积后,得到冰体压强-面积曲线后,与已被ISO(19906)[7]采用,Masterson提出的P=7.4A–0.7压力-面积公式作对照验证,如图3(b)所示。由图可知,有限元计算结果与规范中的曲线在碰撞面积0.1~0.75 m2区域内有较小出入,在撞击面积0.75~3 m2区域内吻合的非常好。在实际的船-冰碰撞问题研究中,撞击时的接触面积一般大于0.75 m2,因此本文提出的多表面失效冰本构模型可以较为准确地应用在船-冰数值模拟中。图3(a)为撞击过程中冰压力云图,可以看出撞击区域存在高、低压区,算例中的高压区最大静水应力约为67.4 MPa,低压区静水应力约为2 MPa,与Gagnon实验数据较为一致。
|
图 3 撞击分析图 Fig. 3 Impact analysis pictures |
为了验证本文自定义的海冰材料相较其他海冰材料更加适用于船冰碰撞问题的研究,对柱形冰撞击船体舷侧板架试验进行数值仿真[8],并进行对比分析。
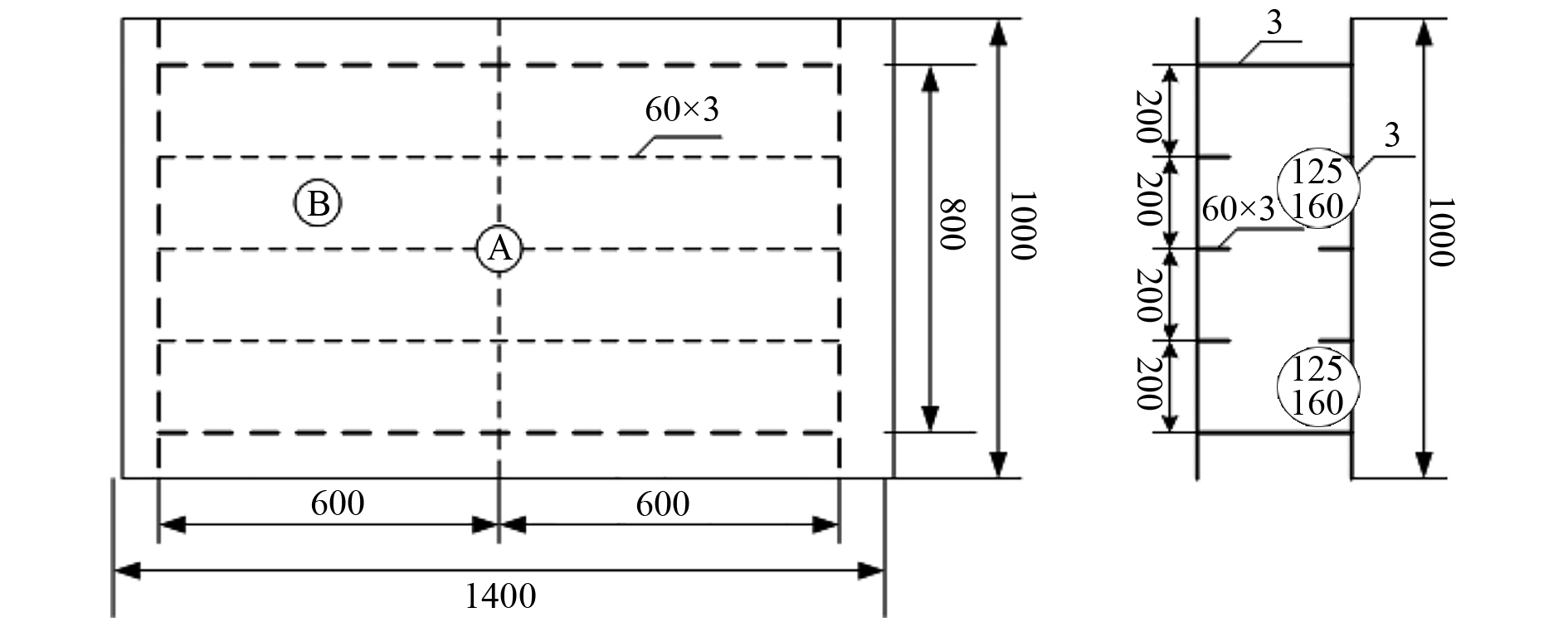
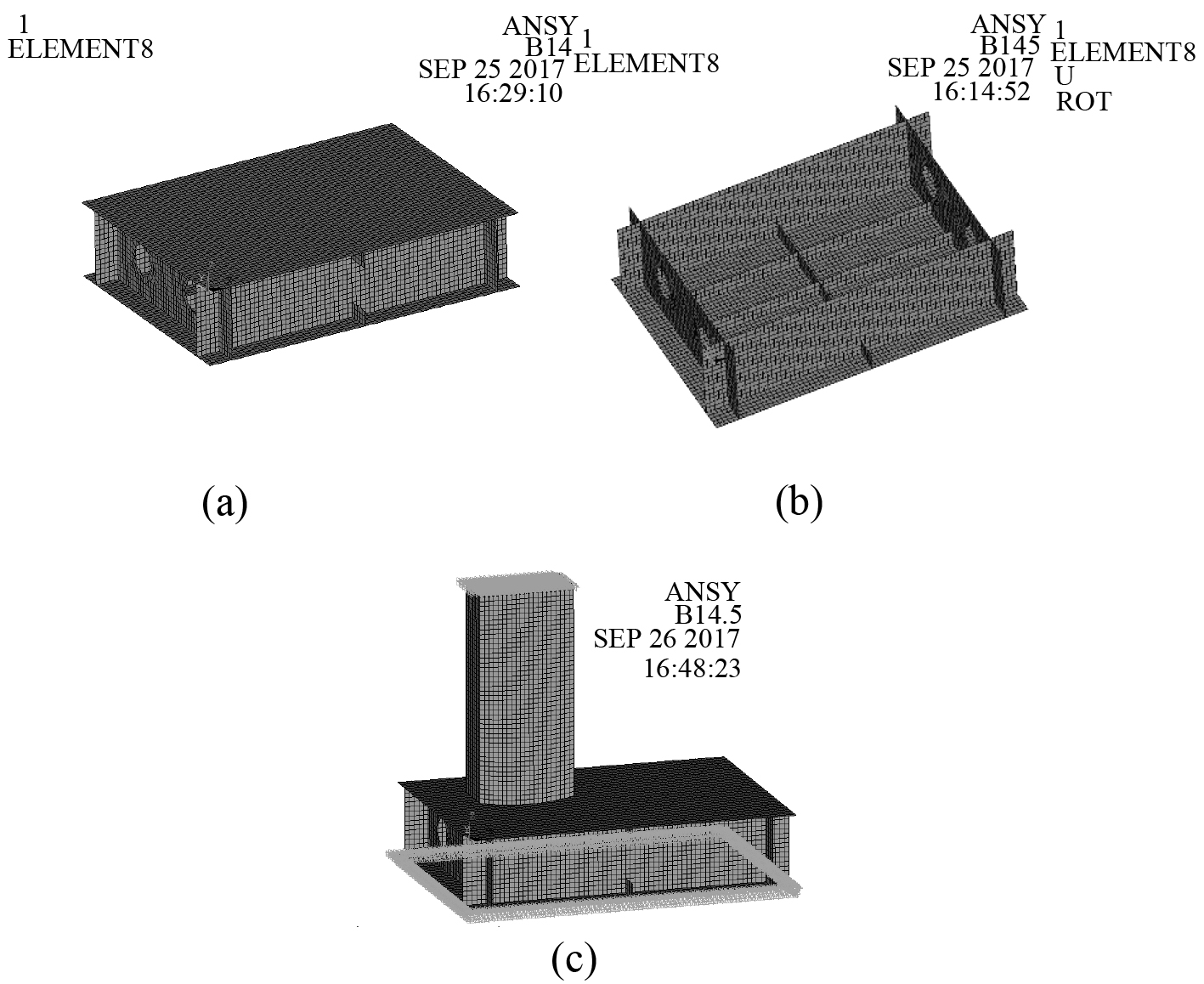
冰体和舷侧板架结构的仿真模型尺寸与试验保持一致,缩尺比舷侧板架结构模型和有限元模型分别如图4和图5所示。按照实际试验中模型底部四周边界固定在地面上,所以舷侧板架结构有限元模型底部四周边界施加全约束。
|
图 4 缩尺比舷侧板架结构模型图(单位:mm) Fig. 4 The reduced scale model figure of side grillage structure |
|
图 5 有限元模型图 Fig. 5 Finite element model |
使用多表面失效模型作为冰体材料对本文所述的柱形冰撞击舷侧板架结构某点位置(拟为图4中B点)进行数值模拟,结果如图6~图8所示。

|
图 6 冰体撞击舷侧板架结构分析 Fig. 6 Analysis of the structure of the side frame of the ice body impacting on the side of the side |
|
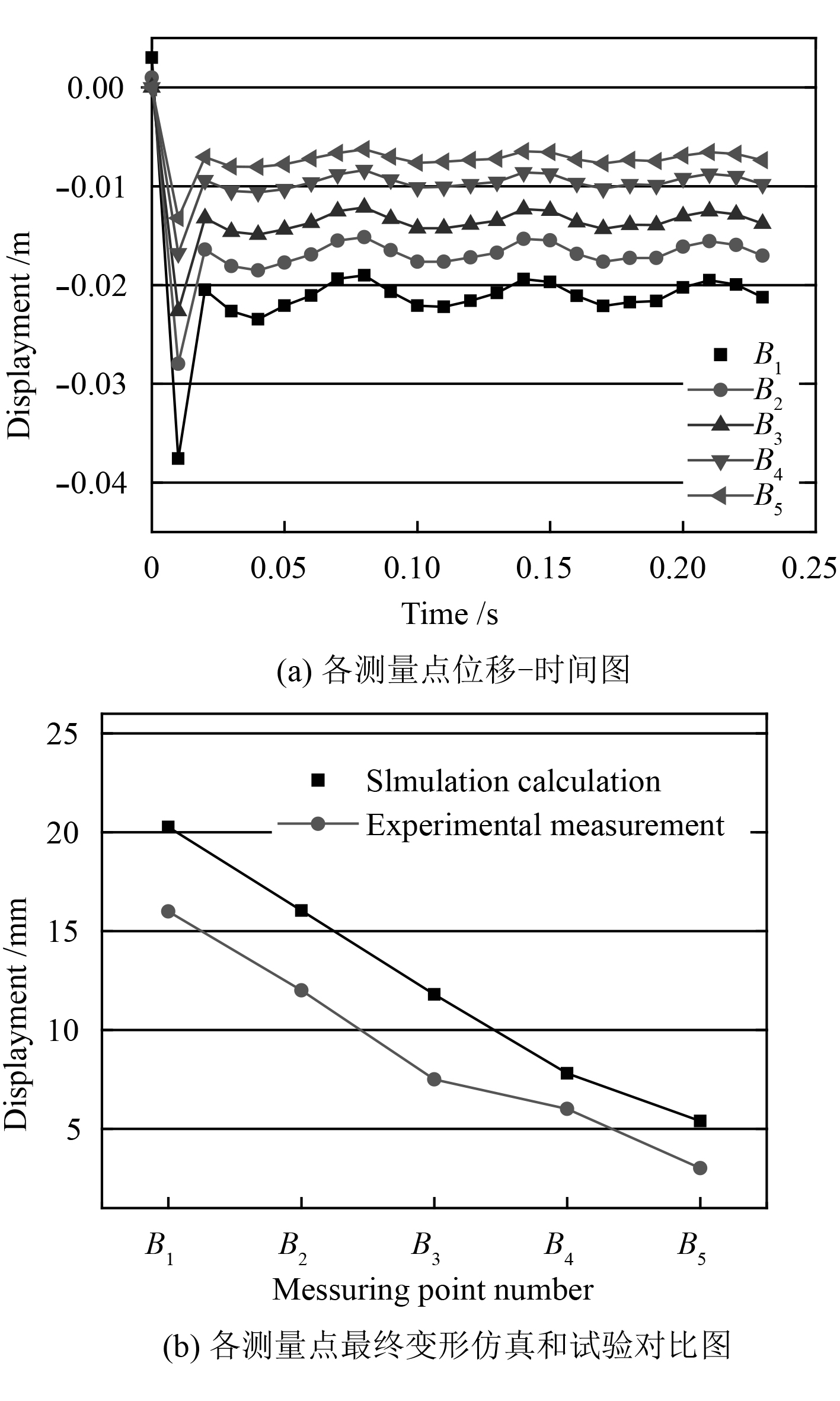
图 8 板架最终变形分析 Fig. 8 Analysis of final deformation of plate frame |
图6(a)为冰体撞击舷侧板架结构示意图,可以看出,柱状冰下表面和板架接触时未发生明显破碎,板架受撞击后变形明显;图6(b)为撞击后冰体示意图,可以看出冰体接触面破碎较为均匀,接触面四周破碎情况较之中部更为明显,整体受力均匀,和实际试验中所观测到的接触过程稍有差距,但在可接受范围内。
图7(a)为受多表面失效冰体模型撞击后舷侧板架结构应力云图;图7(b)为撞击后舷侧板架结构的变形云图,从图中可知,撞击后垂直方向板架的最大变形出现在撞击位置,为25.02 mm,由中间往四周逐渐减小,和试验观测的结果基本吻合。

|
图 7 舷侧板架撞击结果分析图 Fig. 7 The result diagram of the rear frame |
在图4中撞击位置B点处设为测量点B1,并沿图4坐标系中的(–1,–1)方向等距设置测量点B2,B3,B4和B5。5个测量点在垂直方向位移随时间变化如图8(a)所示,撞击后的最终变形(垂直方向位移)与试验中5个测量点测得最终变形数据对比如图8(b)所示。可以看出,利用多表面失效本构模型作为冰材料数值仿真所获得的板架最终变形结果和实际试验所得的变形结果相近。仿真结果的最大变形量为20.3 mm,试验测得最大变形量为16 mm,变形趋势基本吻合。表明本文的基于线弹性多表面失效海冰动力本构模型适合模拟船-冰碰撞问题。
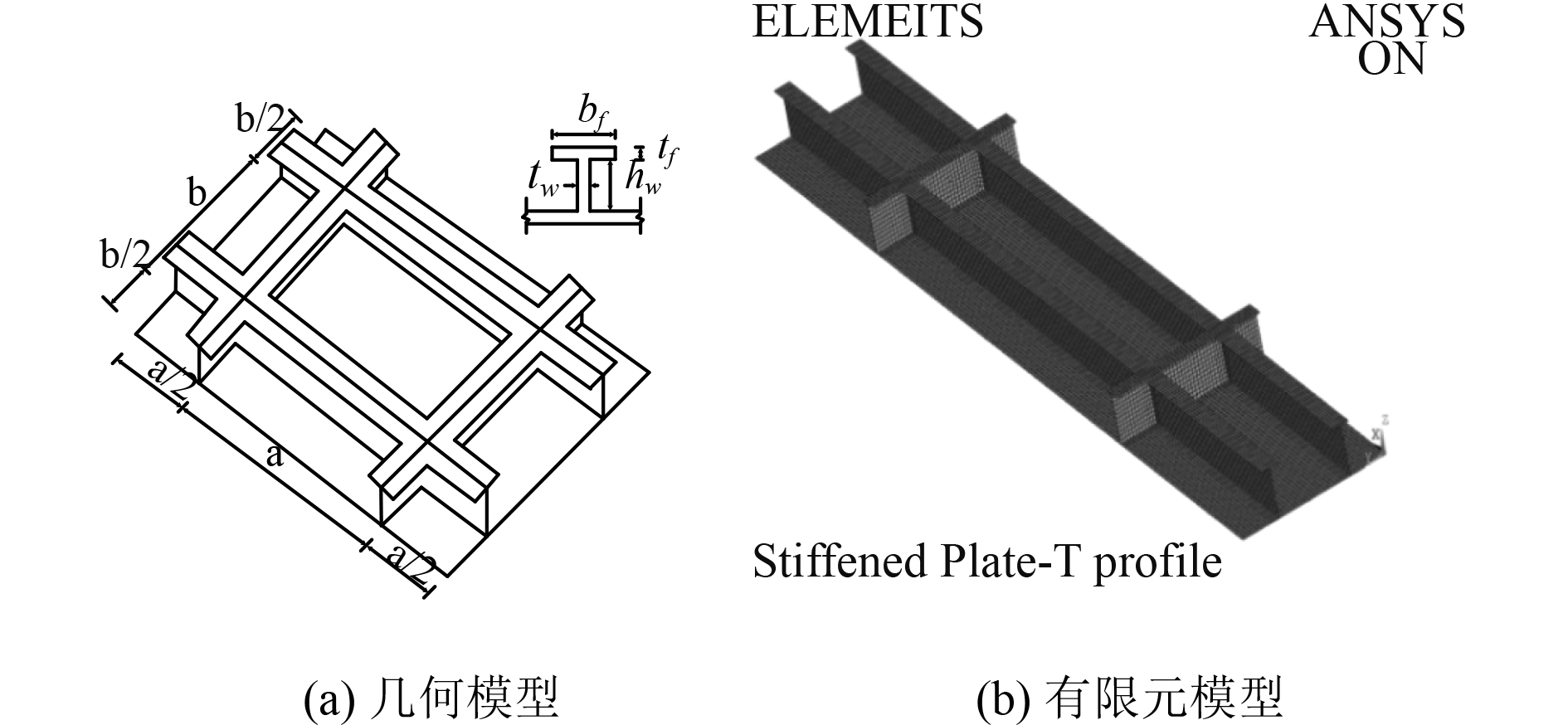
2 计算模型在本文探讨凹陷损伤对加筋板极限强度的影响中,选用计算模型如图9所示,几何尺寸如表1所示。加筋板模型选用低温下高强钢动力本构模型材料,其弹性模量E=2.1E5 MPa,泊松比γ=0.3,静态屈服强度σv=384.6 MPa。海冰模型选用多表面失效海冰动力本构模型材料,考虑到在不同局部形状海冰撞击船体结构中碰撞力和内能总和最大为正方体海冰[9],计算中海冰选取400 mm×400 mm×400 mm正方体模型。
|
|
表 1 双跨梁加筋板几何尺寸 Tab.1 Thedimensions of the double span beam stiffened panel |
|
图 9 双跨梁加筋板模型示意图 Fig. 9 Calculation modelof the doe span beublam stiffened panel |
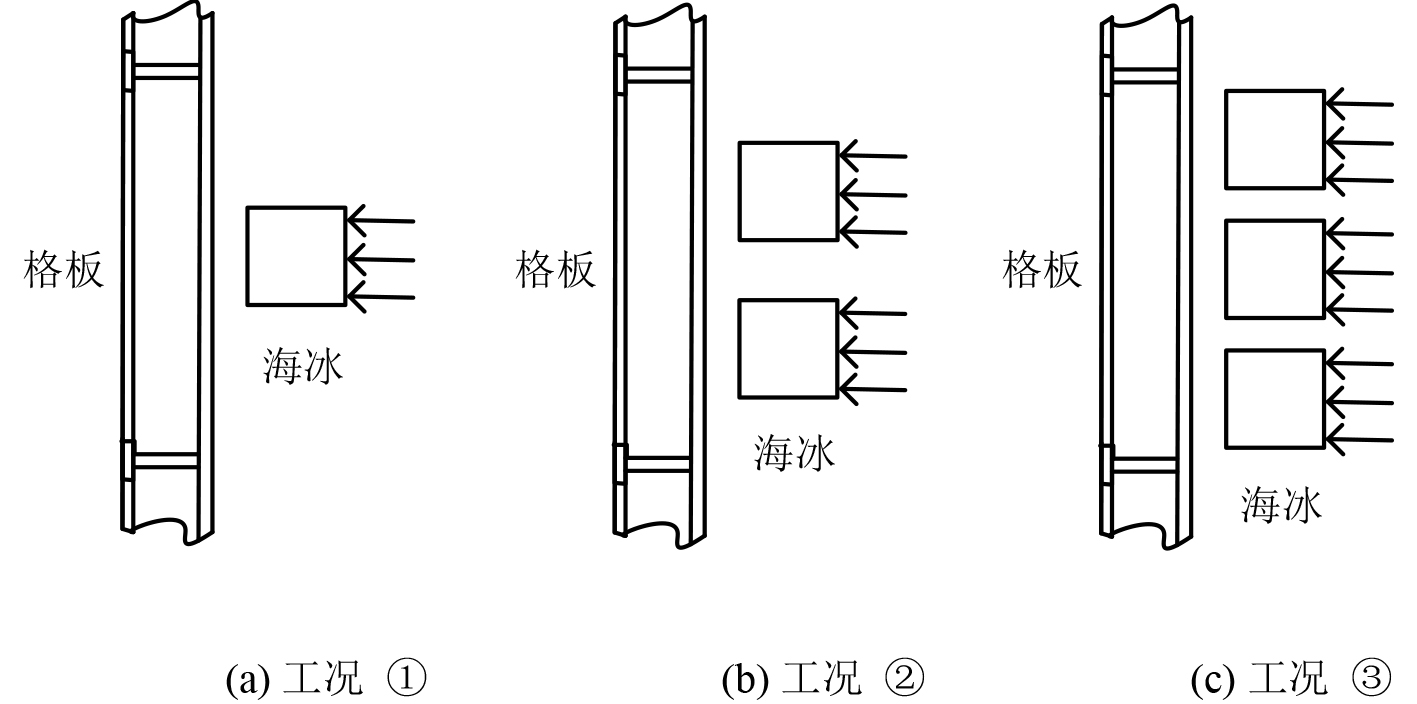
结合实际船冰碰撞事故,本文分别设计3种工况下海冰以不同的速度撞击双跨梁加筋板,如图10所示。
|
图 10 3种船冰碰撞工况示意图 Fig. 10 A sketch map of three kinds of ship-ice collision |
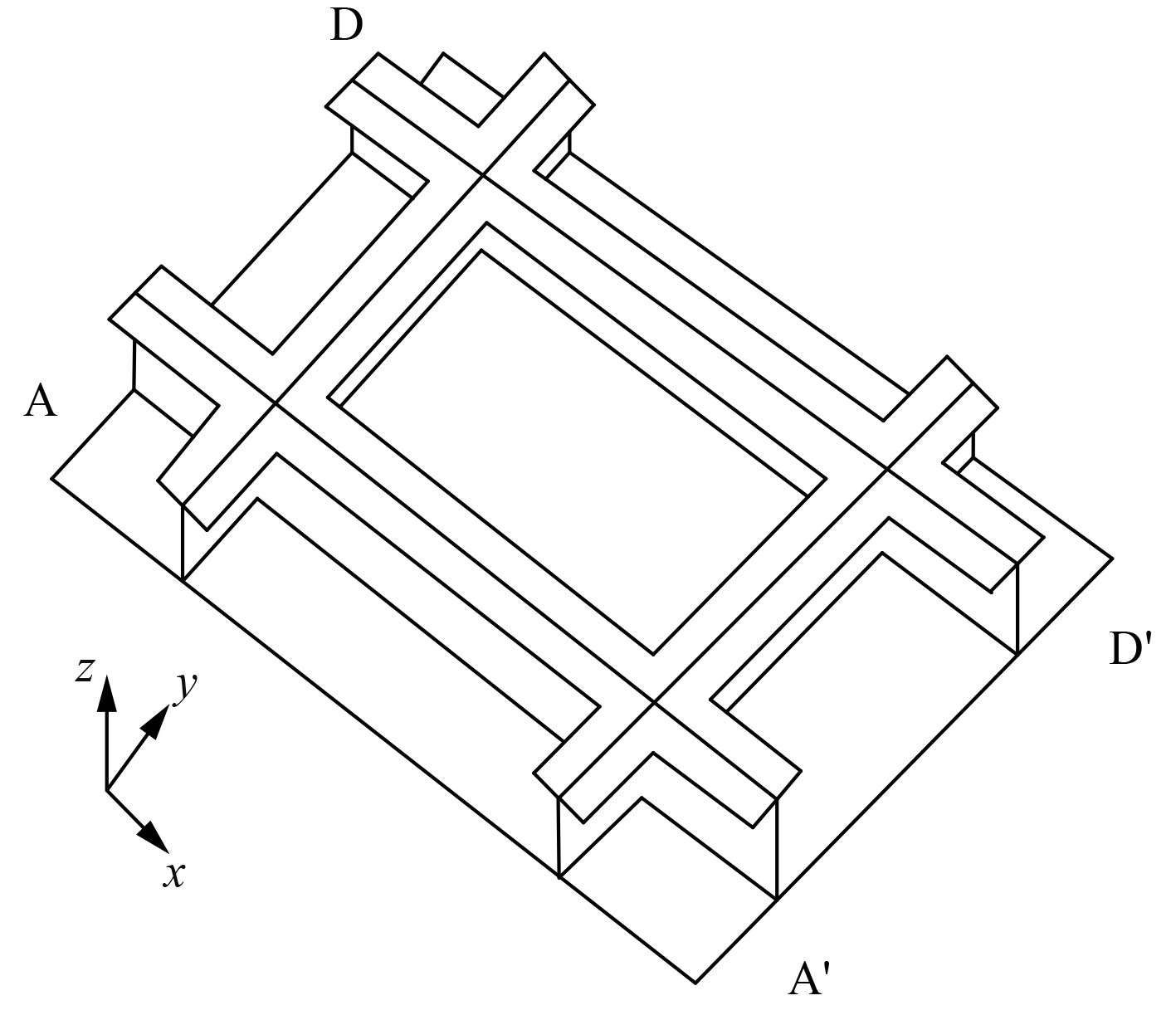
船冰发生碰撞后,计算含损伤加筋板剩余极限强度时的边界条件设置按照实际情况,如图11所示。其中边界A-A′和D-D′的Rx=Rz=0,Uy=0;边界A-D的Ry=Rz=0,Uz=0;边界A′-D′的Ry=Rz=0,Ux=Uz=0。
|
图 11 加筋板模型边界条件示意图 Fig. 11 Boundary condition diagram of stiffened plate model |
本文主要基于Ls-dyna对不同工况下的船冰碰撞进行仿真模拟,并将碰撞后含碰撞凹陷损伤加筋板上所有节点的位移导入Ansys中,最后基于弧长法进行极限强度计算分析。
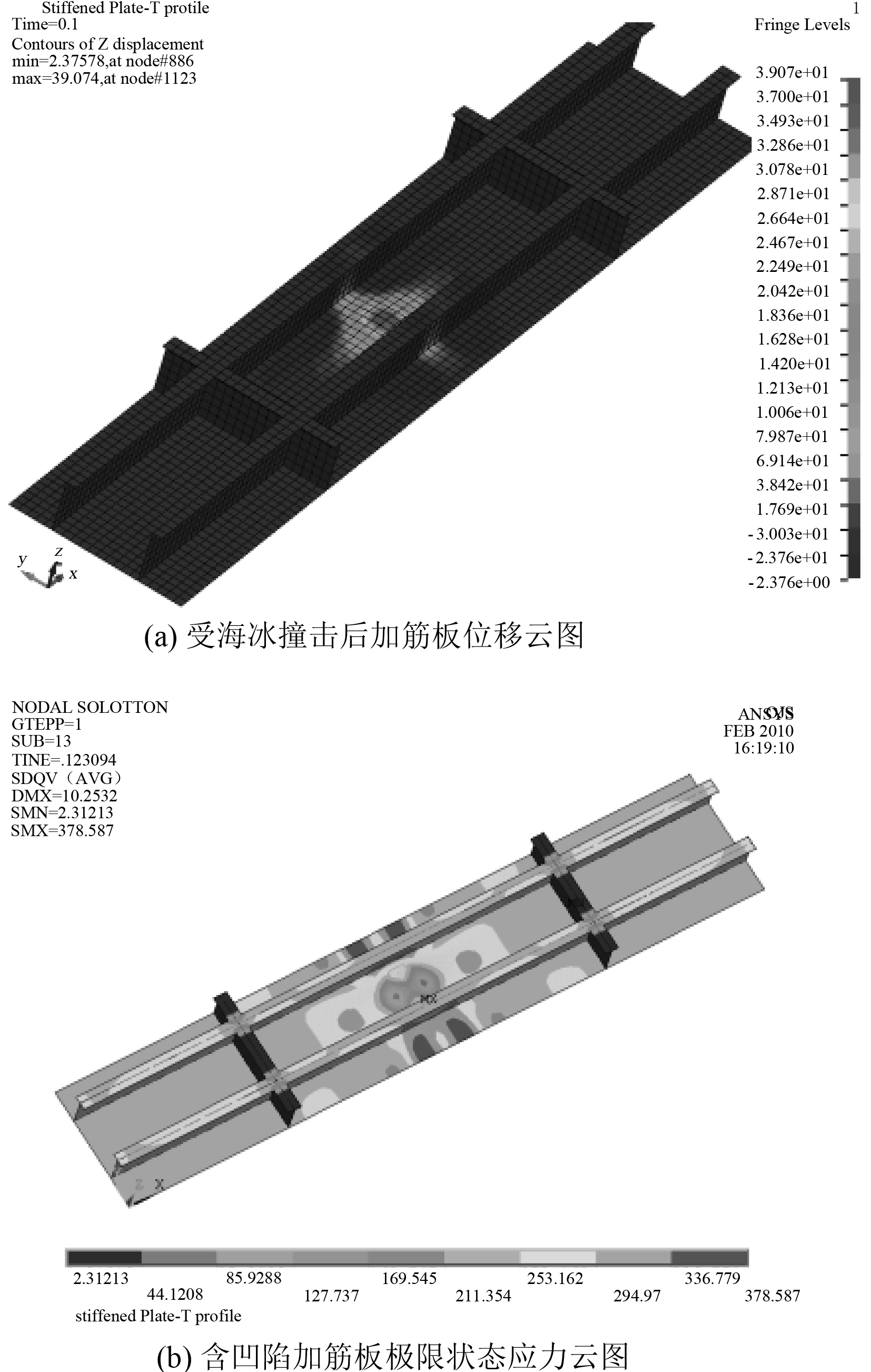
工况1下分别以2 m/s,4 m/s,6 m/s(工况1.1,1.2,1.3)的海冰撞击速度撞击加筋板板格后剩余极限强度的计算结果如图12~图15所示。
|
图 12 有限元分析结果图(2 m/s) Fig. 12 Finite element analysis results (2 m/s) |

|
图 13 有限元分析结果图(4 m/s) Fig. 13 Finite element analysis results (4 m/s) |

|
图 14 有限元分析结果图(6 m/s) Fig. 14 Finite element analysis results (6 m/s) |
|
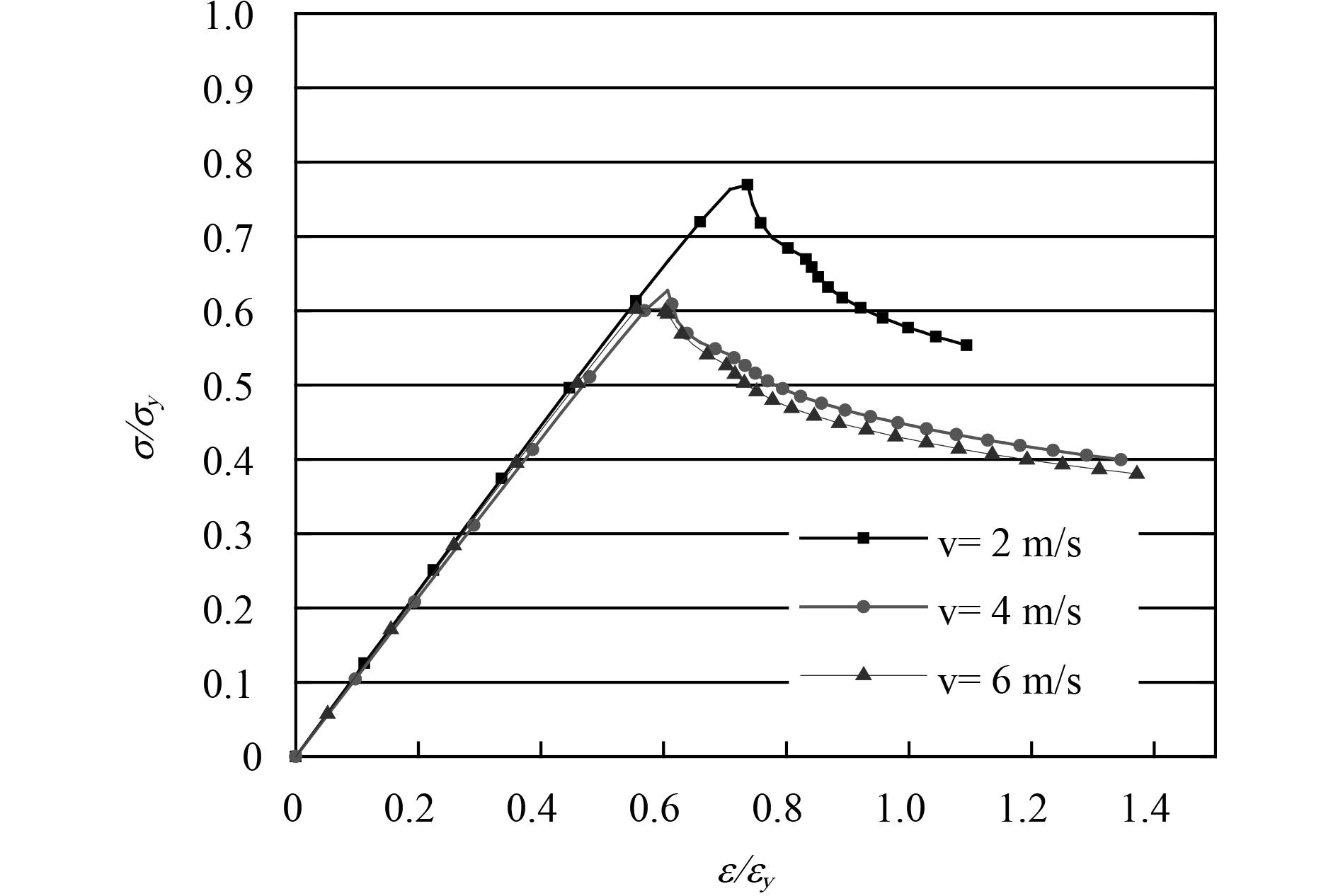
图 15 第①组应力-应变曲线图 Fig. 15 Group1 stress-strain curve |
从图12~图15中可以看出,加筋板屈曲主要集中在加筋板中部,即海冰撞击位置,加强筋发生了明显变形,含凹陷加筋板板格发生明显屈曲。由计算结果可得在工况1中,随着海冰撞击速度提高,所造成的凹陷面积和深度增加,对加筋板极限强度的衰减作用越明显。
工况2及工况3中不同速度海冰撞击加筋板板格后剩余极限强度的计算结果类似工况1。根据3种工况下的计算结果,含不同面积和深度凹陷时的加筋板无量纲极限强度如表2所示。
|
|
表 2 含不同面积和深度凹陷时的加筋板无量纲极限强度 Tab.2 Dimensionless limit strength of stiffened plates with different area and depth depression |
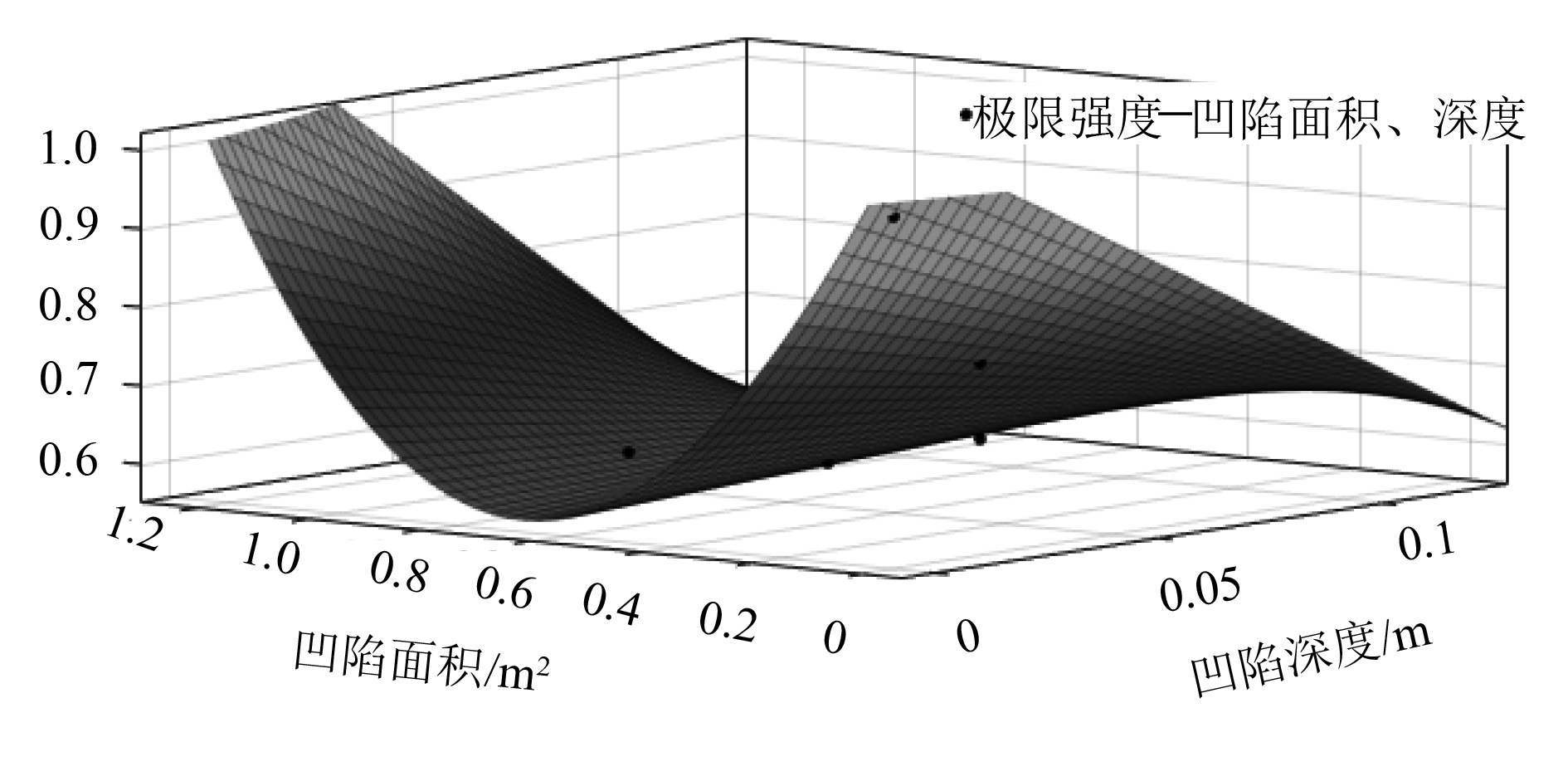
利用Matlab拟合不同的凹陷面积和深度对加筋板极限强度影响关系,如式(1)和图16所示。
|
图 16 式(1)拟合曲线图 Fig. 16 Fitting curve of formula (1) |
| $ \begin{split} \frac{{{\sigma _{duD}}}}{{{\sigma _u}}}=& f({D_{dep}},{A_{dep}})=a + b \cdot {D_{dep}} + c \cdot {A_{dep}} +\\ & d \cdot {D_{dep}} \cdot {A_{dep}} + e \cdot {A_{dep}}^2 +\\ & f \cdot {D_{dep}} \cdot {A_{dep}}^2 + g \cdot {A_{dep}}^3\text{。} \end{split} $ | (1) |
式中:
加筋板格板处凹陷对加筋板极限强度的衰减主要体现在凹陷面积上,凹陷面积和深度对加筋板极限强度的衰减作用随着面积和深度的增加而递减。计算结果可用于极地船舶结构设计中,在允许一定程度凹陷变形的情况下设计结构和航线,可以充分地利用船舶材料,提升经济效益。
4 结 语本文结合Derradji-Aouat各向同性三维失效准则和弹脆性破坏模式,提出基于线弹性的多表面失效海冰本构模型。利用Ls-dyna二次开发技术,编译生成相应的求解器,并与球形冰撞击刚性板和柱形冰撞击船体舷侧板架仿真对比分析。再利用Ls-dyna模拟海冰与船体加筋板碰撞,并将含凹陷损伤加筋板模型导入Ansys中进行加筋板剩余极限强度的计算,得到考虑凹陷影响的加筋板极限强度。本文所得结论表明:
1)根据Derradji-Aouat各向异性三维失效准则和弹脆性破坏模式,提出了适用于船-冰碰撞问题研究的基于线弹性的多表面失效海冰本构模型;
2)利用Ls-dyna二次开发技术,将多表面失效海冰本构模型编写入Ls-dyna用户自定义材料库中,生成新的求解器;
3)通过球形冰撞击钢板和柱形冰撞击舷侧板架结构试验的数值仿真,验证了包含自定义海冰本构模型求解器在船-冰碰撞模拟中的准确性;
4)加筋板格板处凹陷对加筋板极限强度的衰减主要体现在凹陷面积上,并且凹陷面积和深度对加筋板极限强度的衰减作用随着面积和深度的增加而逐步减弱。
| [1] |
GAGNON R E. A numerical model of ice crushing using a foam analogue[J]. Cold Regions Science and Technology, 2011, 65(3): 335-350. DOI:10.1016/j.coldregions.2010.11.004 |
| [2] |
DERRADJI-At A. Multi-surface failure criterion for saline ice in the brittle regime[J]. Cold Regions Science and Technology, 2003, 36(1–3): 47-70. |
| [3] |
QI K L, LIU J, LIU S W, et al. Strength assessment of polar ships under ice loads using direct calculation method[J]. Journal of Ship Mechanics, 2014, 18(6): 662-677. |
| [4] |
XU D, LIU J, LIU S W. Research on limit load criteria for polar ships under ice loads[J]. Journal of Ship Mechanics, 2014, 18(3): 280-290. |
| [5] |
DERRADJI-At A. A unified failure envelope for isotropic fresh water ice and iceberg ice[C]// 2000.
|
| [6] |
DERRADJI-At A. Multi-surface failure criterion for saline ice in the brittle regime[J]. Cold Regions Science and Technology, 2003, 36(1–3): 47-70. |
| [7] |
TIMCO G W, SUDOM D. Revisiting the sanderson pressure–area curve: defining parameters that influence ice pressure[J]. Cold Regions Science & Technology, 2013, 95(11): 53-66. |
| [8] |
张健. 冰载荷作用下船舶结构动态响应及损伤机理[M]. 北京: 国防工业出版社, 2015.
|
| [9] |
胡志强, 高岩, 姚琪. 一种理想弹塑性模拟的冰材料本构模型[J]. 船舶与海洋工程, 2016(1): 65-73. HU Zhi-qiang, GAO Yan, YAO Qi. An ideal elastoplastic constitutive model for ice materials[J]. Ship and Ocean Engineering, 2016(1): 65-73. |
 2019, Vol. 41
2019, Vol. 41
