指向精度是衡量导弹发射筒发射精度的一项重要指标,为导弹提供了初始的出筒角度,是导弹是否能够准确命中目标的关键因素之一。因此,若要保证导弹发射时具有必要的精度值,在进行导弹发射筒总体设计时,必须要对导弹发射筒的指向精度进行评估和控制。
本文以某舰载倾斜固定式导弹发射筒(以下称导弹发射筒)为研究对象,通过剖析导弹发射筒总体结构,确定了影响导弹发射筒指向精度的因素,对导弹发射筒各关键部件的制造和安装误差对指向精度的影响进行研究,运用基于均方根值(RMS)和最大值(Maximum)相结合的误差分析理论对导弹发射筒的指向精度进行统计计算,结合数据对比分析,提出一套可靠且系统的研究方法,在一定程度上解决了影响导弹发射筒指向精度各个因素之间的相位角问题,较为客观地反映了指向误差的真实情况,提高了导弹发射筒总体设计的合理性和经济性。
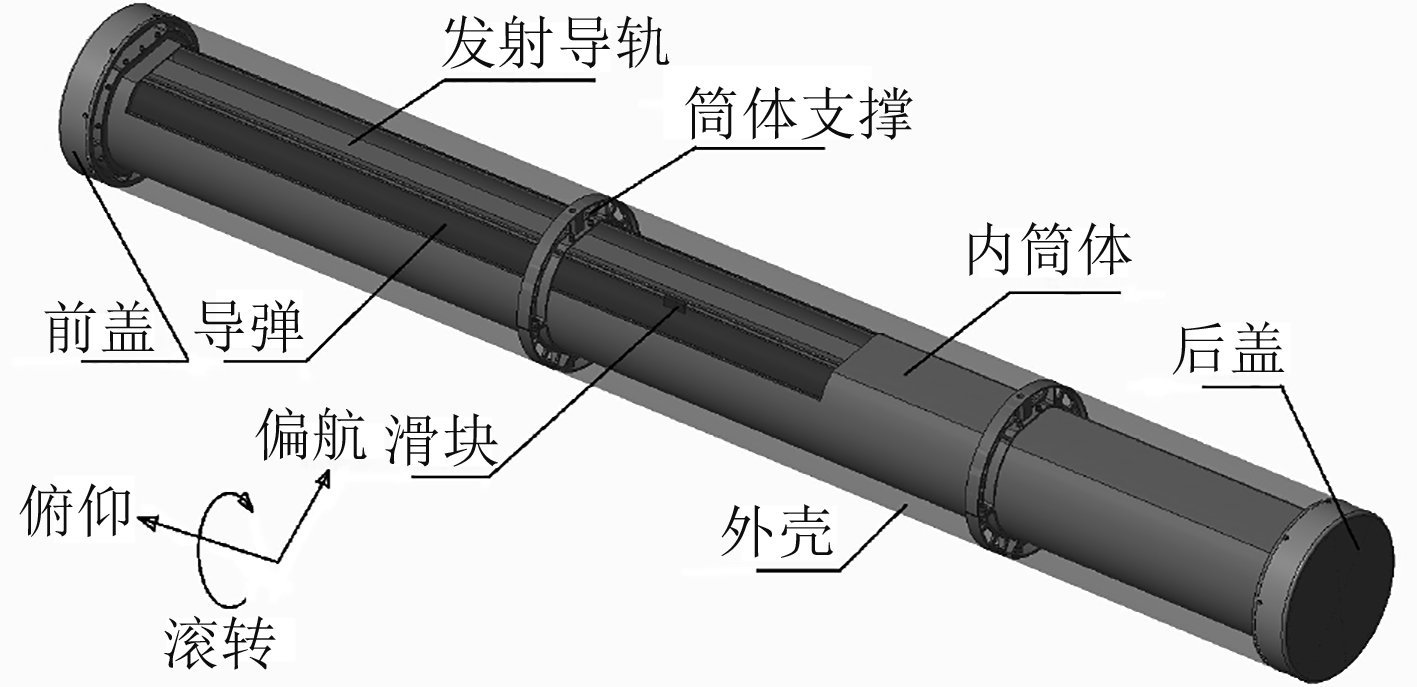
1 影响导弹发射筒指向精度因素分析 1.1 导弹发射筒结构如图1所示,导弹发射筒由导弹和发射筒组成。发射筒由内筒体、发射导轨、筒体支撑、前后盖和外壳等组成。其中,内筒体、外壳均由轻质合金薄壁材料成型,两者之间通过前后筒体支撑等连接成圆柱型框架夹层结构,保证发射筒体的结构刚强度;筒体支撑设置在内筒下部,通过固定件实现与舰上发射支架进行连接;内筒体上部安装有发射导轨,导弹通过自身滑块挂在发射导轨上;发射时,导弹沿发射导轨运动直至出筒,获得初始发射角和出筒速度。
|
图 1 导弹发射筒结构示意图 Fig. 1 The structure schematic diagram of a missile launch canister |
导弹发射筒指向误差是指导弹实际瞄准线与理想瞄准线之间的偏差,指向精度的变化可以延伸成重要的弹道偏差,有可能影响导弹正常飞行[1]和命中概率。
因此,在导弹发射筒研制过程中,指向精度的评估是十分重要的环节,需要剖析多误差源的影响[2],对误差指标进行合理的精度分析和分配,使其在各自限定的范围内指导导弹发射筒的结构型式设计和制造公差选择,为提高总体精度指明工作重点和努力方向,在改进武器系统设计的同时,节省经费并缩短研制周期。
根据某导弹发射筒的结构型式,决定其指向精度的主要有导弹和发射筒两方面。在精度分配时,需要综合衡量导弹的制导能力和定位方式、发射筒的制造难度以及结构复杂度等多种因素的影响,以达到二者合理地匹配,刻意强调和限制某一方面也不科学。
1.3 影响导弹发射筒指向精度的因素分析导弹发射筒安装在舰上基座后,导弹轴线相对于导弹发射筒的安装基准面,在俯仰、偏航和滚转3个方向均有定位误差要求,以此来保证导弹的发射精度。
导弹发射筒的准确指向受到各部分几何误差的影响,几何误差主要是由于部件加工、装配的不准确导致的制造误差以及由于外部载荷作用等原因造成的运动误差等[3]。由导弹发射筒的结构布局和工作原理可知,影响导弹发射筒指向精度的关键部件主要有:导弹滑块、发射导轨、内筒体和筒体支撑。外部影响主要是导弹发射筒工作时承受的振动和冲击载荷。由此确定的影响因素主要包括以下几个方面:导弹滑块与导弹中心线安装精度、导弹滑块与发射导轨配合精度[1]、发射导轨制造和安装精度、发射筒内筒体安装面制造精度、筒体支撑制造精度以及与内筒体安装精度、发射筒与舰上发射支架定位精度、发射筒的结构刚度。以下针对各项因素的影响逐一进行分析研究。
1.3.1 导弹的影响在对导弹的影响进行分析时,将导弹视为一个刚性体,只考虑导弹的制造误差和在发射筒内的初始定位精度,不考虑导弹的制导精度和扰动等因素的影响。
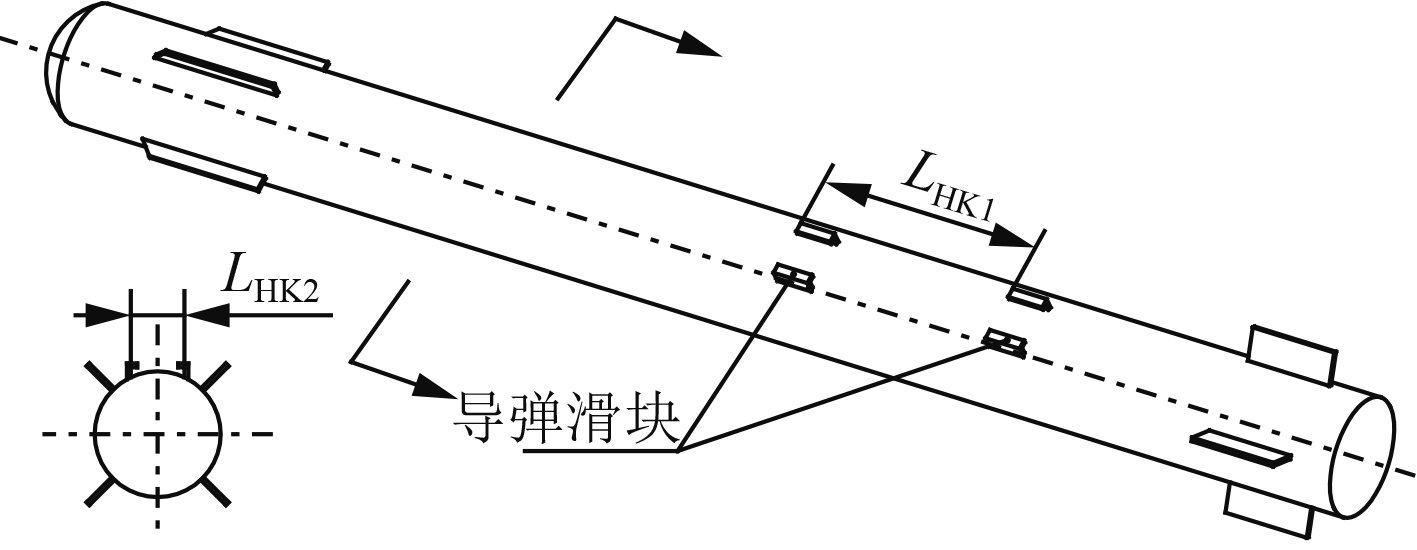
导弹对指向精度的影响主要取决于导弹滑块的安装精度以及与发射导轨的定位精度。导弹滑块位于导弹顶部,为了保证导弹发射时获得较高的初速度和发射精度,设计时应尽量保证导弹在出筒过程中,导弹滑块与发射导轨配合时间尽可能长。如图2所示,某舰载导弹设置了2个滑块,分别位于导弹的中部和后部。导弹滑块通过与发射导轨配合,为导弹提供初始发射精度。
|
图 2 某舰载导弹结构示意图 Fig. 2 The structure schematic diagram of a ship-based missile |
导弹滑块导轨配合面与导弹中心的轴向平行度误差为δPX1,导弹前后滑块之间的距离为LHK1。则由于导弹滑块导轨配合面与导弹中心的轴向平行度影响所产生的俯仰误差βD1为:
| $ {{\rm{\beta }}_{{{D_{1}}}}} = {\rm{arctan}}\left( {{{\rm{\delta }}_{{{PX_{1}}}}}/{{{L}}_{{{HK_{1}}}}}} \right){\text{。}} $ | (1) |
导弹滑块导轨配合面与导弹中心的横向平行度误差为δPX2,导弹滑块配合面宽度为LHK2,则由于导弹滑块导轨配合面与导弹中心的平行度影响所产生的滚转误差γD1为:
| $ {{\rm{\gamma }}_{{{D_{1}}}}} = {\rm{arctan}}\left( {{{\rm{\delta }}_{{{PX_{2}}}}}/{{{L}}_{{{HK_{2}}}}}} \right){\text{。}} $ | (2) |
导弹前后滑块与导弹中心线对称度误差为δDC1,导弹前后滑块之间的距离为LHK1。则由于导弹前后滑块与导弹中心线对称度影响所产生的偏航误差αD1为:
| $ {{\rm{\alpha }}_{{{D_{1}}}}} = {\rm{arctan}}\left( {{{\rm{\delta }}_{{{DC_{1}}}}}/{{{L}}_{{{HK_{1}}}}}} \right){\text{。}} $ | (3) |
导弹滑块与发射导轨侧向间隙为δJX1,发射导轨长度为LDG1,则由于导弹滑块与发射导轨侧向间隙影响所产生的偏航误差αD2为:
| $ {{\rm{\alpha }}_{{{D_{2}}}}} = {\rm{arctan}}\left( {{{\rm{\delta }}_{{{JX_{1}}}}}/{{{L}}_{{{DG_{1}}}}}} \right){\text{。}} $ | (4) |
导弹滑块与发射导轨垂向间隙为δJX2,发射导轨长度为LDG1,则由于导弹滑块与发射导轨垂向间隙影响所产生的俯仰误差βD2为:
| $ {{\rm{\beta }}_{{{D_{2}}}}} = {\rm{arctan}}\left( {{{\rm{\delta }}_{{{JX_{2}}}}}/{{{L}}_{{{DG_{1}}}}}} \right){\text{。}} $ | (5) |
发射导轨安装在发射筒的内筒体内侧顶部,与导弹滑块配合,实现导弹在发射筒内的初始安装和固定;保证在导弹发射时约束导弹并赋予导弹起始运动的方向及合适的离轨速度[4],是影响导弹发射筒指向精度的关键部件,其加工和装配水平直接决定导弹的初始角度。
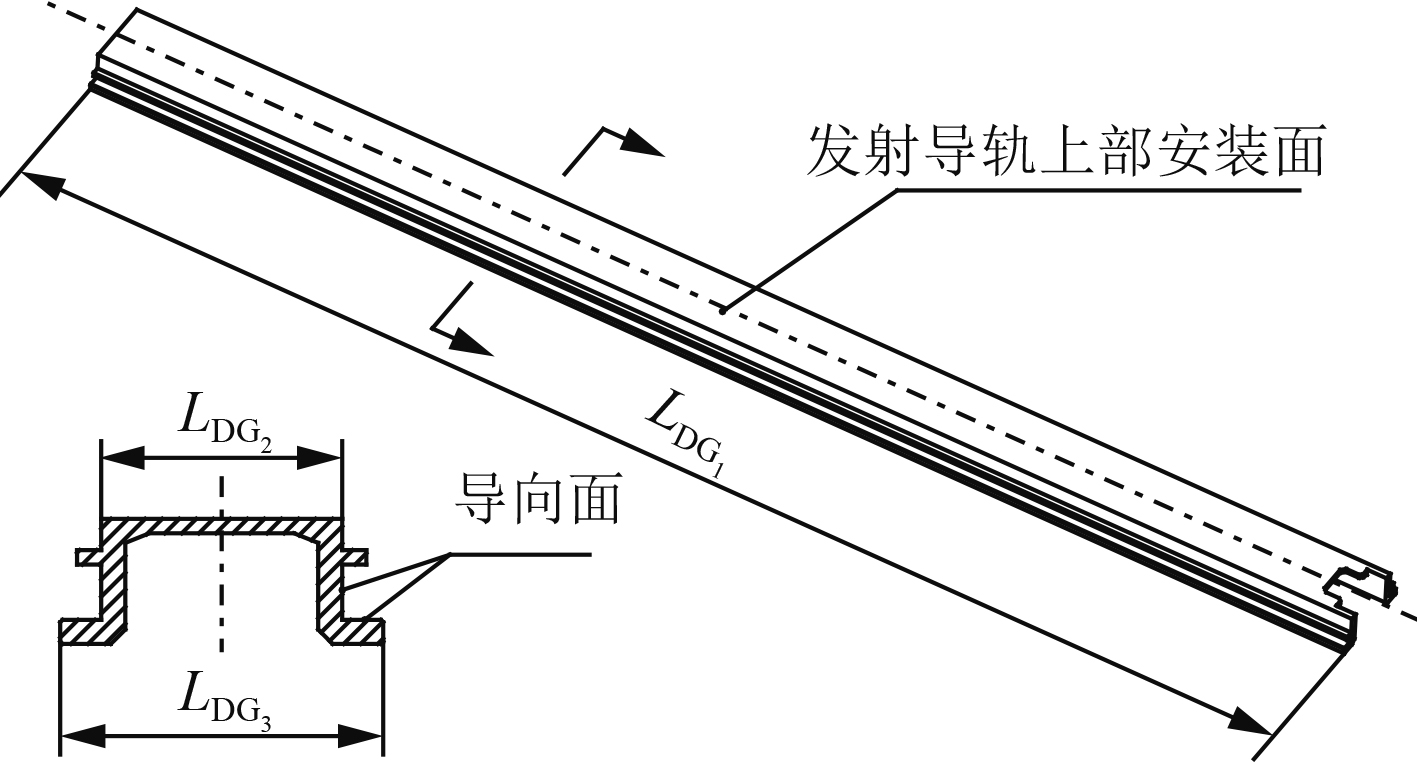
如图3所示,发射导轨的加工精度主要包括发射导轨上部安装面以及各导向面的直线度、倾斜度和平行度等形位公差[1],分别产生俯仰误差、滚转误差以及偏航误差;发射导轨的安装精度也是产生指向误差的重要因素,会引起偏航误差。
|
图 3 发射导轨结构示意图 Fig. 3 The structure schematic diagram of launching guide |
1)发射导轨上部安装面加工精度的影响
发射导轨上部安装面轴向直线度误差为δZX1,发射导轨长度为LDG1,则由于发射导轨上部安装面轴向直线度影响所产生的俯仰误差βT1为:
| $ {{\rm{\beta }}_{{{T_{1}}}}} = {\rm{arctan}}\left( {{{\rm{\delta }}_{{{ZX_{1}}}}}/{{{L}}_{{{DG_{1}}}}}} \right){\text{。}} $ | (6) |
发射导轨上部安装面横向倾斜度误差为δQX1,发射导轨上部安装面宽度为LDG2。则由于发射导轨上部安装面横向倾斜度影响所产生的滚转误差γT1为:
| $ {{\rm{\gamma }}_{{{T_{1}}}}} = {\rm{arctan}}\left( {{{\rm{\delta }}_{{{QX_{1}}}}}/{{{L}}_{{{DG_{2}}}}}} \right){\text{。}} $ | (7) |
2)发射导轨与导弹滑块配合面加工精度的影响
发射导轨导弹滑块配合面与安装面轴向平行度误差为δPX3,发射导轨长度为LDG1,则由于发射导轨导弹滑块配合面与安装面轴向平行度影响所产生的俯仰误差βT2为:
| $ {{\rm{\beta }}_{{{T_{2}}}}} = {\rm{arctan}}\left( {{{\rm{\delta }}_{{{PX_{3}}}}}/{{{L}}_{{{DG_{1}}}}}} \right){\text{。}} $ | (8) |
发射导轨导弹滑块配合面与安装面横向平行度为δPX4,发射导轨导弹滑块配合面宽度为LDG3,则由于发射导轨导弹滑块配合面与安装面横向平行度影响所产生的滚转误差γT2为:
| ${{\rm{\gamma }}_{{{T_{2}}}}} = {\rm{arctan}}\left( {{{\rm{\delta }}_{{{PX_{4}}}}}/{{{L}}_{{{DG_{3}}}}}} \right){\text{。}} $ | (9) |
发射导轨导弹滑块配合面与导轨中心线对称度误差为δDC2,发射导轨长度为LDG1,则由于发射导轨导弹滑块配合面与导轨中心线对称度影响所产生的偏航误差αT1为:
| ${{\rm{\alpha }}_{{{T_{1}}}}} = {\rm{arctan}}\left( {{{\rm{\delta }}_{{{DC_{2}}}}}/{{{L}}_{{{DG_{1}}}}}} \right){\text{。}} $ | (10) |
3)发射导轨安装精度的影响
发射导轨侧向工作面中心线与内筒首尾刻线安装误差为δAZ1,发射导轨长度为LDG1,则由于发射导轨安装精度影响所产生的偏航误差αT2为:
| $ {{\rm{\alpha }}_{{{T_{2}}}}} = {\rm{arctan}}\left( {{{\rm{\delta }}_{{{AZ_{1}}}}}/{{{L}}_{{{DG_{1}}}}}} \right){\text{。}} $ | (11) |
如图4所示,发射筒的内筒体用于连接发射导轨和筒体支撑,是发射筒的主承力部件。由于内筒体加工及安装要素较多,其制造精度对发射筒的指向精度影响较大。因此,对内筒体的成型质量和制造精度提出了较高的要求。

|
图 4 内筒体结构示意图 Fig. 4 The structure schematic diagram of inner cylinder |
1)发射筒内筒导轨安装面制造精度的影响
发射筒内筒导轨安装面与内筒中心线的轴向平行度误差为δPX5,内筒导轨安装面长度为LNT1,则由于发射筒内筒导轨安装面与内筒中心线的平行度影响所产生的俯仰误差βT3为:
| $ {{\rm{\beta }}_{{{T_{3}}}}} = {\rm{arctan}}\left( {{{\rm{\delta }}_{{{PX_{5}}}}}/{{{L}}_{{{NT_{1}}}}}} \right){\text{。}} $ | (12) |
发射筒内筒导轨安装面与内筒中心线的横向平行度误差为δPX6,内筒导轨安装面宽度为LNT2,则由于发射筒内筒导轨安装面与内筒中心线的平行度影响所产生的滚转误差γT3为:
| $ {{\rm{\gamma }}_{{{T_{3}}}}} = {\rm{arctan}}\left( {{{\rm{\delta }}_{{{PX_{6}}}}}/{{{L}}_{{{NT_{2}}}}}} \right){\text{。}} $ | (13) |
2)发射筒内筒筒体支撑安装面制造精度的影响
发射筒内筒筒体支撑安装面与内筒中心线的轴向平行度误差为δPX7,内筒筒体支撑安装面长度为LNT3,则由于发射筒内筒筒体支撑安装面与内筒中心线的平行度影响所产生的俯仰误差βT4为:
| $ {{\rm{\beta }}_{{{T_{4}}}}} = {\rm{arctan}}\left( {{{\rm{\delta }}_{{{PX_{7}}}}}/{{{L}}_{{{NT_{3}}}}}} \right){\text{。}} $ | (14) |
发射筒内筒筒体支撑安装面与内筒中心线的横向平行度误差为δPX8,内筒筒体支撑安装面宽度为LNT4,则由于发射筒内筒筒体支撑安装面与内筒中心线的平行度影响所产生的滚转误差γT4为:
| $ {{\rm{\gamma }}_{{{T_{4}}}}} = {\rm{arctan}}\left( {{{\rm{\delta }}_{{{PX_{8}}}}}/{{{L}}_{{{NT_{4}}}}}} \right){\text{。}} $ | (15) |
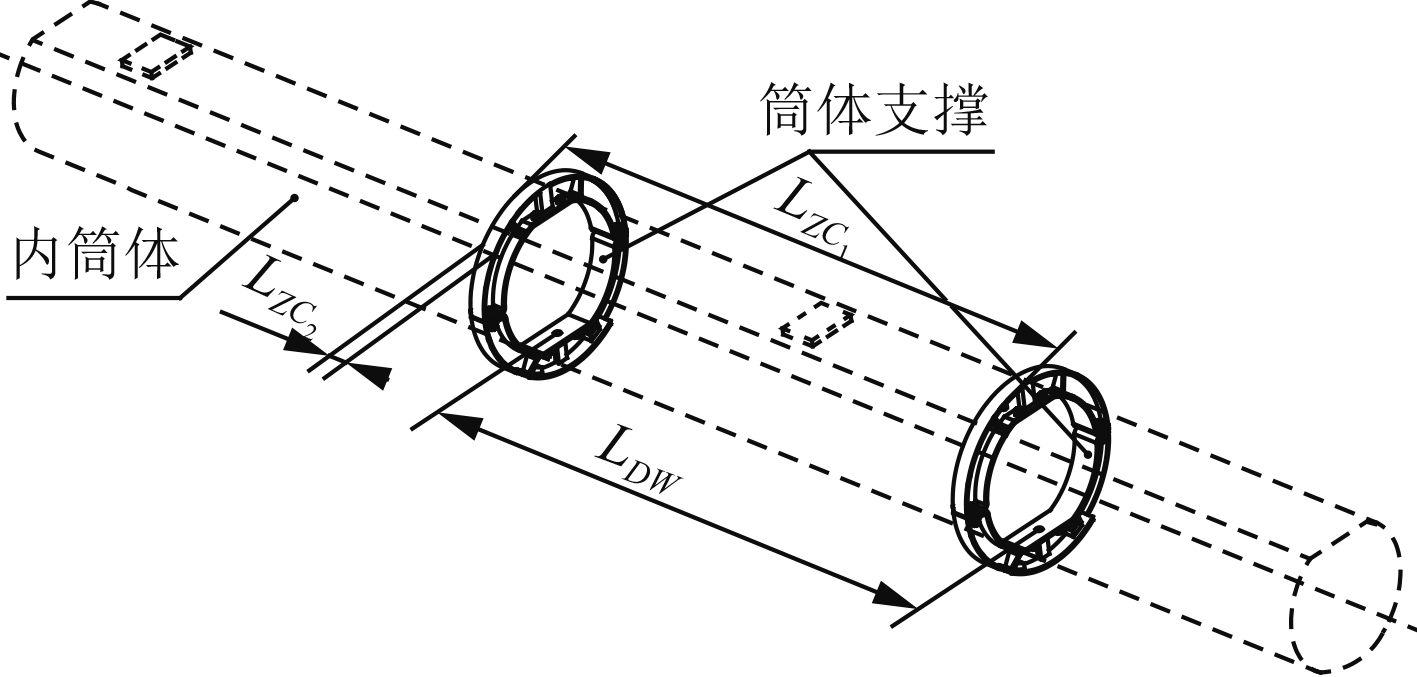
如图5所示,筒体支撑安装在内筒体上,通过与发射支架的安装接口,实现发射筒与发射支架的固定;在发射支架上安装完毕后,使用定位销来固化发射筒与发射支架的相对位置,以保证导弹发射筒的指向精度。
|
图 5 筒体支撑结构示意图 Fig. 5 The structure schematic diagram of cylinder support |
1)筒体支撑制造精度的影响
筒体支撑安装面与其中心线的轴向平行度误差为δPX9,筒体支撑安装面长度为LZC1,则由于筒体支撑安装面与其中心线的平行度影响所产生的俯仰误差βT5为:
| ${{\rm{\beta }}_{{{T_{5}}}}} = {\rm{arctan}}\left( {{{\rm{\delta }}_{{{PX_{9}}}}}/{{{L}}_{{{ZC_{1}}}}}} \right){\text{,}} $ | (16) |
筒体支撑安装面与其中心线的横向平行度误差为δPX10,筒体支撑安装面宽度为LZC2。则由于筒体支撑安装面与其中心线的平行度影响所产生的滚转误差γT5为:
| $ {{\rm{\gamma }}_{{{T_{5}}}}} = {\rm{arctan}}\left( {{{\rm{\delta }}_{{{PX_{10}}}}}/{{{L}}_{{{ZC_{2}}}}}} \right){\text{。}} $ | (17) |
2)筒体支撑与内筒安装精度的影响
筒体支撑中心刻线与内筒艏艉刻线安装偏差为δAZ2,内筒筒体支撑安装面长度为LNT3,则由于筒体支撑中心刻线与内筒艏艉刻线安装偏差影响所产生的偏航误差αT3为:
| $ {{\rm{\alpha }}_{{{T_{3}}}}} = {\rm{arctan}}\left( {{{\rm{\delta }}_{{{AZ_{2}}}}}/{{{L}}_{{{NT_{3}}}}}} \right){\text{。}} $ | (18) |
发射筒定位销孔与发射架定位销之间的配合间隙为δJX3,发射筒前后定位销之间的距离为LDW,则由于发射筒定位销孔与发射架定位销之间的配合间隙影响所产生的偏航误差αT4为:
| $ {{\rm{\alpha }}_{{{T_{4}}}}} = {\rm{arctan}}\left( {{{\rm{\delta }}_{{{JX_{3}}}}}/{{{L}}_{{{DW}}}}} \right){\text{。}} $ | (19) |
发射筒的强度和刚度应能够承受导弹在吊装、装填、贮存、运输和发射过程中产生的振动和冲击载荷,包括轴向、横向和法向3个方向的过载要求。这些作用于发射筒上的不平衡载荷会引起导弹瞄准线产生变化[1],对发射筒的偏航误差和俯仰误差产生动态的影响。这也是影响导弹发射筒指向精度的重要因素之一。
通过对发射筒进行有限元计算分析,可得出由于过载载荷引起的横向变形为Δ横向,法向变形为Δ法向,发射筒内筒体长度为LNT5,则发射筒结构刚度对偏航误差、俯仰误差的影响为:
| $ {{\rm{\alpha }}_{{\rm{T}}{\text{结构刚度}}}} = {\rm{arctan}}({{\rm{\Delta }}_{{\text{横向}}}}/{{{L}}_{{{NT_{5}}}}}){\text{,}} $ | (20) |
| $ {{\rm{\beta }}_{{\rm{T}}{\text{结构刚度}}}} = {\rm{arctan}}({{\rm{\Delta }}_{{\text{法向}}}}/{{{L}}_{{{NT_{5}}}}}){\text{。}} $ | (21) |
通过对影响导弹发射筒指向精度的各个因素进行分析,结果如表1所示。
|
|
表 1 指向误差汇总 Tab.1 Pointing error summary |
表1中序号1~2和3~6描述的分别为导弹和发射筒的结构固有静态指向误差;序号7描述的是由于发射筒受到不平衡载荷引起的动态指向误差。
2 导弹发射筒指向误差统计方法 2.1 统计方法对于传统的误差计算方法一般是将各种因素产生的指向误差简单地作代数运算,但由于各种误差不是同时处于最大值和完全相同的相位角,这种最大值误差统计方法得出的计算结果虽然安全但不能得到比较经济的设计,价值有限[5],不能体现产品真实的指向精度。
本文运用一种均方根值和最大值相结合的统计方法。以发射筒为例,首先将发射筒静态指向误差和动态指向误差进行分类;然后将同类各项误差进行平方相加,然后取其均值[6];最后将均方处理后静态指向误差和动态指向误差进行代数运算。同理计算出导弹的指向精度后,与发射筒指向精度取代数和,将所得结果近似认为是导弹发射筒的指向精度。这种统计方法可以保证在具有合理的安全裕度的前提下,得到较为经济的设计。
1)导弹发射筒的偏航误差α偏航误差统计方法如下:
| $ \begin{split} {\alpha _{\text{偏航误差}}} =& {\alpha _D} + {\alpha _T} = {\alpha _D} + \left( {{\alpha _{{\rm{T}}{\text{静态}}}} + {\alpha _{{\rm{T}}{\text{动态}}}}} \right)=\\ & \sqrt {\displaystyle\sum\limits_{{{k}} = 1}^{{n}} {{\alpha _{{\rm{Dk}}}}^2} } + \left( {\sqrt {\displaystyle\sum\limits_{{{j}} = 1}^{{m}} {{\alpha _{{\rm{Tj}}}}^2} } + {\alpha _{{\rm{T}}{\text{结构刚度}}}}}\!\! \right){\text{。}} \end{split} $ | (22) |
式中:αD为导弹的偏航误差;αT为发射筒的偏航误差;αT静态为发射筒的静态偏航误差;αT动态为发射筒的动态偏航误差。
2)导弹发射筒的俯仰误差β俯仰误差统计方法如下:
| $ \begin{split} {\beta _{\text{俯仰误差}}} &= {\beta _D} + {\beta _T} = {\beta _D} + \left( {{\beta _{{\rm{T}}{\text{静态}}}} + {\beta _{{\rm{T}}{\text{动态}}}}} \right)=\\ & \sqrt {\displaystyle\sum\limits_{{{k}} = 1}^{{n}} {{\beta _{{\rm{Dk}}}}^2} } + \left( {\sqrt {\displaystyle\sum\limits_{{{j}} = 1}^{{m}} {{\beta _{{\rm{Tj}}}}^2} } + {\beta _{{\rm{T}}{\text{结构刚度}}}}} \right){\text{。}} \end{split} $ | (23) |
式中:βD为导弹的俯仰误差;βT为发射筒的俯仰误差;βT静态为发射筒的静态俯仰误差;βT动态为发射筒的动态俯仰误差。
3)导弹发射筒的滚转误差γ滚转误差统计方法如下:
| ${\gamma _{\text{滚转误差}}} = {\gamma _{\rm{D}}} + {\gamma _{\rm{T}}} = \sqrt {\sum\limits_{{{k}} = 1}^{{n}} {{\gamma _{{\rm{Dk}}}}^2} } + \sqrt {\sum\limits_{{{j}} = 1}^{{m}} {{\gamma _{{\rm{Tj}}}}^2} } {\text{。}}$ | (24) |
式中:γD为导弹的滚转误差;γT为发射筒的滚转误差。
2.2 统计结果和数据分析在导弹发射筒设计过程中,根据设计输入阶段的初始精度分配,对导弹发射筒各部件选择了相应的公差范围,对导弹发射筒的静态误差进行了分析计算。采用Ansys有限元分析方法,对发射筒动态指向精度进行仿真,仿真结果如图6所示。运用本文提出的RMS+Maximum统计方法,对导弹发射筒初始精度分配进行复核复算,最终确定了产品尺寸链并优化了各零部件的公差,指导了产品制造时合理的工艺选择。

|
图 6 发射筒有限元仿真结果 Fig. 6 Finite element simulation results of launch canister |
采用“激光垂准仪+标准靶标”的试验方法,对导弹发射筒静态指向精度进行测量;发射筒动态指向精度采用有限元仿真结果。导弹发射筒指向误差数据的对比情况如表2所示。
|
|
表 2 指向误差数据对比表 Tab.2 Pointing error data contrast table |
对比可知,本文所提出的RMS+Maximum统计方法计算出来的数据结果满足初始精度分配指标,在一定程度上消除了同类各项误差之间的相位角问题,较为符合产品生产加工中设备及人员的实际条件,与实际产品的测量结果符合度较高,并具有合理的安全裕度,在一定程度上可指导总体精度指标的确定,具有一定的现实价值和实用性。
3 提高导弹发射筒指向精度的措施 3.1 提高各关键部件的加工和安装精度导弹发射筒指向精度与各关键部件的加工和安装精度关系十分密切。因此,产品试制时,在工艺、设备、人员等条件允许的情况下,在精度分配指标合理的范围内,尽可能提高发射导轨、内筒、筒体支撑等关键部件的加工精度和形位公差等级,增强互换性。利用定位工装和修配手段减少或消除装配误差,以此提高导弹发射筒的指向精度。
3.2 合理的进行结构设计导弹发射筒结构型式的优劣直接影响其指向精度。因此,在导弹发射筒设计过程中,在结构刚度和负载允许的前提下,合理的布置总体结构,尽可能的减少零件数量,以一体式设计代替分级组装结构,减少中间环节。在导弹和发射筒等关键配合处设置可调结构或功能,通过后期修配和标定等手段,提高导弹发射筒的指向精度。
3.3 减少误差源误差源越多,则对导弹发射筒的累积影响就越大。因此,在条件允许的情况下,可最大限度地减少误差源[7],以提高指向精度。比如,通过采用锥销或夹紧套等措施,可有效地消除导弹发射筒和发射支架的配合间隙误差。另外,导弹滑块与发射导轨侧向和垂向间隙也可以通过增加止挡块等措施予以消除,减少误差源,提高导弹发射筒的指向精度。
总之,合理制定关键部件的制造精度、优化结构设计、减少误差源,是提高导弹发射筒指向精度的最重要的途径,三者只能有机的处理,不能片面强调某一方面,比如对精度过低的部件而想只用改进结构的方法获得较高的指向精度,这也是不现实的。
4 结 语通过本文的相关论述,使导弹发射筒指向误差研究有了一个较为具体的理论体系,结合多种统计方法与实测结果的符合度分析,对如何提高导弹发射筒的指向精度提出了有效的解决途径,减少了总体精度指标确定的不合理性以及后续设计工作的盲目性,对于导弹发射筒的总体设计和制备工作具有一定的指导意义和应用价值。
| [1] |
姚昌仁, 张波. 火箭导弹发射装置设计[M]. 北京: 北京理工大学出版社, 1998.
|
| [2] |
徐挺, 李斐, 王霞. 指导系统精度分析及误差分配方法[J]. 四川兵工学报, 2014, 35(3): 18-20. XU Ting, LI Fei, WANG Xia. Accuracy analysis and error distribution of guidance system[J]. Journal of Sichuan Ordance, 2014, 35(3): 18-20. DOI:10.11809/scbgxb2014.03.005 |
| [3] |
王晨晨, 胡祥涛. 光电稳定平台指向误差建模与分析[J]. 新型工业化, 2014, 4(2): 86-90. WANG Chen-chen, HU Xiang-tao. The modeling and analysis of opto-electronic stabilized platform pointing accuracy[J]. The Journal of New Industrialization, 2014, 4(2): 86-90. |
| [4] |
吴秉贤, 严世泽, 龚龙兴. 火箭发射装置结构分析[M]. 北京: 国防工业出版社, 1988.
|
| [5] |
叶期传, 徐辅仁, 王新华. 用概率统计法计算齿轮机构的回差[J]. 机电设备, 2003(1): 16-19. YE Qi-chuan, XU Fu-ren, WANG Xin-hua. Calculating the return stagnant angle of the gearing by use of probability statistic[J]. Mechanical and Electrical Equipment(Marine), 2003(1): 16-19. DOI:10.3969/j.issn.1005-8354.2003.01.003 |
| [6] |
张家华. 某型跟踪雷达传动误差及回差测量方法[J]. 舰船电子对抗, 2002, 25(2): 40-41. ZHANG Jia-hua. Measurement method of transmission error and return stagnant for a tracking radar[J]. Shipboard Electronic Countermeasure, 2002, 25(2): 40-41. DOI:10.3969/j.issn.1673-9167.2002.02.012 |
| [7] |
孙新学, 李文武, 荣茜, 等. 提高机械传动精度的方法和措施[J]. 机床与液压, 2004(3): 166-170. SUN Xin-xue, LI Wen-wu, RONG Qian, et al. Methods and measures to improve the precision of mechanical transmission[J]. Machine Tool & Hydraulics, 2004(3): 166-170. |
 2019, Vol. 41
2019, Vol. 41
