目前研究水中兵器在水中运动状态的方法主要有实验和数值模拟2种方法。实验方法成本高、周期长、结果不精确。数值模拟方法分为解运动微分方程法和CFD方法,前者对运动的微分方程进行精确的求解,但是忽略水下流场的复杂状况,是一种简单化和理想化的求解方法。后者利用CFD软件可以有效模拟水下真实状况,特别是水下复杂流场的模拟和运动状态的监视,更加符合实际情况。
本文采用重叠网格方法和6-DOF方法对水中兵器在水下侧向流中的运动状态进行数值仿真,研究了鱼雷发射速度对鱼雷轨迹[1]和姿态角的影响,为鱼雷安全发射提供理论依据,研究质心浮心的距离对姿态角的影响,得到最优的质浮心间距,为鱼雷运动的稳定性提供理论依据。模拟鱼雷发射后的运动状态,得到鱼雷结构参数和发射参数对于运动状态的影响[6]。为鱼雷结构设计的优化和发射参数的调整以及鱼雷发射的运动控制和调整提供理论支持。可以有效地减少水中兵器研制过程中的湖试和海试次数,有效地降低研制费用。
1 模型简介 1.1 鱼雷模型 1.1.1 几何模型几何模型如图1所示。

|
图 1 鱼雷几何模型 Fig. 1 The geometry model of torpedo |
网格模型如图2所示。鱼雷及水池的网格数量200万左右,在头尾等曲率大、尺寸变化较大的地方做了网格加密,以保证网格质量。

|
图 2 鱼雷及水池网格模型 Fig. 2 The mesh model of torpedo and tank |
鱼雷外包裹一层嵌套网格,此网格大小与外部流场网格大小一致,重叠网格区域网格数量30万左右。
2 数值仿真 2.1 模型设置本文主要模拟鱼雷在发射后的纵向和轴向的质心运动轨迹,以及绕Y轴的姿态角变化规律。水池的X+,X–,Z+,Z–设置为对称面,Y–为速度入口,Y+为压力出口。选择隐式非稳态模型,湍流模型选择K-Epsilon模型,选择有限体积法中的分离流求解方法。
2.2 数值仿真方法简介 2.2.1 重叠网格方法重叠网格方法[7]是一种区域分割与网格组合的策略。首先复杂流场区域按网格生成的需要被分解,并在各个区域内生成高质量的网格块,网格块之间可能共享边界,也可能共享一片区域,其次对所有网格块进行预处理,将多余的网格节点删除,然后建立网格块的流场变量在重叠区域边界上的传递关系。网格预处理使得网格块重新组合成1套可用的计算网格,最后每个分块网格根据各自网格类型使用不同的求解器并行独立运算,流场信息在重叠区域通过差值运算进行交流和耦合,最终使得流场收敛并获得整个计算域的流场分布。
本文研究对象运动幅度大,时间步长小,重叠网格技术可以较好地模拟鱼雷运动过程的状态变化。该方法的网格分为背景区域和重叠网格区域(见图3),背景区域为整个水池的计算域,重叠区域为包含鱼雷的运动区域,在数值计算时2个区域通过交界面进行数据交换,利用重叠网格相对背景网格的运动代替鱼雷相对水池的运动。

|
图 3 重叠网格模型 Fig. 3 The overset mesh model |
6-DOF模型采用STAR-CCM+中的六自由度求解模型[4]来定义鱼雷质量、质心位置、转动惯量、发射速度、发射角度等参数,视鱼雷为刚体,将其动量方程和动量矩方程对时间t求导,利用六自由度求解器求解鱼雷运动参数。
3 仿真结果与分析STAR-CCM+[3]提供强大的后处理功能,用以对计算结果进行分析处理,也可以用可视化方法对鱼雷及水池流场予以显示。本文首先对质心在浮心100 mm前,发射速度为10 m/s的鱼雷进行数值仿真,对比试验数据,分析模型可靠性。
图4~图5可见鱼雷发射在不同时刻的速度云图,鱼雷发射后2 s内基本平稳前进,同时由于负浮力作用向下运动。可以观察到鱼雷头部下方速度大于头部上方速度,尾部上方速度大于尾部下方速度,鱼雷绕Y轴正向转动。

|
图 4 速度云图(t=1 s) Fig. 4 Contour of velocity when time is 1 s |

|
图 5 速度云图(t=2 s) Fig. 5 Contour of velocity when time is 2 s |
图6显示鱼雷运动2 s后流场的绝对压力分布图,水池上方绝对压力较小,下方绝对压力较大,鱼雷上表面压力较小下表面压力较大。且头部压力略大于尾部压力,故鱼雷有向下的倾角。
|
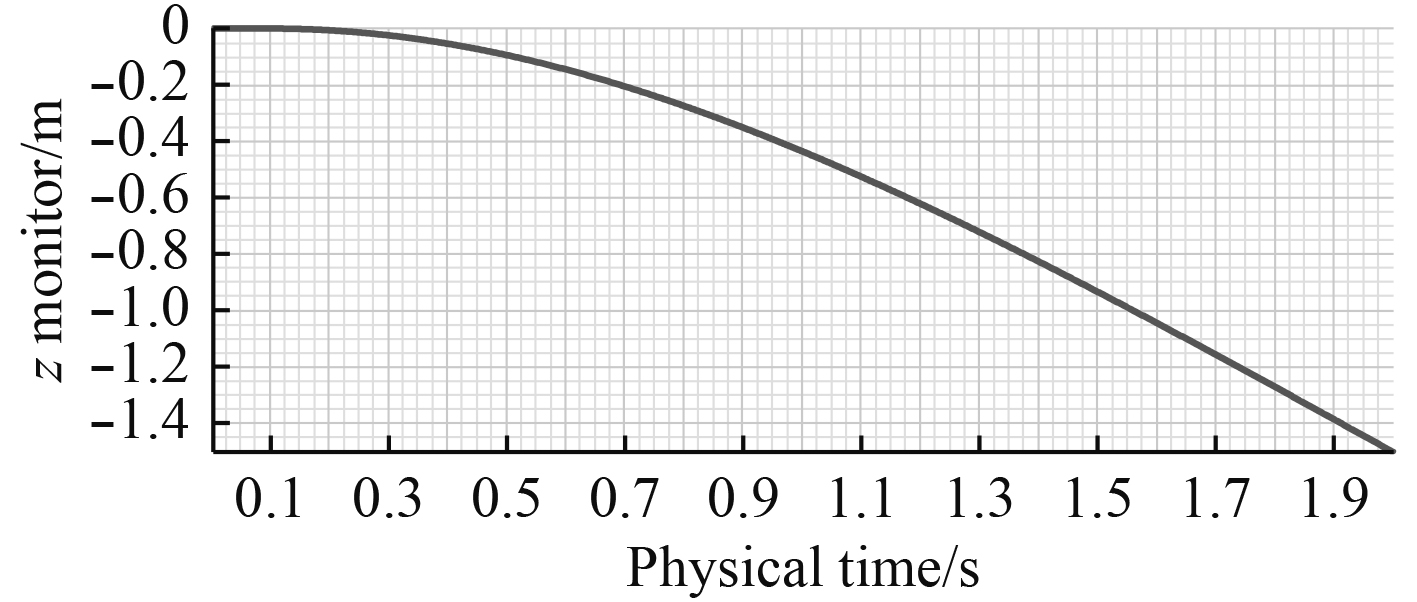
图 8 Z轴向位移 Fig. 8 The distance of Z axis |

|
图 6 压力云图(t=2 s) Fig. 6 Contour of Absolute pressure when time is 2 s |
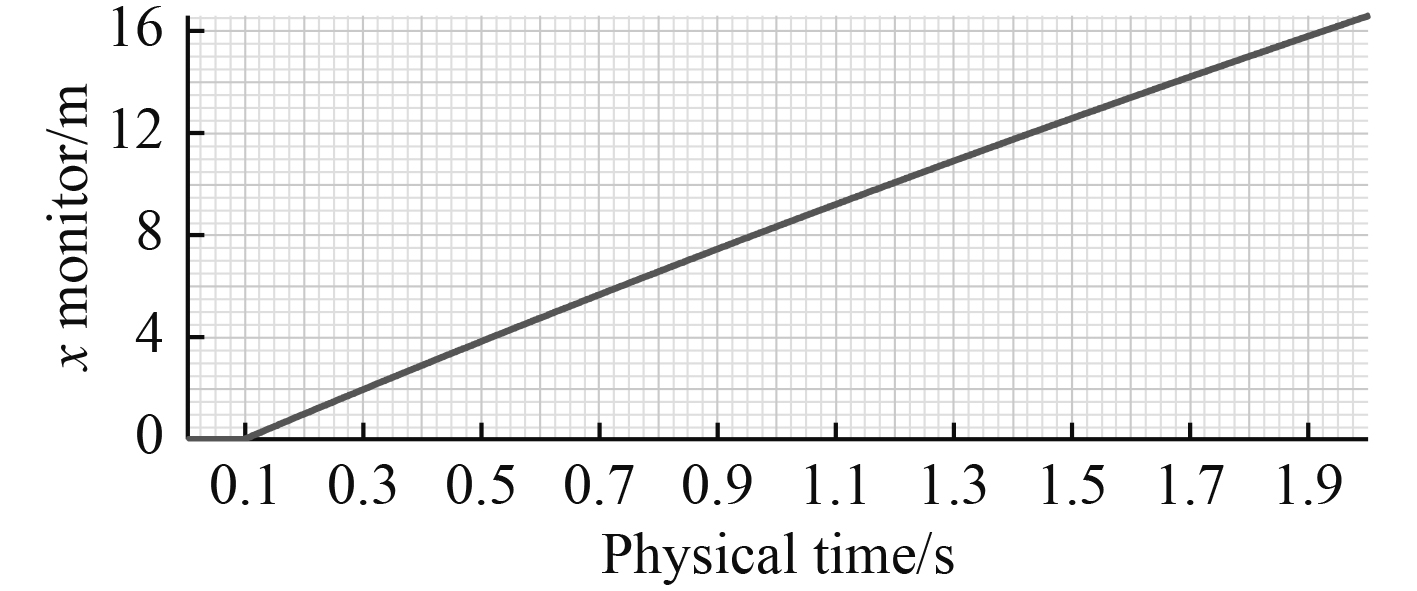
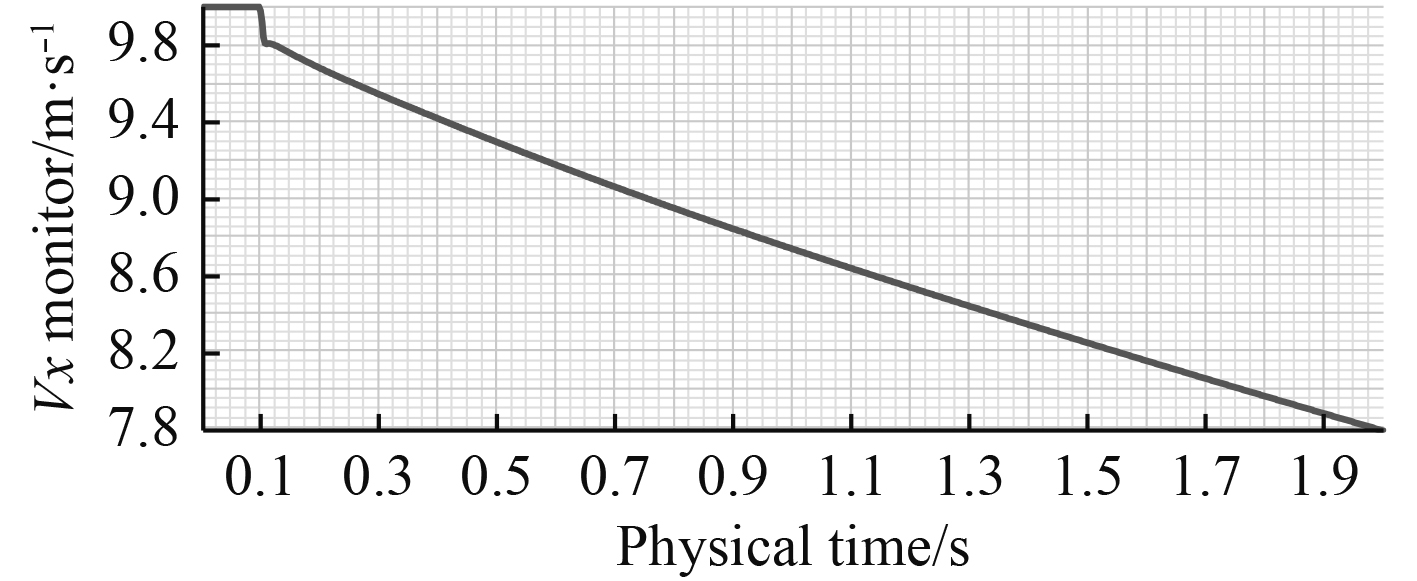
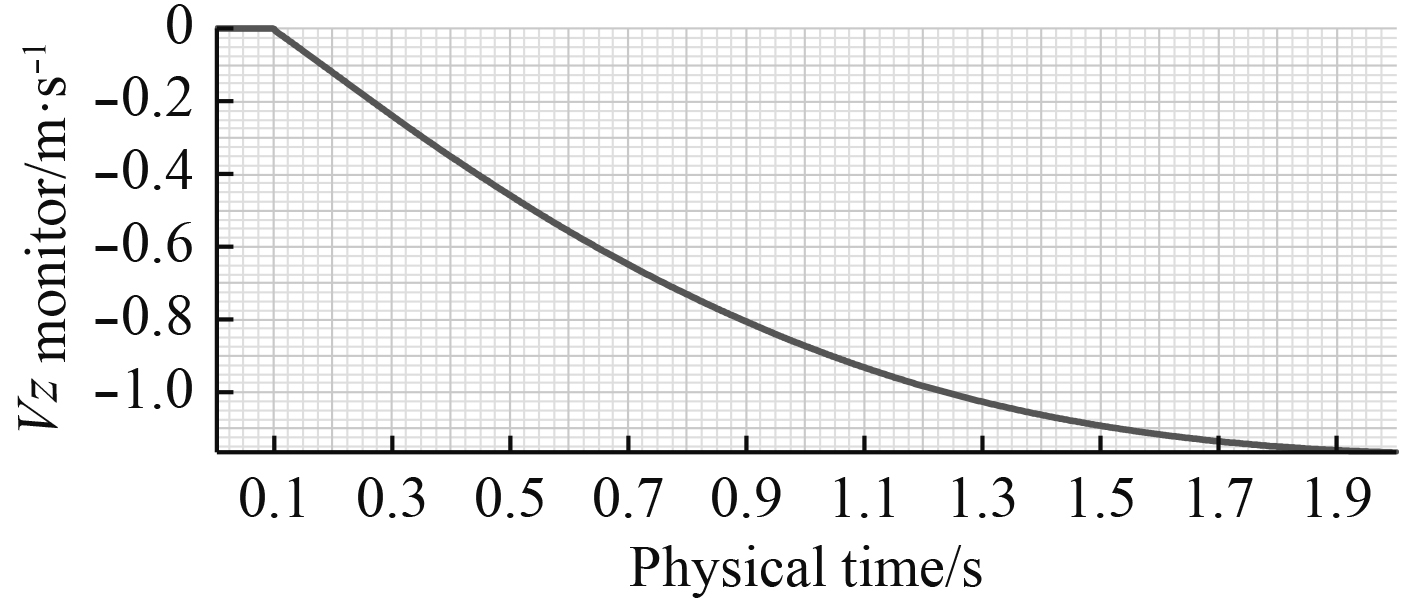
图7~图12为鱼雷在运动过程中的数值模拟仿真结果。可得2 s内鱼雷沿X轴前进16.59 m沿Z轴向下运动1.51 m。图11显示鱼雷沿X轴的速度由初始的10 m/s逐渐减小,2 s时速度约为7.77 m/s。图12显示鱼雷沿Z轴的速度由0 m/s逐渐增大,至2 s时速度约为1.167 m/s。
|
图 7 X轴向位移 Fig. 7 The distance of X axis |
|
图 11 鱼雷的X轴向速度 Fig. 11 The velocity of Torpedo on X axis |
|
图 12 鱼雷的Z轴向速度 Fig. 12 The velocity of Torpedo on Z axis |
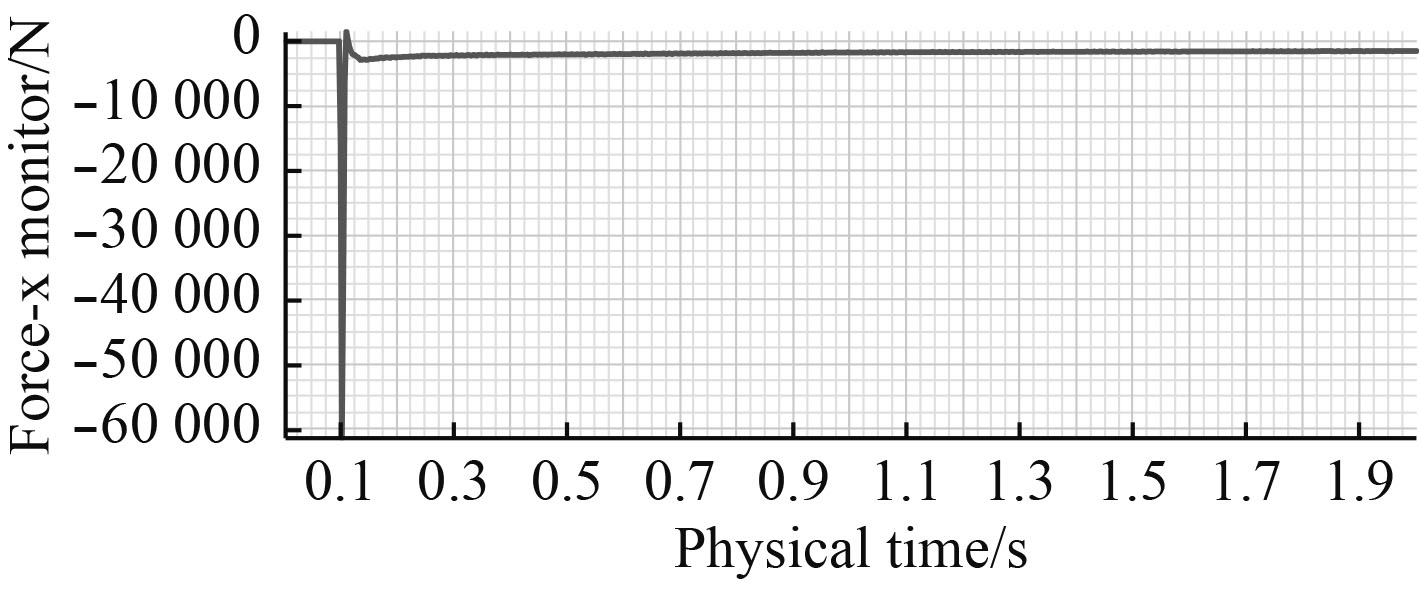
鱼雷在运动过程的X轴向受力即鱼雷运动过程阻力,由图9可见鱼雷在发射瞬间鱼雷阻力由较大迅速缩小[2],0.15 s后阻力缓慢减小,2 s时阻力约1 437 N。启动瞬间要克服惯性故阻力较大,启动后由于鱼雷无动力前进,速度缓慢减小,由式(1)可得阻力与速度平方成正比关系,故阻力也随之减小。
|
图 9 鱼雷X轴向受力 Fig. 9 The force of Torpedo on X axis |
| $ {{{F}}_{\rm{x}}}{\rm{ = }}{c_x}\rho \frac{{{\nu _x}^2}}{2}{s_m}\text{。} $ | (1) |
式中:
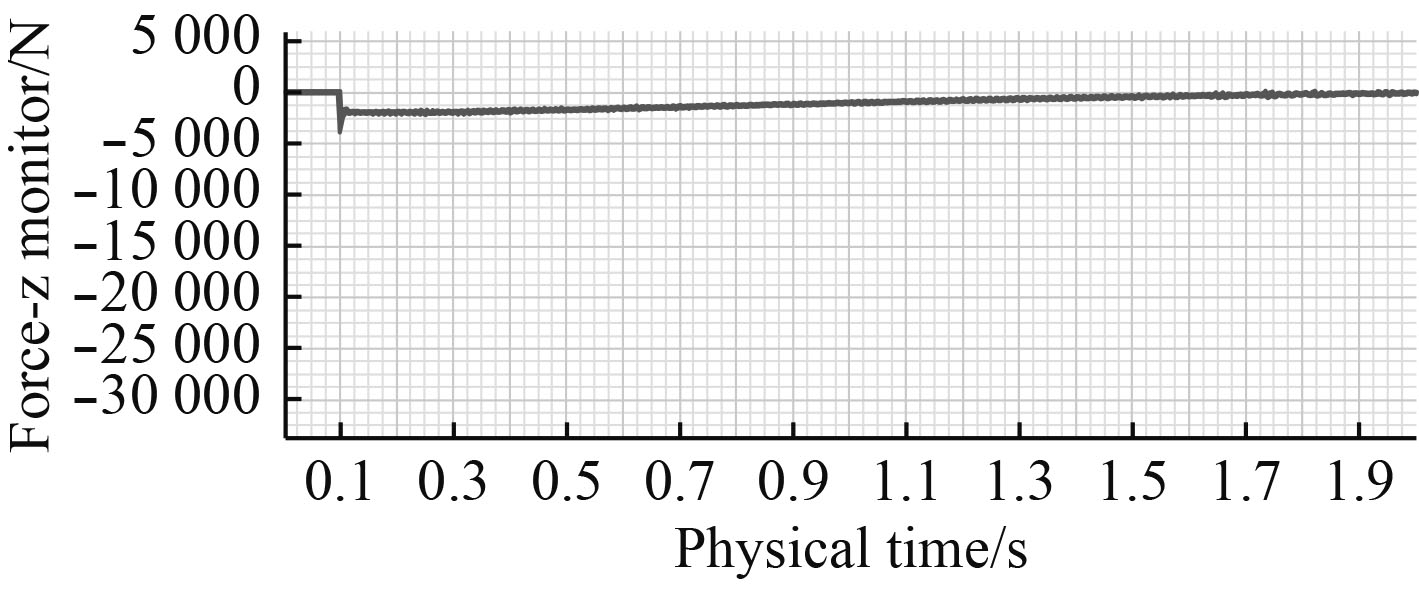
鱼雷在运动过程中的Z轴向力为鱼雷的负浮力减去鱼雷的下沉阻力。由图10可得鱼雷在下沉过程中Z轴向受力在下沉瞬间由较大急剧减小,0.15 s后趋于稳定,0.15~2 s沿Z轴力缓慢减小,1.2 s后沿Z轴的力为94 N。由式(2)得下沉阻力与下沉速度平方成正比,鱼雷的下沉阻力随速度的增大而变大,故鱼雷的Z轴向受力随速度增大而减小。
|
图 10 鱼雷的Z轴向受力 Fig. 10 The force of torpedo on Z axis |
| ${F_z} = P - {c_z}\rho \frac{{{\nu _z}^2}}{2}{s_m}\text{。}$ | (2) |
式中:
|
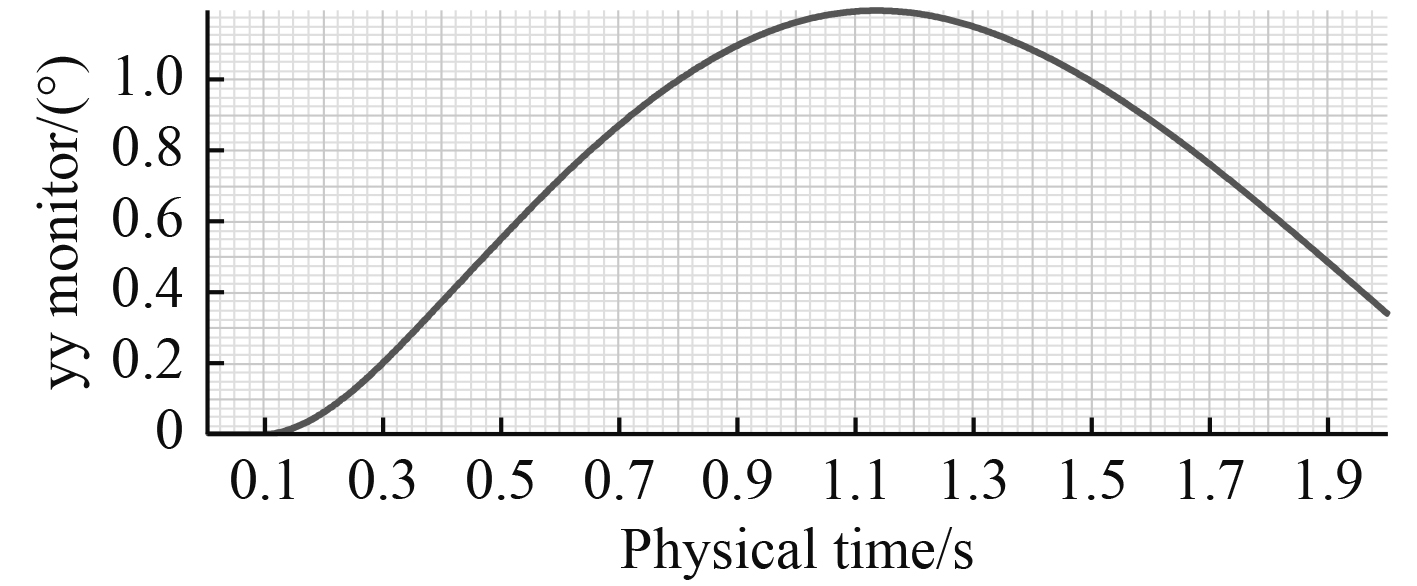
图 13 俯仰角 Fig. 13 The angle of pitch |
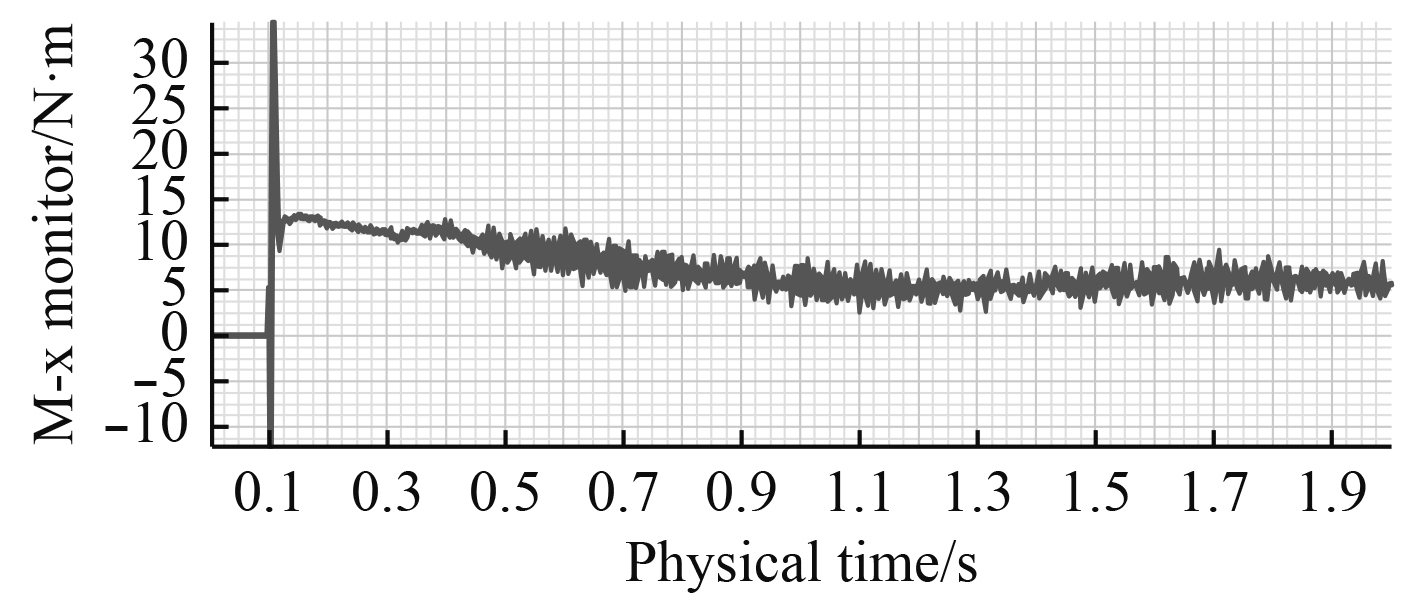
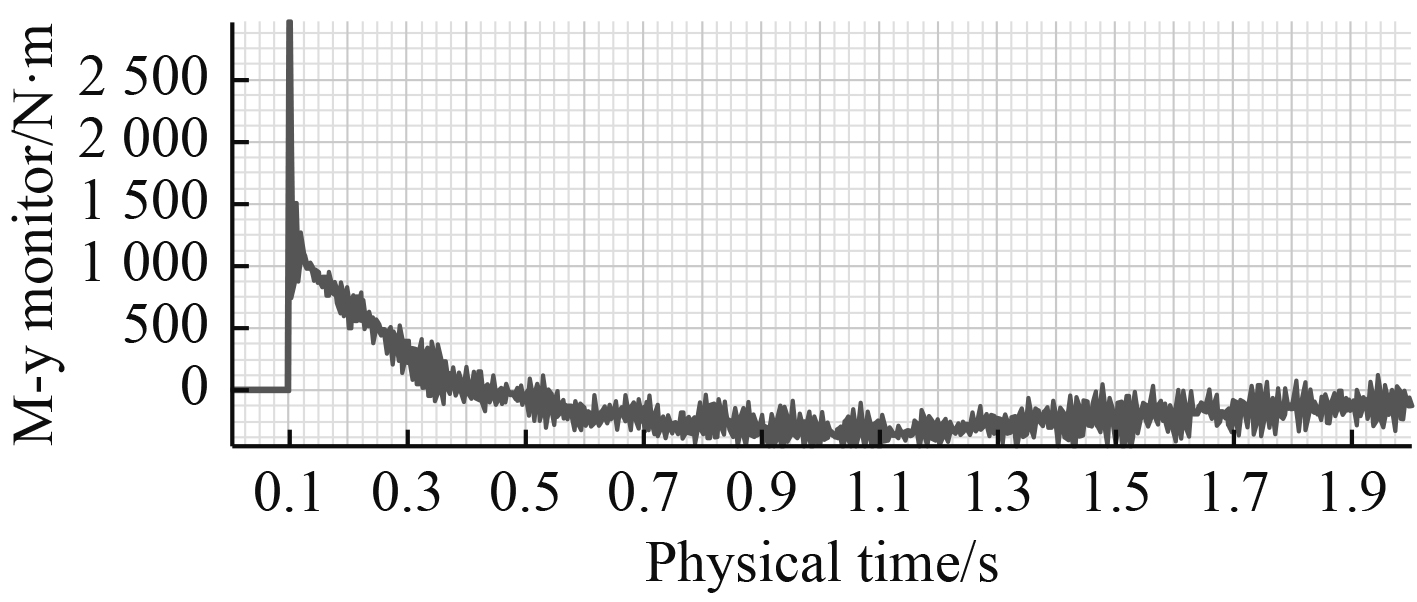
鱼雷绕Y轴的转动角度在0°~1°之间。其主要原因是鱼雷在运动过程绕Y轴的力矩决定,图14显示绕Y轴的力矩先正后负,但绝对值较小。故鱼雷在运动过程中绕Y轴的角度先变大后变小且幅度较小。
|
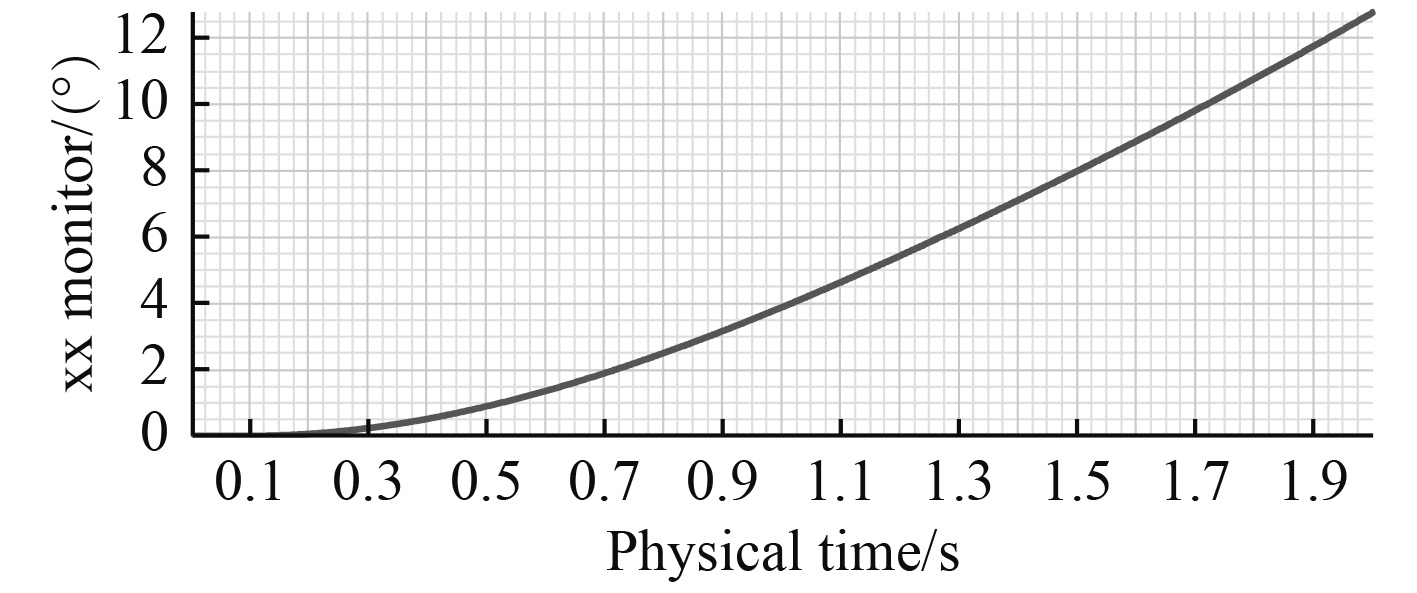
图 15 横滚角 Fig. 15 The angle of roll |
|
图 16 横滚力矩 Fig. 16 The moment of rall |
|
图 14 俯仰力矩 Fig. 14 The moment of pitch |
由于鱼雷的质浮心在Y方向有2 mm的间距,即质心侧移,故鱼雷在无动力前进过程中会出现绕X轴的转矩,在转矩作用下会出现绕X轴的转角。
| $ {\varphi _0}{\rm{ = }}\frac{{\Delta {M_p}}}{{Gh}}{\nu ^2} + \frac{{{z_G}}}{h}\text{。} $ |
式中:
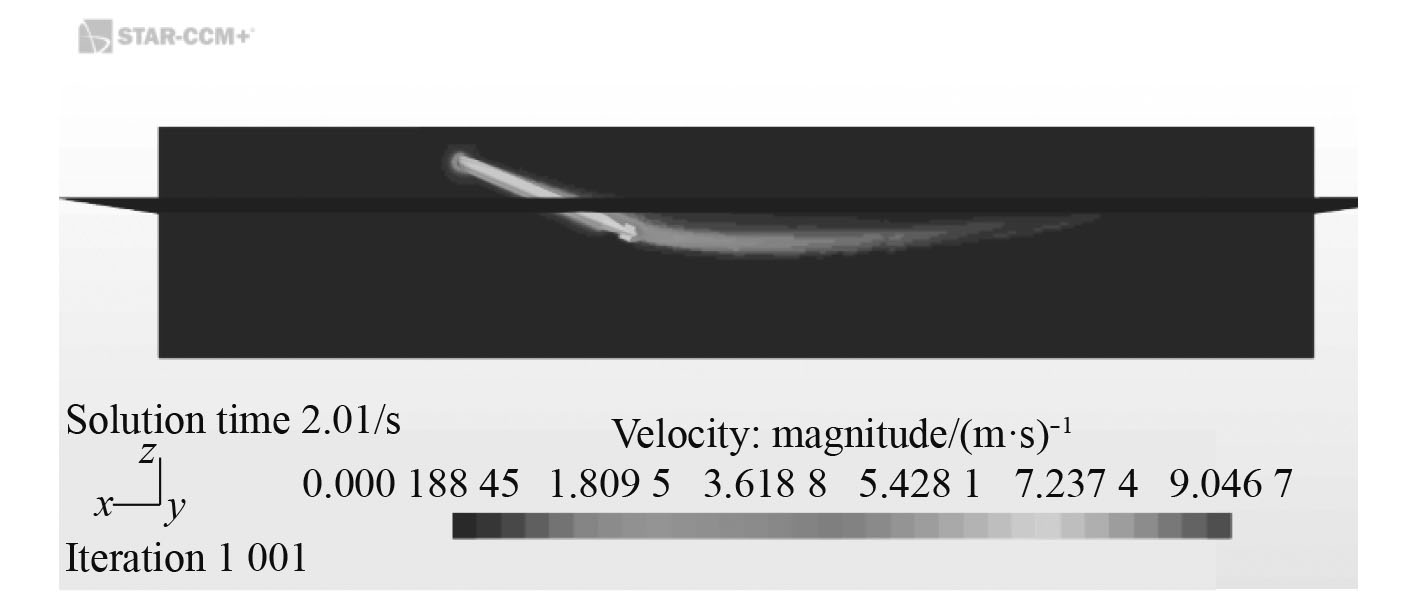
鱼雷质浮心间距对鱼雷出管后的运动状态有重要的影响,选择合适的质浮心间距可以有效起到稳定鱼雷运动作用。本文设置质心位于浮心前为正值,质心位于浮心后为负值,分别选取–300 mm,–100 mm,0 mm,100 mm,300 mm对鱼雷出管后无动力阶段进行数值仿真,得到结果如图17~图21所示。
|
图 17 质心在浮心前300 mm的速度云图 Fig. 17 Contour of velocity when center of mass at 300 mm before center of buoyancy |

|
图 18 质心在浮心前100 mm的速度云图 Fig. 18 Contour of velocity when center of mass at 100 mm before center of buoyancy |

|
图 19 质心在浮心前0 mm的速度云图 Fig. 19 Contour of velocity when center of mass at 0 mm before center of buoyancy |

|
图 20 质心在浮心后100 mm的速度云图 Fig. 20 Contour of velocity when center of mass at 100 mm behind center of buoyancy |

|
图 21 质心在浮心前300 mm的速度云图 Fig. 21 Contour of velocity when center of mass at 300 mm behind center of buoyancy |
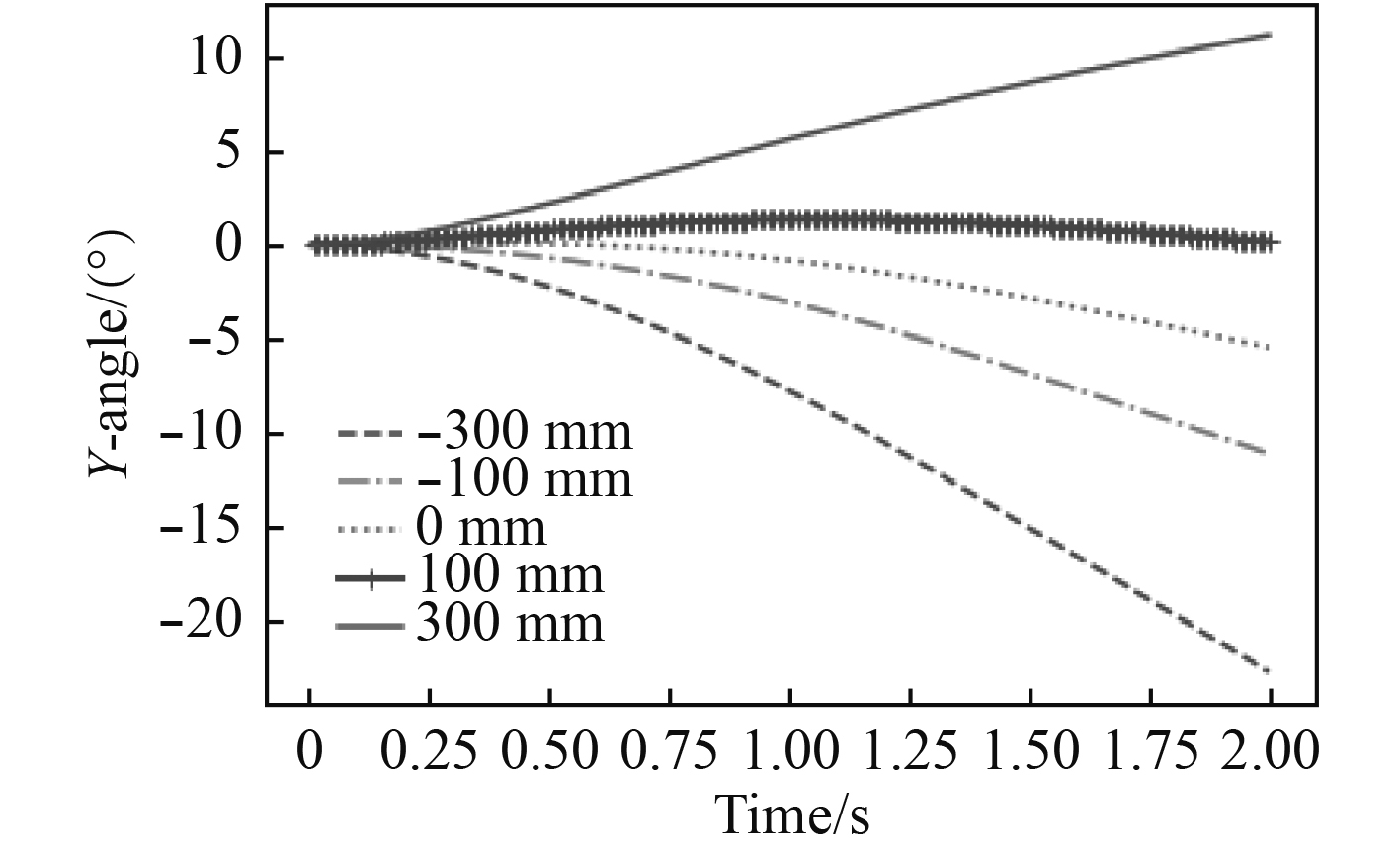
图22显示鱼雷在不同质浮心间距下前进绕Y轴的转角变化,+300 mm的转角约11°,+100 mm的转角变化最小,约为1°,0 mm的转角约–4°,–100 mm的转角约–10°,–300 mm的转角最大约23°,故在鱼雷总体结构设计时应取质浮心间距为+100 mm。
|
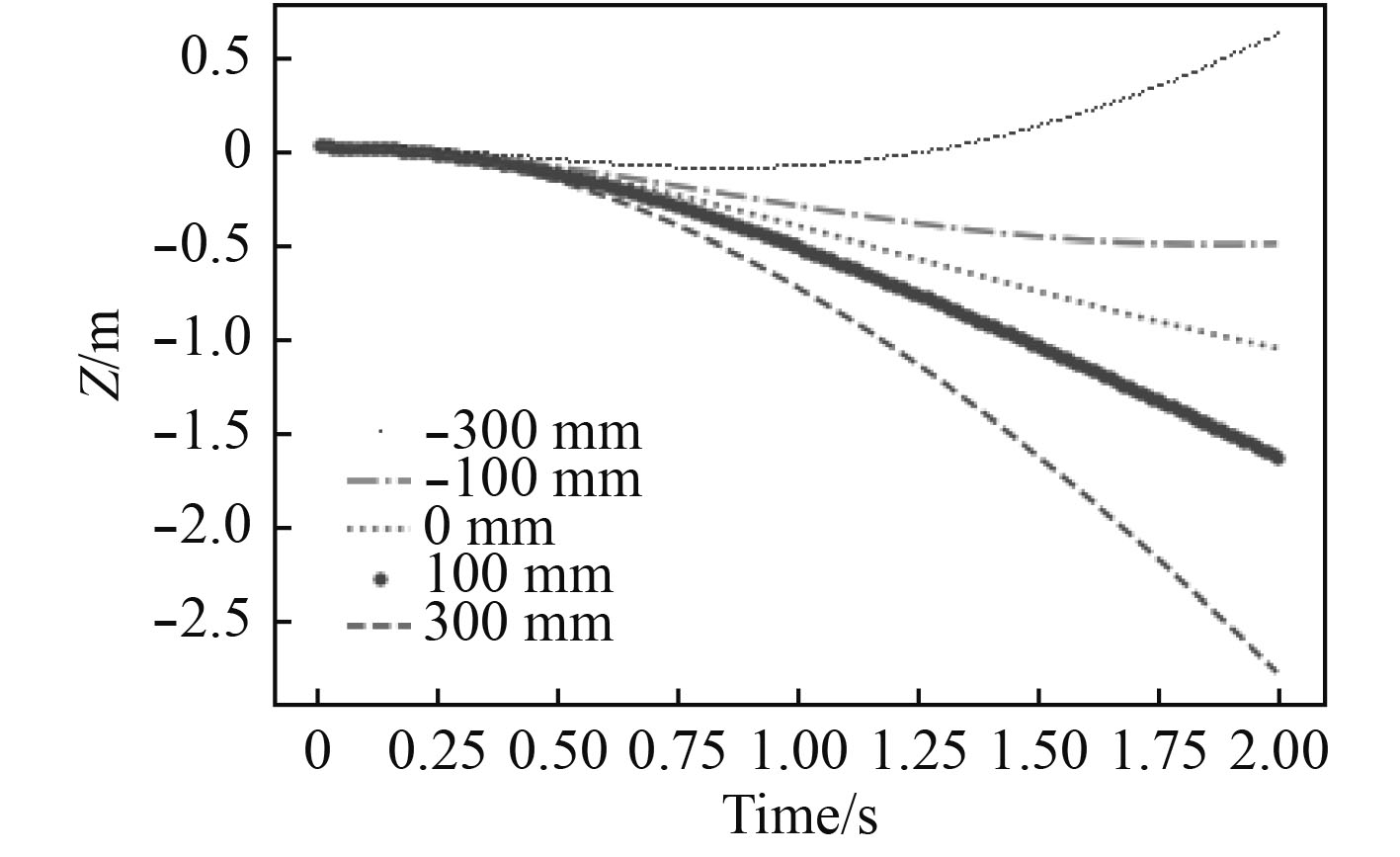
图 24 鱼雷不同质浮心间距下Z轴向位移 Fig. 24 The displacement of Z-axis with different distance between the center of mass and center of buoyancy |
|
图 22 鱼雷不同质浮心间距下俯仰角 Fig. 22 The angle of pitch with different distance between the center of mass and center of buoyancy |
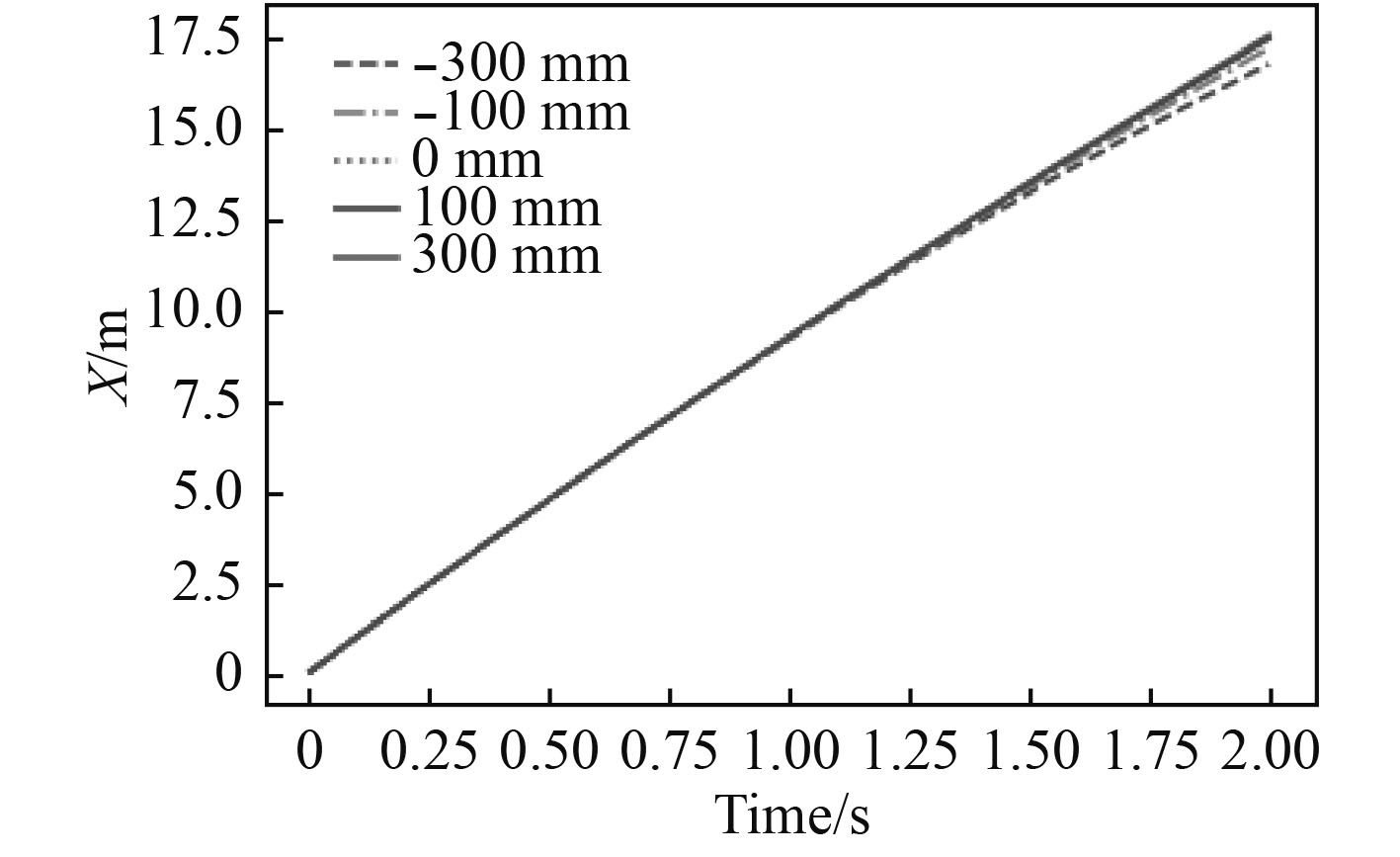
由图23可得质浮心间距对于鱼雷的X轴向位移响并不大,对Z轴向位移影响较大,主要由于鱼雷不同的质浮心间距使得俯仰力矩发生变化,鱼雷发生偏转,引起质心沿Z轴的变化较大,
|
图 23 鱼雷不同质浮心间距下的X轴向位移 Fig. 23 The displacement of X-axis with different distance between the center of mass and center of buoyancy |
本文利用STAR-CCM+软件的重叠网格方法和6-DOF方法对鱼雷水下运动状态进行模拟仿真。得到以下结论:
1)鱼雷发射后不同运动时刻的速度云图和压力云图,结合云图分析鱼雷运动状态。
2)得到鱼雷运动的质心轨迹图、姿态角变化,结合受力和力矩对运动轨迹和姿态进行分析,结合运动方程分析了速度变化曲线的原因。
3)研究了不同质浮心间距对于鱼雷发射稳定性的影响,得到质浮心+100 mm时鱼雷航行最平稳,可以作为鱼雷结构设计的参考。
本文在仿真中为了简化鱼雷发射模型,只考虑了Y轴向转动,忽略了鱼雷运动时绕X轴及Z轴的转动以及Y轴方向的位移。模拟理想情况下鱼雷发射的运动状态,忽略水下复杂海流状况。本文只研究了X轴向的质浮心间距对鱼雷发射稳定性的影响[8],忽略了Y轴向、Z轴向的质浮心间距对鱼雷运动状态的影响。实际水下流场情况复杂,鱼雷运动的状态应考虑更多参数,将需进一步的深入研究。
| [1] |
段浩. 鱼雷发射技术[M]. 北京: 国防工业出版社, 2015.
|
| [2] |
潘光. 鱼雷力学[M]. 陕西: 陕西师范大学出版社, 2013.
|
| [3] |
李明. STAR-CCM+与流场计算[M]. 北京: 机械工业出版社. 2017.
|
| [4] |
房萍萍. 计及侧向流影响的自治水下航行器6-DOF运动仿真[D]. 天津: 天津大学, 2014.
|
| [5] |
宋保维. 气动不平衡式鱼雷发射器内弹道流场仿真研究[J]. 鱼雷技术, 2008, 16(2): 46-49. SONG Bao-wei. Simulation of inner trajectory flow field for pneumatic imbalance torpedo launcher[J]. Torpedo Technology, 2008, 16(2): 46-49. DOI:10.3969/j.issn.1673-1948.2008.02.012 |
| [6] |
董明阳. 假海试验设施复杂内流场仿真[J]. 鱼雷技术, 2015, 23(1): 66-70. DONG Ming-Yang. Simulation on complicatd inner flow field in false sea test facility[J]. Torpedo Technology, 2015, 23(1): 66-70. DOI:10.3969/j.issn.1673-1948.2015.01.015 |
| [7] |
杨壮涛. 小型浮标在波浪作用下运动响应研究[D]. 昆明: 中国舰船研究院, 2018.
|
| [8] |
曹永辉, 石秀华. 水下航行器轨迹跟踪控制与仿真[J]. 计算机仿真, 2006, 23(7): 19-21. CAO Yong-hui, SHI Xiu-hua. Trajectory tracking control and simulation of AUV[J]. Computer Simulation, 2006, 23(7): 19-21. DOI:10.3969/j.issn.1006-9348.2006.07.006 |
 2019, Vol. 41
2019, Vol. 41
