主动信号处理中,当使用相位编码信号在接收端进行相关匹配的时候,会同时产生主瓣和不需要的旁瓣。主动声呐系统探测单个目标时,距离旁瓣的影响较小。但需要探测2个或者2个以上的目标时,大功率信号的旁瓣必将影响小功率信号目标的检测,尤其当所探测目标的功率相差较大时,小功率目标往往会淹没在大功率目标的旁瓣中,必将导致检测不到小功率的目标[1]。因此,为了预防上述情况发生,必须采取一些算法来抑制大功率目标的旁瓣级。按照体积不变的原理,旁瓣不可能全部被抑制,依据尽量降低旁瓣同时尽量提高主旁瓣比的思路,在实现相位编码声呐低旁瓣的问题上进行大量研究。
目前,研究方向分为两方面:一是选择好的码字来获得好的相关性,这种方法没有普适意义,不能满足保密和抗干扰的需求;二是通过信号处理的方式来实现旁瓣压制,相比第一种波形设计方法,它具有码字无限制、不易被敌方破解的特点,因此成为研究热点[2]。Petre Stoica和Jian Li等在零多普勒的条件下提出了一种时间(或距离)高分辨率的多相位编码波形设计方法[3]。曾祥能等在接收端对相位编码使用Woo滤波处理技术产生的均匀旁瓣结构,抑制了输出的旁瓣区能量[4]。李从风等提出了恒模波形设计方法,有效抑制了多相编码特定区间的自相关函数旁瓣[5]。
以上的波形设计方法,只考虑了目标静止,多普勒频移为0的情况,不能有效解决目标有多普勒频移时,相位编码存在的旁瓣峰值过高,造成弱目标丢失的问题。本文针对此问题,提出一种针对低速运动目标,有多普勒频移的波形设计方法。
1 离散模糊度函数 1.1 相位编码脉冲在雷达和声呐等应用中,为了保证发射功率最大,一般采用的波形都是相位调制(phase modulation)方式,可以是恒相位(CW单频)、线性变化相位(LFM)和非线性变化相位,此时发射波形的幅度不变,因此功率或能量不变。对多脉冲雷达,主要是设计不同脉冲间的相位;而对于声呐,就是把单个脉冲划分成多个子脉冲,每个子脉冲的中心频率相同,但初始相位不同。相位编码脉冲的具体表达式为[6]。
| $x\left( n \right) = {e^{j{\phi _n}}}{\text{,}}$ | (1) |
式中,
| $\sum\limits_{n = 1}^N {{{\left| {x\left( n \right)} \right|}^2}} = N{\text{。}}$ | (2) |
主动声呐发射的编码脉冲是模拟信号(即连续时间信号)经过采样和量化得来的,模拟信号经理想的方波信号调制后,得到的基带波形可表示为:
| $s\left( t \right) = \sum\limits_{n = 1}^N {x\left( n \right){p_n}} \left( t \right){\text{,}}$ | (3) |
式中,
| ${\int_0^{{T_p}} {\left| {p\left( t \right)} \right|} ^2}{\rm d}t = 1{\text{,}}$ | (4) |
其中
式(3)可以进一步表示为:
| $s\left( t \right) = \sum\limits_{n = 0}^{N - 1} {x\left( n \right)} p\left( {t - n{T_r}} \right){\text{,}}$ | (5) |
式中:
| $ {v_0}\left( t \right) = {a_t}s\left( t \right)\exp \left[ {j\left( {2{\text{π}} {f_0}t + \phi } \right)} \right] {\text{。}}$ | (6) |
式中:
根据式(3),广义的离散模糊度函数表达式为[7]:
| $ \begin{split} & \chi \left( {\tau ,f} \right) = \int_0^T {\left( {\sum\limits_{n = 1}^N {x\left( n \right){p_n}\left( t \right)} } \right)} \left( {\sum\limits_{m = 1}^N {{x^*}\left( m \right){p_m}\left( {t - \tau } \right)} } \right)\times\\ & {e^{j2{\text{π}} f\left( {t - \tau } \right)}}{\rm d}t = \\ &\sum\limits_{m = 1}^N {\sum\limits_{n = 1}^N {{x^*}\left( m \right)\left( {\int_0^T {{p_n}\left( t \right){p_m}\left( {t - \tau } \right){e^{j2{\text{π}} f\left( {t - \tau } \right)}}{\rm d}t} } \right)} } x\left( n \right){\text{,}} \end{split} $ | (7) |
式中:
设时间延迟
| $ \begin{split} \!\! \chi \left( {k{t_p},f} \right) = &\sum\limits_{m = 1}^N {\sum\limits_{n = 1}^N {{x^*}\left( m \right)\left( {\int_{\left( {n - 1} \right){t_p}}^{n{t_p}} {{{\left| {{p_n}\left( t \right)} \right|}^2}{e^{j2{\text{π}} f\left( {t - k{t_p}} \right)}}{\rm d}t} } \right)}\times }\!\!\!\!\!\!\!\!\!\!\! \\ & {\delta _{m + k,n}}x\left( n \right) = {\frac{{{e^{j{\text{π}} f{t_p}}}\sin \left( {{\text{π}} f{t_p}} \right)}}{{{\text{π}} f{t_p}}}} \times \\ &\sum\limits_{n = 1}^N {x\left( n \right)} {x^*}\left( {n - k} \right){e^{ - j2{\text{π}} f{t_p}\left( {n - k} \right)}}{\text{,}} \end{split} $ | (8) |
值得注意的是
设频移
| $ \chi \left( {k{t_p},\frac{p}{{N{t_p}}}} \right) = {e^{j{\text{π}} \frac{p}{N}}}\sin c\left( {{\text{π}}\frac{p}{N}} \right)\bar r\left( {k,p} \right){\text{,}} $ | (9) |
式中
| $ \bar r\left( {k,p} \right) = \sum\limits_{n = 1}^N {x\left( n \right)} {x^*}\left( {n - k} \right){e^{ - j2{\text{π}} f{t_p}\left( {n - k} \right)}}{\text{,}} $ | (10) |
在低速目标的探测中,多普勒频移非常小(
| $\left| {\chi \left( {k{t_p},\frac{p}{{N{t_p}}}} \right)} \right| \approx \bar r\left( {k,p} \right){\text{,}}$ | (11) |
式中,
在以下的波形设计分析中,主要关心对于序列
| $\mathop {\min }\limits_{\left\{ {x\left( n \right)} \right\}} {C_1} = {\sum\limits_{k \in \kappa } {\sum\limits_{p \in \rho } {\left| {\bar r\left( {k,p} \right)} \right|} } ^2}{\text{,}}$ | (12) |
式中,
按照式(11)所定义的符号,假定
| $ \begin{split} &\left\{ {{x_1}\left( n \right) = x\left( n \right)} \right\}_{n = 1}^N{\text{,}} \\ &\left\{ {{x}_{2}}\left( n \right)=x\left( n \right){{e}^{j2{\text{π}} \frac{n}{N}}} \right\}_{n=1}^{N}{\text{,}} \\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\vdots \\ &\left\{ {{x_P}\left( n \right) = x\left( n \right){e^{j2{\text{π}}\frac{{n\left( {P - 1} \right)}}{N}}}} \right\}_{n = 1}^N{\text{。}} \end{split} $ | (13) |
值得注意的是
| $ \begin{split} &{r_{ml}}\left( k \right) = \sum\limits_{n = 1}^N {{x_m}} \left( n \right)x_l^*\left( {n - k} \right) = \\ &{e^{j2{\text{π}} \frac{{\left( {m - 1} \right)k}}{N}}}\sum\limits_{n = 1}^N {x\left( n \right){x^*}} \left( {n - k} \right){e^{ - j2{\text{π}} \frac{{\left( {n - k} \right)\left( {l - m} \right)}}{N}}}{\text{。}} \end{split}$ | (14) |
显而易见,
举例,
从前面的分析可知,最小化式(14)的旁瓣级等同于减小离散模糊度函数的旁瓣级,也就是式(12)的准则
定义
| ${{X}} = {\left[ {{{{X}}_1} \cdots {{{X}}_P}} \right]_{\left( {N + K - 1} \right) \times K{P}}}{\text{,}}$ | (15) |
其中:
| ${{{X}}_m} = \left[ {\begin{array}{*{20}{c}} {{x_m}\left( 1 \right)}&{}&0 \\ \vdots & \ddots &{} \\ \vdots &{}&{{x_m}\left( 1 \right)} \\ {{x_m}\left( N \right)}&{}& \vdots \\ {}& \ddots & \vdots \\ 0&{}&{{x_m}\left( N \right)} \end{array}} \right]{\text{,}}$ | (16) |
| ${{X}}_m^H{{{X}}_l} = {\left[ {\begin{array}{*{20}{c}} {{r_{ml}}\left( 0 \right)}&{r_{ml}^*\left( 1 \right){\text{ }}}& \cdots &{{\text{ }}r_{ml}^*\left( {N - 1} \right)} \\ {{r_{ml}}\left( 1 \right){\text{ }}}&{{r_{ml}}\left( 0 \right)}& \ddots & \vdots \\ {{\text{ }} \vdots {\text{ }}}& \ddots & \ddots &{r_{ml}^*\left( 1 \right)} \\ {{r_{ml}}\left( {N - 1} \right)}& \cdots &{{r_{ml}}\left( 1 \right)}&{{r_{ml}}\left( 0 \right)} \end{array}} \right]_{N \times N}}{\text{,}}$ | (17) |
矩阵
另外,由于
| ${\hat C_1} = {\left\| {{{{X}}^H}{{X}} - N{{{I}}_{KP}}} \right\|^2}{\text{。}}$ | (18) |
注意到,如果矩阵
| $ \mathop {\min }\limits_{{{X}},{{U}}} {\left\| {{{X}} - \sqrt N {{U}}} \right\|^2}{\text{,}} $ |
| $ s.t.\left| {x\left( n \right)} \right| = 1,n = 1, \cdots ,N{\text{,}} $ |
| $ {x_m}\left( n \right) = x\left( n \right){e^{j2{\text{π}} \dfrac{{n\left( {m - 1} \right)}}{N}}}{\text{。}} $ | (19) |
式中:
1)随机的选取现有的序列来初始化序列
2)固定
| ${{U}} = {{{U}}_1}{{U}}_1^H{\text{,}}$ | (20) |
式中,
3)固定
| $ \begin{split} & {\left\| {{{X}} - \sqrt N {{U}}} \right\|^2}{\text{ = }}\sum\limits_{n = 1}^N {\sum\limits_{l = 1}^{KP} {{{\left| {{\mu _{nl}}x\left( n \right) - {f_{nl}}} \right|}^2}} } = \\ & const - 2\sum\limits_{n = 1}^N {\operatorname{Re} \left[ {\left( {\sum\limits_{l = 1}^{KP} {{{\left| {\mu _{nl}^*{f_{nl}}} \right|}^2}} } \right){x^*}\left( n \right)} \right]} {\text{。}} \end{split} $ | (21) |
这里,const不完全取决于
| $ \begin{split} &\left[ {{\mu _{n1}} \cdots {\mu _{n,KP}}} \right] = \\ &{\left[ {\underbrace {1 \cdots 1}_K\underbrace {{e^{j2{\text{π}} \frac{n}{N}}} \cdots {e^{j2\pi \frac{n}{N}}}}_K \cdots \underbrace {{e^{j2{\text{π}}\frac{{n\left( {p - 1} \right)}}{N}}} \cdots {e^{j2{\text{π}} \frac{{n\left( {p - 1} \right)}}{N}}}}_K} \right]_{1 \times KP}}{\text{,}}\!\!\!\!\!\! \end{split} $ | (22) |
| $ {\phi _n} = \arg \left( {\sum\limits_{l = 1}^{KP} {\mu _l^*{f_{nl}}} } \right),\begin{array}{*{20}{c}} {}&{n = 1, \cdots ,N}{\text{。}} \end{array} $ | (23) |
4)重复第2步和第3步直到收敛。
3 性能分析仿真1:随机相位编码的模糊度函数及等高线图。
随机相位序列的表达式为
| $x\left( n \right) = {e^{j\phi \left( n \right)}}{\text{,}}$ | (24) |
式中:
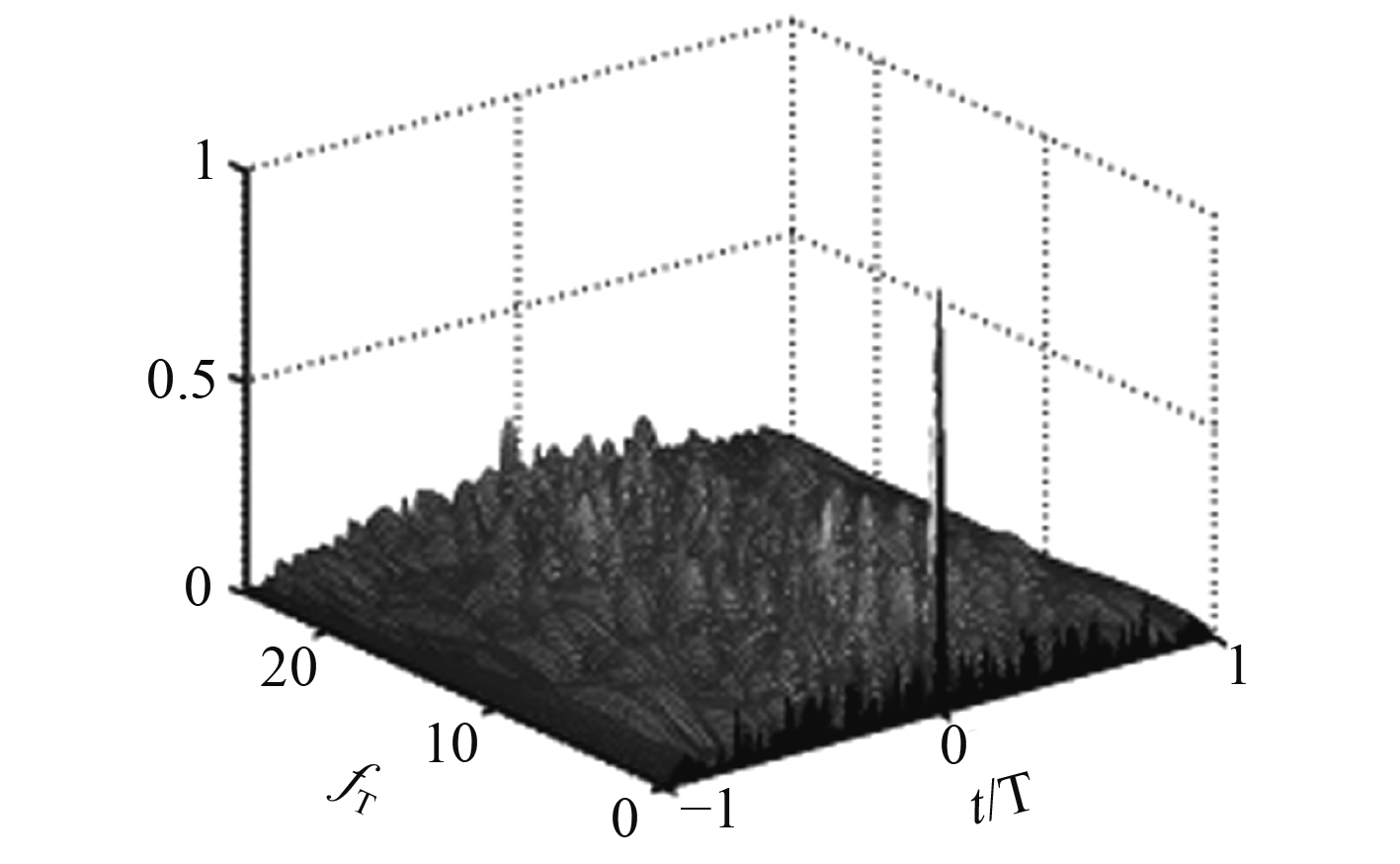
图1为随机相位编码的模糊度函数图,可以发现,随机相位序列的模糊度函数是图钉型的。
|
图 1 随机相位序列的模糊度函数图 Fig. 1 The AF of a length-50 random-phase sequence, 3D plot of the positive Doppler plane |
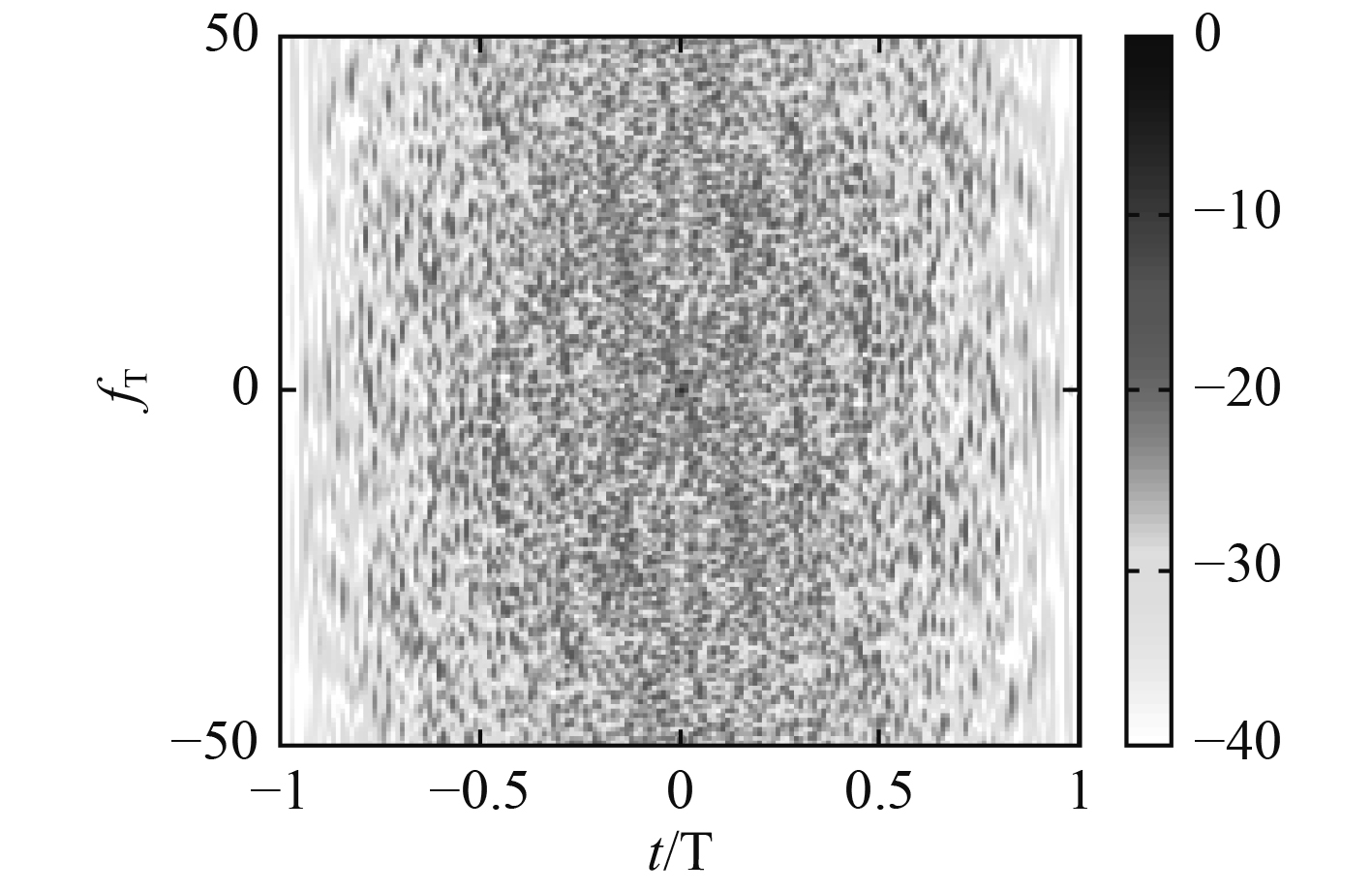
图2为随机相位编码的模糊度函数等高线图,图中颜色越深,代表能量越高。
|
图 2 随机相位序列的模糊度函数等高线图 Fig. 2 The AF of a length-50 random-phase sequence, 2D plot of the positive Doppler plane |
值得注意的是,在图2中,在时延为0处,有一条垂直的窄白线。这是因为,模糊度函数在时延为零处的切割实质是
| $\begin{split} & \chi \left( {0,f} \right) = \int_{ - \infty }^{ + \infty } {u\left( t \right)} u{\left( t \right)^*}{e^{ - i2{\text{π}} ft}}{\rm d}t = \int_0^T {{e^{ - i2{\text{π}}ft}}} {\rm d}t = \\ & \frac{{1 - {e^{ - j2{\text{π}} fT}}}}{{j2{\text{π}} f}} = {e^{ - j{\text{π}} fT}}T\sin c\left( {{\text{π}} fT} \right){\text{,}} \end{split} $ | (25) |
这里,
所以
仿真2:初始序列是长度N=100, K=10, P=3的随机相位编码时所设计编码的模糊度函数等高线图。
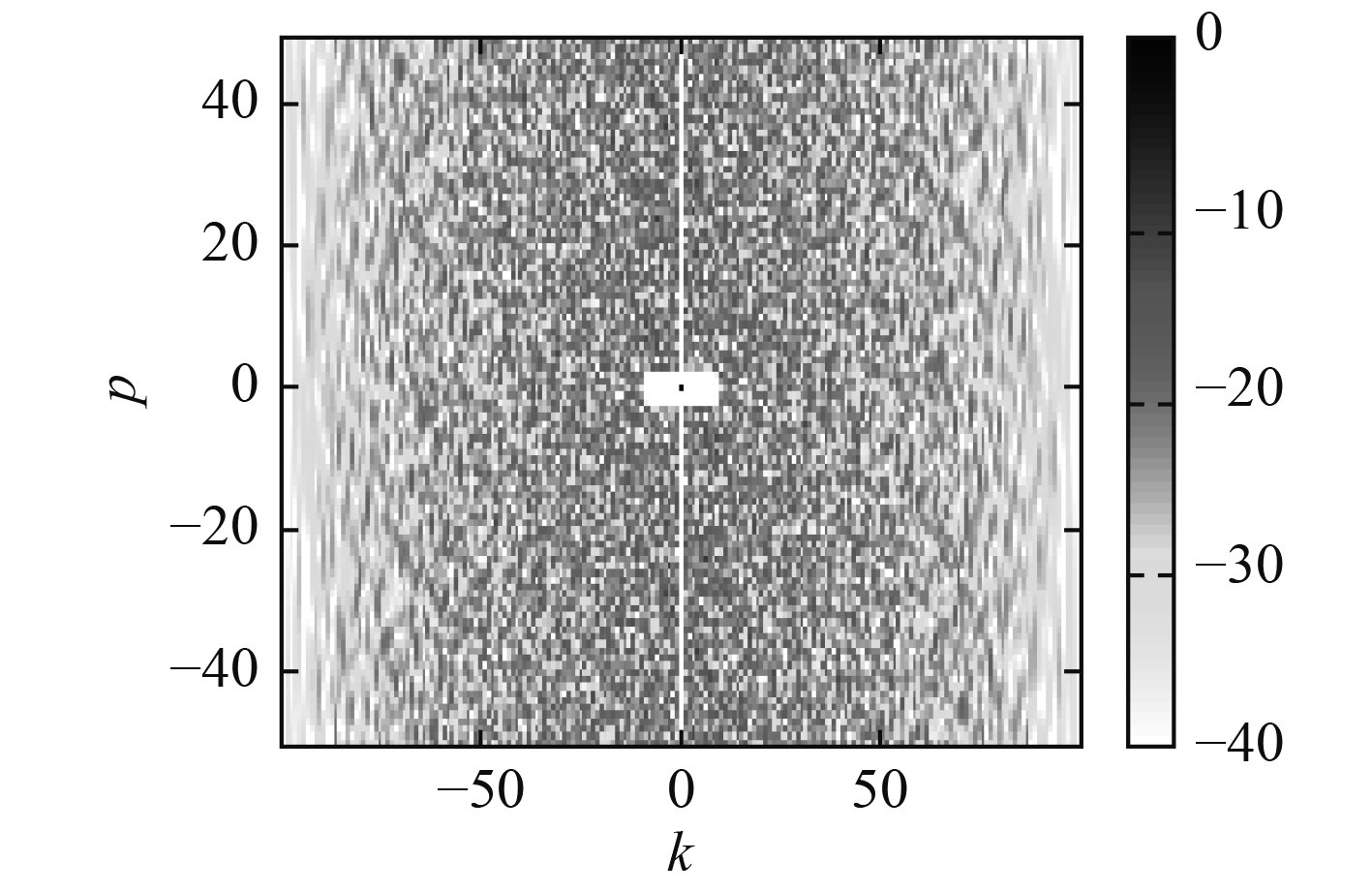
观察图3可以发现,所设计序列的模糊度函数等高线图在原点中心出现较小的白色方形区域,这说明,算法对于原点附近的旁瓣有很强的抑制作用。
|
图 3
设计编码的离散模糊度函数等高线图(用相同长度的随机编码作为算法的初始序列)
Fig. 3
A synthesized discrete-AF:
|
仿真3:N,K不变,增加P时所设计编码的离散模糊度函数等高线图。
设定初始序列是长度N=100随机相位序列,且K=10不变。通过增加P值的方法来设计不同P值下的单位模序列
|
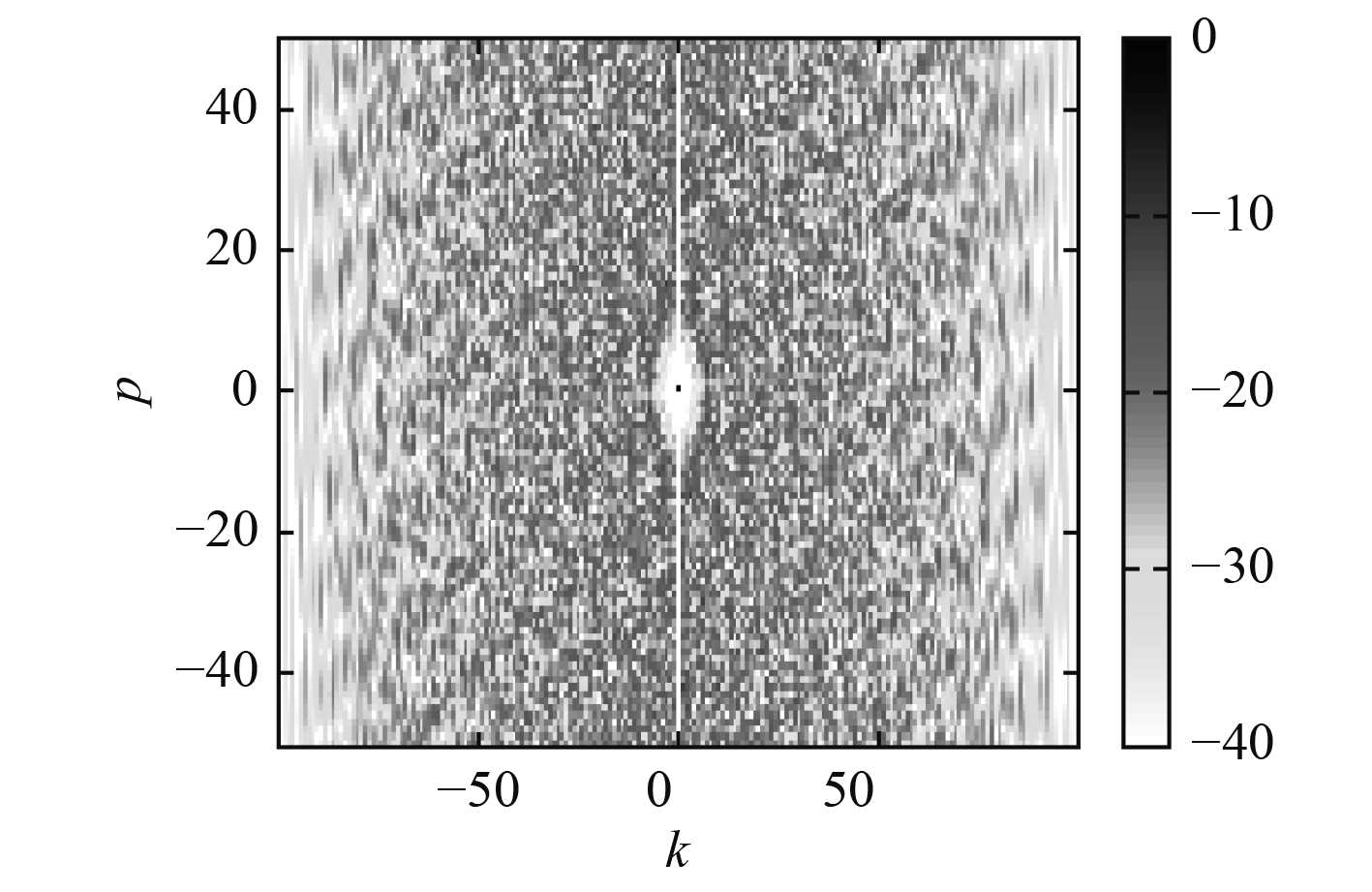
图 4
K=10,P=15时设计编码的模糊度函数等高线图
Fig. 4
A synthesized discrete-AF:
|
|
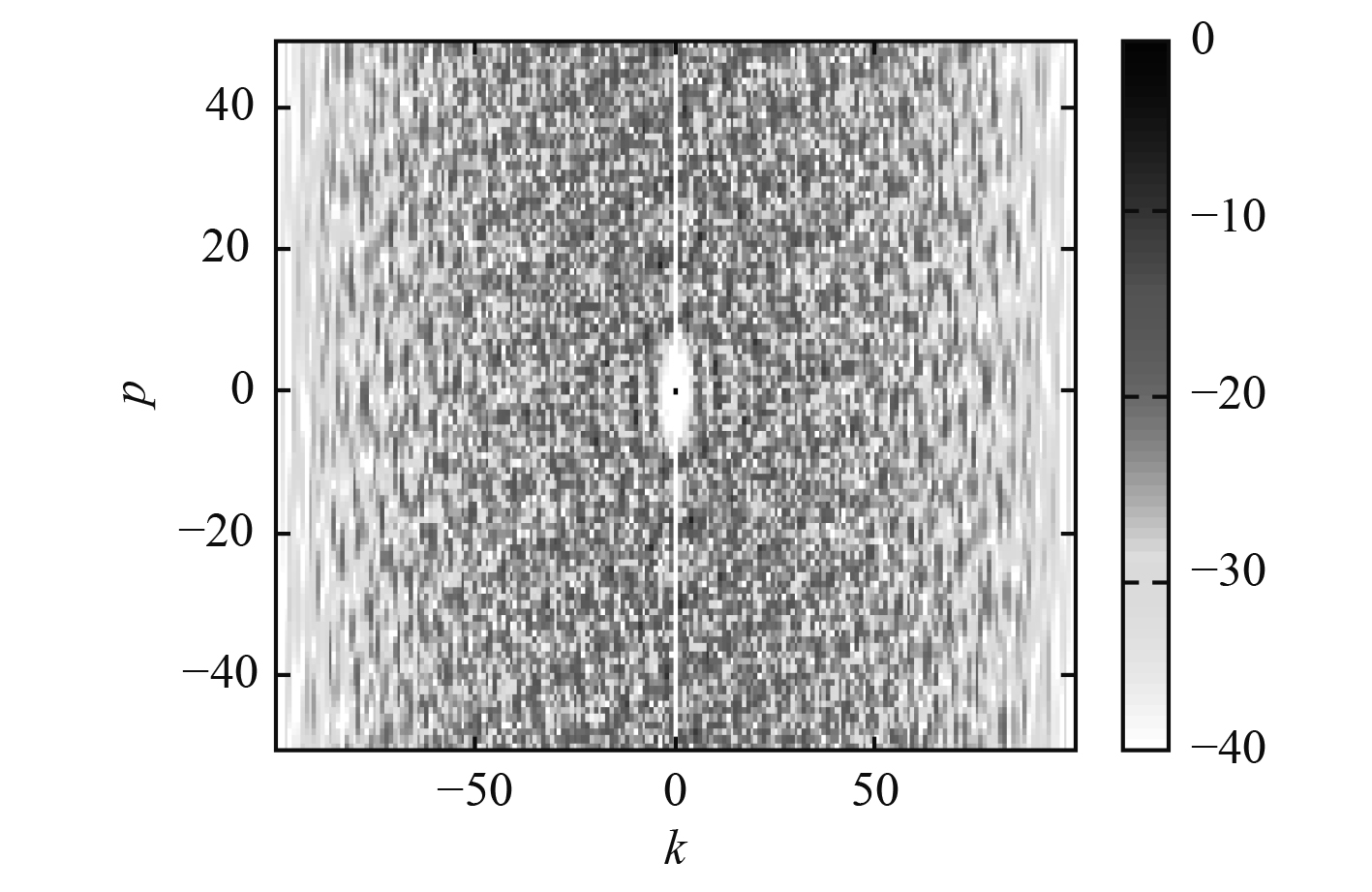
图 5
K=10,P=50时设计编码的模糊度函数等高线图
Fig. 5
A synthesized discrete-AF:
|
在图4和图5中,在N和K不变的情况下,展示了不同P值下,所设计序列的模糊度函数等高线图,对比图4和图5可以发现,通过增大P值,可以增大所设计序列的白色区域,但观察图4和图5可以发现,P从15增大到50时,所设计序列的模糊度函数的白色区域并没有继续增大。具体原因为当P较大时,式(18)不再成立,这种情况下,本文所提出的算法不再适用。
仿真4:N,P不变,增加K时所设计序列的离散模糊度函数等高线图。
假设初始序列是长度N=100随机相位序列,且P=1不变。通过增加K值的方法来设计不同K值下的单位模序列
|
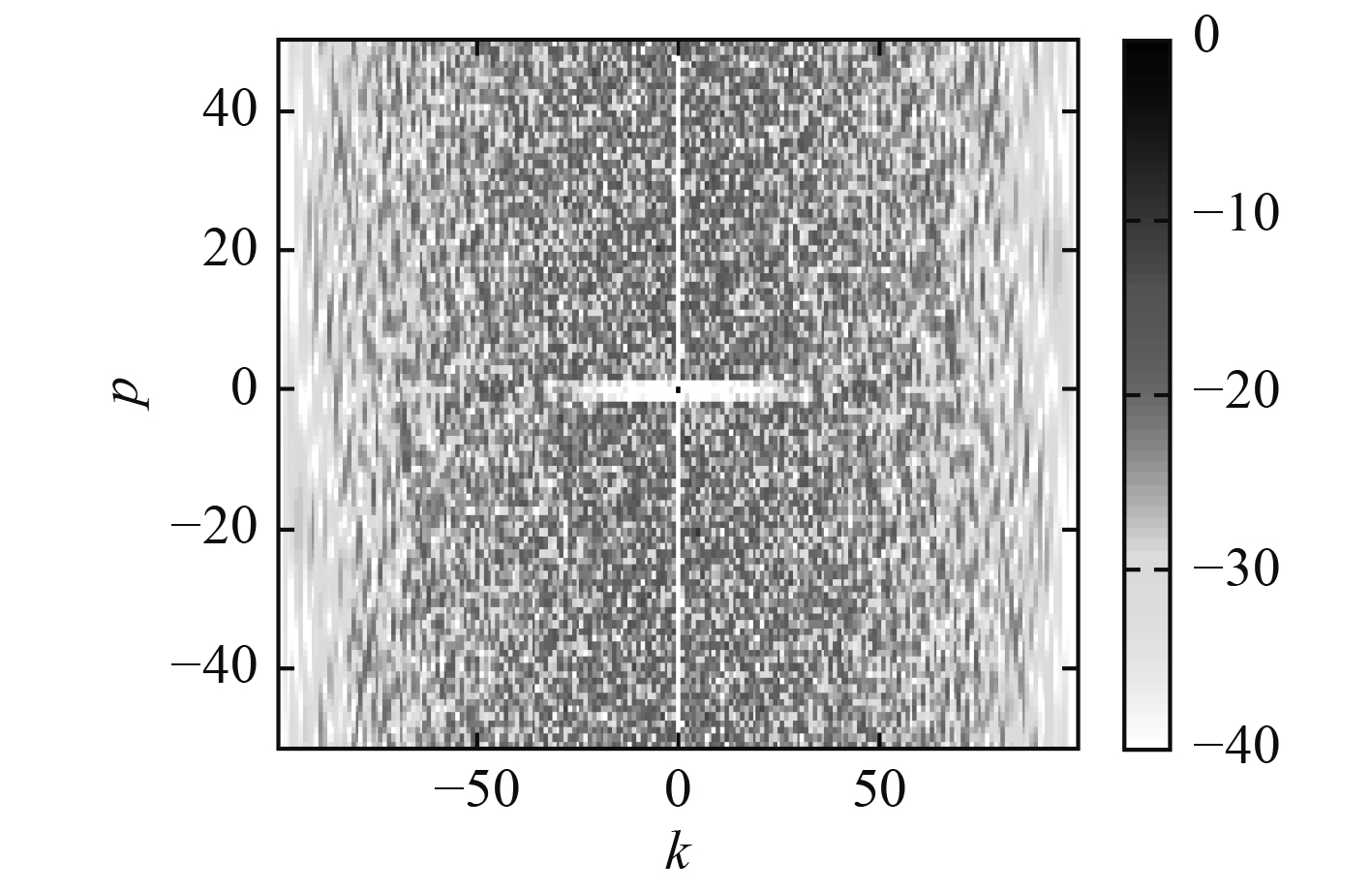
图 6
K=30,P=1 时设计编码的模糊度函数等高线图
Fig. 6
A synthesized discrete-AF:
|
|
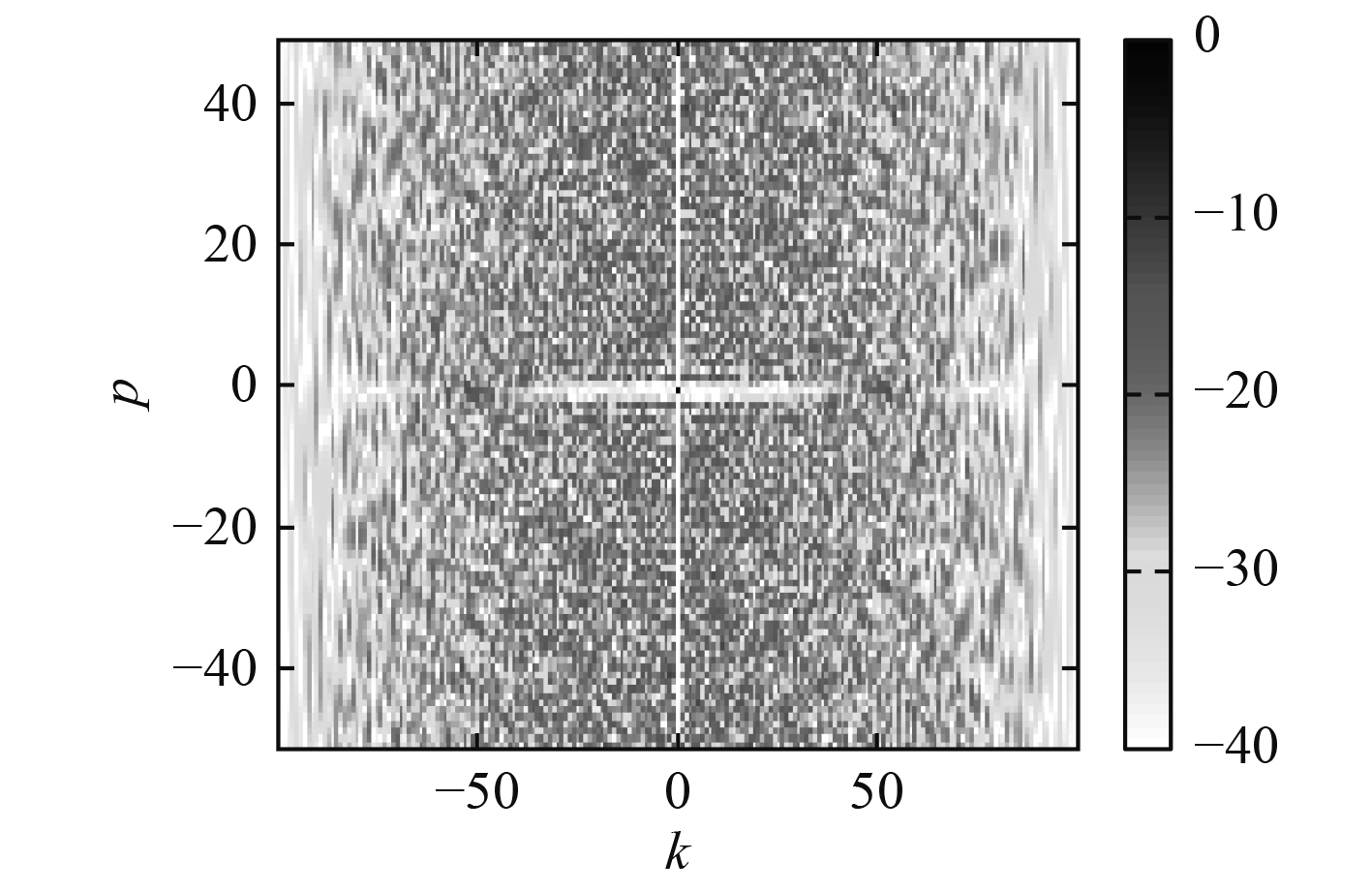
图 7
K=50,P=1时,设计编码的模糊度函数等高线图
Fig. 7
A synthesized discrete-AF:
|
在图6和图7中,在N和P不变的情况下,展示了不同K值下,所设计序列的模糊度函数,对比图6和图7可以发现,通过增大K值,可以增大所设计序列的白色区域,值得注意的是,虽然图7白色区域范围较大,但白色区域内部仍有旁瓣,也就是说,算法的抑制旁瓣的性能有所下降。因为在式(21)中,
综上,本文所设计波形是一种离散模糊度函数原点附近旁瓣级极低的波形,但低旁瓣级局限在一个很小的区域,而且要求K和P的取值接近原点。
4 结 语针对低速运动目标的探测问题,本文提出一种相位编码优化算法,可以有效抑制模糊度函数特定区域旁瓣级。同时引进了离散模糊度函数的概念,并对其定义及其性质进行介绍,提出一种最小化离散模糊度函数附近旁瓣级的算法,这个算法可以用来在时延多普勒平面的原点附近设计图钉型离散模糊度函数。通过计算机仿真发现,在K和P值接近原点的情况下,本文所提出的算法对离散模糊度函数原点附近的旁瓣级有很好的抑制作用。
| [1] |
LEE K PATTON, BRILIAN D RIGLING. Phase retrieval for ra-dar waveform optimization[J]. IEEE Transactions onAerospace and Electronic Systems, 2012, 48(4): 3287-3302. DOI:10.1109/TAES.2012.6324705 |
| [2] |
N ZHANG, SW GOLOMB.. Polyphase sequence with low autocorrelations[J]. IEEE Trans Inf.Theory, 1993, 5(39): 1085-1089. |
| [3] |
PETRE STOICA, HAO HE, JIAN LI. New algorithms for designing unimodular sequences with good correlati-on properties[J]. IEEE Transactions on Signal Processing, 2009, 57(4): 1415-1425. DOI:10.1109/TSP.2009.2012562 |
| [4] |
曾祥能, 张永顺, 何峰, 等. 相位编码信号的综合旁瓣能量改善技术[J]. 电波科学学报, 2012, 2(1): 30-35. |
| [5] |
李风从, 赵宜楠, 乔晓林. 抑制特定区间距离旁瓣的恒模波形设计方法[J]. 电子与信息学报, 2013, 35(3): 532-536. |
| [6] |
STOICA P, H LI.. New algorithms for designing unimodular sequences with good correl-ation properties[J]. IEEE Transactions on Signal Proce-ssing, 2009, 57(4): 1415-1425. DOI:10.1109/TSP.2009.2012562 |
| [7] |
STEIN S. Algorithms for ambiguity function processing[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1981, 29(3): 1425-1435. |
| [8] |
FULVIO GINI, ANTONIO DE MAIO, LEE PATTON. Waveform design and diversity for advanced radar systems. 2012.
|
 2019, Vol. 41
2019, Vol. 41
