2. 江苏科技大学 能源与动力工程学院,江苏 镇江 212003
2. School of Energy and Power Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China
舰船面临一个被探测的严重风险——磁信号。磁信号为人们提供了发现舰船的存在或位移的手段,实现定位。为了保证舰船航行安全,对于“钢筋铁骨”的舰船所采取的防护措施是进行消磁。
采用舰船消磁实验来模拟真实舰船的消磁过程,是普遍的研究方法。
舰船消磁实验,具体分为2个过程,一是测磁工作;二是消磁工作。测磁工作是为了消磁工作做准备,前者完成好坏直接影响了后续的消磁绕组的布置,决定了消磁工作的成功率。测磁工作是在模拟的地磁场环境下,一般所包含设备有矩形坑道、无磁钢轨、测磁传感器(磁探头)、磁性体舰船模型、行车等;消磁工作包含测磁完毕后线圈绕组的布置、安匝的调整、电流的输入等[1]。
载具是测磁工作中的重要组成部分,理论上它与移动的行车作用等同,起着承载磁性体舰船模型的作用,同时为了规避原有行车静态性的缺点,实现动态性的测磁过程,载具在原理和结构上做了非常大的改动,可以模拟真实舰船在海上所产生的航向和姿态的改变。具体讲,舰船消磁实验中,在模拟的地磁场环境下,当载具携带磁性体的舰船模型在无磁轨道上行进时,船模随着载具的摆动发生航向和姿态变化引起自身感应磁场的变化,改变了磁场强度和分布,预先布置的磁探头可以对舰船模型不同位置的磁场信号进行实时动态测量,获取感应磁场纵向、横向、垂向分量,为消磁绕组的布设提供理论计算数据,完成后续消磁工作。整个过程既能够真实模拟实船的运动,同时比较接近实船测量法的数据采集。
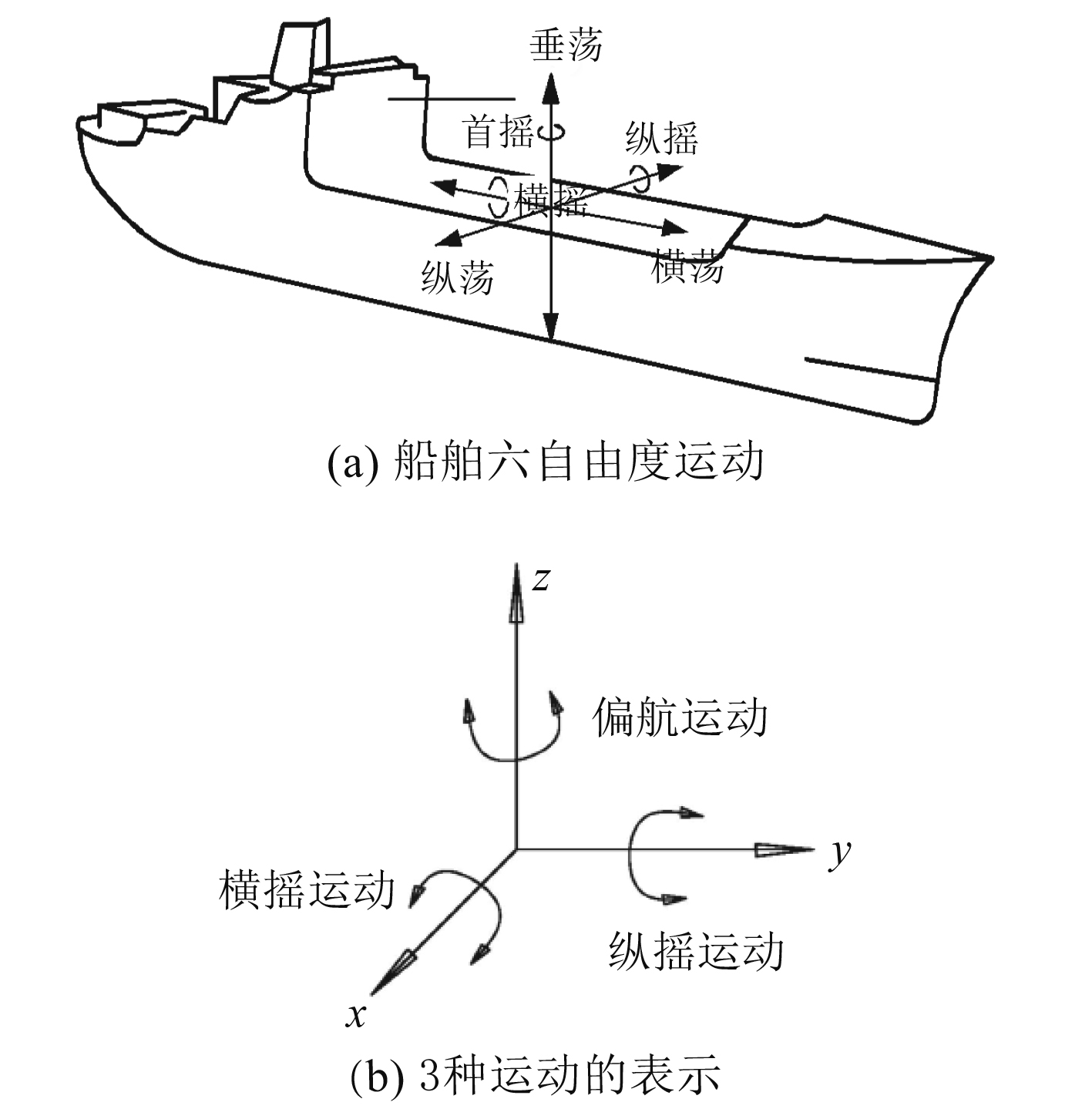
1 运动功能分析舰船航行时,受到海上风、浪、流的影响,会产生6个自由度摇荡运动,即绕3个坐标轴的往复摇荡(进退、横荡、升沉)和旋转摇荡(横摇、纵摇、首尾摇)[2],如图1(a)所示。
|
图 1 各种运动在坐标系中的表示 Fig. 1 Representation of various motion in coordinate |
载具能够模拟真实舰船在海上产生的航向和姿态改变动作,携带磁性体舰船模型完成横摇、纵摇、偏航3个基本运动,将上述运动在空间坐标系里做相关定义,如图1(b)所示。此外,还能够完成行进运动以及调整舰船模型航向的运动。
通过上述分析,所设计的载具需要完成绕固定的坐标轴
区别于真实舰船航行时的运动参数,载具携带磁性体舰船模型完成各种运动时,具有特定要求,即载具携带舰船模型以较小的恒速度在无磁钢轨上匀速行进;同时航向及姿态以一定角度变化;当偏航时,及时调整航向。
基本的运动类型以及运动范围,如表1所示。
|
|
表 1 基本运动类型与运动范围 Tab.1 The type and range of motion |
载具的结构设计方案,如图2所示。其构成元素有基座(移动小车)、转动平台、约束机构球轴承、传动机构、绞盘、电机(含减速器)及驱动绳索。采用对称结构设计,4根绳索的一端与转动平台相连接,另一端通过基座上的传动机构与电机驱动的绞盘相连接。由于驱动绳索存在着单向受力特性,需要有冗余力实现转动平台的力闭合,因此要实现

|
图 2 载具的三维模型 Fig. 2 3D model of the carrier |
分析闭环空间机构的自由度,一般采用Kutzbach Grubler公式[4]来计算,即
| $ F = 6(n - g - 1) + \sum\limits_{i = 1}^g {{f_i}} \text{。} $ |
式中:
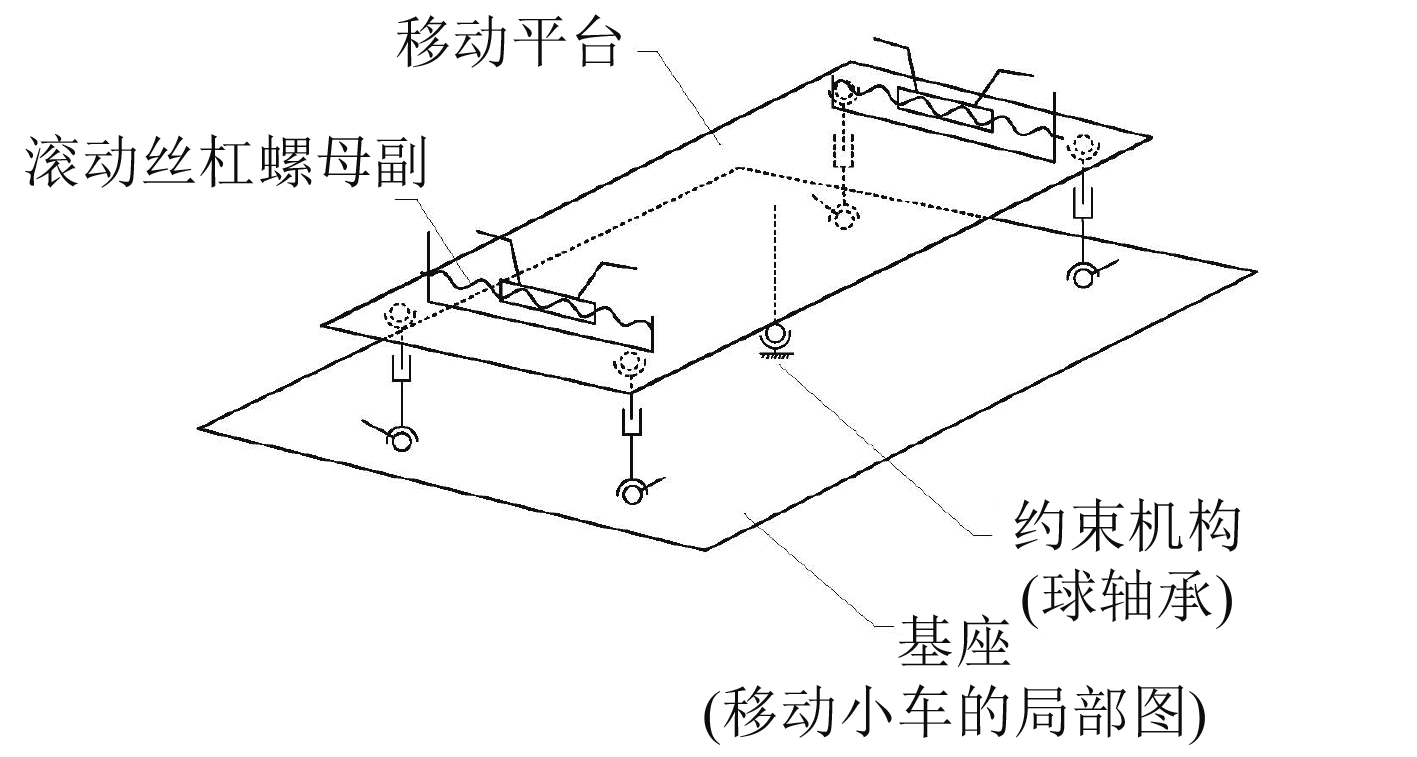
在研究过程中,各驱动绳索始终保持张紧状态,将其理想化,认为绳索具有足够的刚性,能够实现运动副的作用。任意一条驱动绳索都可以等效地看作是一端为球副、另一端为球销副,中间为移动副[5]。可由图2机构的三维模型抽象出载具的等效机构简图,如图3所示。
|
图 3 等效机构简图 Fig. 3 Simplified diagram of equivalent mechanism |
由上面的机构等效简图分析并计算其自由度,机构的总构件数目为10(每条驱动绳索等效为2个构件,1个转动平台,基座(移动小车)与约束机构球轴承看做1个构件),共13个运动副(4个球销副,4个移动副,5个球面副(含1个球轴承)),共有27个自由度,由公式计算可得到:
| $ F = 6(10 - 13 - 1) + 27 = 3\text{。} $ |
综上,所研究的载具分为3层,实现5个自由度的运动。下层:移动小车在牵引绳索牵引下沿着轨道实现前后移动,完成1个移动自由度,模拟舰船在正常航行;中间层:在4根驱动绳索的协调控制下,转动平台实现空间三维转动,完成3个转动自由度,模拟舰船横摇、纵摇和偏航3种姿态和航向改变的动作;上层:对称布置的滚珠丝杠螺母副,当舰船偏航时,它们沿相反方向驱动舰船模型达到调整航向的任务,完成1个回转自由度。因此,所设计的载具能够实现期望的运动功能,并满足舰船消磁实验测磁工作的要求。
3 动力学分析动力学分析主要研究机构运动与力的关系,建立精确的动力学模型对于研究机构动力学非常重要。动力学模型是常说的动力学方程,通过推导动力学方程来研究机构动力学问题。载具的动力学模型可理解为,转动平台绕着固定坐标系中心点
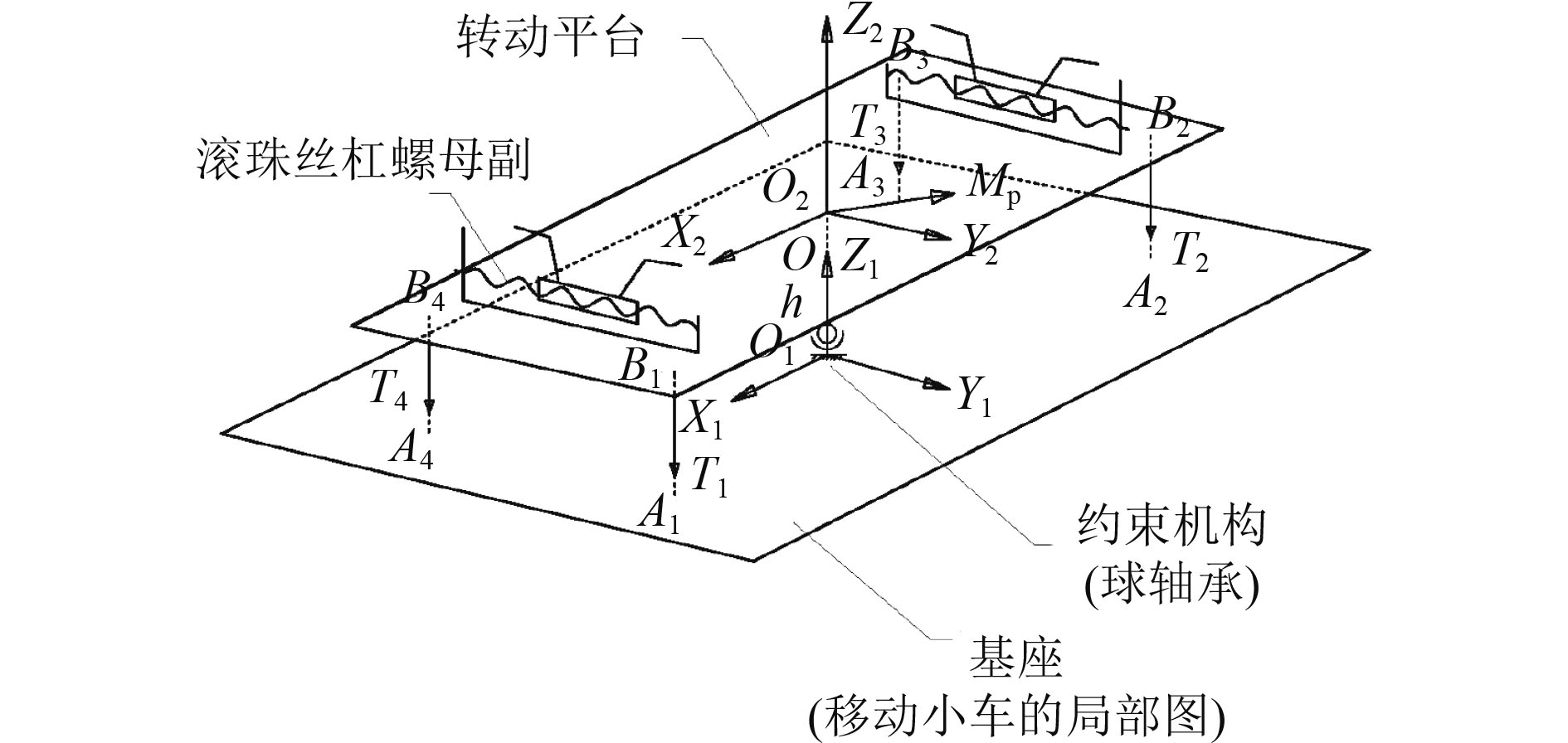
转动平台的受力分析,如图4所示。
|
图 4 载具转动平台受力简图 Fig. 4 Stress diagram of the rotating platform of the carrier |
根据转动平台受力简图,可建立如下动力学方程:
| $ \left\{ {\begin{array}{*{20}{c}} {\displaystyle\sum\limits_{i = 1}^4 {{{{T}}_i} + {{F}} + {{Q}} + m{{g}} + {{{F}}_c} = 0} }\text{,}\\ {\displaystyle\sum\limits_{i = 1}^4 {{}^1{{{R}}_2}{}^2{{{b}}_i} \times {{{T}}_i} + {{{M}}_p} + {{{M}}_c} = 0} }\text{。} \end{array}} \right. $ | (1) |
其中:
| $ {{{F}}_c}=m{{v}}_c^{'}\text{,} $ | (2) |
| $ {{{M}}_c} = - {{{I}}_c}{}^1{{\omega }}_2^{'} - {}^1{{{\omega }}_2} \times ({{{I}}_c}{}^1{{{\omega }}_2})\text{。} $ | (3) |
式中:
将上述动力学方程写成矩阵形式,即
| $ {{UV}} = {{W}}\text{,} $ | (4) |
其中:
| $ {{W}} = {\left[ {\begin{array}{*{20}{c}} {{{{W}}_1}}&{{{{W}}_2}} \end{array}} \right]^{\rm T}} = \left[ {\begin{array}{*{20}{c}} { - ({{F}} + {{Q}} + m{{g}} + {{{F}}_c})}\\ { - ({{{M}}_p} + {{{M}}_c})} \end{array}} \right]\text{。} $ | (5) |
式(5)建立了转动平台动力学模型,将其作为载具的动力学模型。
4 动力学仿真 4.1 机构的运动参数转动平台的运动参数为:单独运动时:横摇运动±8°/0.5 Hz,纵摇运动±3°/0.5 Hz,偏航运动±8°/0.5 Hz;联动时:横摇、纵摇以及偏航运动均为±1°/2 Hz,工作载荷为2 000 kg(包含舰船模型与转动平台的质量),转动平台做正弦摆动,如表2所示。
|
|
表 2 机构的运动参数 Tab.2 Motion parameters of the mechanism |
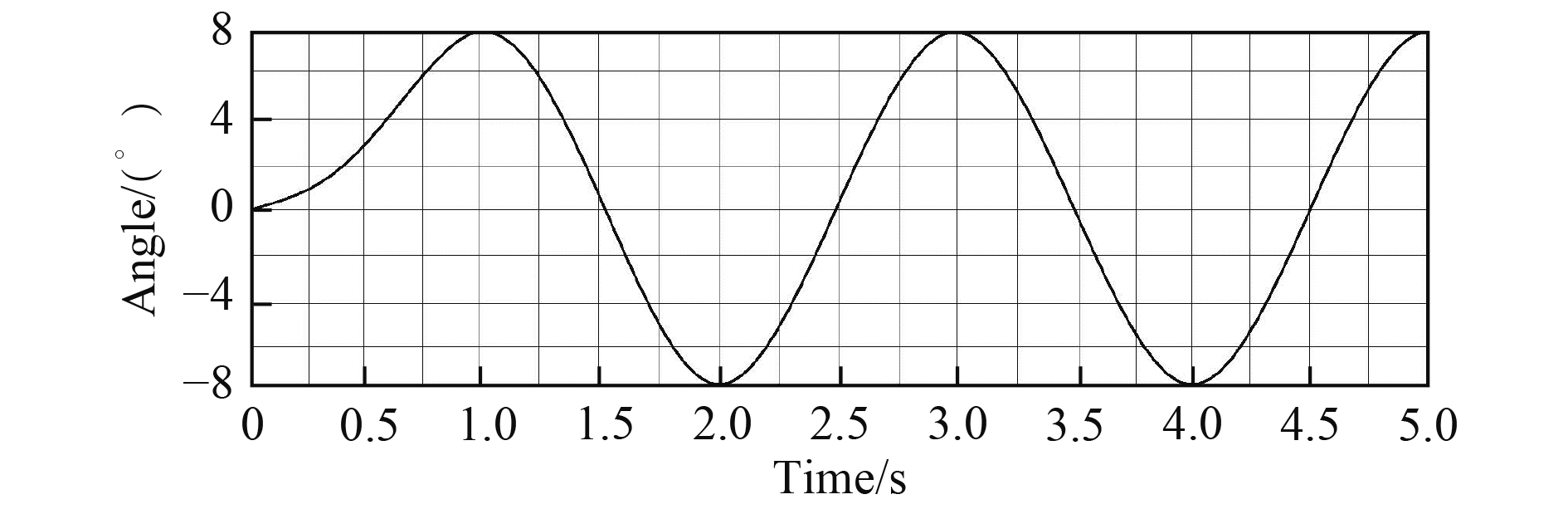
以横摇为例,若转动平台做正弦运动。初始时,摆动角度为0,速度为0。当横摇运动±8°/0.5 Hz时,时间为5 s,一开始时在0~8°内做半个周期的正弦运动,之后在±8°之间做正弦摆动,得到上面单独运动曲线图,如图5所示。
|
图 5 转动平台做横摇运动时的曲线 Fig. 5 The curve of rotating platform doing rolling motion |
动力学仿真,最期望得到的是在转动平台携带舰船模型做横摇、纵摇、偏航单独运动以及3种运动联动时的摆动角度、驱动绳索的拉力、速度变化曲线。运用多体动力学软件ADAMS给出了横摇、纵摇、偏航及联动时的仿真结果,如图6~图9所示。
|
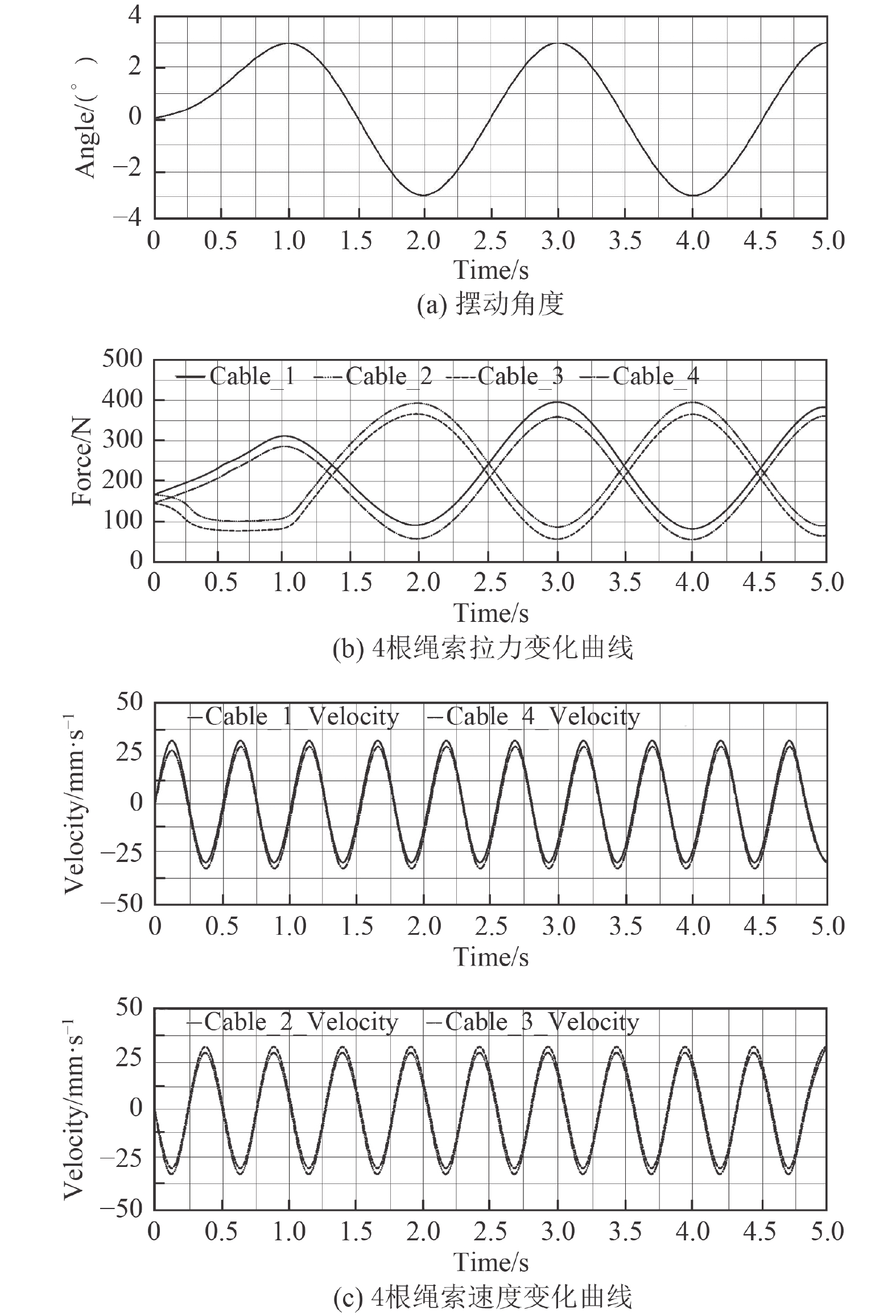
图 6 转动平台做横摇运动时仿真曲线 Fig. 6 Simulation curve of rotating platform carried out rolling motion |
|
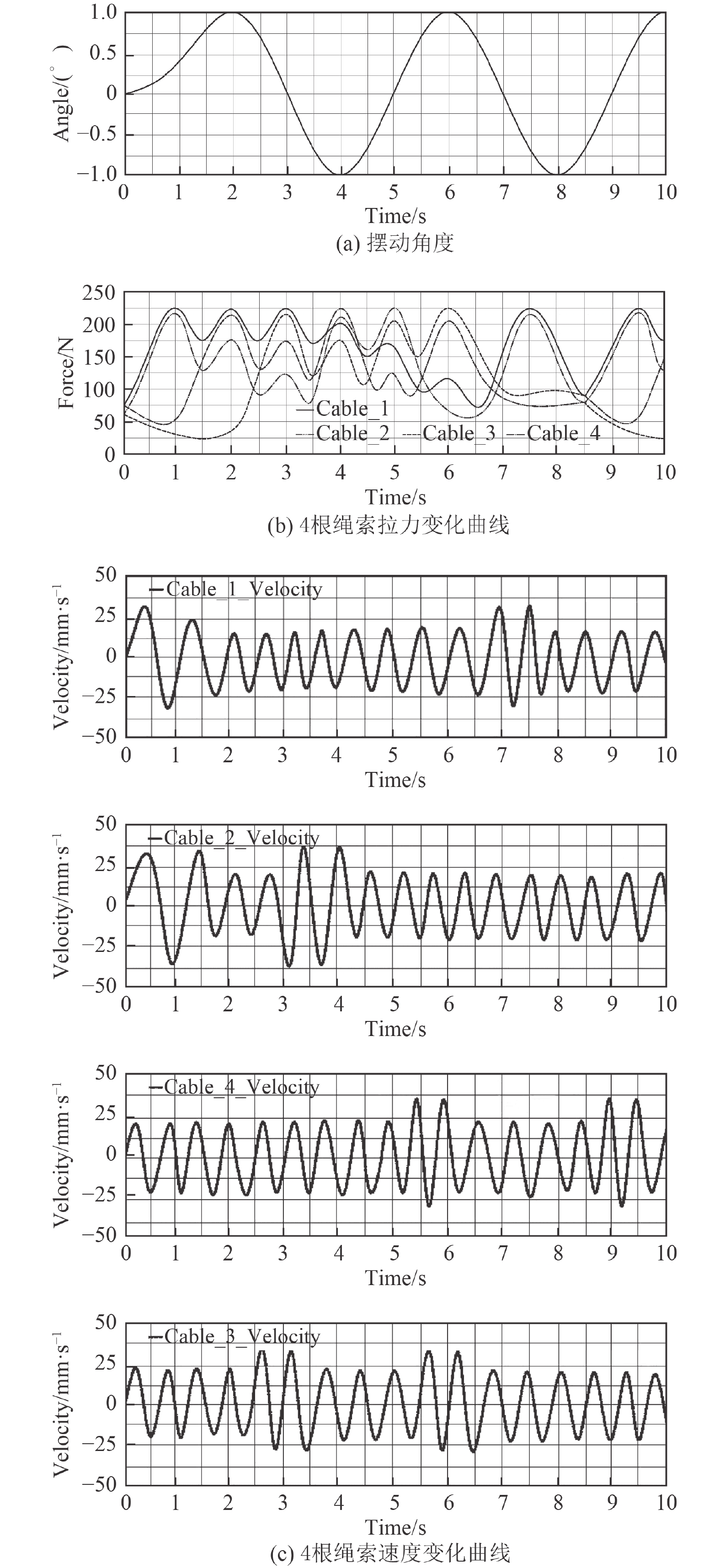
图 9 转动平台做联动运动时仿真曲线 Fig. 9 Simulation curve of rotating platform doing coupling motion |
1)从图6可以看出,当转动平台携带舰船模型做横摇运动时,初始时保持静止状态,转动平台摆角与速度值均为0,而绳索拉力值不为0,主要是为了保证转动平台平衡,绳索需处于张紧状态,所以初始时拉力保持定值。
运动时,图6(a)中转动平台从0~8°半个周期内做上升运动,对应图6(b)中绳索
2)从图7可以看出,当转动平台携带舰船模型做纵摇运动时,初始时保持静止状态,转动平台摆角与速度的值均为0;为了保证转动平台平衡,绳索需处于张紧状态,故各根绳索拉力值不为0。

|
图 7 转动平台做纵摇运动时仿真曲线 Fig. 7 Simulation curve of rotating platform doing pitching motion |
运动时,图7(a)中转动平台从0~3°半个周期内做上升运动,对应图7(b)中绳索
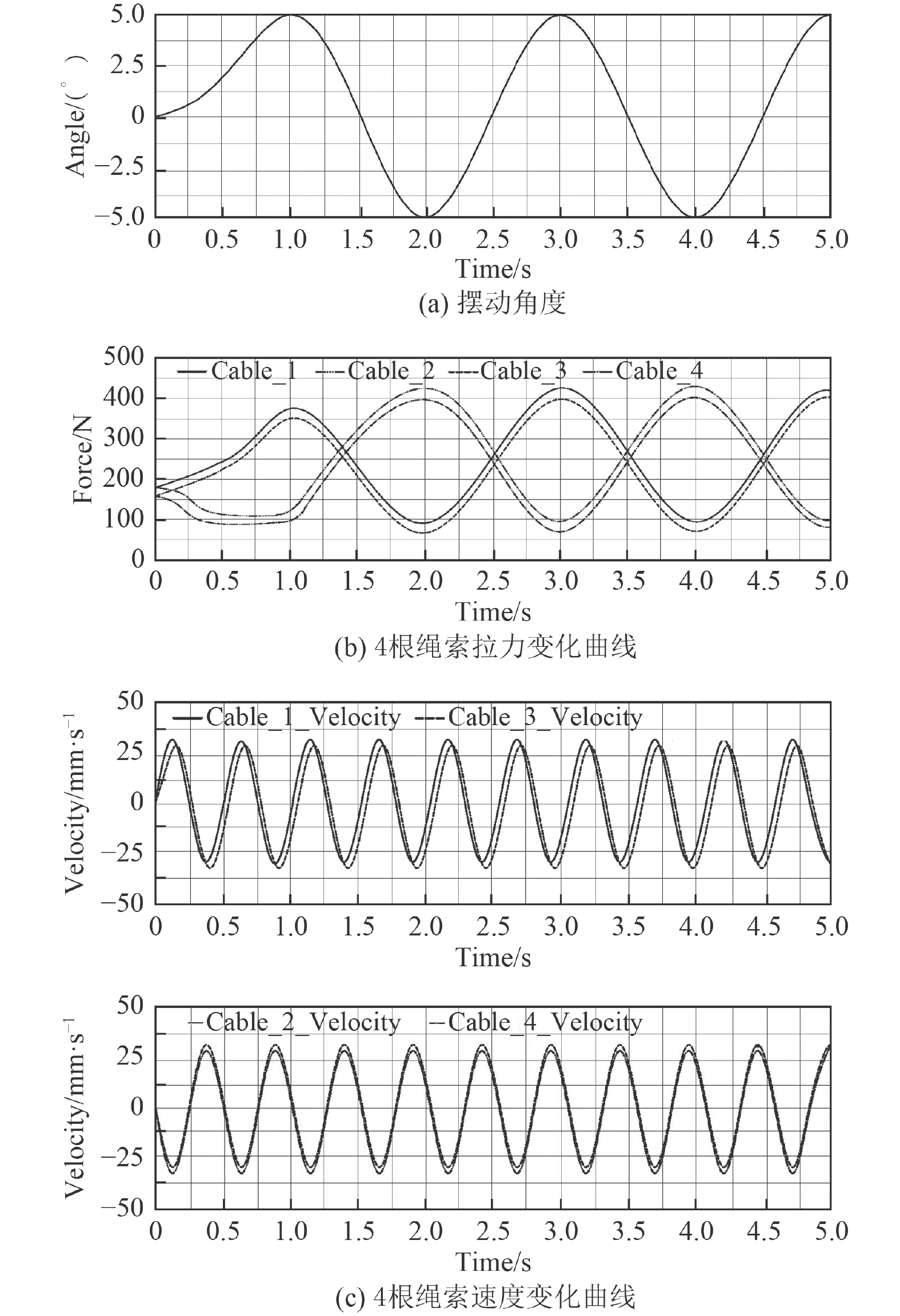
3)从图8可以看出,当转动平台携带舰船模型做偏航运动时,初始时保持静止状态,转动平台摆角与速度的值均为0;为保证转动平台平衡,绳索需处于张紧状态,故绳索拉力值不为0。
|
图 8 转动平台做偏航运动时仿真曲线 Fig. 8 Simulation curve of rotating platform doing yawing motion |
运动时,图8(a)中转动平台从0~5°半个周期内做上升运动,对应图8(b)中绳索
4)从图9可以看出,当转动平台携带舰船模型做联动运动时,初始时保持静止状态,转动平台摆角与速度值均为0,绳索拉力值不为0。
运动时,图9(a)中转动平台从0~1°半个周期内做上升运动,从1°~–1°做的是周期性正弦摆动。
分析绳索拉力的变化情况:图9(b)中,转动平台在0~3 s内,做横摇运动时的绳索
通过动力学仿真分析,对真实工作情况中的驱动绳索、转动平台等关键部件的受力与运动进行研究,反映了载具的真实工作情况,进一步验证了载具的运动性能,满足了设计要求,达到了舰船消磁实验的要求。
| [1] |
刘胜道, 王巍, 肖存龙. 低磁钢舰艇消磁系统绕组安匝调整[J]. 船电技术, 2013, 33(4): 25-27. DOI:10.3969/j.issn.1003-4862.2013.04.008 |
| [2] |
冯铁城, 朱文蔚, 顾树华. 船舶操纵与摇荡(修订本)[M]. 国防工业出版社, 1989.
|
| [3] |
张立勋, 刘攀, 王克义, 等. 绳索牵引并联康复机器人的建模与控制[J]. 哈尔滨工程大学学报, 2009, 30(1): 81-85. DOI:10.3969/j.issn.1006-7043.2009.01.014 |
| [4] |
严传续. 小型船舶运动模拟器研究[D]. 哈尔滨: 哈尔滨工程大学, 2008.
|
| [5] |
禹润田. 新型绳驱动并联踝关节康复机构设计及分析[D]. 北京: 北京交通大学, 2015. 3.
|
| [6] |
陈立平. 机械系统动力学分析及ADAMS应用教程[M]. 北京: 清华大学出版社, 2005.
|
 2019, Vol. 41
2019, Vol. 41
