海洋立管是连接海底井口与海洋平台或钻井船的重要构件,兼具油气传输与钻探生产,是海洋工程中必不可少的重要设备。由于波浪和水流的作用,立管两侧会产生交替脱落的漩涡,从而引起一个周期性的可变力,使得立管发生横向和流向的位移振动,称之为涡激振动(Vortex-induced Vibration, VIV)。VIV会对立管产生严重的结构疲劳破坏作用,减少其使用寿命,增加工程风险和成本。目前工程中抑制立管的涡激振动主要采用附加螺旋列板的方法[1~2]。杨加栋等[3]分析表明,对于相同的列板高度和螺距,一般选用3螺头的列板。李红艳等[4~5]对多组螺高螺距工况进行数值分析,认为螺高螺距分别取0.25D,17.5D(D为管径)时为最佳。Michael Breuer等[6~7]在对圆柱绕流进行数值模拟时试用了多种模型,对比发现,大雷诺数条件下采用大涡模拟的模型计算结果最好。目前多数对涡激振动抑制措施的研究以单一立管为设计对象[8~11],而实际工程中立管常以管群的方式出现。管群排列紧密,互相影响,使其运动响应比单立管时更加复杂[12~15]。研究深海立管涡激振动的同时考虑管群的相互作用更具有现实意义。本文运用三维数值模拟的方法,分别对单、双立管的水动力系数以及尾流场漩涡脱落情况进行分析,对附加螺旋列板对串列双立管升阻力系数及尾流场漩涡脱落的影响进行了模拟研究。
1 数学模型 1.1 大涡模拟的控制方程当流体为湍流状态时,非稳态连续性方程和N-S方程联合求解得到:
| $ \begin{split} & \!\!\!\!\!\!\frac{\partial }{{\partial t}}(\rho {u_i}) + \frac{\partial }{{\partial {x_j}}}(\rho {u_i}{u_j}) = \rho {F_i} - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}(2\mu {s_{ij}})\text{,} \\ & \!\!\!\!\!\!{s_{ij}} = \frac{1}{2}\left[ {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right] \text{。} \end{split} $ | (1) |
式中:F为质量力;ρ为密度;t为时间;p为压力;μ为流体的动力粘性系数;x,u分别为笛卡儿坐标系下的位置和速度分量。
大涡模拟方法是指在一定的空间区域内对N-S方程进行平均,从而在流场中滤掉小尺度的涡而导出大尺度涡所满足的方程的方法。小涡对大涡的影响会体现在大涡方程中,再通过亚格子尺度模型来模拟小涡的影响。
| $ \frac{{\partial {u_i}}}{{\partial t}} + \frac{{\partial \overline {{u_i}{u_j}} }}{{\partial {x_j}}} = - \frac{1}{\rho }\frac{{\partial \bar p}}{{\partial {x_i}}} + \nu \frac{{\partial {}^2\overline {{u_i}} }}{{\partial {x_j}\partial {x_j}}}\text{,} $ | (2) |
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0 \text{,} $ | (3) |
令
| $ \overline {{\tau _{ij}}} = - (\overline {{u_i}{u_j}} - \overline {{u_i}} \overline {{u_j}} ) \text{,} $ | (4) |
为亚格子尺度雷诺应力,则式(2)可写作
| $ \frac{{\partial \overline {{u_i}} }}{{\partial t}} + \frac{{\partial \overline {{u_i}} \overline {{u_j}} }}{{\partial {x_j}}} = - \frac{1}{\rho }\frac{{\partial \overline p }}{{\partial {x_i}}} + \nu \frac{{{\partial ^2}\overline {{u_i}} }}{{\partial {x_j}\partial {x_j}}} + \frac{{\partial {{\overline \tau }_{ij}}}}{{\partial {x_j}}}\text{,} $ | (5) |
令
| $ {u'_j} = {u_j} - \overline {{u_j}} \text{,} $ | (6) |
代表小尺度运动。将速度分解式代入式(4),得
| $ \overline {{\tau _{ij}}} = (\overline {{u_i}} \overline {{u_j}} - \overline {\overline {{u_i}} \overline {{u_j}} } ) - (\overline {\overline {{u_i}} {{u'}_j}} + \overline {{{u'}_i}\overline {{u_j}} } ) - \overline {{{u'}_i}{{u'}_j}} \text{。} $ | (7) |
圆柱体在运动的流体中因为所受的涡激力产生流向和横向的运动,其运动方程为:
| $ \begin{split} & mx + cx + kx = {F_x}(t) \text{,} \\ & my + cy + ky = {F_y}(t)\text{。} \end{split} $ | (8) |
式中:c为结构阻尼系数;k为弹簧刚度系数;Fx(t)为流向的阻力;Fy(t)为横向的升力。
1.3 水动力系数圆柱的阻力和升力系数:
| $ \begin{split} & {C_d}(t) = \frac{{{F_x}(t)}}{{\displaystyle\frac{1}{2}\rho U_c^2}} = \displaystyle\frac{{\int {p(t)\cos \alpha {\rm d}A} }}{{\frac{1}{2}\rho U_c^2}} \text{,} \\ & {C_l}(t) = \frac{{{F_y}(t)}}{{\displaystyle\frac{1}{2}\rho U_c^2}} = \displaystyle\frac{{\int {p(t)\sin \alpha {\rm d}A} }}{{\frac{1}{2}\rho U_c^2}} \text{。} \end{split} $ | (9) |
式中:A为圆柱的迎流面积;α为来流与压力的夹角;Uc为来流速度。
2 数值模拟结果分析 2.1 几何模型及工况设置参考以往的实验和数值模拟结论[16],选取矩形流域时为避免下游壁面边界对圆柱周围流场产生影响,圆柱中心至下游壁面间距离需大于14.5D(D为圆柱直径),侧壁至圆柱中心间距离需大于8D,其中。本算例流场区域如图1所示,圆柱中心距上游10D,距下游25D,与两侧壁面距离均取10D,展向长度取为10D。对于串列双立管,立管圆心间距分别取3D,5D,8D,上游立管距各壁面距离同上。螺旋列板的几何尺寸包括螺距P、板高H以及螺头数等。大量的实验和数值计算表明,螺距P对列板的涡激振动抑制效率影响不大,板高H、螺头数及覆盖率是影响涡激振动抑制效率的主要因素,而板高取0.25D时抑制效果最佳。文中涉及列板均选为三螺头,螺距P为17.5,板高H为0.25D,列板的截面形状选为三角形,如图2所示。

|
图 1 流域模型 Fig. 1 Model of fluid field |

|
图 2 附加螺旋列板 Fig. 2 Model of riser with helical strakes |
在SolidWorks中建立光滑立管的物理模型及计算区域,导入ICEM CFD中,将流域分成9个区域划分网格,考虑到不同区域网格对流场变化的影响,以立管模型为中心,周围3D范围内网格加密,中间区域采用o-grid剖分,其网格质量达0.6以上。圆柱体的网格划分使用结构化六面体网格,而螺旋列板网格划分使用非结构化的四面体网格。具体网格划分如图3所示。前后侧面分别设置为速度入口和出流边界,其他侧面设置为无滑移壁面。湍流模型采用大涡模拟的方法,流体域介质是水,采用稳定性较高的SIMPLEC方法进行压力和速度耦合。压力项采用Standard离散格式,对动量方程的离散采用中心差分格式,对时间的离散采用二阶隐式。通过光滑单圆柱工况的模拟结果验证其可靠性。

|
图 3 网格划分 Fig. 3 Mesh generation |
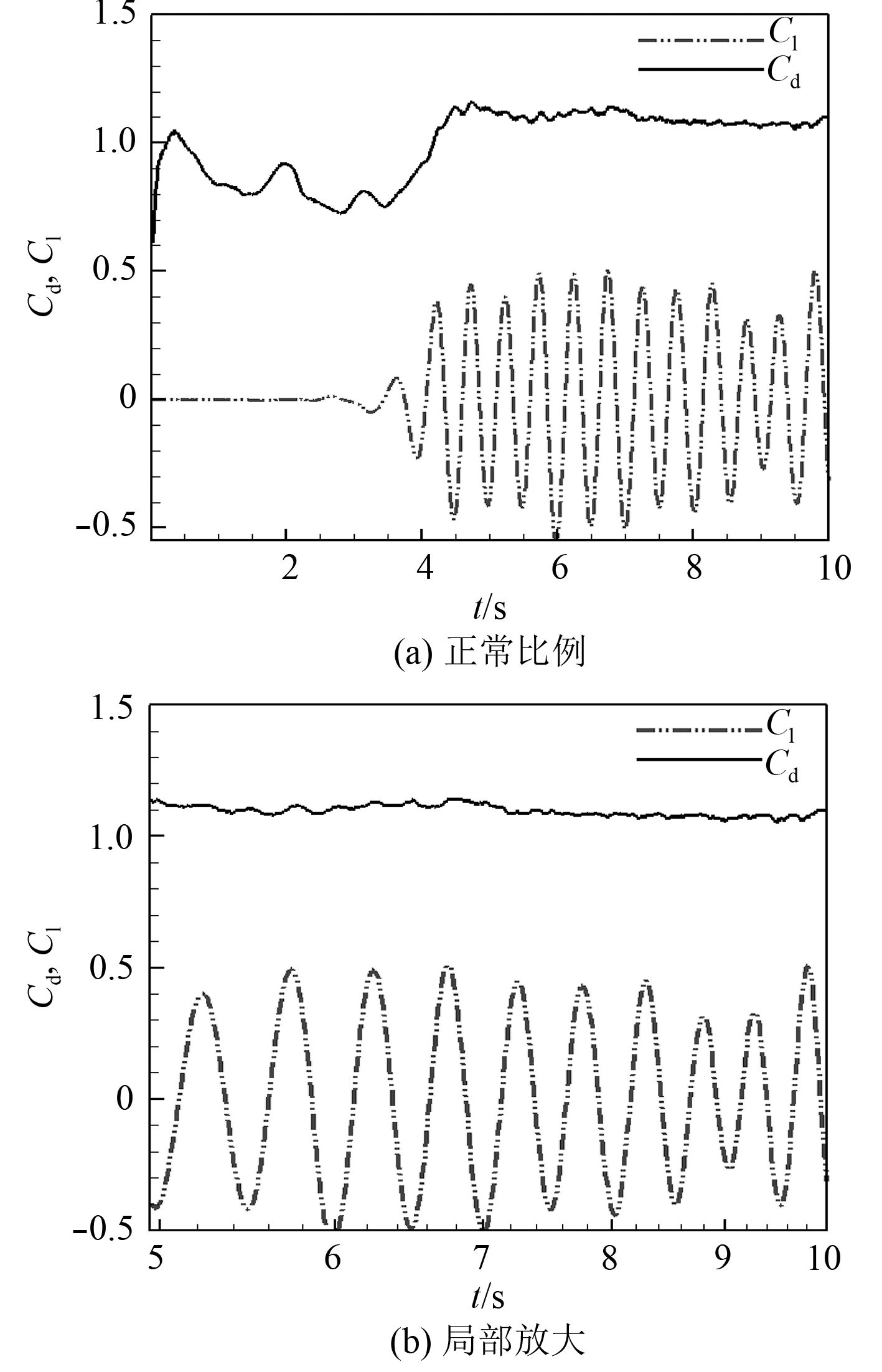
本文采用Re=3 900的均匀来流,光滑单立管的平均阻力系数Cd值为1.006,升力系数最大振幅在0.5左右。由图4可看出,阻力系数振动频率是升力系数振动频率的2倍。对升力系数进行快速傅里叶变换得到立管的振动频率fs=1.92,换算得相应的St数为0.20,与以往实验及模拟[17-19]经验总结的亚临界雷诺数范围内,St在0.19~0.23之间相符。
|
图 4 光滑单管阻力系数与升力系数曲线 Fig. 4 Drag and lift coefficients of smooth riser |
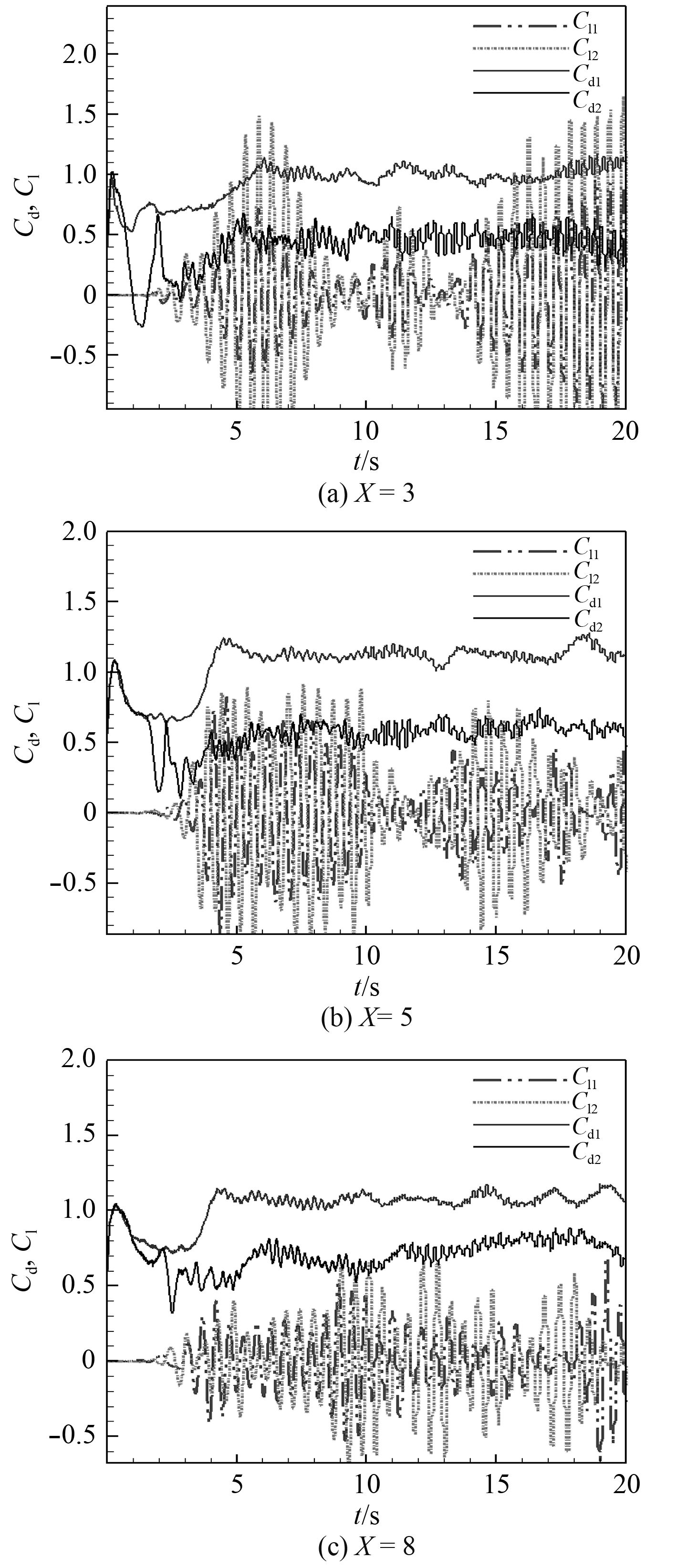
由图5和图6可以看出,双立管情况下,上游立管的升阻力系数与单立管升阻力系数相似,由于上游立管剪切层的脱落和下游立管本身的漩涡脱落造成下游立管力的叠加效应,使其受力情况复杂。下游立管阻力系数较单立管有明显减小,而升力系数振动幅值显著增大,当然,这也与双立管间距有关。本文图表中均用X表示双立管间的顺流向距离与立管直径的比值。
|
图 5 光滑双立管的受力系数 Fig. 5 Drag and lift coefficients of double smoothed risers |

|
图 6 附加列板后双立管的受力系数 Fig. 6 Drag and lift coefficients of risers with helical strakes |
由表1可见,立管间距为3D(X=3)时,上游立管升阻力系数近似于单立管的升阻力系数,下游立管平均阻力系数明显减小,而升力系数幅值较单立管增加了1.57倍;立管间距为5D(X=5)时,下游立管阻力系数比3倍管径时有所增大,升力系数幅值减小,但仍比单立管时大;立管间距为8 D(X=8)时,下游立管平均阻力系数继续增大,但仍小于单管的阻力系数,且升力系数幅值最小,接近单管时的升力系数。
|
|
表 1 双立管间距不同时立管受力系数分析 Tab.1 Drag and lift coefficient of risers with different X |
由于下游圆柱受上游圆柱尾流及自身漩涡脱落的双重影响,出现了下游立管阻力系数比单立管小的现象,而随着立管间距从3 D增加到8 D,下游的阻力系数也回升至单立管时的状态。
2.5 附加螺旋列板双立管结果分析双立管附加螺旋列板前后阻力系数均值以及升力系数标准差列于表2。双立管间距为3 D时,附加列板后前柱阻力系数增大,后柱减小且均值为负值。前后柱升力标准差都降低,前柱比后柱降低幅度更大。立管间距为5 D时,前柱阻力系数增大,后柱阻力系数减小,升力标准差显著降低。立管间距为8 D时,前柱阻力系数增大,后柱阻力系数与光滑管近似,升力系数标准差仍有显著降低。
|
|
表 2 附加列板前后立管受力系数分析 Tab.2 Drag and lift coefficients of smoothed riser and risers with helical strakes |
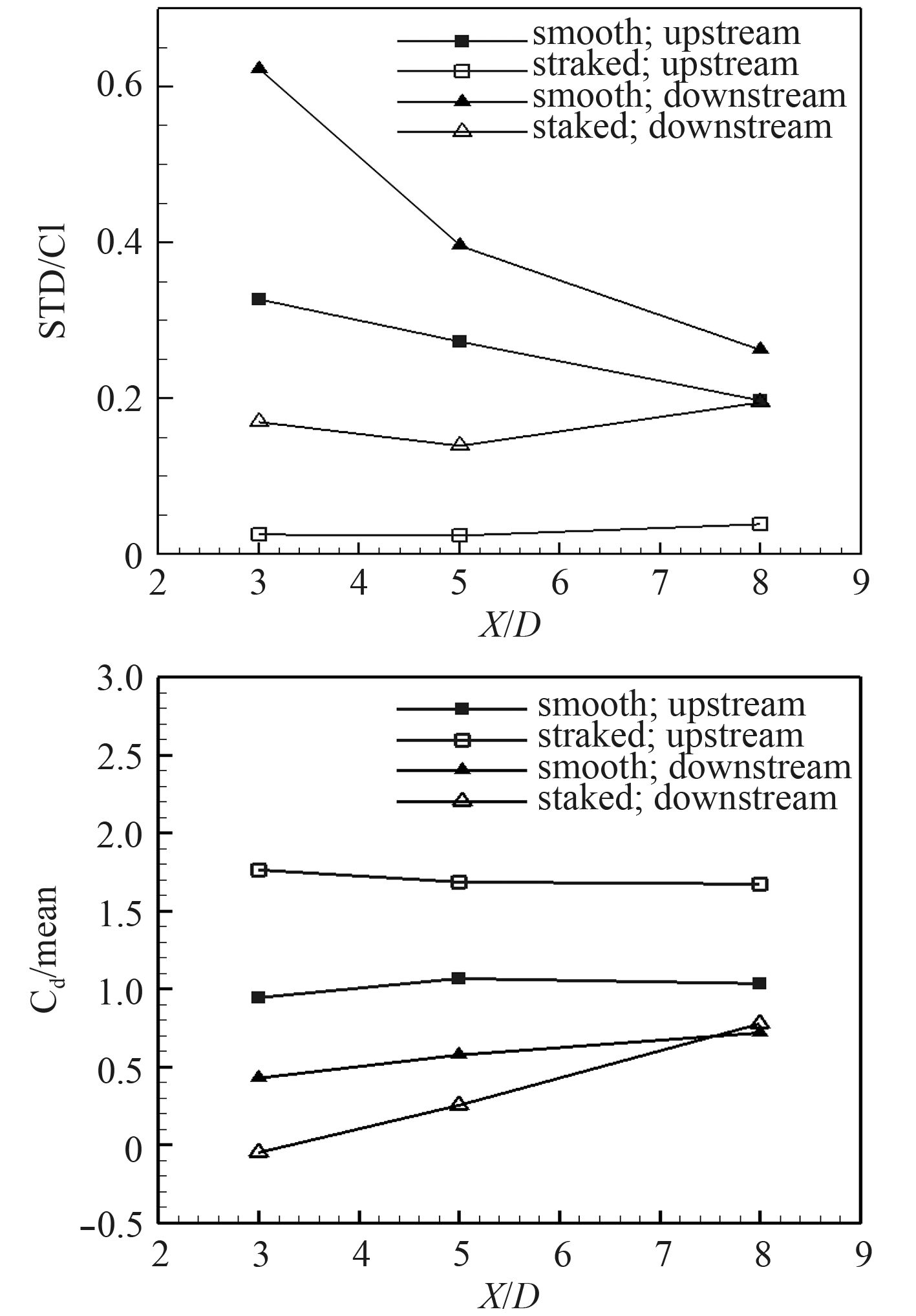
附加螺旋列板后两管间的流动情况复杂。上游立管附加的列板对来流起到分流作用,在上游立管尾流的作用下,下游立管尾流场依然存在相当量的漩涡脱落,导致其发生了大幅振动,其中横向振动占主要作用。附加螺旋列板后,立管阻力系数略微增大,但升力系数幅值显著降低。由图7可以明显看出,双立管间距为3 D时,附加螺旋列板后双立管升力系数的降幅最大,随着双立管间距增加,升力系数的降幅明显减小。而升力是影响立管涡激振动最主要的因素,因此,立管间距为3 D时螺旋列板抑制效率最高,立管间距为8 D时螺旋列板抑制效率最低。并且附加螺旋列板双立管之间的相互作用与光滑双立管之间的相互作用总体趋势相似。
|
图 7 附加螺旋列板前后升力标准差和阻力均值的对比 Fig. 7 Standard deviation of lift coefficients and mean drag coefficient of smoothed riser and risers with helical strakes |
由图8可以看出,光滑双立管之间有完整的漩涡脱落,其尾涡的脱落呈现2P,2S,P+S多种脱落模式。附加螺旋列板后,由于列板的分流作用,在圆柱后形成了间距很小,近乎平行的尾涡。

|
图 8 光滑双立管与附加螺旋列板双立管涡量切片图 Fig. 8 Vorticity slice graph of smoothed riser and risers with helical strakes |
本文对Re=3 900的均匀来流下串列双立管及附加螺旋列板双立管进行数值模拟,模拟分析了不同管间距对立管受力的影响以及附加螺旋侧板对双立管涡激振动的抑制作用,主要结论如下:
1)对于双立管情况,上游立管受力与单立管情况相似,而下游立管受到来自上游立管脱落的剪切层以及自身脱落的漩涡的力的叠加影响,受力情况复杂,与单立管情况相比,其阻力系数明显减小,而升力系数幅值增大。
2)研究发现,立管间距为3 D时上下游立管间的相互影响较大,导致下游立管升力系数幅值显著增加;立管间距为5 D时,下游立管升力系数的增加趋于平缓;立管间距为8 D时,上下游立管间相互影响最小,升阻力系数接近单立管情况。
3)螺旋列板可以有效地抑制双立管的涡激振动。附加螺旋列板后,双立管升力系数幅值显著降低,从而减少了立管的振幅响应,但是阻力系数比光滑管时更大。双立管加板前后,上下游立管之间相互作用的总体趋势相似。并且由于列板的分流作用,彻底破坏了立管的脱涡方式,在立管后形成间距很小,近乎平行的尾涡。
| [1] |
GAO Yun, FU Shi-xiao, CAO Jing, et al. Experimental study on response performance of VIV of a flexible riser with helical strakes[J]. China Ocean Engineering, 2015, 29(5). |
| [2] |
HUANG S. VIV suppression of a two-degree-of-freedom circular cylinder and drag reduction of a fixed circular cylinder by the use of helical grooves[J]. Journal of Fluids and Structures, 2011, 27(7): 1124-1133. DOI:10.1016/j.jfluidstructs.2011.07.005 |
| [3] |
杨加栋, 张晓灵, 杜宝银, 等. 螺旋列板——深水立管涡激振动抑制装置[J]. 海洋技术, 2010, 29(4): 88-92, 116. DOI:10.3969/j.issn.1003-2029.2010.04.020 |
| [4] |
李红艳, 朱仁庆, 王玲. 剪切流中螺旋侧板抑制柔性立管涡激振动的数值模拟[J]. 江苏科技大学学报(自然科学版), 2016, 30(05): 417-423. DOI:10.3969/j.issn.1673-4807.2016.05.002 |
| [5] |
付世晓, 王德禹. 深水立管涡激振动模型试验报告[D]. 上海: 上海交通大学, 2011.
|
| [6] |
BREUER M. A challenging test case for large eddy simulation: high Reynolds number circular cylinder flow[J]. International Journal of Heat and Fluid Flow, 2000, 21(5): 648-654. DOI:10.1016/S0142-727X(00)00056-4 |
| [7] |
乔永亮, 桂洪斌, 刘祥鑫. 三维圆柱绕流数值模拟湍流方法的选择[J]. 水利水运工程学报, 2016(3): 119-125. |
| [8] |
E R RANJITH, A S SUNIL. Lipp in pauly. analysis of flow over a circular cylinder fitted with helical strakes[J]. Procedia Technology, 2016, 24. |
| [9] |
YU Heng-xu, MI Wei-jian, ZHOU Tong-ming, et al. Experimental and numerical studies on the suppression of vortex induced vibrations using helical Strakes[C]// Proceedings of the 2011 International Conference on Advances in Construction Machinery and Vehicle Engineering 2011: 6.
|
| [10] |
盛磊祥, 陈国明.螺旋列板绕流流场CFD分析[J].中国造船, 2010, 51(01): 78–83.
|
| [11] |
LEE Kee Quen, AMINUDIN Abu, NAOMI Kato, PAUZIAH Muhamad, ASNIZAH Sahekhaini, HANIDA Abdullah. Investigation on the effectiveness of helical strakes in suppressing VIV of flexible riser[J]. Applied Ocean Research, 2014, 44. |
| [12] |
曹淑刚, 黄维平, 周阳, 等. 并列双立管涡激振动特性的数值和实验研究[J]. 船海工程, 2015, 44(2): 130-135. DOI:10.3963/j.issn.1671-7953.2015.02.033 |
| [13] |
陈海明, 黄维平. 基于CFX-CFD软件的并列双立管升阻力研究[J]. 中国水运(下半月), 2010, 10(7): 107-108. DOI:10.3969/j.issn.1006-7973-C.2010.07.057 |
| [14] |
贾晓荷. 单圆柱及双圆柱绕流的大涡模拟[D]. 上海: 上海交通大学, 2008.
|
| [15] |
魏东泽. 基于雷诺相似的串列双立管涡激振动研究[D].青岛: 中国海洋大学, 2012.
|
| [16] |
T E TEZDUYAR, R SHIH.. Numerical Experiments on downstream boundary of flow past cylinder[J]. Journal of Engineering Mechanics, 1991, 117: 4. |
| [17] |
KRAVCHENKO A G, MOIN P. Numerical studies of flow over a circular cylinder at Re = 3 900
[J]. Physics of Fluids, 2000, 12(2): 403-417. DOI:10.1063/1.870318 |
| [18] |
ROSHKO A. On the development of turbulent wakes from vortex streets[R]. NACA report 1191, NACA, USA, 1954.
|
| [19] |
LIE H, KAASEN K E. Modal analysis of measurements from a large-scale VIV model test of a riser in linearly sheared flow[J]. Journal of Fluids and Structures, 2006, 22(4): 557-575. DOI:10.1016/j.jfluidstructs.2006.01.002 |
 2019, Vol. 41
2019, Vol. 41
