AUV是水下机器人的一种,是无缆式水下机器人,习惯上称为自主式水下航行器(Autonomous Underwater Vehicle,AUV)[1],近年来AUV作为一种别具特色的海洋应用装备在海洋物探、定位打捞、军事侦察等领域呈现出强劲的发展势头,正成为一种新的隐蔽性好、机动性高的水下作业平台,已经具有相当的搭载能力和水下续航能力,但由于海水对电磁波(包括可见光在内)的吸收和反射等效应,AUV等水下航行器要实现精确的定位和导航是一件很高难度的事情。目前水下自主航行器的水下自身定位导航都是以惯性导航为基础,主要依靠陀螺仪系统,精确地感知水下自主航行器运动姿态的变化,结合加速度传感器,通过实时速度对时间的积分推算水下自主航行器在水下行进的距离和方向从而解算出自身的位置。这种技术的局限性在于测量误差一定存在,并且随着时间积分在不断累积和放大。
迄今为止,水下目标定位跟踪的主要手段仍是依赖于几何原理的水声学定位方法[2],对于水下AUV等自主航行器的定位和跟踪主要通过短基线或者超短基线声学定位系统进行,由于这2种方法的工作原理是测量船舶和AUV的相对位置关系,对于AUV的定位精度受测量船本身的位置精度影响较大,且这2种测量方法相对于水声长基线定位方法精度较低,不适用于水下精确定位的场合,长基线测量系统独立于深度测量,所以其精度非常高[3]。
本文介绍一种适用于水下固定试验场的水下航行器运动自导航及轨迹跟踪方法,主要应用于水下自主航行器的海上测试。由于水声通信是当前唯一可在水下进行远程信息传输的通信形式[4],水声通信与水声网络由于在海洋信息应用领域的不断扩大而取得了很大的进步[5],采用在水下试验场海底预先布设位置已知的定位基元,采用同步式水声精确测距技术,实现AUV等航行器在水下自动获取自身的位置信息和运动轨迹信息以及实现岸站或船载平台精确掌握AUV等航行器在水下的位置和运动轨迹信息。
1 轨迹跟踪方法介绍轨迹跟踪是对目标进行连续定位,本文介绍的方法采用声学长基线定位原理,声学长基线定位包括同步定位、异步定位和应答式定位。
同步定位是指发射端使用与接收端同步的定位发射机,可通过水下合作目标上装载高精度铷钟守时系统来实现[6],根据信号发射和接收端时间同步测距原理,通过至少3个距离值解算完成目标位置信息。
异步定位是指通过发出的定位信号到达一对定位基元的时间差来确定定位信标发射模块(即目标)所在的双曲面,再利用另外2对基元确定另外2个双曲面,3个双曲面交汇在一起就可以确定目标位置。
应答方式是声基元和合作目标之间通过询问和应答的方式测距,所以二者均需要收发声信号的能力[3]。通过信号发射时间和回码时间延时解算得到声基元与声信标之间的双倍声程,从而得到二者之间的距离,获得至少3个距离值计算得到定位目标的大地坐标。
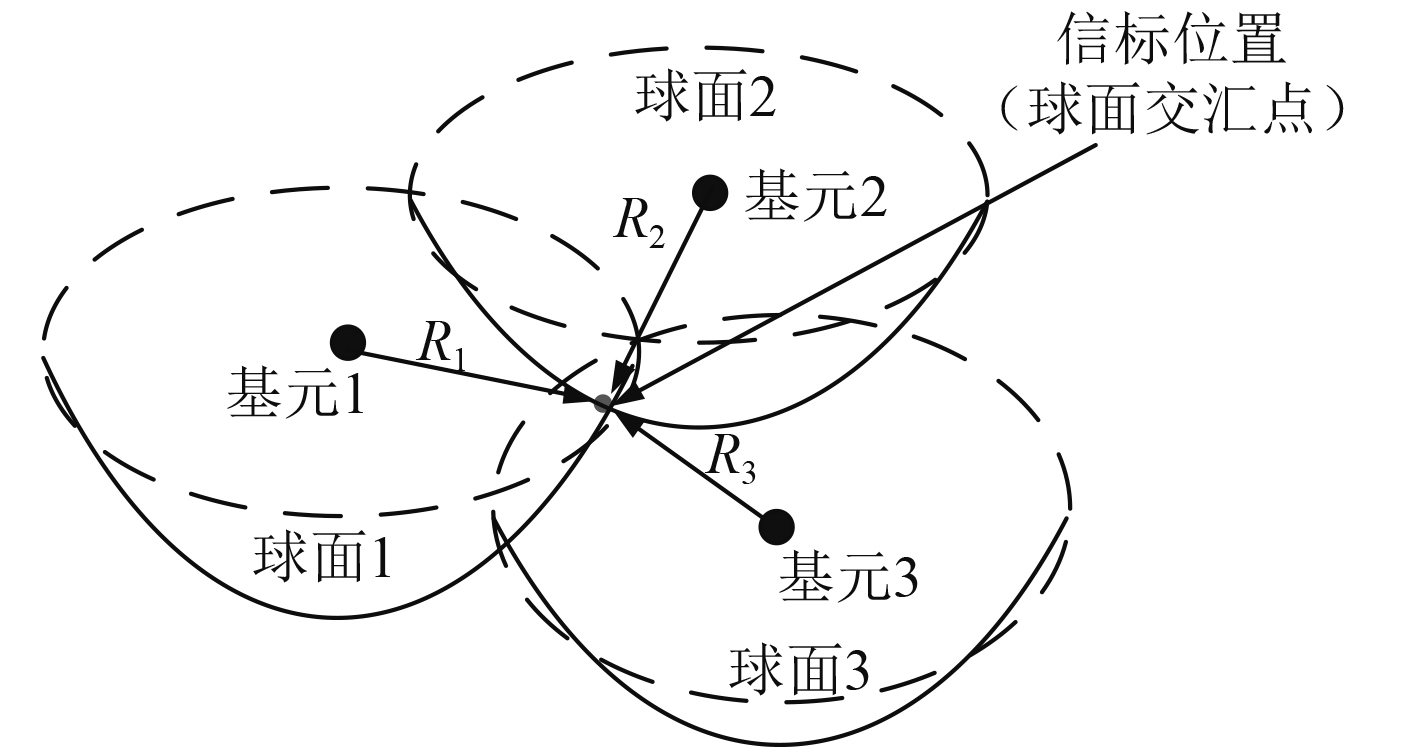
本文采用声学长基线同步定位原理,多个定位基元的三维空间位置可以视为已知量,定位信标接收水下基元基阵发射的信号,不同位置基元发射的信号频率不同,信号接收端可据此分辨出接收时刻不同,基元与定位信标的声程(即信号发射时间与信标接收到的时间差),与水中声速相乘就得出3个基元与定位信标的距离。数学模型如图1所示。
|
图 1 长基线三圆定位原理数学模型 Fig. 1 Mathematical model of long baseline three-circle position principle |
| ${R_i} = c \cdot \Delta {t_i} = \sqrt {{{(x - {X_i})}^2} + {{(y - {Y_i})}^2} + {{(z - {Z_i})}^2}}\text{。} $ | (1) |
其中:
从模型上看,定位信标到基元的距离可以看作是以基元为中心的球体半径,意味着信标在该球面上。信标与2个基元的距离,则意味着目标位于这2个球面相交的曲线上,该曲线为一圆周,2个距离还是不能提供足够的信息求出一个三维解,因此还需要第3个距离来计算目标位置。3个球面相交汇就可以得到一个完整的三维解。
2 定位精度分析 2.1 固定目标定位精度分析由式(1)可知,目标定位误差主要由定位基阵的水平位置误差、时间测试误差和平均声速误差引起,下面通过蒙特卡罗反演方法仿真分析这3个误差源对目标定位精度的影响。
假设一个5 km×2.5 km的定位基阵,在阵元位置误差0.5 m、时间测试误差0.05 ms、声速误差0.5‰的定位精度仿真结果如图2所示。

|
图 2 固定目标精度仿真结果 Fig. 2 Simulation results of fixed target precision |
由图2可以看出系统定位误差≤3.5 m,在基阵中心位置的定位误差≤0.5 m。
2.2 运动目标定位精度分析系统的一种工作方式是定位基阵作为接收端,同运动目标信号发射端工作在同步状态。运动目标发射定位信号,定位基阵接收定位信号后,利用长基线定位原理对目标进行定位解算。目标发射的定位信号传输到基阵这段时间内,目标处于运动状态,定位系统解算出的目标位置是目标发射信号时刻的位置,并不是定位基阵接收到信号后进行解算时刻的位置,所以这种工作方式下的定位结果会产生滞后,但是目标的运动不影响定位精度,因为目标发射信号不会影响到接收信号的时延。这种模式是定位系统可延时知道目标的精确位置,但运动目标不能解算自己的位置。
系统的另一种工作模式是定位基阵各阵元发射信号,运动目标接收不同阵元的信号时延,然后根据长基线定位原理解算自己的位置。这种工作方式目标解算自身的位置没有滞后,但是目标的运动会使系统的测时产生误差。对于一个固定目标收到不同阵元i的时延为ti。但是由于目标一直在运动,导致阵元t1的时延不是t1而是t1+Δt,其他阵元相应也会有时延误差,这个误差将会影响系统定位精度。对于固定目标的定位系统,影响系统定位精度有阵元误差、测时误差和声速误差。对于运动目标定位系统,目标运动引入了新的测时误差,不会影响阵元误差和声速误差。下面将重点从运动目标带来的测时误差来分析系统定位精度。
长基线定位系统定位解算时最少需要3个阵元来完成目标定位,下面从最小阵元数的三元阵来分析运动目标定位系统的定位精度。
首先证明系统定位精度不受基阵发射信号时刻的影响。假设固定目标位于A点处,基阵t0时刻发射信号,目标t1时刻收到阵元1的信号,t2时刻收到阵元2的信号,t3时刻收到阵元3的信号,用t1,t2,t3对目标定位,系统定位精度没有受到影响。同样情况下,目标运动时,目标的起始位置为A,目标在收到阵元1的信号时位置为B,收到阵元1的时延是
| $\Delta {t_2} = \frac{{{V_2}({L_2} - {L_1})}}{{1\;500}}/1\;500\text{。}$ | (2) |
式中:
同理可推出阵元3产生的测时误差如下:
| $\Delta {t_3} = \frac{{{V_3}({L_3} - {L_1})}}{{1\;500}}/1\;500\text{。}$ | (3) |
式中:
从式(2)和式(3)可以得出如果速度一定的情况下,导致测时误差主要是阵元间距差。阵元距离目标的距离差越小系统定位精度越高,换言之如果同时收到3个阵元的信号(3个阵元和目标距离一致),则系统准确定出目标位置,目标的运动不会对系统带来任何误差影响。
下面就不同阵型来分析目标定位精度。
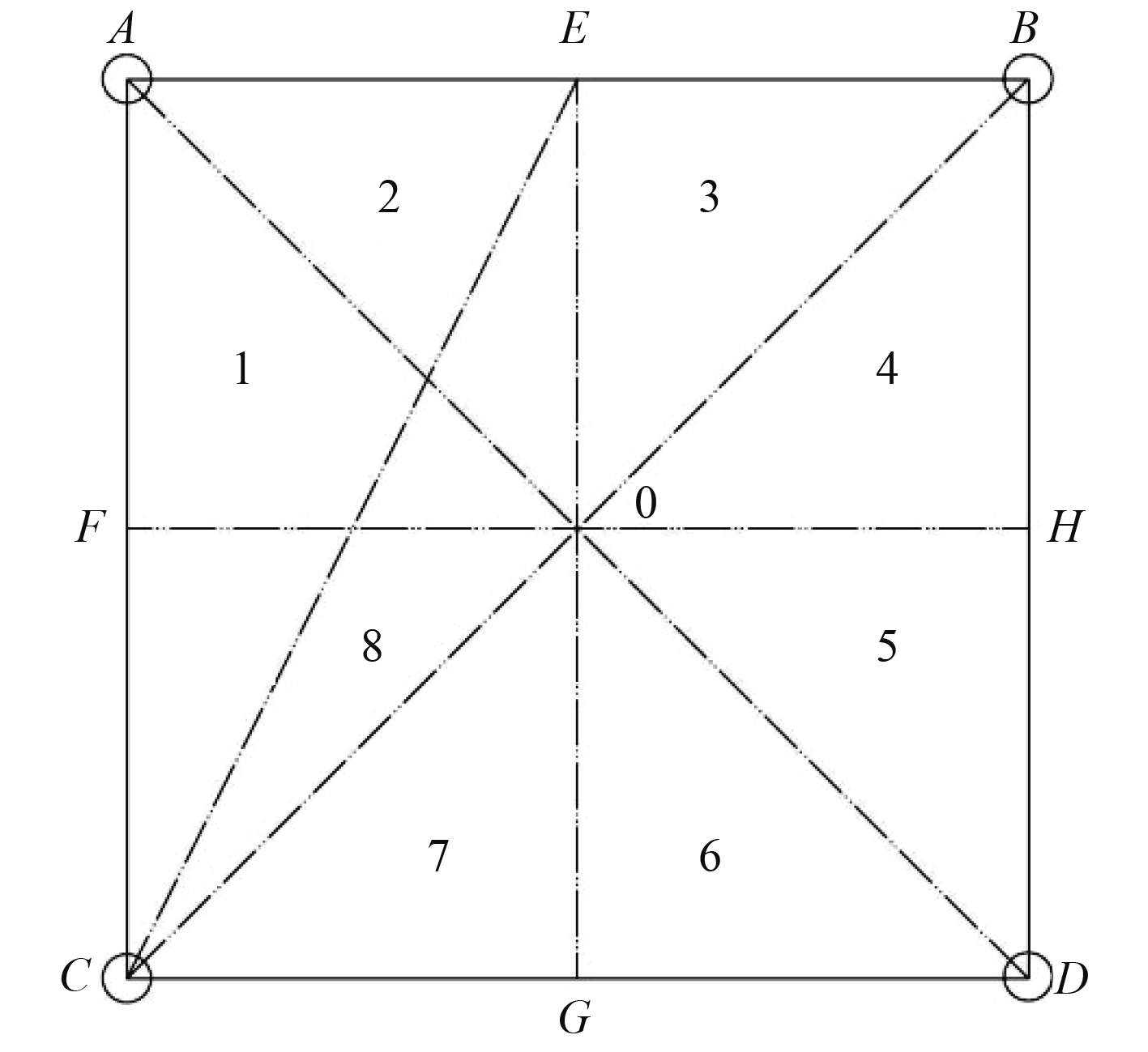
如图3所示的正方形阵,正方形的边长为L,4个阵元分别为A B C D。
|
图 3 正方形阵 Fig. 3 Square array |
如果目标位于A点,目标最先收到阵元A的信号,然后收到阵元B C的信号,最后收到阵元D的信号。根据理论分析虽然最先收到A阵元的信号,使用B C D三阵元来定位,则误差更小。采用B C D三阵元来定位,测时误差为
| $\Delta {t_D} = \frac{{{V_D}(\sqrt 2 - 1)L}}{{1\;500}}/1\;500\text{,}$ | (4) |
式中,
同理可以证明目标在区域1和2内使用B C D定位精度要高;目标在区域3和区域4内使用A C D定位精度要高;目标在区域5和区域6内使用A B C定位精度要高;目标在区域7和8内使用A B D定位精度要高。同理可以计算出定位精度最差的点的位置E F G H。例如E点采用B C D三阵元来定位。
| $\Delta {t_D} = \frac{{{V_D}(\sqrt 5 /2 - 1/2)L}}{{1\;500}}/1\;500\text{,}$ | (5) |
式中,
理论上O点的误差最小,为0,因为O点到各个阵元间的距离相同。
如果在O点增加一个阵元,则E F G H四点的定位误差为0,定位误差最大点则为A B C D四点,测时误差为
| $\Delta {t_D} = \frac{{{V_D}(\sqrt 2 - 1)L}}{{1\;500}}/1\;500\text{。}$ | (6) |
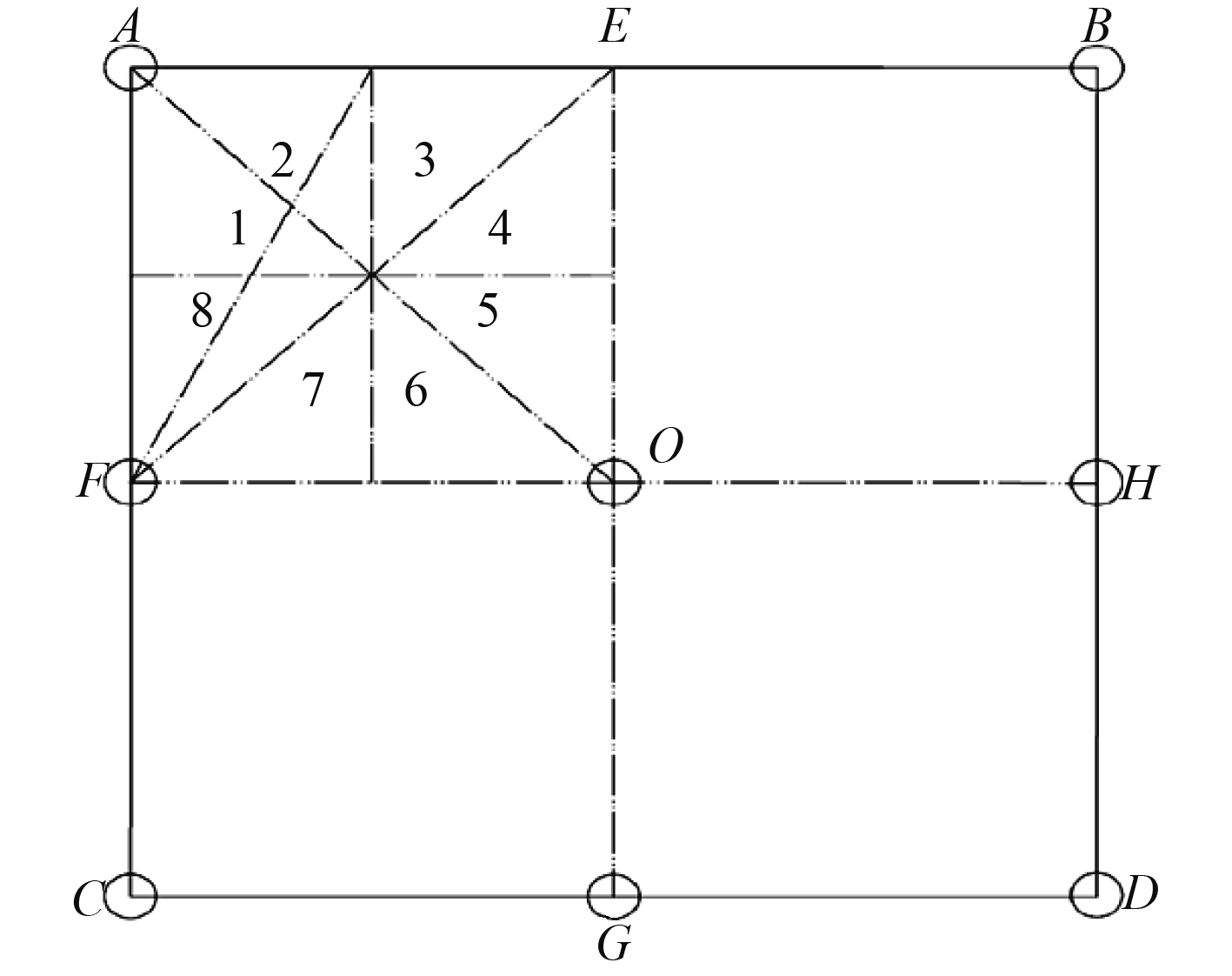
如果要覆盖长度2 L的范围,方形阵需要9个阵元,如图4所示,但是每4阵元的精度如上面4阵元精度所分析。
|
图 4 正方形9阵元 Fig. 4 Square 9-element array |
如图5的正六边形阵,阵元间距为L,7个阵元分别为A B C D E F O。

|
图 5 正六边形阵 Fig. 5 Normal hexagonal array |
由于该阵型多方位对称性,所以只分析AOI该区域的精度,其他对称方位的精度即可得出。理论上这个阵型的6个顶点和中心位置的误差都为0,如A点可以采用B O F三阵元来定位,3个阵元到A点距离相等。而且中心位置O点与多个阵元间的距离都相等,因此定位精度最高。对于AOI区域,误差最大处在边界位置,首先计算I点误差,I点采用A B O三阵元定位,计算可得:
| $\Delta {t_o} = \frac{{{V_o}(\sqrt 3 /2 - 1/2)L}}{{1\;500}}/1\;500\text{,}$ | (7) |
式中,
误差最大点应该位于AI之间的某个点上,这个点应该就是2个阵型的变换点,比如为G点,在AG之间采用B O F三阵元定位,在GI之间采用A B O三阵元定位,在G点采用B O F三阵元定位或采用A B O三阵元定位,定位误差一样。所以在G处应满足:
| $ \left( {{{GO - GA}}} \right){{ = }}\left( {{{GF - GB}}} \right)\text{,} $ |
(GO-GA)为在A B O三阵元定位时,最长距离减去最短距离;(GF-GB)为在B O F三阵元定位时,最长距离减去最短距离。
| $\Delta {t_o} = \frac{{{V_o} \cdot 0.543 \cdot L}}{{1\;500}}/1\;500\text{,}$ | (8) |
G的位置满足AG=0.338 L。
从原理上解G点和I点使用C D E三阵元来解算误差会更小,但是考虑到声信号作用距离和信噪比的影响,选取更近的阵元来解算。
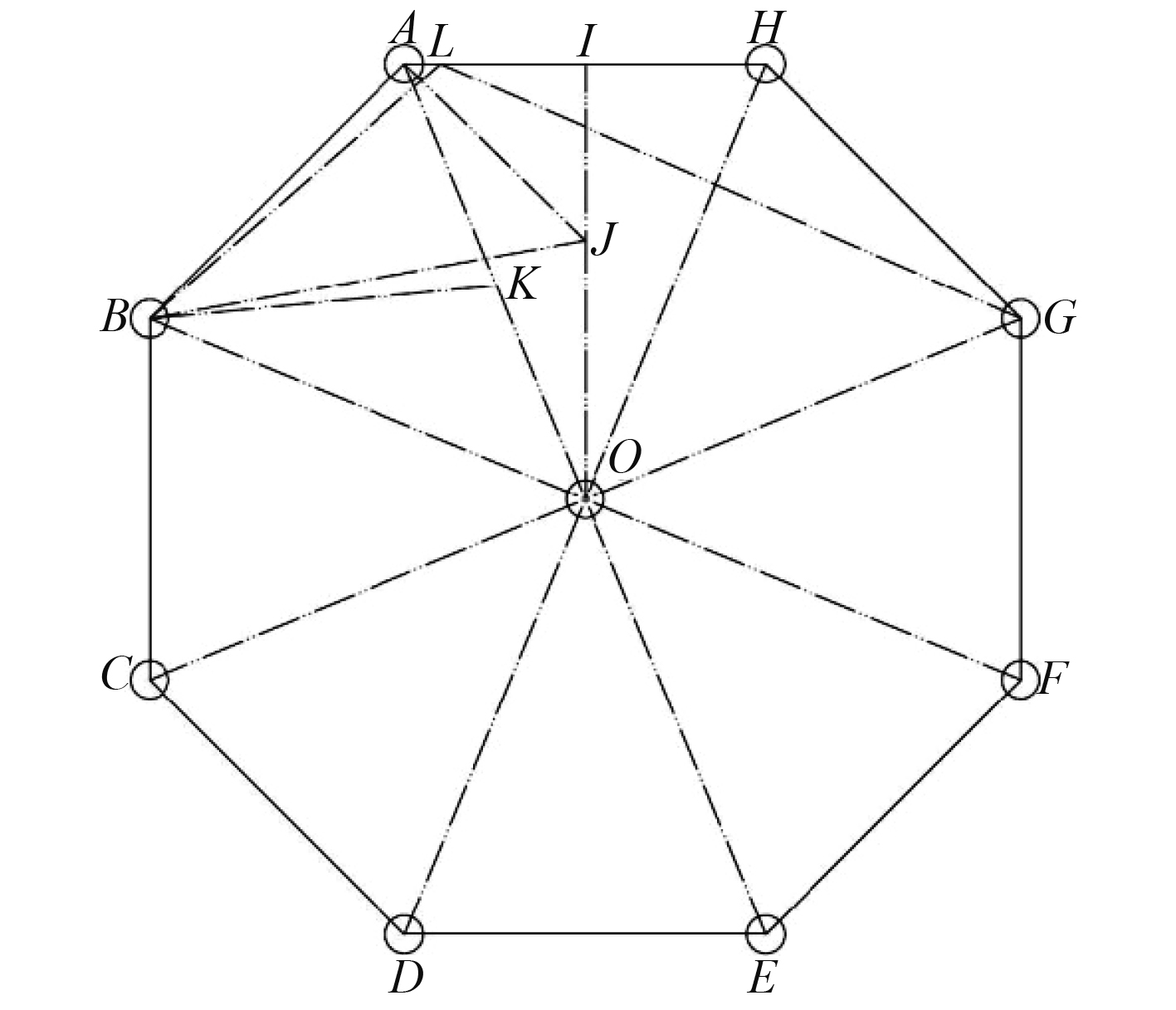
如图6所示的正八边形阵,中心阵元到边上阵元间距为L,9个阵元分别为A B C D E F G H O。
|
图 6 正八边形阵 Fig. 6 Normal octagonal array |
由于该阵型多方位对称性,所以只分析AOI该区域的精度,其他对称方位的精度即可得出。
对于AOI区域,误差最大都在边界,首先分析IO边上,接近I点则用B O G三阵元定位,接近O点则用A B H三阵元定位。误差最大点就是2个阵型转换处,假设为J点,则在
| $\Delta {t_o} = \frac{{{V_o} \cdot (0.937 - 0.541) \cdot L}}{{1\;500}}/1\;500\text{,}$ | (9) |
计算得
| $\Delta {t_o} = \frac{{{V_o} \cdot 0.543 \cdot L}}{{1\;500}}/1\;500\text{。}$ | (10) |
再次分析AI边上,接近I点则用B O G三阵元定位,接近A点则用B O H三阵元定位。误差最大点就是2个阵型转换处,假设为L点,则在
| $\Delta {t_o} = \frac{{{V_o} \cdot (0.96 - 0.512) \cdot L}}{{1\;500}}/1\;500\text{,}$ | (11) |
计算得
| $\Delta {t_o} = \frac{{{V_o} \cdot 0.448 \cdot L}}{{1\;500}}/1\;500\text{。}$ | (12) |
最后分析AO边上,接近O点则用A B H三阵元定位,接近A点则用B O H三阵元定位。误差最大点就是2个阵型转换处,假设为K点,则在
| $\Delta {t_o} = \frac{{{V_o} \cdot (0.737 - 0.5) \cdot L}}{{1\;500}}/1\;500\text{,}$ | (13) |
计算得
| $\Delta {t_o} = \frac{{{V_o} \cdot 0.237 \cdot L}}{{1\;500}}/1\;500\text{。}$ | (14) |
综上分析正八边形阵的最大误差为
| $ \Delta {t_o} = \frac{{{V_o} \cdot 0.448 \cdot L}}{{1\;500}}/1\;500{\text{。}} $ |
经过上述分析,覆盖范围2 L的长度。
采用正方形阵,最大误差为
| $ \Delta {t_D} = \frac{{{V_D}(\sqrt 5 /2 - 1/2)L}}{{1\;500}}/1\;500 = \frac{{{V_D} \cdot 0.618 \cdot L}}{{1\;500}}/1\;500\text{,} $ | (15) |
采用正六边形阵时,系统最大误差为
| $\Delta {t_o} = \frac{{{V_o} \cdot 0.543 \cdot L}}{{1\;500}}/1\;500\text{,}$ | (16) |
采用正八边形阵时,系统最大误差为
| $\Delta {t_o} = \frac{{{V_o} \cdot 0.448 \cdot L}}{{1\;500}}/1\;500\text{。}$ | (17) |
经上述分析建议采用正八边形阵,系统误差最小。
如果采用正八边形阵型,覆盖范围5 km,相当于计算中的L为2.5 km,目标速度10 kn(5 m/s),目标直指O点运动(目标所有速度分量都指向O),最大的测时误差2.4 ms,产生的最大距离误差3.7 m。经上述仿真固定目标最大误差3.5 m,所以系统最大误差7.2 m。
通过上述分析,在不同区域,可以选择不同的阵元来解算,但是在实际使用中,并不知道目标在什么区域,无法预先判断。所以在工程实现上,在一定时间范围内接收到多个阵元信号,然后通过计算找到时延差值最小的3组阵元信号作为定位解算的数据来进行长基线定位。此外通常声学定位系统的频率选择是根据使用的范围和要求的精度来确定,但是声学界就精度与频率的关系问题还在研究,一般情况下频率越高精度越高[7],本文不做探究。
3 工程实现方法根据上述定位原理和精度分析,设计水下运动目标自导航运动轨迹跟踪系统,系统组成如图7所示。
|
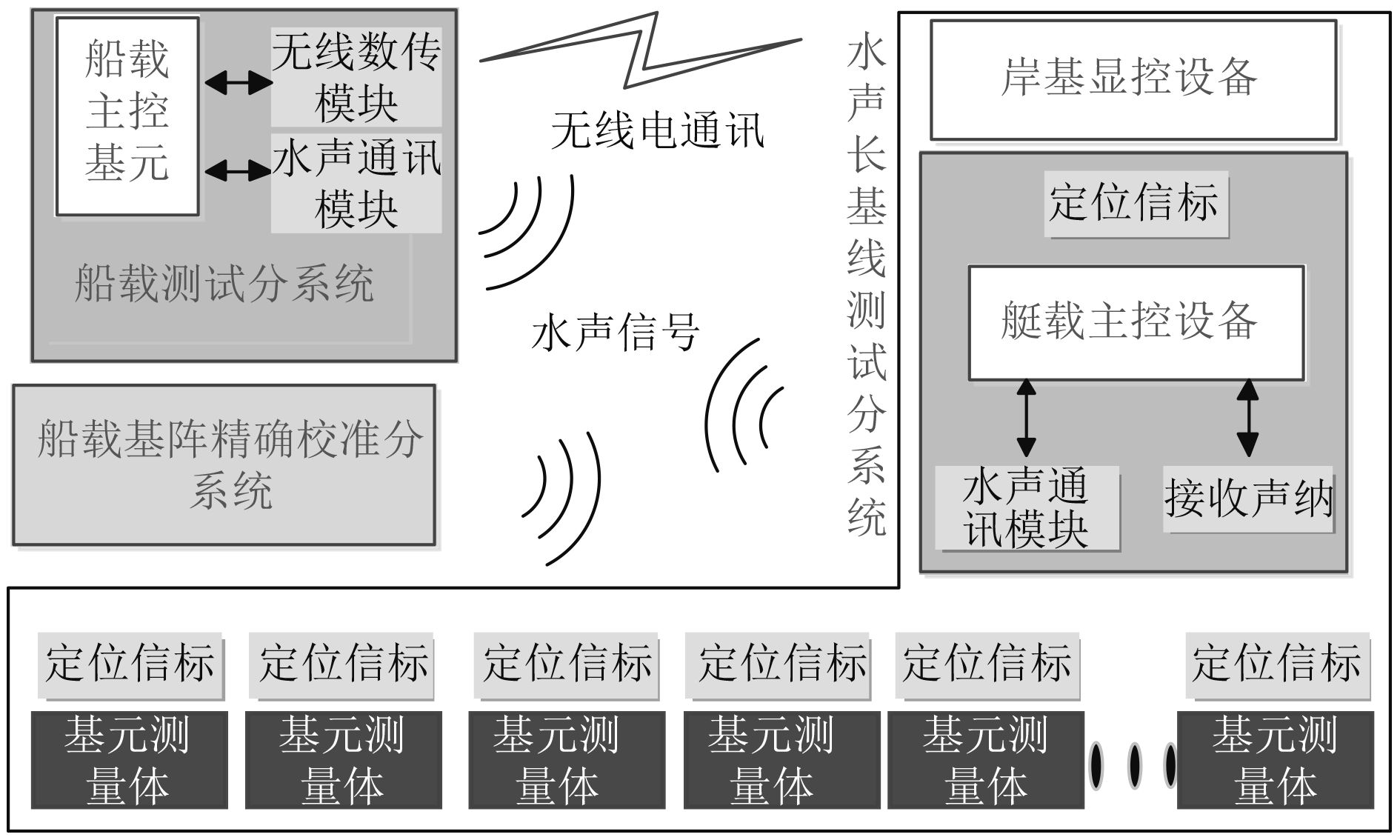
图 7 系统组成框图 Fig. 7 System composition block diagram |
水下运动目标自导航及运动轨迹跟踪系统由水声长基线测试分系统、船载测试分系统和船载基阵精确校准分系统组成。
水声长基线测试分系统主要用于对水下运动目标进行水声长基线同步定位,使运动目标能够获取自身在实验区水下的位置、速度及机动情况,同时水下定位基阵获取其与水下运动目标的距离信息,并将距离信息通过中继浮标上的无线电数传模块发送给船载测试子系统,通过软件计算将定位及轨迹跟踪结果实时上传岸基显控设备,在岸基指挥中心实时地显示运动目标在试验区水下的航速、航迹及机动情况等态势信息,便于岸站试验指挥人员掌握水下运动目标(AUV)当前方位,进行试验现场指挥。该系统包括多枚水下基元测量体、艇载主控设备、中继浮标和岸基显控设备等。
船载测试子系统用于接收中继浮标数据,通过软件计算,在试验船上实时地显示运动目标在试验区水下的航速和航迹、机动情况等态势信息,并将测试结果进行处理后通过无线数传电台上传岸基显控设备。
船载基阵精确校准分系统装配在试验测量船上,对水声长基线测试系统的基元测量体的布放点进行精确定位,并定期进行水下基元测量体的位置校准,水下基阵精确校准系统采用水声超短基线定位设备,在水下定位基元上加装应答式定位信标,采用超短基线的定位原理进行多次定位修正,获取其精确的位置信息。
系统工作时,首先根据定位区域的大小,合理规划定位基阵布放阵型,本系统根据实际需求在海底按照正六边形布放固定式长基线定位阵,阵列由7个水下定位基元潜标组成,每个定位基元相距1 km,每个水下基元的精确位置信息要通过船载基阵精确校准分系统进行精确标定,并将位置信息装订在水下运动目标(AUV)内,每个水下定位基元为水声收发一体。水下运动目标利用至少3个基元发射的定位信号进行自我定位并做出轨迹,进而实现自导航和位置修正。岸站或者船载平台同时利用至少3个基元距运动目标的距离信息对水下合作目标进行定位,掌握其位置信息,并通过跟踪算法测出其运动轨迹。
系统进行轨迹跟踪时,首先水下运动合作目标(比如AUV)上加装的定位信标定时对外发射水声定位信号,定位基元(如1#,2#,3#潜标)接收定位信号并通过同步定位原理计算获得距离信息,通过水下光缆将距离信息传送给中继浮标,通过无线数传电台将数据传送给岸站或船载平台,由多个距离信息解算出水下运动目标的位置信息提供给岸站人员,完成水下运动目标的轨迹跟踪。
在跟踪定位过程执行一次后,水下7个定位基元同时发射声学定位信号,每个水下定位基元发射信号频率不同,水下运动目标上的声学换能器同步接收多路声学定位信号,经信号分离后解算出自身距离多个水下基元的距离信息,由多个距离信息解算出自身的位置信息,实现自导航和自身位置修正。
水下运动目标轨迹跟踪定位和自导航定位由事先设定好的时间间隔交替进行,完成系统整体功能。正六边形布放固定式长基线定位阵,每个定位基元相距1 km,则在定位区域内,水下运动目标距离定位基元最远距离约为2 km,按海水中声速约为1 531 m/s(25 ℃)计算[8],则信号最远传输时间约为1.33 s,可取时间间隔为1.5 s。
系统工作时序如图8所示。
|
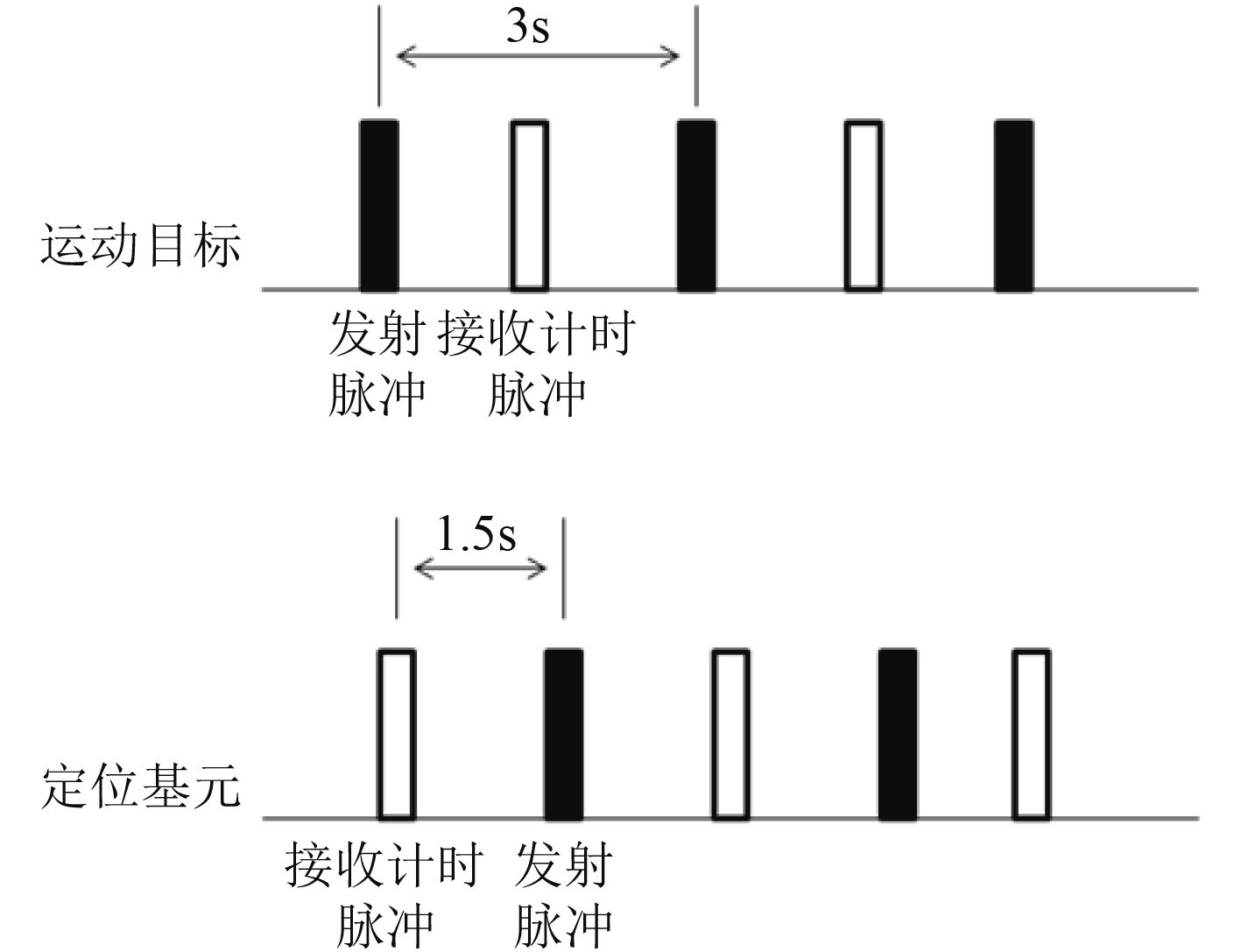
图 8 系统工作时序图 Fig. 8 System working sequence |
运动目标上的声学发射机发射定位声学脉冲,每隔3 s发射下一个定位脉冲,发射完定位脉冲后1.5 s接收机开启接收计时。定位基元上的声学接收机接收定位声学脉冲,每隔3 s清空计时,重新开启接收计时,开启接收计时后1.5 s发射机发送定位脉冲。系统完成一个完整的跟踪定位和自导航周期为3 s。
系统整体工作态势图9所示。

|
图 9 系统工作态势图 Fig. 9 System working situation map |
本文介绍一种针对水下自主航行器运动轨迹的直接测试方法,方法简捷直观,测试精度相对于短基线和超短基线声学定位较高,在工程实现方面切实可行,可应用于水下固定试验场,在试验场中对AUV,UUV,ROV等水下合作运动目标进行轨迹跟踪定位,同时也可实现水下运动目标的自导航和位置修正,对于水下运动目标的回转半径、航速保持、惯性导航精度等指标测试提供技术手段和支持。
| [1] |
马伟锋, 胡震. AUV的研究现状与发展趋势[J]. 火力与指挥控制, 2008, 33(6): 10-13. DOI:10.3969/j.issn.1002-0640.2008.06.003 |
| [2] |
江南, 黄建国, 李姗. 长基线水下目标定位新技术研究[J]. 仪器仪表学报, 2004, 25(4): 77-80. |
| [3] |
于运治, 姜璐, 郭志强. 一种水下精确定位方法及其误差分析[J]. 四川兵工学报, 2011, 32(9): 121-123. DOI:10.3969/j.issn.1006-0707.2011.09.039 |
| [4] |
蔡惠智, 刘云涛, 蔡慧, 等. 水声通信及其研究进展[J]. 物理, 2006, 35(12): 1038-1042. DOI:10.3321/j.issn:0379-4148.2006.12.011 |
| [5] |
许肖梅. 水声通讯与水声网络的发展与应用[J]. 声学技术, 2009, 28(6): 811-814. DOI:10.3969/j.issn1000-3630.2009.06.026 |
| [6] |
陈云飞, 李桂娟, 贾兵, 等. 水下合作目标三维定位技术[J]. 舰船科学技术, 2010, 32(5): 48-51. |
| [7] |
吴永亭, 周兴华, 杨龙. 水下声学定位系统及其应用[J]. 海洋测绘, 2003, 23(4): 18-21. DOI:10.3969/j.issn.1671-3044.2003.04.006 |
| [8] |
陈逸伦. 一种基于GPS实现水下定位的有效方法[J]. 科学技术与工程, 2011, 11(31): 7754-7757. DOI:10.3969/j.issn.1671-1815.2011.31.035 |
 2019, Vol. 41
2019, Vol. 41
