2. 上海交通大学海洋水下工程科学研究院有限公司,上海 200231
2. Shanghai Jiaotong University Underwater Engineering Institute Co., Ltd., Shanghai 200231, China
水下滑翔机(underwater glider)是一种利用净浮力驱动,以锯齿形状轨迹进行航行的新型水下自主机器人,具有成本低、续航强、能耗少、噪声小等特点,在海洋研究、环境监测、资源勘探以及军事侦察等领域都有着广阔的应用前景[1]。
路径规划问题是水下滑翔机研究领域的热点问题之一。很多学者对水下滑翔机的路径规划问题做了研究:Alvarez研究了水下滑翔机与浮标组成的优化采样问题,利用遗传算法对水下滑翔机进行路径规划[2]。文献[3]采用改进的A*算法,考虑了水下滑翔机水下不可控的特性,对其进行路径规划。文献[4]根据海洋环境和深度数据,结合RRT算法和A*算法,规划了能耗较优的路径。Pereira[5]将最小化碰撞风险作为目标,对水下滑翔机进行路径规划。朱心科[6]基于能耗模型,采用两步链式Lin-Kemighan算法对水下滑翔机的海洋采样路径进行优化。
本文通过改进传统的人工势场法来解决水下滑翔机在海流作用下躲避静态障碍物、动态障碍物的路径规划问题。提出对传统人工势场法的改进方法,将水下滑翔机的运动约束引入到人工势场法中;之后,将海流力引入势场力模型,并推出航向角公式,最后,以HUST-2号水下滑翔机为例在不同环境下进行仿真试验。
1 改进的人工势场法人工势场法算法高效、生成路径平滑,适用于路径实时性及安全性要求较高的路径规划任务[7]。但本身也存在局部极值、目标不可达差等缺陷。
其原理是在目标点处设置引力场,障碍物周围设置斥力场,物体在2种势场力共同作用下运动,最终到达目标位置。
1.1 改进斥力势场函数采用传统的斥力势场函数,当目标点在障碍物势场的影响距离内时,运动物体无法到达目标位置,因此考虑在斥力势场函数中加入与目标点的位置关系[8]。新的斥力势场函数为:
| $ {U_{reps}}(X) = \left\{ \begin{aligned} & {\frac{1}{2}{\eta _r}{{\left( {\frac{1}{{\rho (X,{X_o})}} - \frac{1}{{{\rho _0}}}} \right)}^2}{\rho ^2}(X,{X_g})} {,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \rho (X,{X_o}) \leqslant {\rho _0}} {\text{;}}\\ & 0,\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad {\rho (X,{X_o}) > {\rho _0}} {\text{。}} \end{aligned} \right. $ | (1) |
式中:
相应斥力函数为(用
| $ {\overrightarrow F _{reps}}(X) = \left\{ \begin{aligned} &{{\overrightarrow F }_{reps1}}(X) \cdot \nabla \rho (X,{X_o}) - {{\overrightarrow F }_{reps2}}(X) \times \\ & \nabla \rho (X,{X_g}),\quad {\rho (X,{X_o})\leqslant {\rho _0}}{\text{;}}\\ &0, \quad\quad\quad\quad\ {\rho (X,{X_o}) > {\rho _0}}{\text{。}} \end{aligned} \right. $ | (2) |
式中:
物体在运动过程中,除目标点外,当斥力与引力的合力为0时,会陷入局部极值,最简单的情况如障碍物处于运动物体与目标点的连线上会出现受力为0,从而停止运动或震荡不前[9]。考虑引入局部引力势场,驱使物体逃逸出来继续运动。局部引力势场为:
| $ {U_{local}}(X) = \left\{ {\begin{array}{*{20}{c}} {\dfrac{\varepsilon }{{{\rho ^2}(X,{X_g})}}}&{,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \rho (X,{X_g}) > {\rho _g}} {\text{;}}\\ 0&{,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \rho (X,{X_g}) \leqslant {\rho _g}} {\text{。}} \end{array}} \right. $ | (3) |
式中:
改进后的引力场
| $ {U_{att}}(X) = \left\{ \begin{aligned} &{\dfrac{1}{2}{\xi _a}{\rho ^2}(X,{X_g})} , \quad\quad\quad\quad\quad\rho (X,{X_g}) > {\rho _g}\\ &{\text{且}}{F_{total}}\left( X \right) \ne 0{\text{;}}\\ &{\dfrac{1}{2}{\xi _a}{\rho ^2}(X,{X_g}) + \frac{\varepsilon }{{{\rho ^2}(X,{X_g})}}} , \ \rho (X,{X_g}) > {\rho _g}\\ &{\text{且}}{F_{total}}\left( X \right) = 0{\text{;}}\\ &0{, \quad\quad\quad\quad\quad\quad\quad\quad\quad\ \ \rho (X,{X_g}) \leqslant {\rho _g}}{\text{。}} \end{aligned} \right. $ | (4) |
式中,
水下滑翔机在水中航行时可能会遇到动态障碍物,引入速度势场可以把动态障碍物考虑进来[10]。
将水下滑翔机与动态障碍物的速度分别用
| $ {U_{repv}}(X) = \left\{ \begin{aligned} & {{\eta _v}\left| {\left\| {\overrightarrow V - {{\overrightarrow V }_o}} \right\|\sin \phi } \right| = {\eta _v}{V_{or}}\left| {\sin \phi } \right|} ,\\ &\quad\quad\quad{\rho (X,{X_o}) \leqslant {\rho _0}}{\text{;}}\\ & 0, \quad\quad {\rho (X,{X_o}) > {\rho _0}} {\text{。}} \end{aligned} \right. $ | (5) |
式中:
速度斥力函数
| $ {U_{rep}}(X) = \left\{ \begin{aligned} &{{U_{reps}}(X) \!+\! {U_{repv}}(X)}, {\rho (X,\!{X_o}) \leqslant{\rho _0} {\text{且}} \cos \phi > 0}{\text{,}}\!\\ &{{U_{reps}}(X)},{\rho (X,{X_o}) \leqslant {\rho _0} {\text{且}} \cos \phi \leqslant 0}{\text{,}}\!\\ &0, {\rho (X,{X_o}) > {\rho _0}}{\text{。}} \end{aligned} \right. $ | (6) |
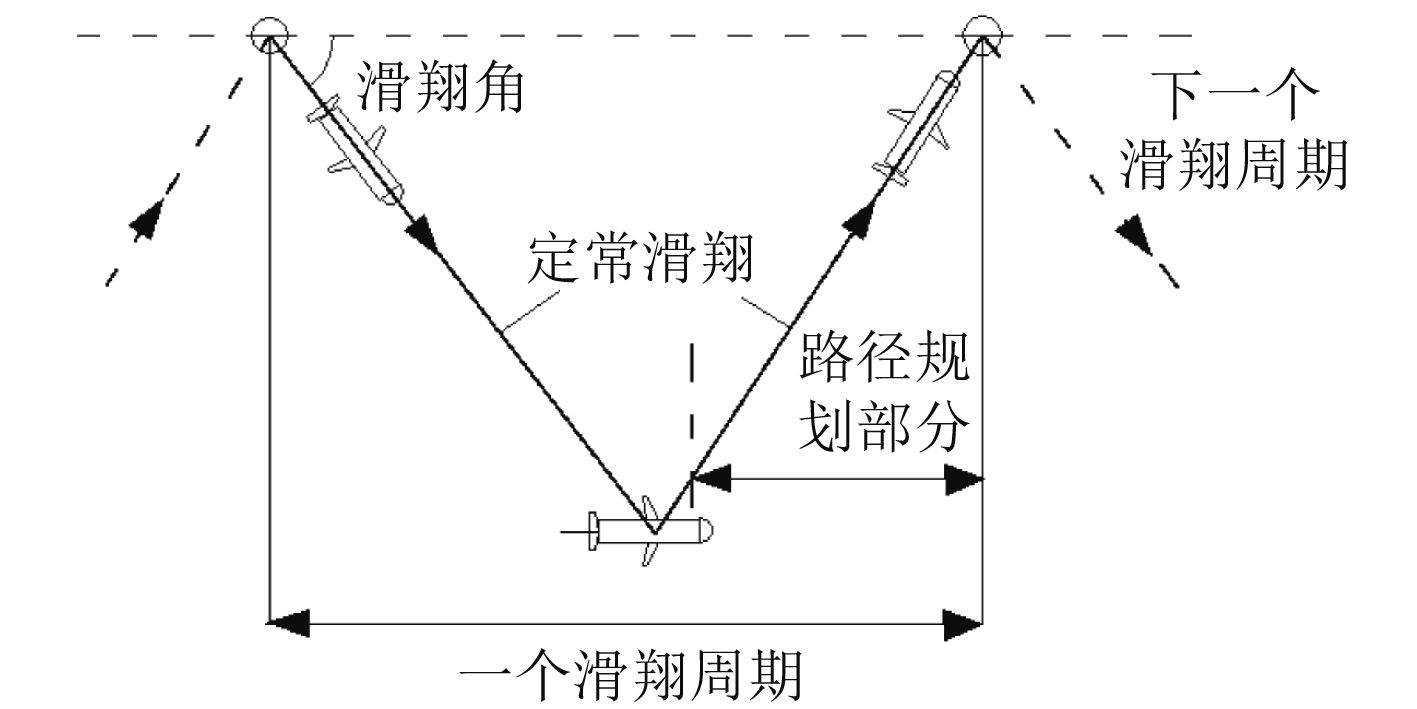
水下滑翔机在航行过程中,主要是沿锯齿形状轨迹做周期性运动。在理想情况下(没有海流以及水中障碍物),以一定滑翔角
|
图 1 水下滑翔机一个周期内的运动情况 Fig. 1 Movement of underwater glider in one cycle |
路径起点的运动参数会影响之后路径的形状,所以将路径规划起点处的运动参数约束为水下滑翔机的速度大小及滑翔角方向。此外,与一些智能水下机器人相比,水下滑翔机机动性和回转性相对较差,主要体现为有最小回转半径
传统人工势场法中,
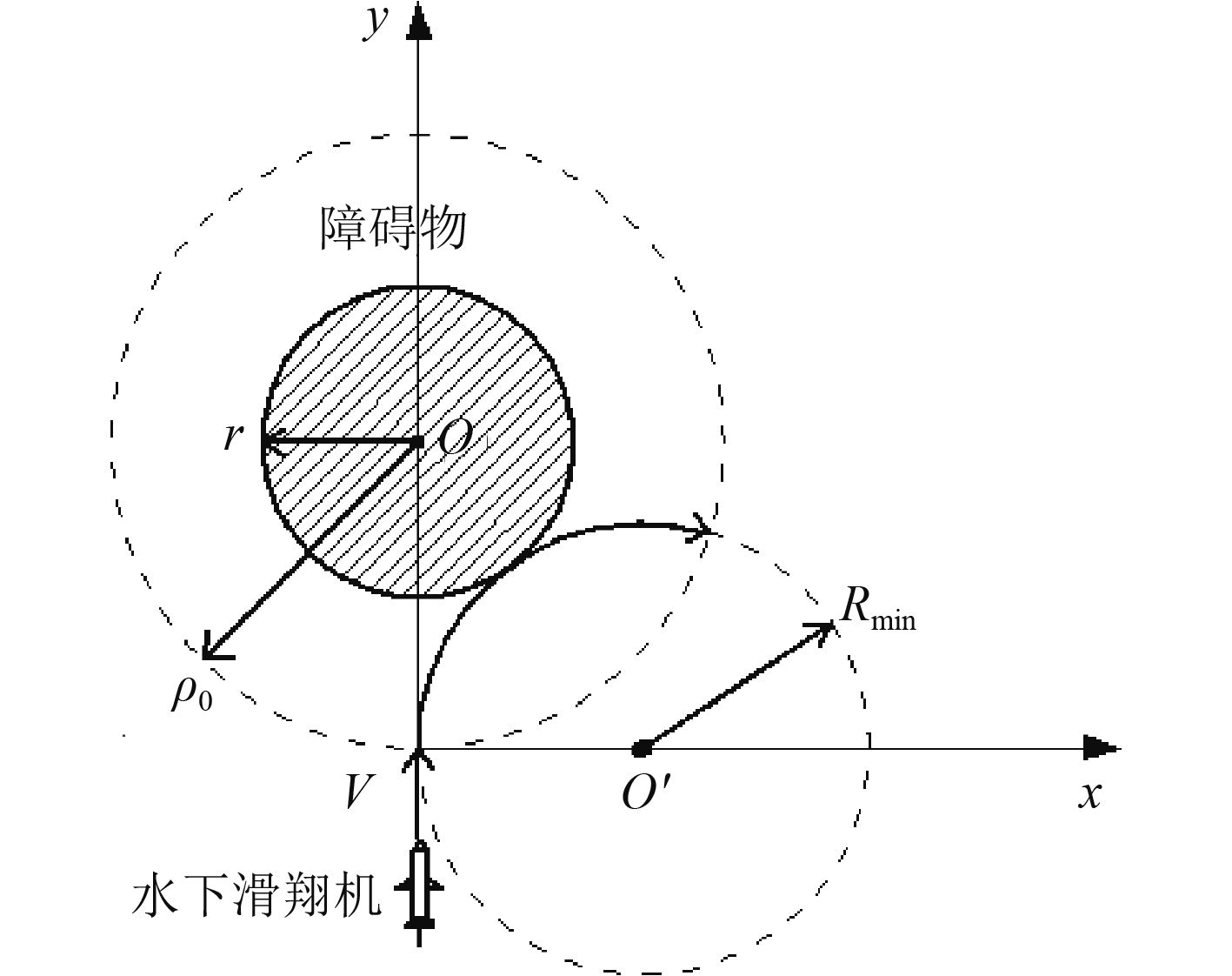
为简化讨论,不考虑障碍物具体形状,表示为包含障碍物轮廓的外包圆,如图2所示。将水下滑翔机外包圆半径
|
图 2 临界情况示意图 Fig. 2 Diagram of the critical situation |
考虑水下滑翔机运动轨迹相切于障碍物边界的临界情况,水下滑翔机受到虚拟向心力的作用以恒定速率
将圆
| $ \begin{split} &(4{R_{\min }}^2 + 4{\rho _0}^2){x^2} + [8{R_{\min }}r({\rho _0} - r) + 4{R_{\min }}{\left( {{\rho _0} - r} \right)^2}- \\ &8{R_{\min }}{\rho _0}^2]x + {[2r({\rho _0} - r) + {({\rho _0} - r)^2}]^2} = 0{\text{。}} \end{split} $ | (7) |
为使圆
因为
| ${\rho _{\min }} = \sqrt {{r^2} + 2Rr}{\text{,}} $ | (8) |
由于水下滑翔机的回转半径
当障碍物半径足够大时,相对于水下滑翔机的最小回转半径而言,障碍物表面接近平面,此时易得
| ${\rho _{\min }} = {R_{\min }} + r{\text{,}}$ | (9) |
对应的
水下滑翔机在海洋中航行的速度较小(实际应用的水下滑翔机航速
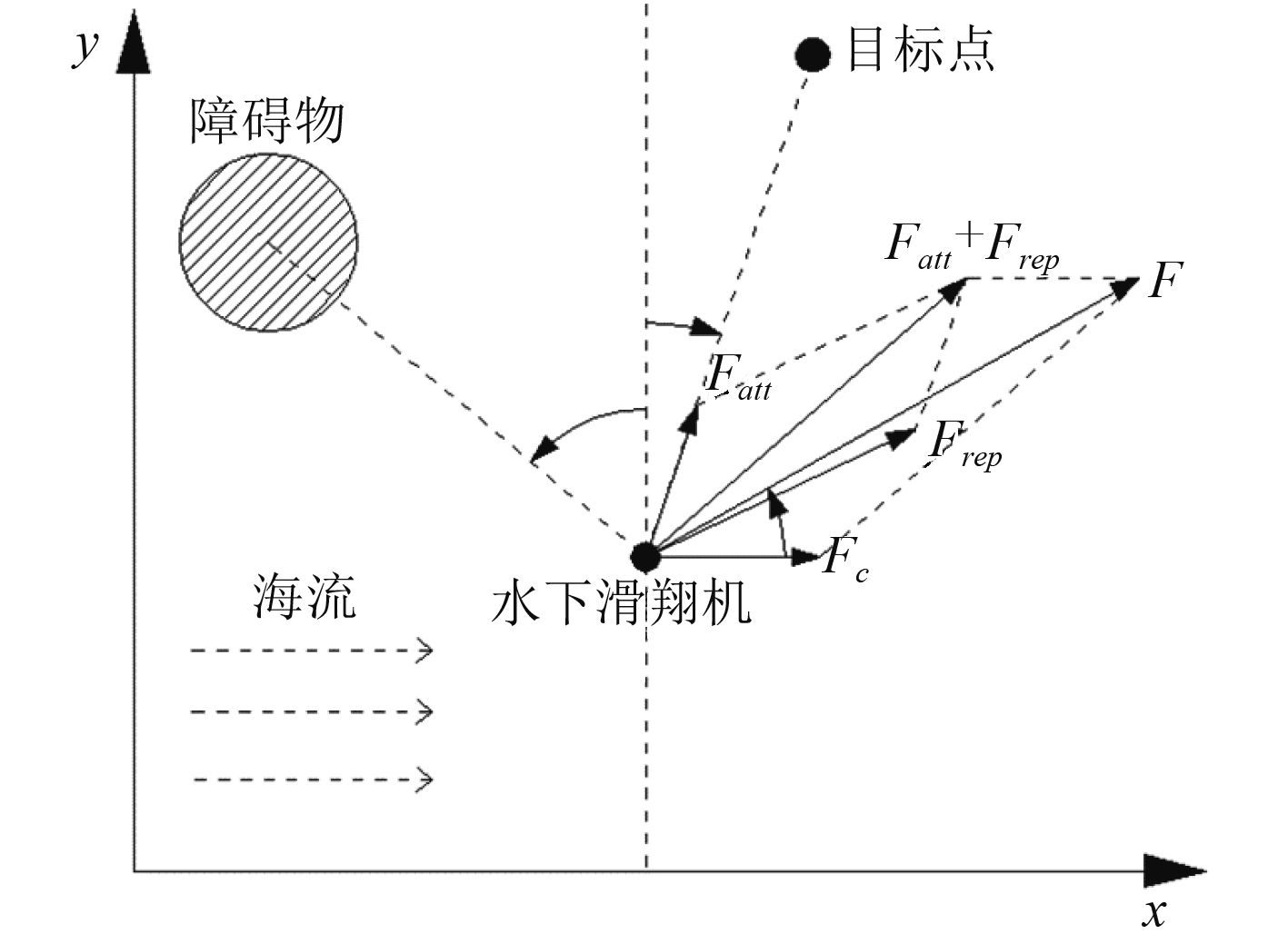
在海洋环境中,大部分海流的整体流动方向呈水平方向,而且在有限的区域和时间段内流动比较稳定[12]。这里考虑水平方向上的定常海流力
|
图 3 水下滑翔机总受力示意图 Fig. 3 Diagram of the whole forces of underwater glider |
图中,
| $ \varphi \! =\! \arctan \frac{{{F_{att,x}} \!\!+\!\! \displaystyle\sum\limits_{i \!=\! 1}^n {(F_{reps1,x}^i \!\!+\!\! F_{reps2,x}^i \!\!+\! F_{repv,x}^i)} \!\!+\!\! {F_c}}}{{{F_{att,y}} \!\!+\!\! \displaystyle\sum\limits_{i \!=\! 1}^n {(F_{reps1,y}^i \!\!+\! F_{reps2,y}^i \!\!+\!\! F_{repv,y}^i)} }}{\text{。}} $ | (10) |
其中,
每运动一个步长后重新进行受力分析,并根据式(10)重新计算航向角
设定路径规划范围为水下滑翔机单个周期内的上升阶段,起始点坐标为(5 m,–145 m),目标点坐标为(150 m,0 m)。水下滑翔机速度
静态障碍物信息见表1,动态障碍物的参数及运动信息见表2。考虑最小回转半径约束,由式(8)计算障碍物1的影响半径为
|
|
表 1 静态障碍物信息 Tab.1 Information of static obstacles |
|
|
表 2 动态障碍物信息 Tab.2 Information of dynamic obstacle |
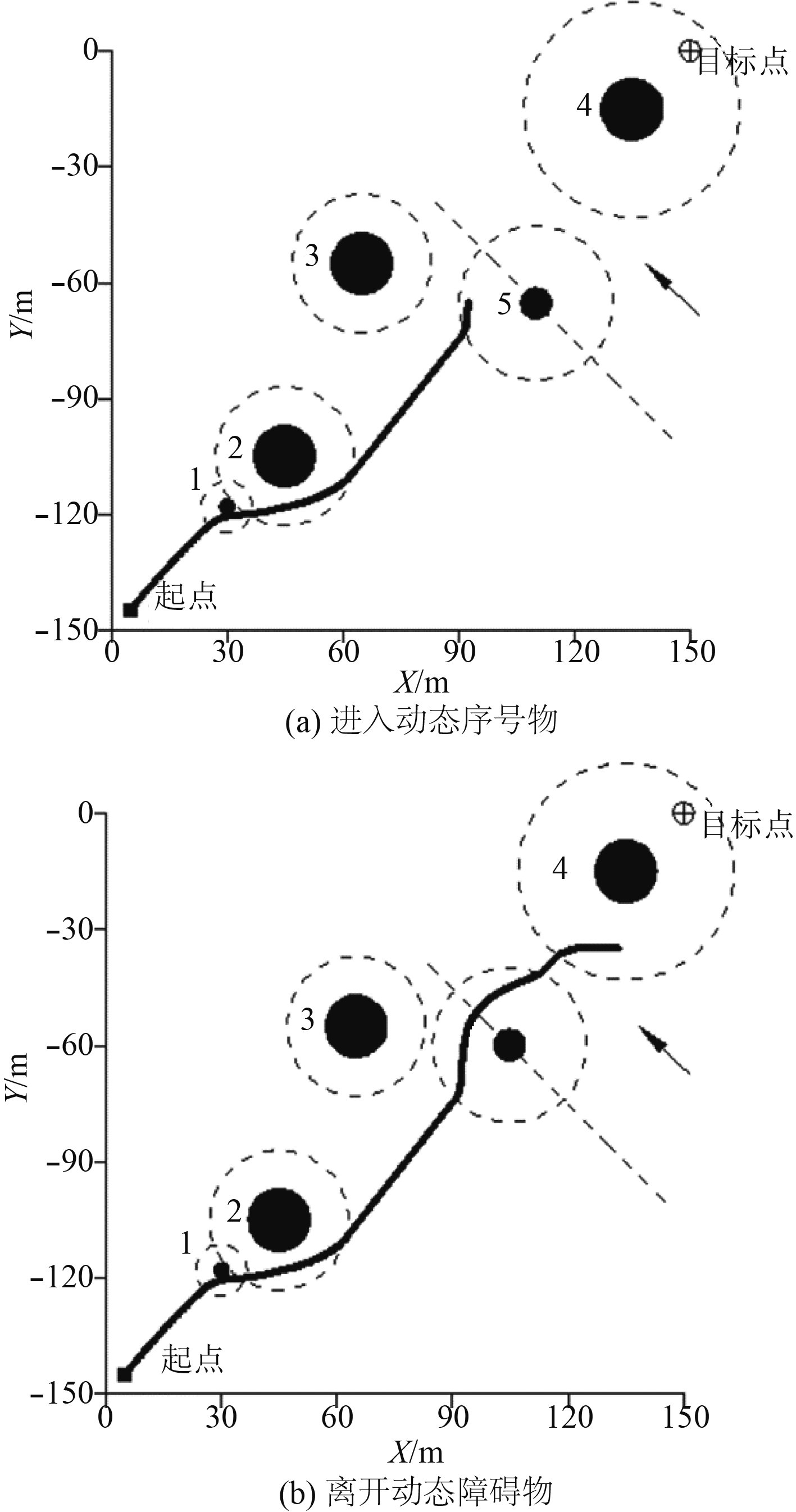
水下滑翔机进入、离开动态障碍物影响范围的过程如图4所示。最终路径规划结果如图5所示。
|
图 4 躲避动态障碍物过程 Fig. 4 Process of avoiding dynamic obstacle |
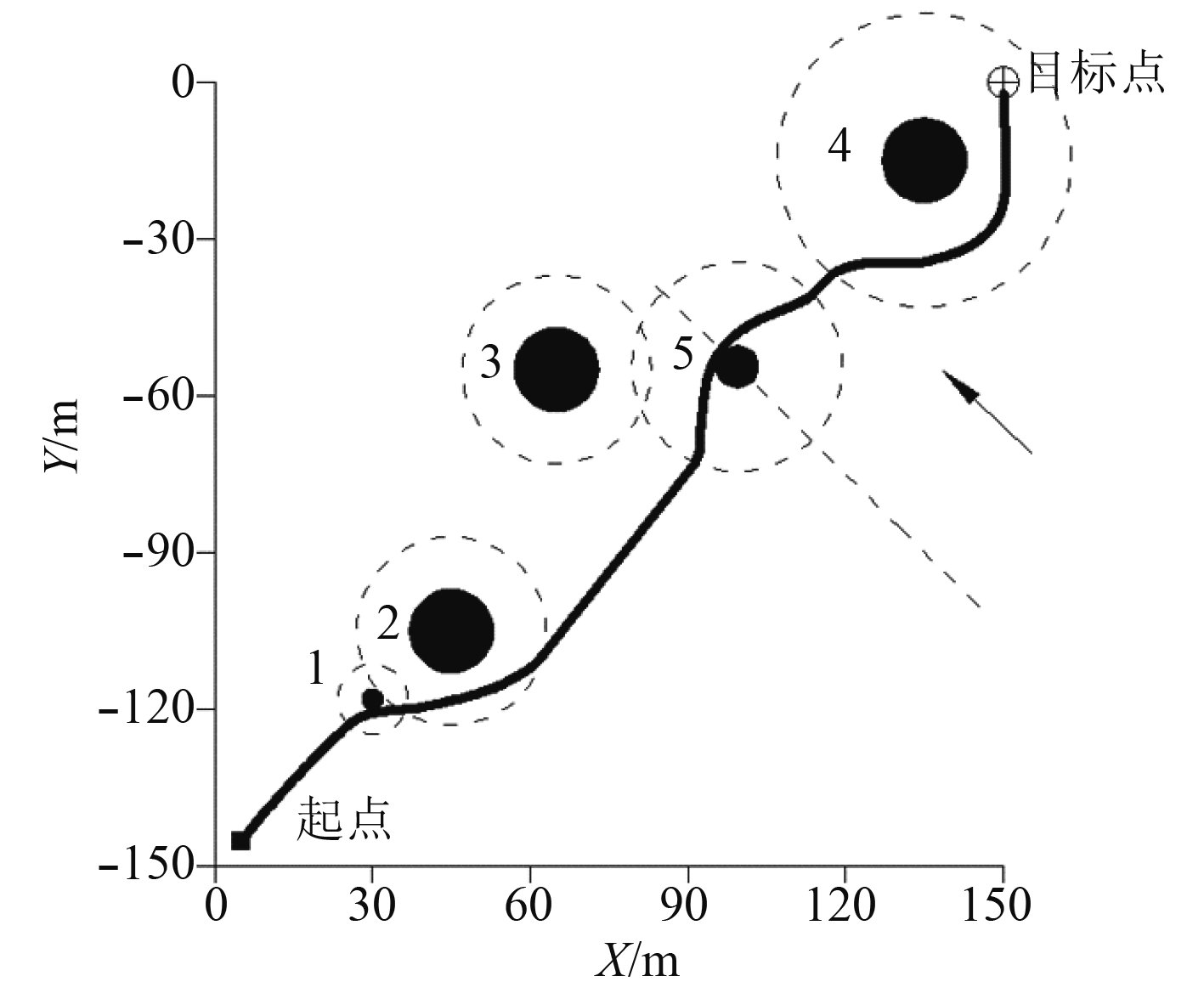
|
图 5 动态环境下的最终路径规划结果 Fig. 5 Path planning result in dynamic environment |
由图4和图5可知,采用改进的人工势场法可使水下滑翔机有效避开静态和动态障碍物,规划出安全的航行路径到达目标点。过程中没有出现局部极值以及目标不可达现象,说明对人工势场法的改进有效。且得到的路径较平滑,符合滑翔机运动特点。
4.2 定常海流对路径规划的影响在同样的动态环境引入海流作用,设定海流方向水平向右,流速
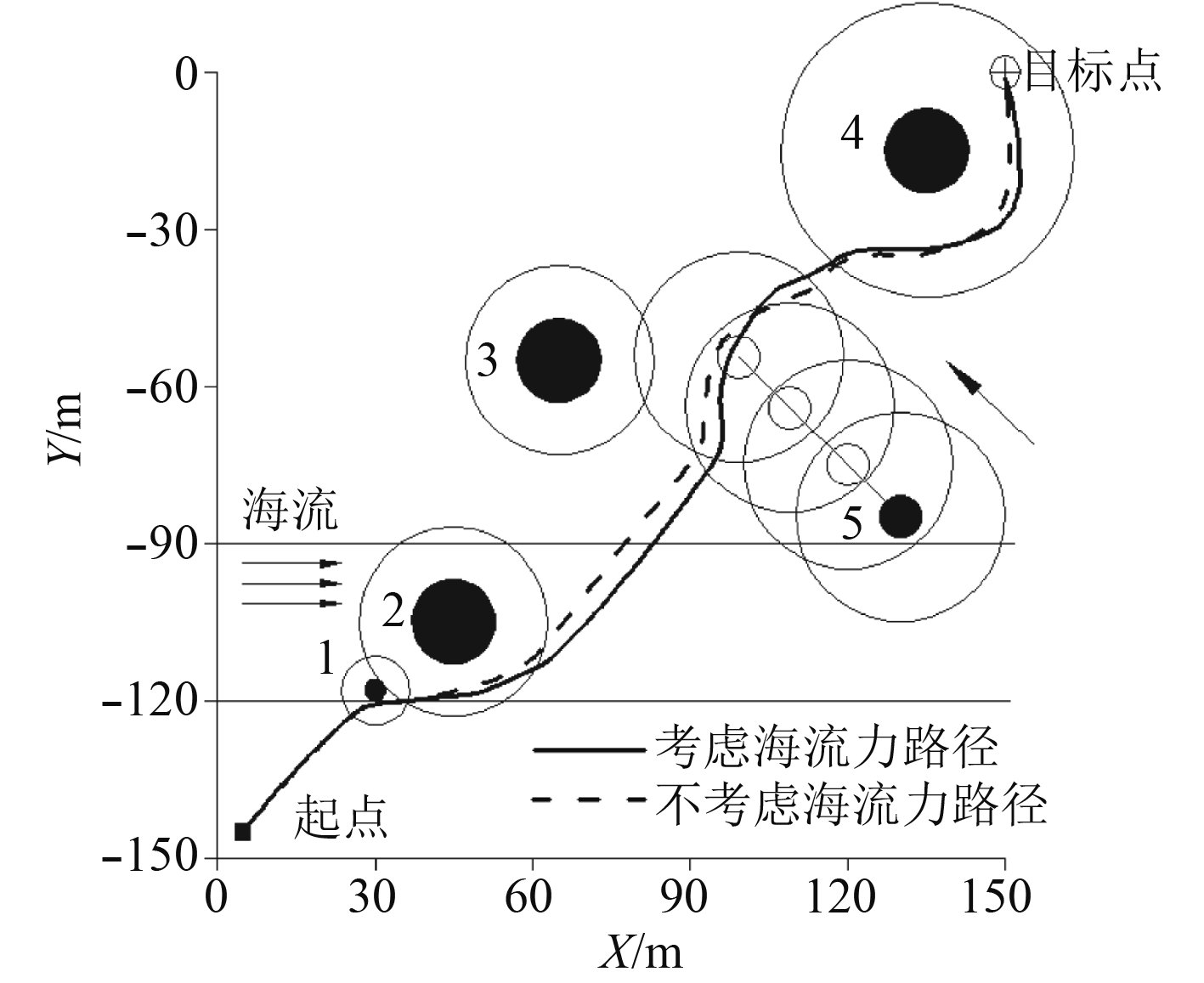
|
图 6 常值海流作用下的动态路径规划 Fig. 6 Dynamic path planning with constant current |
通过比较图6中2条路径可知:在海流作用下,路径会发生较为明显的偏移,而且会影响离开海流区域后的航路走向,但势场法的原理决定最终仍会到达目标点。
为对比不同流速的常值海流对路径规划的影响,分别引入0.2 m/s,0.4 m/s,0.6 m/s三种常值海流,仿真结果如图7所示。可知,海流流速越大,对路径干扰越大。且在障碍物影响范围外,没有海流作用的路径方向稳定,而海流作用的路径则呈现不规则变向运动,这在实际航行中会增加水下滑翔机的能耗。
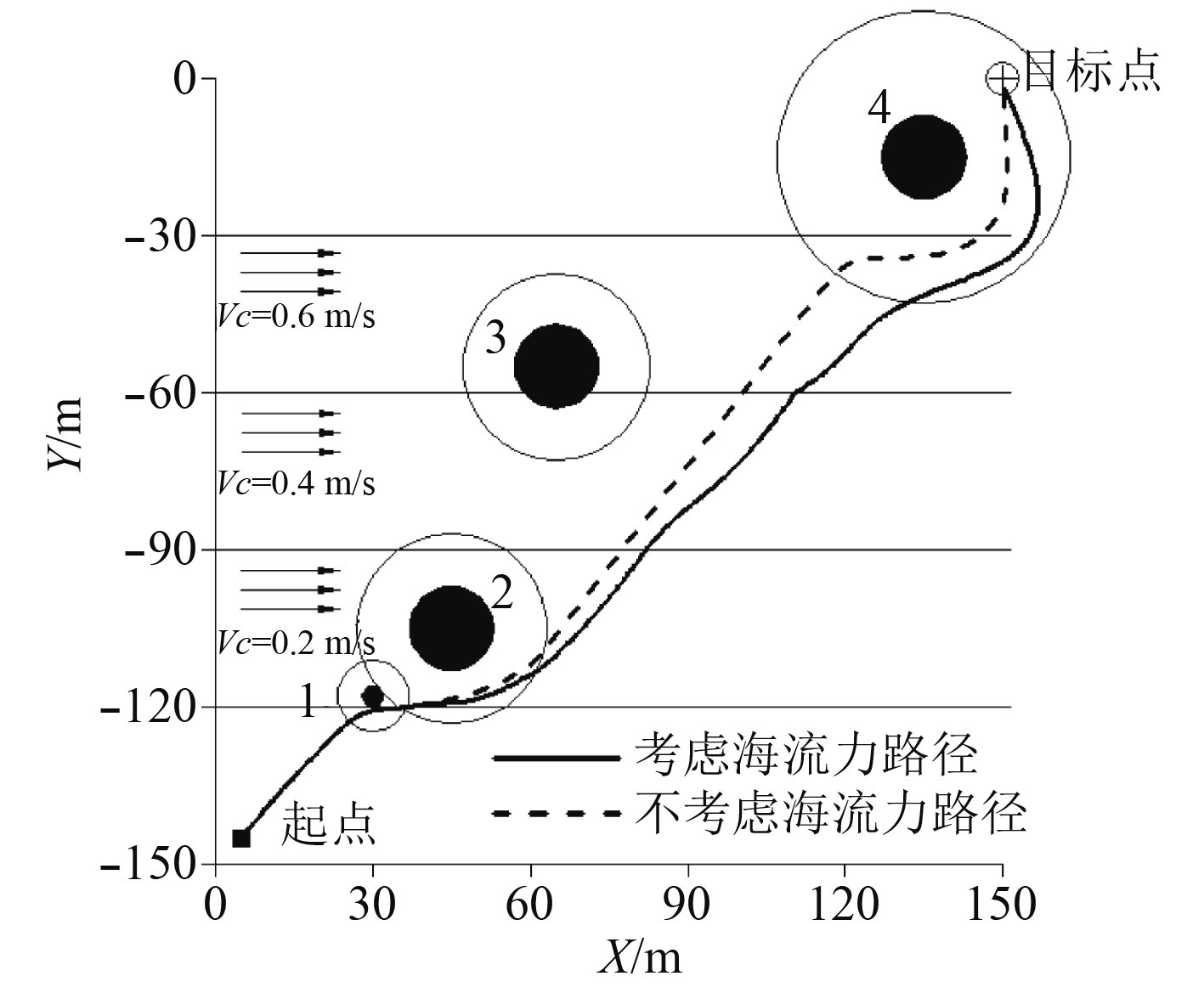
|
图 7 不同海流作用下的静态路径规划 Fig. 7 Static path planning with different currents |
本文提出一种改进的人工势场方法,对海流作用下水下滑翔机在单个周期下的避障问题作了研究。改进的人工势场法综合考虑了传统人工势场法缺陷、动态障碍物、水下滑翔机运动约束以及海流的影响。结果显示采用的改进人工势场法能使水下滑翔机在无海流和有海流的情况下成功避开静态和动态障碍物。另外,本文只考虑了定常海流对路径规划的影响,对于复杂海流等情况对路径规划的影响,还需作更多研究。
| [1] |
赵宝强. 基于粒子群改进算法的水下滑翔机路径优化[J]. 舰船科学技术, 2015, 37(8): 140-145. ZHAO Bao-qiang. Underwater glider path optimization based on improved particle swarm algorithm[J]. Ship Science and Technology, 2015, 37(8): 140-145. DOI:10.3404/j.issn.1672-7649.2015.08.029 |
| [2] |
ALVAREZ A, GARAU B, CAITI A. Combining networks of drifting profiling floats and gliders for adaptive sampling of the Ocean[C]// IEEE International Conference on Robotics and Automation. IEEE, 2007:157–162.
|
| [3] |
FERNÁNDEZ-PERDOMO E, CABRERA-GÁMEZ J, HERNÁNDEZ-SOSA D, et al. Path planning for gliders using regional ocean models: application of pinzón path planner with the ESEOAT model and the RU27 trans-Atlantic flight data[C]// Oceans. IEEE, 2010:1–10.
|
| [4] |
RAO D, WILLIAMS S B. Large-scale path planning for Underwater Gliders in ocean currents[J]. 2009.
|
| [5] |
PEREIRA A A, BINNEY J, HOLLINGER G A, et al. Risk-aware path planning for autonomous underwater vehicles using predictive ocean models[J]. Journal of Field Robotics, 2013, 30(5): 741-762. DOI:10.1002/rob.2013.30.issue-5 |
| [6] |
朱心科, 俞建成, 王晓辉. 能耗最优的水下滑翔机采样路径规划[J]. 机器人, 2011, 33(3): 360-365. ZHU Xin-ke, YU Jian-cheng, WANG Xiao-hui. Sampling path planning of underwater glider for optimal energy consumption[J]. Robot, 2011, 33(3): 360-365. |
| [7] |
张殿富, 刘福. 基于人工势场法的路径规划方法研究及展望[J]. 计算机工程与科学, 2013, 35(6): 88-95. DOI:10.3969/j.issn.1007-130X.2013.06.015 |
| [8] |
王奎民, 赵玉飞, 侯恕萍, 等. 一种改进人工势场的UUV动碍航物规避方法[J]. 智能系统学报, 2014(1): 47-52. |
| [9] |
KIM Y, GU D W, POSTLETHWAITE I. Real-time path planning with limited information for autonomous unmanned air vehicles[M]. Pergamon Press, Inc. 2008.
|
| [10] |
李惠光, 李旭锋, 邹立颖, 等. 动态环境下基于人工势场的足球机器人路径规划[J]. 国外电子测量技术, 2008, 27(5): 27-30. DOI:10.3969/j.issn.1002-8978.2008.05.010 |
| [11] |
WU Z, ZHAO M, WANG Y, et al. Path Planning for Underwater Gliders with Motion Constraints[M]// Mechanism and Machine Science. Springer Singapore, 2017.
|
| [12] |
曹璟. 复杂环境下AUV路径规划方法研究[D]. 青岛: 中国海洋大学, 2011.
|
| [13] |
顾建农, 张志宏, 王冲, 等. 水下滑翔机定常螺旋回转运动特性分析[J]. 中国造船, 2017(3): 68-79. GU Jian-nong, ZHANG Zhi-hong, WANG Chong, et al. Analysis of steady spiral gyration motion characteristics of underwater glider[J]. Shipbuilding of China, 2017(3): 68-79. DOI:10.3969/j.issn.1000-4882.2017.03.022 |
 2019, Vol. 41
2019, Vol. 41
