2. 哈尔滨工程大学,黑龙江 哈尔滨 150001
2. Harbin Engineering University, Harbin 150001, China
水面船舶在海上航行时,不可避免地遭遇随机风浪的干扰,由此将引起船舶六自由度运动姿态的随机运动。航向(首摇)的校正作用一般是靠自动舵控制系统承担,对于未加装减摇装置系统的船舶,其横摇运动是欠驱动系统,将会对船舶的稳定性、船上人员的舒适感、船载设备的运行性能和武备系统的命中率产生较大的影响。此外,横摇运动也将耦合影响航向的保持性能及航行的安全性[1-3]。
船舶动力学、运动学研究结果表明[4-5],船舶航行时,舵叶上除了能生成首摇控制力(矩)外,还能够生成可观的横摇扶正力(矩),加之首摇运动动态特性处在较低频率域,而横摇运动相对首摇运动而言,处在较高频率域,这使得有可能寻求在不添装减摇装置系统情况下,通过合理的设计自动舵控制系统和策略,在保证航行方向稳定的同时,显著地减少船的横摇运动。
本文提出的矢量舵是在普通的后缘开襟形成一个独立的可动面—翼舵,从而与主舵形成2个相对独立的矢量控制。翼舵相当于一个可调整舵叶双侧曲率不对称度的控制面,通过翼舵控制面的转动控制,可改变舵叶双侧面曲率的不对称度,从而增大舵叶上的水动力(系数),即控制力(矩),实现提高舵效之目的。
目前,工程上应用的带有翼舵的航向控制系统,均为基于舵和翼舵是线性连动的控制面,没有实现矢量控制面,而实际上,在
本文提出了矢量舵减横摇控制系统技术,设计了
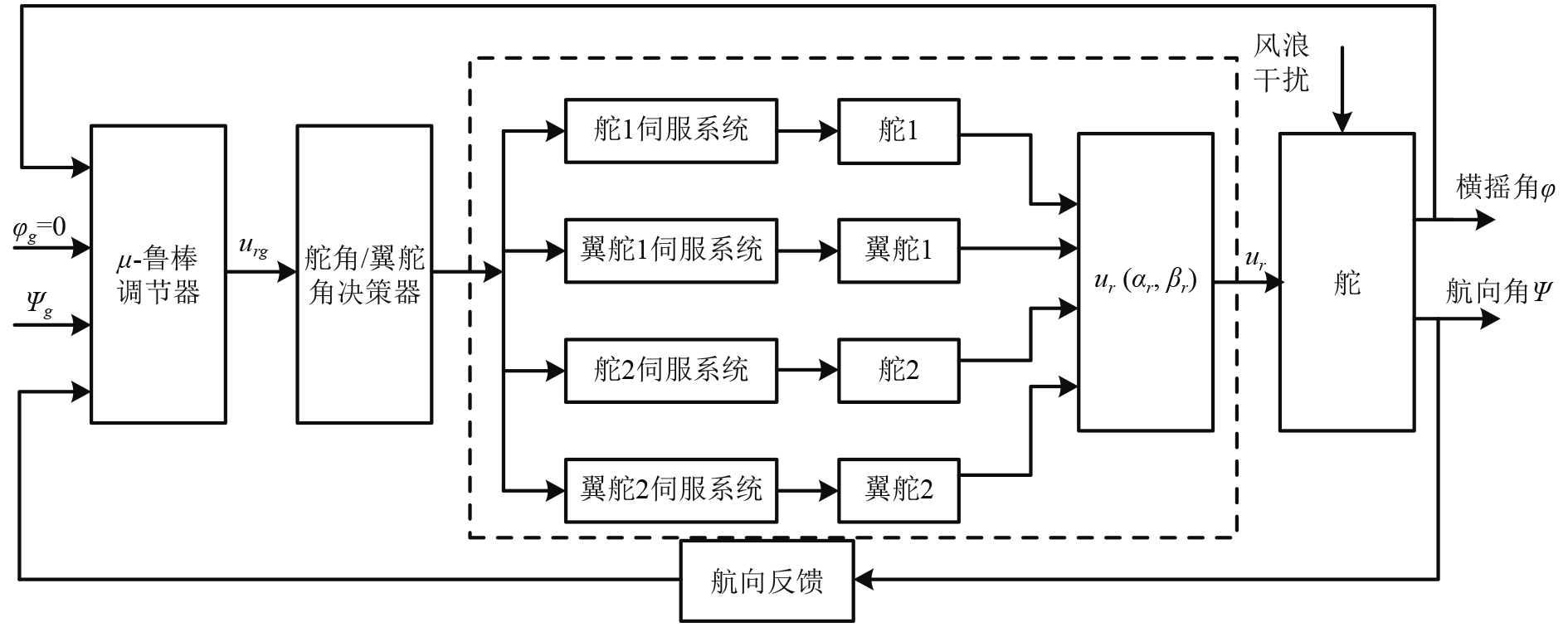
船舶矢量减横摇控制系统结构原理图如图1所示。
|
图 1 船舶矢量舵减横摇控制系统结构原理图 Fig. 1 Schematic diagram of the structure of ship vector rudder anti-roll control system |
该系统主要有控制器(控制策略)、主舵角和翼舵角协调决策分配器,舵和翼舵组成的矢量舵、舵角、翼舵角矢量传动装置,舵、翼舵伺服驱动系统,横摇反馈信号传感器等构成。
船体横荡,首摇,横摇三自由度运动非线性模型为[9]:
| $ \left\{ {\begin{aligned} & \begin{array}{l} {\rm{m}}(\dot v + ur) = - {m_y}\dot y - {m_x}ur + {Y_v}v + {Y_r}r + {Y_{v\left| v \right|}}v\left| v \right| +\\ {Y_{r\left| r \right|}}r\left| r \right|+ {Y_{vvr}}{v^2}r + {Y_{vrr}}v{r^2} + {Y_r}({\alpha _r},{\beta _r}) + {Y_d}\text{,} \end{array}\\ & \begin{array}{l} {I_{\rm{z}}}\dot r = - \Delta {I_z}\dot r + {N_v}v + {N_r}r + {N_{v\left| v \right|}}v\left| v \right| + \\ {N_{r\left| r \right|}}r\left| r \right| + {N_{vvr}}{v^2}r + {N_{vrr}}v{r^2}+ {N_\varphi }\varphi + {N_{v\left| \varphi \right|}}v\left| \varphi \right| +\\ {N_{r\left| \varphi \right|}}r\left| \varphi \right| + {N_r}({\alpha _r},{\beta _r}) + {N_d}\text{,} \end{array}\\ & \begin{array}{l} {I_x}\dot p = - \Delta {I_x}\dot p - 2{N_p}p - Wh\varphi - {z_H}( - {m_y}\dot v -\\ {m_x}ur + {Y_v}v + {Y_r}r + {Y_{v\left| v \right|}}v\left| v \right|+ {Y_{r\left| r \right|}}r\left| r \right| + {Y_{vvr}}{v^2}r +\\ {Y_{vrr}}v{r^2}){\rm{ + }} {K_r}({\alpha _r},{\beta _r}) + {K_d}\text{。} \end{array} \end{aligned}} \right. $ | (1) |
式中:
舵/翼舵产生的对船体的横荡力
| $\begin{split} & {Y_r}({\alpha _r},{\beta _r}) = (1 + {\alpha _H}){P_N}\cos {\alpha _r} \text{,}\\ & {N_r}({\alpha _r},{\beta _r}) = - (1 + {\alpha _H}){x_R}{P_N}\cos {\alpha _r} \text{,} \\ & {K_r}({\alpha _r},{\beta _r}) = (1 + {\alpha _H}){z_R}{P_N}\cos {\alpha _r} \text{。} \end{split} $ | (2) |
式中:
| ${\alpha _H}{\rm{ = 1}}{\rm{.052}}{{\rm{C}}_b} + 0.125\text{。}$ | (3) |
考虑到舵/翼舵在水中的实际受力情况,有:
| $\begin{split} & {Y_r}({\alpha _r},{\beta _r}) = (1 + {\alpha _H}){P_y} \text{,}\\ & {N_r}({\alpha _r},{\beta _r}) = - (1 + {\alpha _H}){x_R}{P_y} \text{,}\\ & {K_r}({\alpha _r},{\beta _r}) = (1 + {\alpha _H}){z_R}{P_y} \text{,}\\ & {P_y}{\rm{ = }}\frac{1}{2}\rho {\upsilon ^2}{S_p}{C_{yr}}\left( {{\alpha _r},{\beta _r}} \right) \text{。} \end{split} $ | (4) |
式中:
由于受到船体伴流的影响,导致
矢量舵产生的控制力矩
| $\begin{split} {u_r}({\alpha _r},{\beta _r}) = & {A_0} + {a_1}{\alpha _r} + {a_2}{\alpha _r}^2 + \cdots + {a_m}{\alpha _r}^m +\\ & {b_1}{\beta _r} + {b_2}{\beta _r}^2 +\cdots + {b_m}{\beta _r}^m +\\ & {c_1}{a_r}{\beta _r} + {c_2}{\alpha _r}^2{\beta _r} + \cdots + {c_{m - 1}}{\alpha _r}^{m - 1}{\beta _r} + \\ & {d_2}{a_r}{\beta _r}^2 + {d_3}{\alpha _r}{\beta _r}^3 + \cdots + {d_{m - 1}}{\alpha _r}{\beta _r}^{m - 1} \text{。} \end{split} $ | (5) |
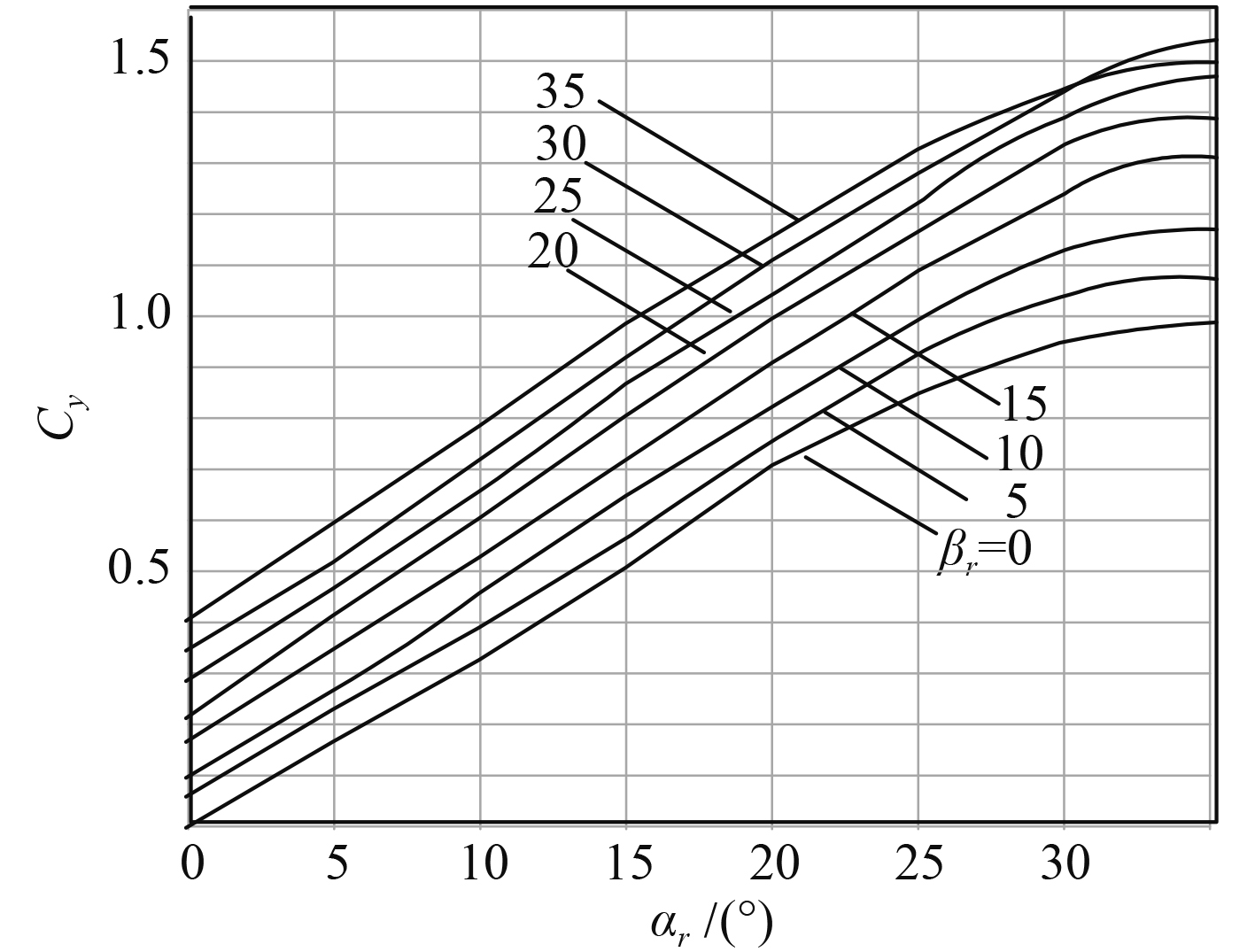
由于舵为对称剖面,当
|
图 2 舵/翼舵升力系数图谱 Fig. 2 Rudder / wing rudder lift coefficient map |
| $\begin{split} {c_r}({\alpha _r},{\beta _r}) = & 1.47{\alpha _r} + 3.04{\alpha _r}^2 - 3.82{\alpha _r}^3 - 1.46{\alpha _r}^4 + \\ & 0.29{\beta _r} + 3.86{\beta _r}^2 - 10.45{\beta _r}^3{\rm{ + }}8.37{\beta _r}^4 + \\ & {\rm{ 0}}{\rm{.50}}{a_r}{\beta _r} - 4.09{\alpha _r}^2{\beta _r} + 7.61{\alpha _r}^3{\beta _r} + \\ & 4.43{\alpha _r}{\beta _r}^2 - 4.59{\alpha _r}{\beta _r}^3 \text{。} \end{split} $ | (6) |
其中:
| ${u_r}({\alpha _r},{\beta _r}) = \frac{1}{2}\rho {V^2}{S_r}{L_r}{c_r}\left( {{\alpha _r},{\beta _r}} \right)\text{。}$ | (7) |
式中:
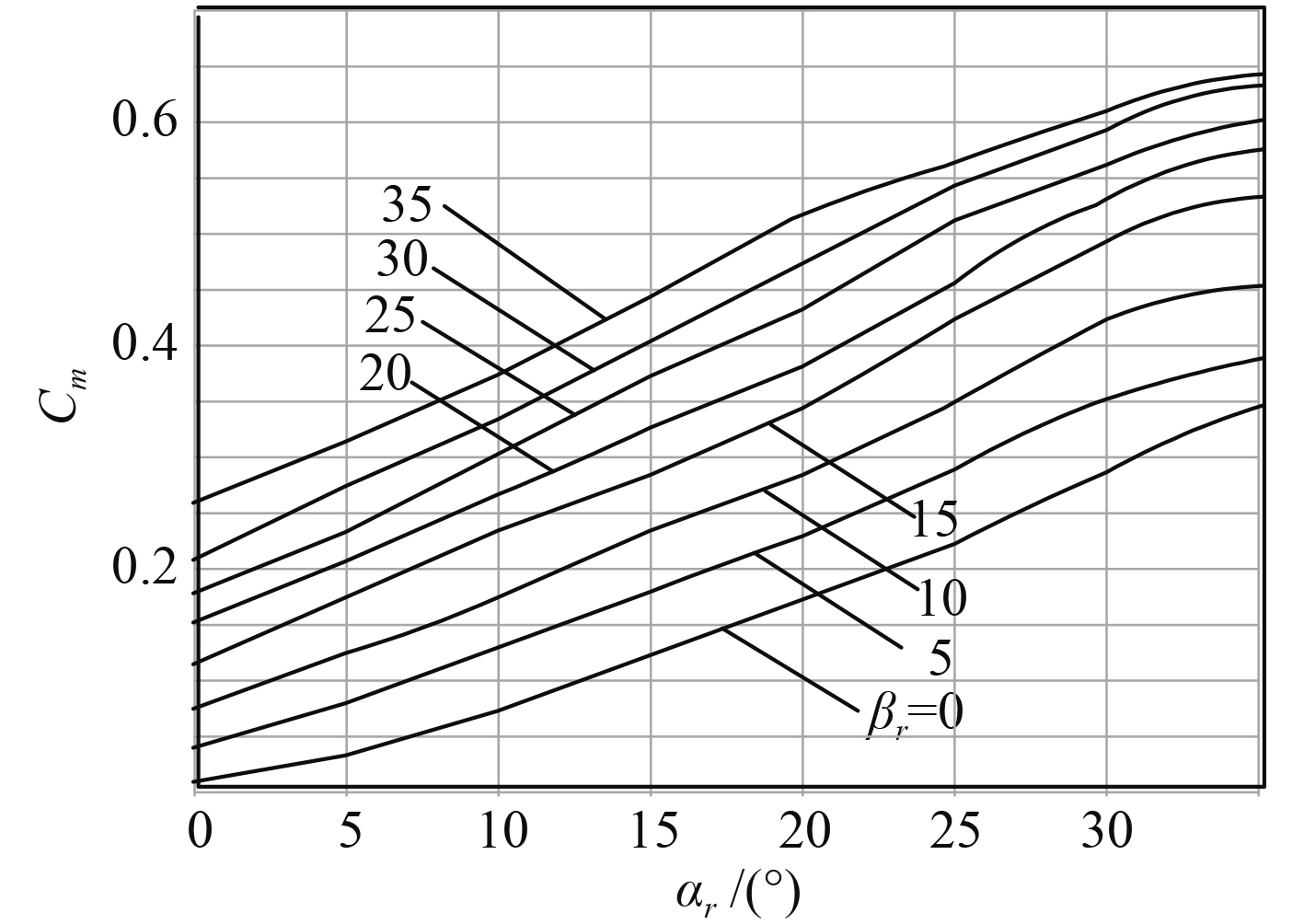
相同的方法,根据图3的扭矩系数试验曲线图谱,得到舵扭矩系数回归模型[12]:
|
图 3 舵扭矩系数图谱 Fig. 3 Torque factor map |
| $\begin{split} {c_{mr}}({\alpha _r},{\beta _r}) =& 0.356\;6{\alpha _r} + 0.143\;4{\alpha _r}^2 + 1.210\;3{\alpha _r}^3 - \\ & 1.482\;8{\alpha _r}^4 + 0.381\;2{\beta _r} + 0.374\;1{\beta _r}^2 -\\ & 0.971\;2{\beta _r}^3{\rm{ + 0}}{\rm{.693\;9}}{\beta _r}^4 {\rm{ + 0}}{\rm{.111\;3}}{a_r}{\beta _r} + \\ &\! 0.720\;1{\alpha _r}^2{\beta _r}\! -\! 1.194\;8{\alpha _r}^3{\beta _r} \!+\! 2.257\;6{\alpha _r}{\beta _r}^2 -\!\!\!\!\!\!\!\!\!\! \\ & 3.103\;8{\alpha _r}{\beta _r}^3 - 0.623\;1{\alpha _r}^2{\beta _r}^2 \text{。} \end{split} $ | (8) |
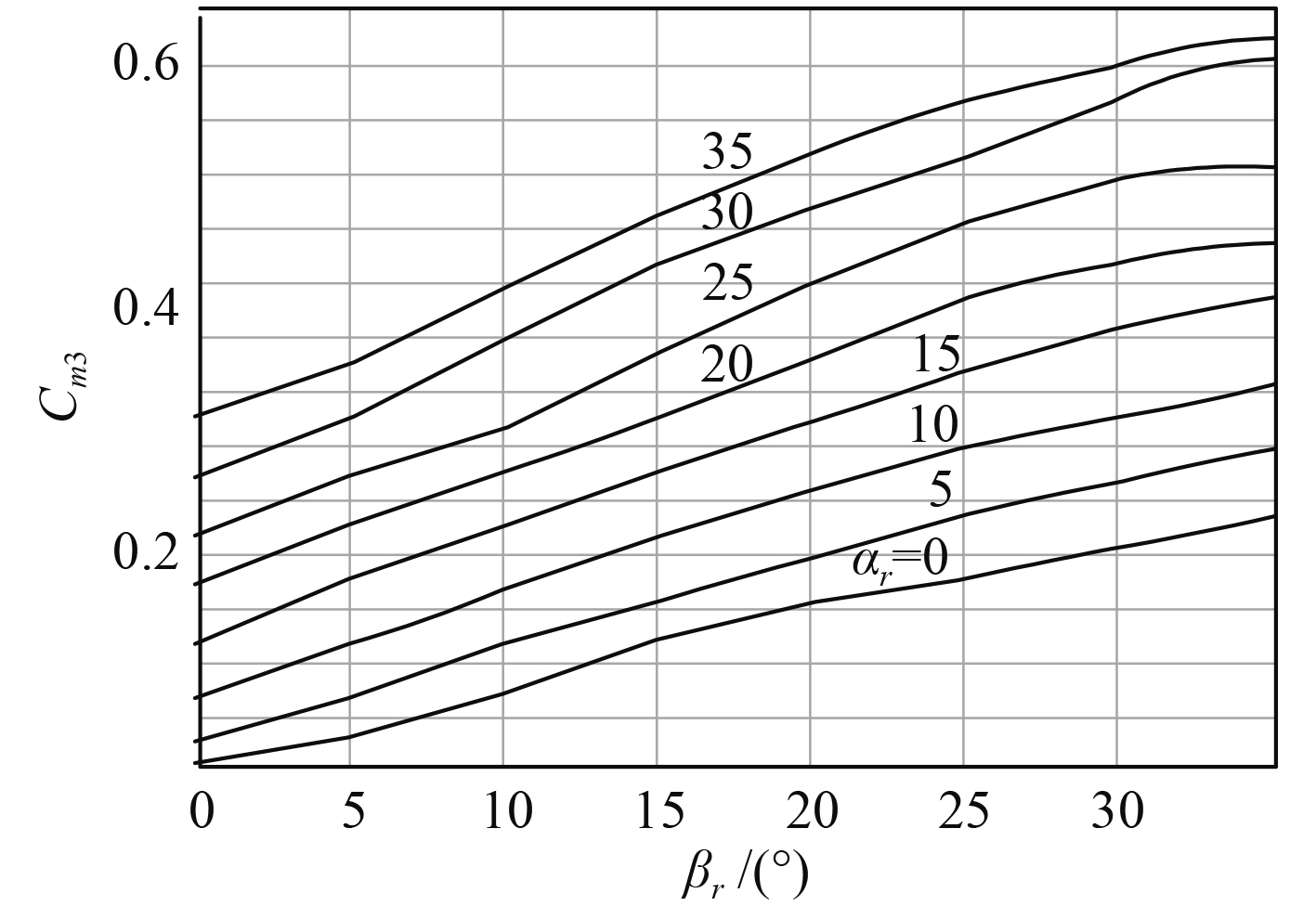
根据图4的翼舵扭矩系数试验曲线图谱,得到翼舵扭矩系数回归模型:
|
图 4 舵扭矩系数图谱 Fig. 4 Torque factor map |
| $\begin{split} {c_{m3r}}({\alpha _r},{\beta _r}) =& 0.432\;4{\alpha _r} + 0.110\;0{\alpha _r}^2 - 0.511\;6{\alpha _r}^3+ \\ & 0.350\;6{\alpha _r}^4 + 0.347\;4{\beta _r} + 0.232\;1{\beta _r}^2 +\\ & 0.942\;7{\beta _r}^3 - 1.333\;5{\beta _r}^4 {\rm{ + 0}}{\rm{.241\;9}}{a_r}{\beta _r} +\\ & 1.892\;3{\alpha _r}^2{\beta _r} \!-\! 2.443\;2{\alpha _r}^3{\beta _r} \!+\! 0.424\;6{\alpha _r}{\beta _r}^2-\!\!\!\!\!\!\!\! \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \\ & 0.752\;8{\alpha _r}{\beta _r}^3 - 0.731\;0{\alpha _r}^2{\beta _r}^2 \text{。} \end{split} $ | (9) |
图5、图6和图7分别给出了舵/翼舵升力系数、舵扭矩系数和翼舵扭矩系数由图谱采样数据得到的曲面与拟合的回归模型计算得到的曲面之相对误差曲面(相对误差为图谱采样计算值与回归模型计算值的差值除以图谱采样计算值)。
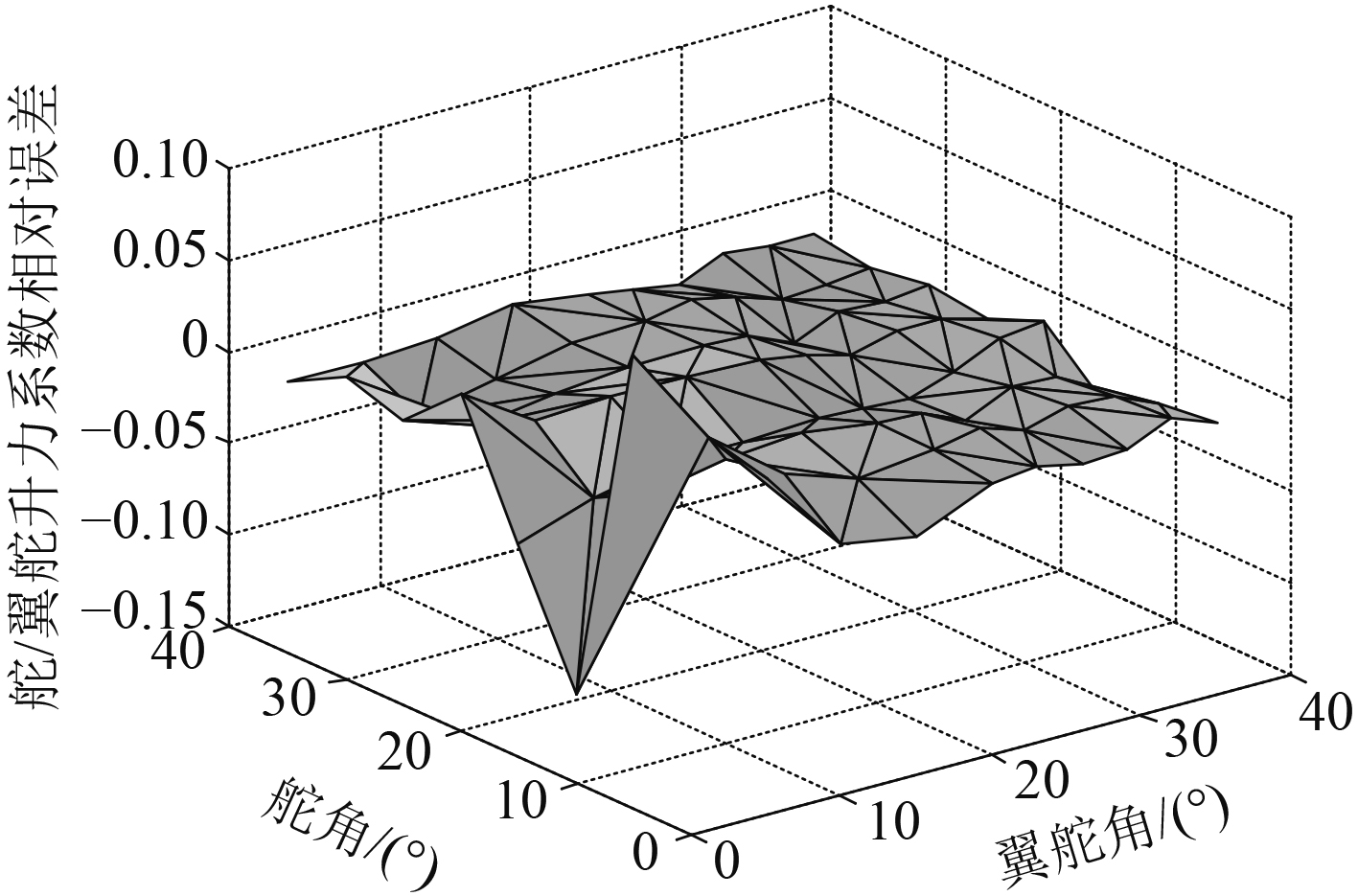
|
图 5 舵/翼舵升力系数相对误差曲面 Fig. 5 Relative error surface of rudder/finger rudder lift coefficient |
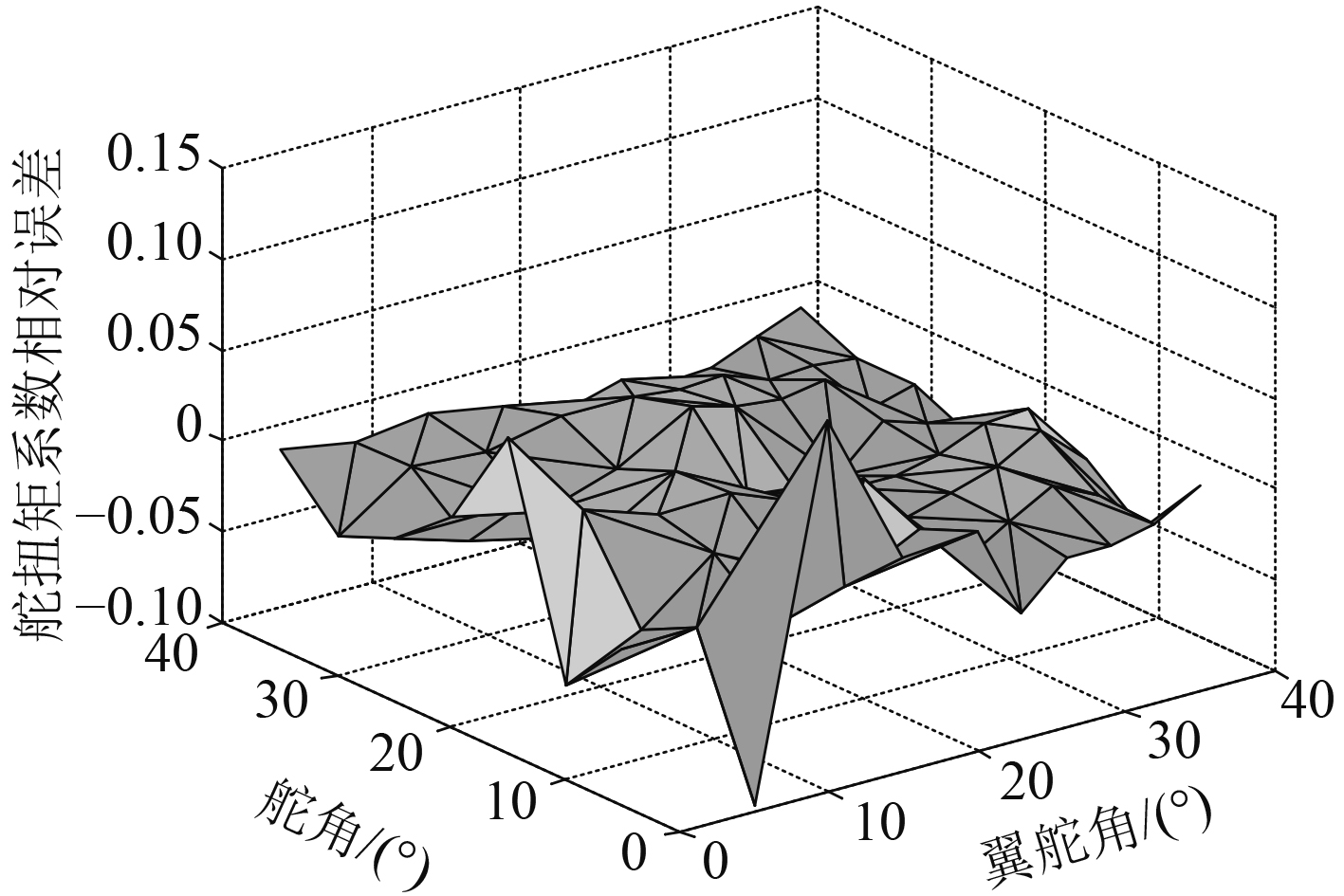
|
图 6 舵扭矩系数相对误差曲面 Fig. 6 Relative error surface of rudder torque coefficient |

|
图 7 翼舵扭矩系数相对误差曲面 Fig. 7 Relative error surface of torque coefficient of wing rudder |
将式(1)中模型的非线性项和横荡影响并入到参数摄动和广义干扰项,忽略横荡的影响和方程中非线性项,得到简化的首摇/横摇线性耦合模型为[13]:
| $\left\{ \!\!\!\!\begin{array}{l} \left( {{I_x}{\rm{ + }}{a_{\varphi \varphi }}} \right)\ddot \varphi + {b_{\varphi \varphi }}\dot \varphi + {c_{\varphi \varphi }}\varphi + {a_{\varphi \psi }}\ddot \psi + {b_{\varphi \psi }}\dot \psi = {K_r}({\alpha _r},{\beta _r}) + {K_d}\text{,} \\ \left( {{I_z}{\rm{ + }}{a_{\psi \psi }}} \right)\ddot \psi + {b_{\psi \psi }}\dot \psi + {a_{\psi \varphi }}\ddot \varphi + {b_{\psi \varphi }}\dot \varphi = {N_r}({\alpha _r},{\beta _r}) + {N_d}\text{。} \\ \end{array} \right.$ | (10) |
记
| $\begin{split} & \dot X = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0&1&0 \end{array}} \\ { - E_1^{ - 1}{E_2}} \end{array}} \right]X + \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0&0 \end{array}} \\ {E_1^{ - 1}} \end{array}} \right]\left[ \begin{array}{l} {K_r}({\alpha _r},{\beta _r}) \\ {N_r}({\alpha _r},{\beta _r}) \\ \end{array} \right] +\\ & \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0&0 \end{array}} \\ {E_1^{ - 1}} \end{array}} \right]\left[ \begin{array}{l} {K_d} \\ {N_d} \\ \end{array} \right] y = CX,C = \left[ {\begin{array}{*{20}{c}} 1&0&0 \end{array}} \right] \text{。} \end{split} $ | (11) |
其中:
| $ {E_1} = \left[\!\!\!\! {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{I_x}{\rm{ + }}{a_{\varphi \varphi }}}&{{a_{\varphi \psi }}} \end{array}} \\ {\begin{array}{*{20}{c}} {{a_{\psi \varphi }}}&{{I_z}{\rm{ + }}{a_{\psi \psi }}} \end{array}} \end{array}} \!\!\!\!\right], {E_2} = \left[\!\!\!\! {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{c_{\varphi \varphi }}}&{{b_{\varphi \varphi }}}&{{b_{\varphi \psi }}} \end{array}} \\ {\begin{array}{*{20}{c}} 0&{{b_{\psi \varphi }}}&{{b_{\psi \psi }}} \end{array}} \end{array}}\!\!\!\!\right]\text{。} $ | (12) |
将系统状态方程中由控制量舵/翼舵产生的状态
| $\begin{aligned} & {{\dot X}_1} = \left[\!\!\!\! {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0&1&0 \end{array}} \\ { - E_1^{ - 1}{E_2}} \end{array}} \!\!\!\!\right]{X_1} + \left[\!\!\!\! {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0&0 \end{array}} \\ {E_1^{ - 1}} \end{array}} \!\!\!\!\right]\left[ \!\!\!\!\begin{array}{l} {K_r}({\alpha _r},{\beta _r}) \\ {N_r}({\alpha _r},{\beta _r}) \\ \end{array} \!\!\!\! \right] \text{,} \\ & {{\dot X}_2} = \left[\!\!\!\! {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0&1&0 \end{array}} \\ { - E_1^{ - 1}{E_2}} \end{array}} \!\!\!\!\right]{X_2} + \left[\!\!\!\! {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0&0 \end{array}} \\ {E_1^{ - 1}} \end{array}} \!\!\!\!\right]\left[ \!\!\!\!\begin{array}{l} {K_d} \\ {N_d} \\ \end{array} \!\!\!\!\right]\text{,} \\ & y = CX = C{X_1} + C{X_2} \text{。} \end{aligned} $ | (13) |
定义广义干扰
| $\left[ \!\!\!\!\begin{array}{l} {K_r}({\alpha _r},{\beta _r}) \\ {N_r}({\alpha _r},{\beta _r}) \\ \end{array} \!\!\!\! \right]{\rm{ = }}\left[\!\!\!\! \begin{array}{l} \left( {1{\rm{ + }}{a_H}} \right){z_R} \\ - \left( {1{\rm{ + }}{a_H}} \right){x_R} \\ \end{array} \!\!\!\! \right]{P_y}({\alpha _r},{\beta _r}) = {B_R}{P_y}({\alpha _r},{\beta _r})\text{,}$ | (14) |
得到:
| $\left\{ \begin{split} & {{\dot X}_1} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0&1&0 \end{array}} \\ { - E_1^{ - 1}{E_2}} \end{array}} \right]{X_1} + \left[ {\begin{array}{*{20}{c}} 0 \\ {E_1^{ - 1}{B_R}} \end{array}} \right]{P_y}({\alpha _r},{\beta _r})\text{,} \\ & y = C{X_1} + \omega\text{。} \\ \end{split} \right.$ | (15) |
这样就将系统的奇异控制问题变换为非奇异的标准控制问题。
记
| $M\left( q \right) = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {A\left( q \right)}&{B\left( q \right)} \end{array}} \\ {\begin{array}{*{20}{c}} {C\left( q \right)}&{D\left( q \right)} \end{array}} \end{array}} \right]\text{。}$ | (16) |
根据仿射参数摄动系统的线性分式表示问题的解法[14],求得:
| $\begin{split} & M(g) = {F_u}({P_M},\Delta ) \text{,} \\ & \Delta = diag({c_{\varphi \varphi }},{b_{\varphi \varphi }},{b_{\varphi \psi }},{b_{\psi \varphi }},{b_{\psi \psi }},{a_{\varphi \varphi }},{a_{\varphi \psi }},{a_{\psi \varphi }},{a_{\psi \psi }}) \text{,} \\ \end{split} $ | (17) |
| ${P_M} = \left[ {\begin{array}{*{20}{c}} {{P_{M11}}}&{{P_{M12}}} \\ {{P_{M21}}}&{{P_{M22}}} \end{array}} \right]\text{,}$ | (18) |
假设对象参数
| $\Delta = {F_u}({P_\Delta },{\Delta _\delta })\text{,}$ | (19) |
| ${\Delta _\delta } = diag({\delta _1},{\delta _2},{\delta _3},{\delta _4},{\delta _5},{\delta _6},{\delta _7},{\delta _8},{\delta _9})\text{。} $ | (20) |
且
| $M(\delta ) = {F_u}(P,{\Delta _\delta })\text{。}$ | (21) |
其中:
| $P = \left[ {\begin{split} {{F_l}({P_\Delta },{P_{M11}})}\;\;\;\;{{P_{\Delta 12}}{{(I - {P_{M11}}{P_{\Delta 22}})}^{ - 1}}{P_{M12}}} \\ {{P_{M21}}{{(I - {P_{\Delta 22}}{P_{M11}})}^{ - 1}}{P_{\Delta 12}}}\;\;\;\;\;{{F_u}({P_M},{P_{\Delta 21}})} \end{split}} \right]\text{。}$ | (22) |
图8为船舶舵/翼舵减摇鲁棒控制系统的原理结构图。
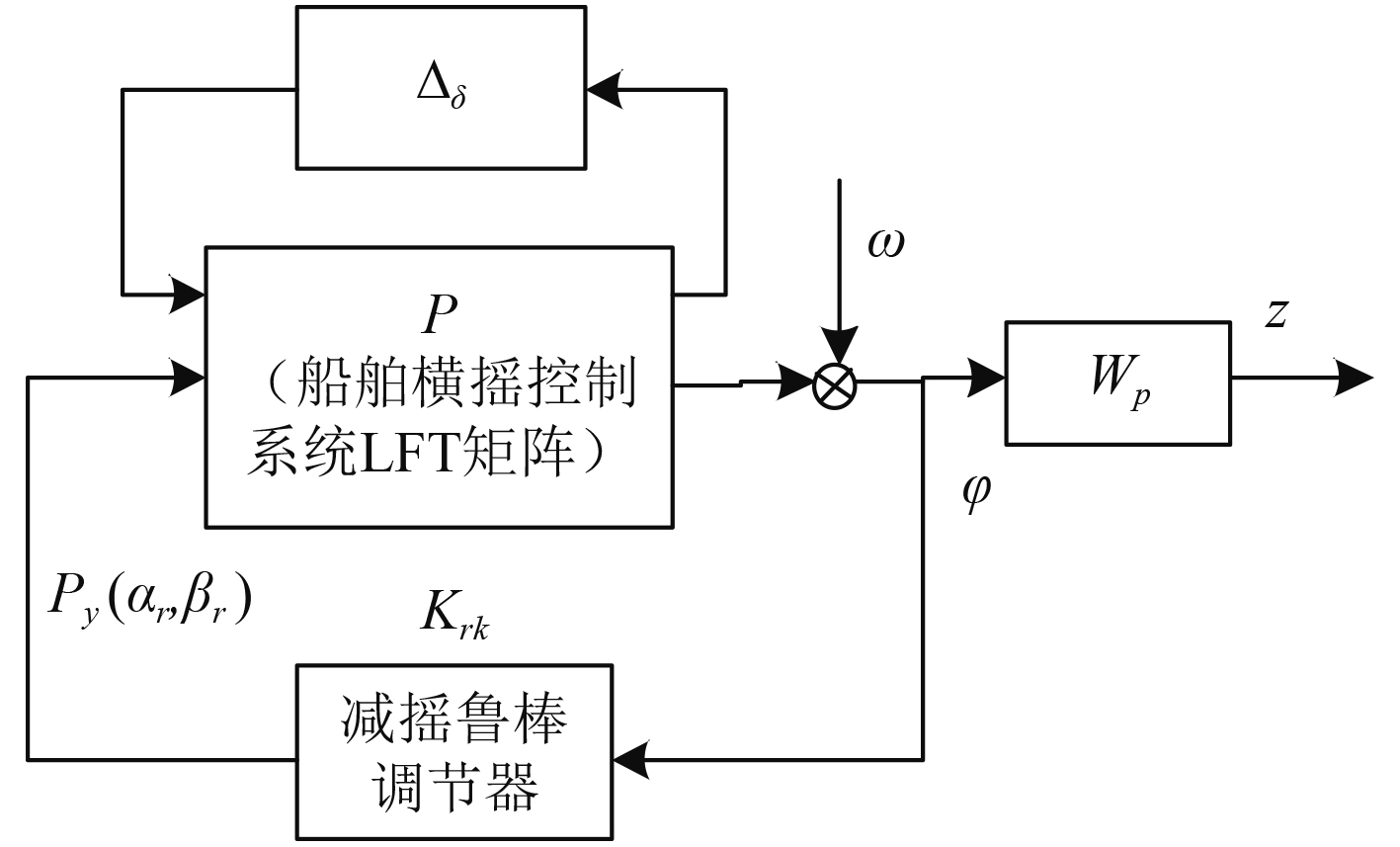
|
图 8
船舶舵/翼舵减摇
|
船减摇控制策略设计的目标为:
| ${W_p} = \frac{{0.39s}}{{{s^4} + 2.46{s^3} + 1.29{s^2} + 0.84s + 0.19}}\text{,} $ | (23) |
| ${W_r} = \frac{{0.03{s^2} + 0.03s + 0.01}}{{{s^2} + 100s + 0.001}}\text{。} $ | (24) |
利用Matlab中的D-K迭代算法求取船减摇控制器传递函数[10],
| $ {k_{rk}}\left( s \right) = \frac{{ - 8.89(s + 100)(s + 0.94)({s^2} + 0.08s + 0.003)}}{{(s + 5.10)(s + 0.63)(s + 0.05)({s^2} + 5.01s + 21.4)}}\text{。} $ | (25) |
智能决策指标函数就是在矢量舵提供所需控制力矩
若记
| $ \begin{split} {J_r}\left( {k + 1} \right) =& \int {_{{\alpha _r}\left( k \right)}^{{\alpha _r}\left( {k + 1} \right)}} {M_{\alpha r}}\left( {\theta ,{\beta _r}\left( k \right)} \right){\rm d}\theta + \\ & \int {_{{\alpha _r}\left( {k + 1} \right) + {\beta _r}\left( k \right)}^{{\alpha _r}\left( {k + 1} \right) + {\beta _r}\left( {k + 1} \right)}} {M_{\beta r}}\left( {{\alpha _r}\left( {k + 1} \right),\theta } \right){\rm d}\theta \text{,} \end{split} $ | (26) |
| ${M_{\alpha r}}{\rm{ + }}{M_{\alpha N}} + {M_{\alpha J}} + {M_{\alpha h}} + {M_{\alpha f}} = 0\text{,} $ | (27) |
| ${M_{\beta r}}{\rm{ + }}{M_{\beta N}} + {M_{\beta J}} + {M_{\beta h}} + {M_{\beta f}} = 0\text{。} $ | (28) |
其中:
| $\begin{split} {J_r}\left( {k + 1} \right) =& \displaystyle\frac{1}{2}\rho {V^2}{S_{\alpha r}}{L_{\alpha r}}\int {_{{\alpha _r}\left( k \right)}^{{\alpha _r}\left( {k + 1} \right)}} {c_{\alpha r}}\left( {\theta ,{\beta _r}\left( {k{\rm{ + }}1} \right)} \right){\rm d}\theta + \\ & \left( {{M_{\alpha J}} + {M_{\alpha h}} + {M_{\alpha f}}} \right)\left( {{\alpha _r}\left( {k{\rm{ + }}1} \right) - {\alpha _r}\left( k \right)} \right) + \\ & \displaystyle\frac{1}{2}\rho {V^2}{S_{\beta r}}{L_{\beta r}}\int {_{{\alpha _r}\left( {k + 1} \right) + {\beta _r}\left( k \right)}^{{\alpha _r}\left( {k + 1} \right) + {\beta _r}\left( {k + 1} \right)}} {c_{\beta N}}\times \\ &\left( {{\alpha _r}\left( {k{\rm{ + }}1} \right),\theta } \right)d\theta + \left( {{M_{\beta J}} + {M_{\beta h}} + {M_{\beta f}}} \right) \times\\ &\left( {{\beta _r}\left( {k{\rm{ + }}1} \right) - {\beta _r}\left( k \right)} \right) \text{。} \end{split} $ | (29) |
其中:
矢量舵上产生的控制力矩
| ${u_r}({\alpha _r}(k + 1),{\beta _r}(k + 1)) = {K_r}(k + 1)\text{,} $ | (30) |
考虑到舵角、舵角速度、翼舵角、翼舵角速度均有限制,故有:
| $ \begin{split} & \left| {{\alpha _r}(k + 1)} \right| \leqslant {\alpha _{r\max }} \text{,} \\ & \left| {{{\dot \alpha }_r}(k + 1)} \right| \leqslant {{\dot \alpha }_{r\max }} \text{,} \\ & \left| {{\beta _r}(k + 1)} \right| \leqslant {\beta _{r\max }} \text{,} \\ & \left| {{{\dot \beta }_r}(k + 1)} \right| \leqslant {{\dot \beta }_{r\max }} \text{。} \end{split} $ | (31) |
舵角/翼舵角决策规则为在保证
| $\begin{split} & {J_r}(k + 1)\min \text{,} \\ & {u_r}({\alpha _r}(k + 1),{\beta _r}(k + 1)) = {N_r}(k + 1) \text{,} \\ & \left| {{\alpha _r}(k + 1)} \right| \leqslant {\alpha _{r\max }} \text{,} \\ & \left| {{{\dot \alpha }_r}(k + 1)} \right| \leqslant {{\dot \alpha }_{r\max }} \text{,} \\ & \left| {{\beta _r}(k + 1)} \right| \leqslant {\beta _{r\max }} \text{,} \\ & \left| {{{\dot \beta }_r}(k + 1)} \right| \leqslant {{\dot \beta }_{r\max }} \text{。} \end{split} $ | (32) |
舵角/翼舵角最优智能决策追求的是[16]在决策规则约束下快速精确地寻优给出
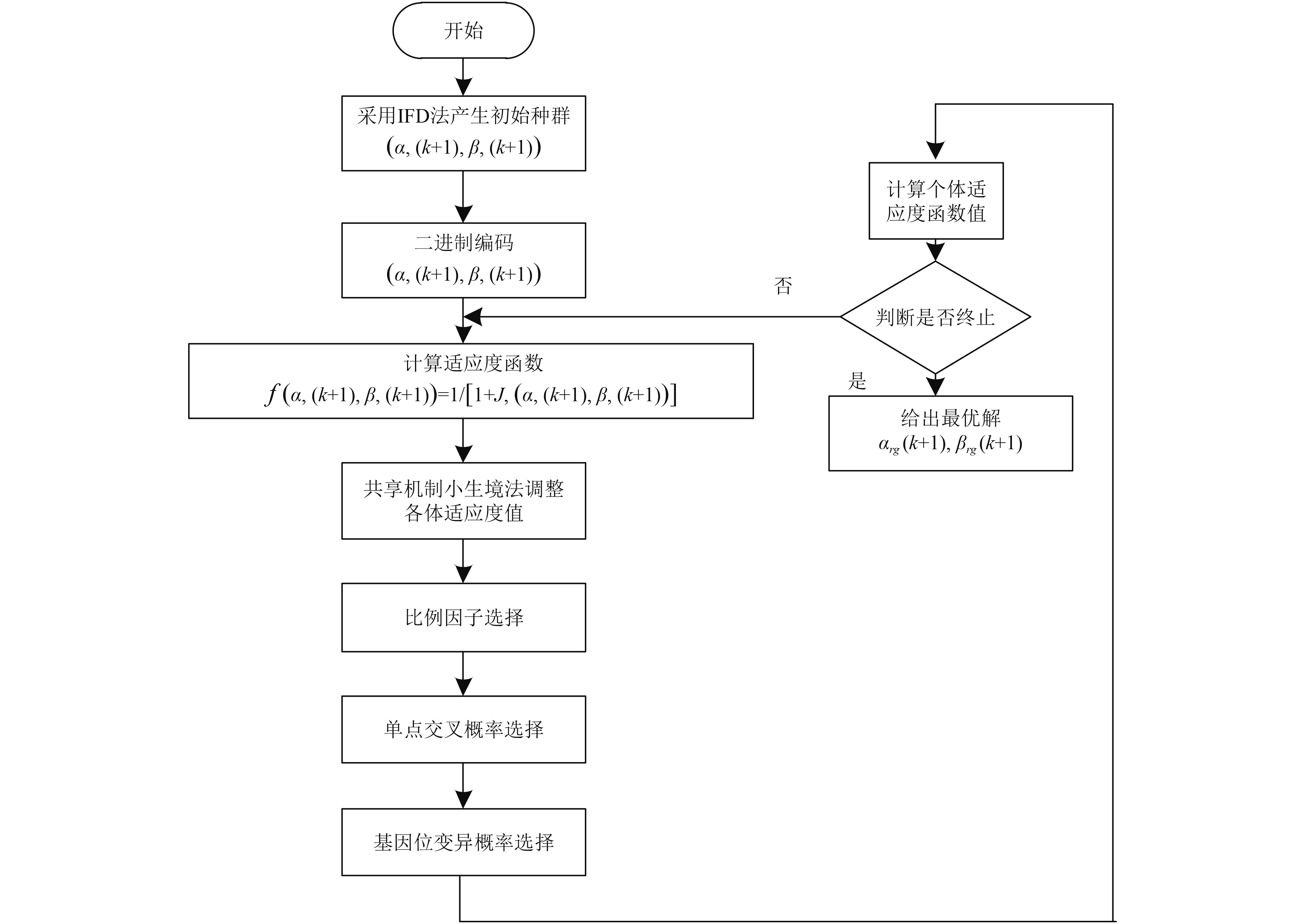
|
图 9 舵角/翼舵角改进GA智能协调决策分配器实现流程图 Fig. 9 Flow diagram of the improved intelligent coordination decision distributor for rudder angle / wing rudder angle |
本文对某船矢量舵减横摇控制系统进行数字仿真,并给出了仿真试验结果。
仿真条件:船水动力参数见参考文献[1],海浪有义波高
|
|
表 1 |
|
|
表 2 |
|
|
表 3 |
|
|
表 4 |
仿真实验结果表明:1)船舶矢量舵减横摇控制系统能有效地减小横摇,在有利浪向下,减摇率达50%,这是非常可观的,说明了舵减摇的有效性;2)系统在横浪时减摇效果最显著;3)在尾斜浪时减摇效果最差,这是由于舵叶与水流相对速度和横摇首摇运动分频特性引起的,即舵只能减小较高频域的横摇,而对较低频域横摇无能为力;4)
本文提出由舵和翼舵构成的矢量舵减横摇控制系统,设计了系统
| [1] |
王勇. 随机波浪中船舶航行非线性横摇稳定性评估分析[J]. 舰船科学技术, 2018, 40(2): 4-6. WANG Yong. Evaluation and analysis of nonlinear rolling stability of ships in random waves[J]. Ship Science and Technology, 2018, 40(2): 4-6. |
| [2] |
DO K D. Global robust adaptive path-tracking control of underactuated ships under stochastic disturbances[J]. Ocean Engineering, 2016, 111: 267-278. DOI:10.1016/j.oceaneng.2015.10.038 |
| [3] |
CHAI W, NAESS A, LEIRA B J. Stochastic roll response for a vessel with nonlinear damping models and steady heeling angles in random beam seas[J]. Ocean Engineering, 2016, 120: 202-211. DOI:10.1016/j.oceaneng.2016.05.019 |
| [4] |
刘胜. 现代船舶控制工程[M]. 北京: 科学出版社, 2010.
|
| [5] |
刘胜, 于萍, 方亮, 等. 船舶舵减横摇H∞鲁棒控制研究
[J]. 中国造船, 2007(3): 35-43. LIU Sheng, YU Ping, FANG Liang, et al. H∞ Robust control system of ship rudder roll damping [J]. Shipbuilding of China, 2007(3): 35-43. DOI:10.3969/j.issn.1000-4882.2007.03.005 |
| [6] |
CHAI W, NAESS A, LEIRA B J. Stochastic nonlinear ship rolling in random beam seas by the path integration method[J]. Probabilistic Engineering Mechanics, 2016, 44: 43-52. DOI:10.1016/j.probengmech.2015.10.002 |
| [7] |
屈高敏, 李继广. 流体矢量推进特性分析和控制[J]. 兵器装备工程学报, 2018(3): 62-67. QU Gao-min, LI Ji-guang. Fluid vector propulsion characteristics analysis and control[J]. Journal of Ordnance Equipment Engineering, 2018(3): 62-67. DOI:10.11809/bqzbgcxb2018.03.013 |
| [8] |
ZHAO D, GUO C, SU Y. Hydrodynamic performance of ichthyoid rudder at different rudder angle settings[J]. Journal of Coastal Research, 2016, 32(5): 1184-1195. |
| [9] |
LIU S, FANG L, LI G Y, et al. Fin/flap fin joint control for ship anti-roll system[C]// IEEE International Conference on Mechatronics and Automation. IEEE, 2009: 386–391.
|
| [10] |
贾欣乐, 杨盐生. 船舶运动数学模型——机理建模与辨识建模[M]. 大连: 大连海事大学出版社, 1999.
|
| [11] |
冯崇谦. 船用襟翼舵[M]. 北京: 国防工业出版社, 1989.
|
| [12] |
王磊, 唐为民, 郭亚军. 飞艇推力矢量转向系统支架的静动态特性分析[J]. 四川兵工学报, 2014, 35(6): 85-86+90. WANG Lei, TANG Wei-min, GUO Ya-jun. Analysis of static and dynamic characteristic for bracket of thrust vector steering mechanism for airship platform[J]. Journal of Sichuan Armamenties, 2014, 35(6): 85-86+90. DOI:10.11809/scbgxb2014.06.024 |
| [13] |
LIU S, SONG Y, Fin/flap fin anti-roll control for ship based on MSA-PSO intelligent allocation[C]// Proceeding of the 33nd Chinese Control Conference, 2014: 8607–8611.
|
| [14] |
ZHANG X K, ZHANG Q, REN H X, et al. Linear reduction of backstepping algorithm based on nonlinear decoration for ship course-keeping control system[J]. Ocean Engineering, 2018, 147: 1-8. DOI:10.1016/j.oceaneng.2017.10.017 |
| [15] |
WANG Y, CHAI S, KHAN F, et al. Unscented Kalman Filter trained neural networks based rudder roll stabilization system for ship in waves[J]. Applied Ocean Research, 2017, 68: 26-38. DOI:10.1016/j.apor.2017.08.007 |
| [16] |
张云峰, 胡国仁. 遗传优化算法在船舶航向混合智能控制中的应用[J]. 舰船科学技术, 2017, 39(8A): 22-24. ZHANG Yun-feng, HU Guo-ren. Application of genetic optimization algorithm in ship routing mixed intelligent control[J]. Ship Science and Technology, 2017, 39(8A): 22-24. |
 2019, Vol. 41
2019, Vol. 41
