推进轴系是船舶动力系统的重要组成部分,其与船舶推进电机直接相连,中间由多个径向滑动轴承进行支承。径向滑动轴承的承载特性对船舶推进轴系运行稳定性具有显著的影响[1],特别是靠近螺旋桨端的尾轴承,由于推进轴系很大一部分质量集中在螺旋桨端,尾轴承刚度变化对推进轴系运行稳定性的影响更为明显。径向滑动轴承的支承刚度与其工作状态有关[2],在理想的工作状态下,径向滑动轴承内承载的轴颈中心线保持稳定。但是在实际工作过程中,由于推进轴系振动等多方面因素的影响,轴颈中心线承载部位往往并不固定。
目前,关于轴承承载特性国内外学者已进行大量的研究工作,积累了一定的研究资料。戴惠良等[3]对轴承液膜压力计算方法进行研究;Meruane等[4]基于无限短轴承假设对雷诺方程进行分析,通过对液膜压力积分求得液膜承载力,同时采取对位移扰动求偏导的方式获得轴承的刚度系数;B.C.Majumdar等[5]采用扰动法对轴承的液膜刚度进行相关研究;朱汉华等[6]对轴系转速与轴承液膜刚度之间的关系进行研究,研究结果显示随着转速增加,轴承液膜动态刚度不断降低。杨家友等[7]基于轴承的不同工作状态详细探究了轴承的承载特性,但均忽略了推进轴系振动因素对轴承承载特性的影响,然而实际运行过程中推进轴系的振动无法避免,故有必要对轴承承载特性进行更深入的研究。
张新宝等[8]已分析了轴系校中因素对轴承液膜特性的影响,本文将在此基础上进一步研究推进轴系振动因素对轴承承载特性的作用规律。首先推导能合理表征轴承润滑特性的Reynolds方程,然后建立轴承液膜承载力和承载刚度的分析模型,编制相关Matlab计算分析程序,根据某推进轴系的振动响应参数通过计算求得轴承承载特性的变化规律。研究结果揭示了振动幅值、振动频率等推进轴系振动因素对轴承承载特性的影响规律,同时也对轴承的合理设计以及船舶推进轴系稳定运行提供了理论指导。
1 Reynolds方程的求解原理根据流体润滑理论,在船舶推进轴系正常运行的条件下,忽略切向速度变化因素及径向速度变化因素的影响,轴承的液膜润滑状态可以简化为无量纲形式:
| $ \frac{\partial }{{\partial x}}\left( {\frac{{{h^3}}}{\eta }\frac{{\partial p}}{{\partial x}}} \right) + \frac{\partial }{{\partial z}}\left( {\frac{{{h^3}}}{\eta }\frac{{\partial p}}{{\partial z}}} \right) = 6U\frac{{\partial h}}{{\partial x}}\text{。} $ | (1) |
式中:油粘度,N·s/m2;h为液膜厚度,m;p为夜膜压力,N/m2;x为轴承沿圆周方向的坐标;z为轴承向坐标;U为轴颈线速度,m/s。
式(1)可利用有限差分法进行求解,将轴瓦内表面由偏位角处展开成一平面,然后将该平面划分成大小为m×n的网格。以圆周
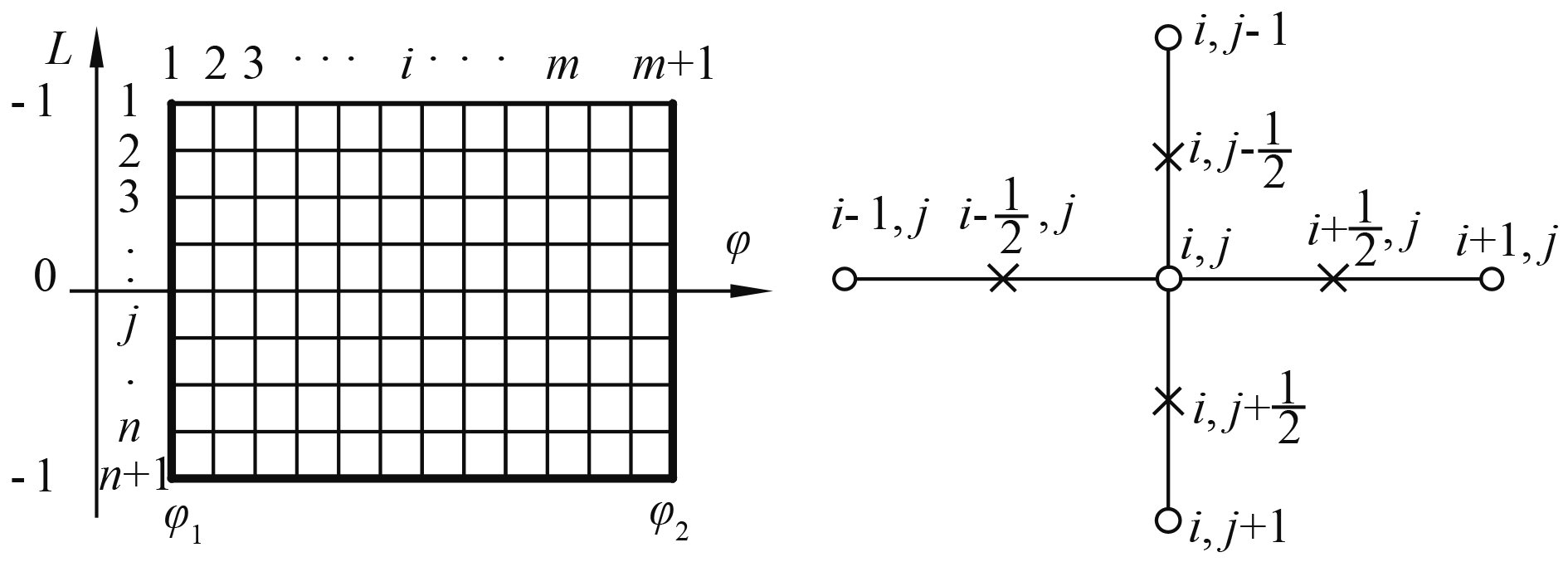
|
图 1 轴瓦平面网格划分与差商示意图 Fig. 1 Bearing shell mesh and differential quotient diagram |
推进轴系运行时在激振力的作用下,轴颈会在轴承孔内产生扰动,轴承所受力的大小并不是保持不变的。轴承负荷的来源主要有2个方面:1)轴系自重引起的负荷F1,在推进轴系运行过程中保持不变,可以通过现有的相关校中计算方法获得;2)激振力引起的轴承附加载荷F2,会随振动不断变化,激振力引起的附加载荷F2可采用传递矩阵法求得。
推进轴系可视为以轴承为支撑点的带有若干集中质量的多跨距梁横向振动系统,将整个系统离散化为足够数量的轴段,其中螺旋桨及联轴节等视为集中质量处理,轴承支撑点、集中质量重心和不同直径轴段连接处作轴段分界点处理,从螺旋桨端起依次对各分界点进行编号1,2,···,n。分界点之间的轴段离散成无质量的梁,其原本质量按重心不变原则集中到轴段两端,即分界点处。
其中质量单元的传递矩阵为:
| $\left\{ {\begin{array}{*{20}{c}} {{y_{\rm{z}}}} \\ {{\theta _z}} \\ M \\ Q \end{array}} \right\}_i^R = \left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&1&0 \\ { - k + m{\omega ^2}}&0&0&1 \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{y_z}} \\ {{\theta _z}} \\ M \\ Q \end{array}} \right\}_i^L,$ | (2) |
无均布质量等截面轴的传递矩阵为:
| $ \left\{ {\begin{array}{*{20}{c}} {{y_z}} \\ {{\theta _z}} \\ M \\ Q \end{array}} \right\}_i^L = \left[ {\begin{array}{*{20}{c}} 1&{{l_i}}&{\dfrac{{{l^2}}}{{2EJ}}}&{\dfrac{{{l^3}}}{{6EJ}}} \\ 0&1&{\dfrac{l}{{EJ}}}&{\dfrac{{{l^2}}}{{2EJ}}} \\ 0&0&1&{{l_i}} \\ 0&0&0&1 \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{y_z}} \\ {{\theta _z}} \\ M \\ Q \end{array}} \right\}_{i - 1}^R\text{。} $ | (3) |
式中:yz为分界点挠度;θz为分界点转角;M为分界点弯矩;Q为分界点剪力;上标L、R分别表示单元的左端和右端;i为分界点编号;l为轴段长度;EJ为横截面抗弯刚度;k为轴承刚度;m为分界点质量;ω为运行频率。
将各个单元的传递矩阵按编号从左到右依次相乘求得累积矩阵,代入激振力的影响,即可求得F2。轴承负荷F表示为:
| $ F = {F_1} + {F_2} = {F_1} + {A_2}\sin wt, $ | (4) |
其中A2表示轴承刚度不变时F2的幅值,其大小取决于激振力以及试验台的结构参数。实际计算时需选择合理的k值,其大小也会对振动响应数值构成影响,进而影响轴承负荷近似计算结果的准确性。
2.2 液膜刚度的计算轴系稳定运行时,轴颈偏位角θ和偏心率ε稳定在一确定部位,使得液膜水平方向合力为0,并且竖直方向的合力等于轴承所受负荷。其中液膜水平方向合力Fx和竖直方向上合力Fy可表达为:
| $ \left\{ {\begin{array}{*{20}{c}} {{F_x} = \displaystyle\int_{ - 1}^1 {\displaystyle\int_0^{2{\text{π}} } {{p_{ij}}\sin \left( {\theta + \varphi } \right){\rm d}\varphi {\rm d}\lambda } } }\approx\\ { \displaystyle\sum\nolimits_{i = 1}^{m + 1} {\sum\nolimits_{j = 1}^{n + 1} {{p_{ij}}\sin \left( {\theta + {\varphi _i}} \right)\Delta \varphi \Delta \lambda } } },\\ {{F_y} = \displaystyle\int_{ - 1}^1 {\int_0^{2{\text{π}} } {{p_{ij}}\cos \left( {\theta + \varphi } \right){\rm d}\varphi {\rm d}\lambda } } }\approx\\ { \displaystyle\sum\nolimits_{i = 1}^{m + 1} {\sum\nolimits_{j = 1}^{n + 1} {{p_{ij}}\cos \left( {\theta + {\varphi _i}} \right)\Delta \varphi \Delta \lambda } } }\text{。} \end{array}} \right. $ | (5) |
编写程序迭代求出偏心率ε和偏位角θ,即可得出液膜承载力大小。
轴承支反力与轴颈扰动的关系实际上是非线性的,当力和位移的扰动均极微小时,可以将其处理为线性关系。因此,可采用载荷增量法对液膜刚度进行求解。
轴颈由原来的平衡位置发生偏移到建立并稳定到新的平衡。假设轴颈沿x,y方向上的微小扰动Δx,Δy引起的液膜压力增量分别记为ΔFx,ΔFy,由此可得液膜刚度系数表达式:
| $ \left\{ {\begin{array}{*{20}{c}} {{K_{xx}} = {{\lim }_{\Delta x \to 0}}\dfrac{{\Delta {F_x}}}{{\Delta x}} = \dfrac{{\partial {F_x}}}{{\partial x}}},\\ {{K_{yx}} = {{\lim }_{\Delta x \to 0}}\dfrac{{\Delta {F_y}}}{{\Delta x}} = \dfrac{{\partial {F_y}}}{{\partial x}}},\\ {{K_{xy}} = {{\lim }_{\Delta y \to 0}}\dfrac{{\Delta {F_x}}}{{\Delta y}} = \dfrac{{\partial {F_x}}}{{\partial y}}},\\ {{K_{yy}} = {{\lim }_{\Delta y \to 0}}\dfrac{{\Delta {F_y}}}{{\Delta y}} = \dfrac{{\partial {F_y}}}{{\partial y}}}\text{。} \end{array}} \right. $ | (6) |
轴承动力模型如图2所示。本文采用在轴颈的平衡位置上加小扰动位移而计算液膜力增量的方法来求解液膜刚度,具体计算模型如图3所示。
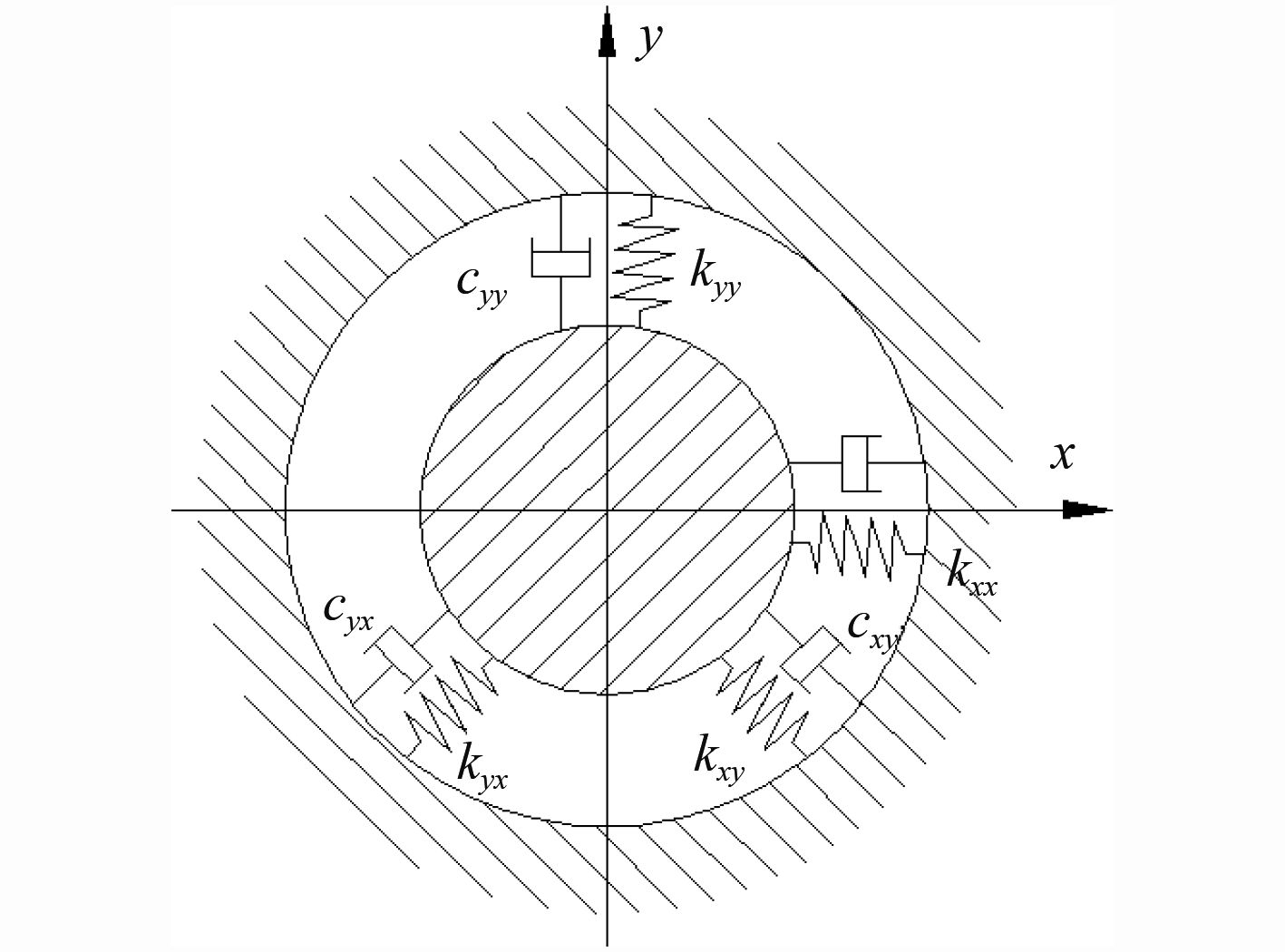
|
图 2 轴承的刚度阻尼简化模型 Fig. 2 Bearing stiffness and damping simplified model |

|
图 3 扰动位移示意图 Fig. 3 Disturbance displacement diagram |
假设轴颈的轴心沿x(水平)方向从O1移动一个小距离Δx到O2,如图3(a)所示,记初始的轴颈偏心距和偏位角分别为e1,θ1,则由几何关系可得出新的轴颈平衡位置处的偏心距e2为:
| $ {e_2} \!=\! \sqrt {O{M^2} \!+\! {{\left( {{O_1}M \!+\! \Delta x} \right)}^2}} \!=\! \sqrt {e_1^2 \!+\! \Delta {x^2} \!+\! 2\Delta x{e_1}\sin {\theta _1}} , $ | (7) |
新的平衡位置处的偏位角θ2可表示为:
| $ {\theta _2} = {\cos ^{ - 1}}\left( {OM/{e_2}} \right) = {\cos ^{ - 1}}\left( {{e_1}\cos {\theta _1}/{e_2}} \right)\text{。} $ | (8) |
由式(7)和式(8)可得新的轴颈位置处的液膜分力
| $ \left\{ {\begin{array}{*{20}{c}} {{K_{xx}} = \dfrac{{F'_x - {F_x}}}{{\Delta x}}},\\ {{K_{yx}} = \dfrac{{F'_y - {F_y}}}{{\Delta x}}}\text{。} \end{array}} \right. $ | (9) |
同理也可求出轴承液膜刚度Kxy,Kyy,本文主要研究振动因素对轴承承载刚度Kyy的影响。选取合适的位移量对于液膜刚度的求解十分重要,代入现有程序中进行试算,逐步减小位移量直至液膜刚度值趋于稳定。
3 算例分析在推进轴系工作过程中,尾管后轴承因其支承位置特殊受激振力的影响极其明显,本文以某船舶推进轴系对其尾管后轴承承载特性的影响为例进行计算分析,尾管后轴承具体参数如表1所示。分别研究推进轴系激振力的幅值、频率及安装参数对轴承承载力及承载刚度的影响规律。
|
|
表 1 尾管后轴承结构参数 Tab.1 Stern tube bearing structure parameter table |
船舶推进轴系运行过程中,由于工作情况等因素影响,推进轴系激振力的大小并不保持恒定。现以尾管后轴承为例,探究推进轴系激振力的幅值对轴承承载力及承载刚度的影响。
保持激振力频率大小不变,改变激振力幅值的大小,得到结果如图4和图5所示。
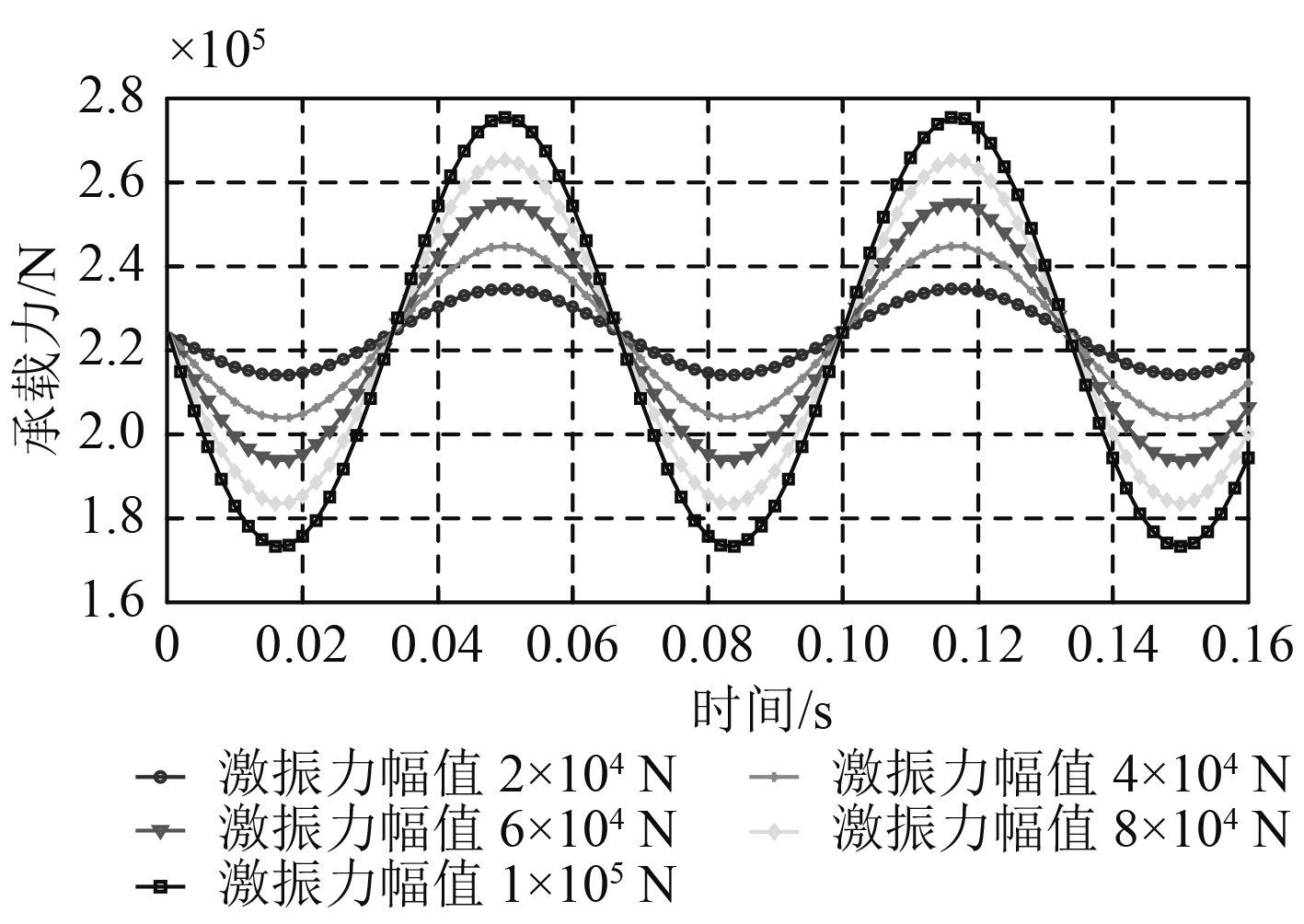
|
图 4 激振力幅值对轴承承载力影响 Fig. 4 The effect of exciting frequency on bearing capacity |
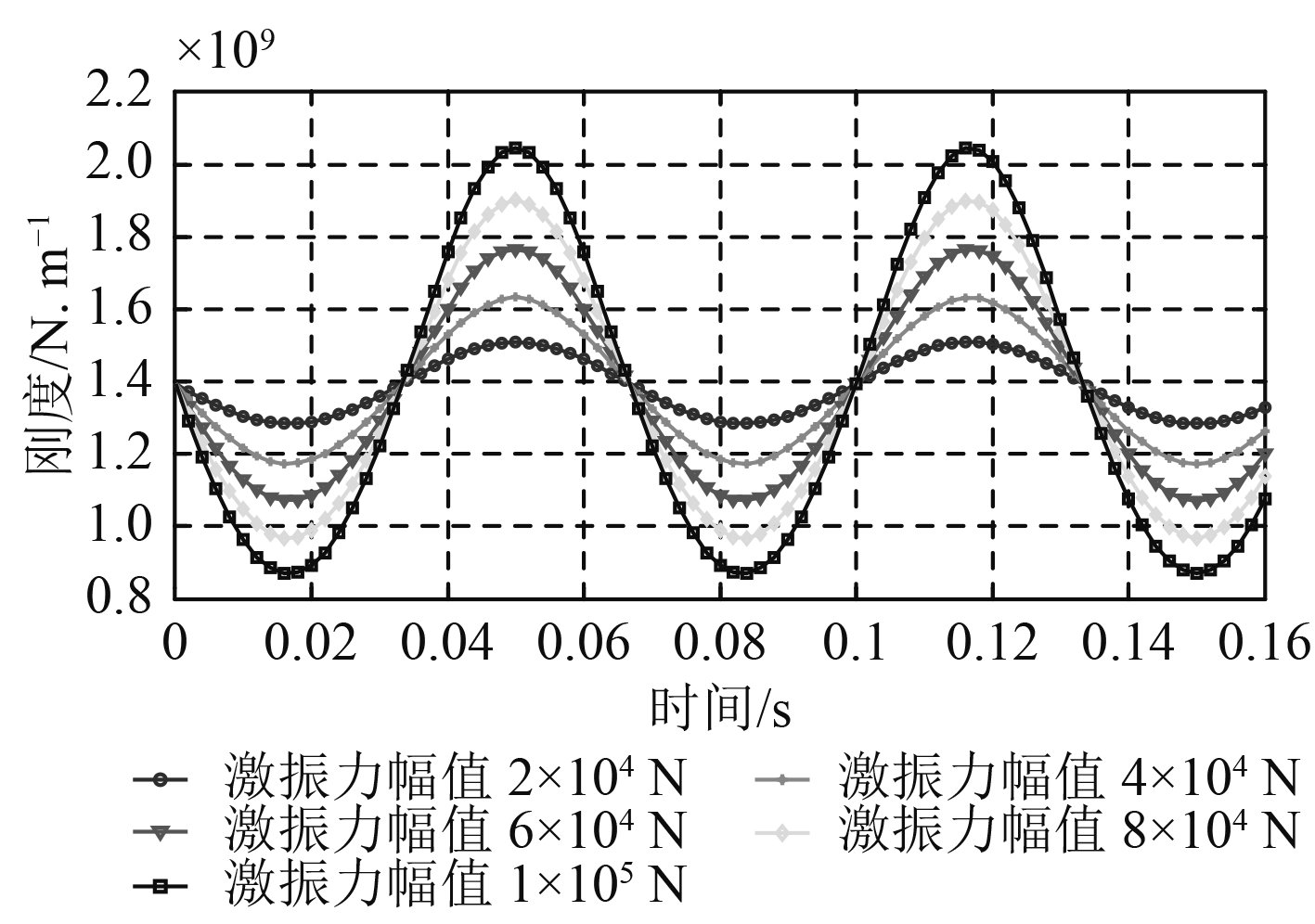
|
图 5 激振力幅值对轴承承载刚度影响 Fig. 5 The effect of exciting frequency on bearing stiffness |
从图4可以看出,随着激振力振幅增加,轴承承载力波动范围也随之增加,且与激振力幅值大小成正比关系,若激振力幅值进一步增加,承载力计算结果可能出现负值,即导致轴承承载失效,这是轴承正常工作时所不能允许的。结合图5可以看出,轴承承载刚度也随轴承承载力增加而增加,与承载力的变化趋势类似,但当激振力振幅增加时,轴承承载刚度的波动范围明显提升,且激振力幅值越大,波动范围增加的速度越快,加速削弱了轴承承载的稳定性。
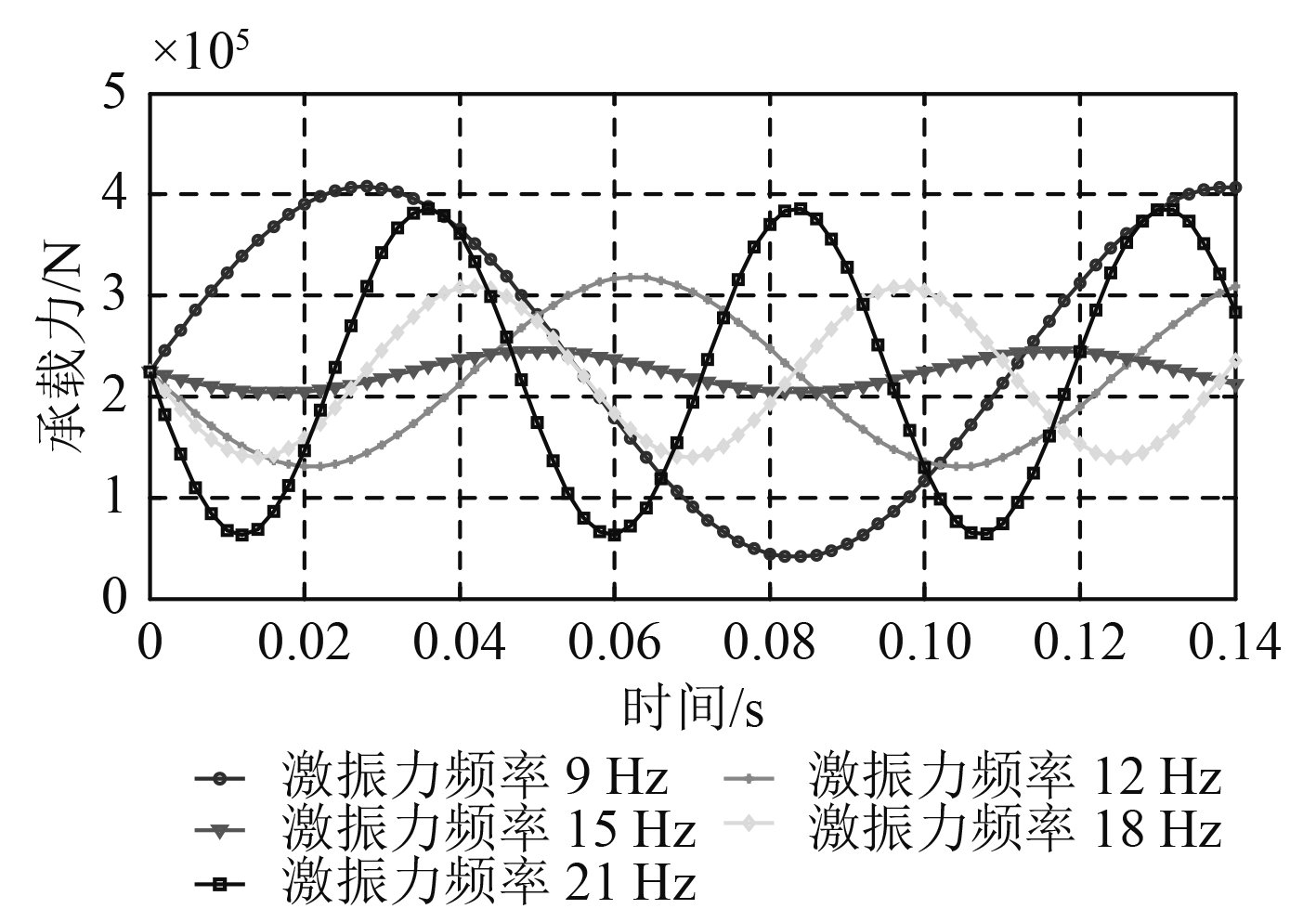
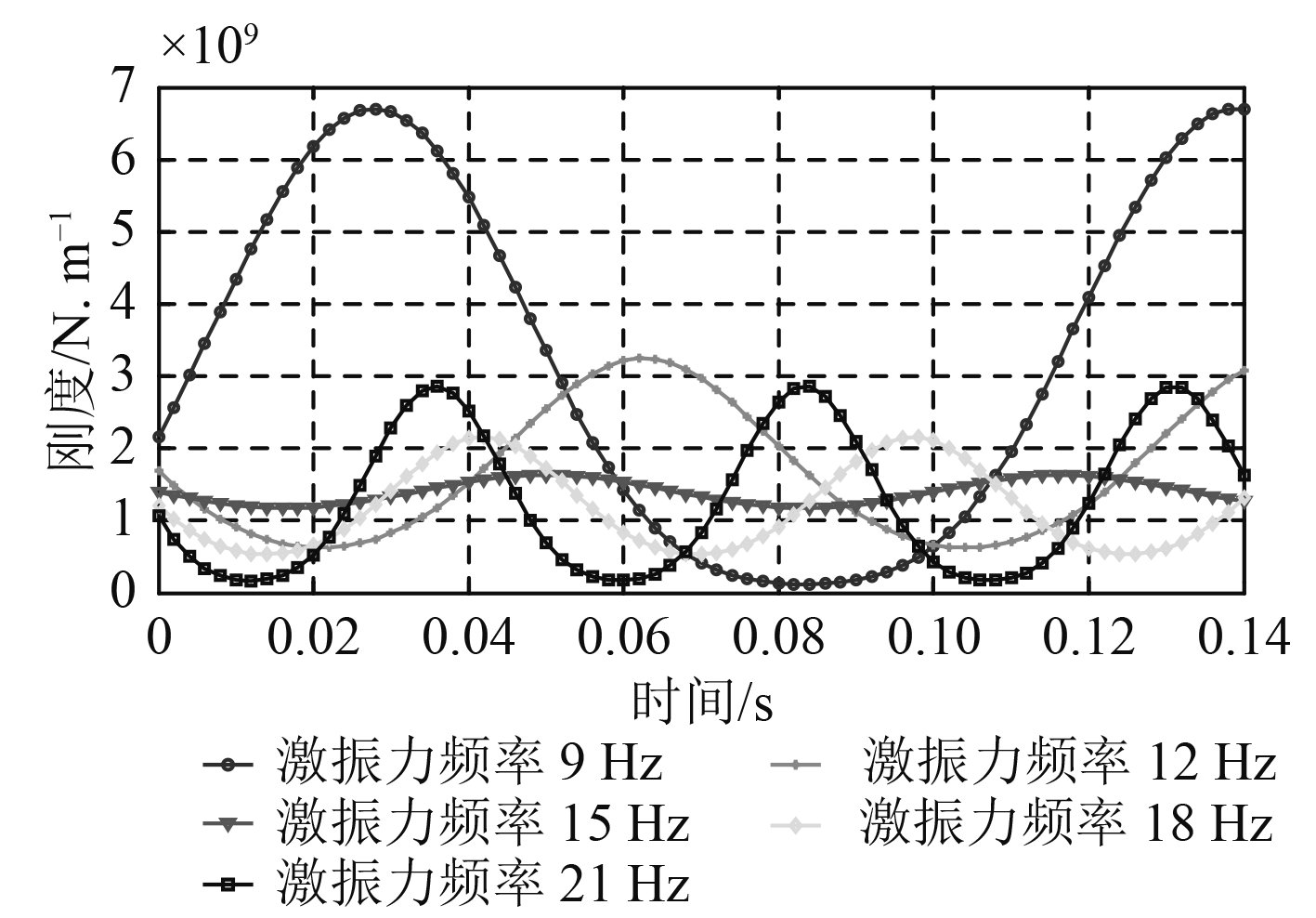
3.2 推进轴系激振力频率的影响如果推进轴系转速发生改变,激振力频率也会相应发生改变,从而对轴承承载力及承载刚度造成一定程度的影响,结果如图6和图7所示。
|
图 6 激振力频率对轴承承载力影响 Fig. 6 The effect of exciting frequency on bearing capacity |
|
图 7 激振力频率对轴承承载刚度影响 Fig. 7 The effect of exciting frequency on bearing stiffness |
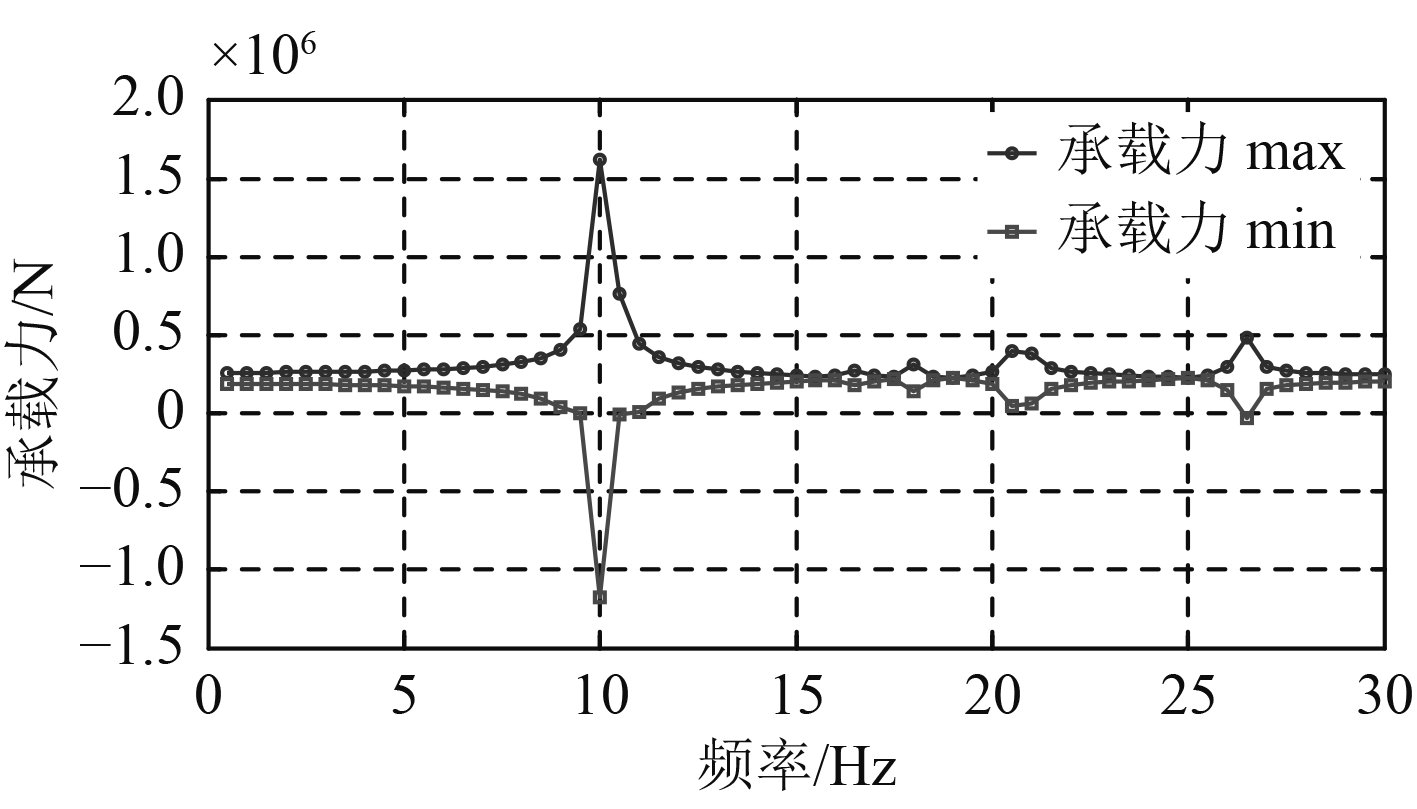
从图6可以看出,随着激振力频率改变,轴承承载力波动范围也随之改变,且在部分频率区段,由于接近推进轴系共振频率,轴承承载力波动范围过大,导致轴承承载失效,而部分频率区段轴承承载力波动很小,轴承承载情况十分稳定。结合图7可以看出,轴承承载刚度波动情况也随激振力频率改变而改变,且轴系转速越高,轴承的承载刚度越稳定,承载能力更强;而轴系共振频率区段会出现明显的轴承刚度强化效应,该区段不仅极易产生轴承承载失效现象,而且承载刚度极不稳定,实际轴承工作过程中应予以规避,本文所分析多支承船舶推进轴系的承载力与运行频率间的关系曲线如图8所示。选择合理的频率范围,可以使轴承承载刚度更为稳定,提升轴承承载的稳定性。
|
图 8 频率与承载力幅值关系曲线 Fig. 8 Frequency and bearing force amplitude curve |
在船舶推进轴系运行过程中,轴承承载力及刚度大小会随激振力的变化产生相应改变,主要得出以下结论:
1)激振力幅值越大,轴承承载力及承载刚度的波动范围越大,且承载刚度的波动范围增加越明显,降低激振力的幅值大小可有效改善轴承的承载性能。
2)轴承承载力及承载刚度的波动范围随激振力频率改变而改变,部分频率范围甚至导致轴承承载失效,选择合理的运行频率,适当增加转速,可以提高轴承承载的稳定性。
3)合理设计轴承结构参数,同时提高轴承的安装精度,可以有效改善轴承的承载性能,保证推进轴系的运行稳定性。
| [1] |
周继良, 邹鸿均. 船舶轴系校中原理及其应用[M]. 北京: 人民交通出版社.1985.
|
| [2] |
耿厚才. 船舶轴系的动态校中计算[J]. 中国造船, 2006, 47(3): 51-56. GENG Hou-cai. Dynamic alignment calculations for marine shafting[J]. Shipbuilding of China, 2006, 47(3): 51-56. DOI:10.3969/j.issn.1000-4882.2006.03.007 |
| [3] |
戴惠良, 刘思仁, 张亮. 滑动轴承油膜压力的新算法[J]. 机床与液压, 2011, 39(11): 27-28. DAI Hui-liang, LIU Si-ren, ZHANG Liang. A new algorithm of oil pressure for a sliding bearing[J]. Machine tool&Hydraulics, 2011, 39(11): 27-28. |
| [4] |
MERUANE V, PASCUAL R. Identification of nonlinear dynamic coefficients in plain journal bearings[J]. Tribology International, 2008, 41: 743-754. DOI:10.1016/j.triboint.2008.01.002 |
| [5] |
B C MAJUMDAR, R PAI, D J HARGREAVES. Analysis of water lubricated journal bearings with multiple axial grooves[J]. Proc. Instn. Mech. Engrs, Part J, Journal of Engineering Tribology, 2004, 218: 135-146. |
| [6] |
朱汉华, 严新平, 刘正林, 等. 转速对油膜刚度与螺旋桨轴振动影响研究[J]. 船海工程, 2007, 36(4): 83-85. ZHU Han-hua, YAN Xin-ping, LIU Zheng-lin, et al. Research on the influence of rotation speed upon rigidity of lubricant oil film and vibration of propeller shaft[J]. Ship & Ocean Engineering, 2007, 36(4): 83-85. DOI:10.3963/j.issn.1671-7953.2007.04.026 |
| [7] |
杨家友. 水润滑轴承液膜刚度特性及对轴系振动的影响研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.
|
| [8] |
张新宝, 顾兴晨. 轴系轴承不对中夹角误差对其承载特性的影响[J]. 舰船科学技术, 2017, 39(2): 97-102. ZHANG Xin-bao, GU Xing-chen. Influence of misalignment angle error of shafting bearing on the load-bearing properties of the bearing[J]. Ship Science and Technology, 2017, 39(2): 97-102. DOI:10.3404/j.issn.1672-7619.2017.02.020 |
 2019, Vol. 41
2019, Vol. 41
